как решить в точке с абсциссой, алгоритм, формула, примеры
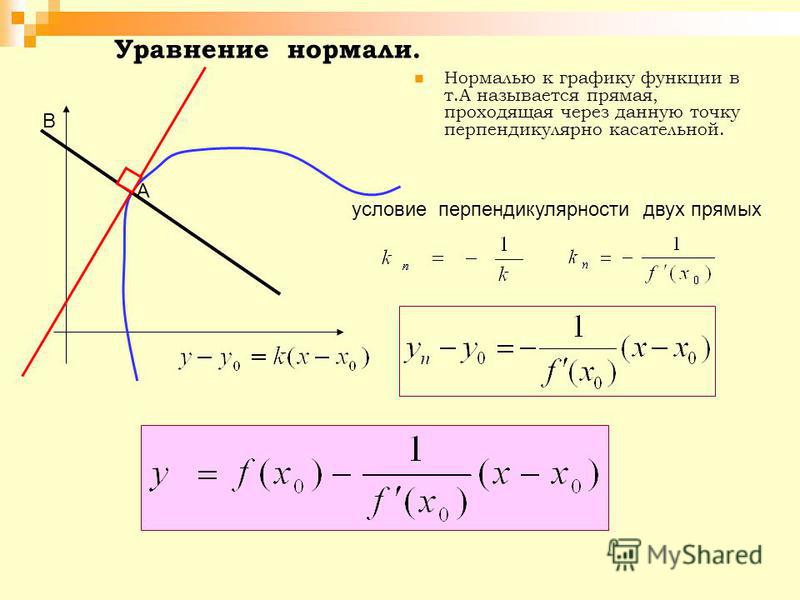
Вывод уравнения касательной к графику функции
ОпределениеКасательная к графику функции f(x) — это прямая y=f(x) в точке x0, если она проходит через точку через точку A(x0; f(x0)) и имеет угловой коэффициент f´(x0).
Выведем уравнение касательной.
Рассмотрим кривую y=f(x).
Выберем на ней точку A с координатами (x0,y0), проведем касательную AB в этой точке.
Угловой коэффициент касательной равен производной от функции f в точке x0: k=f′(x0)
Уравнение прямой AB, проведенной через две точки: (yB−yA)=k(xB−xA).
Для A(x0,y0), B(x,y) получаем:
(y−y0)=k(x−x0)
y=k(x−x0)+y0
y=f′(x0)(x−x0)+f(x0)
Вывод: уравнение касательной к кривой y=f(x) в точке x0 задается следующей формулой:
y=f´(x0)(x-x0)+f(x0), при условии, что производная f´(x0)=a≠∞ — существует и конечна.
Чтобы записать уравнение касательной с угловым коэффициентом в виде y=kx+b, нужно раскрыть скобки и привести подобные:
y=f′(x0)(x−x0)+f(x0)=f′(x0)x+f(x0)−f′(x0)⋅x0
f′(x0)=k, f(x0)-f′(x0)⋅x0=b
Вывод: уравнение касательной с угловым коэффициентом будет выглядеть следующим образом: y=kx+b.
Смысл элементов уравнения касательной
A(x0;y0) — точка касания касательной и графика с координатами (x0;y0).
y=f(x) — график функции.
B(x;y) — произвольная точка на касательной с координатами (x;y).
f(x0) — значение функции в точке х0.
f´(x) — производная. f´(x)=tgx=k, то есть равна угловому коэффициенту.
f´(x0) — значение производной в точке х0.
b — вычисленное числовое значение.
Алгоритм построения касательной к графику функции
Дано: уравнение кривой y=f(x), абсцисса точки касания х0.
Необходимо вывести уравнение касательной.
Решение:
- Найти значение функции в точке касания f(x0)
- Найти общее уравнение производной f′(x)
- Найти значение производной в точке касания f′(x0)
- Записать уравнение касательной y=f′(x0)(x−x0)+f(x0), привести его к виду y=kx+b
В итоге получаем уравнение касательной в виде y=kx+b.
Как построить касательную к графику функции в точке с заданной абсциссой
Следуя алгоритму построения, построим касательную к графику в точке с заданной абсциссой.
Дано: f(x)=x²+3, x0=1
Построить касательную к графику.
Решение:
- Вычислить значение функции в точке х0, f(x0)=(x0)²+3=4
- Вычислить производную, f´(x)=2x
- Вычислить значение производной в точке х0, f´(x0)=2×0=2
- Подставить значения в уравнение касательной, f(x)=f´(x0)(x-x0)+f(x0)=2(х-1)+4=2х+2
- Построить линейный график по уравнению y=2x+2
Примеры решения задач
ЗадачаНаписать уравнение касательной к графику функции f(x)=x³-2x²+3 в точке x0=1.
Решение:
- Нахождение значения функции в точке х0: f(1)=1³-2*1²+3=2
- Нахождение производной: f´(x)=3x²-4x
- Значение производной в точке х0: f´(1)=3*1²-4*1=-1
- Составление уравнения касательной по вычисленным значениям: y=2+(-1)(х-1)=2-х+1=-х+3
Ответ: y=-х+3.
10 класс. Алгебра. Производная. Применение производной к исследованию функции. — Уравнение касательной к графику функции.
Комментарии преподавателяУравнение касательной к графику функции
На предыдущих занятиях были рассмотрены задачи на технику дифференцирования.
Это очень важные задачи, и нахождение производных необходимо в разных задачах, в том числе и в составлении уравнения касательной.
Построим кривую (см. рис.1).
Рис. 1. График функции .
Зафиксируем точку . Если , то значение функции равно . Значит, имеем точку с координатами (.
Задача: составить уравнение касательной. Более строгая формулировка – написать уравнение касательной к функции в точке с абсциссой , в которой — существует.
Уравнение касательной – это прямая, которая задается формулой
Любая прямая, в том числе и касательная, определяется двумя числами: и . Исходя из геометрического смысла производной (тангенс угла наклона касательной) – это есть угловой коэффициент .
Параметр найдем из условия, что касательная проходит через точку (, то есть .
.
Стало быть .
Запишем уравнение касательной
.
Или, .
Получили уравнение касательной к кривой в точке с абсциссой .
Смысл каждого элемента, который входит в уравнение касательной.
1) ( – точка касания касательной и графика функции.
2) — угловой коэффициент касательной к графику функции.
3) – произвольная точка на касательной.
Очень много задач, когда задана точка, которая не лежит на графике функции, и через нее надо провести касательную к данной функции. Надо четко понимать, что – это произвольная точка на касательной.
Итак, получили уравнение касательной, проанализировали смысл каждого элемента этой касательной, и теперь приведем пример, и на нем изложим методику построения касательной.
Задача.
К кривой в точке с абсциссой провести касательную. Проиллюстрируем поиск касательной на рисунке (см. рис.2).
Рис. 2. Касательная к графику функции .
Зафиксируем точку . Значение функции в этой точке равно 1.
Алгоритм составления уравнения касательной к графику функции:
1) Найти и точку касания.
— дано.Точка касания: (;.
2) Найти производную в любой точке .
.
3) Найти значение производной в точке с абсциссой .
.
4) Выписать и проанализировать уравнение касательной.
.
Упрощаем и получаем: .
Ответ: .
Задача 1.
Пусть дано уравнение касательной .
Найдите точки пересечения касательной с осями координат.
Если , то . – это первая точка.
Если , то . — вторая точка.
Итак, первая точка – это точка с координатами . Вторая точка – точка пересечения с осью , точка с координатами (см. рис.3).
Рис.3. Точки пересечения касательной к графику функции с осями координат. Задача 2.
Найти длину отрезка касательной, которая отсекается осями координат, то есть надо найти длину отрезка .
Рассмотрим прямоугольный треугольник (Рис. 3). Длина катета равна 1. Длина катета . Длину отрезка из прямоугольного треугольника найдем по теореме Пифагора:
Задача 3.
Найти площадь треугольника, образованного касательной и осями координат. Ясно, что это площадь треугольника (Рис. 3) — площадь треугольника, образованного касательной и осями координат.
Следующая задача для самостоятельного решения.
Найдите радиус окружности, вписанной в треугольник . Радиус окружности, описанной около треугольника .
Рассмотрим пример.
Дана функция . Написать уравнение касательной к данной кривой в точке с данной абсциссой.
Рассмотрим графическую иллюстрацию (см. рис.4).
Рис. 4. Касательная к графику функции .
Нахождение точки касания.
1. Точка касания имеет координаты .
2.
Найти .
3. Найти
И, последнее действие, – написать уравнение касательной.
4. .
Упростим и получим .
Заметим в точке синусоида и касательная соприкасаются. В районе точки синусоида и прямая почти не различаются.
Итак, мы вывели уравнение касательной. Рассмотрели все элементы этой касательной. Выяснили их смысл. Сформулировали одну из методик нахождения касательных в конкретных функциях, в конкретных точках и решили некоторые сопутствующие задачи.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/uravnenie-kasatelnoy-k-grafiku-funktsii
http://v.5klass.net/zip/457286d0df8865f8084b5db13cbd6e95.zip
http://school.xvatit.com/index.php?title=%D3%F0%E0%E2%ED%E5%ED%E8%E5_%EA%E0%F1%E0%F2%E5%EB%FC%ED%EE%E9_%EA_%E3%F0%E0%F4%E8%EA%F3_%F4%F3%ED%EA%F6%E8%E8
http://itest.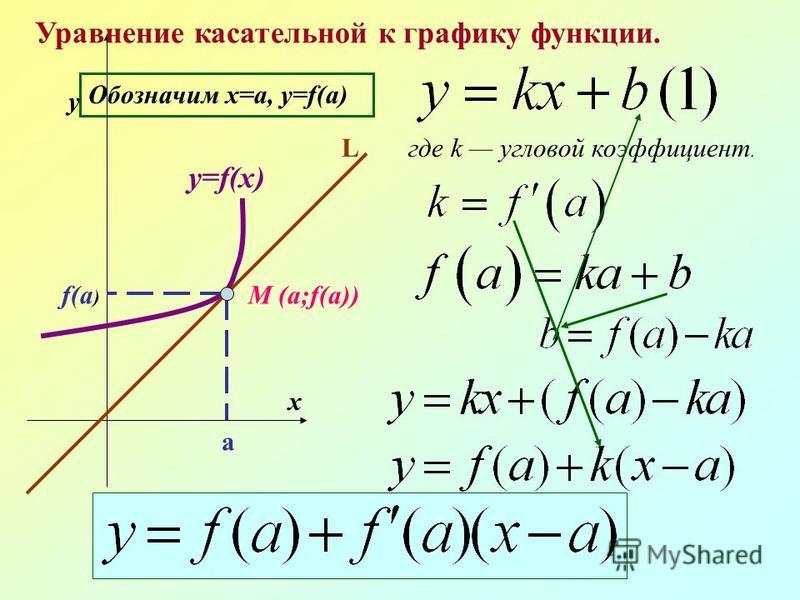
kz/lekciya_uglovoj_koehfficzient_kasatelnoj_i_ee_uravnenie_ru
http://www.postupivuz.ru/vopros/12822.htm
2+3х+5 в точке (-4,9)
Исчисление
Селин С.
спросил 25.03.20Подписаться І 1
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Диана Г. ответил 26.03.20
Репетитор
5,0 (368)
Экспертное онлайн-исчисление AP, исчисление колледжа, репетитор всех уровней математики
Об этом репетиторе ›
Об этом репетиторе ›
Привет, Селин. Чтобы найти уравнение касательной, я всегда начинаю с точки — наклона:
y — y 1 = m (x — x 1 )
Нам уже дана точка (-4 , 9), поэтому мы подставим эти значения вместо x 
Чтобы найти наклон касательной, м, нужно найти производную данной функции и подставить x = -4:
f'(x) = 2x + 3
f'(-4 ) = 2(-4) + 3 = -5, поэтому m = -5.
Теперь запишите уравнение в форме точки-наклона:
y — 9 = -5 (x + 4)
Если вам нужно записать уравнение в форме точки-точки, решите для y:
y = — 5x -11
В стандартной форме уравнение будет таким: 5x + y = -11
Надеюсь, это поможет. Пожалуйста, дайте мне знать, если у вас есть еще вопросы.
Голосовать за 0 голос против
Подробнее
Отчет
ЖАК Д. ответил 26.03.20
Репетитор
4,8 (62)
Физика, Химия, Математика — Без проблем!
Об этом репетиторе ›
Об этом репетиторе ›
Производная функции, вычисленной в точке, представляет собой наклон касательной к кривой в этой точке.
df/dx = 2x +3 с использованием степенного закона и что константы имеют производную от нуля.
df/dx(x = -4) = 2(-4) + 3 = -5
Это наклон касательной
Вы можете представить его в виде y = mx + b input x = — 4, y = 9 и m = -5 —> найдите b или
Вы можете изменить определение уклона между произвольной точкой на линии (x,y) и известной вам точкой (-4, 9):
(y-9)/(x+4) = -5 решить for y = …
Надеюсь, это поможет.
Голосовать за 0 голос против
Подробнее
Отчет
Тим Т. ответил 25.03.20
Репетитор
4.9 (702)
Математика: от K-12 классов до Advanced Calc, Ring Theory, Cryptography
См. таких репетиторов
Смотрите таких репетиторов
Эй! Давайте решим это?
Итак, мы должны найти уравнение касательной по заданной функции и точке.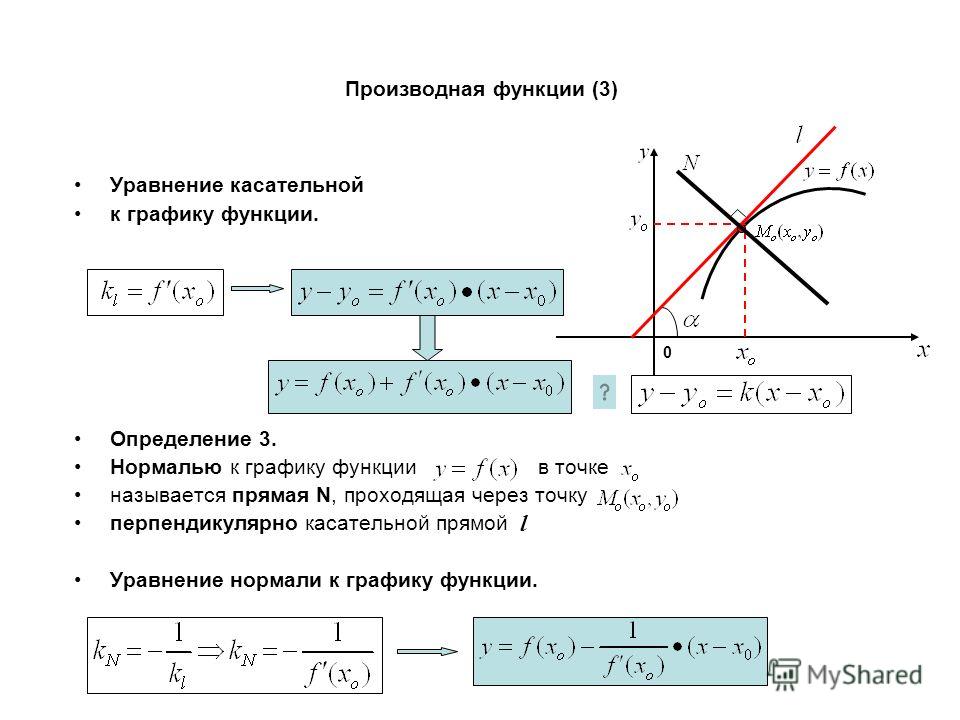
Во-первых, мы берем первую производную от f, используя степенное правило, такое, что
f ‘(x) = 2x + 3
Затем мы оцениваем, используя x = -4 данной точки (-4,9) и подставим его в производную таким образом, что
f ‘(-4) = 2(-4) + 3 = -5
Затем мы используем формулу точки-наклона, чтобы найти уравнение касательной прямой, такое что
y — y1 = f’ (-4) ( x — x1)
y — 9 = (-5)(x — (-4))
y — 9 = -5(x + 4)
y — 9 = -5x — 20 ……. Затем добавьте 9, чтобы
y = -5x — 11
Надеюсь, это помогло!
Голосовать за 0 Голосовать против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Видео с вопросами: Найдите уравнение касательной прямой к обратной функции — учитывая только исходную функцию и точку на кривой
Стенограмма видео
Рассмотрим функцию 𝑓 от 𝑥, которая равна 𝑥 в пятой степени минус два 𝑥 в кубе плюс три 𝑥 плюс два и точка четыре, один. Найдите наклон касательной к обратной ей функции 𝑓, обратной в указанной точке 𝑃. Найдите уравнение касательной к графику обратной функции 𝑓 в указанной точке 𝑃.
Вопрос дает нам функцию 𝑓 от 𝑥, которая является полиномом пятой степени и четвертой точки, один. Первая часть этого вопроса требует, чтобы мы нашли наклон касательной к нашей обратной функции 𝑓 в точке 𝑃.
И если мы находим касательную к нашей обратной функции 𝑓 в точке 𝑃, то точка 𝑃 должна лежать на нашей кривой 𝑦 равна обратной функции 𝑓 от 𝑥. И что это нам говорит? Что ж, когда мы вводим четыре в нашу обратную функцию 𝑥, наш выход должен быть один. Другими словами, обратная функция 𝑓, оцененная в четыре, равна единице.
Теперь помните, что наклон нашей касательной в этой точке будет как раз равен наклону нашей обратной функции в этой точке. И мы знаем формулу для нахождения наклона обратной функции. Производная нашей обратной функции 𝑓 в точке 𝑎 равна единице, деленной на 𝑓 простое число, оцененное как обратная функция 𝑓 из 𝑎. И это предполагает, что 𝑎 находится в области определения нашей обратной функции 𝑓 и что 𝑓 простое число не равно нулю в этой точке.
Мы хотим найти наклон нашей кривой в точке четыре, один. Поэтому мы установим 𝑎 равным четырем. И мы уже нашли выражение для обратной функции 𝑓 в четыре. Оно равно единице. Таким образом, мы получаем наклон нашей обратной функции 𝑓 при 𝑥 равно четырем, равным единице, деленной на 𝑓 простое число единицы.
Итак, нам нужно найти выражение для 𝑓 простого числа 𝑥. А 𝑓 из 𝑥 — это просто многочлен. Таким образом, мы можем сделать это, используя правило степени для дифференцирования. Применяя правило степени для дифференцирования каждого из наших членов 𝑓 из 𝑥, мы получаем, что 𝑓 простое число 𝑥 равно пяти 𝑥 в четвертой степени минус шесть 𝑥 в квадрате плюс три. Итак, теперь мы можем использовать это выражение для вычисления единицы, деленной на 𝑓 простое число единицы. Это равно единице, деленной на пять, умноженной на один в четвертой степени, минус шесть, умноженная на один в квадрате, плюс три.
Итак, мы показали наклон нашей обратной функции в точке четыре, один равен половине. И помните, это будет то же самое, что и наклон нашей касательной.
Вторая часть нашего вопроса требует, чтобы мы нашли уравнение касательной к нашему графику обратной функции 𝑓 в точке 𝑃. Первое, что нам нужно сделать, это запомнить общий вид уравнения прямой. Линия наклона 𝑚, проходящая через точки 𝑦 единица, 𝑥 единица, будет иметь уравнение 𝑦 минус 𝑦 единица, равная 𝑚 умноженная на 𝑥 минус 𝑥 единица.