9 класс геометрия » Векторы. Понятие вектора» | План-конспект урока по геометрии (9 класс) на тему:
Тема: «Понятие вектора. Модуль и направление вектора. Равные вектора».
Цель: — ввести определение вектора, нулевого вектора, длины вектора, коллинеарных векторов, равных векторов, сонаправленных и противоположно направленных векторов,
— развитие навыков выполнения рисунков; правильности обозначения векторов;
— воспитывать внимательность и аккуратность при обозначении и построении
векторов, взаимопомощь при изучении темы.
Ход урок:
1. Организационный момент
«Образование – это не количество прослушанных уроков, а количество понятых. Так что, если хотите идти вперед, то поспешайте медленно и будьте внимательны»
2. Мотивация урока.
Мой первый слог — почтенный срок,
Коль прожит он недаром;
Модель второго на столе,
Румяна, с пылу с жару. (Век-тор)
Группа туристов вышла в трехдневный поход. На туристической базе было известно, что за день группа проходит 30 км. На следующий день группа связалась по рации с турбазой и только успела передать, что один из туристов повредил ногу и не может двигаться дальше, как связь прервалась. Что предпринять руководителю туристической базы? Что необходимо знать, чтобы как можно скорее прийти на помощь группе?
На туристической базе было известно, что за день группа проходит 30 км. На следующий день группа связалась по рации с турбазой и только успела передать, что один из туристов повредил ногу и не может двигаться дальше, как связь прервалась. Что предпринять руководителю туристической базы? Что необходимо знать, чтобы как можно скорее прийти на помощь группе?
Спасибо за ваши предложения. Сегодня мы узнаем ответы на этот и многие другие вопросы, связанные с определением положения тела в произвольный момент времени. Мы ближе познакомимся с понятием вектора, перемещения, научимся изображать векторы, определять их направление.
3. Актуализация опорных знаний.
Приведите примеры:
-скалярные величины (имеют числовое значение): масса, площадь, длина, объём, время, температура.
— векторные величины (имеют числовое значение и направление): сила, перемещение, скорость, ускорение, вес.
4. Изучение нового материала.
Многие величины полностью характеризуются своими численными: длина, площадь, температура, цена.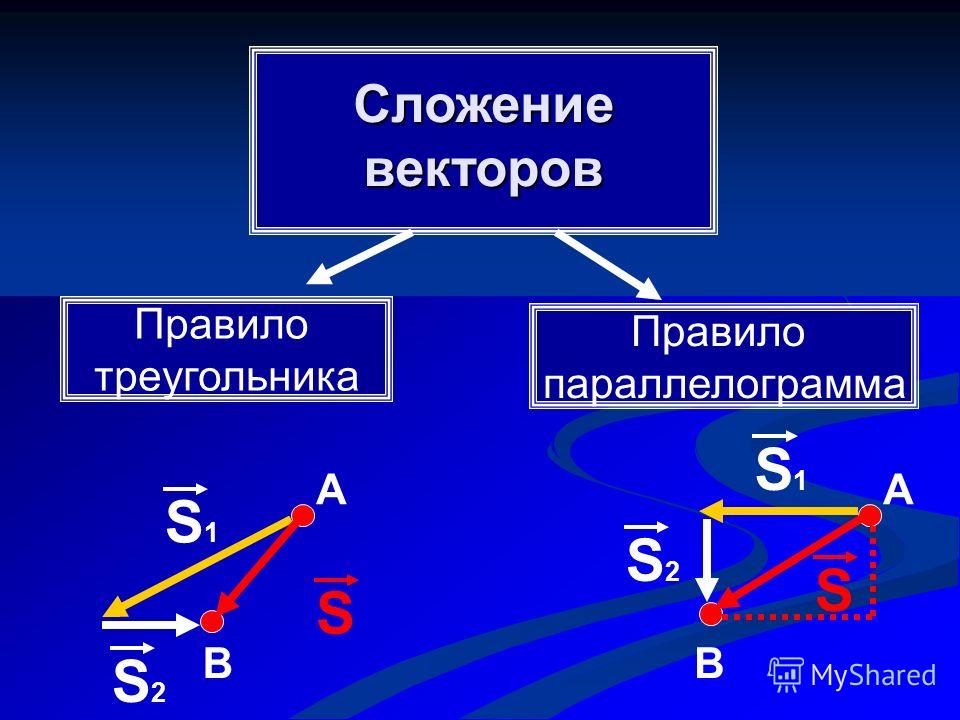 Их называют скалярными величинами или скалярами. Но есть и такие величины, которые характеризуются не только своим численным значением, но и направлением: сила, скорость, перемещение. Например, мало знать, что скорость поезда равна 50 км/ ч. Надо знать еще в каком направлении движется этот поезд. Указать направление можно, например, стрелкой.
Их называют скалярными величинами или скалярами. Но есть и такие величины, которые характеризуются не только своим численным значением, но и направлением: сила, скорость, перемещение. Например, мало знать, что скорость поезда равна 50 км/ ч. Надо знать еще в каком направлении движется этот поезд. Указать направление можно, например, стрелкой.
Так, поезд движется со скоростью 50 км/ч из пункта А в пункт В. Величины, которые характеризуются не только своими числовыми значениями, но направлением, называются векторными величинами или векторами.
Из курса физики вам знакомы такие величины.
Пусть на тело действует сила 8 Н. Надо еще знать, в каком направлении действует сила.
Стрелка показывает направление силы, а длина отрезка соответствует в выбранном масштабе числовому значению силы.
Рассмотрим отрезок произвольной величины. Его концы – граничные точки отрезка. На данном отрезке можно отметить 2 направления.
Чтобы выбрать одно из направлений, одну граничную точку отрезка назовем началом, другую – концом. Теперь будем считать, что отрезок направлен от начала к концу.
Теперь будем считать, что отрезок направлен от начала к концу.
Отрезок, для которого обозначены начало и конец, называется направленным отрезком или вектором.
На рисунке вектор обозначается отрезком со стрелкой, показывающей направление вектора. Обозначается вектор двумя заглавными латинскими буквами со стрелкой над ними, например , где А – начало вектора, В – конец вектора.
Вектор – направленный отрезок.
,
А – начало вектора
В В – конец вектора
А
Задание 1: Назовите векторы, изображенные на рис.85, 86.
Задание 2: (№406) Отметьте три точки А, В и С, не лежащие на одной прямой. навертите векторы АВ, ВС и АС.
Также любая точка плоскости – вектор. В данном случае вектор называется нулевым, т.е начало вектора совпадает с его концом. Обозначается такой вектор двумя одинаковыми заглавными латинскими буквами — или .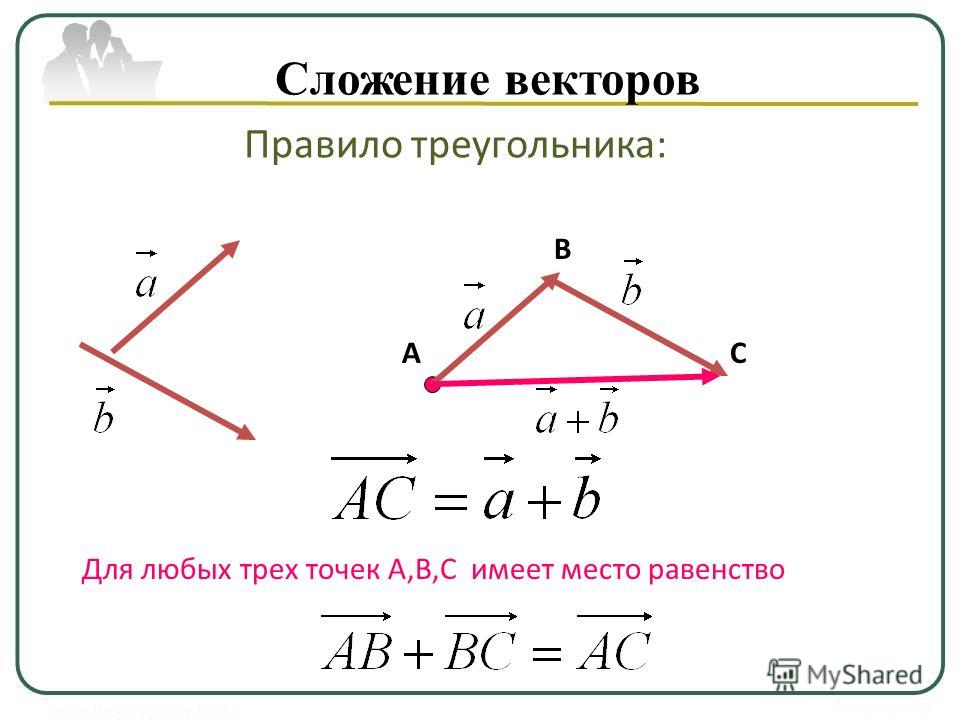
Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина вектора обозначается (⏐⏐). Длина нулевого вектора считается равной нулю: ⏐⏐=0.
Коллинеарные векторы – это ненулевые векторы, если они лежат на параллельных прямых или на одной прямой: | | .
а) сонаправленные векторы.
↑↑ .
б) противоположно направлены.
↑↓ .
Т.к. у нулевого вектора начало и конец совпадают, поэтому определенного направления он не имеет.
Задание 3: По рис. 87-90 назвать виды векторов.
Ненулевые векторы называются равными, если их модули равны и они сонаправлены. Любые два нулевых вектора равны.
=
Задание 4: (№417) (Работа в парах) По рис. 97 назвать виды векторов.
Пусть дана точка А и А – начало вектора . Тогда вектор отложен от точки А.
От любой точки М можно отложить вектор, равный данному вектору , и притом только один.
5. Историческая справка.
Как институт без ректора,
Так геометрия без вектора!
Теория векторов развивалась в XIX в. параллельно с теорией систем линейных уравнений. Направленные отрезки использовал Арган (J.R. Argand, 1768–1822) в работе «Опыт некоторого представления мнимых величин … «, опубликованной в 1806 году. Эти отрезки Арган обозначал символами →a, →b и т.п. Мëбиус обозначал отрезок с началом в точке A и концом в точке B символом AB . Он считается одним из основателей теории векторов. Термин «вектор» ввел Гамильтон приблизительно в 1845 году. Он же определил скалярное и векторное произведения векторов в 1853 году.
6. Закрепление знаний.
Графически: № 407, 409, 411.
У доски: № 415, 418.
7. Самостоятельная работа учащихся.
Решить в парах № 419.
Задание на повторение: (из курса «Геометрия 7 класс»)
Фронтальный опрос «Дальше, дальше…». Класс разбит на 3 команды. За каждый верный ответ-жетон.
- Что такое геометрия?
- Что такое планиметрия?
- Приведите примеры плоских и неплоских фигур.
- Опишите понятие точка.
- Опишите понятие прямая.
- Опишите понятие плоскость.
- Что означает запись А, В?
- Сформулируйте основное свойство расположения точки на прямой.
- Что такое луч?
- Как обозначается луч?
- Какие лучи называются дополнительными?
- Что такое отрезок?
- Что такое концы отрезка?
- В каких единицах измеряется отрезок?
- Сформулируйте основное свойство измерения отрезков.
- Что такое середина отрезка?
- Что такое расстояние между двумя точками?
- какая фигура называется углом?
- Как обозначаются углы?
- В каких единицах измеряются углы?
- Какой угол называется острым?
- Какой угол называется прямым?
- Какой угол называется тупым?
- Какой угол называется развернутым?
- Сформулируйте основное свойство измерения углов.

- Что такое биссектриса угла?
- Какие углы называются равными?
8.Итоги урока. Рефлексия. Д/з.
Сообщение « Из истории векторов».
- Что ты понял сегодня на уроке?
- Чего ты сегодня не понял на уроке?
- При выполнении каких заданий ты ошибся и почему?
- Укажи причины успехов и неудач своей деятельности.
- Что вам дало изучение понятия вектор?
- Каков смысл сегодняшнего урока?
Мировая наука начиналась с геометрии. Человек не может по настоящему развиваться культурно и духовно, если он не изучал в школе геометрию. Геометрия возникла не только из практических, но и духовных потребностей человека.
Геометрия 9 класс В Е К Т О Р Ы (Обобщающий урок)
Вы можете ознакомиться и скачать
Геометрия 9 класс В Е К Т О Р Ы (Обобщающий урок) .
Презентация содержит 21 слайдов. Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Слайды и текст этой презентации
Описание слайда:
Геометрия 9 класс В Е К Т О Р Ы (Обобщающий урок)
Слайд 2
Описание слайда:
Понятие вектора
Многие физические величины, характеризуются не только своим числовым значением, но и направлением в пространстве.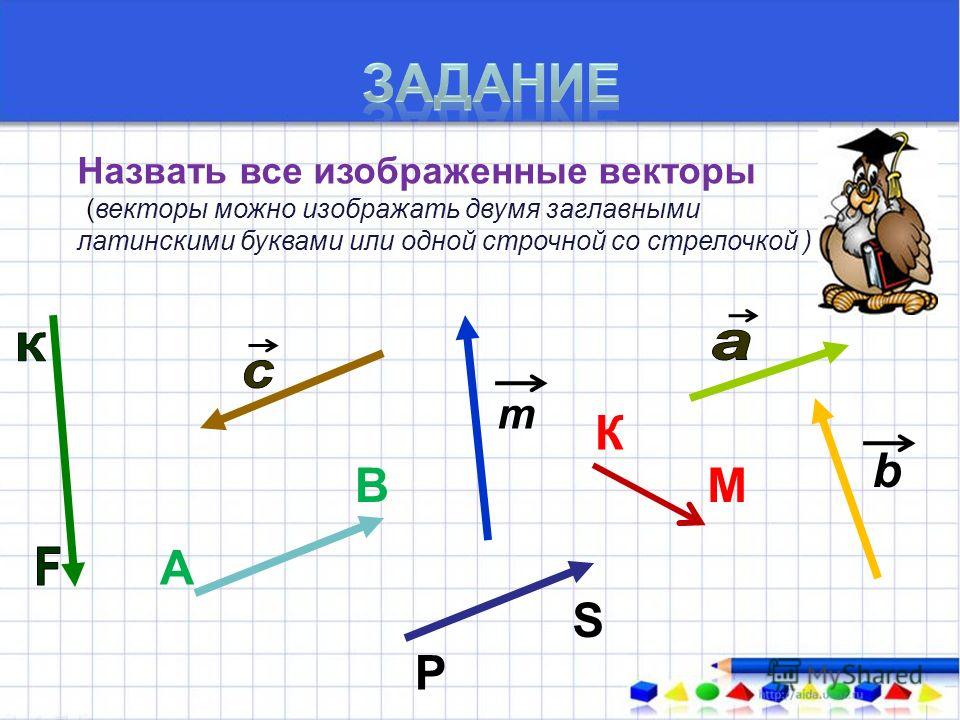 Такие физические величины называются ВЕКТОРАМИ.
Проверь себя! Какие из данных величин являются векторными: вес, сила, отрезок, ускорение, скорость, масса ?
Такие физические величины называются ВЕКТОРАМИ.
Проверь себя! Какие из данных величин являются векторными: вес, сила, отрезок, ускорение, скорость, масса ?
Слайд 3
Описание слайда:
История
В 19 веке параллельно с теорией систем линейных уравнений развивалась теория векторов. Направленные отрезки использовал Жан Робер АРГАН (Argand, 1768-1822, швейцарский математик), ввел термин «модуль комплексного числа» (1814-1815) в работе «Опыт некоторого представления мнимых величин…», опубликованной в 1806 году. Эти отрезки Арган обозначал символами а ,в .
Одним из основателей теории векторов считается Август Фердинанд Мебиус (1790-1868, немецкий математик), он обозначал отрезок с началом в точке А и концом в точке В символом АВ.
Термин «вектор» ввел Вильям Роуэн Гамильтон (1805-1865, директор астрономической обсерватории Дублинского университета и президент Ирландской Академии наук) приблизительно в 1845 году.
Слайд 4
Описание слайда:
ВЕКТОР — НАПРАВЛЕННЫЙ ОТРЕЗОК.
Слайд 5
Описание слайда:
Р а в е н с т в о в е к т о р о в
ВЕКТОРЫ называются равными, если они сонаправлены и их длины равны. .
а = в, если а в и а = в .
Слайд 6
Описание слайда:
Д л и н а в е к т о р а Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ .Обозначается длина вектора АВ (вектора а ) так : АВ ( а ). Длина нулевого вектора равна нулю: 0 = 0
Слайд 7
Описание слайда:
СОНАПРАВЛЕННЫЕ ПРОТИВОПОЛОЖНО ВЕКТОРЫ НАПРАВЛЕННЫЕ ВЕКТОРЫ СОНАПРАВЛЕННЫЕ ПРОТИВОПОЛОЖНО ВЕКТОРЫ НАПРАВЛЕННЫЕ ВЕКТОРЫ
Слайд 8
Описание слайда:
К О Л Л И Н Е А Р Н Ы Е В Е К Т О Р Ы
Ненулевые векторы называются к о л л и н е а р н ы м и , если они лежат либо на одной прямой, либо на параллельных прямых.
Слайд 9
Описание слайда:
С Л О Ж Е Н И Е В Е К Т О Р О В ПРАВИЛО ПРАВИЛО ТРЕУГОЛЬНИКА ПАРАЛЛЕЛОГРАММА
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
В Ы Ч И Т А Н И Е В Е К Т О Р О В Р а з н о с т ь ю в е к т о р о в а и в называется такой вектор, сумма которого с вектором в равна вектору а .
Слайд 12
Описание слайда:
З А К Р Е П Л Е Н И Е И З У Ч Е Н Н О Г О
З А Д А Н И Я (устно)
1). Укажите на рисунке 1:
а) сонаправленные векторы
б) противоположно направлен-
ные векторы
в) равные векторы
2).Укажите на рисунке 2:
а) пары коллинеарных векторов
б) векторы , длины которых
равны (трапеция равнобедренная)
Укажите на рисунке 1:
а) сонаправленные векторы
б) противоположно направлен-
ные векторы
в) равные векторы
2).Укажите на рисунке 2:
а) пары коллинеарных векторов
б) векторы , длины которых
равны (трапеция равнобедренная)
Слайд 13
Описание слайда:
3).На рис. 3 изображён треугольник МNL Найти: а) MN + NL б) MN — ML в ) ML — MN
Слайд 14
Описание слайда:
4).На рис.4 изображён параллелограмм MNKE. Найти: MN + ME ME + EK KN + KE
Слайд 15
Описание слайда:
Разложение вектора на плоскости по двум неколлинеарным векторам
Если векторы a и b коллинеарны и а ≠0, то существует такое число k, что в=k а.
Слайд 16
Описание слайда:
Координаты вектора
Слайд 17
Описание слайда:
Простейшие задачи в координатах: 1.Координаты середины отрезка 2. Вычисление длины вектора по его координатам. 3. Расстояние между двумя точками.
Слайд 18
Описание слайда:
П Р О В Е Р Ь С Е Б Я !
1). Верно ли утверждение:
а) Если а=в , то а в
б) Если а=в , то а и в коллинеарны
в) Если а=в , то а в
г) Если а в , то а = в
2).
Слайд 19
Описание слайда:
П Р О В Е Р Ь С Е Б Я ! 3) Найдите вектор х из условия: EF- LM- EL+ x =MK 4) Выпишите координаты вектора с, если его разложение по координатным векторам имеет вид с = -6i +2j 5) Дано а{-2;4}, d{3;-1}. Найдите координаты вектора к =2а –d 6) OA- радиус-вектор точки А, ОА{-5;4}.Какие координаты имеет точка А? 7) Найти координаты вектора RT? Если R(-1;5) , T(6;2). 8) Найдите длину вектора s{3;4}
Слайд 20
Описание слайда:
1. а) да 2. а) PR 3. FK 6. A(-6;4)
б) да б) QT 4. c{-6;2} 7.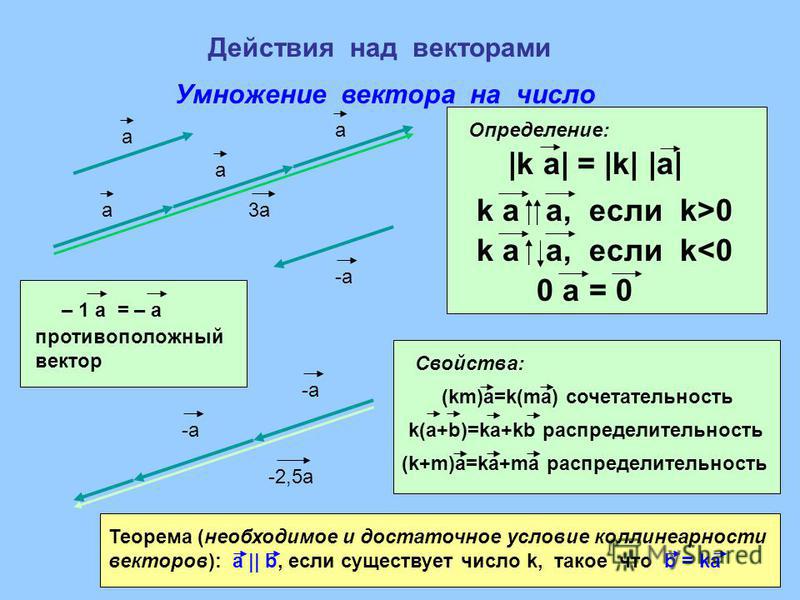 RT{7;-3}
в) нет в) RP 5. k{-7;9} 8. ISI=5
г) нет
RT{7;-3}
в) нет в) RP 5. k{-7;9} 8. ISI=5
г) нет
Слайд 21
Описание слайда:
Скаляры и векторы
Физика — математическая наука. Основные понятия и принципы имеют математическую основу. В ходе нашего изучения физики мы столкнемся с множеством понятий, имеющих математическую основу, связанную с ними. Хотя наш акцент часто будет делаться на концептуальной природе физики, мы будем уделять значительное и постоянное внимание ее математическому аспекту.
Движение объектов можно описать словами. Даже у человека, не знакомого с физикой, есть набор слов, которые можно использовать для описания движущихся объектов. Слова и фразы, такие как  Мы будем расширять этот словарь такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгое определение. Математические величины, используемые для описания движения объектов, можно разделить на две категории. Величина является либо вектором, либо скаляром. Эти две категории можно отличить друг от друга по их различным определениям:
Мы будем расширять этот словарь такими словами, как расстояние , смещение , скорость , скорость и ускорение . Как мы вскоре увидим, эти слова связаны с математическими величинами, имеющими строгое определение. Математические величины, используемые для описания движения объектов, можно разделить на две категории. Величина является либо вектором, либо скаляром. Эти две категории можно отличить друг от друга по их различным определениям:
- Скаляры — это величины, которые полностью описываются только величиной (или числовым значением).
- Векторы — это величины, полностью описываемые как величиной, так и направлением.
Оставшаяся часть этого урока будет посвящена нескольким примерам векторных и скалярных величин (расстояние, перемещение, скорость, скорость и ускорение). По мере прохождения урока уделяйте особое внимание векторному и скалярному характеру каждой величины. По мере того как мы переходим к другим разделам учебного пособия по физике и знакомимся с новыми математическими величинами, обсуждение часто начинается с определения новой величины как вектора или скаляра.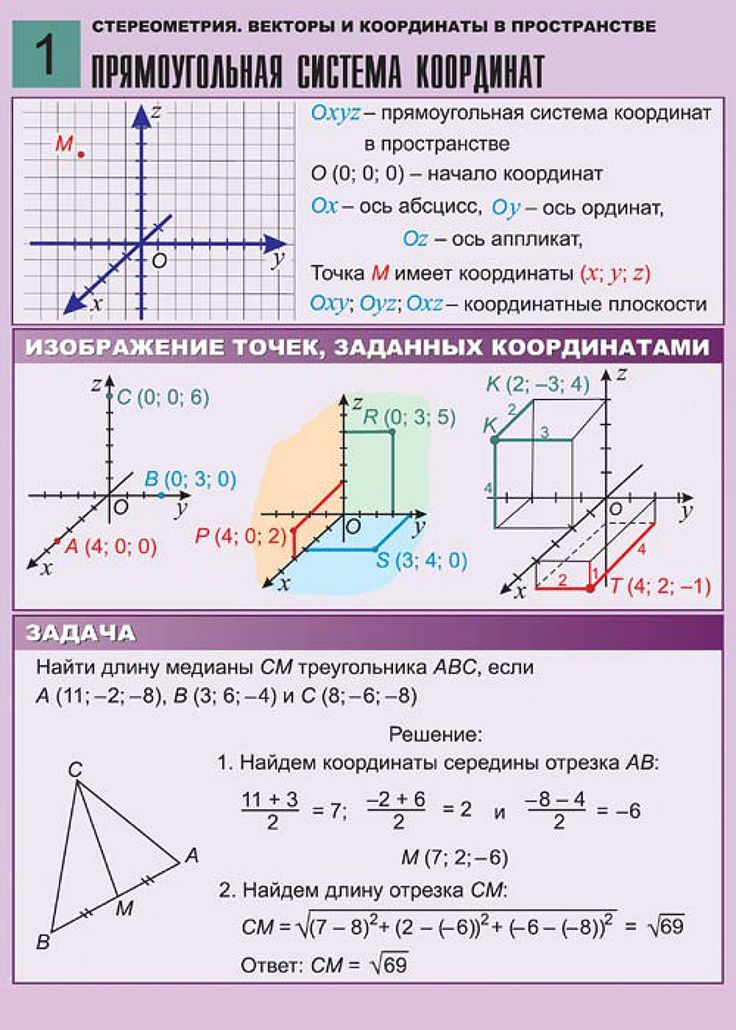
Проверьте свое понимание
1. Чтобы проверить свое понимание этого различия, рассмотрите следующие количества, перечисленные ниже. Классифицируйте каждую величину как векторную или скалярную. Нажмите кнопку, чтобы увидеть ответ.
| Количество | Категория |
|---|---|
| а. 5 м | |
| б. 30 м/с, Восток | |
| в. 5 миль, Север | |
| д. 20 градусов Цельсия | |
| эл. 256 байт | |
| ф. 4000 калорий |
Следующий раздел:
Перейти к следующему уроку:
Нахождение компонентов вектора
Как упоминалось ранее в этом уроке, любой вектор, направленный под углом к горизонтали (или вертикали), можно рассматривать как состоящий из двух частей (или компонент). То есть любой вектор, направленный в двух измерениях, можно рассматривать как имеющий две компоненты. Например, если цепь тянет вверх под углом ошейник собаки, то возникает сила натяжения, направленная в двух измерениях. Эта сила натяжения имеет две составляющие: направленную вверх и направленную вправо составляющую. В качестве другого примера рассмотрим самолет, который перемещается на северо-запад из международного аэропорта О’Хара (в Чикаго) в пункт назначения в Канаде. Вектор смещения плоскости находится в двух измерениях (северо-запад). Таким образом, этот вектор смещения имеет две составляющие: северную и западную.
То есть любой вектор, направленный в двух измерениях, можно рассматривать как имеющий две компоненты. Например, если цепь тянет вверх под углом ошейник собаки, то возникает сила натяжения, направленная в двух измерениях. Эта сила натяжения имеет две составляющие: направленную вверх и направленную вправо составляющую. В качестве другого примера рассмотрим самолет, который перемещается на северо-запад из международного аэропорта О’Хара (в Чикаго) в пункт назначения в Канаде. Вектор смещения плоскости находится в двух измерениях (северо-запад). Таким образом, этот вектор смещения имеет две составляющие: северную и западную.
В этом разделе мы изучаем два основных метода определения величин компонент вектора, направленного в двух измерениях. Процесс определения величины вектора известен как разрешение вектора . Мы рассмотрим два метода векторного разрешения:
- метод параллелограмма
- тригонометрический метод
Метод параллелограмма векторного разрешения включает использование точно нарисованной масштабированной векторной диаграммы для определения компонентов вектора. Кратко говоря, этот метод включает в себя рисование вектора в масштабе в указанном направлении, рисование параллелограмма вокруг вектора таким образом, чтобы вектор был диагональю параллелограмма, и определение величины компонентов (сторон параллелограмма) с использованием масштаба. . Если кто-то хочет определить компоненты, направленные вдоль традиционных осей координат x и y, то параллелограмм представляет собой прямоугольник со сторонами, вытянутыми по вертикали и горизонтали. Пошаговая процедура использования метода параллелограмма векторного разрешения:
Кратко говоря, этот метод включает в себя рисование вектора в масштабе в указанном направлении, рисование параллелограмма вокруг вектора таким образом, чтобы вектор был диагональю параллелограмма, и определение величины компонентов (сторон параллелограмма) с использованием масштаба. . Если кто-то хочет определить компоненты, направленные вдоль традиционных осей координат x и y, то параллелограмм представляет собой прямоугольник со сторонами, вытянутыми по вертикали и горизонтали. Пошаговая процедура использования метода параллелограмма векторного разрешения:
- Выберите масштаб и точно нарисуйте вектор для масштабирования в указанном направлении.
- Нарисуйте параллелограмм вокруг вектора: начиная с конца вектора, нарисуйте вертикальные и горизонтальные линии; затем нарисуйте горизонтальные и вертикальные линии в начале вектора; нарисованные линии встретятся, образуя прямоугольник (частный случай параллелограмма).
- Нарисуйте компоненты вектора. Компонентами являются сторон параллелограмма.
 Хвост компонентов начинается в хвосте вектора и тянется по осям до ближайшего угла параллелограмма. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо).
Хвост компонентов начинается в хвосте вектора и тянется по осям до ближайшего угла параллелограмма. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо). - Осмысленно пометьте компоненты векторов символами, чтобы указать, какой компонент представляет какую сторону. Компонент сил, направленный на север, может быть обозначен F север . Компонент скорости, направленный вправо, может быть обозначен как v x ; и т. д.
- Измерьте длину сторон параллелограмма и с помощью шкалы определите величину компонентов в реальных единиц. Обозначьте величину на схеме.
Пошаговая процедура, описанная выше, проиллюстрирована на диаграмме ниже, чтобы показать, как вектор скорости с величиной 50 м/с и направлением 60 градусов выше горизонтали может быть разделен на две составляющие. На диаграмме показано, что вектор сначала рисуется в масштабе в указанном направлении; вокруг вектора начерчен параллелограмм; компоненты обозначены на схеме; и результат измерения длины компонентов вектора и преобразования в м/с с использованием шкалы. (ПРИМЕЧАНИЕ: поскольку разные компьютерные мониторы имеют разное разрешение, фактическая длина вектора на вашем мониторе может быть меньше 5 см.)
(ПРИМЕЧАНИЕ: поскольку разные компьютерные мониторы имеют разное разрешение, фактическая длина вектора на вашем мониторе может быть меньше 5 см.)
Тригонометрический метод разрешения вектора
Тригонометрический метод разрешения вектора включает использование тригонометрических функций для определения компонентов вектора. Ранее в уроке 1 было описано использование тригонометрических функций для определения направления вектора. Теперь в этой части урока 1 тригонометрические функции будут использоваться для определения компонентов одного вектора. Вспомните из предыдущего обсуждения, что тригонометрические функции связывают отношение длин сторон прямоугольного треугольника с мерой острого угла внутри прямоугольного треугольника. Таким образом, тригонометрические функции можно использовать для определения длины сторон прямоугольного треугольника, если известна мера угла и длина одной стороны.
Метод использования тригонометрических функций для определения компонентов вектора следующий:
- Построить грубый эскиз (масштаб не требуется) вектора в указанном направлении.
 Обозначьте его величину и угол, который он образует с горизонтом.
Обозначьте его величину и угол, который он образует с горизонтом. - Нарисуйте прямоугольник вокруг вектора так, чтобы вектор был диагональю прямоугольника. Начиная с хвоста вектора, нарисуйте вертикальные и горизонтальные линии. Затем нарисуйте горизонтальные и вертикальные линии в начале вектора. Нарисованные линии сойдутся, образуя прямоугольник.
- Нарисуйте компоненты вектора. Компонентами являются сторон прямоугольника. Хвост каждой компоненты начинается в хвосте вектора и тянется по осям до ближайшего угла прямоугольника. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо).
- Осмысленно пометьте компоненты векторов символами, чтобы указать, какой компонент представляет какую сторону. Составляющая силы, направленная на север, может быть обозначена как F 9.0129 север . Направленная вправо составляющая скорости силы может быть обозначена как v x ; и т. д.
- Чтобы определить длину стороны, противоположной указанному углу, используйте функцию синуса.
 Замените модуль вектора на длину гипотенузы. С помощью алгебры решите уравнение для длины стороны, противоположной указанному углу.
Замените модуль вектора на длину гипотенузы. С помощью алгебры решите уравнение для длины стороны, противоположной указанному углу. - Повторите описанный выше шаг, используя функцию косинуса, чтобы определить длину стороны, примыкающей к указанному углу.
Описанный выше метод показан ниже для определения компонентов силы, действующей на Фидо. Поскольку сила натяжения в 60 ньютонов действует на Фидо вверх и вправо под углом 40 градусов, компоненты этой силы можно определить с помощью тригонометрических функций.
Таким образом, вектор, направленный в двух измерениях, имеет две компоненты, то есть влияние в двух отдельных направлениях. Величину влияния в заданном направлении можно определить с помощью методов векторного разрешения. Здесь описаны два метода векторного разрешения — графический метод (метод параллелограмма) и тригонометрический метод.
Используйте виджет Компоненты вектора ниже, чтобы разложить вектор на его компоненты.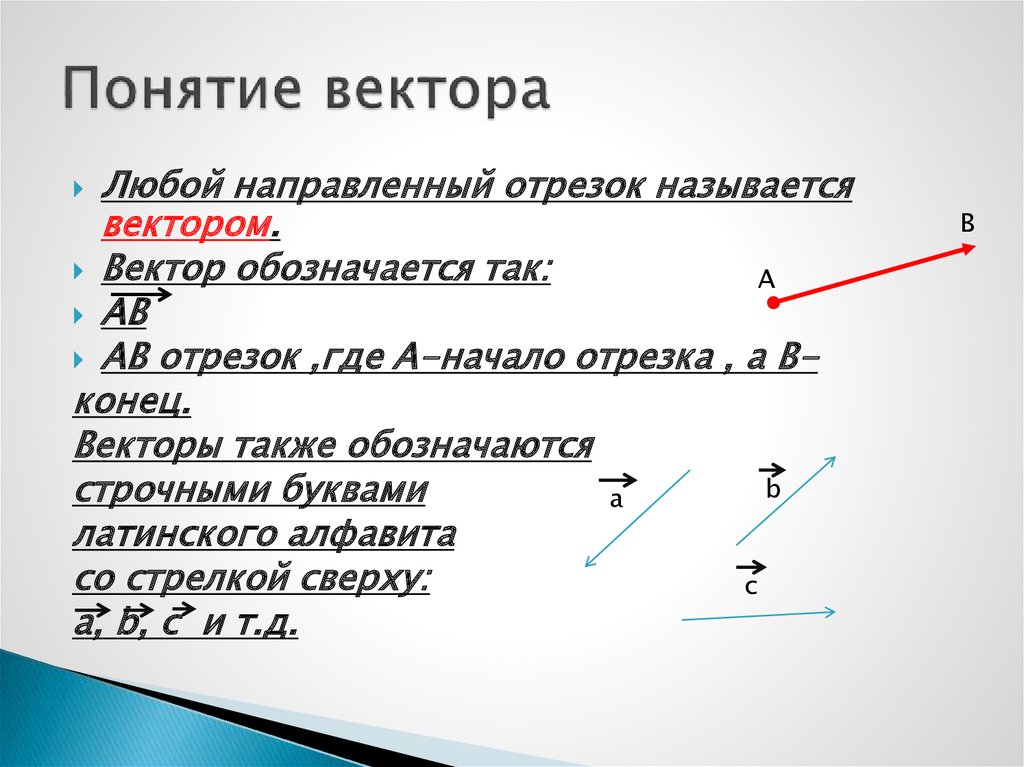


 Хвост компонентов начинается в хвосте вектора и тянется по осям до ближайшего угла параллелограмма. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо).
Хвост компонентов начинается в хвосте вектора и тянется по осям до ближайшего угла параллелограмма. Обязательно поместите стрелки на эти компоненты, чтобы указать их направление (вверх, вниз, влево, вправо). Обозначьте его величину и угол, который он образует с горизонтом.
Обозначьте его величину и угол, который он образует с горизонтом.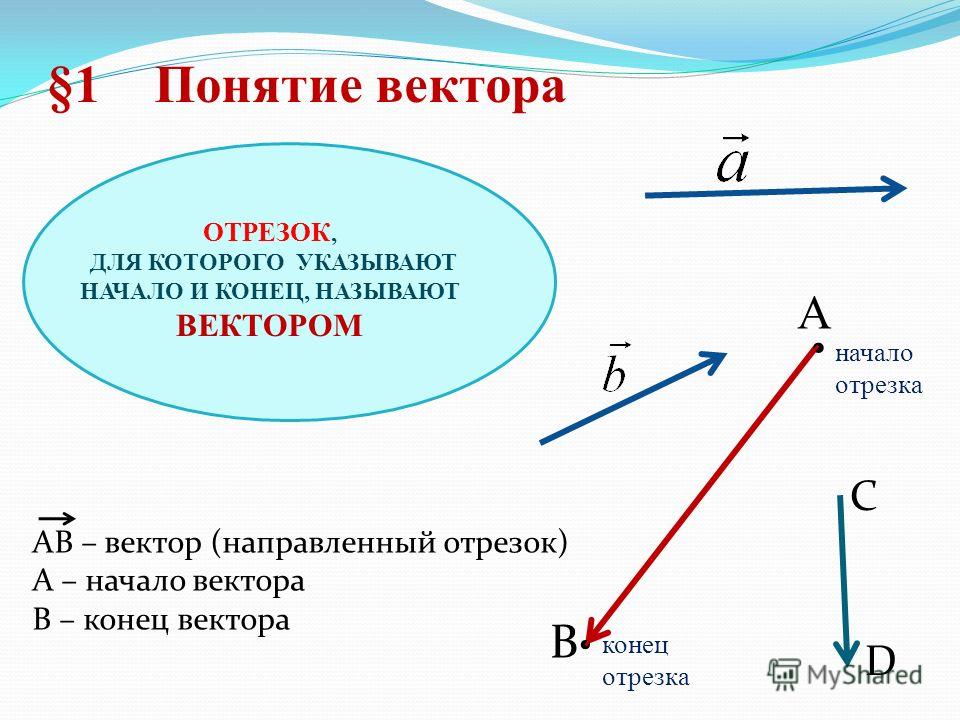 Замените модуль вектора на длину гипотенузы. С помощью алгебры решите уравнение для длины стороны, противоположной указанному углу.
Замените модуль вектора на длину гипотенузы. С помощью алгебры решите уравнение для длины стороны, противоположной указанному углу.