Найти при каком значении параметра а определитель а 0: 22. При каком значении параметра λ матрица A является вырожденной? А=(2 5 ) (-λ 20)

Приложение 1 Домашние задания Домашнее задание № 1. Определители.

Задача 1. Найти при каком значении параметра α определитель

Ответ: α=3.

Задача 2. Найти при каком значении α определитель :

Ответ: α = 2;

Задача 3. Найти при каком значении α определитель :

Ответ: α = 1;

Задача 4. Найти при каком значении α определитель :

Ответ: α = — 7;

Задача 5. Найти при каком значении α определитель :

Ответ: α = -16;

Задача 6. Найти при каком значении α определитель :

Ответ: α = — 11;

Задача 7. Найти при каком значении α определитель :

Ответ: α = 20;

Задача 8. Найти при каком значении α определитель :

Ответ: α = 12

Задача 9. Найти значение определителя :

Ответ: =

Задача 10. Найти значение определителя:

, Ответ: =ad — вс;

Задача 11. Найти значение определителя:

, Ответ: =2a — 5в;

Задача 12. Вычислить определитель

, Ответ: = 5

Задача 13. Вычислить определитель

Ответ: = — 1;

Задача 14. Вычислить определитель

Ответ: = — 9;

Задача 15. Вычислить определитель

Ответ: = — 11;

Задача 16. Вычислить определитель

Ответ: = 6;

Задача 17. Вычислить определитель

Ответ: = 5;

Задача 18. Разложением по первой строке вычислить определитель

Ответ: =

Задача 19. Разложением по первой строке вычислить определитель

Ответ: =2а₁₂ – 3а₁₁;

Задача 20. Разложением по первой строке вычислить определитель

Ответ: =2а₁₃ – 3а₁₂;

Задача 21. Разложением по первой строке вычислить определитель

Ответ: =

2а₁₃ – 3а₁₂;

Задача 1. Дана матрица

Найти сумму двух следующих ее элементов а₁₁+ а₃₂.

Ответ: (-7).

Задача 2. Дана матрица найти сумму а₁₂+ а₂₃.

Ответ: ( — 4).

Задача 3. Найти сумму элементов, расположенных на главной диагонали.

Ответ: 15.

Задача 4. Найти сумму элементов, расположенных на второй диагонали.

Ответ: 9.

Задача 5. Указать тип матрицы

Ответ: трапециевидная.

Задача 6. Указать тип матрицы

Ответ: единичная.

Задача 7. Указать тип матрицы

Ответ: верхняя.

Задача 8. Указать тип матрицы

Ответ: нижняя.

Задача 9. Указать тип матрицы

Ответ: симметричная.

Задача 10. Найти сумму двух следующих матриц

Ответ:

Задача 11. Найти сумму двух следующих матриц

Ответ: ;

Задача 12. Найти сумму двух следующих матриц

Ответ: ;

Задача 13. Найти сумму двух следующих матриц

Ответ:

Задача 14. Из матрицы А вычесть матрицу В:

Ответ: ;

Задача 15. Матрицу умножить на число λ=2.

Ответ: λ•А=;

Задача 16. Найти произведение А и В:

Ответ: ;

Задача 17. Найти произведение А и В:

Ответ:

Задача 18. При каком значении параметра λ матрица

является вырожденной.

Ответ: λ = — 2

Задача 19. При каком значении параметра λ матрица является вырожденной.

. Ответ: λ= -2;

Задача 20. При каком значении параметра λ матрица является вырожденной.

. Ответ: λ= — 8;

Задача 21. При каком значении параметра λ матрица является вырожденной.

. Ответ: λ= 3;

Задача 22. При каком значении параметра λ матрица является вырожденной.

. Ответ: λ= — 3;

Задача 23. При каком значении параметра λ матрица является вырожденной.

.

Ответ: λ = 2;

Задача 24. Вычислить определители произведения матриц А и В

, ,

Ответ: =0;

Задача 25. Вычислить определители произведения матриц А и В

, ,

Ответ: =24;

Задача 26. Вычислить определители произведения матриц А и В

, ,

Ответ: =45;

Задача 27. Вычислить определители произведения матриц А и В

, ,

Ответ: = — 26;

Задача 28. Вычислить определители произведения матриц А и В

, ,

Ответ: =9;

Задача 29. Найти ранг матрицы

Ответ: r = 1

Задача 30. Найти ранг матрицы

Ответ: r = 2

Задача 31. Найти ранг матрицы

Ответ: r = 2

Задача 32. Найти ранг матрицы

Ответ: r = 1

Задача 33. Найти ранг матрицы

Ответ: r = 2

Задача 34. При каком значении параметра λ матрица А не имеет обратной.

Ответ:

Задача 35. При каком значении параметра λ матрица А не имеет обратной.

, , Ответ: = 8;

Задача 36. При каком значении параметра λ матрица А не имеет обратной.

, , Ответ: = — 6;

Задача 37. При каком значении параметра λ матрица А не имеет обратной.

, , Ответ: = — 3;

Задача 38. При каком значении параметра λ матрица А не имеет обратной.

, , Ответ: = 3;

Задача 39. При каком значении параметра λ матрица А не имеет обратной.

, Ответ: = — 16;

Сообщество Экспонента

• Публикация
• 24.12.2022

Системы связи

Скачать материалы семинара можно тут.

Недавно у нас в офисе прошел офлайн-семинар, который собрал на одной площадке специалистов данной тематики для обмена знаниями и опытом, чтобы вооружившись последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G.

• 5G
• ИИ
• Искусственный интеллект

24.12.2022

• вопрос
• 23.12.2022

Глубокое и машинное обучение(ИИ), Робототехника и беспилотники, ПЛИС и СнК, Системы управления, Электропривод и силовая электроника, Радиолокация, Автоматизация испытаний, Системы связи, Цифровая обработка сигналов, Верификация и валидация, Математика и статистика, Изображения и видео

Здравствуйте! Есть такая вот статья. Мне в Matlab надо написать формулу, чтобы в результате получить диаграмму, как на рисунке 4 на статье. Только вот я не понимаю, какую формулу можно было бы написат…

Здравствуйте! Есть такая вот статья. Мне в Matlab надо написать формулу, чтобы в результате получить диаграмму, как на рисунке 4 на статье. Только вот я не понимаю, какую формулу можно было бы написат…

2 Ответа

• Отвеченный вопрос
• 21. 12.2022

Другое, Математика и статистика, Цифровая обработка сигналов

Есть массив экспериментальных данных (9 спектров при разных концентрациях), который я пытаюсь описать спектрами нескольких форм (в данном примере для упрощения только одна форма со спектром x(2,: ) и…

Есть массив экспериментальных данных (9 спектров при разных концентрациях), который я пытаюсь описать спектрами нескольких форм (в данном примере для упрощения только одна форма со спектром x(2,: ) и…

6 Ответов

• вопрос
• 20.12.2022

Глубокое и машинное обучение(ИИ)

Здравствуйте, подскажите пожалуйста ссылки и статьи на тему работы с нейронной сетью, созданной с помощью Matlab, через js, nodejs. 

Здравствуйте, подскажите пожалуйста ссылки и статьи на тему работы с нейронной сетью, созданной с помощью Matlab, через js, nodejs. 

1 Ответ

• MATLAB-программирование
• javascript

20. 2 (вольт — частотная корректировка) 3. Добавить вентиляторную…

1 Ответ

• ПЧ
• Скалярное управление
• АД

14.12.2022

• Отвеченный вопрос
• 13.12.2022

Другое, Математика и статистика, Цифровая обработка сигналов

Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…

Здравствуйте. Подскажите пожалуйста как (и можно ли вообще) решить систему квадратных уравнений. eqn1=(x-y)/(A0-x-y)/(m0-x-2*y)==K1; eqn2=y/(x-y)/(m0-x-2*y)==K2; То есть выразить переменные x и y чер…

7 Ответов

• Публикация
• 07.12.2022

Электропривод и силовая электроника

Наша команда представила решение для электроэнергетической отрасли на базе КПМ РИТМ. В очередной раз мы провели демонстрацию работы стенда с терминалами РЗиА (ВАЖНО! — мы не занимаемся рекламой сипротеков, на их месте может быть любой терминал, в том числе и В. ..

На прошлой неделе прошел международный форум «Электрические сети», который объединил десятки ведущих представителей профессионального сообщества электроэнергетики, а также задал вектор развития для внедрения новых прорывных технологий.

• Электропривод
• электроэнергетика

07.12.2022

• Публикация
• 07.12.2022

Робототехника и беспилотники

В докладе будет рассказано о применении алгоритмов обучения с подкреплением к различным задачам: от простых игровых задач до задачи навигации мобильного робота. Также будут представлены результаты сравнения различных алгоритмов в задачах избежания столкновения…

Приглашаем на вебинар «Обучение с подкреплением: от игр к реальным задачам», который пройдет 13 декабря в 10:00.

В настоящее время технологии обучения с подкреплением активно применяются во многих сферах: от ритейла до автономных транспортных средств. Может быть лучше: основной сложностью этого подхода является отсутствие размеченных данных, и, к сожалению, нет формализованного подхода как данные могут быть размечены для этой задачи. Другая сложность — это формализация функции вознаграждения. От удачного ее выбора зависит конечный успех настройки алгоритма управления.

• MATLAB
• Simulink
• САУ
• МОП
• Модельно ориентированное проектирование
• Искусственный интеллект

07.12.2022

• вопрос
• 07.12.2022

Системы связи, Цифровая обработка сигналов, ПЛИС и СнК, Другое

Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA.  Мне необходимо построить сигнал с данной модуляцией и…

Здравствуйте! У меня вопрос по поводу дифференциальной квадратурной фазовой модуляции (DQPSK), которая применяется в стандарте связи TETRA.  Мне необходимо построить сигнал с данной модуляцией и…

13 Ответов

• вопрос
• 07. 12.2022

Изображения и видео, Математика и статистика, Автоматизация испытаний, Другое

Добрый день, мне нужно выполнить в матлаб вычитание постоянного наклона для изображения, полученного атомно-силовым микроскопом. Изображение представляет собой квадратную матрицу. Для этого требуется…

Добрый день, мне нужно выполнить в матлаб вычитание постоянного наклона для изображения, полученного атомно-силовым микроскопом. Изображение представляет собой квадратную матрицу. Для этого требуется…

6 Ответов

Плоскость определения трассировки

\(\newcommand{\trace}{\operatorname{tr}} \newcommand{\real}{\operatorname{Re}} \newcommand{\imaginary}{\operatorname{Im}} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)

¶

Предположим, что у нас есть два резервуара, Бак \(A\) и Бак \(B\text{,}\), оба имеют объем \(V\) литров и оба заполнены соляным раствором. Предположим, что чистая вода поступает в бак \(A\) со скоростью \(r_{\text{in}}\) литров в минуту, а солевая смесь поступает в бак \(A\) из бака \(B\) со скоростью скорость \(r_B\) литров в минуту. Рассол также поступает в бак \(B\) из бака \(A\) со скоростью \(r_A\) литров в минуту. Наконец, рассол сливается из резервуара \(B\) со скоростью \(r_{\text{out}}\), так что объем в каждом резервуаре остается постоянным (рис. 3.7.1).

Рис. 3.7.1 Пример смешивания с двумя резервуарами

Если \(x(t)\) и \(y(t)\) — количество соли в резервуаре \(A\) и резервуаре \(B\text{,} \) соответственно, то наша задача может быть смоделирована линейной системой двух уравнений,

\начать{выравнивать*} \frac{dx}{dt} \amp = \text{скорость входа} — \text{скорость выхода} = — r_A \frac{x}{V} + r_B \frac{y}{V}\\ \frac{dy}{dt} \amp = \text{ставка на входе} — \text{скорость на выходе} = r_A \frac{x}{V} — r_B \frac{y}{V} — r_{\text{ out}} \frac{y}{V}. \конец{выравнивание*}

Кроме того, \(r_A = r_B + r_{\text{out}}\text{,}\), поскольку объем в баке \(B\) постоянен. Следовательно, наша система теперь становится

\начать{выравнивать*} \frac{dx}{dt} \amp = — r_A \frac{x}{V} + r_B \frac{y}{V}\\ \frac{dy}{dt} \amp = r_A \frac{x}{V} — r_A \frac{y}{V}. \конец{выравнивание*}

Если у нас есть начальные условия \(x(0) = x_0\) и \(y(0) = y_0\text{,}\), то несложно сделать вывод, что количество соли в каждом баке будет приближаться к нулю при \(t \to \infty\text{,}\) и мы будем иметь устойчивое равновесное решение при \((0, 0)\text{.}\) Определение характера равновесного решения является более сложным вопросом . Например, возможно ли, чтобы равновесное решение было спиральным стоком? Одним из решений является изучение следоопределяющая плоскость .

Подраздел 3.7.1. Плоскость определения трассы

¶

Ключ к решению системы

\begin{уравнение*} \begin{pmatrix} х’\у’ \end{pматрица} знак равно \begin{pmatrix} а и б \\ CD \end{pматрица} \begin{pmatrix} х\у \end{pматрица} знак равно А \begin{pmatrix} х\у \end{pматрица} \end{уравнение*}

определяет собственные значения \(A\text{.}\) Чтобы найти эти собственные значения, нам нужно вывести характеристический многочлен \(A\text{,}\) 92 — Т \ лямбда + Д. \end{уравнение*}

Мы можем использовать след и определитель, чтобы установить природу решения линейной системы.

Теорема 3.7.2.

Если \(2 \times 2\) матрица \(A\) имеет собственные значения \(\lambda_1\) и \(\lambda_2\text{,}\), то след \(A\) равен \(\ lambda_1 + \lambda_2\) и \(\det(A) = \lambda_1 \lambda_2\text{.}\)

Доказательство

Доказательство следует из прямого вычисления. Действительно, мы можем переписать характеристический полином как 92 — 4D}}{2}. \end{уравнение*}

Следовательно, \(T = \lambda_1 + \lambda_2\) и \(D = \lambda_1 \lambda_2\text{.}\)

Теорема Теорема 3.7.2 говорит нам, что мы можем определить определитель и след матрицы \(2 \times 2\) по ее собственным значениям. Таким образом, мы должны быть в состоянии определить фазовый портрет системы \({\mathbf x}’ = A {\mathbf x}\), просто исследуя след и определитель \(A\text{.}\) Поскольку собственные значения \(A\) равны

92 — 4D\) не зависит от замены координат по теореме Теорема 3. 7.4. То есть нам нужно рассматривать только системы \({\mathbf x}’ = A {\mathbf x}\text{,}\), где \(A\) — одна из следующих матриц:

\begin{уравнение*} \begin{pmatrix} \альфа и \бета\\ -\бета и \альфа \end{pmatrix}, \begin{pmatrix} \лямбда & 0 \\ 0 & \мю \end{pmatrix}, \begin{pmatrix} \лямбда & 0 \\ 0 & \лямбда \end{pmatrix}, \begin{pmatrix} \лямбда & 1 \\ 0 & \лямбда \end{pматрица}. \end{уравнение*} 92/4\)

Ситуация с различными действительными собственными значениями несколько сложнее. Предположим, что у нас есть система

.

\begin{уравнение*} {\mathbf х}’ знак равно \begin{pmatrix} \лямбда & 0 \\ 0 & \мю \end{pматрица} {\ mathbf х} \end{уравнение*}

с различными собственными значениями \(\lambda\) и \(\mu\text{.}\) У нас будет три случая для рассмотрения, если ни одно из наших собственных значений не равно нулю:

• Оба собственных значения положительные (источник). 92/4\)

  Пример 3.7.8

  Вернемся к проблеме перемешивания, которую мы предложили в начале этого раздела. Задача может быть смоделирована системой уравнений

  \начать{выравнивать*} \frac{dx}{dt} \amp = — r_A \frac{x}{V} + r_B \frac{y}{V}\\ \frac{dy}{dt} \amp = r_A \frac{x}{V} — r_A \frac{y}{V}\\ х(0) \амп = х_0\\ у(0) \амп = у_0. \конец{выравнивание*}

  Матрица, соответствующая этой системе, равна

  . 92} \lt 0, \end{уравнение*}

  мы находимся ниже параболы в плоскости определителя трассы и знаем, что наше решение должно быть узловым стоком.

  Подраздел 3.7.2. Параметризованные семейства линейных систем.

  ¶

  Плоскость определения трассы является примером плоскости параметров . Мы можем скорректировать элементы матрицы \(A\) и тем самым изменить значение следа и определителя.

  Пример 3.7.9

  92 — 4D = 4 — 8a = 0 \qquad \text{или}\qquad a = \frac{1}{2}. \end{уравнение*}

  Таким образом, в точке \(a = 1/2\text{.}\) происходит бифуркация. Если \(a \gt 1/2\text{,}\) мы имеем спиральный сток. Если \(a \lt 1/2\text{,}\) у нас есть сток с действительными собственными значениями. Более того, если \(a \lt 0\text{,}\) наша раковина становится седлом (рис. 3.7.10).

  Рисунок 3.7.10 Однопараметрическое семейство линейных систем

  Напомним, что гармонический осциллятор можно смоделировать уравнением второго порядка

  92} + b \frac{dx}{dt} + k x = 0, \end{уравнение*}

  , где \(m > 0\) — масса, \(b \geq 0\) — коэффициент демпфирования, а \(k \gt 0\) — жесткость пружины. Если мы перепишем это уравнение как систему первого порядка, мы получим

  \begin{уравнение*} {\mathbf х}’ знак равно \begin{pmatrix} 0 и 1 \\ -к/м & — б/м \end{pматрица} {\mathbf х}. \end{уравнение*}

  Таким образом, для гармонического осциллятора \(T = -b/m\) и \(D= k/m\text{.}\) Если мы используем плоскость определения следа для анализа гармонического осциллятора, нам нужно рассматривать только себя со вторым квадрантом (Рисунок 3.7.11).

  Рис. 3.7.11. Однопараметрическое семейство для гармонического осциллятора

  . Если \((T, D) = (-b/m, k/m)\) лежит выше параболы, мы имеем недодемпфированный осциллятор. Если \((T, D) = (-b/m, k/m)\) лежит ниже параболы, мы имеем передемпфирующий осциллятор. Если \((T, D) = (—b/m, k/m)\) лежит на параболе, то мы имеем критически затухающий осциллятор. Если \(b = 0\text{,}\) у нас есть незатухающий осциллятор.

  Пример 3.7.12

  Теперь давайте посмотрим, что произойдет с нашим гармоническим осциллятором, если мы зафиксируем \(m = 1\) и \(k = 3\) и позволим затуханию \(b\) варьироваться от нуля до бесконечности. Мы можем переписать нашу систему как 92 = 12\) или когда \(b = 2 \sqrt{3}\text{.}\) Если \(b = 0\text{,}\) мы имеем чисто мнимые собственные значения. Это незатухающий гармонический осциллятор. Если \(0 \lt b \lt 2 \sqrt{3}\text{,}\) собственные значения являются комплексными с ненулевой действительной частью — случай недодемпфирования. Если \(b = 2 \sqrt{3}\text{,}\), собственные значения отрицательны и повторяются — случай критического затухания. Наконец, если \(b \gt 2 \sqrt{3}\text{,}\) мы имеем случай передемпфирования. 2/4\) на \(TD\)-плоскости. Точки на плоскости определителя следа соответствуют следу и определителю линейной системы \({\mathbf x}’ = A {\mathbf x}\text{.}\) Поскольку след и определитель матрицы определяют собственных значений \(A\text{,}\) мы можем использовать плоскость следа-детерминанта для параметризации фазовых портретов линейных систем.

• Плоскость следа-детерминанта полезна для изучения бифуркаций.

Подраздел Упражнения

¶

Классификация точек равновесия

Классифицируйте точки равновесия системы \(\mathbf x’ = A \mathbf x\) на основе положения \((T, D)\) в плоскости определителя трассы в группе упражнений 3.7.1–8. Нарисуйте фазовый портрет от руки, а затем используйте Sage , чтобы проверить результат.

1

\(A = \begin{pmatrix} 1\ампер 2\ 3\ампер 4 \end{pmatrix}\)

Решение

\((T,D) = (5,-2)\) является узловым седлом.

2

\(A = \begin{pmatrix} 4\ампер 2\ 3\ампер 2 \end{pmatrix}\)

Решение

\((T,D) = (6,2)\) является узловым источником.

3

\(A = \begin{pmatrix} -3\ампер -8\ 4 амп -6 \end{pmatrix}\)

Решение

\((T,D) = (-9,50)\) — спиральный сток.

4

\(A = \begin{pmatrix} 4\амп -5\ 3\ампер 2 \end{pmatrix}\)

Решение

\((T,D) = (6,23)\) является спиральным источником.

5

\(A = \begin{pmatrix} -11\ампер 10\ 4 амп -5 \end{pmatrix}\)

Решение

\((T,D) = (-16,15)\) является узловым стоком.

6

\(A = \begin{pmatrix} 5\амп -3\ -8 \ампер -6 \end{pmatrix}\)

Решение

\((T,D) = (-1,-54)\) является узловым седлом.

7

\(A = \begin{pmatrix} 4\амп -15\ 3 амп -8 \end{pmatrix}\)

Решение

\((T,D) = (-4,13)\) является спиральным стоком.

8

\(A = \begin{pmatrix} 4\ампер 11\ -8 \амп -3 \end{pmatrix}\)

Решение

\((T,D) = (1,76)\) является спиральным источником.

Однопараметрические семейства и бифуркации

Каждая из следующих матриц в группе упражнений 3.7.9–14 описывает семейство дифференциальных уравнений \(\mathbf x’ = A \mathbf x\), которое зависит от параметра \(\alpha\text{.}\) Для каждого семейства с одним параметром нарисуйте кривую в плоскости определителя трассы, определяемой \(\alpha\text{.}\). Определите любые значения \(\alpha\), при которых меняется тип системы. Эти значения представляют собой бифуркационных значений \(\alpha\text{.}\)

9

\(A = \begin{pmatrix} \альфа\усилитель 3\\ -1 \амп 0 \end{pmatrix}\)

10

\(A = \begin{pmatrix} \альфа\усилитель 3\\ \альфа\ампер 0 \end{pmatrix}\)

11

\(A = \begin{pmatrix} \ альфа \ усилитель 2 \\ \ альфа \ усилитель \ альфа \end{pmatrix}\)

12

\(A = \begin{pmatrix} 1\ампер 2\ \альфа\ампер 0 \end{pmatrix}\)

13

\(A = \begin{pmatrix} \альфа\ампер 1\\ 1 \амп\альфа — 1 \end{pmatrix}\) 92} \end{pmatrix}\)

15

Рассмотрим двухпараметрическое семейство линейных систем

\begin{уравнение*} \begin{pmatrix} х’ \\ у’ \end{pmatrix} знак равно \begin{pmatrix} \альфа и \бета\\ 1 и 0 \end{pматрица} \begin{pmatrix} x \\ y \end{pmatrix}. \end{уравнение*}

Определите все области \(\alpha\beta\)-плоскости, где эта система имеет седло, сток, спиральный сток и т.д.

16

Рассмотрим двухпараметрическое семейство линейных систем

\begin{уравнение*} \begin{pmatrix} х’ \\ у’ \end{pmatrix} знак равно \begin{pmatrix} \альфа и \бета\\ \бета и \альфа \end{pматрица} \begin{pmatrix} x \\ y \end{pmatrix}. \end{уравнение*}

Определите все области \(\alpha\beta\)-плоскости, где эта система имеет седло, сток, спиральный сток и т.д.

17

Рассмотрим двухпараметрическое семейство линейных систем

\begin{уравнение*} \begin{pmatrix} х’ \\ у’ \end{pmatrix} знак равно \begin{pmatrix} \альфа & -\бета \\ \бета и \альфа \end{pматрица} \begin{pmatrix} x \\ y \end{pmatrix}. \end{уравнение*}

Определите все области \(\alpha\beta\)-плоскости, где эта система имеет седло, сток, спиральный сток и т.д.

Подраздел 3.7.4 Проект—

¶ Видео с вопросами

: нахождение значения определителя, включающего неизвестные, с использованием свойств

Если det [𝑥, 4 и 4, 𝑦] = 0, det [𝑦, 9 и 9, 𝑧] = 0 и det [𝑥, 1 и 1, 𝑧] = 0, найти det [𝑥, 1, 2 и 0, 𝑦, 3 и 0, 0, 𝑧].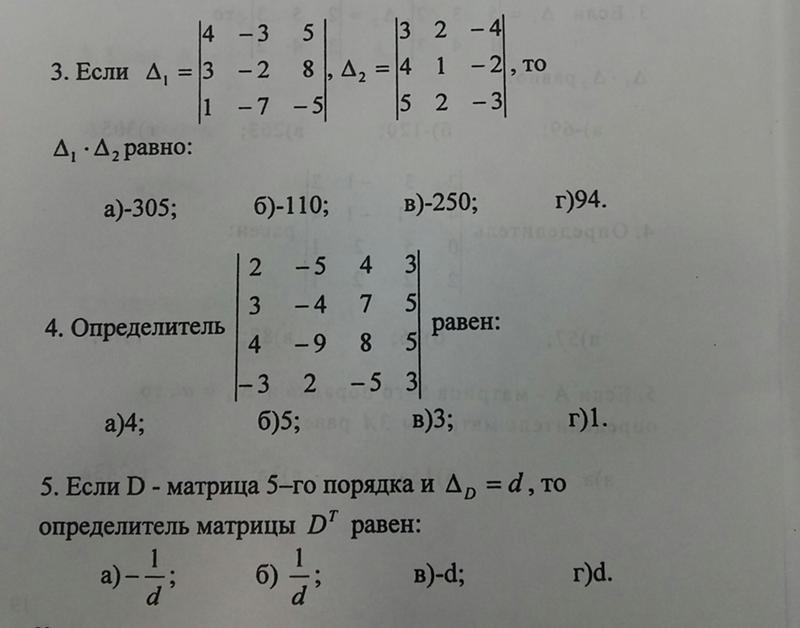

Стенограмма видео

Если определитель матрица два на два 𝑥, четыре, четыре, 𝑦 равна нулю; определитель матрица два на два 𝑦, девять, девять, 𝑧 равна нулю; и определитель матрица два на два 𝑥, один, один, 𝑧 равна нулю, найти определитель матрица три на три 𝑥, один, два, ноль, 𝑦, три, ноль, ноль, 𝑧.

В этом вопросе нам говорят, что определитель трех матриц два на два равен нулю. И каждая из этих трех матриц содержит три неизвестных: 𝑥, 𝑦 и 𝑧. Нам нужно использовать эту информацию, чтобы определите определители матрицы три на три, включающей три неизвестные. Итак, чтобы ответить на этот вопрос, мы нужно начать с поиска выражения для определителей матрица три на три. И у нас может возникнуть соблазн сделать это расширяя первую строку. Однако есть намного проще метод.

Нужно заметить, что эта матрица является верхней треугольной матрицей. Все записи ниже основного диагонали равны нулю. Затем мы можем оценить это определителя, вспомнив одно из свойств определителя, которое гласит, что если мы пытаемся найти определитель квадратно-треугольной матрицы, тогда это просто равно произведению всех элементов на главной диагонали. Поэтому, поскольку это верхний треугольной матрицы, определитель этой матрицы является произведением элементов на его главная диагональ: 𝑥 раз 𝑦 раз 𝑧.

Следовательно, чтобы ответить на этот вопрос, нам нужно определить значение 𝑥, 𝑦 и 𝑧 из трех заданных детерминанты. И для этого нам понадобится оценить каждую из трех детерминант. Начнем с первого определитель. Мы хотим оценить определитель матрицы два на два. И мы делаем это, находя разность произведений его диагоналей. Определитель этой матрицы равен 𝑥 раз 𝑦 минус четыре раза четыре. И мы можем упростить это, так как четырежды четыре равно 16. Определитель этой матрицы равен 𝑥𝑦 минус 16. Но помните, в вопрос определитель этой матрицы равен нулю. Таким образом, мы имеем, что ноль равно 𝑥𝑦 минус 16. Мы можем найти выражение для 𝑥𝑦 прибавив 16 к обеим частям уравнения. У нас есть, что 𝑥𝑦 равно 16.

Давайте теперь применим этот же процесс ко второму определителю. Сначала вычислим определитель этой матрицы, взяв разность произведений диагоналей. Это 𝑦 раз 𝑧 минус девять раз девять. И тогда, поскольку девять раз девять 81, это упрощает, чтобы дать нам 𝑦𝑧 минус 81. И помните, нам сказано в Вопрос этот определитель равен нулю. Таким образом, мы можем установить это равным нулю а затем добавьте 81 к обеим частям уравнения. Получаем, что 𝑦 умножить на 𝑧 равно 81.

Теперь нам нужно применить этот процесс в последний раз к третьему и последнему определителю. Сначала возьмем разницу в произведения диагоналей. Определитель этой матрицы равен 𝑥 умножить на 𝑧 минус один раз на один, что упрощает получение 𝑥𝑧 минус один. И мы знаем, что этот определитель равен нулю. Затем мы можем добавить один к обеим сторонам уравнения, чтобы определить, что 𝑥, умноженное на 𝑧, должно быть равно единице.

И в этот момент мы можем заметить что-то интересное. У нас есть три уравнения, включающие наши переменные 𝑥, 𝑦 и 𝑧. И левая сторона каждого из эти три уравнения входят в наше выражение для определителя. Таким образом, мы можем попытаться найти выражение для этого определителя, взяв произведение каждого из этих трех уравнения. Во-первых, взяв произведение в левой части этих трех уравнений мы получаем 𝑥𝑦 раз 𝑦𝑧 раз 𝑥𝑧. Тогда это будет равно произведение правой части каждого уравнения: 16 умножить на 81 умножить на один.

Теперь упростим это уравнение. Во-первых, в левой части уравнение, у нас есть два множителя 𝑥, два множителя 𝑦 и два множителя 𝑧. Так что это упрощает дать нам 𝑥 в квадрате умножить на 𝑦 в квадрате на 𝑧 в квадрате. Далее мы можем упростить правая часть уравнения. 16 умножить на 81 умножить на один — 1296. Теперь мы почти готовы найти значение этого определителя. Нам просто нужно использовать наши законы exponents, чтобы взять постоянный показатель степени двух вне выражения. 𝑥 в квадрате раз 𝑦 в квадрате раз 𝑧 в квадрате 𝑥 раз 𝑦 раз 𝑧 все в квадрате. А это площадь выражение, значение которого мы хотим найти. Итак, у нас есть 𝑥 раз 𝑦 раз 𝑧 квадрат равен 1,296.