Найти проекцию вектора на вектор онлайн: Онлайн калькулятор. Проекция вектора на вектор

Как найти проекцию вектора: на ось, другой вектор

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение проекции вектора: формула, примеры

В данной публикации мы рассмотрим, что такое проекция вектора на ось или на другой вектор, и приведем формулу, с помощью которой можно найти значение этой проекции. Также разберем примеры решения задач по этой теме.

• Нахождение проекции вектора
• Примеры задач

Нахождение проекции вектора

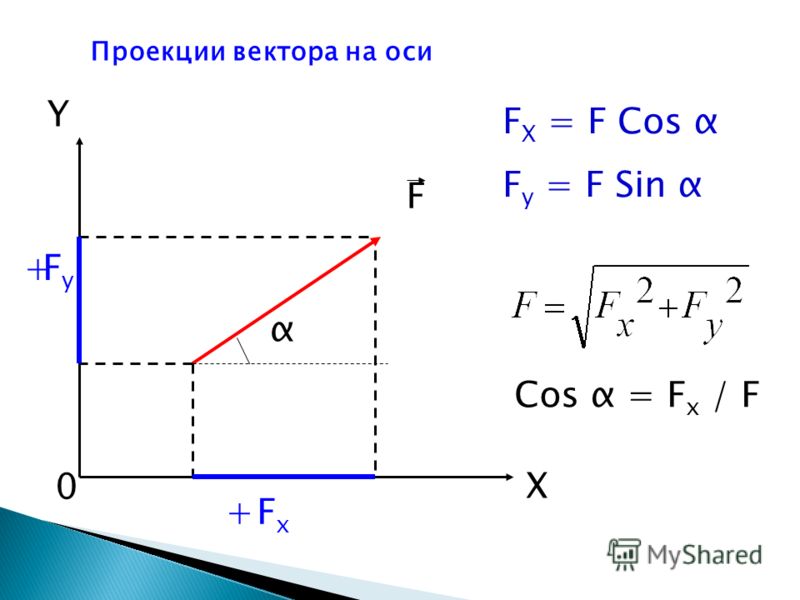
Проекция вектора AB на ось l – это число, которое равняется отрезку A₁B₁. Точки A₁ и B₁ при этом являются проекциями точек A и B на ось l.

Проекция вектора a на направление вектора b – это число, которое равно проекции a на ось, проходящую через b.

Формула для нахождения проекции вектора на вектор

Рассчитать проекцию a на направление b можно следующим образом:

Примеры задач

Задание 1
Найдем проекцию вектора a = {3; 5} на b = {2; 8}.

Решение:

1. Сперва посчитаем скалярное произведение заданных векторов:

a · b = 3 · 2 + 5 · 8 = 46

2. Теперь вычислим длину (модуль) b:

3. Остается только воспользоваться формулой выше для нахождения проекции вектора:

Задание 2
Вычислим проекцию вектора a = {4; -7; 5} на b = {11; 3; 6}.

Решение:
Поочередно выполняем те же самые действия, что и в примере, разобранном выше.

a · b = 4 · 11 + (-7) · 3 + 5 · 6 = 53

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Образцы решения задач по векторной алгебре

Задание 1: Коллинеарны ли векторы и , разложенные по векторам и , где

Решение:

1. Вычислим проекции векторов на оси координат:

2. Два вектора коллинеарны, если их проекции на оси координат пропорциональны, следовательно, проверим пропорциональность проекций векторов на оси координат:

не коллинеарны.

Задание 2: Перпендикулярны ли векторы ?

Решение: Два вектора перпендикулярны, если их скалярное произведение равно 0, скалярное произведение векторов, заданных проекциями на оси координат, вычисляется по формуле:, где вычислим скалярное произведение:

векторы не перпендикулярны.

Задание 3: Компланарны ли векторы ?

Решение: Три вектора компланарны, если смешанное произведение векторов равно 0, смешанное произведение векторов вычисляется по формуле: , гдевычислим смешанное произведение векторов:

векторы не компланарны.

Задание 4: При каком значении векторы где , перпендикулярны?

Решение:

1) Для определения , при котором векторы перпендикулярны, необходимо использовать условие перпендикулярности двух векторов (это условие было рассмотрено в задании 2) мы сможем найти из условия: , для этого найдем проекции векторов и на оси координат, заданных координатами точек начала и конца вектора. В этом случае проекции вектора на оси координат равны разности координат точек, задающих конец и начало вектора

Итак: векторы и перпендикулярны при и при

Задание 5: Даны точки:

Найти:

1. ;

2. ;

3. ;

4. орт вектора ;

5. ;

6. ;

Решение:

1. Из определения скалярного произведения следует, что проекцию вектора на вектор можно вычислить по формуле: , где скалярное произведение векторов вычисляется по формуле: где и длина вектора: итак, в нашем случае, формула принимает вид: для нахождения необходимо найти проекции векторов на оси координат, заданных координатами точек начала и конца векторов, скалярное произведение и длину соответствующего вектора:

на основании формулы, выше написанной, получим:

.

2. Для нахождения длины вектора воспользуемся формулой:, для этого найдем проекции векторов на оси координат (смотри пункт 1), так же найдем сумму векторов по правилу сложения векторов, заданных проекциями на оси координат:

;

Итак:

3. Угол между векторами можно найти из определения скалярного произведения: в нашем случае формула принимает вид: находим проекции векторов на оси координат (смотри пункты 1 и 2), вычисляем скалярное произведение векторов, заданных своими проекциями на оси координат, вычисляем длины векторов:

Итак

4. Направление вектора определяется углами , образованными им с осями координат Косинусы этих углов (направляющие косинусы вектора) определяются по формулам: Направляющие косинусы вектора связаны соотношением мы имеем вектор единичной длины, такой вектор называется ортом для нахождения орта вектора необходимо каждую проекцию вектора на оси координат разделить на его длину орт вектора .

Итак: орт вектора

5. Скалярное произведение векторов вычисляем по формуле:

(см. пункты 1 и 2), вычислим проекции векторов на оси координат и скалярное произведение векторов :

Итак:

6. Векторное произведение векторов вычисляется по формуле:

, где

Находим проекции векторов на оси координат:

Найдем , , .

Итак:

7. Смешанное произведение векторов вычисляется по формуле:

, где Итак:

Задание 6: Даны координаты вершин пирамиды:

Вычислить:

1. объем пирамиды;

2. длину ребра ;

3. площадь грани ;

Решение:

1. Объем пирамиды равен объема параллелепипеда, а объем параллелепипеда вычисляется на основании геометрического смысла смешанного произведения объем

параллелепипеда, построенного на векторах как на ребрах равен:

Найдем проекции соответствующих векторов на оси координат:

Тогда объем пирамиды равен:

Вычислим объем по указанной формуле:

;

2. Длина ребра

; (смотри пункт 5,3)

3. Площадь грани вычисляется по формуле:

так как грань треугольник, а площадь треугольника можно вычислить как половину площади параллелограмма, а площадь параллелограмма равна длине векторного произведения векторов, на которых построен параллелограмм на основании свойств векторного произведения найдем проекции векторов на оси координат:

;

Образцы билетов к коллоквиуму

1

1. Минор и алгебраическое дополнение элемента определителя. Приведите пример.

2. Выведите уравнение прямой, проходящей через две данные точки.

3. При каком значении векторы и будут коллинеарны?

4. Найти проекцию вектора на вектор , если

А(-2,5,7), В(-5,0,4), С(1,4,7).

2

1.Дайте определение векторного произведения двух векторов.

2. Выведите каноническое уравнение прямой на плоскости.

3. При каком значении векторы и будут ортогональны?

4. Найдите площадь треугольника АВС, используя векторное произведение векторов, если А(-2,5,7),

В(-5,0,4), С(1,4,7).

3

1. Вектор. Основные понятия. Линейные операции над векторами в геометрической форме.

2. Выведите уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору..

3. При каком значении векторы и будут коллинеарны?

4. Решите уравнение .

4

T$ на подпространство, натянутое на векторы $\{x, y\}$, где $x = [6; 1; -3]$, $y = [1; 0; 2]$.

Мне сказали посмотреть на ортогональный базис, спроецировать вектор на каждый элемент базиса, а затем сложить их. Итак, я использую формулу проекции для $t$ и $x$, $t$ и $y$, а затем складываю эти два вместе?

• линейная алгебра

$\endgroup$

1

$\begingroup$

В общем случае процедура нахождения ортогональной проекции вектора $\vec v$ на подпространство $\operatorname{span}(\vec a_1, \vec a_2, \dots, \vec a_k)$ такова:

$1.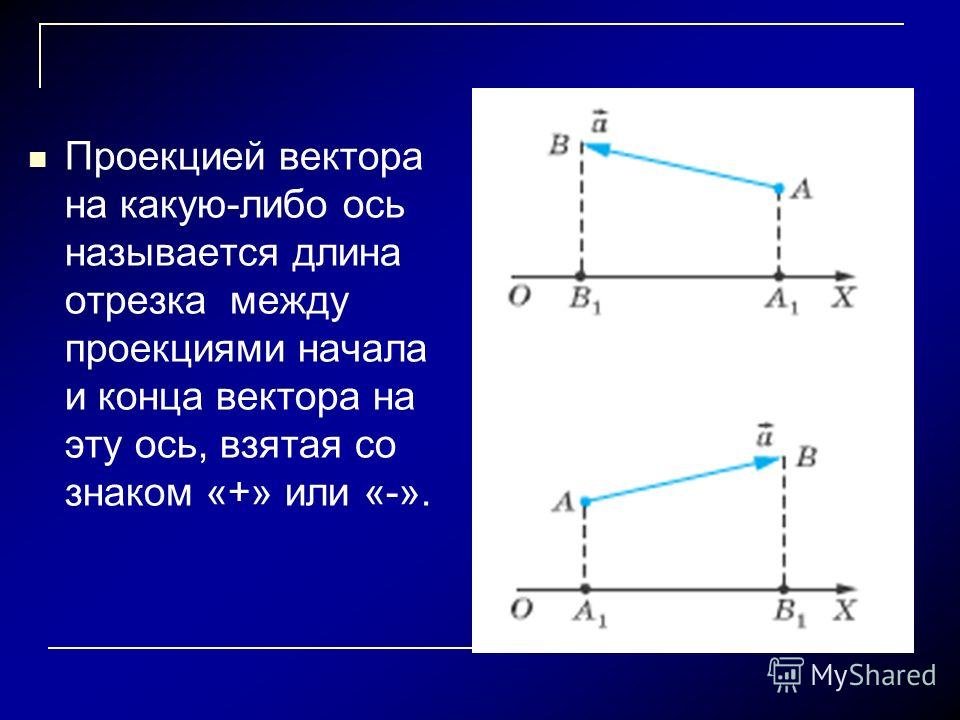 k\operatorname{proj}_{\vec b_i }\vec v$$ 93$, натянутых на $x$ и $y$. Как вы уже правильно заметили, нужно рассматривать ортонормированный базис $W$. Вы можете применить процесс Грама–Шмидта к $x$ и $y$, чтобы получить такой базис. Этот базис будет состоять из двух векторов (поскольку $W$ двумерен), скажем, $x’$ и $y’$.

Тогда проекция $p_W(t)$ $t$ на $W$ задается выражением $$ p_W(t) = \langle t, x’ \rangle x’ + \langle t, y’ \rangle y’.$$

$\endgroup$

$\begingroup$

Метод, который вы указали, хорош, и в основном это то, что рекомендуют два других ответа.

Однако это требует расчета двух проекций. Это не обременительно, но есть более простой способ спроецировать трехмерный вектор на двумерную плоскость, определяемую двумя линейно независимыми векторами.

1) Найдите векторное произведение двух векторов, определяющих плоскость.

2) Найдите проекцию вашего вектора на этот вектор.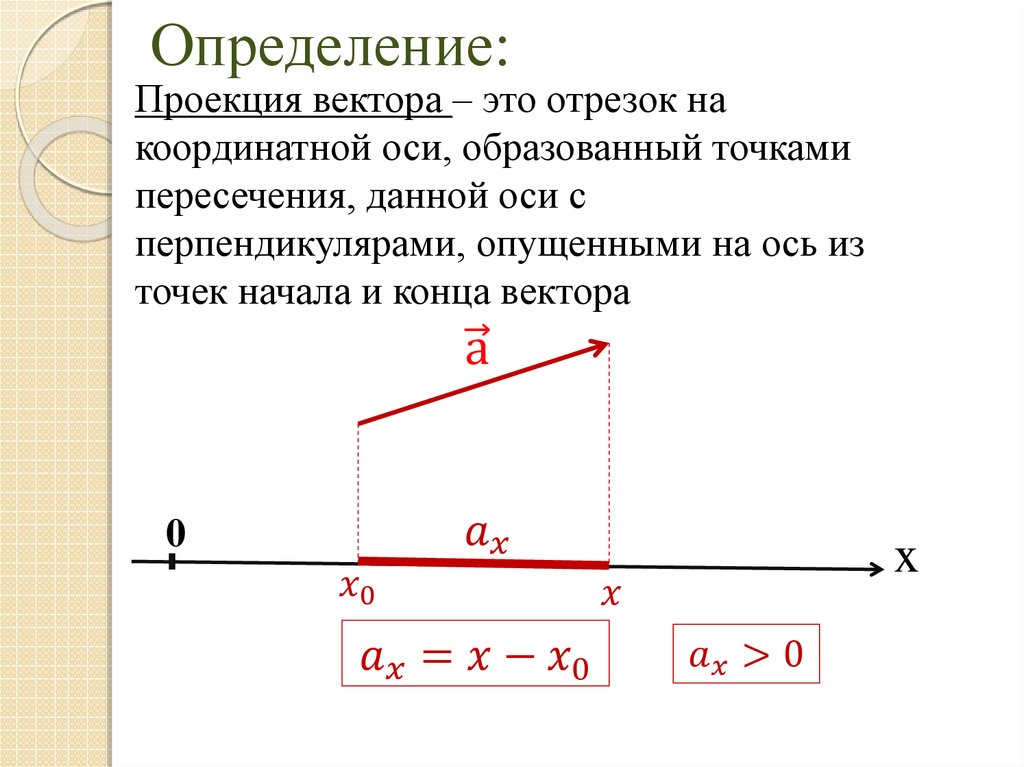

3) Вычтите эту проекцию из исходного вектора.

Теперь у вас есть проекция исходного вектора на плоскость. Для этого потребовалось только одно проекционное вычисление, одно перекрестное произведение и одно вычитание. Другой метод требует двух проекционных расчетов и добавления. Поскольку перекрестные произведения проще, чем проекции, этот метод проще. Заметим также, что этот метод даже не требует, чтобы два базисных вектора плоскости были ортогональны друг другу, а только то, что они линейно независимы.

$\endgroup$

Проекции: определения, описательные, векторные и типы

Существует два типа проекций, о которых вам необходимо знать на данном этапе: скалярные проекции и v векторные проекции .

Скалярная проекция просто дает длину в конкретном направлении . Результатом этого является скаляр, который количественно определяет эту сумму. С другой стороны, проекция вектора ‘‘ проецирует длину одного вектора в направлении другого. Один из способов думать об этом, как если бы «тень» вектора отбрасывалась поверх другого вектора.

Скалярная проекция

Начнем с самого простого для концептуального понимания. Скалярная проекция вектора определяет, насколько скалярная часть вектора находится в определенном направлении. Он находится с использованием скалярного произведения вектора с единичным вектором в рассматриваемом направлении.

Скалярная проекция вектора на единичный вектор – это скаляр, заданный скалярным произведением : или

Рис.

Решение

«Горизонтальное направление» лежит вдоль оси x, поэтому единичный вектор, который мы будем использовать, равен . Вектор в векторной записи равен .

Интуитивно вы, возможно, уже поняли, что скалярная проекция должна быть равна 3, поскольку по определению состоит из 3 единиц по горизонтали (и 4 по вертикали).

Мы можем показать это и с помощью скалярного произведения:

Следовательно, скалярная проекция в горизонтальном направлении равна 3,

Проекция вектора

Проекция вектора — это проекция одного вектора на другой. Он берет длину одного вектора и проецирует его в направлении другого, создавая новых вектора с направлением второго.

Рисунок 2 Рисунок 2

Рисунок 3 Если вы посмотрите на рисунок 3, вектор c является вектором в направлении оси x , поэтому b также является проекцией a в направлении вектора c.

В математической записи это записывается как . Мы знаем, что вектор должен быть равен , поэтому он таков, что ортогонален вектору c .

Эта ортогональность является важным свойством для нахождения проекции a на L. Помните «точечный продукт»? Так как он ортогонален линии L, то их скалярное произведение должно быть равно нулю . Используя эту информацию, мы можем вывести формулу векторной проекции a в направлении b .

Получение формулы вектора проекции

Чтобы полностью понять, что делает вектор проекции, может быть полезно посмотреть, как его получить. Сначала рассмотрим вектор v , лежащий на прямой L . Поскольку находится в направлении L, мы можем записать его как скаляр, кратный вектору v .

С помощью скалярного произведения:

Поскольку скалярное произведение вектора на самого себя равно квадрату длины этого вектора, мы получаем:

.

Итак, .

Проекция вектора вектора a на вектор v равна .

У нас есть вектор и вектор . Найдите проекцию x на v .

Используя формулу:

Следовательно, .

обозначен синей стрелкой на схеме ниже.

Рисунок 4

Проекции – основные выводы с единичным вектором

в рассматриваемом направлении

Формула скалярной проекции x на направление u равна

Векторная проекция проецирует длину одного вектора в направлении другого на L, ортогонален прямой L

Проекция вектора a на прямую L вектора v равна .

Часто задаваемые вопросы о проектах

Скалярная проекция дает скалярную длину в определенном направлении. С другой стороны, векторная проекция «проецирует» длину одного вектора в направлении другого.

Двумя примерами проекции являются скалярная проекция и векторная проекция.

Скалярная проекция дается скалярным произведением.

Как скалярная, так и векторная проекция выполняются с применением соответствующих формул.

Проекции в геометрии не подпадают под действие статьи. Тем не менее, они имеют сферическую, цилиндрическую, коническую и азимутальную проекции.

Итоговый опрос по прогнозам

Вопрос

Какие существуют два типа прогнозов?

Показать ответ

Ответ

Скалярная проекция и векторная проекция.

Показать вопрос

Вопрос

Какова формула векторной проекции?

Показать ответ

Ответ

Проекция вектора a на прямую L вектора v равна

Показать вопрос

Вопрос

Объясните проекцию вектора словами.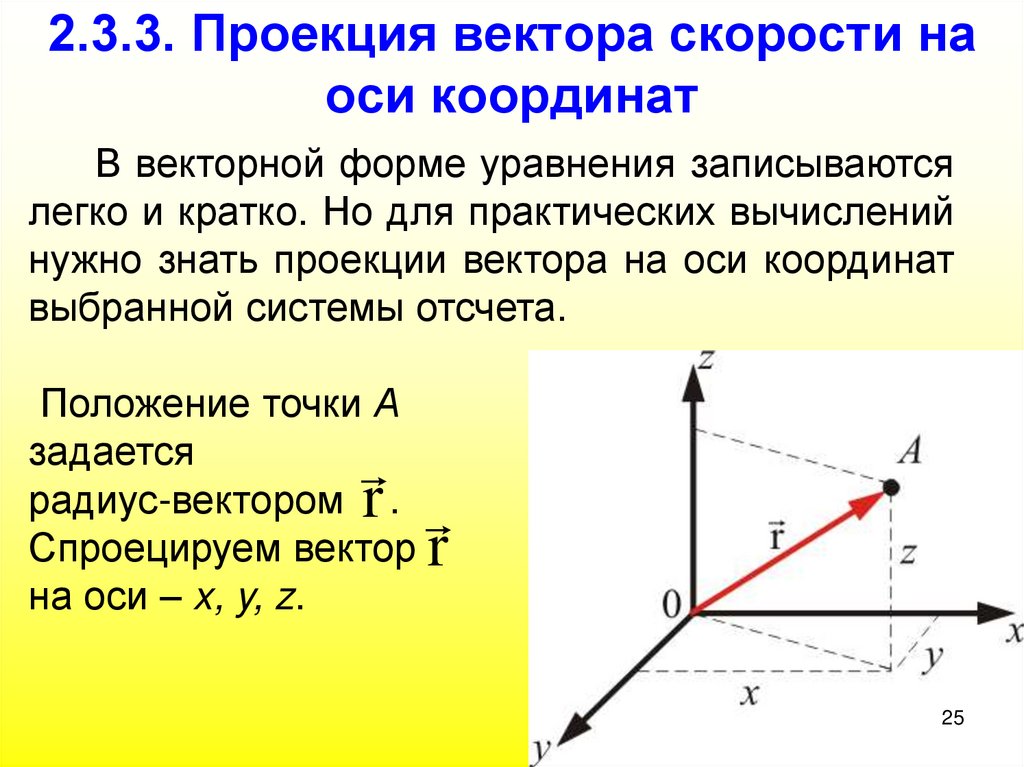

Показать ответ

Ответ

Проекция вектора «проецирует» длину одного вектора в направлении другого.

Показать вопрос

Вопрос

Объясните словами скалярную проекцию.

Показать ответ

Ответ

Скалярная проекция вектора показывает, насколько вектор направлен в определенном направлении.

Показать вопрос

Вопрос

(пересмотр) В чем разница между скаляром и вектором?

Показать ответ

Ответ

Скаляр — это величина, имеющая только величину (например, длину). Вектор имеет как величину 90 120, так и направление 90 121.

Показать вопрос

Вопрос

Предположим, мы хотим найти проекцию вектора a на L. Какое отношение имеет  к L?

Показать ответ

Ответ

ортогонален L.

Показать вопрос

Вопрос

(пересмотр) Какова формула скалярного произведения?

Показать ответ

Ответ

Показать вопрос

Вопрос

Определение ортогональности.

Показать ответ

Ответ

Если два вектора ортогональны, то они перпендикулярны друг другу (т. е. находятся под прямым углом).

Показать вопрос

Вопрос

Что такое скалярное произведение ортогональных векторов?

Показать ответ

Ответ

Показать вопрос

Вопрос

Что из следующего является формулой для проекции вектора a на линию L вектора v ?

Показать ответ

Ответ

Показать вопрос

Вопрос

Что такое вектор в терминах a и б ?

Показать ответ

Ответ

Показать вопрос

Вопрос

Чему равен вектор b через a и линию L?

Показать ответ

Ответ

Вектор b известен как ‘ проекция a на прямую L’, т.