Найти проекцию вектора на плоскость онлайн. Калькулятор онлайн.Вычисление проекции вектора на вектор
Пусть на плоскости задана прямая l и пересекающая ее прямая m . Проекцией вектора на прямую l параллельно прямой m (вдоль прямой m ) называется вектор (рис.1.13,а). Если прямая m перпендикулярна прямой l , то проекция называется ортогональной.
Пусть в пространстве дана прямая l и пересекающая ее плоскость \rho . Проекцией вектора \vec{a}=\overrightarrow{AB} на прямую l параллельно плоскости \rho (вдоль плоскости \rho ) называется вектор \vec{a}_l=\overrightarrow{AB}_l , началом которого служит проекция A_l , начала A , а концом — проекция B_l конца B вектора \overrightarrow{AB} (рис. 1.13,6). Если плоскость \rho перпендикулярна прямой l , то проекция называется ортогональной.
Проекция вектора на плоскость
Пусть в пространстве задана плоскость я и пересекающая ее прямая \rho
. Проекцией вектора \vec{a}=\overrightarrow{AB}
на плоскость \rho
параллельно прямой m
(вдоль прямой m
) называется вектор \vec{a}_{\rho}=\overrightarrow{AB}_{\rho}
, началом которого служит проекция A_{\rho}
начала A
, а концом — проекция B_{\rho}
конца B
вектора \overrightarrow{AB}
(рис.
Свойства проекций векторов
1. Проекции вектора на параллельные прямые (или на параллельные плоскости) равны.
2. Проекции равных векторов равны.
3. Проекция суммы векторов равна сумме их проекций.
4. Проекция произведения вектора на число равна произведению этого числа на проекцию вектора, другими словами, отношение коллинеарных векторов равно отношению их проекций (если оно определено).
5. Проекция линейной комбинации векторов равна линейной комбинации проекций.
Рассмотрим эти свойства для проекций векторов на прямую l параллельно прямой m . Для проекций векторов на плоскость или на прямую параллельно плоскости доказательства аналогичные.
Докажем первое свойство. Пусть \vec{a}_l
— проекция вектора \vec{a}
на прямую l
вдоль прямой m
, а \vec{a}_l
— проекция вектора \vec{a}
на прямую l»
вдоль той же прямой m
, причем прямые l
и l»
параллельные (рис.
Докажем второе свойство. Пусть на плоскости даны равные векторы \overrightarrow{AB} и \overrightarrow{CD} , не параллельные прямой m (см. рис. 1.16). Построим равные им векторы \mathop{\overrightarrow{A_lB»}= \overrightarrow{AB}}\limits_{.} и \mathop{\overrightarrow{C_lD»}= \overrightarrow{CD}}\limits_{.} . Из равенства \mathop{\overrightarrow{A_lB»}= \overrightarrow{C_lD»}}\limits_{.} следует, что четырехугольник A_lB»D»C_l — параллелограмм, а треугольники A_lB»B_l и C_lD»D_l равны по стороне и двум прилежащим углам
\big(A_lB»=C_lD»,\qquad \angle B»A_lB_l=\angle D»C_lD_l,\qquad \angle A_lB»B_l=\angle C_lD»D_l
как углы с соответственно параллельными сторонами). Следовательно, \mathop{\overrightarrow{A_lB_l}= \overrightarrow{C_lD_l}}\limits_{. }
, т.е. равные векторы, не параллельные прямой m
, имеют равные проекции. Если же векторы параллельны прямой m
, то их проекции также равны, как нулевые векторы. Второе свойство доказано.
}
, т.е. равные векторы, не параллельные прямой m
, имеют равные проекции. Если же векторы параллельны прямой m
, то их проекции также равны, как нулевые векторы. Второе свойство доказано.
Доказательство третьего свойства очевидно для векторов \overrightarrow{AB} и (рис. 1.17): проекция вектора \overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC} равна сумме проекций и \overrightarrow{B_lC_l} , векторов \overrightarrow{AB} и \overrightarrow{BC} , т.е. \overrightarrow{A_lC_l}= \overrightarrow{A_lB_l}+ \overrightarrow{B_lC_l} . Для произвольных векторов \vec{a} и \vec{b} (у которых конец вектора \vec{a} не совпадает с началом вектора \vec{b} ) доказательство сводится к рассмотренному случаю для равных им векторов \overrightarrow{AB}=\vec{a} и \overrightarrow{BC}=\vec{b} , так как равные векторы имеют равные проекции (по второму свойству).
Доказательство четвертого свойства следует из теоремы Фалеса (см. разд. В.2). На рис.1.18 изображены векторы \overrightarrow{AB}
и \overrightarrow{AC}=\lambda\overrightarrow{AB}
(\lambda>0)
, а также их проекции \overrightarrow{A_lB_l}
и \overrightarrow{A_lC_l}
. По теореме Фалеса \frac{AC}{AB}=\frac{A_lC_l}{A_lB_l}=\lambda
, следовательно, \overrightarrow{A_lC_l}= \lambda\overrightarrow{A_lB_l}
, что и требовалось доказать. В случае \lambda
По теореме Фалеса \frac{AC}{AB}=\frac{A_lC_l}{A_lB_l}=\lambda
, следовательно, \overrightarrow{A_lC_l}= \lambda\overrightarrow{A_lB_l}
, что и требовалось доказать. В случае \lambda
Пятое свойство проекций следует из третьего и четвертого.
Теорема 1.1 (о проекциях вектора на пересекающиеся прямые).
1. Если на плоскости заданы две пересекающиеся прямые l_1 и l_2 , то любой вектор \vec{a} на плоскости можно однозначно представить в виде суммы своих проекций \vec{a}_1 и \vec{a}_2 на эти прямые (проекции на каждую прямую берутся вдоль другой прямой), т.е. .
2. Если в пространстве заданы три прямые l_1,l_2 и l_3 , пересекающиеся в одной точке и не лежащие в одной плоскости, то любой вектор \vec{a} в пространстве можно однозначно представить в виде суммы своих проекций \vec{a}_1,\vec{a}_2,\vec{a}_3 на эти прямые (проекции на каждую прямую берутся вдоль плоскости, содержащей две другие прямые), т.е. .
В самом деле, пусть прямые l_1
и l_2
пересекаются в точке O
(рис. 1.19,а). Приложим вектор \vec{a}
к точке O
, т.е. рассмотрим вектор \overrightarrow{OA}=\vec{a}
. По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство \overrightarrow{OA}=\vec{a}_1+\vec{a}_2
, которое равносильно доказываемому равенству \vec{a}=\vec{a}_1+\vec{a}_2
, так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.
1.19,а). Приложим вектор \vec{a}
к точке O
, т.е. рассмотрим вектор \overrightarrow{OA}=\vec{a}
. По правилу параллелограмма сложения векторов (см. разд. 1.2) получаем равенство \overrightarrow{OA}=\vec{a}_1+\vec{a}_2
, которое равносильно доказываемому равенству \vec{a}=\vec{a}_1+\vec{a}_2
, так как равные векторы имеют равные проекции (см. свойство 2 проекций). Единственность представления следует из однозначности нахождения проекций вектора.
Если же вектор \vec{a} коллинеарен одной из прямых, например l_1 , то соответствующие проекции имеют вид: \vec{a}_1=\vec{a},~\vec{a}_2=\vec{o} и равенство \vec{a}=\vec{a}_1+\vec{a}_2=\vec{a}+\vec{o} , очевидно, выполняется.
Аналогично доказывается второе утверждение.
Замечание 1.3.
Справедливы утверждения, обратные к указанным в теореме 1.1.
Если вектор на плоскости равен сумме двух неколлинеарных векторов, т.е. \vec{a}=\vec{a}_1+\vec{a}_2
, то слагаемые \vec{a}_1
и \vec{a}_2
являются проекциями вектора \vec{a}
на прямые, содержащие векторы \vec{a}_1
и \vec{a}_2
соответственно.
Если вектор в пространстве равен сумме трех некомпланарных векторов, т.е. \vec{a}=\vec{a}_1+\vec{a}_2+\vec{a}_3 , то слагаемые \vec{a}_,\vec{a}_2 и \vec{a}_3 являются проекциями вектора \vec{a} на прямые, содержащие векторы \vec{a}_,\vec{a}_2,\vec{a}_3 соответственно.
В самом деле, отложим от произвольной точки O
векторы \overrightarrow{OA}=\vec{a},\,\overrightarrow{OA_1}=\vec{a}_1,\,\overrightarrow{OA_2}=\vec{a}_2,\,\overrightarrow{OA_3}=\vec{a}_3
(рис.1.19,6). Тогда из равенства \vec{a}=\vec{a}_1+\vec{a}_2+\vec{a}_3
следует, что \overrightarrow{OA}=\overrightarrow{OA_1}+\overrightarrow{OA_2}+\overrightarrow{OA_3}
, т.е. вектор — является диагональю параллелепипеда, построенного на векторах (отсюда следует правило параллелепипеда сложения трех некомпланарных векторов). Поэтому \overrightarrow{OA_1},\,\overrightarrow{OA_2},\,\overrightarrow{OA_3}
— проекции вектора \overrightarrow{OA}
на прямые l_1,\,l_2,\,l_3
(проекция на каждую прямую берется вдоль плоскости, проходящей через две другие прямые).
Пример 1.5. Если прямая пересекает стороны AB,~BC,~CA треугольника ABC (или их продолжения) в точках C_1,~B_1,~C_1 соответственно, то
\frac{\overrightarrow{AC_1}}{\overrightarrow{BC_1}}\cdot\frac{\overrightarrow{BA_1}}{\overrightarrow{CA_1}}\cdot\frac{\overrightarrow{CB_1}}{\overrightarrow{AB_1}}=1.
Решение. Найдем отношения проекций векторов на прямую AB вдоль прямой A_1C_1 (рис. 1.20). Для этого через точку B проведем прямую BB_2 , параллельную прямой A_1C_1 . По свойству 4 проекций имеем:
\frac{\overrightarrow{AC_1}}{\overrightarrow{BC_1}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{B_2B_1}};~~~~\frac{\overrightarrow{BA_1}}{\overrightarrow{CA_1}}=\frac{\overrightarrow{B_2B_1}}{\overrightarrow{CB_1}}.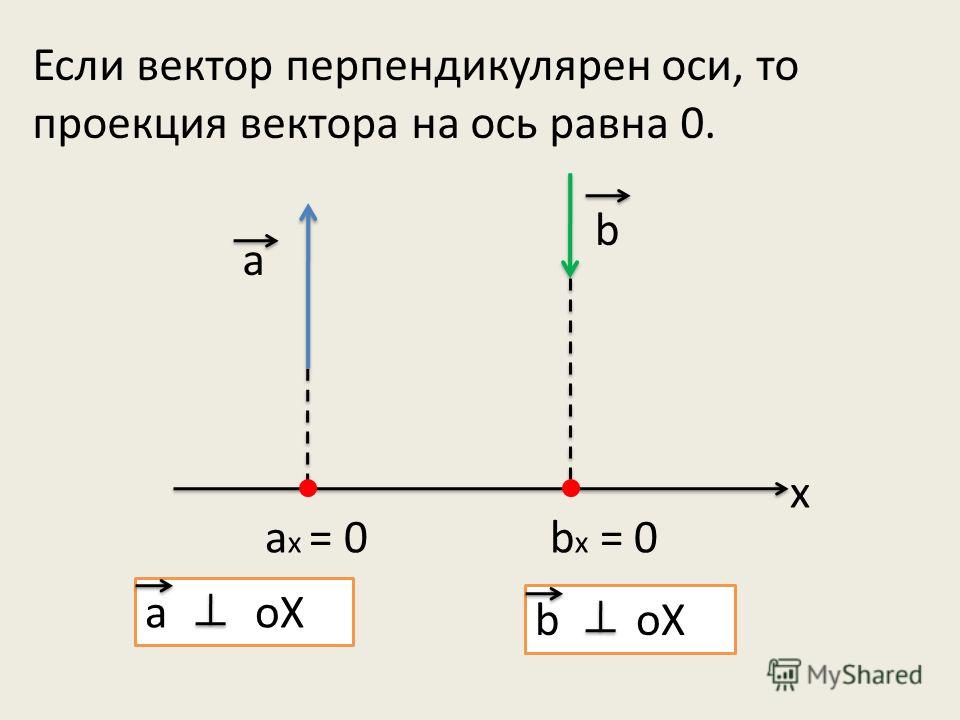
Перемножая эти пропорции, получаем \frac{\overrightarrow{AC_1}}{\overrightarrow{BC_1}}\cdot\frac{\overrightarrow{BA_1}}{\overrightarrow{CA_1}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}} , что равносильно доказываемому равенству.
Заметим, что доказанное утверждение является частью теоремы Менелая.
Пример 1.6. Если на сторонах AB,~BC,~CA треугольника ABC взяты соответственно точки A_1,~B_1,~C_1 так, что прямые AA_1,~BB_1,~CC_1 пересекаются в одной точке, то
\frac{\overrightarrow{AC_1}}{\overrightarrow{BC_1}}\cdot\frac{\overrightarrow{BA_1}}{\overrightarrow{CA_1}}\cdot\frac{\overrightarrow{CB_1}}{\overrightarrow{AB_1}}=-1.
Решение. Пусть прямые пересекаются в точке Q (рис.1.21). Через точку C_1 проведем прямые C_1B_2 и C_1A_2 параллельно BB_1 и AA_1 соответственно. По свойству проекций (свойство 4):
\frac{\overrightarrow{AB_1}}{\overrightarrow{B_2B_1}}=-\frac{\overrightarrow{AB}}{\overrightarrow{BC_1}};~~~\frac{\overrightarrow{BA_1}}{\overrightarrow{A_2A_1}}=\frac{\overrightarrow{AB}}{\overrightarrow{AC_1}};~~~\frac{\overrightarrow{CA_1}}{\overrightarrow{A_2A_1}}=\frac{\overrightarrow{CQ}}{\overrightarrow{C_1Q}}=\frac{\overrightarrow{CB_1}}{\overrightarrow{B_2B_1}}
Учитывая эти равенства и свойства отношений коллинеарных векторов (см, разд. 1.2.1), преобразуем левую и правую части последнего равенства:
1.2.1), преобразуем левую и правую части последнего равенства:
\begin{gathered}\frac{\overrightarrow{CQ}}{\overrightarrow{C_1Q}}=\frac{\overrightarrow{CA_1}}{\overrightarrow{A_2A_1}}=\frac{\overrightarrow{CA_1}}{\overrightarrow{BA_1}}\cdot\frac{\overrightarrow{BA_1}}{\overrightarrow{A_2A_1}}=\frac{\overrightarrow{CA_1}}{\overrightarrow{BA_1}}\cdot\frac{\overrightarrow{AB}}{\overrightarrow{AC_1}}\\\frac{\overrightarrow{C_1Q}}{\overrightarrow{CQ}}=\frac{\overrightarrow{B_2B_1}}{\overrightarrow{CB_1}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}}\cdot\frac{\overrightarrow{B_2B_1}}{\overrightarrow{AB_1}}=\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}}\cdot\left(-\frac{\overrightarrow{BC_1}}{\overrightarrow{AB}}\right)\end{gathered}
Запишем произведение правых частей этих равенств, учитывая, что произведение левых частей равно единице:
\frac{\overrightarrow{CA_1}}{\overrightarrow{BA_1}}\cdot\frac{\overrightarrow{AB}}{\overrightarrow{AC_1}}\cdot\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}}\cdot\left(-\frac{\overrightarrow{BC_1}}{\overrightarrow{AB}}\right)=-\frac{\overrightarrow{BC_1}}{\overrightarrow{AC_1}}\cdot\frac{\overrightarrow{CA_1}}{\overrightarrow{BA_1}}\cdot\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}}\cdot\frac{\overrightarrow{AB}}{\overrightarrow{AB}}=-\frac{\overrightarrow{BC_1}}{\overrightarrow{AC_1}}\cdot\frac{\overrightarrow{CA_1}}{\overrightarrow{BA_1}}\cdot\frac{\overrightarrow{AB_1}}{\overrightarrow{CB_1}}=1
Найдем обратное отношение \frac{\overrightarrow{AC_1}}{\overrightarrow{BC_1}}\cdot\frac{\overrightarrow{BA_1}}{\overrightarrow{CA_1}}\cdot\frac{\overrightarrow{CB_1}}{\overrightarrow{AB_1}}=-1
, что и требовалось доказать.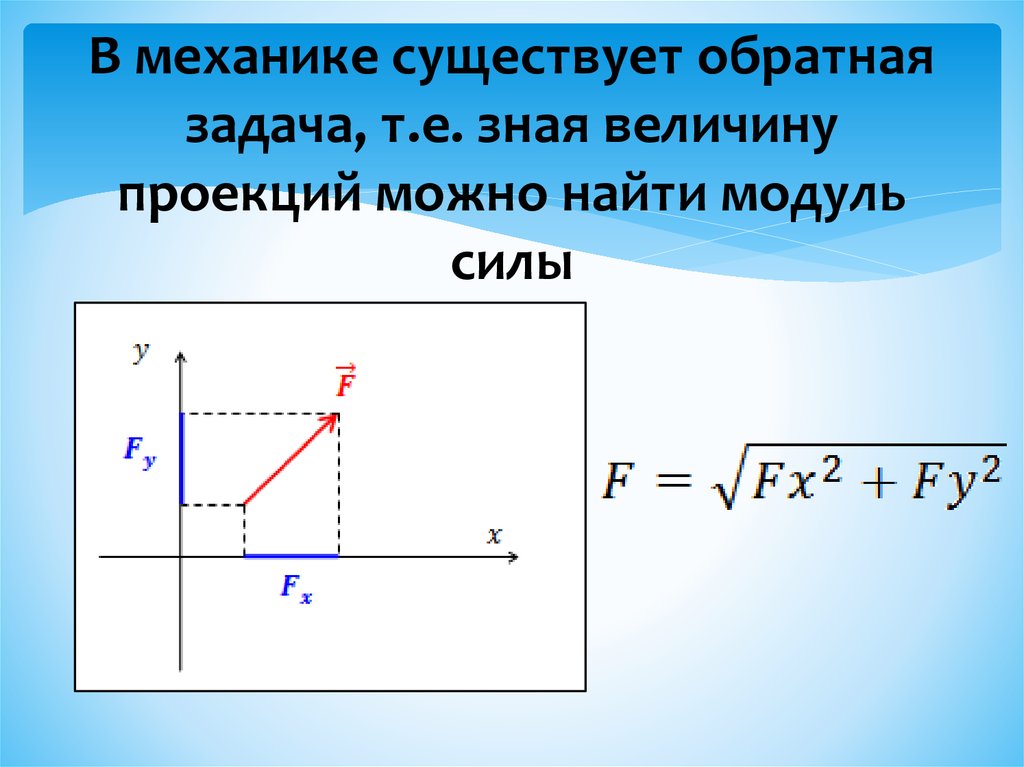
Заметим, что доказанное утверждение является частью теоремы Чевы.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX! Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b) или
Где a b — скалярное произведение векторов , |a| — модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Заданы :две координаты вектора
три координаты вектора
a: ; ;
b: ; ;
Классификация проекций вектора
Виды проекций по определению проекция вектора
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).

- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
| Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак. | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак. |
| Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак. | Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак. |
| Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB. | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB. |
| Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор). | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор). |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что .
Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.
Действительно, длина вектора равна 2, а направление противоположно направлению оси.
а на ось или какой-либо другой вектор существуют понятия ее геометрической проекции и числовой (или алгебраической) проекции. Результатом геометрической проекции будет вектор, а результатом алгебраической – неотрицательное действительное число. Но перед тем, как перейти к этим понятиям вспомним необходимую информацию.
Предварительные сведения
Основное понятие – непосредственно понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $\overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $\overline{a}\overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $\overline{a}↓\overline{d}$
Определение 6
Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|\overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Геометрическая проекция
Как мы уже сказали ранее, результатом геометрической проекции будет вектор.
Определение 8
Геометрической проекцией вектора $\overline{AB}$ на ось будем называть такой вектор, который получается следующим образом: Точка начала вектора $A$ проецируется на данную ось. Получаем точку $A»$ — начало искомого вектора. Точка конца вектора $B$ проецируется на данную ось. Получаем точку $B»$ — конец искомого вектора. Вектор $\overline{A»B»}$ и будет искомым вектором.
Рассмотрим задачу:
Пример 1
Постройте геометрическую проекцию $\overline{AB}$ на ось $l$, изображенные на рисунке 6.
Проведем из точки $A$ перпендикуляр к оси $l$, получим на ней точку $A»$. Далее проведем из точки $B$ перпендикуляр к оси $l$, получим на ней точку $B»$ (рис. 7).
7).
Проектирование различных линий и поверхностей на плоскость позволяет построить наглядное изображение предметов в виде чертежа. Будем рассматривать прямоугольное проектирование, при котором проектирующие лучи перпендикулярны плоскости проекции. ПРОЕКЦИЕЙ ВЕКТОРА НА ПЛОСКОСТЬ считают вектор = (рис. 3.22), заключенный между перпендикулярами, опущенными из его начала и конца.
Рис. 3.22. Векторная проекция вектора на плоскость.
Рис. 3.23. Векторная проекция вектора на ось.
В векторной алгебре часто приходится проектировать вектор на ОСЬ, то есть на прямую, имеющую определенную ориентацию. Такое проектирование выполняется легко, если вектор и ось L лежат в одной плоскости (рис. 3.23). Однако задача усложняется, когда это условие не выполнено. Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Построим проекцию вектора на ось, когда вектор и ось не лежат в одной плоскости (рис. 3.24).
Рис. 3.24. Проектирование вектора на ось
в общем случае.
Через концы вектора проводим плоскости, перпендикулярные прямой L. В пересечении с этой прямой данные плоскости определяют две точки А1 и B1 — вектор , который будем называть векторной проекцией данного вектора. Задача нахождения векторной проекции может быть решена проще, если вектор приведен в одну плоскость с осью, что возможно осуществить, так как в векторной алгебре рассматриваются свободные векторы.
Наряду с векторной проекцией, существует и СКАЛЯРНАЯ ПРОЕКЦИЯ, которая равна модулю векторной проекции, если векторная проекция совпадает с ориентацией оси L, и равна величине, ей противоположной, если векторная проекция и ось L имеют противоположную ориентацию. Скалярную проекцию будем обозначать:
Векторная и скалярная проекции не всегда терминологически разделяются строго на практике. Обычно пользуются термином «проекция вектора», подразумевая под этим скалярную проекцию вектора. При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
При решении же необходимо четко эти понятия различать. Следуя установившейся традиции, будем использовать термины «проекция вектора», подразумевая скалярную проекцию, и «векторная проекция» — в соответствии с установленным смыслом.
Докажем теорему, позволяющую вычислять скалярную проекцию заданного вектора.
ТЕОРЕМА 5. Проекция вектора на ось L равна произведению его модуля на косинус угла между вектором и осью, то есть
(3.5)
Рис. 3.25. Нахождение векторной и скалярной
Проекций вектора на ось L
( и ось L одинаково ориентированы).
ДОКАЗАТЕЛЬСТВО . Выполним предварительно построения, позволяющие найти угол G Между вектором и осью L. Для этого построим прямую MN, параллельную оси L и проходящую через точку О — начало вектора (рис. 3.25). Угол и будет искомым углом. Проведем через точки А и О две плоскости, перпендикулярные оси L. Получим:
Так как ось L и прямая MN параллельны.
Выделим два случая взаимного расположения вектора и оси L.
1. Пусть векторная проекция и ось L одинаково ориентированны (рис. 3.25). Тогда соответствующая скалярная проекция .
2. Пусть и L ориентированы в разные стороны (рис. 3.26).
Рис. 3.26. Нахождение векторной и скалярной проекций вектора на ось L ( и ось L ориентированы в противоположные стороны).
Таким образом, в обоих случаях справедливо утверждение теоремы.
ТЕОРЕМА 6. Если начало вектора приведено к некоторой точке оси L, и эта ось расположена в плоскости s, вектор образует с векторной проекцией на плоскость s угол , а с векторной проекцией на ось L — угол , кроме того сами векторные проекции образуют между собой угол , то
Как найти проекцию вектора — онлайн справочник для студентов
ФОРМУЛА
Чтобы найти проекцию вектора
\(\ \overline{a} \) на вектор \(\ \overline{b} \), необходимо разделить скалярное произведение этих векторов на длину (модуль) вектора \(\ \overline{b} \) , т.е.
\(\ \Pi_{\mathrm{p}_{\overline{b}} \overline{a}}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|} \)
Если векторы заданы на плоскости и имеют координаты \(\ \Pi_{\mathrm{p}_{\overline{b}} \overline{a}}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|} \) , то проекция вектора \(\ \overline{a} \) на вектор \(\ \overline{b} \) рассчитывается по формуле:
\(\ \Pi_{\mathrm{p}_{\overline{b}} \overline{a}}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|}=\frac{a_{x} \cdot b_{x}+a_{y} \cdot b_{y}}{\sqrt{b_{x}^{2}+b_{y}^{2}}} \)
Если векторы заданы в пространстве, то есть они имеют координаты \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \) ,то проекция вектора \(\ \overline{a} \text { на } \overline{b} \) вектор рассчитывается по формуле:
\(\ \Pi_{\mathrm{p}_{\overline{b}} \overline{a}}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|}=\frac{a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}}{\sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}} \)
ПРИМЕРЫ ПРОЕКЦИИ ВЕКТОРА НА ВЕКТОР
ПРИМЕР
\(\ \Pi p_{\overline{b}} \overline{a}=\frac{(\overline{a}, \overline{b})}{|b|}=\frac{a_{x} \cdot b_{x}+a_{y} \cdot b_{y}}{\sqrt{b_{x}^{2}+b_{y}^{2}}} \)
Подставляя в него координаты указанных векторов, получаем:
\(\ \Pi \mathrm{p}_{\overline{b}} \overline{a}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|}=\frac{-1 \cdot 3+0 \cdot(-4)}{\sqrt{3^{2}+(-4)^{2}}}=\frac{-3+0}{\sqrt{9+16}}=\frac{-3}{\sqrt{25}}=-\frac{3}{5} \)
ПРИМЕР
\(\ \Pi \mathrm{p}_{\overline{b}} \overline{a}=\frac{(\overline{a}, \overline{b})}{|\overline{b}|}=\frac{a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}}{\sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}} \)
мы получим:
\(\ \Pi p_{b} \overline{a}=\frac{(\overline{a}, b)}{|b|}=\frac{-2 \cdot(-2)+3(-1)+0 \cdot 5}{\sqrt{(-2)^{2}+(-1)^{2}+5^{2}}}=\frac{4-3+0}{\sqrt{4+1+25}}=\frac{1}{\sqrt{30}} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Как найти разность векторов Как найти сумму векторов Как найти вектор по точкам Периодические десятичные дроби
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Линейные операции.
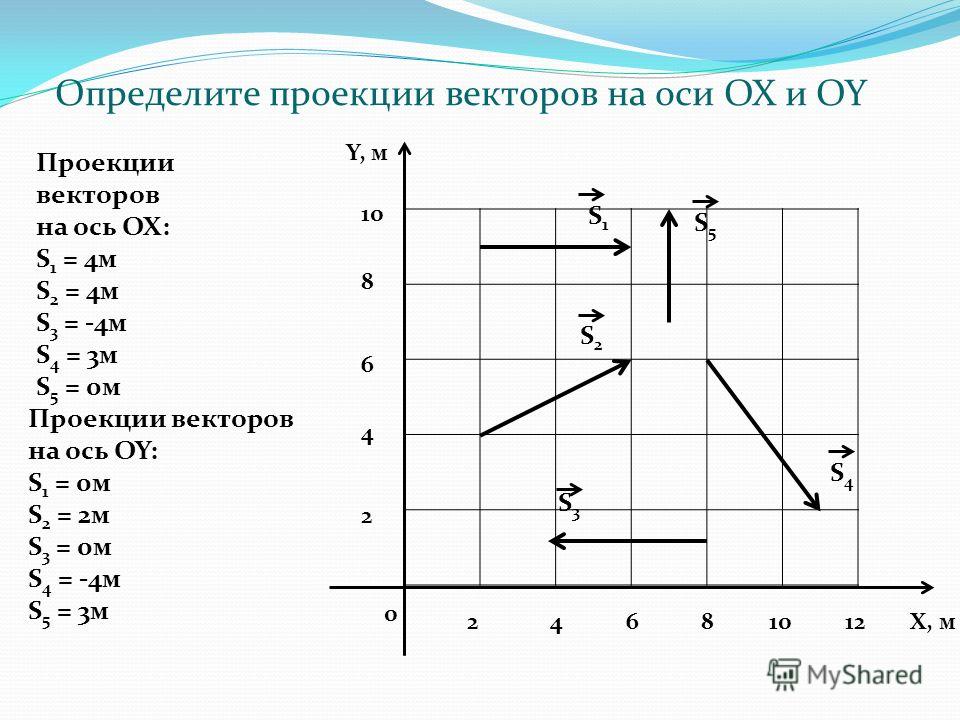 Проекция вектора на ось. Скалярное произведение векторов. Базис векторов. Тема 5
Проекция вектора на ось. Скалярное произведение векторов. Базис векторов. Тема 5Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема 1-6. Линейные операции. Проекция вектора на ось. Скалярное произведение векторов. Базис векторов. Векторное произведение
Раздел II. Векторная алгебраТема 1-6.
Линейные операции. Проекция
вектора на ось. Скалярное
произведение векторов. Базис
векторов. Векторное
произведение векторов.

Смешанное произведение
векторов
2. Основные определения векторной алгебры
• Вектором называется направленный отрезок.• Длиной a вектора a называется длина задающего
его направленного отрезка.
• Нулевым вектором называется вектор нулевой
длины.
• Единичным вектором называется вектор длины 1.
• Векторы называются равными, если равны их длины
и они одинаково направлены.
• Векторы называются коллинеарными, если они лежат
на параллельных прямых.
• Векторы называются компланарными, если они
параллельны одной плоскости (лежат в одной
плоскости).
3. Линейные операции
1) Сложение: (первые три правила для векторов компланарных,т.е. лежащих в одной плоскости)
4. Линейные операции
2) Вычитание:3) Умножение на число:
5. Свойства линейных операций
6. Проекция вектора на ось
7. Свойства проекций:
8. Скалярное произведение векторов
Если скалярное произведение векторов равно нулю, то вектора называютортогональными.

9. Скалярное произведение в координатах Применение скалярного произведения
10. Базис векторов
11. Чаще всего пользуются прямоугольным базисом
14. Векторное произведение векторов
17. Смешанное произведение векторов
19. РЕШЕНИЕ ЗАДАЧ
Примеры вычисления длины вектораПример. Найти длину вектора a = {2; 4; 4}.
Решение: |a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Определение равенства векторов
Пример. При каком значении параметра n вектора a = {1; 2; 4} и b = {1; 2; 2n}
равны.
Решение:
Проверим равенство компонентов векторов
ax = bx = 1
ay = by = 2
az = bz => 4 = 2n => n = 4/2 = 2
Ответ: при n = 2 вектора a и b равны.
Пример умножения вектора на число
Пример . Найти произведение вектора a = {1; 2} на 3.
Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.
Примеры на сложение (вычитание ) векторов
Пример 1. Найти сумму векторов a = {1; 2} и b = {4; 8}.
Решение: a + b = {1 + 4; 2 + 8} = {5; 10}
Примеры вычисления проекции вектора
Пример.
 Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.
Найти проекцию вектора a = {1; 4; 0} на вектор b = {4; 2; 4}.Решение:
Найдем скалярное произведение этих векторов
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12
Найдем модуль вектора b
|b| = √42 + 22 + 42 = √14 + 4 + 16 = √36 = 6
Найдем проекцию вектора a на вектор b
Примеры вычисления скалярного произведения векторов
Пример . Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.
Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример . Найти скалярное произведение векторов a и b, если их длины
|a| = 3, |b| = 6, а угол между векторами равен 60˚.
Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Вычисление угла между векторами
Пример. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.
Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
Примеры задач с направляющими косинусами вектора
Пример.
 Найти направляющие косинусы вектора a = {3; 4}.
Найти направляющие косинусы вектора a = {3; 4}.Решение:
Найдем модуль вектора a:
|a| = √32 + 42 = √9 + 16 = √25 = 5.
Найдем направляющие косинусы вектора a:
22. Определение линейной зависимости
Пример. Проверить будут ли вектора a = {1; 1; 1}, b = {1; 2; 0}, c = {0; -1; 1} линейнонезависимыми.
Данное решение показывает, что система имеет множество решений, то есть
существует не нулевая комбинация значений чисел x1, x2, x3 таких, что линейная
комбинация векторов a, b, c равна нулевому вектору, например: -a + b + c = 0, а
это значит вектора a, b, c линейно зависимы.
Коллинеарность векторов
Пример. найти значение параметра n при котором вектора a = {3; 2} и b =
{9; n} коллинеарны.
Пример. Какие из векторов a = {1; 2; 3}, b = {4; 8; 12}, c = {5; 10; 12}
коллинеарны?
Ортогональность векторов
Пример . Проверить являются ли вектора a = {3; -1} и b = {7; 5}
ортогональными.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16
Ответ: так как скалярное произведение не равно нулю, то вектора a и b не
ортогональны.
Пример . Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1}
будут ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 4
2n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Вычисление координат
Пример. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).
Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты
точки A(3; -4; 3).
Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8
ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Вычисление векторного произведения
Пример. Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Смешанное произведение векторов
Пример. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1;
1}, c = {1; 2; 1}.
Компланарность векторов
Пример. Проверить компланарны ли три вектора a = {1; 2; 3}, b = {1; 1;
1}, c = {1; 2; 1}.
27. Базис векторов
English Русский Правила
Скалярный продукт — Math Insight
Скалярный продукт — Math InsightСкалярное произведение
Скалярное произведение двух векторов основано на проекции одного вектора на другой. Предположим, у нас есть два вектора $\vc{a}$ и $\vc{b}$, и мы хотим подсчитайте, какая часть $\vc{a}$ указывает в том же направлении, что и вектор $\vc{b}$. Нам нужна величина, которая была бы положительной, если бы два вектора в одинаковых направлениях, нуль, если они перпендикулярны, и отрицательный если два вектора указывают почти в противоположных направлениях. Мы определим скалярное произведение между векторами, чтобы получить эти величины.
Но сначала обратите внимание на вопрос «сколько $\vc{a}$ указывает в том же направлении, что и вектор $\vc{b}$»
не имеет ничего общего с величиной (или длиной) $\vc{b}$;
оно основано только на его направлении. (Напомним, что вектор имеет величину и направление.)
Ответ на этот вопрос не должен зависеть от величины $\vc{b}$, а только от ее направления.
Чтобы избежать путаницы, вызванной величиной $\vc{b}$, давайте масштабируем вектор так, чтобы его длина равнялась единице.
Другими словами, давайте заменим $\vc{b}$ единичным вектором, указывающим в том же направлении, что и $\vc{b}$.
Мы назовем этот вектор $\vc{u}$, который определяется формулой
$$\vc{u} = \frac{\vc{b}}{\|\vc{b}\|}.$$
(Напомним, что вектор имеет величину и направление.)
Ответ на этот вопрос не должен зависеть от величины $\vc{b}$, а только от ее направления.
Чтобы избежать путаницы, вызванной величиной $\vc{b}$, давайте масштабируем вектор так, чтобы его длина равнялась единице.
Другими словами, давайте заменим $\vc{b}$ единичным вектором, указывающим в том же направлении, что и $\vc{b}$.
Мы назовем этот вектор $\vc{u}$, который определяется формулой
$$\vc{u} = \frac{\vc{b}}{\|\vc{b}\|}.$$
Скалярное произведение $\vc{a}$ с единичным вектором $\vc{u}$, обозначаемое
$\vc{a} \cdot \vc{u}$, определяется как проекция $\vc{a}$ в
направление $\vc{u}$ или количество, на которое указывает $\vc{a}$
в том же направлении, что и единичный вектор $\vc{u}$.
Предположим на мгновение, что $\vc{a}$ и $\vc{u}$ указывают на
подобные направления.
Затем вы можете представить $\vc{a} \cdot \vc{u}$ как длину тени
$\vc{a}$ на $\vc{u}$, если их хвосты были вместе и
солнце светило с направления, перпендикулярного $\vc{u}$. Образовав прямоугольный треугольник с $\vc{a}$ и этой тенью, вы
может использовать геометрию, чтобы вычислить это
\begin{gather}\vc{a} \cdot \vc{u} = \|\vc{a}\| \cos\тета,
\label{dot_product_unit}
\конец{собрать}
где $\theta$ — угол между $\vc{a}$ и $\vc{u}$.
Образовав прямоугольный треугольник с $\vc{a}$ и этой тенью, вы
может использовать геометрию, чтобы вычислить это
\begin{gather}\vc{a} \cdot \vc{u} = \|\vc{a}\| \cos\тета,
\label{dot_product_unit}
\конец{собрать}
где $\theta$ — угол между $\vc{a}$ и $\vc{u}$.
Если бы $\vc{a}$ и $\vc{u}$ были перпендикулярны, тени не было бы. Это соответствует случаю, когда $\cos\theta = \cos\pi/2=0$ и $\vc{a} \cdot \vc{u}=0$. Если бы угол $\theta$ между $\vc{a}$ и $\vc{u}$ был больше, чем $\pi/2$, тогда тень не попала бы в $\vc{u}$. Так как в этом случае $\cos\theta
Но нам нужно вернуться к скалярному произведению $\vc{a}\cdot \vc{b}$, где
$\vc{b}$ может иметь величину, отличную от единицы.
Это скалярное произведение $\vc{a}\cdot \vc{b}$ должно зависеть от величины обоих
векторы, $\|\vc{a}\|$ и $\|\vc{b}\|$,
и быть симметричным относительно этих векторов.
Следовательно, мы не хотим определять $\vc{a}\cdot \vc{b}$ точно
проекция $\vc{a}$ на $\vc{b}$;
мы хотим, чтобы он сводился к этой проекции для случая, когда $\vc{b}$ является единичным вектором. Мы можем сделать это очень легко: просто подставьте определение $\vc{u}=\frac{\vc{b}}{\|\vc{b}\|}$ в определение скалярного произведения уравнения \eqref{dot_product_unit }.
Это приводит к определению, что скалярное произведение $\vc{a} \cdot \vc{b}$,
деленная на величину $\|\vc{b}\|$ $\vc{b}$, является проекцией $\vc{a}$ на $\vc{b}$.
$$\frac{\vc{a}\cdot \vc{b}}{\|\vc{b}\|} = \|\vc{a}\| \cos\тета.$$
Затем, если мы умножим на сквозное на $\|\vc{b}\|$, мы получим хороший
симметричное определение скалярного произведения $\vc{a} \cdot \vc{b}$.
\начать{собирать}
\vc{a}\cdot \vc{b} = \|\vc{a}\| \|\vc{b}\|\cos\тета.
\метка{dot_product_definition}\тег{2}
\конец{собрать}
Мы можем сделать это очень легко: просто подставьте определение $\vc{u}=\frac{\vc{b}}{\|\vc{b}\|}$ в определение скалярного произведения уравнения \eqref{dot_product_unit }.
Это приводит к определению, что скалярное произведение $\vc{a} \cdot \vc{b}$,
деленная на величину $\|\vc{b}\|$ $\vc{b}$, является проекцией $\vc{a}$ на $\vc{b}$.
$$\frac{\vc{a}\cdot \vc{b}}{\|\vc{b}\|} = \|\vc{a}\| \cos\тета.$$
Затем, если мы умножим на сквозное на $\|\vc{b}\|$, мы получим хороший
симметричное определение скалярного произведения $\vc{a} \cdot \vc{b}$.
\начать{собирать}
\vc{a}\cdot \vc{b} = \|\vc{a}\| \|\vc{b}\|\cos\тета.
\метка{dot_product_definition}\тег{2}
\конец{собрать}
Рисунок геометрической интерпретации $\vc{a} \cdot \vc{b}$ почти идентична приведенной выше картинке для $\vc{a} \cdot \vc{u}$. Нам просто нужно помнить, что мы должны делить на $\|\vc{b}\|$ чтобы получить проекцию $\vc{a}$ на $\vc{b}$.
В следующем интерактивном апплете вы можете изучить этот
геометрическую интерпретацию скалярного произведения и проследить, как оно зависит
от векторов и угла между ними. (Сообщаемый номер не должен
зависит от длины $\|\vc{b}\|$, так как мы разделили на эту величину.)
(Сообщаемый номер не должен
зависит от длины $\|\vc{b}\|$, так как мы разделили на эту величину.)
Скалярное произведение как проекция. Скалярное произведение векторов $\vc{a}$ (синий) и $\vc{b}$ (зеленый) при делении на величину $\vc{b}$ является проекцией $ \vc{a}$ на $\vc{b}$. Эта проекция показана отрезком красной линии от хвоста $\vc{b}$ до проекции головы $\vc{a}$ на $\vc{b}$. Вы можете изменить векторы $\vc{a}$ и $\vc{b}$, перетащив точки на их концах или перетащив сами векторы. Обратите внимание, что скалярное произведение положительно для острых углов и отрицательно для тупых. Сообщаемое число не зависит от $\|\vc{b}\|$ только потому, что мы разделили на эту величину.
Дополнительная информация об апплете.
Геометрическое определение уравнения \eqref{dot_product_definition} проясняет свойства скалярного произведения.
Из формулы сразу видно, что скалярное произведение $\vc{a}\cdot\vc{b}$ положительно для острых углов и отрицательно для тупых.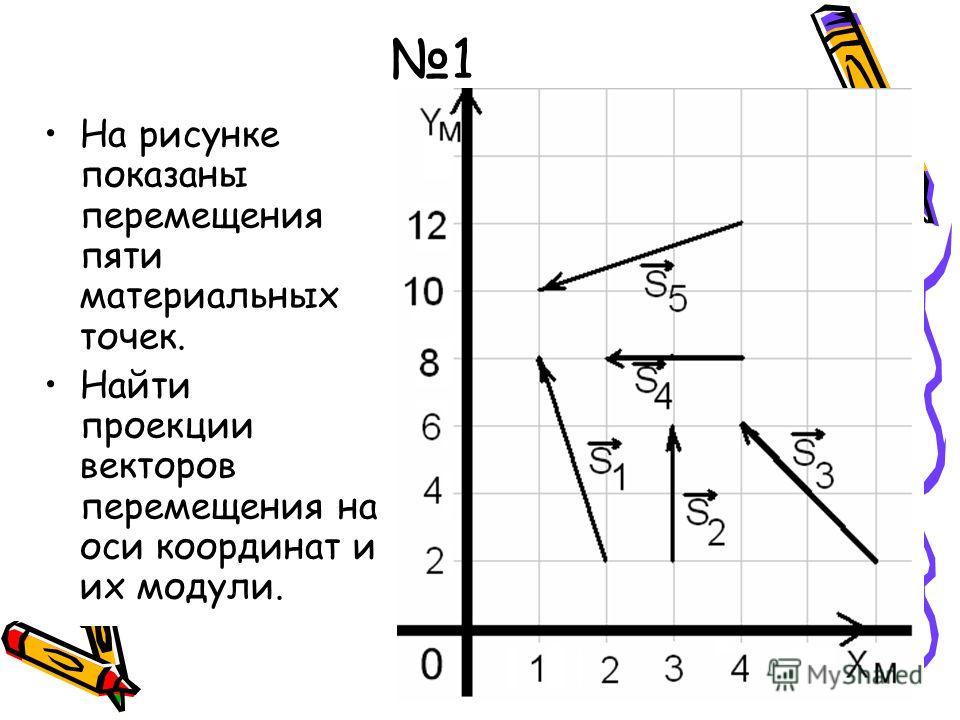 Формула показывает, что скалярное произведение растет линейно с длиной обоих векторов и является коммутативным, т. е. $\vc{a} \cdot \vc{b} = \vc{b} \cdot \vc{a}$.
Формула показывает, что скалярное произведение растет линейно с длиной обоих векторов и является коммутативным, т. е. $\vc{a} \cdot \vc{b} = \vc{b} \cdot \vc{a}$.
Однако геометрическая формула \eqref{dot_product_definition} неудобна для вычисления скалярного произведения, когда нам заданы векторы $\vc{a}$ и $\vc{b}$ через их компоненты. Для облегчения таких вычислений мы выводим формулу скалярного произведения через компоненты вектора. Имея на руках такую формулу, мы можем пробежаться по примерам вычисления скалярного произведения.
Навигация по нитям
Векторная алгебра
Математика 2374
Похожие страницы
V5 Проекция векторов | Учебная лаборатория
Открыть изображение
В разделе Разрешение векторов мы узнали, как разрешать векторы в двух измерениях по горизонтальной и вертикальной осям. Также возможно разрешить один вектор вдоль линии другого вектора (вместо осей x-y).
(см. также линейные графики)
Узнайте, как найти проекцию (разрешение) одного вектора в направлении второго вектора.
Существует два типа векторной проекции:
Скалярная проекция
Векторная проекция
Для скалярной проекции мы вычисляем длину (скалярную величину) вектора в определенном направлении.
Для векторной проекции мы вычисляем векторную составляющую вектора в заданном направлении.
Часто на курсах физики, инженерии и математики вас просят разложить вектор на две составляющие вектора, перпендикулярные друг другу. Например, на диаграмме ниже вектор \(\vec{a}\) является проекцией \(\overrightarrow{F}\) в горизонтальном направлении, а \(\vec{b}\) является проекцией \(\overrightarrow{F}\) в вертикальном направлении.
Вы можете проецировать вектор в любом направлении, не только по горизонтали и вертикали.
В этом модуле обсуждаются как скалярные, так и векторные проекции.
Скалярная проекция
Рассмотрим следующую диаграмму:
Пусть \(\overrightarrow{PQ}=\vec{a}\) и \(\overrightarrow{PS}=\vec{b}. {2}}\\
& =\sqrt{4+9+1}\\
& =\sqrt{14}
\end{выравнивание*}\]
{2}}\\
& =\sqrt{4+9+1}\\
& =\sqrt{14}
\end{выравнивание*}\]
\[\begin{выравнивание*} \cos\left(\theta\right) & =\frac{\text{смежный}}{\text{гипотенуза}}\\ & =\frac{\left|\overrightarrow{PR}\right|}{\left|\vec{a}\right|}. \end{align*}\] Перестановка дает, \[\begin{align*} \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\cos\left(\theta\right). & \влево(1\вправо) \end{align*}\] Это можно записать в терминах скалярного произведения.22 Скалярное произведение (или скалярное произведение) двух векторов \[\begin{align*} \vec{a} & =a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\\ \vec{b} & =b_{1}\vec{i}+b_{2}\vec{j}+b_{3}\vec{k} \end{align*}\] определяется как \[\begin{align*} \vec{a}\cdot\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\cos\left(\theta\right) \end{align*}\] Альтернативное определение: \[\begin{align*} \vec{a}\cdot\vec{b} & =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}. \end{выравнивание*}\]
Мы знаем \[\begin{align*}
\vec{a}\cdot\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\cos\left(\theta\right)
\end{align*}\] и так \[\begin{align*}
\cos\left(\theta\right) & =\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right |}. \end{align*}\]
\end{align*}\]
Подстановка этого выражения для \(\cos\left(\theta\right)\) в уравнение\(\left(1\right)\) выше дает:
\[\begin {выровнять*} \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\cos\left(\theta\right)\\ \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\cdot\left|\vec{b }\справа|}\\ & =\frac{\vec{a}\cdot b}{\left|\vec{b}\right|}\\ & =\vec{a}\cdot\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\vec{a}\cdot\шляпа{b} \end{выравнивание*}\]
где \(\hat{b}=\frac{\vec{b}}{\left|\vec{b}\right|}\) — единичный вектор в направлении \(\vec{b} \).33 Единичный вектор для вектора \(\vec{b}\) обозначается \(\hat{b}\) и представляет собой вектор \(\vec{b}\), деленный на его длину \( \влево|\vec{b}\вправо|\). Это \[\begin{align*} \шляпа{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}. \end{align*}\] Единичный вектор — это вектор длины один в направлении исходного вектора.
Скалярная проекция вектора \(\vec{a}\) в направлении вектора \(\vec{b}\) определяется как: 9{2}}\\ & =\sqrt{25+4+4}\\ & =\sqrt{33} \end{alignat*}\]
поэтому \[\begin{alignat*}{1} \шляпа{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\frac{(5,-2,2)}{\sqrt{33}}\\ & =\frac{1}{\sqrt{33}}(5,-2,2) \end{alignat*}\]
, поэтому скалярная проекция \(\vec{a}\) в направлении \(\vec{b}\):
\[\begin{alignat*}{ 1} \vec{a}\cdot\hat{b} & =(2,3,1)\cdot\frac{(5,-2,2)}{\sqrt{33}}\\ & =\frac{\left(2\times5\right)+\left(3\times\left(-2\right)\right)+\left(1\times2\right)}{\sqrt{33}} \\ & =\frac{10-6+2}{\sqrt{33}}\\ & =\frac{6}{\sqrt{33}}.
\end{выравнивание*}\]
Векторная проекция
Векторная проекция вектора \(\vec{a}\) в направлении вектора \(\vec{b}\) — это вектор в направлении \(\vec{b}\ ) с величиной, равной длине прямой линии \(PR\) или \(\left|\overrightarrow{PR}\right|\), как показано ниже.
Следовательно, векторная проекция \(\vec{a}\) в направлении \(\vec{b}\) есть скалярная проекция, умноженная на единичный вектор в направлении \(\vec{b }\).
9009{2}}\\ & =\frac{\left(2\times5+3\times\left(-2\right)+1\times2\right)\left(5,-2,2\right)}{33}\\ & =\frac{\left(10-6+2\right)\left(5,-2,2\right)}{33}\\ & = \ гидроразрыва {\ влево (6 \ вправо) \ влево (5, -2,2 \ вправо)} {33} \end{alignat*}\]Векторная проекция \(\vec{a}\) в направлении \(\vec{b}\) равна
\[\begin{alignat*}{1} \frac{6\left(5,-2,2\right)}{33} & =\frac{6}{33}\left(5,-2,2\right)\\ & =\frac{2}{11}\left(5\hat{i}-2\hat{j}+2\hat{k}\right). \end{выравнивание*}\]
Пример 2
Если \(\vec{a}=(1,-2,2)\) и \(\vec{b}=(5,-2,2)\) найти:
\( (a)\) Скалярная проекция \(\vec{a}\) в направлении \(\vec{b}\).
\((b)\) Векторная проекция \(\vec{a}\) в направлении \(\vec{b}\).
Решение:
\((a)\) Скалярная проекция \(\vec{a}\) в направлении \(\vec{b}\) равна \(\vec{a}\cdot\ шляпа{б}\).
Если \[\begin{alignat*}{1} \vec{b} & =(5,-2,2) \end{alignat*}\]
, затем \[\begin{alignat*}{1} \влево|\vec{b}\вправо| & =\sqrt{33} \end{выравнивание*}\]
и \[\begin{alignat*}{1} \шляпа{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\frac{\left(5,-2,2\right)}{\sqrt{33}}\\ & =\frac{1}{\sqrt{33}}\left(5,-2,2\right). \end{alignat*}\]
Поэтому \[\begin{alignat*}{1} \vec{a}\cdot\hat{b} & =\left(1,-2,2\right)\cdot\frac{\left(5,-2,2\right)}{\sqrt{33} }\\ & =\ frac{\left(\left(1\times5\right)+\left(\left(-2\right)\times\left(-2\right)\right)+\left(2\times2\ вправо)\вправо)}{\sqrt{33}}\\ & = \ гидроразрыва {\ влево (5 + 4 + 4 \ вправо)} {\ sqrt {33}} \\ & =\frac{13}{\sqrt{33}}. \end{alignat*}\] Скалярная проекция равна \(13/\sqrt{33}.\)
\((b)\) Векторная проекция \(\vec{a}\) в направлении \(\vec{b}\) равна \(\left(\vec{a}\cdot\hat {b}\right)\hat{b}\)
из части \((a)\) \[\begin{alignat*}{1} \vec{a}\cdot\hat{b} & =\frac{13}{\sqrt{33}} \end{alignat*}\]
, так что векторная проекция \(\vec{a}\) в направлении \(\vec{b}\) равна \[\begin{alignat*}{1} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & =\left(\frac{13}{\sqrt{33}}\right)\frac{(5,- 2,2)}{\sqrt{33}}\\ & =\frac{13(5,-2,2)}{33}\\ & =\frac{13}{33}(5,-2,2)\\ & =\frac{13}{33}\left(5\шляпа{i}-2\шляпа{j}+2\шляпа{k}\право) \end{alignat*}\] Векторная проекция \(\frac{13}{33}(5,-2,2)\) или \(\frac{13}{33}\left(5\hat{ i}-2\шляпа{j}+2\шляпа{k}\право)\)
Упражнение 1
Для \(\vec{a}=\left(2,3,1\right)\) , \(\vec{b}=\left(5,0,3\right)\) , \(\vec{c}=\left(0,0,3\right)\) и \(\vec{d}=\left(-2,2,-1\right)\) найти:
9{\circ}=0\) и см. уравнение (1) выше.
Скалярная проекция \(\vec{a}\) в направлении \(\vec{b}\).

Ответ: \(\frac{13}{34}\)Векторная проекция \(\vec{a}\) в направлении \(\vec{b}\).
Ответ: \(\frac{13}{34}\left(5,0,3\right)\)Скалярная проекция \(\vec{c}\) в направлении \(\vec{b}\).
Ответ: \(\frac{9}{\sqrt{34}}\)Векторная проекция \(\vec{c}\) в направлении \(\vec{a}\).
Ответ: \(\frac{3}{14}\left(2,3,1\right)\)Векторная проекция \(\vec{d}\) в направлении \(\vec{a}\).
Ответ: \(\frac{1}{14}\left(2,3,1\right)\)Векторная проекция \(\vec{b}\) в направлении \(\vec{d}\).
Ответ: \(\frac{-13}{9}\left(-2,2,-1\right)\)Скачать эту страницу: Проекция векторов V5 (PDF 150 КБ)
Что дальше… V6 Векторное уравнение прямой
Математика — Проекции прямых на плоскости
Мы хотим найти компонент прямой A, который проецируется на плоскость B и составляющая прямой А, проецируемая на нормаль плоскости.
Здесь мы рассмотрели проекции линий на линии.
Ориентация плоскости определяется вектором нормали B, как описано здесь.
Для этого мы будем использовать следующие обозначения:
- A || B = компонент линии A, который проецируется на плоскость B, в других слова вектор в точку на плоскости, где, если взять нормаль в этом точку, он перехватит конец вектора A.
- A B = компонент линии A проецируется на нормаль плоскости B.
Мы также будем использовать:
- |A| = скалярная величина вектора A.
- θ = угол между вектором А и нормаль к плоскости В
- = единичный вектор в направлении из А
Итак: = А / |А|
Соотношение между этими величинами
Если сложить параллельную и перпендикулярную составляющие, то получим исходную вектор, который дает нам следующее уравнение:
A = A || B + A B
Таким образом, если у нас есть перпендикулярная составляющая, мы можем вычислить параллельную составляющую.
и наоборот.
Расчет проекции на плоскость
Из приведенной выше диаграммы скалярная величина проекции на плоскость |А| sin(θ) и его направление равно вдоль плоскости (перпендикулярной нормали B).
Чтобы найти нужное направление, сначала возьмем взаимно перпендикулярный вектор к A и B, это дается перекрестным произведением A x B (которое находится за пределами страницы на приведенной выше схеме). Теперь возьмем вектор, взаимно перпендикулярный это и вектор B, это дает нам направление, которое мы хотим.
Итак, направление:
B × (A × B)
или: (B × A) × B
Нам нужно нормализовать это, поэтому единичный вектор в требуемом направлении:
x
Из приведенной выше диаграммы величина проекции на плоскость равна:
|A| sin(θ)
Таким образом, проекция на плоскость:
A || В = |А| sin(θ) ×
Но с этой страницы мы знаем что: × = грех (θ) так:
А || В = |А| Икс х
но = А / |А| а также = В / |В|
так:
А || B = B × (A×B / |B|) / |B
Расчет перпендикулярной составляющей
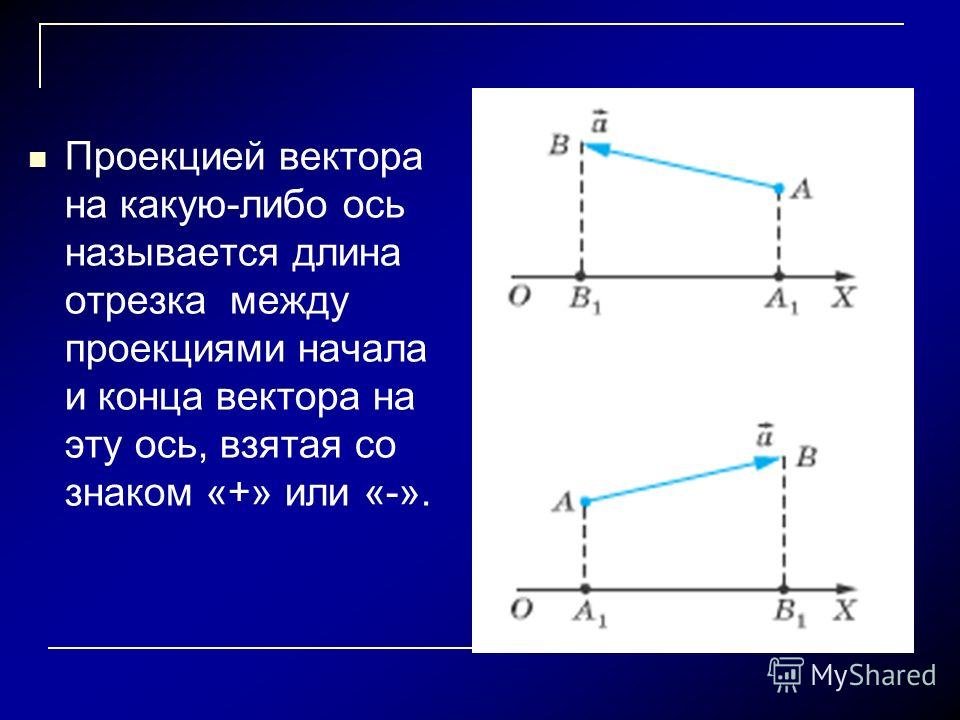
|Из диаграммы выше скалярная величина перпендикулярной составляющей |А| cos(θ) и его направление равно в направлении вектора B.
Итак, если мы умножим |A| потому что (θ) единичным вектором вдоль B, то есть B/|B|
Итак, нам нужен вектор:
A B = |A| потому что (θ) * В/|В|
Мы можем использовать скалярное произведение векторов, чтобы вычислить это, из этого страницы мы знаем, что:
AB = |A| |Б| cos(θ)
Следовательно, объединение этих уравнений дает:
A B = AB * B/|B| 2
Альтернатива с использованием Клиффорда или геометрической алгебры
Информацию о Клиффорде/геометрической алгебре см. здесь. В геометрической алгебре представлены бивекторами.
В этом случае:
- A является вектором
- B — бивектор (представляющий плоскость)
Внешнее произведение
Эквивалент векторного произведения в геометрической алгебре, но не ограничено умножением векторов на векторы, оно увеличивается до степени операнда следующим образом:
- скаляр вектор = вектор
- вектор вектор = бивектор
- бивектор вектор = три вектора
Внутренний продукт
Это эквивалент скалярного произведения в геометрической алгебре, но не ограничивается умножением векторов на векторы, он уменьшается до степени операнда следующим образом:
- вектор вектор = скаляр
- бивектор вектор = вектор
- трехвектор вектор = бивектор
Таким образом, внутренние и внешние продукты симметричны следующим образом:
Для проекции линии на линию у нас было:
- А || В = АВ / В
- А В = (А Б) / Б
В этом случае мы можем использовать точно такие же уравнения, но B теперь представлен по бивектору.
Альтернатива с использованием матричного представления
(Моя исходная работа находится на этой странице до того, как Ксавьер указал на несоответствия)
Начиная с уравнений векторной алгебры, полученных выше, мы имеем:
параллельный компонент = A || B = B × (A × B) / |B|²
перпендикулярная компонента =A B = AB * B / |B|²
Чтобы преобразовать эти уравнения из векторных в матричные, мы можем использовать следующие матричные эквиваленты перекрестное и точечное произведение:
Чтобы заменить перекрестное произведение, мы можем использовать кососимметричную матрицу, как описано на этой странице:
Б×А = [~B][A] =
0 -Бз По Бз 0 -Бх -По Бх 0
Топор Ай Аз Чтобы заменить скалярное произведение, результат должен быть скалярным (или матрицей 1×1, которую мы можем получить, умножив на транспонирование B или просто умножив на скалярный множитель: (Ax * Bx + Ay * By + Az * Bz)
BA =
Бх По Бз
Топор Ай Аз перпендикулярная составляющая
Итак, давайте вычислим полные условия для перпендикулярной составляющей:
A B = AB * B / |B|² =
Бх * (Ах * Бх + Ау * Ви + Аз * Бз)
/(Bx² + By² + Bz²)По * (Ax * Bx + Ay * By + Az * Bz)
/(Bx² + By² + Bz²)Бз * (Ах * Бх + Ау * Бы + Аз * Бз)
/(Bx² + By² + Bz²)Предполагая, что B нормализовано (Bx² + By² + Bz²=1), и разделение A и B дает:
A B =
Bx² Бх*По Бх*Бз По*Вх К² По*Бз Бз*Бх Бз*По Бз²
Топор Ай Аз параллельный компонент
Мы можем вычислить параллельный компонент в терминах матриц:
А || B = B × (A × B) / |B|²
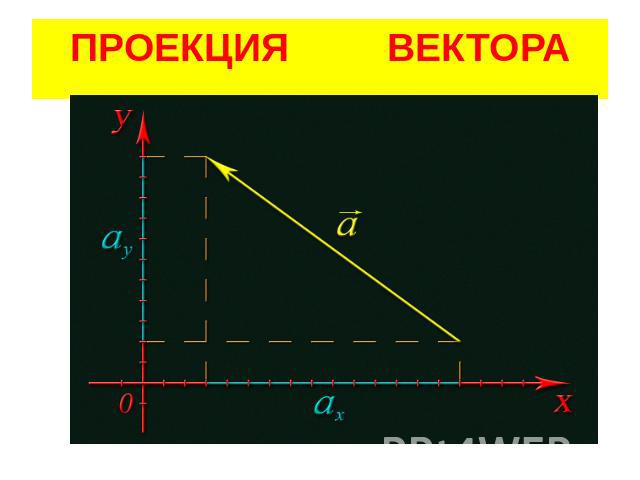
Перекрестное произведение антикоммутирует, т.
е. изменение порядка операндов на противоположное меняет знак, поэтому мы получаем:
A || B = — B × (B × A) / |B|²
Преобразование этого уравнения в матричное уравнение с использованием кососимметричной матрицы, как описано выше, дает:
A || B = — [~B][~B][A] / |B|²
Вычеркивание терминов:
A || В = —
0 -Бз По Бз 0 -Бх -По Бх 0
0 -Бз По Бз 0 -Бх -По Бх 0
Топор Ай Аз /(Bx² + By² + Bz²) Предполагая, что B нормализовано (Bx² + By² + Bz²=1), и умножение двух членов косой матрицы дает:
A || В = —
-Bz² — By² Бх*По Бх*Бз По*Вх -Bz² — Bx² По*Бз Бз*Бх Бз*По -Bx² — By²
Топор Ай Аз Ввод ведущего члена ‘-‘ в матрицу дает:
A || В =
Бз² + Бай² -Bx*By -Бх*Бз -By*Bx Bz² + Bx² -By*Bz -Бз*Бх -Бз*По Бх² + Вх²
Топор Ай Аз , снова используя (Bx² + By² + Bz²=1) по ведущей диагонали:
A || В =
1 — Bx² -Bx*By -Бх*Бз -By*Bx 1 — По² -By*Bz -Бз*Бх -Бз*По 1 — Бз²
Топор Ай Аз проверка результата
Мы можем проверить приведенные выше результаты, потому что перпендикулярная и параллельная компоненты должны складываться, чтобы получить исходный вектор A, другими словами:
А = А || B + A B
Подстановка значений матрицы:
A || Б + А Б
1 — Bx² + Bx² -Bx*By + Bx*By -Бх*Бз+Бх*Бз -By*Bx+By*Bx 1 — By² + By² -By*Bz+By*Bz -Bz*Bx + Bz*Bx -Bz*By+Bz*By 1 — Бз²+ Бз²
Топор Ай Аз Сокращение равных и противоположных значений дает:
A || Б + А Б
1 0 0 0 1 0 0 0 1
Топор Ай Аз Следовательно, часть B сводится к единичной матрице [I], и у нас остается вектор A, который нам и нужен.

 \end{выравнивание*}\]
\end{выравнивание*}\]

 и наоборот.
и наоборот. Итак, если мы умножим |A| потому что (θ)
единичным вектором вдоль B, то есть B/|B|
Итак, если мы умножим |A| потому что (θ)
единичным вектором вдоль B, то есть B/|B|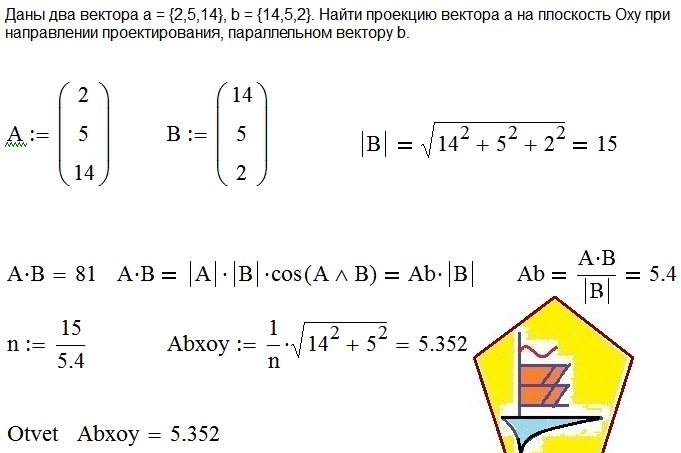
 е. изменение порядка операндов на противоположное меняет знак, поэтому мы получаем:
е. изменение порядка операндов на противоположное меняет знак, поэтому мы получаем: