Сложение и вычитание матриц.
Навигация по странице:
- Сложение матриц
- Вычитание матриц
- Свойства сложения и вычитания матриц
- Примеры сложения и вычитания матриц
Онлайн калькулятор. Сложение и вычитание матриц.
Складывать и вычитать можно матрицы одного размера в результате получается матрица того же размера.
Определение.
Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:
сij = aij + bij
Определение.
Вычитание матриц (разность матриц) A — B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц
сij = aij — bij
Свойства сложения и вычитания матриц
- Ассоциативность: (A + B) + C = A + (B + C)
- A + Θ = Θ + A = A, где Θ — нулевая матрица
- A — A = Θ
- Коммутативность: A + B = B + A
Примеры задач на сложение и вычитание матриц
Пример 1.
| Найти сумму матриц A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 |
Решение:
| A + B = | 4 | 2 | + | 3 | 1 | = | 4 + 3 | 2 + 1 | = | 7 | 3 | ||||||||
| 9 | 0 | -3 | 4 | 9 + (-3) | 0 + 4 | 6 | 4 |
Пример 2
| Найти разность матриц A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 |
Решение:
| A — B = | 4 | 2 | — | 3 | 1 | = | 4 — 3 | 2 — 1 | = | 1 | 1 | ||||||||
| 9 | 0 | -3 | 4 | 9 — (-3) | 0 — 4 | 12 | -4 |
Пример 3
| Найти значение матрицы С = 2A + 3B, если A = | 4 | 2 | и B = | 3 | 1 | . | ||||
| 9 | 0 | -3 | 4 | |||||||
| 4 | -6 | 9 | 1 |
Решение:
| C = 2A + 3B = 2 | 4 | 2 | + 3 | 3 | 1 | = | 2·4 + 3·3 | 2·2 + 3·1 | = | 17 | 7 | ||||||||
| 9 | 0 | -3 | 4 | 2·9 + 3·(-3) | 2·0 + 3·4 | 9 | 12 | ||||||||||||
| 4 | -6 | 9 | 1 | 2·4 + 3·9 | 2·(-6) + 3·1 | 35 | -9 |
Онлайн калькуляторы с матрицами.
Упражнения с матрицами.
Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Сложение и вычитание матриц
Сложение и вычитание матриц определяется как и для массивов, то есть поэлементно. Эти операции требуют чтобы обе матрицы имели одинаковую размерность, или одна из них была скаляром (в последнем случае MATLAB прибавляет (или вычитывает) данный скаляр из всех элементов матрицы). Если размерности матриц не совпадают, в командное окно выдается со-общение об ошибке (красным цветом)
Error using ==> +
Matrix dimensions must agree.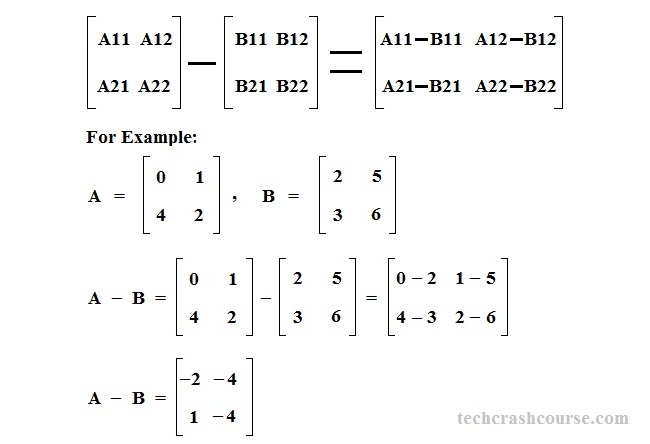
Векторное произведение и транспонирование матриц
Вектор-строка и вектор-столбец могут быть перемножены в любом порядке (оператор умно-жения * расположен на верхнем регистре клавиши с цифрой 8). Результатом будет или ска-ляр ( внутреннее произведение) или матрица (внешнее произведение). Для приведенных выше векторов v и u имеем :
x = v*u
x =
2
X = u*v
X =
6 0 -3
2 0 -1
8 0 -4
Для действительных
матриц, операция транспонирования меняет взаимное местоположение
элементов aij aji, симметричных
относительно главной диагонали.
X = B’
X =
8 3 4
1 5 9
6 7 2
Транспонирование превращает вектор-строку в вектор-столбец и наоборот. Если x и y оба яв-ляются действительными векторами, то произведение x*y не определено, но оба произве-дения x’*y и y’*x дают один и тот же скаляр. Это соотношение используется так часто, что имеет три различных имени: скалярное произведение, внутреннее произведение и точечное произведение.
Для комплексного вектора или матрицы, z, величина z’ обозначет комплексно-сопряженное транспонирование. В MATLAB-е предусмотрены
также поэлементные операции над
элеме-нтами массивов. Признаком
поэлементных операций служит точка после обозначения пере-менной. Так,
транспонирование элементов матрицы z как массива чисел обозначается z.’,
по аналогии с другими операциями на
массивами чисел. Например, если
В MATLAB-е предусмотрены
также поэлементные операции над
элеме-нтами массивов. Признаком
поэлементных операций служит точка после обозначения пере-менной. Так,
транспонирование элементов матрицы z как массива чисел обозначается z.’,
по аналогии с другими операциями на
массивами чисел. Например, если
z = [1+2i 3+4i]
то
z‘ =
1-2i
3-4i
тогда как z.’ есть
z.’ =
1+2i
Для комплексных
векторов, два скалярных произведения x’*y и y’*x комплексно сопряжены, а
скалярное произведение x’*x комплексного
вектора с самим собой есть действительное
число.
Произведение матриц
Для произведения двух совместимых А и В матриц в MATLAB–е достаточно записать в ко-мандной строке С = А*В . MATLAB самостоятельно проверит совместимость размерностей матриц и выдаст результат. Если матрицы несовместимы, выдается сообщение об ошибке:
Error using ==> *
Inner matrix dimensions must agree. Индексирование (Subscripts)
Для краткого рассмотрения некоторых основных понятий, связанных с индексированием дву-мерных массивов (матриц), введем «волшебную» матрицу 4-го порядка:
F = magic(4)
F =16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Элемент в i-ой строке и j-ом столбце матрицы F обозначается через F (i,j).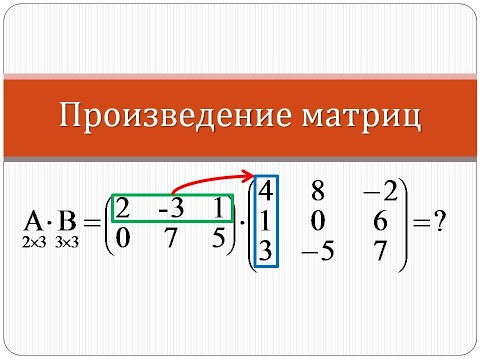 Например, F (4,2) есть число в четвертой
строке и втором столбце. Для нашего
волшебного квадрата, F(4,2) есть 14.
Таким образом, можно вычислить сумму
элементов четвертого столбца матрицы F, напечатав
Например, F (4,2) есть число в четвертой
строке и втором столбце. Для нашего
волшебного квадрата, F(4,2) есть 14.
Таким образом, можно вычислить сумму
элементов четвертого столбца матрицы F, напечатав
F (1,4) + F (2,4) + F (3,4) + F (4,4)
Это дает ответ
ans =
34
но, как мы увидим в дальнейшем, не является самым элегантным способом суммирования элементов одного столбца.
Имеется также
возможность обращения к элементам
матрицы при помощи одного индекса, F(k).
Это обычный способ обращения к элементам
векторов (строк или столбцов). Но в
MATLAB-е такой способ индексирования можно
применить и к двумерным (в общем случае
– многомерным) матрицам, так как система
MATLAB хранит все многомерные массивы
чи-сел в виде одного длинного
вектора-столбца, сформированного из
столбцов исходной матри-цы. Так, для
нашего волшебного квадрата, F (8) есть
другой способ обращения к начени 14
хранящемуся в F (4,2).
Так, для
нашего волшебного квадрата, F (8) есть
другой способ обращения к начени 14
хранящемуся в F (4,2).
Если вы попытаетесь использовать элемент, находящийся вне размеров матрицы, это приве-дет к сообщению об ошибке
t = F (4,5)
Сложение и вычитание матриц. — КиберПедия
Сложение и вычитание матриц.
Суммой A+B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij+bij для всех i=1,mи j=1,n.
Аналогичное определение вводят и для разности матриц:
Разностью A−B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij−bij для всех i=1,m и j=1,n.
Умножение матрицы на число.
Произведением матрицы Am×n=(aij) на число α называется матрица Bm×n=(bij), где bij=α⋅aijдля всех i=1,m¯¯¯¯¯¯¯¯ и j=1,n¯¯¯¯¯¯¯.
Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.
Произведение двух матриц.
Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.
Произведением матрицы Am×n=(aij) на матрицу Bn×k=(bij) называется матрица Cm×k=(cij), для которой каждый элемент cij равен сумме произведений соответствующих элементов i-й строки матрицы Aна элементы j-го столбца матрицы B:
Вопрос 2. Определители квадратных матриц. Свойства определителей.
Определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.
I. Определитель матрицы первого порядка
Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а11:
.
II. Определитель матрицы второго порядка
Определитель матрицы второго порядка
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
.
Например, пусть
.
III. Определитель матрицы третьего порядка
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Пример. Вычислить определитель третьего порядка:
Решение.
Определитель матрица, которого более высокого порядка лучше всего находить через приведение к треугольному виду матрицы.
Вопрос 3. Обратная матрица. Элементарные преобразования.
Для применения этого метода в одну матрицу записывают заданную матрицу A и единичную матрицу E, т.е. составляют матрицу вида (A|E) (эту матрицу называют также расширенной).
К элементарным преобразованиям в данной ситуации относят такие действия:
1. Смена мест двух строк.
2. Умножение всех элементов строки на некоторое число, не равное нулю.
3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на любой множитель.
Пример
Найти матрицу A−1, если
Решение
В этом примере будет найдена обратная матрица методом Гаусса. Расширенная матрица, имеющая в общем случае вид (A|E), в данном примере примет такую форму:
Расширенная матрица, имеющая в общем случае вид (A|E), в данном примере примет такую форму:
Вопрос 6. Метод Гаусса.
На первом этапе нужно записать расширенную матрицу системы:
. По какому принципу записаны коэффициенты, думаю, всем видно.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: .
Вернемся к нашей системе . Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Ответ:
Пример
Задание. Проверить, являются ли функции и эквивалентными бесконечно малыми при .
Решение. Проверим вначале, что данные функции являютсябесконечно малыми функциями в точке :
Найдем предел отношения этих функций:
Ответ. Заданные функции и являются эквивалентными бесконечно малыми.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
.
Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x)и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Так как b + cесть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то
.
Пример. .
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) иg(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .
Следствие 1. Постоянный множитель можно выносить за знак предела:
.
Следствие 2. Предел степени равен степени предела:
.
Пример. .
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.
.
Доказательство. Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное
Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное
.
Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c2≠0.
Примеры.
- .
- .
- Рассмотрим . При x→1 числитель дроби стремится к 1, а знаменатель стремится к 0. Но так как , т.е. есть бесконечно малая функция при x→1, то .
Теорема 4. Пусть даны три функции f(x), u(x) иv(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞), то и функция f(x)стремится к тому же пределу, т.е. если
, то .
Смысл этой теоремы понятен из рисунка.
Теорема 5. Если при x→a (или x→∞) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b, то этот предел не может быть отрицательным: b≥0.
Доказательство. Доказательство проведем методом от противного. Предположим, что b<0, тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a. Но тогда y не стремится к пределу b при x→a, что противоречит условию теоремы.
Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента xудовлетворяют неравенству f(x)≥ g(x) и имеют пределы , то имеет место неравенство b≥c.
Доказательство. По условию теоремы f(x)-g(x) ≥0, следовательно, по теореме 5 , или .
Пример
Задание. Исследовать на непрерывность функцию
Решение. Функция определена в любой точке из . Найдем приращение заданной функции произвольной точке :
Тогда
А тогда делаем вывод, что функция является непрерывной.
Ответ. Функция является непрерывной.
Правила дифференцирования.
Если у функций f(x) и g(x) существуют производные, то
Производная сложной функции:
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
Уравнение касательной к графику функции y=f(x) в точке x0 :
Пример
Задание. Найти наибольшее и наименьшее значение функции на отрезке .
Решение. Находим производную функции:
Находим точки, в которых производная равна нулю:
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку . Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
Таким образом,
Ответ.
Пример
Задание. Найти интервалы выпуклости/вогнутости функции
Найти интервалы выпуклости/вогнутости функции
Решение. Найдем вторую производную заданной функции:
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение :
Исследуем знак второй производной слева и справа от полученной точки:
Так как на промежутке вторая производная , то на этом промежутке функция выпукла; в силу того, что на промежутке вторая производная — функция вогнута. Так как при переходе через точку вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
Ответ. Точка — точка перегиба графика функции.
На промежутке функция выпукла, на промежутке функция вогнута.
Определение
Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .
Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Определение
Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Определение
Прямая называется наклонной асимптотой графика функции , если
Замечание
(условиях существования наклонной асимптоты)
Если для функции существуют пределы и , то функция имеет наклонную асимптоту при .
Замечание
Горизонтальная асимптота является частным случаем наклонной при .
Замечание
Если при нахождении горизонтальной асимптоты получается, что , то функция может иметь наклонную асимптоту.
Замечание
Кривая может пересекать свою асимптоту, причем неоднократно.
Задание. Найти асимптоты графика функции
Решение. Область определения функции:
а) вертикальные асимптоты: прямая — вертикальная асимптота, так как
б) горизонтальные асимптоты: находим предел функции на бесконечности:
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты :
Таким образом, наклонная асимптота: .
Ответ. Вертикальная асимптота — прямая .
Наклонная асимптота — прямая .
Замечание
Схема представлена как примерная. Пункты исследования можно опускать, если они дают банальную информацию, или переставлять, если обнаруживаются интересные особенности поведения графика.
Замечание
Для уточнения графика можно найти некоторые дополнительные точки, но иногда удается обойтись и без них.
Замечание
Рекомендуется строить график одновременно с исследованием функции, нанося на координатную плоскость информацию по завершении каждого пункта исследования.
Задание. Исследовать функцию и построить ее график.
Решение. 1) Область определения функции.
2) Четность, нечетность.
Функция общего вида.
3) Точки пересечения с осями.
а) с осью :
то есть точки
б) с осью : в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые и — вертикальные асимптоты.
б) горизонтальные асимптоты:
то есть прямая — горизонтальная асимптота.
в) наклонные асимптоты :
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
Найдем точки, в которых первая производная равна нулю или не существует: для любого из области определения функции; не существует при и .
Таким образом, функция убывает на всей области существования.Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.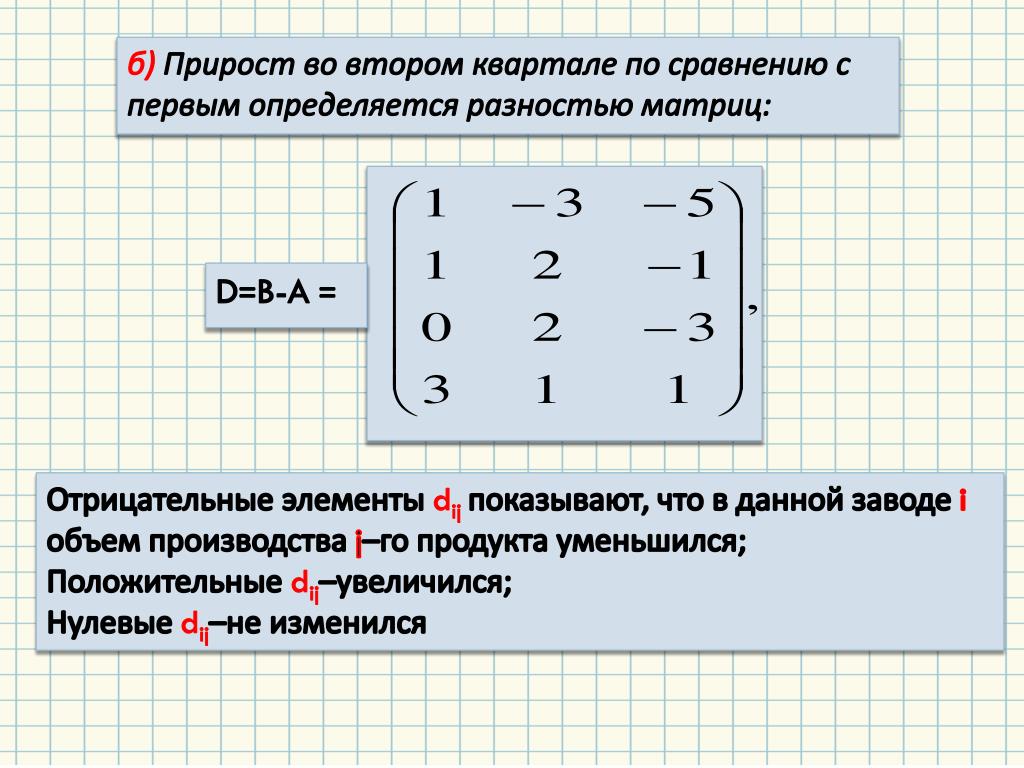
Найдем точки, в которых вторая производная равна нулю или не существует: ; при и вторая производная не существует.
Таким образом, на промежутках и функция вогнута, а на промежутках и — выпукла. Так как при переходе через точку вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
Пример
Функция является первообразной для функции , так как
Совокупность всех первообразных функции , определенных на заданном промежутке, называется неопределенным интегралом от функции и обозначается символом . То есть
Знак называется интегралом, — подынтегральным выражением, — подынтегральной функцией, а — переменной интегрирования.
Пример
2. Производная от неопределенного интеграла равна подынтегральной функции
Пример
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
Пример
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
Пример
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
Пример
6. Если , то и , где функция — произвольная функция с непрерывной производной.
Пример
Известно, что , а тогда
Основные формулы
Замечание
После нахождения интеграла по новой переменной необходимо вернуться к первоначальной переменной .
Замечание
В некоторых случаях целесообразно делать подстановку , тогда
Пример
Задание. Найти интеграл
Найти интеграл
Решение. Сделаем замену переменной: , далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.
Ответ.
Замечание
В некоторых случаях формулу интегрирования частями нужно применять неоднократно.
Формулу интегрирования по частям целесообразно применять к интегралам следующего вида:
1) ; ;
Здесь — многочлен степени , — некоторая константа. В данном случае в качестве функции берется многочлен, а в качестве — оставшиеся сомножители. Для интегралов такого типа формула интегрирования по частям применяется раз.
Примеры решения интегралов данным методом
Пример
Задание. Найти интеграл
Решение. В исходном интеграле выделим функции и , затем выполним интегрирование по частям.
Ответ.
Вопрос 28. Основные понятия теории вероятностей.
Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание.
Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: {выпало 66} и {выпало не 66}, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).
Испытанием называется эксперимент с очерченным набором возможных взаимоисключающих результатов. Эти результаты называются исходами.
Эти результаты называются исходами.
Случайное событие — это подмножество множества исходов испытания.
Любое случайное событие может состоять из одного или нескольких исходов испытания (тогда это событие возможно) или не содержать ни одного исхода (невозможное событие). Например, «выпало больше 77» — невозможное событие для испытания «бросание кубика». Отдельно определяют достоверное событие, то есть такое, которое включает в себя все исходы данного испытания.
Исходы, входящие в событие, называются благоприятными для этого события.
Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.
Свойства м(х)
1. Математическое ожидание постоянной величины равно самой постоянной, т. е. М(С) = С, С = const.
е. М(С) = С, С = const.
С имеет одно значение, равноеС,с вероятностьюp = 1,М(С)=С .1 = С.
Определим произведение постоянной СнаХкак дискретную случайную величину , возможные значения которой равны произведениямСна возможные значенияХ. Вероятность равна вероятностямХ. Например, если имеет вероятность , то имеет также вероятность .
2. М(СХ) = С . М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величинаX задана законом распределения:
Тогда имеет закон распределения:
Случайные величины XиYназываютнезависимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая.
Произведение – случайная величинаXY, возможные значения которой равны произведениям каждого возможного значенияХна каждое возможное значениеY. ВероятностиXY равны произведению соответствующих вероятностейXиY.
ВероятностиXY равны произведению соответствующих вероятностейXиY.
3. , гдеX,Y– независимые дискретные случайные величины.
Пусть законы распределения вероятностей этих величин:
Составим значения, которые могут принимать Закон распределения:
4. M(X+Y) = M(X) + M(Y).
Возможные значения случайной величины X+Yравна сумме возможных значенийXиY, а вероятностьX+Yравна произведению вероятностей слагаемых.
Теорема.М(Х) числа появлений событийАвnнезависимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытанииp.
Иначе, М(Х) биноминального распределения равно .
Сложение и вычитание матриц.
Суммой A+B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij+bij для всех i=1,mи j=1,n.
Аналогичное определение вводят и для разности матриц:
Разностью A−B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij−bij для всех i=1,m и j=1,n.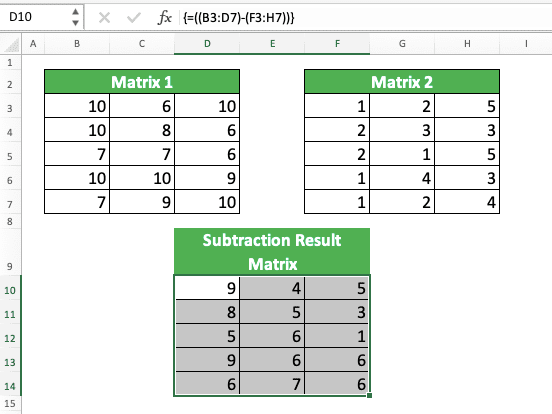
Умножение матрицы на число.
Произведением матрицы Am×n=(aij) на число α называется матрица Bm×n=(bij), где bij=α⋅aijдля всех i=1,m¯¯¯¯¯¯¯¯ и j=1,n¯¯¯¯¯¯¯.
Попросту говоря, умножить матрицу на некое число – означает умножить каждый элемент заданной матрицы на это число.
Произведение двух матриц.
Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать.
Произведением матрицы Am×n=(aij) на матрицу Bn×k=(bij) называется матрица Cm×k=(cij), для которой каждый элемент cij равен сумме произведений соответствующих элементов i-й строки матрицы Aна элементы j-го столбца матрицы B:
Руководство по вычитанию матриц NumPy
Введение
Вычитание двух матриц в NumPy — довольно распространенная задача. Самый простой способ вычесть две матрицы в NumPy — использовать оператор — , который является упрощением метода np. — специального метода NumPy, предназначенного для вычитания массивов и других подобных массивам объектов, таких как матрицы. . subtract()
subtract()
Примечание: Объектом, подобным массиву, в NumPy считается любой объект, который может быть передан в np.array() , чтобы он создавал объект, имеющий тип ndarray .
В этом руководстве вы узнаете, как вычесть две матрицы в NumPy, используя как оператор - , так и метод np.subtract() , когда использовать любой из них, и получите более глубокое понимание всех нюансов. метода np.subtract() в NumPy.
Как вычесть две матрицы в NumPy
В алгебре две матрицы можно вычесть, только если обе они имеют такое же количество строк и столбцов , что означает, что они имеют одинаковую форму . Предположим, у вас есть две матрицы одинаковой формы, которые вы хотите вычесть:
matrix1 = np.array([[2, 4, 0], [9, 1, 7]]) матрица2 = np.массив ([[2, 2, 1], [3, 5, 8]])
Примечание: Перед вызовом любого из методов NumPy, таких как метод np.array() в первый раз, вы должны импортировать модуль NumPy в свой проект с помощью import numpy as np
Как видите, две матрицы имеют одинаковую форму, а это означает, что matrix1.shape равно matrix2.shape — оба равны (2, 3) . Этот факт имеет решающее значение, поскольку в противном случае и оператор - , и метод np.subtract() не будут вести себя должным образом.
Примечание: Свойство shape любого объекта ndarray (массив или матрица) сохраняет форму этого объекта в форме (m, n) , где m представляет количество строк, а n представляет количество столбцов в матрице.
Теперь вы можете вычесть эти две матрицы с помощью оператора - :
resultMatrix = matrix1 - matrix2
Вот так просто! Эта строка равна следующей строке:
resultMatrix = np.subtract(matrix1, matrix2)
В обоих этих случаях resultMatrix будет иметь точно такое же значение, как и ожидалось:
[ 0 2 -1] [ 6 -4 -1]
Вычитание двух матриц разной формы в NumPy
В предыдущем разделе показан наиболее интуитивно понятный способ использования вычитания в NumPy. Правила алгебры гласят, что вы можете вычесть две матрицы только в том случае, если они имеют одинаковую форму, поэтому в предыдущем разделе описан единственный тип вычитания матриц, который математически действителен.
Однако библиотека NumPy позволяет методу np.subtract() работать, даже если матрицы аргументов равны не такой формы . Это делается с помощью механизма под названием широковещательная передача , который определяет, как NumPy обрабатывает массивы различных форм во время арифметических операций. В конечном итоге они уравниваются по форме, и происходит обычное вычитание.
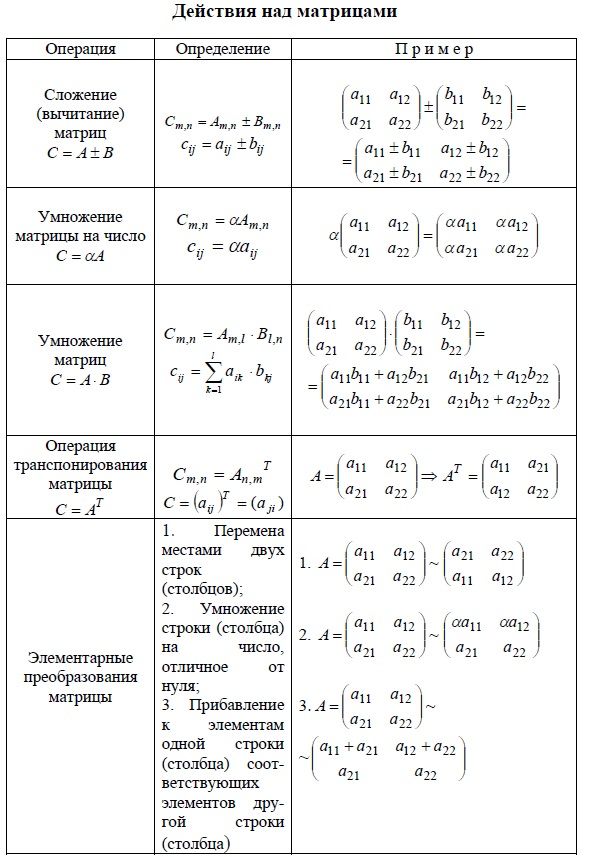
Например, рассмотрим две следующие матрицы:
rowMatrix = np.array([1, 2, 3]) columnMatrix = np.array ([[1], [2], [3]])
Эти матрицы определенно имеют разную форму, rowMatrix.shape равно (1, 3) , а columnMatrix.shape равно (3, 1) . Это может ввести вас в заблуждение, заставив думать, что вы не можете выполнить их вычитание в NumPy, но это определенно возможно (хотя и косвенно, поскольку они автоматически транслируются перед вычитанием):
resultMatrix = np.subtract( матрица строк, матрица столбцов)
Примечание: resultMatrix будет иметь точно такое же значение, если вы используете - оператор вместо np.subtract() метод
resultMatrix будет иметь следующее значение:
[ 0 1 2] [-1 0 1] [-2 -1 0]
Хотя этот результат может показаться немного нелогичным, но давайте воспользуемся им, чтобы проиллюстрировать механизм вещания простыми словами.
Что такое вещание NumPy?
Чтобы вычесть columnMatrix из rowMatrix , они оба должны иметь одинаковую форму. Поскольку эти две матрицы не соответствуют упомянутому критерию, вступает в действие механизм вещания. Это гарантирует растяните , чтобы они оба имели совместимые формы. Таким образом,
Поскольку эти две матрицы не соответствуют упомянутому критерию, вступает в действие механизм вещания. Это гарантирует растяните , чтобы они оба имели совместимые формы. Таким образом, rowMatrix является растянутым , так что он формирует матрицу формы (3, 3) :
> Исходная `resultMatrix`: [1 2 3] > Рассылка `resultMatrix`: [1 2 3] [1 2 3] [1 2 3]
Аналогичным образом columnMatrix также растягивается для формирования матрицы (3, 3) :
> Исходная `resultMatrix`: [1] [2] [3] > Рассылка `resultMatrix`: [1 1 1] [2 2 2] [3 3 3]
Теперь, когда у вас есть две измененные матрицы одинаковой формы, можно выполнить над ними вычитание. Результирующая матрица такая же, как resultMatrix из приведенного выше примера.
[1 2 3] [1 1 1] [0 1 2] [1 2 3] - [2 2 2] = [-1 0 1] [1 2 3] [3 3 3] [-2 -1 0]
Предупреждение: Широковещательная передача — гораздо более сложный механизм, чем описанный здесь, поэтому мы настоятельно рекомендуем вам использовать его с осторожностью или проводить дополнительные исследования по этой теме. Например, некоторая другая комбинация двух матричных форм даст
Например, некоторая другая комбинация двух матричных форм даст ValueError , потому что эти формы не могут транслироваться в одну и ту же форму.
Когда использовать
np.subtract() Метод вместо — Оператор Основываясь на том, что вы видели до сих пор, вы можете сделать вывод, что вы можете использовать как - , так и subtract() взаимозаменяемо довольно много в любое время вы хотите. Это почти верно, но в некоторых случаях вам следует рассмотреть возможность использования метода np.subtract() вместо - оператор.
По сути, оператор - является абстракцией метода np.subtract() . При вызове оператор - фактически вызовет np.subtract() с параметрами по умолчанию. Таким образом, единственный вариант использования, в котором вы можете рассмотреть возможность использования np.subtract() вместо оператора - , — это когда вы хотите настроить предопределенное поведение вычитания по умолчанию в NumPy. Мы рассмотрим несколько аргументов, с которыми может быть интересно поэкспериментировать.
Мы рассмотрим несколько аргументов, с которыми может быть интересно поэкспериментировать.
Во-первых, давайте посмотрим на объявление метода np.subtract() :
numpy.subtract(x1, x2, /, out=None, *, where=True, cast='same_kind', order='K', dtype=None, subok=True[ подпись, extobj]) =
Помимо нескольких обычных и не требующих пояснений аргументов, раздел объявления, который, скорее всего, привлечет ваше внимание, это , так что давайте сначала проясним, что он означает. В NumPy, ufunc означает универсальную функцию , таким образом, этот аргумент сигнализирует о том, что метод np.subtract() является универсальной функцией.
Универсальные функции в NumPy работают с массивами (точнее, ndarrays ) поэлементно. Они могут эффективно перебирать элементы двух ndarrays и выполнять предопределенную операцию над соответствующими элементами. Например,
Например, np.subtract() вычтет два соответствующих элемента из двух ндаррейс . Таким образом, вы можете думать об универсальных функциях как о базовых, предопределенных функциях, которые позволяют вам выполнять множество основных математических операций с ndarrays .
Теперь мы можем описать некоторые другие интересные аргументы:
-
x1(обязательно)- первый входной массив (или другие подобные массиву объекты)
- должен иметь ту же форму, что и
x2, либо транслироваться в той же форме, что и 9.0005 x2
-
x2(обязательно)- второй входной массив (или другие подобные массиву объекты)
- должен иметь ту же форму, что и
x1, либо транслироваться в ту же форму, что иx1.
-
вых.(опционально)- используется, если вы хотите указать место для хранения результата
- если не указано, создается новый объект для хранения результата
- , если указано, это должен быть объект
ndarrayили кортеж изndarrayиНетобъектов - указанный объект должен иметь форму, которую два входных массива передают в
-
, где(опционально)- используется, если вы хотите указать некоторые элементы входного массива, над которыми не будет выполняться
ufunc - значение по умолчанию
True, поэтомуnp.вычтет все соответствующие элементы из subtract()
subtract() x1иx2 - , если вы не хотите вычитать элементы в определенной позиции в массиве
из, вы можете передать массив логических значений, который имеет ту же форму, что и массивиз, и установить значениеFalseдля этих позиций.
- используется, если вы хотите указать некоторые элементы входного массива, над которыми не будет выполняться
-
dtype(дополнительно)- используется для указания типа матрицы результатов
- по умолчанию, он равен типу входных массивов
Заключение
Ищете ли вы простой способ вычитания двух матриц с помощью NumPy или пытаетесь вспомнить более сложные концепции, связанные с методом np.subtract(), это руководство поможет вам. Основная цель этого руководства состояла в том, чтобы дать вам ответ на оба этих вопроса.
Во-первых, мы рассмотрели простой и интуитивно понятный способ вычитания двух матриц в модуле NumPy. Наряду с этим мы обсудили сходства и различия между
Наряду с этим мы обсудили сходства и различия между - оператор и метод np.subtract() . После этого мы проиллюстрировали концепцию вещания в NumPy, но мы советуем вам углубиться в тему вещания.
В конце концов, мы предоставили вам подробный обзор метода np.subtract() в NumPy, поэтому вы можете настроить его поведение по умолчанию, чтобы сделать его более подходящим для некоторых более конкретных случаев использования.
Сложение и вычитание матриц | Колледж Алгебра
Результаты обучения
- Определение размеров матрицы.
- Сложите и вычтите две матрицы.
Чтобы решить задачу, подобную описанной для футбольных команд, мы можем использовать матрицу , которая представляет собой прямоугольный массив чисел. Строка в матрице — это набор чисел, выровненных по горизонтали. Столбец в матрице представляет собой набор чисел, выровненных по вертикали.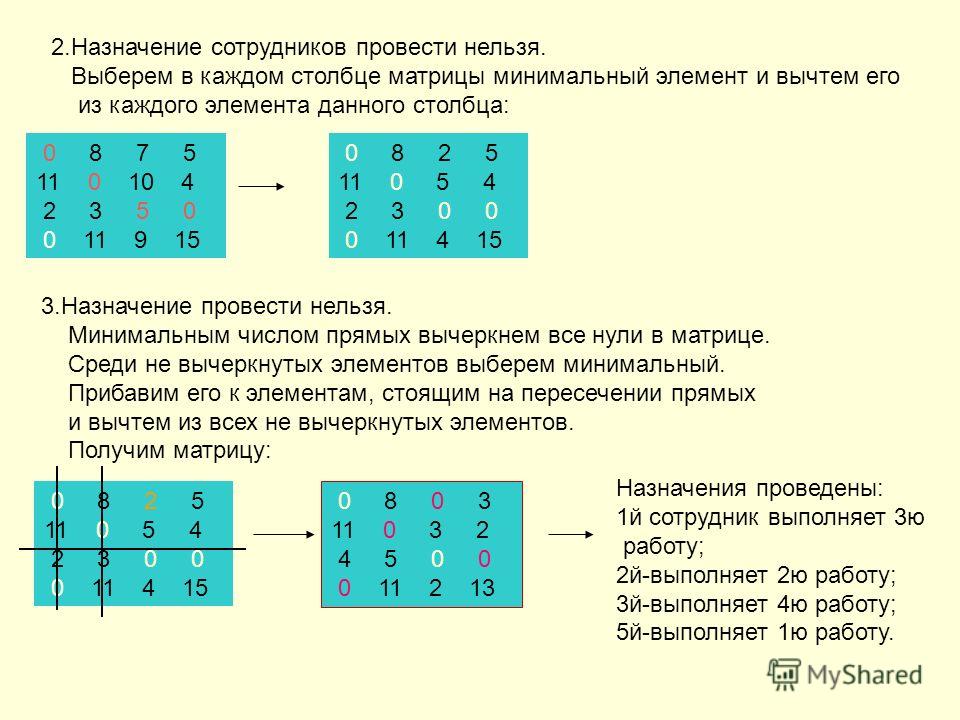 Каждое число представляет собой запись , иногда называемую элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами. Например, ниже показаны три матрицы с именами [latex]A,B,\text{}[/latex] и [latex]C[/latex].
Каждое число представляет собой запись , иногда называемую элементом матрицы. Матрицы (во множественном числе) заключаются в [ ] или ( ) и обычно называются заглавными буквами. Например, ниже показаны три матрицы с именами [latex]A,B,\text{}[/latex] и [latex]C[/latex].
[латекс]A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{массив}\right],B=\left[\begin{array}{ccc}1& 2& 7\ \ 0& -5& 6\\ 7& 8& 2\end{массив}\right],C=\left[\begin{массив}{c}-1\\ 0\\ 3\end{массив}\begin{массив} {c}3\\ 2\\ 1\end{массив}\right][/latex]
Описание матриц
Матрица часто упоминается по ее размеру или измерениям: [latex]\text{ }m\text { }\times \text{ }n\text{ }[/latex] с указанием [latex]m[/latex] строк и [latex]n[/latex] столбцов. Элементы матрицы определяются сначала по строке, а затем по столбцу. Например, чтобы найти запись в матрице [latex]A[/latex], идентифицированную как [latex]{a}_{ij},\text{}[/latex], мы ищем запись в строке [latex]i, \text{}[/latex] столбец [latex]j[/latex]. В матрице [latex]A[/latex], показанной ниже, записью в строке 2 столбца 3 является [latex]{a}_{23}[/latex].
В матрице [latex]A[/latex], показанной ниже, записью в строке 2 столбца 3 является [latex]{a}_{23}[/latex].
[латекс]A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {a}_{21} & {a}_{22}& {a}_{23}\\ {a}_{31}& {a}_{32}& {a}_{33}\end{массив}\right][ /latex]
Квадратная матрица — это матрица с размерами [latex]\text{ }n\text{ }\times \text{ }n,\text{}[/latex], что означает, что она имеет тот же номер строк как столбцов. Матрица [latex]3\times 3[/latex] выше является примером квадратной матрицы.
Матрица строк — это матрица, состоящая из одной строки с размерами [latex]1\text{ }\times \text{ }n[/latex].
[латекс]\влево[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\end{массив}\right][/latex ]
Матрица столбцов — это матрица, состоящая из одного столбца с размерами [latex]m\text{ }\times \text{ }1[/latex].
[латекс]\left[\begin{array}{c}{a}_{11}\\ {a}_{21}\\ {a}_{31}\end{array}\right][ /latex]
Матрица может использоваться для представления системы уравнений.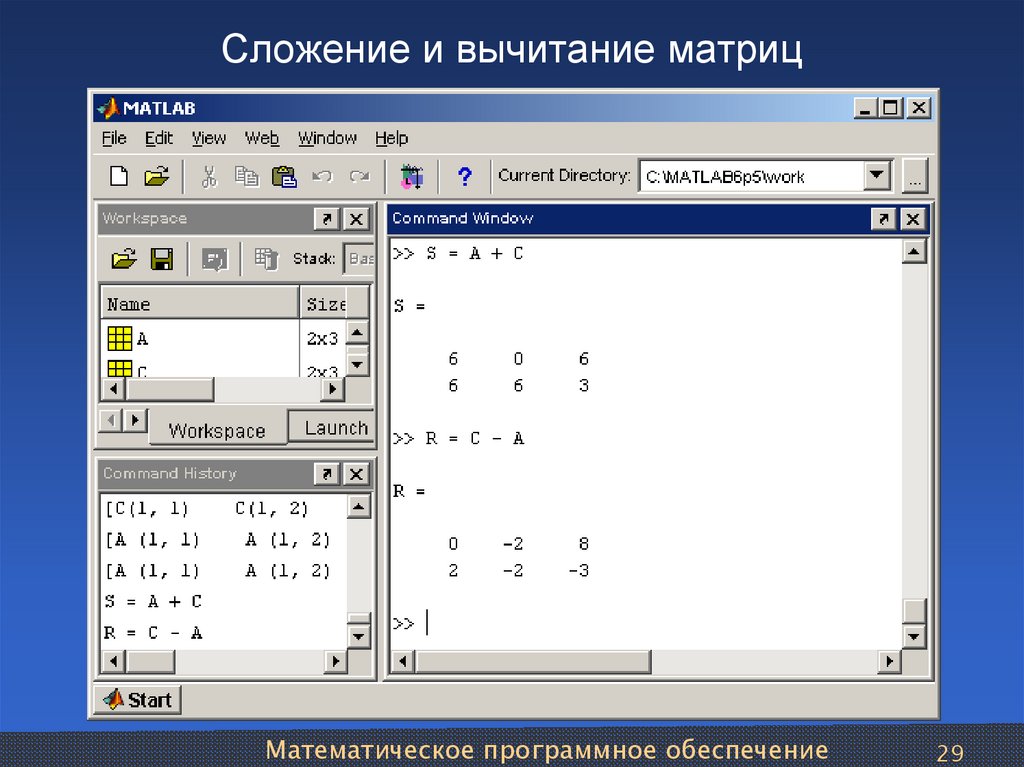 В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто облегчают решение систем уравнений, потому что они не перегружены переменными. Мы исследуем эту идею подробнее в следующем разделе, но сначала мы рассмотрим основные матричные операции .
В этих случаях числа представляют собой коэффициенты переменных в системе. Матрицы часто облегчают решение систем уравнений, потому что они не перегружены переменными. Мы исследуем эту идею подробнее в следующем разделе, но сначала мы рассмотрим основные матричные операции .
A Общее примечание: Матрицы
A Матрица представляет собой прямоугольный массив чисел, который обычно обозначается заглавной буквой: [latex]A,B,C,\text{}[/latex] и так далее. Каждая запись в матрице обозначается как [latex]{a}_{ij}[/latex], так что [latex]i[/latex] представляет строку, а [latex]j[/latex] представляет столбец. Матрицы часто упоминаются по их размерам: [латекс]m\times n[/латекс] указывает [латекс]m[/латекс] строк и [латекс]n[/латекс] столбцов.
Пример: нахождение размеров заданной матрицы и поиск элементов
заданная матрица [latex]A:[/latex]
- Каковы размеры матрицы [latex]A?[/latex]
- Что представляют собой записи в [latex]{a}_{31}[/latex] и [latex]{a}_{22}?[/latex]
[латекс]A=\left[\begin{array}{rrrr}\hfill 2& \hfill & \hfill 1& \hfill 0\\ \hfill 2& \hfill & \hfill 4& \hfill 7\\ \hfill 3& \ hfill & \hfill 1& \hfill -2\end{массив}\right][/latex]
Показать раствор
Попробуйте
Сложение и вычитание матриц
Мы используем матрицы для перечисления данных или представления систем. Поскольку записи являются числами, мы можем выполнять операции над матрицами. Мы добавляем или вычитаем матрицы, добавляя или вычитая соответствующие элементы.
Поскольку записи являются числами, мы можем выполнять операции над матрицами. Мы добавляем или вычитаем матрицы, добавляя или вычитая соответствующие элементы.
Для этого записи должны совпадать. Поэтому сложение и вычитание матриц возможны только тогда, когда матрицы имеют одинаковые размеры . Мы можем добавить или вычесть матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\текст{ }[/латекс] и другую матрицу [латекс]\текст{ }3\текст{ }\times \text{ }3\text{ }[/latex] матрица, но мы не можем складывать или вычитать матрицу [latex]\text{ }2\text{ }\times \text{ }3\text{ }[/latex] и матрица [latex]\text{ }3\text{ }\times \text{ }3\text{ }[/latex], поскольку некоторым элементам в одной матрице не будет соответствующего элемента в другой матрице.
A Общее примечание: сложение и вычитание матриц
Даны матрицы [латекс]А[/латекс] и [латекс]В[/латекс] одинакового размера, сложение и вычитание [латекс]А[/латекс] и [латекс ]B[/latex] создаст матрицу [latex]C[/latex] или матрицу [latex]D[/latex] того же размера.
[латекс]A+B=C\текст{ такой, что }{a}_{ij}+{b}_{ij}={c}_{ij}[/latex]
[латекс]A-B= D\text{ такое, что }{a}_{ij}-{b}_{ij}={d}_{ij}[/latex]
Сложение матриц коммутативно.
[латекс]А+В=В+А[/латекс]
Это тоже ассоциативно.
[латекс]\влево(А+В\вправо)+С=А+\влево(В+С\вправо)[/латекс]
Пример: нахождение суммы матриц
Нахождение суммы [латекс]А [/latex] и [latex]B \text{}[/latex] заданы
[latex]A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right] \text{ и }B=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right][/latex]
Показать решение
Пример: добавление матрицы
A и Matrix BНайдите сумму [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}4& 1\\ 3& 2\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 5& 9\\ 0& 7\end{массив}\right][/latex]
Показать решение
Пример: нахождение разности двух матриц
Найдите разность [латекс]А[/латекс] и [латекс]В[/латекс].
[латекс]A=\left[\begin{array}{cc}-2& 3\\ 0& 1\end{array}\right]\text{ и }B=\left[\begin{array}{cc} 8& 1\\ 5& 4\end{массив}\right][/латекс]
Показать раствор
Пример: нахождение суммы и разности двух матриц 3 x 3
Даны [латекс]А[/латекс] и [латекс]В:[/латекс]
- Найдите сумму.
- Найди разницу.
[латекс]A=\left[\begin{array}{rrr}\hfill 2& \hfill -10& \hfill -2\\ \hfill 14& \hfill 12& \hfill 10\\ \hfill 4& \hfill -2& \ hfill 2\end{массив}\right]\text{ и }B=\left[\begin{array}{rrr}\hfill 6& \hfill 10& \hfill -2\\ \hfill 0& \hfill -12& \hfill - 4\\ \hfill -5& \hfill 2& \hfill -2\end{массив}\right][/latex]
Показать раствор
Попробуйте
Добавьте матрицу [латекс]А[/латекс] и матрицу [латекс]В[/латекс].
[латекс]A=\left[\begin{массив}{rr}\hfill 2& \hfill 6\\ \hfill 1& \hfill 0\\ \hfill 1& \hfill -3\end{массив}\right]\ text{и}B=\left[\begin{array}{rr}\hfill 3& \hfill -2\\ \hfill 1& \hfill 5\\ \hfill -4& \hfill 3\end{array}\right][ /латекс]
Показать решение
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.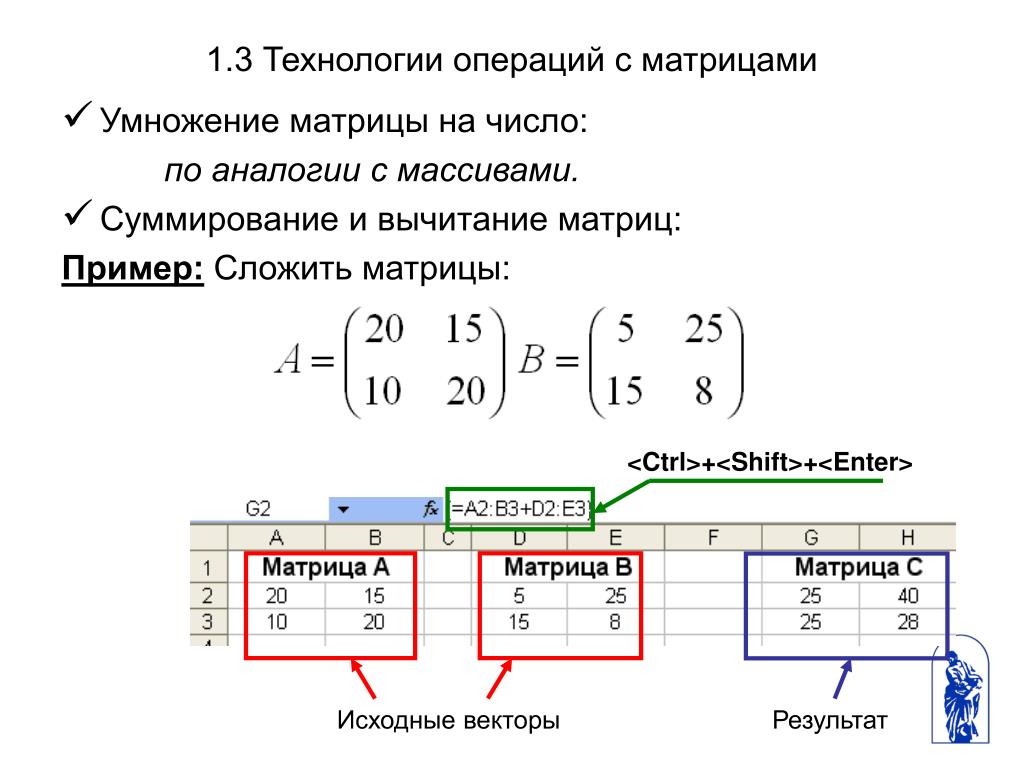
Улучшить эту страницуПодробнее
Вычитание матриц – объяснение и примеры
Есть $ 4 $ основных операций, которые мы можем выполнять с матрицами. Это сложение, вычитание, скалярное умножение и матричное умножение. Матричное вычитание — одна из них, и мы рассмотрим ее в этой статье.
Примечание: Деление матрицы не является определенной операцией. Мы можем разделить матрицу только на скалярное число. Чтобы узнать больше о матричном делении, нажмите здесь.
Определим вычитание матриц:
Вычитание матриц — это операция вычитания двух матриц одного размера путем вычитания соответствующих элементов.
Эта статья покажет, при каких условиях возможно вычитание матриц, вычитание матриц и несколько примеров, показывающих этот процесс.
Когда можно вычитать матрицы?
Можем ли мы вычесть любые матрицы?
Нет!
Мы можем вычитать $2$ матрицы, только если они имеют одинаковую размерность. То есть, если матрицы $2$ имеют одинаковое количество строк и столбцов, то и только тогда мы можем вычитать матрицы $2$ вместе.
То есть, если матрицы $2$ имеют одинаковое количество строк и столбцов, то и только тогда мы можем вычитать матрицы $2$ вместе.
Напомним, что размерность матрицы — это количество строк и количество столбцов. Если в матрице есть $a$ строк и $b$ столбцов, мы можем сказать, что матрица имеет размеры $a\times b$ (произносится как $a$-by-$b$). Чтобы узнать больше о размерах матрицы, ознакомьтесь с этой статьей!
Помните, матрица, полученная в результате операции вычитания матриц, будет того же размера, что и матрицы, из которых она получена.
Как вычитать матрицы?
После того, как мы пришли к выводу, что матрицы имеют одинаковые размеры, мы вычтем $ 2 $ матрицы, вычитая соответствующие элементы друг друга . Рассмотрим Matrix $ A $ и Matrix $ B $, показанные ниже:
$ A = \begin{bmatrix} { 0 } & { 4 } \\ { – 3} & { – 3 } \end {bmatrix} $
$ B = \begin{bmatrix} { – 9 } & 0 \\ 2 & { – 2 } \end {bmatrix} $
Обе матрицы $ A $ и $ B $ имеют $ 2 $ строк и $ 2 $ столбцы. Следовательно, размерность матриц $ 2 \times 2 $, что делает их равными. Это означает, что мы можем вычесть матрицы $2$, вычитая каждую соответствующую запись друг из друга. Процесс показан ниже:
Следовательно, размерность матриц $ 2 \times 2 $, что делает их равными. Это означает, что мы можем вычесть матрицы $2$, вычитая каждую соответствующую запись друг из друга. Процесс показан ниже:
$ A – B = \begin{bmatrix} { 0 – – 9 } & { 4 – 0 } \\ { – 3 – 2 } & { – 3 – – 2 } \ end {bmatrix } $
$ A – B = \begin{bmatrix} { 0 + 9} & { 4 – 0 } \\ { – 3 – 2 } & { – 3 + 2 } \end {bmatrix} $
$ A – B = \begin{bmatrix} { 9 } & { 4 } \\ { – 5 } & { – 1 } \end {bmatrix} $
Теперь рассмотрим две матрицы, показанные ниже:
$ A = \begin{bmatrix} { 0 } & { – 1 } \\ 10 & 2 \ end {bmatrix} $
$ B = \begin{bmatrix} { – 5 } & 0 \\ 6 & 0 \\ 3 & 7 \\ 4 & { – 7 } \end {bmatrix} $
Is $ А – В$ определены?
№
Матрица $A$ имеет размерность $2\times 2$. Матрица $B$ имеет размерность $4\times 2$. Поскольку размеры обеих матриц не равны, вычитание матрицы не определено! Мы не можем вычесть Матрицы $A$ и $B$, потому что не будет соответствующей записи для каждого элемента Матрицы $A$ и Матрицы $B$.
Правила вычитания матриц
Мы можем написать $ 4 $ правила для вычитания матриц. Показано ниже:
- Вычитать можно только матрицы одинаковой размерности (т.е. количество строк первой матрицы должно быть равно количеству строк второй матрицы. Также количество столбцов первой матрицы должно быть равно количеству столбцов вторая матрица.)
- Матрица, полученная в результате вычитания матриц, будет иметь ту же размерность, что и исходные матрицы, из которых она получена.
- Вычитание матриц НЕ коммутативно (т. е. $ A – B \neq B – A $). Когда вы меняете порядок матриц и вычитаете, он дает другой ответ (точно так же, как действительные числа).
- Матричное вычитание является НЕ ассоциативным (т. е. $ (A – B) – C \neq A – (B – C) $).
Давайте рассмотрим несколько примеров Вычитания матриц .
Пример 1 Проверить, задано ли матричное вычитание между матрицей $A$ и матрицей $B$. Если да, вычтите их.
Если да, вычтите их.
$ A = \begin{bmatrix} { 0 } & { – 5 } \\ { – 5 } & { 0 } \end {bmatrix} $
$ B = \begin{bmatrix} { 3 } & { – 4 } \\ { 0 } & { – 5 } \end {bmatrix} $
Решение
Для определения вычитания матриц размерность каждой матрицы должна быть одинаковой.
Матрица $ A $ является матрицей размера $ 2 \times 2 $. Матрица $B$ также является матрицей $2\times 2$. Таким образом, матричное вычитание между Matrix $A$ и $B$ определено.
Теперь давайте вычтем вместе матрицы $2$, вычитая каждый соответствующий элемент матрицы $B$ из каждого соответствующего элемента матрицы $A$. Как показано ниже:
$ A – B = \begin{bmatrix} { 0 – 3 } & { – 5 – – 4 } \\ { – 5 – 0 } & { 0 – – 5 } \end {bmatrix} $
$ A – B = \begin{bmatrix} { – 3 } & { – 5 + 4 } \\ { – 5 } & {0 + 5 } \end{bmatrix} $
$ A – B = \begin {bmatrix} { – 3 } & { – 1 } \\ { – 5 } & { 5 } \end{bmatrix} $
Пример 2
Для матриц $ 2 $, показанных ниже, найдите $С-Д$.
$ C = \begin{bmatrix} { 1 } & { – 1 } \\ 1 & { – 1 } \\ 7 & { – 7 } \end {bmatrix} $
$ D = \begin{bmatrix} { 1 } & { – 2 } & { – 1 } \\ { – 1 } & 0 & { – 1 } \end {bmatrix} $
Решение
Размер матрицы $C$ равен $3\times 2$. Размерность матрицы $D$ равна $2\times 3$. Несмотря на то, что размеры эквивалентны, мы не можем вычесть матрицу $D$ из матрицы $C$. Порядок размеров также важен. Матрица $3\times 2$ не равна матрице $2\times 3$. Таким образом, мы не можем вычесть матрицу $D$ из матрицы $C$.
Мы также можем решать основные алгебраические уравнения с вычитанием матриц. Рассмотрим пример, показанный ниже.
Пример 3Найдите значения $ a $ и $ b $ по следующему уравнению:
$ \begin{pmatrix} { 1 } & { 2 } \\ b & { – 6 } \ end {pmatrix} – \begin{pmatrix} { a } & { – 1 } \\ 0 & { – 3 } \ end {pmatrix} = \begin{pmatrix} { 7 } & { 3 } \\ { – 2 } & { – 3 } \end {pmatrix} $
Решение
Мы можем вычесть соответствующие записи, чтобы найти $ a $ и $ b $. Сначала вычтем соответствующие элементы для $a$ и найдем переменную:
Сначала вычтем соответствующие элементы для $a$ и найдем переменную:
$ 1 – a = 7 $
$ a = 1 – 7 $
$ a = – 6 $
Теперь найдем значение $b $, вычитая соответствующие записи для $b $:
$ b – 0 = – 2 $
$ b = – 2 $
Теперь вы можете попробовать несколько практических вопросов и посмотреть, правильно ли вы ответили на них или нет. Ответы ниже.
Практические вопросы- Рассмотрим следующие матрицы $ 3 $:
$ P = \begin{pmatrix} { – 2 } & { – 2 } \\ 1 & { 1 } \end {pmatrix} $
$ Q = \begin{pmatrix} { – 3 } & { – 3 } \\ { – 3 } & { – 3 } \end {pmatrix} $
$ R = \begin{pmatrix} 1 & 1 \\ 7 & { – 2 } \\ 3 & { – 7 } \end {pmatrix} $
Найти:- $ P – Q $
- $ Q – R $
- $ Q – P $
- Найти значения $ a $, $ b $ и $ c $, заданные следующим уравнением:
$ \begin{pmatrix} { 3 } & { 2 } & 0 \\ b & { – 2 } & 3 \\ 11 & a & -2 \end {pmatrix} – \begin{pmatrix} { 3 } & { 2 } & c \\ 5 & { – 5 } & 3 \\ { – 4 } & { 6 } & 10 \end {pmatrix} = \begin{pmatrix} { 0 } & { 0 } & -9\\ 12 & { 3 } & 0 \\ 15 & -3 & { – 12 } \end {pmatrix} $
Ответы
- Все задачи на $3 $ являются матричным вычитанием.
 Обратите внимание, что, поскольку вычитание матрицы не является коммутативным , ответ на часть $ A $ и часть $ C $ будет другим. Ответы показаны ниже.
Обратите внимание, что, поскольку вычитание матрицы не является коммутативным , ответ на часть $ A $ и часть $ C $ будет другим. Ответы показаны ниже. - Обе матрицы $P$ и $Q$ являются матрицами размера $2\times 2$. Таким образом, мы вычитаем матрицы $2$, вычитая соответствующие элементы. Показано ниже:
$ P – Q = \begin{pmatrix} { – 2 – – 3 } & { – 2 – – 3 } \\ { 1 – – 3 } & {1 – – 3 } \end {pmatrix} $
$ P – Q = \begin{pmatrix} { – 2 + 3 } & { – 2 + 3 } \\ { 1 + 3 } & {1 + 3 } \end {pmatrix} $
$ P – Q = \begin{pmatrix } { 1 } & { 1 } \\ { 4 } & { 4 } \end {pmatrix} $ - Мы не можем вычесть матрицу $R$ из матрицы $Q$, потому что их размеры не совпадают. Матрица $Q$ является матрицей размера $ 2 \times 2$, а матрица $R$ является матрицей размера $3 x 2$.
- Ответ на эту часть вопроса будет отличаться от ответа на часть $ A $, поскольку вычитание матриц не является коммутативным. Вычтем Матрицу $P$ из Матрицы $Q$.

- Обе матрицы $P$ и $Q$ являются матрицами размера $2\times 2$. Таким образом, мы вычитаем матрицы $2$, вычитая соответствующие элементы. Показано ниже:

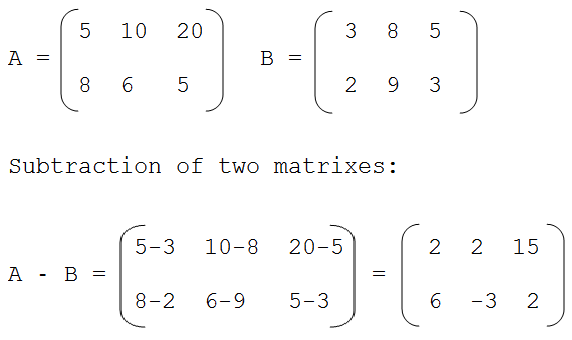 массив ([[2, 2, 1], [3, 5, 8]])
массив ([[2, 2, 1], [3, 5, 8]])
 subtract(matrix1, matrix2)
subtract(matrix1, matrix2)
 array([1, 2, 3])
columnMatrix = np.array ([[1], [2], [3]])
array([1, 2, 3])
columnMatrix = np.array ([[1], [2], [3]])
 subtract()
subtract()  Обратите внимание, что, поскольку вычитание матрицы не является коммутативным , ответ на часть $ A $ и часть $ C $ будет другим. Ответы показаны ниже.
Обратите внимание, что, поскольку вычитание матрицы не является коммутативным , ответ на часть $ A $ и часть $ C $ будет другим. Ответы показаны ниже. 