Чем отличается рациональное число от иррационального: Рациональные и иррациональные числа

Рациональна ли разница между двумя рациональными числами? – Обзоры Вики

Разница между двумя рациональными числами должно быть рациональным числом. … Рациональное число — это число, которое можно записать в форме a/b, где a — целое число, а b — целое число, отличное от нуля.

Отсюда, в чем разница рациональных чисел? Разница между двумя рациональными числами, a/b и c/d, равна результату вычитания меньшего числа из большего. Чтобы найти разницу между рациональными числами или вычесть рациональные числа, мы используем следующую формулу: a/b – c/d = (ad – bc) / bd.

Является ли рациональное число целым числом? Целое число можно представить в виде дроби, присвоив ей знаменатель, равный единице, поэтому любое целое число является рациональным числом.

Кроме того, почему разница двух рациональных чисел всегда рациональна? Поскольку ab и cd — рациональные числа, мы знаем, что a, b, c и d — целые числа. Следовательно, по нашему правилу все ad, bc и bd — целые числа, а поскольку ad и bc — целые числа, наши правила также дают, что ad–bc — это все. … Таким образом, мы имеем, что разность двух рациональных чисел является рациональным числом.

Чем отличаются два иррациональных числа? (i) Разность — иррациональное число: если мы рассмотрим два числа как √3 и √2, то их разность будет равна, √3−√2=√1. Мы видим, что их разность также является иррациональным числом.

Всегда ли разность двух иррациональных чисел иррациональна?

Нет, разница в два иррациональное может быть иррациональным или рациональным. Возьмем два иррациональных числа и увидим, что это не всегда относится к разнице, но бывает и к сумме. & сумма этих двух иррациональных чисел = 2, что является рациональным числом. Это не всегда иррационально.

Может ли разность двух иррациональных чисел быть рациональной? Тем не менее, это возможно иметь два иррациональных числа в сумме, разности, произведении, частном или степени так, чтобы результат был рациональным.

Чему всегда равно произведение двух рациональных чисел? Пусть pl=x,qm=y. ⇒plqm=xy, где y≠0, а x и y — наименьшее представление терма, являющееся рациональным числом. Следовательно, произведение двух рациональных чисел равно всегда рациональное число.

Может ли разность двух иррациональных чисел быть рациональной?

Их разность равна 1. Если два иррациональных числа, то один из может быть рациональным, но не оба (и, конечно, оба могут быть иррациональными). Если оба рациональны, то такова и их сумма, следовательно, рациональна.

Также является ли разность двух разных иррациональных чисел рациональным числом? Чай разница может быть как иррациональной, так и рациональной. Разница между двумя пи и пи равна пи, что иррационально. Разница между pi и pi+1 равна единице, что является рациональным.

Является ли разница двух иррациональных чисел иррациональной?

Нет, сумма двух иррациональных чисел не всегда иррациональна. Рациональное число — это число, которое можно представить как частное или дробь двух целых чисел, числителя p и ненулевого знаменателя q. С другой стороны, иррациональное число — это действительное число, которое нельзя выразить как отношение двух целых чисел.

Является ли произведение двух иррациональных чисел иррациональным? Произведение двух иррациональных чисел не будет иррациональным.

Чему равно произведение двух иррациональных чисел?

Произведение двух иррациональных чисел может быть рациональным или иррациональным в зависимости на два числа. Например, √3×√3 равно 3, что является рациональным числом, а √2×√4 равно √8, которое является иррациональным числом. Поскольку √3,√2,√4 иррациональны.

Какие 2 иррациональных числа составляют рациональное число?

Сумма двух иррациональных чисел является рациональной, если иррациональные части компенсируют друг друга. Сейчас, х + у = 2 — квадрат (3) + квадрат (3) = 2 , которое является рациональным числом.

Может ли сумма целого числа и рационального числа быть целым числом? Отвечать: Это ложь из-за следующего: Пошаговое объяснение: Полученная сумма целого числа и рационального числа.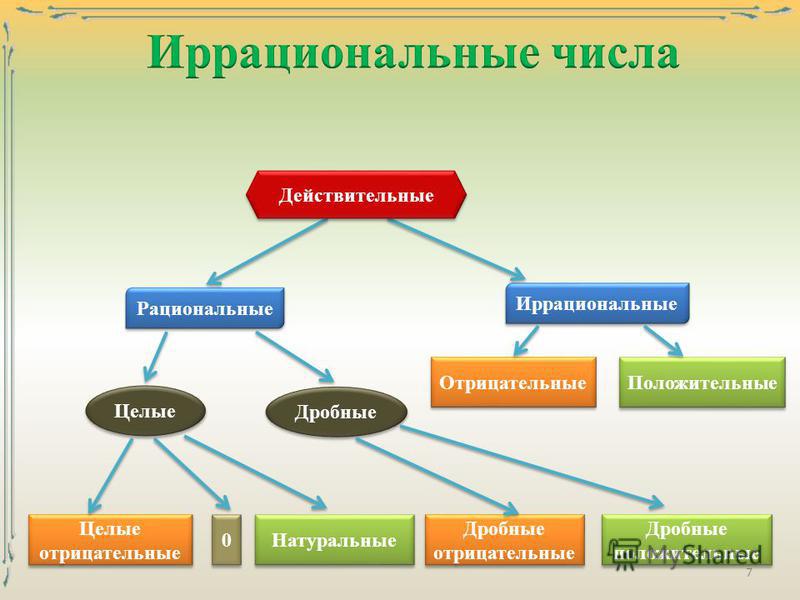

Чему равна сумма или разность рационального и иррационального числа? Сумма или разность рационального числа и иррационального числа равна иррациональный. … Отсюда следует, что добавление или вычитание рационального и иррационального будет иррациональным.

2 — рациональное число?

2 — рациональное число потому что оно удовлетворяет условию рационального числа и может быть записано в форме p/q, что математически представляется как 2/1, где 1≠0.

Чему равно произведение двух отрицательных рациональных чисел? Произведение двух отрицательных рациональных чисел равно всегда позитивный.

Может ли быть целое число?

Целое число включает целые числа и отрицательные целые числа. Целые числа могут быть положительными, отрицательными или нулевыми. Например: 1, -1, 0, 101 и -101. Существует бесконечное количество целых чисел.

Чем отличаются целые и рациональные числа? Рациональное число — это число, которое можно представить в виде дроби между двумя целыми числами. Целое число является рациональным числом, потому что каждое целое число может быть выражено как дробь между собой и 2, оба целых числа. Таким образом, целые числа являются подмножество рациональных чисел для по той же причине.

Чем отличается иррациональное число от целого?

Иррациональные числа бессрочный, повторяющиеся десятичные числа, т. е. десятичное расширение, которое не заканчивается и не становится периодическим, которое не может быть выражено в форме дроби. … Целое число — это полная сущность, которая включает в себя все натуральные числа вместе с их отрицательными значениями и нулем.

В чем разница между рациональными и иррациональными числами, приведите пример каждого из них? Рациональное число включает в себя числа, которые являются конечными или повторяющимися по своей природе. Они состоят из чисел, которые не заканчиваются и не повторяются по своей природе. Иррациональные числа включают в себя сурды, такие как √2, √3, √5, √7 и так далее.

Может ли произведение двух иррациональных чисел быть целым числом?

Произведение любых двух иррациональных чисел (1) Всегда иррациональное число (2) Всегда является рациональным числом (3) Всегда является целым числом (4) Может быть рациональным или иррациональным числом. Рациональные числа представлены в форме p/q, где q не равно нулю.

Всякое ли натуральное число целое? Все целые числа являются целыми (и все натуральные числа целые), но не все целые числа являются целыми числами или натуральными числами. Например, -5 — это целое число, но не целое или натуральное число.

Всякое ли действительное число является целым числом?

Целые числа являются действительными числами, но не все действительные числа являются целыми числами. Вот некоторые различия: Действительные числа включают целые числа, но также включают рациональные, иррациональные, целые и натуральные числа.

Математика. Иррациональные числа.

Иррациональное число (лат. irrationalis — неразумный, от in(ir) — отрицательная приставка и ratio — счёт, отношение) — это число, не являющееся рациональным, то есть целым или дробным.

Термины рациональное число, иррациональное число происходят от латинского слова ratio — разум (буквальный перевод: «рациональное число — разумное число», «иррациональное число — неразумное число»; впрочем, так говорят и в реальной жизни: «он поступил рационально» — это значит, что он поступил разумно; «так действовать нерационально» — это значит, что так действовать неразумно).

Рациональное и иррациональное число: описание и чем они отличаются?

Откуда же произошли следующие термины такие, как:

• Рациональное число.
• Иррациональное число.

А свои корни они извлекли из латинского слова «ratio», что означает «разум». Исходя из дословного перевода:

• Рациональное число — это «разумное число».
• Иррациональное число, соответственно, «неразумное число».

Общее понятие рационального числа

Рациональным числом считается то число, которое можно записать в виде:

1. Обыкновенной положительной дроби.
2. Отрицательной обыкновенной дроби.
3. В виде числа нуль (0).

Иными словами, к рациональному число подойдет следующие определения:

• Любое натуральное число является по своей сути рациональным, так как любое натуральное число можно представить в виде обыкновенной дроби.
• Любое целое число, включительно число нуль, так как любое целое число можно записать как ввиде положительной обыкновенной дроби, в виде отрицательной обыкновенной дроби, так и ввиде числа нуль.
• Любая обыкновенная дробь, и здесь не имеет значение положительная она или отрицательная, тоже напрямую подходит к определению рационального числа.
• Так же в определение можно отнести и смешанное число, конечную десятичную дробь либо бесконечную периодическую дробь.

      

Рассмотрим примеры рациональных чисел:

• Натуральные числа — «4», «202», «200».
• Целые числа — «-36», «0», «42».
• Обыкновенные дроби.

Из вышеперечисленных примеров совершенно очевидно, что рациональные числа могут быть как положительными так и отрицательными. Естественно, число 0 (нуль), которое тоже в свою очередь является рациональным числом, в тоже время не относится к категории положительного или отрицательного числа.

Отсюда, хотелось бы напомнить общеобразовательную программу с помощью следующего определения: «Рациональными числами» — называются те числа, которые можно записать в виде дроби х/у, где х (числитель) — целое число, а у (знаменатель) — натуральное число.

Общее понятие и определение иррационального числа

Помимо «рациональных чисел» нам известны и так называемые «иррациональные числа». Вкратце попробуем дать определение данным числам.

Еще древние математики, желая вычислить диагональ квадрата по его сторонам, узнали о существовании иррационального числа. Исходя из определения о рациональных числах, можно выстроить логическую цепь и дать определение иррациональному числу. Итак, по сути, те действительные числа, которые не являются рациональными, элементарно и есть иррациональными числами. Десятичные дроби же, выражающие иррациональные числа, не периодичны и бесконечны.

Иррациональное число

Примеры иррационального числа

Рассмотрим для наглядности небольшой пример иррационально числа. Как мы уже поняли, бесконечные десятичные непериодические дроби называются иррациональными, к примеру:

• Число «-5,020020002… (прекрасно видно, что двойки разделены последовательностью из одного, двух, трех и т.д. нулей)
• Число «7,040044000444… (здесь ясно, что число четверок и количество нулей каждый раз цепочкой увеличивается на единицу).
• Всем известное число Пи (3,1415…). Да, да — оно тоже является иррациональным.

Вообще все действительные числа являются как рациональными так и иррациональными. Говоря простыми словами, иррациональное число нельзя представить ввиде обыкновенной дроби х/у.

Общее заключение и краткое сравнение между числами

Мы рассмотрели каждое число по отдельности, осталось отличие между рациональным числом и иррациональным:

1. Иррациональное число встречается при извлечении квадратного корня, при делении окружности на диаметр и т. д.
2. Рациональное число представляет обыкновенную дробь.

Выводы:

• Арифметическая операция, произведенная над рациональным числом, кроме деления на 0 (нуль), в конечном результате приведет тоже к рациональному числу.
• Конечный результат же, при совершении арифметической операции над иррациональным числом, может привести как к рациональному так и к иррациональному значению.
• Если же в арифметической операции принимают участие и те и другие числа (кроме деления или умножения на нуль), то результат нам выдаст иррациональное число.

 

Иррациональное число — Википедия

Номер √2 иррационально.

В математика, то иррациональные числа все действительные числа которые не рациональное число. То есть иррациональные числа нельзя выразить как отношение двух целые числа. Когда соотношение длины двух отрезков является иррациональным числом, отрезки также описываются как несоизмеримый, что означает, что у них нет общей «меры», то есть не существует длины («меры»), какой бы короткой она ни была, которую можно было бы использовать для выражения длин обоих из двух данных сегментов как целых кратных сам.

Среди иррациональных чисел есть соотношение π длины окружности к ее диаметру, число Эйлера е, золотое сечение φ, а квадратный корень из двух^[1][2][3]. Фактически, все квадратные корни из натуральные числа, кроме идеальные квадраты, иррациональны.

Как и все действительные числа, иррациональные числа могут быть выражены в позиционная запись, особенно как десятичное число. В случае иррациональных чисел десятичное разложение не прекращается, и заканчиваться повторяющейся последовательностью. Например, десятичное представление π начинается с 3,14159, но конечное количество цифр не может представлять π точно, и не повторяется. И наоборот, завершающее или повторяющееся десятичное раскрытие должно быть рациональным числом. Это доказуемые свойства рациональных чисел и позиционных систем счисления, которые не используются в качестве определений в математике.

Иррациональные числа также можно выразить как непрерывные непрерывные дроби и многие другие способы.

Как следствие Доказательство Кантора что настоящие числа бесчисленный и рациональные счетно, отсюда следует, что почти все реальные числа иррациональны.^[4]

Содержание

• 1 История
  • 1.1 Древняя Греция
  • 1.2 Индия
  • 1.3 Средний возраст
  • 1.4 Современный период
• 2 Примеры
  • 2.1 Квадратные корни
  • 2.2 Общие корни
  • 2.3 Логарифмы
• 3 Типы
  • 3.1 Трансцендентный / алгебраический
• 4 Десятичные разложения
• 5 Иррациональные силы
• 6 Открытые вопросы
• 7 Набор всех иррациональных
• 8 Смотрите также
• 9 Рекомендации
• 10 дальнейшее чтение
• 11 внешняя ссылка

История

Набор действительных чисел (R), который включает рациональные числа (Q), которые включают целые числа (Z), которые включают натуральные числа (N). Действительные числа также включают иррациональные числа (R Q).

Древняя Греция

Первое доказательство существования иррациональных чисел обычно приписывают Пифагорейский (возможно Гиппас из Метапонта ),^[5] кто, вероятно, обнаружил их, определяя стороны пентаграмма. ^[6]Существовавший тогда метод Пифагора должен был утверждать, что должна быть какая-то достаточно маленькая неделимая единица, которая могла бы равномерно вписаться в одну из этих длин, а также в другую. Однако Гиппас в V веке до нашей эры смог сделать вывод, что на самом деле не существовало общей единицы измерения, и что утверждение о таком существовании на самом деле было противоречием. Он сделал это, продемонстрировав, что если гипотенуза из равнобедренный прямоугольный треугольник действительно был соизмеримый с ногой, то одна из этих длин, измеренная в этой единице измерения, должна быть как нечетной, так и четной, что невозможно. Его рассуждения таковы:

• Начните с равнобедренного прямоугольного треугольника со сторонами целых чисел. а, б, и c. Отношение гипотенузы к катету представлено как c:б.
• Предполагать а, б, и c в минимально возможных сроках (т.е. у них нет общих факторов).
• Посредством теорема Пифагора: c² = а²+б² = б²+б² = 2б². (Поскольку треугольник равнобедренный, а = б).
• С c² = 2б², c² делится на 2, а значит, даже.
• С c² даже, c должно быть даже.
• С c четный, делящий c на 2 дает целое число. Позволять у быть этим целым числом (c = 2у).
• Квадрат с обеих сторон c = 2у дает c² = (2у)², или же c² = 4у².
• Подставляя 4у² за c² в первом уравнении (c² = 2б²) дает нам 4у²= 2б².
• Деление на 2 дает 2у² = б².
• С у целое число, а 2у² = б², б² делится на 2, а значит, даже.
• С б² даже, б должно быть даже.
• Мы только что показали, что оба б и c должно быть даже. Следовательно, у них есть общий множитель 2. Однако это противоречит предположению, что у них нет общих множителей. Это противоречие доказывает, что c и б не могут одновременно быть целыми числами, и, следовательно, существование числа, которое не может быть выражено как отношение двух целых чисел.^[7]

Греческие математики назвал это соотношение несоизмеримых величин алогос, или невыразимо. Гиппаса, однако, не хвалили за его усилия: согласно одной легенде, он сделал свое открытие, находясь в море, и впоследствии был выброшен за борт своими товарищами-пифагорейцами, «… за то, что создал во вселенной элемент, который отрицал… доктрину о том, что все явления во Вселенной можно свести к целым числам и их отношениям ».^[8] Другая легенда гласит, что Гиппас был просто изгнан за это откровение. Какими бы ни были последствия для самого Гиппаса, его открытие представляло собой очень серьезную проблему для пифагорейской математики, поскольку оно разрушило предположение о неразрывности числа и геометрии — основу их теории.

Открытие несоизмеримых соотношений указывало на еще одну проблему, с которой столкнулись греки: отношение дискретного к непрерывному. Это было обнаружено Зенон Элейский, который поставил под сомнение концепцию, согласно которой количества дискретны и состоят из конечного числа единиц заданного размера. Согласно прежним греческим концепциям, они обязательно должны быть такими, поскольку «целые числа представляют собой отдельные объекты, а соизмеримое соотношение представляет собой отношение между двумя наборами дискретных объектов»,^[9] но Зенон обнаружил, что на самом деле «[количества] в целом не являются дискретным набором единиц; вот почему появляются отношения несоизмеримых [величин]… Другими словами, [количества] непрерывны ».^[9] Это означает, что вопреки популярной концепции времени не может быть неделимой мельчайшей единицы измерения для любой величины. Фактически, эти количественные единицы обязательно должны быть бесконечный. Например, рассмотрим линейный сегмент: этот сегмент можно разделить пополам, половину — пополам, половину — пополам и так далее. Этот процесс может продолжаться бесконечно, потому что всегда остается разделить другую половину. Чем чаще сегмент делится вдвое, тем ближе единица измерения к нулю, но никогда не достигает точного нуля. Именно это и пытался доказать Зенон. Он попытался доказать это, сформулировав четыре парадокса, который продемонстрировал противоречия, присущие математической мысли того времени. Хотя парадоксы Зенона точно продемонстрировали недостатки современных математических концепций, они не рассматривались как доказательство альтернативы. В представлении греков опровержение обоснованности одной точки зрения не обязательно доказывало обоснованность другой, и поэтому требовалось дальнейшее исследование.

Следующий шаг сделали Евдокс Книдский, который формализовал новую теорию пропорции, которая учитывала как соизмеримые, так и несоизмеримые величины. Центральным в его идее было различие между величиной и числом. Величина «… не была числом, а обозначала такие объекты, как отрезки линий, углы, площади, объемы и время, которые могли изменяться, как мы бы сказали, непрерывно. Величины были противопоставлены числам, которые прыгали от одного значения к другому, от 4 до 5. «^[10] Числа состоят из некоторой наименьшей, неделимой единицы, тогда как величины бесконечно уменьшаются. Поскольку никакие количественные значения не были присвоены величине, Евдокс смог учесть как соизмеримые, так и несоизмеримые отношения, определяя соотношение по величине и пропорции как равенство между двумя отношениями. Убрав количественные значения (числа) из уравнения, он избежал ловушки, связанной с необходимостью выражать иррациональное число в виде числа. «Теория Евдокса позволила греческим математикам добиться огромного прогресса в геометрии, предоставив необходимую логическую основу для несоизмеримых соотношений».^[11] Эта несоизмеримость рассматривается в «Элементах» Евклида, книга X, предложение 9.

В результате различия между числом и величиной геометрия стала единственным методом, который мог учитывать несоизмеримые отношения. Поскольку предыдущие числовые основы все еще были несовместимы с концепцией несоизмеримости, греческий акцент сместился с таких числовых концепций, как алгебра, и сосредоточился почти исключительно на геометрии. Фактически, во многих случаях алгебраические концепции были переформулированы в геометрические термины. Это может объяснить, почему мы все еще понимаем Икс² и Икс³ в качестве Икс в квадрате и Икс куб вместо Икс во вторую степень и Икс в третью степень. Также критически важным для работы Зенона с несоизмеримыми величинами был фундаментальный акцент на дедуктивном мышлении, который явился результатом фундаментального разрушения ранней греческой математики. Осознание того, что некоторые основные концепции существующей теории расходятся с реальностью, потребовало полного и тщательного исследования аксиом и предположений, лежащих в основе этой теории. Исходя из этой необходимости, Евдокс разработал метод истощения, типа сокращение до абсурда что «… установило дедуктивную организацию на основе явных аксиом …», а также «… подкрепило ранее принятое решение полагаться на дедуктивное рассуждение для доказательства».^[12] Этот метод исчерпания — первый шаг в создании исчисления.

Феодор из Кирены доказал иррациональность серпы целых чисел до 17, но остановился на этом, вероятно, потому, что алгебра, которую он использовал, не могла быть применена к квадратному корню из 17.^[13]

Он не был до тех пор Евдокс разработал теорию пропорции, которая учитывала иррациональные, а также рациональные соотношения, что позволило создать прочную математическую основу иррациональных чисел.^[14]

Индия

Геометрические и математические проблемы, связанные с иррациональными числами, такими как квадратные корни, были решены очень рано во время Ведический период в Индии. Ссылки на такие расчеты есть в Самхиты, Брахманы, а Шульба Сутры (800 г. до н.э. или ранее). (См. Bag, Indian Journal of History of Science, 25 (1-4), 1990).

Предполагается, что концепция иррациональности была неявно принята Индийские математики с 7 века до нашей эры, когда Манава (ок. 750 — 690 до н. э.) считали, что квадратные корни чисел, таких как 2 и 61, не могут быть точно определены. ^[15] Однако историк Карл Бенджамин Бойер пишет, что «подобные утверждения малообоснованны и маловероятны».^[16]

Также предлагается, чтобы Арьябхата (V век нашей эры) при вычислении значения числа пи до 5 значащих цифр использовали слово асанна (приближение), означающее, что это не только приближение, но и несоизмеримость (или иррациональность) значения.

Позже в своих трактатах индийские математики писали об арифметике сурдов, включая сложение, вычитание, умножение, рационализацию, а также разделение и извлечение квадратных корней.^[17]

Математикам нравится Брахмагупта (в 628 г.) и Бхаскара I (629 г. н.э.) внесли свой вклад в эту область, как и другие последовавшие за ней математики. В 12 веке Бхаскара II оценили некоторые из этих формул и подвергли их критике, выявив их ограничения.

В течение 14-16 веков Мадхава Сангамаграмы и Керальская школа астрономии и математики обнаружил бесконечная серия для нескольких иррациональных чисел, таких как π и некоторые иррациональные значения тригонометрические функции. Джиешхадева предоставил доказательства для этих бесконечных серий в Юктибхана.^[18]

Средний возраст

в Средний возраст, развитие алгебра к Мусульманские математики разрешил иррациональные числа рассматриваться как алгебраические объекты.^[19] Математики Ближнего Востока также объединили концепции «номер » и «величина «в более общее представление о действительные числа критиковал идею Евклида о соотношения, разработал теорию составных отношений и расширил понятие числа до отношений непрерывной величины.^[20] В своем комментарии к книге 10 Элементы, то Персидский математик Аль-Махани (ум. 874/884) осмотрены и классифицированы квадратичные иррациональные числа и кубические иррациональные числа. Он дал определения рациональных и иррациональных величин, которые он рассматривал как иррациональные числа. Он свободно разбирался с ними, но объясняет их геометрическими терминами следующим образом:^[21]

«Это будет рациональным (величина), когда мы, например, скажем 10, 12, 3%, 6% и т. Д., Потому что его значение произносится и выражается количественно. То, что нерационально, является иррациональным, и его невозможно произнести и представить его значение количественно. Например: корни чисел, таких как 10, 15, 20, которые не являются квадратами, стороны чисел, которые не являются кубами. и Т. Д.«

В отличие от евклидова концепции величин как линий, Аль-Махани рассматривал целые числа и дроби как рациональные величины, а квадратные корни и кубические корни как иррациональные величины. Он также представил арифметический подход к концепции иррациональности, поскольку он относит к иррациональным величинам следующее:^[21]

«их суммы или различия, или результаты их прибавления к рациональной величине, или результаты вычитания такой величины из иррациональной, или рациональной величины из нее».

В Египтянин математик Абу Камил Шуджа ибн Аслам (ок. 850 — 930) был первым, кто принял иррациональные числа как решения квадратные уравнения или как коэффициенты в уравнение, часто в виде квадратных корней, кубических корней и четвертые корни. ^[22] В 10 веке Иракский математик Аль-Хашими предоставил общие доказательства (а не геометрические демонстрации) для иррациональных чисел, поскольку он рассматривал умножение, деление и другие арифметические функции.^[23] Иранский математик, Абу Джафар аль-Хазин (900–971) дает определение рациональных и иррациональных величин, утверждая, что если определенная количество является:^[24]

«содержится в определенной заданной величине один или несколько раз, тогда эта (данная) величина соответствует рациональному числу … Каждый раз, когда эта (последняя) величина составляет половину, треть или четверть данной величины (единицы) или, по сравнению с (единицей), составляет три, пять или три пятых, это рациональная величина. И, в общем, каждая величина, которая соответствует этой величине (т.е. к единице), как одно число к другому, рационально. Если же величина не может быть представлена ​​в виде кратного числа, то часть (1 /п) или части (м/п) данной величины, это иррационально, т. е. это не может быть выражено иначе, как через корни ».

Многие из этих концепций были в конечном итоге приняты европейскими математиками спустя некоторое время после Латинские переводы XII века. Аль-Хассар, марокканский математик из Фес специализируясь на Исламское наследство юриспруденции в 12 веке впервые упоминается использование дробной черты, где числители и знаменатели разделены горизонтальной чертой. В своем обсуждении он пишет: «… например, если вам говорят написать три пятых и одну треть пятого, напишите так: 3153{ displaystyle { frac {3 quad 1} {5 quad 3}}}.»^[25] Это же дробное обозначение вскоре появляется в работах Леонардо Фибоначчи в 13 веке.^[26]

Современный период

17 век увидел мнимые числа стать мощным инструментом в руках Авраам де Муавр, и особенно Леонард Эйлер. Завершение теории сложные числа в 19 ​​веке повлекло за собой разделение иррациональных чисел на алгебраические и трансцендентные числа, доказательство существования трансцендентных чисел и возрождение научных исследований теории иррациональных чисел, в значительной степени игнорируемых с тех пор, как Евклид. В 1872 году были опубликованы теории Карл Вейерштрасс (его ученик Эрнст Коссак), Эдуард Гейне (Журнал Крелля, 74), Георг Кантор (Аннален, 5), и Ричард Дедекинд. В 1869 году Мере взял ту же отправную точку, что и Гейне, но теория обычно относится к 1872 году. Метод Вейерштрасса полностью изложен Сальваторе Пинчерле в 1880 г.,^[27] и Дедекинда получили дополнительную известность благодаря более поздней работе автора (1888 г.) и одобрению Пол Таннери (1894 г.). Вейерштрасс, Кантор и Гейне основывают свои теории на бесконечных рядах, в то время как Дедекинд основывает свои теории на идее вырезать (Шнитт) в системе всех рациональное число, разделив их на две группы, обладающие определенными характерными свойствами. Этот предмет получил более поздние работы от Вейерштрасса, Леопольд Кронекер (Crelle, 101), и Шарль Мере.

Непрерывные дроби, тесно связанные с иррациональными числами (и благодаря Катальди, 1613 г.), привлекли внимание Эйлера и в начале XIX века получили известность благодаря трудам Жозеф-Луи Лагранж. Дирихле также внес свой вклад в общую теорию, как и многие участники, внесшие вклад в приложения этого предмета.

Иоганн Генрих Ламберт доказал (1761), что π не может быть рациональным и что е^п иррационально, если п рационально (если только п = 0).^[28] Хотя доказательство Ламберта часто называют неполным, современные оценки подтверждают его как удовлетворительное, и в действительности для своего времени оно необычайно строгое. Адриан-Мари Лежандр (1794), после введения Функция Бесселя – Клиффорда, предоставили доказательство того, что π² иррационально, откуда сразу следует, что π также иррационально. Существование трансцендентные числа был впервые установлен Лиувиллем (1844, 1851). Потом, Георг Кантор (1873) доказали их существование другой метод, который показал, что каждый интервал в вещественных числах содержит трансцендентные числа. Чарльз Эрмит (1873) впервые доказано е трансцендентный, и Фердинанд фон Линдеманн (1882), исходя из выводов Эрмита, показал то же самое для π. Доказательство Линдеманна было значительно упрощено Вейерштрассом (1885 г.), а еще дальше — Дэвид Гильберт (1893), и, наконец, был сделан элементарным Адольф Гурвиц^{[нужна цитата ]} и Пол Гордан.^[29]

Примеры

Квадратные корни

В квадратный корень из 2 было первым числом, которое оказалось иррациональным, и эта статья содержит ряд доказательств. В Золотое сечение — еще одно известное квадратичное иррациональное число. Квадратные корни из всех натуральных чисел, не являющихся идеальные квадраты иррациональны, и доказательство можно найти в квадратичные иррациональные числа.

Общие корни

Приведенное выше доказательство для квадратного корня из двух можно обобщить, используя основная теорема арифметики. Это утверждает, что каждое целое число имеет уникальная факторизация в простые числа. Используя его, мы можем показать, что если рациональное число не является целым числом, то его целая степень не может быть целым числом, как в самые низкие сроки должен быть основной в знаменателе, который не делится на числитель, в какую бы степень они ни возводились.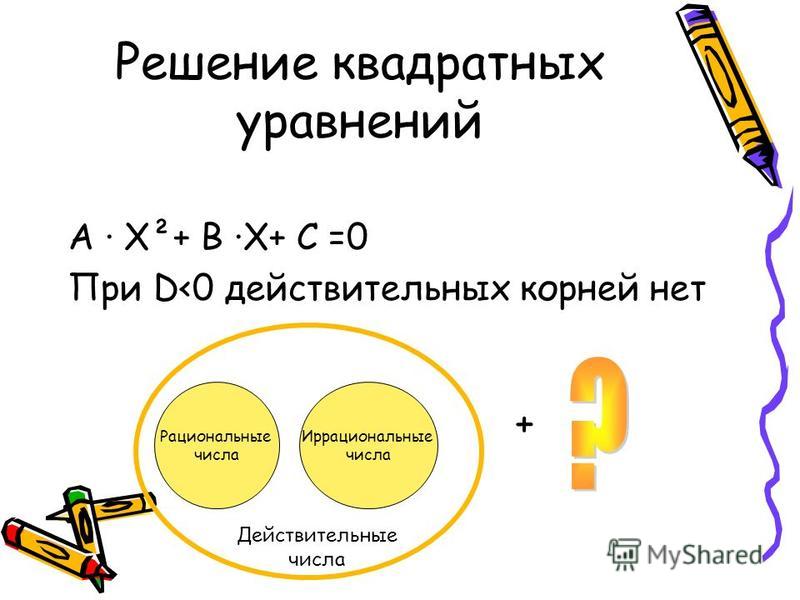 {n}.}

Однако число 2, возведенное в любую положительную целую степень, должно быть четным (потому что оно делится на 2), а число 3, возведенное в любую положительную целую степень, должно быть нечетным (так как ни одно из его главные факторы будет 2). Ясно, что целое число не может быть одновременно четным и нечетным: приходим к противоречию. Мы сделали единственное предположение, что журнал₂ 3 является рациональным (и поэтому выражается как частное целых чисел м/п с п ≠ 0). Противоречие означает, что это предположение должно быть ложным, т.е. log₂ 3 иррационально и никогда не может быть выражено как частное от целых чисел м/п с п ≠ 0.

Такие случаи, как журнал₁₀ 2 можно рассматривать аналогично.

Типы

• Теоретико-числовое различие: трансцендентный / алгебраический
• нормальный / ненормальный (ненормальный)

Трансцендентный / алгебраический

Почти все иррациональные числа трансцендентный и все реальные трансцендентные числа иррациональны (существуют также комплексные трансцендентные числа): в статье о трансцендентных числах приводится несколько примеров. {n-1} + cdots + a_ {1} x + a_ {0} = 0 ;, }

где коэффициенты ая{ displaystyle a_ {i}} целые числа и ап≠0{ displaystyle a_ {n} neq 0}. Любой рациональный корень этого полиномиального уравнения должно иметь вид р /s, куда р это делитель из а₀ и s является делителем а_п. Если настоящий рут Икс0{ displaystyle x_ {0}} полинома п{ displaystyle p} не входит в число этих конечных возможностей, это должно быть иррациональное алгебраическое число. Примерное доказательство существования таких алгебраических иррациональных чисел состоит в том, чтобы показать, что Икс₀  = (2^1/2 + 1)^1/3 является иррациональным корнем многочлена с целыми коэффициентами: он удовлетворяет (Икс³ − 1)² = 2 и, следовательно, Икс⁶ − 2Икс³ — 1 = 0, и этот последний многочлен не имеет рациональных корней (единственными кандидатами для проверки являются ± 1, иИкс₀, будучи больше 1, не является ни одним из них), поэтомуИкс₀ — иррациональное алгебраическое число.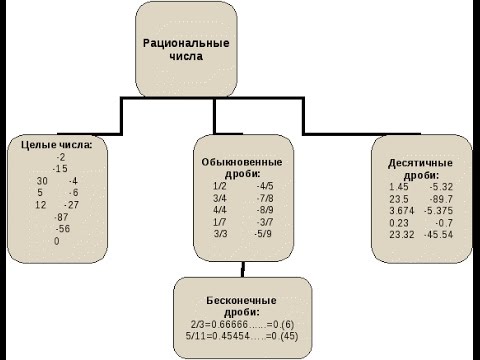

Поскольку алгебраические числа образуют подполе Из действительных чисел многие иррациональные действительные числа могут быть построены путем комбинирования трансцендентных и алгебраических чисел. Например, 3π + 2, π + √2 и е√3 иррациональны (и даже трансцендентны).

Десятичные разложения

Десятичное разложение иррационального числа никогда не повторяется и не заканчивается (последнее эквивалентно повторяющимся нулям), в отличие от любого рационального числа. То же верно и для двоичный, восьмеричный или же шестнадцатеричный расширений, и в целом для расширений в каждом позиционный обозначение с естественный базы.

Чтобы показать это, предположим, что мы делим целые числа п к м (куда м не равно нулю). Когда длинное деление применяется к разделению п к м, Только м остатки возможны. Если 0 появляется как остаток, десятичное раскрытие завершается. Если 0 никогда не встречается, алгоритм может работать не более м — 1 шаг без использования остатка более одного раза. После этого должен повториться остаток, а затем повторяется десятичное разложение.

И наоборот, предположим, что мы столкнулись с повторяющаяся десятичная дробь, мы можем доказать, что это дробь двух целых чисел. Например, рассмотрим:

А=0.7162162162…{ Displaystyle А = 0,7 , 162 , 162 , 162 , ldots}

Здесь повторяется 162, а длина повторения равна 3. Сначала мы умножаем на соответствующую степень 10, чтобы переместить десятичную запятую вправо так, чтобы она находилась прямо перед повторением. В этом примере мы умножим на 10, чтобы получить:

10А=7.162162162…{ Displaystyle 10A = 7,162 , 162 , 162 , ldots}

Теперь умножим это уравнение на 10.^р куда р длина повтора. Это приводит к перемещению десятичной точки перед «следующим» повторением. В нашем примере умножаем на 10³:

10,000А=7162.162162…{ Displaystyle 10,000A = 7 , 162,162 , 162 , ldots}

Результат двух умножений дает два разных выражения с точно такой же «десятичной частью», то есть хвостовой частью 10 000А соответствует концу 10А точно. Здесь и 10000А и 10А имеют .162162162… после десятичной точки.

Следовательно, когда мы вычитаем 10А уравнение из 10 000А уравнение, конец 10А аннулирует хвост из 10,000А оставив нас с:

9990А=7155.{ displaystyle 9990A = 7155.}

потом

А=71559990{ displaystyle A = { frac {7155} {9990}}}

представляет собой отношение целых чисел и, следовательно, рациональное число.

Иррациональные силы

Дов Джарден дал простой не-конструктивное доказательство что существуют два иррациональных числа а и б, так что а^б рационально:^[30]

Учитывать √2^√2; если это рационально, то возьмем а = б = √2. В противном случае возьмите а быть иррациональным числом √2^√2 и б = √2. потом а^б = (√2^√2)^√2 = √2^√2·√2 = √2² = 2, что рационально.

Хотя приведенный выше аргумент не делает выбор между двумя случаями, Теорема Гельфонда – Шнайдера показывает, что √2^√2 является трансцендентный, следовательно, иррационально. {n} e} рационально для некоторого целого числа п>1.{ displaystyle n> 1.}^{[нужна цитата ]}

Набор всех иррациональных

Поскольку реалы образуют бесчисленный множество, рациональными числами которого являются счетный подмножество дополнительных наборов иррациональных чисел неисчислимо.

Под обычным (Евклидово ) функция расстояния d (Икс, у) = |Икс − у|, действительные числа — это метрическое пространство а значит, и топологическое пространство. Ограничение функции евклидова расстояния придает иррациональным числам структуру метрического пространства. Поскольку подпространство иррациональных чисел не замкнуто, индуцированная метрика не является полный. Однако, будучи G-дельта набор — т.е. счетное пересечение открытых подмножеств — в полном метрическом пространстве пространство иррациональных чисел полностью метризуемый: то есть существует метрика на иррациональных числах, порождающая ту же топологию, что и ограничение евклидовой метрики, но относительно которой иррациональные числа полны. Альберт, Джон. «Некоторые нерешенные проблемы теории чисел» (PDF). Отделение математики Университета Оклахомы. (Старший математический семинар, весенний курс 2008 г.)

дальнейшее чтение

• Адриан-Мари Лежандр, Éléments de Géometrie, Примечание IV, (1802 г.), Париж
• Рольф Валлиссер, «О доказательстве Ламбертом иррациональности числа π», в Алгебраическая теория чисел и диофантов анализ, Франц Хальтер-Кох и Роберт Ф. Тихи, (2000), Вальтер де Грюйер

внешняя ссылка

• Парадоксы Зенона и несоизмеримость (нет данных). Проверено 1 апреля 2008 г.
• Вайсштейн, Эрик В. «Иррациональный номер». MathWorld.

в чем разница между рациональным числом и иррациональным числом?

Спросил 8 лет, 11 месяцев назад

Изменено 1 год, 4 месяца назад

Просмотрено 23k раз

$\begingroup$

Я пытался понять разницу между рациональными и иррациональными числами. Я понимаю, что такое рациональное число (число, которое можно выразить как отношение двух чисел p/q).

что делает иррациональное число иррациональным? как можно простым способом доказать, что иррациональное число иррационально? почему тот факт, что отношение двух чисел, которые можно разделить на 2, иррационален? (я прав?)

Я не смог понять выбранный ответ в В чем разница между рациональными и иррациональными — топологически? поэтому, пожалуйста, имейте в виду, что мои математические навыки и понимание в настоящее время слабы (занижение), и я работаю над их улучшением.

Спасибо!

• простые числа
• иррациональные числа
• системы счисления
• рациональные числа

$\endgroup$

2

$\begingroup$

Шутка (но правда): Разница между рациональным числом и иррациональным числом иррациональна.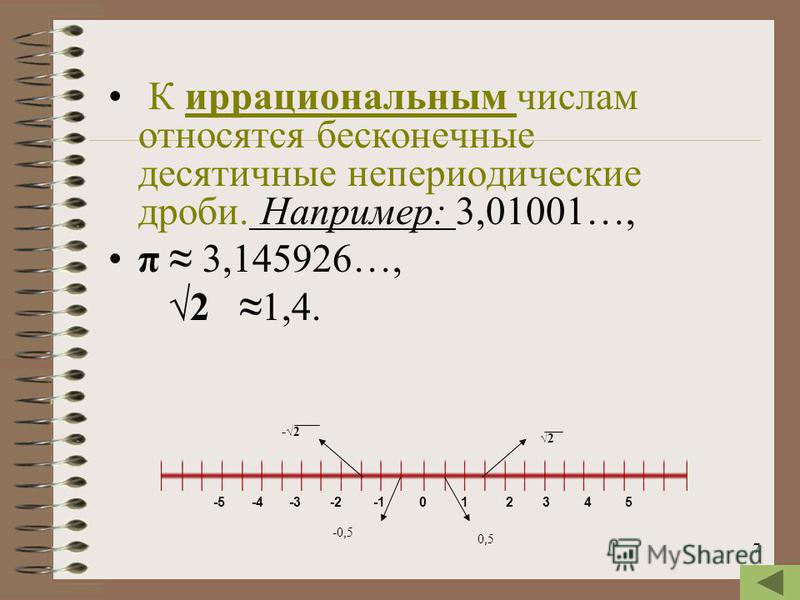 \pi}}$ целым числом, не говоря уже о том, является ли оно рациональным (но практически любой может поспорить, что оно иррационально).

Оказывается, что в некоторых смыслах почти все действительные числа иррациональны и даже трансцендентны (более неприятный зверь). Существуют также различные методы для производства больших объемов иррациональных (и даже трансцендентных) чисел, но большинство чисел, которые на самом деле интересуют людей, либо тривиально рациональны, либо тривиально алгебраичны (не трансцендентны), либо загадочны — никто не знает наверняка, они рациональны или иррациональны.

Частично это объясняется тем, что, хотя очень легко сложить рациональные числа, чтобы получить больше рациональных чисел, вы не можете сложить иррациональные числа, чтобы получить больше иррациональных чисел, очень многими способами. Например, сумма или произведение двух рациональных чисел всегда рационально, но сумма или произведение двух иррациональных чисел может быть рациональным.

$\endgroup$

6

$\begingroup$

Иррациональное число — это просто действительное число, которое не является рациональным. Другими словами, это действительное число, которое нельзя записать как отношение целых чисел.

Классический пример — число $\pi$; давайте попробуем получить некоторое представление об иррациональных числах на этом примере. Возможно, вы знакомы с первыми цифрами десятичной записи $\pi$; \начать{выравнивать} \пи = 3,14159\точки \end{выравнивание} Обратите внимание, что если мы усекаем это десятичное разложение в любой точке, то результирующее число

будет рациональным. Допустим, например, что мы усекаем до десятков, тогда получаем число $3.1$, которое можно записать как \начать{выравнивать} 3,1 = \ гидроразрыва {31} {10} \end{выравнивание} В качестве альтернативы, если мы отрежем два, три или четыре десятичных знака, то получим следующие рациональные числа, которые все лучше и лучше приближаются к $\pi$: \начать{выравнивать} 3. 14 &= \frac{314}{100} \\ 3.141 &= \frac{3141}{1000} \\ 3,1415 &= \фракция{31415}{10000} \end{выравнивание} Мы можем продолжать в том же духе, получая все более и более рациональные приближения к $\pi$, но обратите внимание, что мы никогда не сможем полностью получить $\pi$ только с конечным числом десятичных цифр. Нам нужна полная бесконечная последовательность десятичных цифр, чтобы точно получить число $\pi$. Другими словами, хотя существуют все более и более совершенные рациональные приближения к $\pi$, каждое из которых представляет собой отношение целых чисел, нет возможности точно записать число $\pi$ как такое отношение.

$\endgroup$

2

$\begingroup$

Во-первых, отношение двух четных чисел по-прежнему рационально, так что это неправильно. Во-вторых, доказательство иррациональности зависит от числа. Примеры: $\pi, e, \sqrt 2, \sqrt 3, \sqrt 7, \ldots$ ($\sqrt p$ иррационально, если $p$ простое число)

$\endgroup$

$\begingroup$

Я разместил этот ответ на аналогичный вопрос.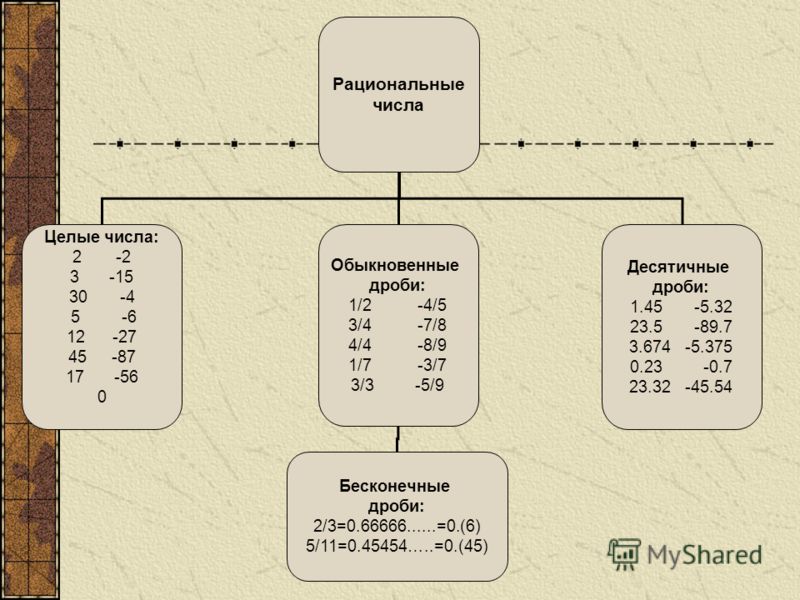

Вопрос, который вы цитируете под заголовком «Какая разница между рациональными и иррациональными — топологически?» на самом деле на несколько другую тему: речь идет не о различии между одним видом чисел и другим, а скорее о различии между набором ВСЕХ чисел одного вида и набором ВСЕХ чисел другого вида. Вам нужно знать некоторую топологию, чтобы понять ответы. Но вопрос, который вы ставите, проще.

$\endgroup$

$\begingroup$

Один из способов представить это — использовать десятичные расширения, с которыми вы, скорее всего, знакомы. Пусть $a$ — число, для удобства рассмотрим только числа от $0$ до $1$ и рассмотрим разложение по основанию 10 $a=0.a_1a_2a_3\dots$, где каждое $a_i$ — целое число от $0$ до $1$. $9$. Десятичное расширение рационального числа либо завершится (заканчивается бесконечным числом $0$), либо завершится повторением одной и той же конечной цепочки чисел до бесконечности.

Принимая во внимание, что иррациональное число не прекратится и не будет повторяться бесконечно много раз.

Тогда легко создать иррациональное число, например, число $0,10100100010000100000\dots$ нерационально. Идти в обратном направлении часто намного труднее, но есть много примеров достаточно доступных доказательств иррациональности. Вы можете прочитать о доказательствах иррациональности $\sqrt2$ и $\sqrt3$, так как они оба довольно просты.

$\endgroup$

$\begingroup$

Чтобы понять, является ли данное число иррациональным, нужно знать, как оно построено.
Учитывая ваши математические способности (как вы утверждаете, они не очень высоки), вам следует проверять числа, в которых нет повторяющихся десятичных знаков.
Например, число $0,1234567…$ и т. д. иррационально (доказательство этого не очень простое).
Теперь вы можете составить иррациональное число самостоятельно: выберите число с апериодическим десятичным например $1. 24681012…$ и вот оно: Вам удалось найти иррациональное!
Еще одна вещь, которую вы должны знать об иррациональных числах, это то, что если вы выберете случайное число из всего множества действительных чисел, вероятность того, что оно иррациональное, равна 100%. (Удивительный факт, не так ли?)

$\endgroup$

2

$\begingroup$

Рациональное число можно записать в виде дробного числа. Однако иррациональное наоборот. Его нельзя записать в виде дроби.

25, 16, 4 — полный квадратный корень. Это тоже рациональные числа. Другое число, такое как 5, 7, 13 и т. д., является иррациональным числом, потому что у этих чисел нет идеального квадратного корня.

Вы можете использовать программу проверки рациональных и иррациональных чисел, если у вас возникли проблемы с проверкой рациональности или иррациональности числа.

0 число также включено в список рациональных чисел.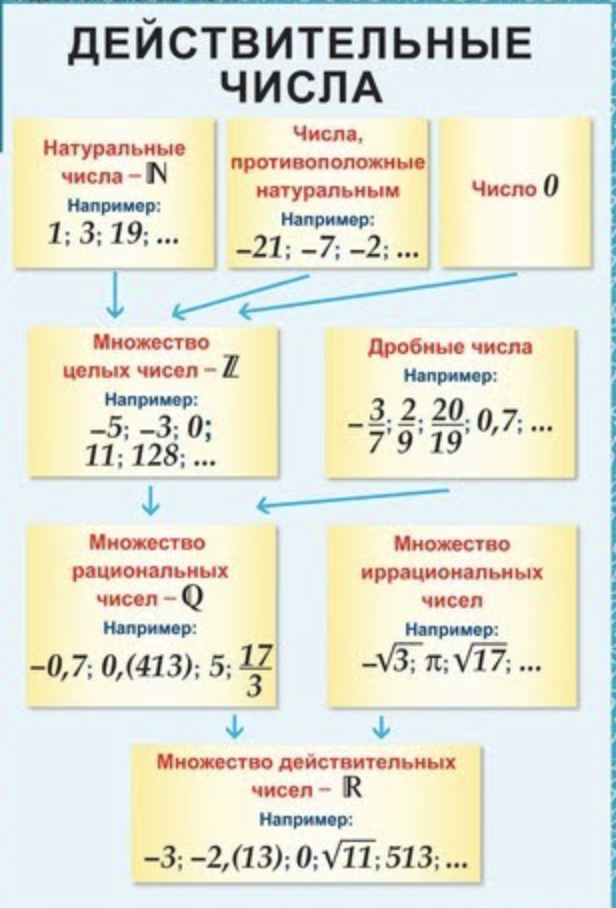

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

7 Различия между рациональными и иррациональными числами

Дом Математика 7 Различия между рациональными и иррациональными числами

Числа можно разделить на различные категории, такие как действительные числа, мнимые числа, рациональные, иррациональные, целые числа, натуральные числа, четные числа, нечетные числа и т. д. В зависимости от того, может ли действительное число быть представлено в виде p/q, мы может классифицировать числа как рациональные и иррациональные числа. В этой статье мы обсудим 7 различий между рациональными и иррациональными числами.

Что такое рациональные числа?

Рациональное число — это тип действительного числа, которое можно представить как отношение двух чисел в виде p/q, где q не равно нулю. Любая дробь с ненулевым знаменателем может рассматриваться как рациональное число. Примеры рациональных чисел: 4, 3, 3/4, 5/8, 0. Число «0» также является рациональным числом.

Что такое иррациональные числа?

Иррациональные числа — это действительные числа, которые не могут быть представлены простой дробью в виде p/q. Другими словами, мы не можем составить отношение для иррационального числа. Примеры включают объемы, круговую диаграмму, число Эйлера, золотое сечение и т. д.

Difference between rational and irrational numbers

COMPARISON	Rational Numbers	Irrational numbers
MEANINGS	Rational numbers are the numbers that can be represented as отношение двух чисел. Они существуют в виде p/q, где q≠0. 2 может быть представлен 2/1.	Иррациональные числа — это числа, которые нельзя представить как отношение двух чисел. Номер 3.14159265358979………. . не может быть представлено в форме p/q.
СВОЙСТВА	Замыкание Свойство: Для двух рациональных чисел, скажем a и b, результаты операций сложения, вычитания и умножения дают рациональное число. 2 + 3 = 5; 2*3 = 6; 2-3 = -1 Распределительное  свойство: Если a, b и c три рациональных числа, [a * (b + c)] = (a * b) + (a * c) Тождество и обратное свойство : Свойство идентичности: 0 — аддитивная идентичность, а 1 — мультипликативная идентичность для рациональных чисел. аддитивная идентичность: 2/4 + 0 = 2/4 обратное свойство: 2/4*1 = 2/4 обратное свойство: Для рационального числа x/y аддитивное обратное свойство равно -x/y и y / x — мультипликативная обратная. a/b + (-a/b) = 0 [2/4 + (-2/4)] a/b*b/a = 1 Коммутативный   Свойство: Для рациональных чисел, сложения и умножения коммутативны. а + b = b + а; a × b = b × a Где a и b рациональны. Ассоциативное свойство: Если x, y и z рациональны, то для сложения: x+(y + z)=(x + y)+z	•Сложение иррационального числа и рационального числа дает иррациональное число. 3 + 3,141592…….. = 6,141592……(иррациональное) • Умножение любого иррационального числа на любое ненулевое рациональное число дает иррациональное число. √3 * 3 = 5,196………..(иррациональное) • Сложение или умножение двух иррациональных чисел может быть рациональным числом. √3 * √3 = 3 (рациональное)
ПРИРОДА	Они в основном включают те числа, которые конечны и повторяются по своей природе. например: 3,4, 4, 5,66, 7,32, 5	Они носят непрерывный или неповторяющийся характер. например: 3.141592……, 1.618033988…….
СОСТОИТ ИЗ	Они состоят из чисел, являющихся полными квадратами.	Они состоят из сурдов, таких как √3, √2, √5 и т. д. равен нулю.	Они не могут быть представлены в дробной форме.
Примеры	2/4, 3/4, 5/8	√5, √3
Применение в реальной жизни
. очень часто используется в экономике, потребительских данных и т. д.	пирог — иррациональное число, используемое при расчете площади и периметра круга, золотое сечение φ = 1,61803398874989…. Корни часто используются в тригонометрии, число Эйлера

Сходства между рациональными и иррациональными числами

И рациональные, и иррациональные числа являются действительными числами. Таким образом, они обладают теми же свойствами, что и вещественные числа.

• Собственность закрытия
• Коммутативная недвижимость
• Ассоциативная недвижимость
• Распределительная собственность

См. Также

• PERIMET0022
• Числовая строка
• Целые числа
• Четные числа
• Арифметическая прогрессия
• Векторы

Предыдущая статья9 Различия между испарением и конденсацией

Следующая статья10 Различия между вогнутой и выпуклой линзой

Поиск

Видео дня

Поддержите нас

Мы хотим делать науку одновременно интересной и бесплатной! Ваш вклад в эту страницу поможет нам донести качественный контент до детей, которые больше всего в нем нуждаются. Если вам нравится, что мы делаем, и вы хотите поддержать нас, вы можете посетить нашу страницу пожертвований ko-fi на www.ko-fi.com/dewwool.

Категории

• Анимация
• Биология
• Блог
• Химия
  • Органическая химия
• Математика
• Физика
  • Оптика и акустика
• Викторина
• Без категории
• Рабочие листы

Комикс дня

Архивы

Архивы Выбрать месяц Октябрь 2022 г. Август 2022 г. Июль 2022 г. Июнь 2022 г. Май 2022 г. Апрель 2022 г. Март 2022 г. Январь 2022 г. Декабрь 2021 г. Ноябрь 2021 г. Октябрь 2021 г. Сентябрь 2021 г. Август 2021 г. Август 2020 Июль 2020 Июнь 2020 Май 2020 Март 2020

Последние сообщения

Рабочие листы отдела | Бесплатный PDF

админ — 10 октября 2022 0

Здесь, в этой статье, мы представляем вам бесплатные загружаемые рабочие листы по делению. Эти рабочие листы помогут учащимся понять концепцию деления и методы…

Рабочие листы на вычитание с перегруппировкой | Бесплатные PDF-файлы

админ — 9 октября, 2022 0

Вычитание может стать сложным, если число, из которого вы «вычитаете», меньше числа, «которое вычитается». Это часто встречается в…

Рабочие листы по вычитанию для 4-го класса | Бесплатный PDF

админ — 9 октября 2022 0

Эта статья содержит рабочие листы с вычитанием четырехзначных чисел, подходящие для учащихся 4 класса. Для простого вычитания двузначных или однозначных чисел вы можете прочитать наш рабочий лист…

Самая популярная

Нагрузка Подробнее

Разница между рациональными и иррациональными номерами

Серия испытаний

от Aina Parasher | Обновлен: 20 июня, 2022

1 UPVOTE0 Комментарии

Share

разница между rational Rational Rational Rational Rational и ilration Comments

. : Давайте подробно изучим разницу между рациональными и иррациональными числами. Положительные целые числа 1, 2, 3 и т. д., которые используются для счета, являются простейшими числами в полной системе счисления. Натуральные числа были с нами на протяжении тысячелетий. Введение обыкновенных дробей, таких как 1/2, 2/3, 6/7 и т. д., было вызвано основными потребностями повседневной жизни. Они известны как рациональные числа. Целые числа, целые числа, натуральные числа, действительные числа и комплексные числа — все это примеры чисел. Действительные числа делятся на две категории:

• Рациональные числа
• Иррациональные числа

Рациональные числа — это целые числа, которые могут быть представлены в виде p/q (и числитель, и знаменатель — целые числа), тогда как иррациональные числа — это те, которые не могут быть выражены дробью. Кроме того, в этой статье мы представили разницу между рациональными и иррациональными числами, а также краткое введение в рациональные числа и иррациональные числа.

Содержание

• 1. В чем разница между рациональными и иррациональными числами?
• 2. Что такое рациональные и иррациональные числа?
• 3. Как отличить рациональные числа от иррациональных?
• 4. Примеры рациональных и иррациональных чисел

Прочитать статью полностью

В чем разница между рациональными и иррациональными числами?

Основное различие между рациональными и иррациональными числами заключается в том, что число, которое можно записать в виде отношения двух целых чисел, называется рациональным числом, тогда как число, которое нельзя представить в виде отношения двух целых чисел, называется иррациональное число. Далее, давайте посмотрим на различные различия, упомянутые в таблице ниже.

Ключевая разница между рациональными и иррациональными числами

Рациональные числа	Иррациональные числа
Рациональные числа могут быть выражены в форме p/q.	Иррациональные числа не могут быть выражены в виде p/q.
И числитель, и знаменатель являются полными числами в рациональных числах, а знаменатель не равен нулю.	Дробь не может быть записана для иррационального числа.
Рациональные числа включают в себя совершенные квадраты, такие как 9, 16, 25 и т. д.	Иррациональные числа включают такие сурды, как 2, 3, 5, 7 и т. д.
В рациональное число входят только конечные и повторяющиеся десятичные дроби. .	Иррациональные числа — это те, чье десятичное представление безгранично, неповторяемо и не имеет шаблона.

Что такое рациональные и иррациональные числа?

Если число можно представить в виде дроби, причем числитель и знаменатель являются целыми числами, а знаменатель — натуральным числом, то оно называется рациональным (ненулевым числом). Все рациональные числа являются целыми числами, дробями, включая смешанные дроби, повторяющимися десятичными дробями, конечными десятичными дробями и так далее.

Если число не может быть уменьшено ни до какой доли целого или натурального числа, оно называется иррациональным числом. Его также можно интерпретировать как иррациональное число. Десятичное расширение иррационального числа не является ни конечным, ни рекуррентным. Surds и необычные числа, такие как пи и e, являются примерами иррациональных чисел.

Здесь также можно проверить систему счисления.

Как отличить рациональные числа от иррациональных?

Все целые числа, дроби и повторяющиеся десятичные дроби являются рациональными числами, и их можно выразить дробями. Следующие условия могут быть использованы для идентификации рациональных чисел:

• Записывается как a/b, где b≠0.
• Соотношение a/b также можно упростить и представить в десятичной форме.

Неразумные числа называются иррациональными. Иррациональные числа могут быть выражены в десятичной форме, но не в виде дробей, что означает, что они не могут быть выражены как отношение двух целых чисел.

После запятой рациональные числа имеют бесконечное количество неповторяющихся цифр.

Примеры рациональных и иррациональных чисел

После обсуждения разницы между рациональными и иррациональными числами. Давайте рассмотрим несколько примеров из этих двух, чтобы полностью понять концепцию рациональных и иррациональных чисел.

• 6 — Рациональное число, завершающееся и неповторяющееся по своей природе.
• 4/5 — Рациональное число в форме p/q и q≠0.
• √7 — Иррациональное число, квадратный корень из числа, не являющегося полным квадратом.
• √16 — Рациональное число, представляет собой квадратный корень из полного квадрата и имеет значение 4,9.0022

Часто задаваемые вопросы о разнице между рациональными и иррациональными числами

• В чем разница между рациональными и иррациональными числами?

  Разница между рациональным и иррациональным числом заключается в том, что рациональное число может быть записано как p/q, где p и q — целые числа, а q не равно нулю. Однако иррациональное число не может быть выражено простыми дробями.

• Как определить разницу между рациональным и иррациональным числом?

  Число является рациональным, если оно является завершающим или повторяющимся десятичным числом, например 1/2 = 0,5.

  Иррациональные числа, такие как 0,31545673…, являются непрерывающимися и неповторяющимися десятичными знаками.

• Все ли рациональные числа являются целыми числами?

  Нет, рациональные числа не всегда являются целыми числами. Все числа, которые заканчиваются или повторяются, являются рациональными числами. Целое число — это любое число, которое больше или равно нулю и не имеет дробной части. Например, 2,9является рациональным, но не целым числом.

• Как определить, является ли число иррациональным?

  Если число нельзя записать в виде p/q, то такие числа называются иррациональными числами. В то время как действительная система счисления имеет бесконечное количество иррациональных чисел, квадратные корни несовершенных квадратов, такие как квадратный корень из 2, и константы пи и е чаще всего используются в математике.

• Какое из следующих чисел не является иррациональным? √7, √5, √16, √11.

  16 — правильный квадрат, поэтому ответ — √16.

  = 4, что является рациональным числом.

  Как мы все знаем, квадратный корень из простых чисел — иррациональное число. Простые числа включают 7, 5 и 11. Таким образом, единственное число, которое не является иррациональным, — это 16.

  No related posts.