Как разделить число на матрицу: Как делить матрицы

Изучаем матрицы в питоне и массивы NumPy в Python

2022-08-01

Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:

Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.

• Матрицы в Python
• NumPy массивы в Python
• Как создать массив NumPy?
  • Массив целых чисел, чисел с плавающей точкой и составных чисел
  • Массив нулей и единиц
  • Использование arange() и shape()
• Операции с матрицами
  • Сложение двух матриц или сумма элементов массива Python
  • Умножение двух матриц Python
  • Транспонирование матрицы питон
• Доступ к элементам матрицы, строкам и столбца
  • Доступ к элементам матрицы
  • Доступ к строкам матрицы
  • Доступ к столбцам матрицы
• Разделение матрицы

Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:

A = [[1, 4, 5], 
    [-5, 8, 9]]

Этот список является матрицей на 2 строки и 3 столбца.

Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.

Давайте посмотрим, как работать с вложенным списком.

A = [[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]]
print("A =", A) 
print("A[1] =", A[1])      # вторая строка
print("A[1][2] =", A[1][2])   # третий элемент второй строки
print("A[0][-1] =", A[0][-1])   # последний элемент первой строки
column = [];        # пустой список
for row in A:
  column.append(row[2])   
print("3rd column =", column)

Когда мы запустим эту программу, результат будет следующий:

A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]
A [1] = [-5, 8, 9, 0]
A [1] [2] = 9
A [0] [- 1] = 12
3-й столбец = [5, 9, 11]

Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .

NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,

• Ознакомьтесь: Как установить NumPy Python?
• Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.

После установки NumPy можно импортировать и использовать его.

NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:

import numpy as np
a = np.array([1, 2, 3])
print(a)               # Вывод: [1, 2, 3]
print(type(a))         # Вывод: <class 'numpy.ndarray'>

Как видите, класс массива NumPy называется ndarray.

Существует несколько способов создания массивов NumPy.

import numpy as np
A = np.array([[1, 2, 3], [3, 4, 5]])
print(A)
A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой
print(A)
A = np. array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)

Когда вы запустите эту программу, результат будет следующий:

[[1 2 3]
 [3 4 5]]
[[1.1 2. 3.]
 [3. 4. 5.]]
[[1. + 0.j 2. + 0.j 3. + 0.j]
 [3. + 0.j 4. + 0.j 5. + 0.j]]

import numpy as np
zeors_array = np.zeros( (2, 3) )
print(zeors_array)
'''
 Вывод:
 [[0. 0. 0.]
  [0. 0. 0.]]
'''
ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype
print(ones_array)      # Вывод: [[1 1 1 1 1]]

Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2

import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
''' 
Вывод:
A = [0 1 2 3]
B = [[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
'''

Узнайте больше о других способах создания массива NumPy .

Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.

Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.

import numpy as np
A = np.array([[2, 4], [5, -6]])
B = np.array([[9, -3], [3, 6]])
C = A + B      # сложение соответствующих элементов
print(C)
''' 
Вывод:
[[11  1]
 [ 8  0]]
 '''

Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .

Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.

import numpy as np
A = np.array([[3, 6, 7], [5, -3, 0]])
B = np.array([[1, 1], [2, 1], [3, -3]])
C = a.dot(B)
print(C)
''' 
Вывод:
[[ 36 -12]
 [ -1   2]]
'''

Мы используем numpy.transpose для вычисления транспонирования матрицы.

import numpy as np
A = np.array([[1, 1], [2, 1], [3, -3]])
print(A.transpose())
''' 
Вывод:
[[ 1  2  3]
 [ 1  1 -3]]
'''

Как видите, NumPy значительно упростил нашу задачу.

Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.

import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0])     # Первый элемент     
print("A[2] =", A[2])     # Третий элемент     
print("A[-1] =", A[-1])   # Последний элемент     

Когда вы запустите эту программу, результат будет следующий:

A [0] = 2
A [2] = 6
A [-1] = 10

Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).

import numpy as np
A = np.array([[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
#  Первый элемент первой строки
print("A[0][0] =", A[0][0])  
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])     

Когда мы запустим эту программу, результат будет следующий:

A [0] [0] = 1
A [1] [2] = 9
A [-1] [- 1] = 19

import numpy as np
A = np. array([[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)

Когда мы запустим эту программу, результат будет следующий:

A [0] = [1, 4, 5, 12]
A [2] = [-6, 7, 11, 19]
A [-1] = [-6, 7, 11, 19]

import numpy as np
A = np.array([[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)

Когда мы запустим эту программу, результат будет следующий:

A [:, 0] = [1 -5 -6]
A [:, 3] = [12 0 19]
A [:, - 1] = [12 0 19]

Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».

Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:

import numpy as np
letters = np. array([1, 3, 5, 7, 9, 7, 5])
# с 3-го по 5-ый элементы
print(letters[2:5])        # Вывод: [5, 7, 9]
# с 1-го по 4-ый элементы
print(letters[:-5])        # Вывод: [1, 3]   
# с 6-го до последнего элемента
print(letters[5:])         # Вывод:[7, 5]
# с 1-го до последнего элемента
print(letters[:])          # Вывод:[1, 3, 5, 7, 9, 7, 5]
# список в обратном порядке
print(letters[::-1])          # Вывод:[5, 7, 9, 7, 5, 3, 1]

Теперь посмотрим, как разделить матрицу.

import numpy as np
A = np.array([[1, 4, 5, 12, 14], 
    [-5, 8, 9, 0, 17],
    [-6, 7, 11, 19, 21]])
print(A[:2, :4])  # две строки, четыре столбца
''' Вывод:
[[ 1  4  5 12]
 [-5  8  9  0]]
'''
print(A[:1,])  # первая строка, все столбцы
''' Вывод:
[[ 1  4  5 12 14]]
'''
print(A[:,2])  # все строки, второй столбец
''' Вывод:
[ 5  9 11]
'''
print(A[:, 2:5])  # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
 [ 9  0 17]
 [11 19 21]]
'''

Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами.

Пожалуйста, оставьте свои мнения по текущей теме статьи. За комментарии, подписки, лайки, дизлайки, отклики огромное вам спасибо!

Вадим Дворниковавтор-переводчик статьи «Python Matrices and NumPy Arrays»

Матрица Эйзенхауэра: что это, как пользоваться, примеры

Тренды

Телеканал

Газета

Pro

Инвестиции

РБК+

Новая экономика

Тренды

Недвижимость

Спорт

Стиль

Национальные проекты

Город

Крипто

Дискуссионный клуб

Исследования

Кредитные рейтинги

Франшизы

Конференции

Спецпроекты СПб

Конференции СПб

Спецпроекты

Проверка контрагентов

РБК Библиотека

Подкасты

ESG-индекс

Политика

Экономика

Бизнес

Технологии и медиа

Финансы

РБК КомпанииРБК Life

РБК Тренды

Фото: Shutterstock

Чтобы не отвлекаться на бесполезные дела и не откладывать важные, нужно верно расставлять приоритеты. В этом помогает Матрица Эйзенхауэра — метод тайм-менеджмента самого продуктивного президента США

1

Что такое матрица Эйзенхауэра

Матрица Эйзенхауэра — это метод тайм-менеджмента, помогающий расставлять приоритеты: делать важное и не тратить время на ненужное. Он подойдет всем, кто хочет разобраться с личным и рабочим временем, научиться планировать расписание, которое не съезжает. Матрица состоит из четырех квадратов: срочно и важно, несрочно и важно, срочно и неважно, несрочно и неважно. Идея такой матрицы отдаленно пересекается со знаменитым «правилом Парето», согласно которому 20% усилий приводят к 80% результата и наоборот.

Матрица Эйзенхауэра

Идея распределять дела по такой методике появилась у 34-го президента США Дуайта Эйзенхауэра, руководившего страной с 1953-го по 1961 год. Эйзенхауэра считают одним из самых продуктивных президентов в истории Штатов.

Метод Эйзенхауэра оформил и популяризировал американский консультант Стивен Кови, описав его в книге «Семь навыков высокоэффективных людей».

Эффективность метода подтверждает исследование 2018 года [1]. Большинство людей выбирают срочные, а не важные дела. Ученые предложили участникам эксперимента выбрать, что делать в первую очередь. Срочные дела выбирали люди, которые описывали себя как «занятые». Зато когда их попросили обдумать последствия выбора той или иной задачи, они отдавали приоритет важным делам.

Читайте также: «Правила делегирования» — подборка РБК Pro

2

Как пользоваться матрицей Эйзенхауэра

Прежде чем заполнять матрицу, отследите в течение нескольких дней, какие задачи вы выполняете и сколько времени они отнимают. После наблюдения положите перед собой список дел и к каждому задайте три вопроса:

1. Была ли задача для меня срочной?
2. Была ли она для меня важной?
3. Я единственный, кто мог это сделать?

Когда распределите задачи по блокам, посмотрите, в каком квадрате их больше всего. Последовательно разбирайтесь с каждым квадратом. В будущем старайтесь оставлять в одном квадрате не больше восьми задач, причем личные и рабочие задачи считаются вместе. А перед тем как добавлять новое дело, завершите одно из списка.

3

Квадрат 1 — срочные и важные

Оперативно подхватить проект, пока коллега на больничном, закрыть задачу, прилетевшую за три часа до дедлайна, вылечить зуб с острой болью, — срочные и важные дела. Они требуют быстрого ответного действия. Обычно у таких задач есть осязаемые дедлайны и последствия, если не выполнить их вовремя. Сюда отнесем дела, возникшие из-за кризисов или форс-мажоров.

Если таких задач большинство. Возможно, у вас проблемы. Задачи в этом квадрате неизбежны, ведь ситуации и события, которыми нельзя управлять, будут происходить всегда. Но если фокусироваться только на срочных и важных делах, можно «заработать» хронический стресс, эмоциональное выгорание и ощущение потери контроля над жизнью. Это приведет к «внутренней миграции» — делам из четвертого квадрата.

Что делать. Старайтесь оставить здесь как можно меньше дел. Разработайте план по достижению актуальных целей. Поставьте дедлайны, составьте расписание. Проверьте в конце недели, что вы успели сделать, какие результаты получились и что будете делать на следующей неделе. Если срочные и важные задачи приходят извне, подумайте, как это предотвратить. Например, поговорите с начальством, коллегами или клиентом о перераспределении нагрузки или поменяйте рабочий план.

4

Квадрат 2 — несрочные и важные

Занятия в тренажерном зале, изучение языков, учеба на образовательных курсах — это задачи, связанные не с решением проблем, а с личным ростом. Эти дела помогают двигаться к долгосрочным целям с самыми ценными результатами. У них может не быть дедлайна или конечного срока, поэтому часто мы заменяем несрочные важные дела задачами из списка срочных.

Подкаст об образовании не поможет зарабатывать больше уже завтра, но поможет спланировать свою образовательную траекторию, чтобы зарабатывать больше в будущем. Это несрочно, но важно.

Если таких задач большинство. Вы расходуете свои ресурсы на то, что считаете важным. Уровень стресса снижается, вы почувствуете себя еще лучше, когда увидите первые результаты своих инвестиций.

Что делать. Это идеальная ситуация. Поддерживайте и сохраняйте ее как можно дольше.

5

Квадрат 3 — срочные и неважные

Сюда попадает проверка электронной почты и мессенджеров, рассылки документов, мытье посуды и другие бытовые дела. Это рутинные задачи, их результата ждут другие люди, но это почти не приближает вас к собственным целям. Автор книги «Сделай это завтра» Марк Форстер называет это занятостью. Занятость мешает делать «настоящую работу».

Если таких задач большинство. В этом квадрате можно увидеть эффект срочности: вы можете чувствовать драйв от поставленных галочек напротив списка дел. Как говорит знаменитый инвестор Уоррен Баффетт, каждым вечером следует задавать себе вопрос: «Стал ли я умнее сегодня, научился ли чему-то новому за день?» Другое дело, когда этот список состоит из мелких задач, которые почти ничего для вас не значат. Вместе с этим возникает ощущение, что вы занимаетесь не тем. Растет недовольство собой и своей жизнью.

Что делать. Стивен Кови советует делегировать такие задачи: службам доставки, личным ассистентам, клининговой службе, подрядчикам. Важно при этом грамотно делегировать задачи, чтобы не растерять уважение сотрудников, избегая при этом проявлений авторитаризма. Если делегирование невозможно — снизить их влияние на расписание. Например, выключать уведомления мессенджеров, ясно обозначать другим, сколько вам нужно времени на задачу, и говорить «нет», если таких дел становится слишком много. Еще один способ — заниматься задачами третьего квадрата, когда в первом и втором уже ничего нет.

6

Квадрат 4 — несрочные и неважные

Сюда попадают просмотры сериалов, пролистывание ленты в соцсетях и сортировка писем вместо ответа на них. Это «убийцы времени»: за этими занятиями мы проводим часы, но не получаем от них практической пользы в долгосрочной перспективе. Конечно, желание отвлечься, отдохнуть, полениться — это естественно. Самого Эйзенхауэра критиковали за игру в гольф в рабочее время. Но гольф и бридж создавали баланс между личным временем и стрессовой работой президента.

В долгосрочной перспективе «убийцы времени» мешают достигать важных целей. Исследование 2019 года, опубликованное в Journal of Applied Psychology, это доказывает [2]. Ученые нашли взаимосвязь между досугом сотрудников и их продуктивностью на следующий день. Исследователи выяснили, что работники, которые накануне долго смотрели передачи, пришли на работу с хорошим настроем. Но к концу недели их настроение ухудшалось, а мотивация падала. При этом работники, которые занимались спортом, йогой, медитацией, слушали музыку и помогали другим, чувствовали себя более спокойными и мотивированными.

Если таких задач большинство. Вы можете застрять в рутине. Из-за этого появится стресс и ощущение эскапизма, бегства от проблем.

Что делать. Фиксируйте время. Это поможет определить главных «убийц времени». Когда их найдете, подумайте, чем их заменить или ограничить.

7

Где собирать матрицу Эйзенхауэра

Блокнот или тетрадь. Не имеет значения, будут ли это разлинованные листы или нет — главное, чтобы вы осознавали границы между квадратами. Чтобы сделать распределение нагляднее, используйте разные цвета и шрифты для каждого блока.

Матрица Эйзенхауэра на бумаге

Todoist. В приложении можно маркировать задачи с помощью четырех уровней приоритетности, которые можно отфильтровать.

Матрица Эйзенхауэра в Todoist

Notion. Оформить матрицу в Notion можно несколькими способами. Например, создать базу с автоматическим присваиванием тега к задачам. Чтобы пользоваться такой матрицей, скопируйте шаблон у автора. Шаблон на английском языке.

Матрица Эйзенхауэра в Notion

Evernote. Это приложение для заметок. В нем есть шаблон матрицы, который можно настроить под себя: выбрать цвета, задачи. Можно заводить отдельную заметку с матрицей на каждый месяц, неделю или день.

Матрица Эйзенхауэра в Evernote

Обновлено 08.06.2022

Текст

Наталья Шацкова

Урок 21. Векторы и матрицы в Mathcad

Павел Демидов 12.11.2014 Уроки Mathcad 2

С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.

Введение

В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:

Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:

Теперь рассмотрим несколько матриц:

Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).

Элемент матрицы можно вывести, используя подстрочные индексы:

Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:

Запомните: первое число – номер строки (или их количество), второе – столбца.

Элементы, выделенные с помощью подстрочных индексов:

Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:

Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:

Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:

Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.

Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.

В Mathcad

Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:

Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:

Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:

Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:

Операции с матрицами

Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:

Транспонирование

Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:

Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:

Поэлементные операции

Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:

Затем выберите все выражение и примените векторизацию:

Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:

Другие поэлементные операции:

Поэлементные операции применимы только к массивам одного размера.

Сложение и вычитание

Сложение и вычитание выполняется поэлементно:

Эта операция также применима лишь к массивам одного размера.

С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):

Скалярное произведение

Умножение на константу работает так:

При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:

Заметьте, что последовательность множителей играет роль:

Скалярное произведение не коммутативно, за исключением особых случаев:

Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:

Векторное произведение

Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:

Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.

Обратная матрица

Обратная матрица определяется только для квадратных матриц:

Произведение матрицы и ее обратной матрицы является единичной матрицей:

Произведение матрицы и единичной матрицы дает изначальную матрицу:

Определитель

Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:

Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:

Для скаляра определитель равен его модулю:

Для вектора команда Определитель вычисляет длину вектора:

Резюме

В этом уроке мы рассмотрели векторы и матрицы (массивы).

1. Элементы массива можно вывести с помощью подстрочного индекса – один индекс для вектор-столбца, два – для других массивов. Первое индекс – для строк, второй – для столбцов.
2. Есть специальные команды для извлечения отдельных строк и столбцов.
3. Векторы и матрицы создаются и редактируются с помощью команд со вкладки Матрицы/таблицы.

Операции над векторами и матрицами, которые мы рассмотрели:

1. Транспонирование.
2. Поэлементные операции.
3. Сложение и вычитание.
4. Скалярное произведение.
5. Векторное произведение.
6. Поиск обратной матрицы.
7. Поиск определителя.

About Павел Демидов

Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.

View all posts by Павел Демидов →

Пользовательские единицы измерения в Mathcad

Урок 22. Линейные уравнения в Mathcad

Массив разделения NumPy

❮ Предыдущий Далее ❯

Разделение массивов NumPy

Разделение — это операция, обратная объединению.

Объединение объединяет несколько массивов в один, а разделение разбивает один массив на несколько.

Мы используем array_split() для разделения массивов, мы передаем массив, который хотим разделить и количество разделений.

Пример

Разделить массив на 3 части:

импортировать numpy как np

arr = np.array([1, 2, 3, 4, 5, 6])

новая ошибка = np.array_split(arr, 3)

print(newarr)

Попробуйте сами »

Примечание: Возвращаемое значение представляет собой массив, содержащий три массива.

Если в массиве меньше элементов, чем требуется, он соответствующим образом подстроится с конца.

Пример

Разделить массив на 4 части:

импортировать numpy как np

arr = np.array([1, 2, 3, 4, 5, 6])

newarr = np.array_split (пример, 4)

печать (новый)

Попробуйте сами »

Примечание: У нас также есть метод split() , но он не будет корректировать элементы, когда элементов меньше исходный массив для разделения, как в примере выше, array_split() работал правильно, но split() завершится ошибкой.

Разбить на массивы

Возвращаемое значение метода array_split() представляет собой массив, содержащий каждое разбиение в виде массива.

Если вы разделите массив на 3 массива, вы можете получить к ним доступ только из результата как любой элемент массива:

Пример

Доступ к разделенным массивам:

импортировать numpy как np

arr = np.array([1, 2, 3, 4, 5, 6])

newarr = np.array_split(arr, 3)

print(newarr[0])
print(newarr[1])
print(newarr[2])

Попробуйте сами »

Разделение двумерных массивов

Использование тот же синтаксис при разбиении двумерных массивов.

Использовать метод array_split() , передать массив ты хочешь разделить и количество сплитов, которые вы хотите сделать.

Пример

Разделить двумерный массив на три двумерных массива.

импортировать numpy как np

arr = np. array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10], [11, 12]])

newarr = np.array_split(arr, 3)

print(newarr)

Попробуйте сами »

В приведенном выше примере возвращаются три двумерных массива.

Давайте посмотрим на другой пример, на этот раз каждый элемент в двумерных массивах содержит 3 элемента.

Пример

Разделить двумерный массив на три двумерных массива.

импортировать numpy как np

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12], [13, 14, 15], [16, 17, 18]])

newarr = np.array_split(arr, 3)

print(newarr)

Попробуйте сами »

Пример выше возвращает три двумерных массива.

Кроме того, вы можете указать, вокруг какой оси вы хотите выполнить разделение.

В приведенном ниже примере также возвращаются три двумерных массива, но они разделены вдоль строка (ось = 1).

Пример

Разделить двумерный массив на три двумерных массива по строкам.

импортировать numpy как np

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12], [13, 14, 15], [16, 17, 18]])

newarr = np.array_split(arr, 3, axis=1)

print(newarr)

Попробуйте сами »

Альтернативное решение использует hsplit() напротив hstack()

Пример

Используйте метод hsplit() для разделения двумерного массива на три двумерных массива по строкам.

импортировать numpy как np

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12], [13, 14, 15], [16, 17, 18]])

newarr = np.hsplit(arr, 3)

print(newarr)

Попробуйте сами »

Примечание: Аналогично альтернативам vstack() и dstack() доступны как vsplit() и dsplit() .

❮ Предыдущий Следующий ❯

NEW

Мы только что запустили
Видео W3Schools

Узнать

ВЫБОР ЦВЕТА

КОД ИГРЫ

Играть в игру

Top Tutorials

900 Справочник Справочник по HTML
Справочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery

Лучшие примеры

ФОРУМ | О

W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения. Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования, куки-файлы и политика конфиденциальности.

Copyright 1999-2022 Refsnes Data. Все права защищены.
W3Schools работает на основе W3.CSS.

Как разделить каждый элемент в списке на Python делитель для элемента в заданном_списке]

Читайте дальше, чтобы узнать о многих других решениях.

Проблема: Как разделить каждый элемент в списке и получить результирующий список, содержащий частные?

Пример:

 li = [38, 57, 76, 95, 114, 161,5]
число = 19
# Какой-то способ разделить каждый элемент li на 19 

Ожидаемый результат:

 [2. 0, 3.0, 4.0, 5.0, 6.0, 8.5] 

Итак, без дальнейших проволочек, давайте углубимся в критический вопрос и узнать различные способы ее решения.

Содержание

Как разделить каждый элемент в списке в Python

Посмотрите это видео на YouTube

Подход:

• Создайте пустой список, в котором будут храниться частные.
• Перебрать все элементы в данном списке, используя цикл for .
• Разделить каждый элемент на заданное число/делитель и добавить результат в результирующий список.
• Наконец, отобразите результирующий список после того, как все частные были вычислены и добавлены к нему.

Код:

 li = [38, 57, 76, 95, 114, 161,5]
число = 19
разрешение = []
для val в ли:
    res. append(значение/число)
Печать (RES) 

Выход:

 [2.0, 3,0, 4,0, 5,0, 6,0, 8,5] 

📌 Прочитайте здесь: Python Loops

в наиболее Pythonic решение данной проблемы.

Подход: Создайте понимание списка таким образом, чтобы:

• Выражение: a/num представляет деление каждого элемента в списке на заданный делитель. Здесь переменная контекста и представляет каждый элемент в данном списке, а num представляет делитель.
• Контекст: Контекст содержит переменную контекста a , которая охватывает все элементы в списке таким образом, что на каждой итерации она представляет элемент с определенным индексом на этой итерации.

Код:

 li = [38, 57, 76, 95, 114, 161,5]
число = 19
res = [a/num для a в ли]
print(res) 

Вывод:

 [2. 0, 3.0, 4.0, 5.0, 6.0, 8.5] 

💎 Краткий обзор списка понятий в Python:

3 компактный способ List 0

2

2 создание списков. Простая формула: [выражение + контекст] .
⦿ Выражение: Что делать с каждым элементом списка?
⦿ Контекст: Какие элементы выбрать? Контекст состоит из произвольного числа операторов вместо и if .
⦿ В примере   [x вместо x в диапазоне (3)]   создается список   [0, 1, 2] .

📌 Рекомендуем прочитать: Понимание списков в Python — полезное иллюстрированное руководство0031 Идея состоит в том, чтобы использовать анонимную лямбда-функцию для вычисления деления каждого элемента на заданный делитель. Вы можете передать каждый элемент списка функции lambda в качестве входных данных с помощью встроенной функции map .

Код:

 li = [38, 57, 76, 95, 114, 161,5]
число = 19
res = список (карта (лямбда x: x / число, li))
print(res) 

Вывод:

 [2.0, 3.0, 4.0, 5.0, 6.0, 8.5] 

💎 Readers Digest:

• Функция map() преобразует одну или несколько итераций в новую, применяя «функцию преобразования» к i-м элементам каждой итерации. Аргументами являются объект функции преобразователя и одна или несколько итераций . Если вы передаете n итераций в качестве аргументов, функция преобразования должна быть n -арной функцией , принимающей n входных аргументов. Возвращаемое значение представляет собой итерируемый объект карты преобразованных и, возможно, агрегированных элементов.

Освоение функции карты в Python [+Видео]

Посмотрите это видео на YouTube

📌 Подробнее о map() читайте здесь: Python map() — наконец осваиваем функцию карты в Python [+Видео]

• Лямбда-функция — это анонимная функция в Python. Он начинается с ключевого слова  lambda , за которым следует список из нуля или более аргументов, разделенных запятыми, двоеточие и возвращаемое выражение. Например, lambda x, y, z: x+y+z  вычислит сумму трех значений аргументов x+y+z .

Давайте поиграем в Finxter — лямбда-функция в Python

Посмотрите это видео на YouTube

📌 Узнайте больше о map() здесь: Лямбда-функции в Python: простое введение

 импортировать numpy как np
li = [38, 57, 76, 95, 114, 161,5]
обр = np.массив(ли)
число = 19рез = обр/число
print(res.tolist()) 

 [2.0, 3.0, 4.0, 5.0, 6.0, 8. 5] 

 импортировать numpy как np
li = [38, 57, 76, 95, 114, 161,5]
обр = np.массив(ли)
число = 19
res = np.divide (обр, число)
print(res.tolist()) 

 [2.0, 3.0, 4.0, 5.0, 6.0, 8.5] 

 numpy.divide(x1, x2, /, out=None, *, where=True, cast='same_kind', order='K', dtype=None, subok=True[ подпись , extobj]) 

 импортировать numpy как np
# Создание 2D списков
а = [[1, 2, 3],
     [4, 5, 6]]
б = [[2, 4, 6],
     [8, 10, 12]]
# Преобразование списков в двумерные массивы NumPy
а = np. массив (а)
б = np.массив (б)
# Разделить 2D-массивы
print(a / b) 

 [[0,5 0,5 0,5] 
 [0,5 0,5 0,5]] 

Мы успешно изучили четыре разных способа деления элементов в данном списке с заданным номером. Я надеюсь, что это руководство помогло ответить на все ваши вопросы. Пожалуйста, подпишитесь на и следите за обновлениями для получения более интересных уроков. Приятного обучения! 🙂

Парсинг веб-страниц с помощью BeautifulSoup

Одним из самых востребованных навыков на Fiverr и Upwork является  парсинг веб-страниц  . Не заблуждайтесь:  извлечение данных с веб-сайтов программными средствами   – это жизненно важный навык в современном мире, который формируется благодаря Интернету и удаленной работе. Этот курс научит вас тонкостям библиотеки BeautifulSoup Python для парсинга веб-страниц.

Шубхам Сайон

Я профессиональный блоггер Python и создатель контента. Я опубликовал множество статей и создал курсы за определенный период времени. В настоящее время я работаю штатным фрилансером и имею опыт работы в таких областях, как Python, AWS, DevOps и Networking.

Вы можете связаться со мной по адресу:

UpWork
LinkedIn

Функция разделения VBA в Excel — объяснение с примерами

При работе с VBA в Excel может возникнуть необходимость разделить строку на разные части на основе разделителя.

Например, если у вас есть адрес, вы можете использовать функцию разделения VBA, чтобы получить разные части адреса, разделенные запятой (которая в данном случае будет разделителем).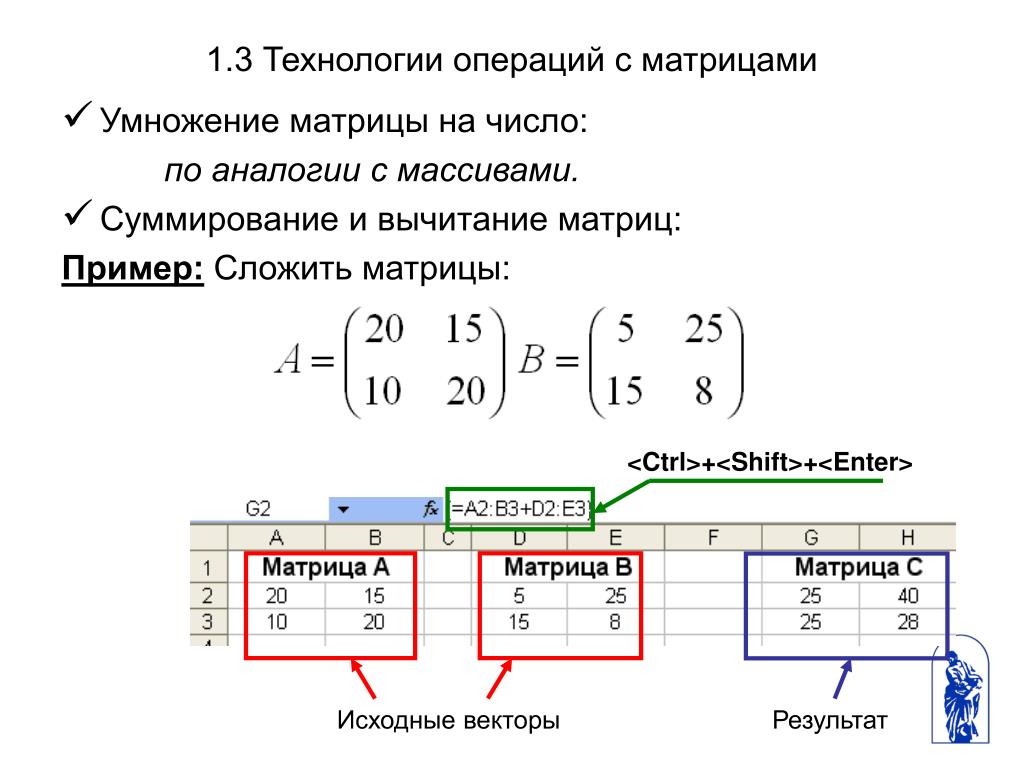

SPLIT — это встроенная строковая функция в Excel VBA, которую можно использовать для разделения текстовой строки на основе разделителя.

Это руководство охватывает:

 Разделить ( Выражение, [Разделитель], [Предел], [Сравнить] ) 

• Выражение: Это строка, которую вы хотите разделить на основе разделителя. Например, в примере с адресом весь адрес будет «выражением». В случае, если это строка нулевой длины («»), функция SPLIT вернет пустой массив.
• Разделитель: Это необязательный аргумент. Это разделитель, который используется для разделения аргумента «Выражение». В нашем примере с адресом запятая — это разделитель, который используется для разделения адреса на разные части. Если вы не укажете этот аргумент, символ пробела считается разделителем по умолчанию. Если вы укажете строку нулевой длины («»), функция вернет всю строку «Выражение».
• Ограничение: Это необязательный аргумент. Здесь вы указываете общее количество подстрок, которые хотите вернуть. Например, если вы хотите вернуть только первые три подстроки из аргумента «Выражение», это будет 3. Если вы не укажете этот аргумент, по умолчанию будет -1, что возвращает все подстроки.
• Сравните: Это необязательный аргумент. Здесь вы указываете тип сравнения, которое вы хотите, чтобы функция SPLIT выполняла при оценке подстрок. Доступны следующие варианты:
  • Когда сравнение равно 0 : Это двоичное сравнение. Это означает, что если ваш разделитель представляет собой текстовую строку (скажем, ABC), то регистр будет чувствительным. «ABC» не будет равно «abc».
  • Когда сравнение равно 1 : это сравнение текста. Это означает, что если ваш разделитель представляет собой текстовую строку (скажем, ABC), то даже если у вас есть «abc» в строке «Выражение», он будет рассматриваться как разделитель.

Теперь, когда мы рассмотрели основы функции SPLIT, давайте рассмотрим несколько практических примеров.

Пример 1. Разделение слов в предложении

Предположим, у меня есть текст — «Быстрая коричневая лиса перепрыгивает через ленивую собаку».

Я могу использовать функцию SPLIT, чтобы получить каждое слово этого предложения как отдельный элемент в массиве.

Приведенный ниже код будет следующим:

 Sub SplitWords()
Dim TextString как строка
Dim Result () как строка
TextStrng = "Быстрая коричневая лиса перепрыгивает через ленивую собаку"
Результат () = Разделить (текстовая строка)
End Sub 

Хотя код не делает ничего полезного, он поможет вам понять, что делает функция Split в VBA.

Функция разделения разделяет текстовую строку и присваивает каждое слово массиву результатов.

Итак, в этом случае:

• Результат(0) сохраняет значение «The»
• Результат(1) сохраняет значение «Быстрый»
• Результат(2) сохраняет значение «Коричневый» и так далее.

В этом примере мы указали только первый аргумент — текст, который необходимо разделить. Поскольку разделитель не указан, в качестве разделителя по умолчанию используется пробел.

Важное примечание.

1. Функция VBA SPLIT возвращает массив, который начинается с основания 0.
2. Когда результат функции SPLIT присваивается массиву, этот массив должен быть объявлен как тип данных String. Если вы объявите его как тип данных Variant, он покажет ошибку несоответствия типа). Обратите внимание, что в приведенном выше примере я объявил Result() как тип данных String.

Пример 2. Подсчет количества слов в предложении

Вы можете использовать функцию РАЗДЕЛИТЬ, чтобы получить общее количество слов в предложении. Хитрость здесь заключается в подсчете количества элементов в массиве, который вы получаете, когда разделяете текст.

Приведенный ниже код покажет окно сообщения с количеством слов:

 Sub WordCount()
Dim TextString как строка
Dim WordCount как целое число
Dim Result () как строка
TextStrng = "Быстрая коричневая лиса перепрыгивает через ленивую собаку"
Результат = Разделить (текстовая строка)
Количество слов = UBound(Результат()) + 1
MsgBox "Количество слов равно" & WordCount
End Sub 

В этом случае функция UBound сообщает нам верхнюю границу массива (т. е. максимальное количество элементов в массиве). Поскольку основание массива равно 0, для получения общего количества слов добавляется 1.

Вы можете использовать аналогичный код для создания пользовательской функции в VBA, которая будет принимать текст в качестве входных данных и возвращать количество слов.

Приведенный ниже код создаст эту функцию:

 Функция WordCount (CellRef As Range)
Dim TextString как строка
Dim Result () как строка
Результат = Разделить (WorksheetFunction.Trim (CellRef.Text), "")
Количество слов = UBound(Результат()) + 1
End Function 

После создания вы можете использовать функцию WordCount, как и любую другую обычную функцию.

Эта функция также обрабатывает начальные, конечные и двойные пробелы между словами. Это стало возможным благодаря использованию функции TRIM в коде VBA.

Если вы хотите узнать больше о том, как эта формула работает для подсчета количества слов в предложении, или хотите узнать о способе подсчета слов с помощью формулы, отличной от VBA, ознакомьтесь с этим руководством.

Пример 3. Использование разделителя, отличного от пробела

В предыдущих двух примерах мы использовали только один аргумент в функции SPLIT, а остальные были аргументами по умолчанию.

Если вы используете другой разделитель, вам нужно указать его в формуле SPLIT.

В приведенном ниже коде функция SPLIT возвращает массив, основанный на запятой в качестве разделителя, а затем показывает сообщение с каждым словом в отдельной строке.

 Подразделитель запятых()
Dim TextString как строка
Dim Result () как строка
Затемнить DisplayText как строку
TextStrng = "The,Quick,Brown,Fox,Jump,Over,The,Lazy,Dog"
Результат = Разделить (TextString, ",")
Для i = LBound(Result()) To UBound(Result())
DisplayText = DisplayText и Результат (i) и vbNewLine
Далее я
MsgBox DisplayText
Конец суб 

В приведенном выше коде я использовал цикл For Next, чтобы просмотреть каждый элемент массива «Результат», назначив его переменной «DisplayText».

Пример 4.

С помощью функции РАЗДЕЛИТЬ вы можете указать количество разделений, которые вы хотите получить. Например, если я ничего не укажу, каждый экземпляр разделителя будет использоваться для разделения строки.

Но если я укажу ограничение 3, то строка будет разбита только на три части.

Например, если у меня есть следующий адрес:

  2703 Winifred Way, Indianapolis, Indiana, 46204  

, я могу использовать функцию Split в VBA, чтобы разделить этот адрес на три части.

Разбивает первые два на основе разделителя-запятой, а оставшаяся часть становится третьим элементом массива.

Приведенный ниже код покажет адрес в трех разных строках окна сообщения:

 Sub CommaSeparator()
Dim TextString как строка
Dim Result () как строка
Затемнить DisplayText как строку
TextStrng = "2703 Winifred Way, Indianapolis, Indiana, 46204"
Результат = Разделить (TextString, ",", 3)
Для i = LBound(Result()) To UBound(Result())
DisplayText = DisplayText и Результат (i) и vbNewLine
Далее я
MsgBox DisplayText
Конец суб 

Одно из практических применений этого может быть, когда вы хотите разделить однострочный адрес в формат, показанный в окне сообщения. Затем вы можете создать пользовательскую функцию, которая возвращает адрес, разделенный на три части (каждая часть в новой строке).

Следующий код сделает это:

 Функция ThreePartAddress(cellRef As Range)
Dim TextString как строка
Dim Result () как строка
Затемнить DisplayText как строку
Результат = Разделить (cellRef, ",", 3)
Для i = LBound(Result()) To UBound(Result())
DisplayText = DisplayText и Обрезать (Результат (i)) и vbNewLine
Далее я
ThreePartAddress = Mid(DisplayText, 1, Len(DisplayText) - 1)
Завершить функцию 

Если у вас есть этот код в модуле, вы можете использовать функцию (ThreePartAddress) в рабочей книге, как и любую другую функцию Excel.

Эта функция принимает один аргумент – ссылку на ячейку с адресом.

Обратите внимание, что для того, чтобы результирующий адрес отображался в трех разных строках, необходимо применить к ячейкам формат переноса текста (он находится на вкладке «Главная» в группе «Выравнивание»). Если формат «Перенос текста» не включен, вы увидите весь адрес в виде одной строки.

Пример 5. Получение названия города из адреса

С помощью функции разделения в VBA вы можете указать, какую часть результирующего массива вы хотите использовать.

Например, предположим, что я разбиваю следующий адрес на основе запятой в качестве разделителя:

 2703 Winifred Way, Indianapolis, Indiana, 46204 

Результирующий массив будет выглядеть примерно так, как показано ниже:

 {"2703 Winifred Way ", "Индианаполис", "Индиана", "46204"} 

Поскольку это массив, я могу отображать или возвращать определенную часть этого массива.

Ниже приведен код пользовательской функции, в которой вы можете указать число, и она вернет этот элемент из массива. Например, если мне нужно имя состояния, я могу указать 3 (поскольку это третий элемент в массиве).

 Функция ReturnNthElement (CellRef как диапазон, ElementNumber как целое число)
Dim Result () как строка
Результат = Разделить (CellRef, ",")
ReturnNthElement = Результат (ElementNumber - 1)
End Function 

Вышеприведенная функция принимает два аргумента: ссылку на ячейку с адресом и номер элемента, который вы хотите вернуть. Функция Split разделяет элементы адреса и присваивает их переменной Result.

Затем он возвращает номер элемента, который вы указали в качестве второго аргумента. Обратите внимание, что поскольку основание равно 0, ElementNumber-1 используется для возврата правильной части адреса.

Эта пользовательская формула лучше всего подходит, когда у вас есть единый формат для всех адресов, т. е. город всегда упоминается после двух запятых. Если данные не согласуются, вы не получите желаемого результата.

Если вам нужно название города, вы можете использовать 2 в качестве второго аргумента. Если вы используете число, превышающее общее количество элементов, будет возвращено значение #VALUE! ошибка.

Вы можете еще больше упростить код, как показано ниже:

 Функция ReturnNthElement(CellRef As Range, ElementNumber As Integer)
ReturnNthElement = Split(CellRef, ",")(ElementNumber - 1)
End Function 

В приведенном выше коде вместо использования переменной Result возвращается только указанный номер элемента.