| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Калькулятор производной в точке
Введение в калькулятор производной в точке
Калькулятор производной — это онлайн-инструмент, который позволяет вычислять производную в заданной точке функции, не прибегая к длительным вычислениям.
Он использует значение функции в качестве входных данных и интервал, с которым вы хотите рассчитать скорость изменения этой функции.
В исчислении производная в точке является важным понятием, которое определяет скорость изменения любой функции. Он аппроксимирует заданную функцию в конце изменения. Мы представляем онлайн-инструмент, который поможет вам рассчитать производные в заданной точке на касательной.
Как использовать пошаговый калькулятор производной в точке?
С помощью этого инструмента нетрудно найти производные в точке, потому что он обеспечивает простое и быстрое решение ваших математических задач. Есть несколько простых и легких шагов, чтобы использовать этот инструмент. Это:
- Запишите значение функции в поле «Введите функцию».
- Выберите порядок производных из «вычисляет с».
- Теперь выберите точку из «Когда x=».
- Нажмите кнопку «Рассчитать» после просмотра функции, которая появляется при вводе входного значения.
Вы получите решение в течение минуты после нажатия кнопки расчета.
Онлайн-калькулятор производной с пошаговой формулой
Производная в точке относится к аппроксимации функции в точке. При этом дифференцировании мы сначала находим производную функции, а затем подставляем в нее точку.
Формула
Пусть f — функция, и в области определения f(x) есть точка x=a. Тогда производная f(x) по точке x=a равна
$$ f'(a) \;=\; \frac{f(a+h)-f(a)}{h} $$
Где,
f’a= Производная в a.
Калькулятор производной в точке использует эту формулу для аппроксимации заданной функции относительно точки.
Как найти производную в точке онлайн-калькулятором?
Этот инструмент несложно найти в Интернете. Вы можете выполнить поиск в своем браузере. Он доступен на сайте калькулятора. На этом сайте также есть множество различных математических инструментов.
Зачем использовать калькулятор формулы производной в точке?
Производная в точке и обычная производная — два запутанных, но важных понятия для учащихся.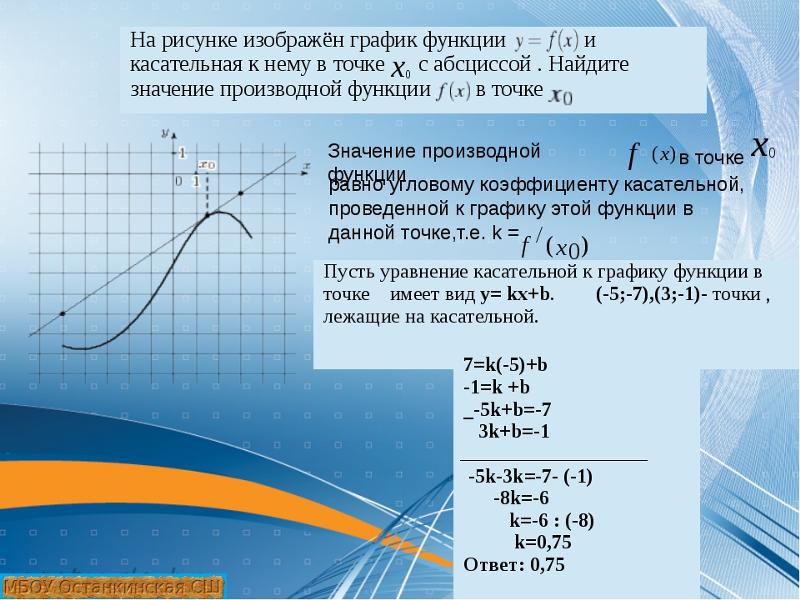
Это понятие помогает найти наклон касательной к графику функции в точке. Поэтому он имеет множество приложений в математике и физике. Например, нахождение наклона в определенной точке выполняется путем нахождения производной в этой точке.
Можно запутаться в формуле при вычислении Производной в точке ручными вычислениями. Это потому, что обычная производная и производная в точке состоят почти из одних и тех же формул. Есть лишь небольшая разница, которая сбивает с толку студентов. Поэтому вам нужно использовать этот инструмент, чтобы избежать путаницы. Если вы хотите быстро найти производную от экстремума, вы также можете воспользоваться онлайн-калькулятором экстремумов.
Преимущества использования калькулятора второй производной в точке
Сегодня, в соответствии с последними технологическими обновлениями, нам необходимо обновить наши методы обучения с его помощью. Итак, следуя этому требованию, мы предлагаем вам калькулятор второй производной в баллах, который может дать вам много преимуществ не только в учебе, но и в улучшении ваших навыков решения задач.