Отрицательные числа рациональные числа: Рациональные числа и действия с ними — что это, определение и ответ

Рациональные числа и действия с ними — что это, определение и ответ

Рациональные числа – это числа, представленные в виде отношения \(\frac{m}{n}\), где m – целое число, а n – натуральное.

Они могут быть как положительными, так и отрицательными.

Целые и дробные числа вместе образуют множество рациональных.

1. Любое целое число является рациональным, потому что его можно записать в виде \(\frac{m}{1}\).

Например:

\(–4 = \frac{- 4}{1}\)

\(2 = \frac{2}{1}\)

\(0 = \frac{0}{1}\)

2. Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.

3. Любое рациональное число можно записать в виде десятичной или периодической дроби.

Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.

Например:

\(\frac{1}{3} = 0,33333333..\)

Повторяющиеся цифры периодической дроби записывают в скобках, например:

\(\frac{1}{3} = 0,(3)\)

\(\frac{5}{11} = 0,45454545 = 0,(45)\)

СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение:

1. Переместительное свойство:

\(a + b = b + a\)

2. Сочетательное свойство:

\(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c\)

3. Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:

\(a + 0 = a\)

\(a + ( — a) = 0\)

Умножение:

1. Переместительное свойство:

\(ab = ba\)

2. Сочетательное свойство:

\(a(bc) = (ab)c = (ac)b = abc\)

3. Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:

\(a \bullet 1 = a\)

\(a \bullet \frac{1}{a} = 1\)

4. Если один из множителей равен нулю, то и всё произведение равно 0:

\(a \bullet 0 = 0\)

\(0 \bullet b = 0\)

\(0 \bullet 0 = 0\)

5. Распределительное свойство:

\((a + b)c = ac + сb\)

ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.

СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:

Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.

Например:

1. Сравним числа 1,5 и 4:

Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.

\(4 > 1,5\)

2. Сравним числа 3,5 и -1:

Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.

\(3,5 > — 1\)

3. Сравним числа -2,5 и -3:

Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.

\(- 2,5 > — 3\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).

Например:

1. Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:

Видим, что \(1 + 2,5 = 3,5\).

Сумма положительных чисел – положительное число.

2. Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.

Получилось, что \(- 1 + ( — 2) = — 3.\)

Сумма отрицательных чисел – отрицательное число.

3. Найдем разность положительных чисел 4 – 1,5. Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:

Получилось, что \(4\ –1,5 = 2,5.\)

Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.

4. Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:

Получим, что \(2–4 = — 2.\)

Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.

5. Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

6. Найдем сумму двух противоположных чисел 3 + (-3). От координаты 3 пройдем 3 отрезка в отрицательном направлении:

Видим, что \(3 + ( — 3) = 0.\)

Сумма двух противоположных чисел \(\mathbf{= 0.}\)

УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

1. Рациональные числа умножаются и делятся не смотря на знак.

2. Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.

Например:

\(3 \bullet 4 = 12\)

\(- 6 \bullet ( — \frac{1}{2}) = 3\)

\(7:( — 2) = — 3,5\)

\(- 12:\frac{1}{3} = — 12 \bullet 3 = — 36\)

Сравнение рациональных чисел

Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.

Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.

Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.

В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы

4 > 1

Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:

Из двух положительных чисел больше то число, модуль которого больше.

Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.

Например, сравним те же числа 4 и 1, применяя вышеприведенное  правило

Находим модули чисел:

|4| = 4

|1| = 1

Сравниваем найденные модули:

4 > 1

Отвечаем на вопрос:

4 > 1

Для отрицательных чисел существует другое правило, выглядит оно следующим образом:

Из двух отрицательных чисел больше то число, модуль которого меньше.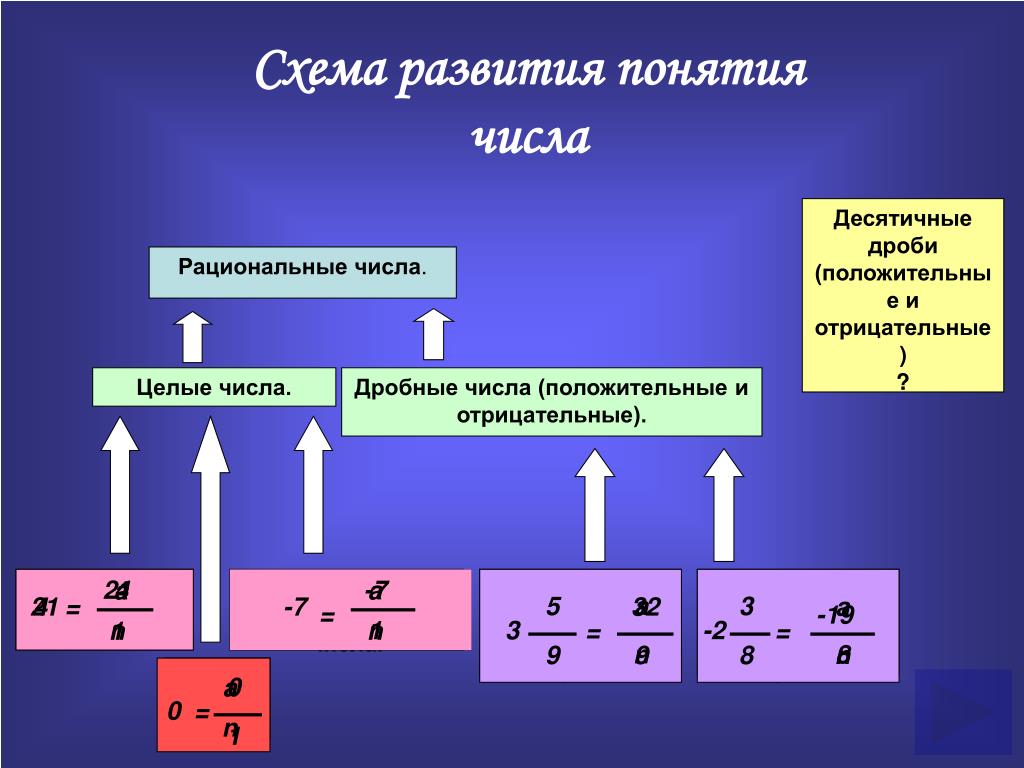

Например, сравним числа −3 и −1

Находим модули чисел

|−3| = 3

|−1| = 1

Сравниваем найденные модули:

3 > 1

Отвечаем на вопрос:

−3 < −1

Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.

Число −3 меньше, чем число −1. Это можно понять, если воспользоваться координатной прямой

Видно, что число −3 лежит левее, чем −1. А мы знаем, что чем левее, тем меньше.

---

Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2

−4 < 2

Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».

Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса

−4 < +2

---

Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.

Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет видоизменять, чтобы сделать его более простым для сравнения и восприятия.

Пример 1. Сравнить рациональные числа

Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что    меньше, чем

---

Пример 2. Сравнить рациональные числа   и 

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем  , потому что модуль числа меньше, чем модуль числа

---

Пример 3. Сравнить числа 2,35 и

Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем что 2,35 больше, чем

2,35 > 

---

Пример 4. Сравнить рациональные числа   и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше.

Значит рациональное  больше, чем  , потому что модуль числа  меньше, чем модуль числа

---

Пример 5. Сравнить рациональные числа 0 и

Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем

---

Пример 6. Сравнить рациональные числа 0 и 

Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем

---

Пример 7. Сравнить рациональные числа 4,53 и 4,403

Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.

Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль

4,530

Далее применим правило сравнения положительных чисел.

Находим модули чисел

|4,530| = 4,530

|4,403| = 4,403

Сравниваем найденные модули:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403

4,53 > 4,403

---

Пример 8. Сравнить рациональные числа   и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число  в неправильную дробь, затем приведём обе дроби к общему знаменателю:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное  больше, чем  , потому что модуль числа  меньше, чем модуль числа 

---

Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.

Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.

Пример 9. Сравнить рациональные числа 15,4 и 2,1256

Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256

|15| = 15

|2| = 2

15 > 2

поэтому и дробь 15,4 больше, чем дробь 2,1256

15,4 > 2,1256

Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа

15,4000   2,1256

154000 > 21256

Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.

---

Пример 10. Сравнить рациональные числа −15,2 и −0,152

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей

|−15| = 15

|−0| = 0

15 > 0

Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.

А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2

 −0,152 > −15,2

---

Пример 11. Сравнить рациональные числа −3,4 и −3,7

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:

|−3| = 3

|−3| = 3

3 = 3

В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули

|−3,4| = 3,4

|−3,7| = 3,7

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7

−3,4 > −3,7

---

Пример 12. Сравнить рациональные числа 0,(3) и 

Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.

Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью  . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)

0,(3)  < 

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Могут ли отрицательные числа быть рациональными числами?

Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.

A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это единственный способ представления чисел в арифметической и алгебраической структуре.

Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.

Числа обычно также известны как цифры — это математические значения, используемые для подсчета, измерений, маркировки и измерения основных величин.

Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Оно представлено цифрами как 2,4,7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.

Типы чисел

Существуют различные типы чисел на множества по действительной системе счисления. Типы описаны ниже:

• Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Множество натуральных чисел представлено ‘ N ’. Это числа, которые мы обычно используем для счета. Набор натуральных чисел можно представить как N = 1, 2, 3, 4, 5, 6, 7,…
• Целые числа: Целые числа — это положительные числа, включая ноль, который считается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен как « W ». Набор может быть представлен как W = 0, 1, 2, 3, 4, 5,…
• Целые числа: Целые числа представляют собой набор чисел, включающий все положительные числа, нуль, а также все отрицательные числа, которые считаются от отрицательной бесконечности к положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается ‘ З ’. Набор целых чисел можно представить в виде Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…
• Десятичные числа: Любые числовое значение, состоящее из десятичной точки, является десятичным числом. Его можно выразить как 2,5, 0,567 и т. д.
• Вещественное число: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается как ‘ R ‘.
• Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается ‘ C ’.
• Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘ Q ’.
• Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается ‘ P ’.

Могут ли отрицательные числа быть рациональными числами?

Ответ:

Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается буквой Q.

Пример: -4 , -6 , -14 , 0 , 1 , 2 , 5 и т.д. числа, форма p/q, большинству людей трудно отличить дроби от рациональных чисел.

При делении рационального числа выходные данные представляются в десятичной форме, которая может быть либо оканчивающейся, либо повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.

Рациональное число — это разновидность действительного числа, имеющая форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.

Здесь ответ на поставленный выше вопрос: ДА отрицательные числа являются рациональными числами как рациональное число включает все целые числа, как положительные, так и отрицательные.

Похожие вопросы …. является рациональным числом.

Ответ:

Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 8.1515…. имеет повторяющиеся цифры.

Следовательно, 8,1515…. является рациональным числом.

Вопрос 2.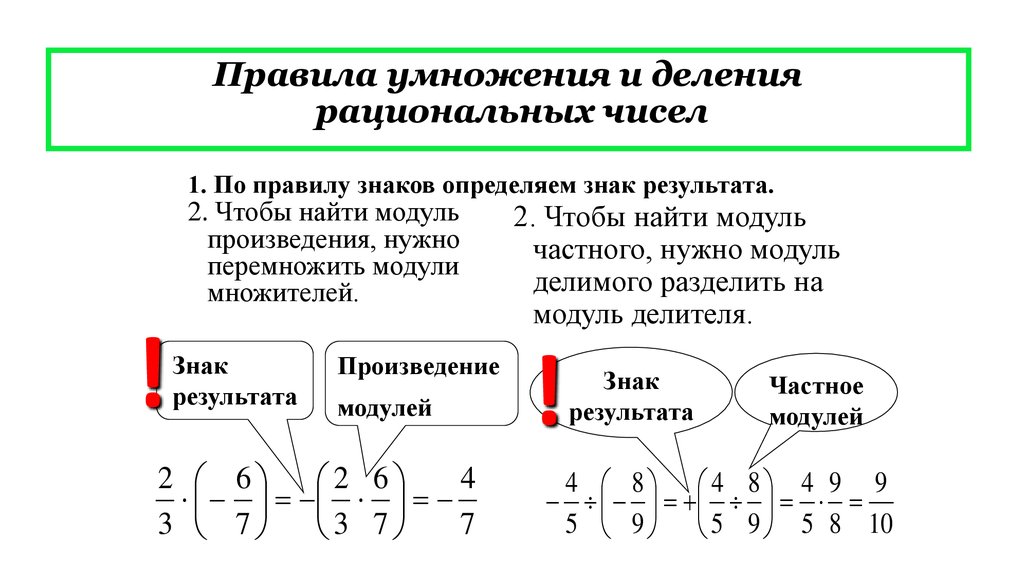 Является ли число π рациональным или иррациональным?

Ответ:

Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.

Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».

Здесь данное число π не может быть выражено в виде p/q.

Значит, π — иррациональное число.

Вопрос 3: Определите, является ли -8 рациональным или иррациональным числом.

Ответ:

Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков.

Рациональное число — это своего рода действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом.

Здесь заданное число -8 является рациональным числом.

Вопрос 4: Является ли -5 рациональным числом или нет?

Ответ:

Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков.

Здесь заданное число -5 является рациональным числом, поскольку целые числа являются частью рационального числа.

Отрицательные рациональные числа — определение, представление, примеры

Рациональные числа определяются как числа, которые могут быть выражены в форме p/q, где q ≠ 0. Когда либо числитель, либо знаменатель p/q имеет отрицательный знак, рациональное число известно как отрицательное рациональное число.

число. В этой статье мы будем больше изучать отрицательные рациональные числа.

1.	Определение отрицательных рациональных чисел
2.	Отрицательные рациональные числа в числовой строке
3.	Стандартная форма отрицательных рациональных чисел
4.	Часто задаваемые вопросы об отрицательных рациональных числах

Определение отрицательных рациональных чисел

Рациональные числа со знаком минус называются отрицательными рациональными числами. При заданном рациональном числе p/q, если одно из значений ‘p’ или ‘q’ отрицательно, мы получаем — p/q, которое является отрицательным рациональным числом. Следовательно, когда знак «минус» ставится перед рациональным числом, это дает нам отрицательное рациональное число. Например: — 4/5, — 7/6 и т.д.

Отрицательные рациональные числа в числовой строке

Представление отрицательных рациональных чисел в числовой строке очень похоже на представление отрицательных целых чисел или отрицательных дробей в числовой строке. Левая часть 0 на числовой прямой представляет отрицательную область, а правая часть 0 представляет положительную область. Давайте рассмотрим шаги для представления отрицательных рациональных чисел на числовой прямой, как показано ниже.

Нанесем на числовую прямую — 2/3.

Шаг I: Нарисуйте числовую линию, отметив 0 в качестве точки отсчета.

Шаг II: Определите рациональные числа, между которыми лежит рациональное число, и отметьте их. — 2/3 лежит между 0 и -1.

Шаг III: Отметьте количество делений между отмеченными на шаге II рациональными числами, равными знаменателю данного рационального числа. Здесь — 2/3 имеет 3 в знаменателе. Таким образом, мы сделаем 3 деления.

Шаг IV: Начиная с 0, двигаться влево на количество шагов, равное числителю заданного рационального числа. Для — 2/3 мы будем двигаться на 2 единицы влево.

Таким образом, мы представили — 2/3 на числовой прямой, как показано выше.

Стандартная форма отрицательных рациональных чисел

Когда числитель и знаменатель отрицательного рационального числа имеют наибольший общий делитель, равный 1, а знаменатель является положительным числом, говорят, что оно имеет стандартную форму. Другими словами, стандартная форма отрицательного рационального числа, скажем, p/q выражается в простейшей форме, в которой знаменатель всегда является положительным числом. Таким образом, мы можем заключить, что для стандартной формы отрицательного рационального числа числитель всегда является отрицательным числом.
Если знаменатель является отрицательным числом, мы умножаем -1 на числитель и знаменатель, чтобы изменить знаменатель на положительное число. Давайте рассмотрим несколько примеров, чтобы понять это.

Пример: Express 8/(-16) в стандартной форме.

Знаменатель данного рационального числа 8/(-16) равен -16, что является отрицательным числом. Следовательно, мы умножаем — 1 и на числитель, и на знаменатель.

[8 × (-1)] / [-16 × (-1)] = — 8/16

Также мы видим, что — 8/16 не является упрощенным. GCF 8 и 16 равен 2. Таким образом, при упрощении — 8/16 = — 1/2. Следовательно, стандартная форма данного отрицательного рационального числа — 1/2.

Статьи по теме

Проверьте эти статьи, связанные с концепцией отрицательных рациональных чисел.

• Рациональные числа
• Номер строки
• Целые числа
• Дроби
• Целые числа

 

Примеры отрицательных рациональных чисел

1. Пример 1: Выразите заданное отрицательное рациональное число -2/4 в стандартной форме.

   Решение: Данное отрицательное рациональное число -2/4 имеет отрицательный числитель и положительный знаменатель, что соответствует правилам стандартной формы. Но -2/4 не в упрощенной форме. НОД 2 и 4 равен 2. Таким образом, упрощая -2/4, мы получаем -1/2. Следовательно, стандартная форма данного рационального числа -2/4 равна -1/2.

2. Пример 2. Представьте отрицательные рациональные числа -1/5, -2/5 и -3/5 на числовой прямой.

   Решение: Мы знаем, что -1/5, -2/5 и -3/5 лежат между рациональными числами 0 и -1.

   Так как знаменатель равен 5, мы произведем 5 делений между 0 и -1 и пометим рациональные числа, перемещаясь влево, что эквивалентно числителям -1/5, -2/5 и -3/5.

   Таким образом, мы представили -1/5, -2/5 и -3/5 на числовой прямой.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по отрицательным рациональным числам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы об отрицательных рациональных числах

Что такое отрицательные рациональные числа?

Отрицательные рациональные числа определяются как рациональные числа со знаком «минус». Для заданного рационального числа x/y, если одно из значений «x» или «y» является отрицательным числом, мы получаем отрицательное рациональное число. Например: — 4/3, — 6/7 и т.д.

Что такое положительные и отрицательные рациональные числа?

Положительное рациональное число определяется как число, которое выражается как a/b, где b ≠ 0, а ‘a’ и ‘b’ являются либо положительными, либо отрицательными числами. Например: 2/3, (-5)/(-7) = 5/7 и т. д. Отрицательное рациональное число очень похоже на положительное рациональное число, за исключением того факта, что либо «а», либо «b» отрицательный. Например: — 1/2, — 3/7 и т. д.

Что такое сумма двух отрицательных рациональных чисел?

Сумма двух отрицательных рациональных чисел всегда является отрицательным рациональным числом.
Например: — 3/5 + (- 4)/5
= — 3/5 — 4/5
= (- 3 — 4) / 5 = — 7/5

Чему равно произведение двух отрицательных рациональных чисел?

Произведение двух отрицательных рациональных чисел всегда является положительным рациональным числом.