3 корень 3 степени из х производная
Вы искали 3 корень 3 степени из х производная? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x корень x производная, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «3 корень 3 степени из х производная».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.

Где можно решить любую задачу по математике, а так же 3 корень 3 степени из х производная Онлайн?
Решить задачу 3 корень 3 степени из х производная вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
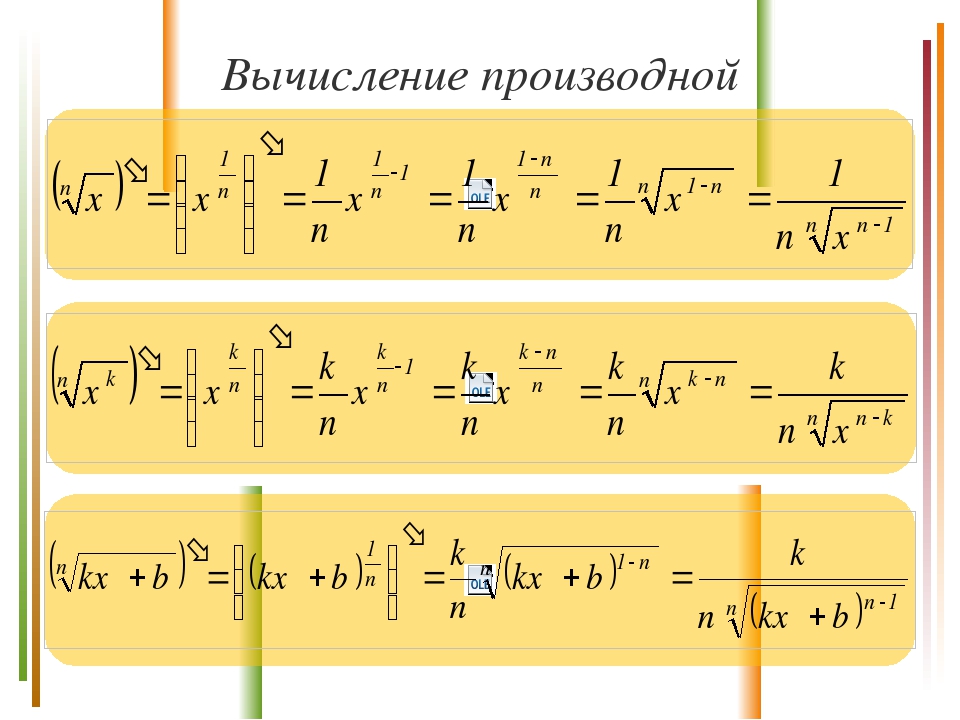
Как найти производную корня
В задачах по математическому анализу иногда требуется найти производную корня. (-⅔).
(-⅔).Продифференцировав все корни, внимательно посмотрите на остальные части примера. Если в ответе у вас получилось очень громоздкое выражение, то наверняка его можно упростить. Большинство школьных примеров составлено таким образом, чтобы в итоге получилось небольшое число или компактное выражение.
Во многих задачах на нахождение производной, корни (квадратные и кубические) встречаются вместе с другими функциями. Чтобы найти производную корня в этом случае, применяйте следующие правила:
• производная константы (постоянного числа, C) равняется нулю: C’ = 0;
• постоянный множитель выносится за знак производной: (k*f)’ = k * (f)’ (f – произвольная функция) ;
• производная суммы нескольких функций равняется сумме производных: (f + g)’ = (f)’ + (g)’;
• производная произведения двух функций равняется… нет, не произведению производных, а следующему выражению: (fg)’ = (f)’g + f (g)’;
• производная частного также равняется не частному производных, а находится согласно следующего правила: (f/g)’ = ((f)’g – f(g)’) / g².
Производная показательно-степенной функции | Математика
Мы рассмотрели общую схему нахождения производной показательно-степенной функции. Производная показательно-степенной функции вычисляется достаточно легко. Рассмотрим конкретные примеры.
Найти производную показательно-степенной функции:
Это показательно-степенная функция, поскольку и основание, и показатель степени содержат переменную x.
Действуем по схеме: сначала логарифмируем обе части по основанию e:
Показатель степени выносим за знак логарифма:
Теперь дифференцируем обе части равенства, с учетом того, что y=y(x), а значит, lny — сложная функция:
Обе части равенства умножаем на y:
Вспоминаем, что по условию y — это x в степени sinx, и подставляем это выражение вместо y:
Действуем по схеме:
Здесь ln(2x+3) — сложная функция, внешняя функция f=lnu. внутренняя u=2x+3:
внутренняя u=2x+3:
Умножаем обе части равенства на y:
Теперь подставляем в вместо y его выражение из условия:
Логарифмируем обе части по основанию e:
Показатель степени выносим за знак логарифма:
Теперь дифференцируем обе части равенства:
√(7-x) сложная функция, внешняя функция f=√u, внутренняя u=7-x:
Теперь обе части умножаем на y:
И в заверщении, заменяем y на соответствующее выражение из условия:
Примеры для самопроверки: найти производную показательно-степенной функции:
Показать решение
Здесь ln(sinx) — сложная функция. f=lnu — внешняя функция, u=sinx — внутренняя:
Умножаем обе части равенства на y:
и заменяем y выражением из условия:
Здесь ln(arcsinx) — сложная функция. Внешняя функция f=lnu, внутренняя u=arcsinx:
Внешняя функция f=lnu, внутренняя u=arcsinx:
Теперь умножаем обе части равенства на y:
И заменяем y на выражение из условия:
Теперь умножаем обе части равенства на y:
И заменяем y на его выражение из условия:
система управления знаниями (инженерия, математика)
Для кого
Система управления техническими знаниями (СУТЗ) позволяет собирать, конструировать, хранить и извлекать знания из базы знаний (БЗ) в формате микрокурсов.
В первую очередь решение адресовано корпоративным заказчикам, для которых нематериальные активы (интеллектуальный капитал и профессиональные инженерные и научные компетенция кадров) имеют ключевое значение.
Система способна представлять техническую информацию в супер-лаконичном виде за счет применения атомарного контента в базе знаний и ее «ручной» систематизации нашими экспертами. С одной стороны, это позволяет на основе поискового запроса клиента динамически формировать микрокурсы по интересующей его теме.
С другой стороны, наличие собственной библиотеки контента (видео, текст, расчеты, библиография и т.д.) дает возможность клиенту оформлять и хранить собственные структурированные знания, добавляя пользовательский контент в свою локальную базу знаний (для КОРП версии).
Важно, что неявные знания и экспертиза, которые находятся в головах сотрудников (даже без создания новых материальных продуктов — отчетов, CAD моделей, математических расчетов и т.д.), трудно поддаются систематизации и оформлению в виде отчужденных знаний.
С одной стороны, это позволяет на основе поискового запроса клиента динамически формировать микрокурсы по интересующей его теме.
С другой стороны, наличие собственной библиотеки контента (видео, текст, расчеты, библиография и т.д.) дает возможность клиенту оформлять и хранить собственные структурированные знания, добавляя пользовательский контент в свою локальную базу знаний (для КОРП версии).
Важно, что неявные знания и экспертиза, которые находятся в головах сотрудников (даже без создания новых материальных продуктов — отчетов, CAD моделей, математических расчетов и т.д.), трудно поддаются систематизации и оформлению в виде отчужденных знаний.
Наш сервис позволяет управлять именно такими знаниями, предлагая в качестве основы систематизированную общеизвестную техническую информацию, облегчающую формализацию знаний сотрудников и сохранение интеллектуального капитала компании.
Из теории инженерии знаний известно, что знания не рождаются сами по себе, они появляются в результате трансформации одних элементов информационного пространства в другие. Мы предлагаем не только и не столько систему менеджмента знаний, но в первую очередь — структурированную, нормализованную и лаконичную базу общеупотребительного математического, инженерного и научного контента, которая постоянно пополняется и улучшается при помощи наших экспертизы.
СУТЗ по умолчанию содержит документы с «живыми» расчетами в среде Mathcad. Немаловажно, что Mathcad имеет бесплатную версию, которую можно использовать как среду расчетов для 50-60% документов базы знаний и как просмотровщик расчетов для 100% документов.
Мы предлагаем не только и не столько систему менеджмента знаний, но в первую очередь — структурированную, нормализованную и лаконичную базу общеупотребительного математического, инженерного и научного контента, которая постоянно пополняется и улучшается при помощи наших экспертизы.
СУТЗ по умолчанию содержит документы с «живыми» расчетами в среде Mathcad. Немаловажно, что Mathcad имеет бесплатную версию, которую можно использовать как среду расчетов для 50-60% документов базы знаний и как просмотровщик расчетов для 100% документов.
Описание технологии
Предположим, потребитель (инженер, студент, музыкант и т.д.) хочет разобраться в основах спектров и начинает искать курс по Фурье-анализу. Скорее всего, он отыщет нужную информацию в курсах по мат.анализу, а при недостатке базовых знаний, будет вынужден обращаться и к предыдущим курсам по математике.
Вероятно, потребителю придется самому отфильтровывать нужную информацию, двигаясь в обратном направлении, т.
Конечно, может встать закономерный вопрос «как же пользователь будет разбираться с определенным интегралом, если ему «не нужны первообразные»?».
Однако в данном случае, ему будет упрощенно объяснено понятие определенного интеграл через соответствующую площадь под графиком кривой и Риманову сумму.
Ведь в данной постановке задачи строгое объяснение не является необходимым, а на практике, для вычисления спектров, интегралы считаются все равно численно, как раз через площадь.
Для реализации динамического формирования микрокурсов нужен, во-первых, контент иного типа («нормализованный») и, во-вторых, соответствующая система управления этим контентом (базой знаний).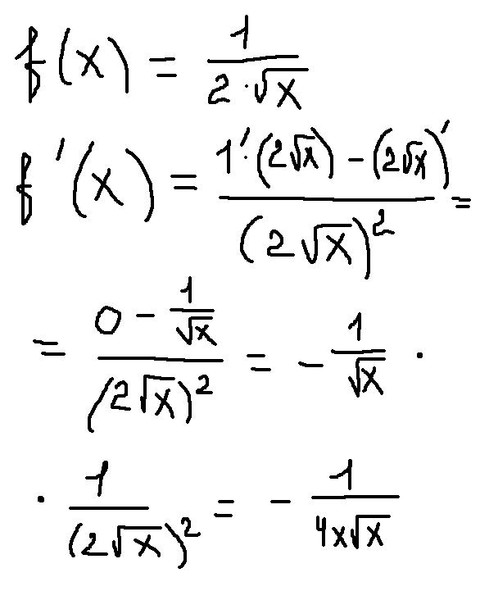
Быстрый старт
Для быстрого знакомства с системой используйте три демонстрационных примера. Оставьте в поле поиска слово «демо» и просто нажмите красную кнопку Найти. В результате, под полем поиска появятся три ссылки — результаты поиска тем по заготовленному слову «демо». Поочередно нажмите каждую из кнопок и работайте с микрокурсами — списками видео, заметок, расчетов и т.д., извлеченных из базы знаний.
При каждом нажатии соответствующая тема будет открываться в виде динамического микрокурса — списка видеороликов, заметок, расчетов или внешних вики-ссылок, извлеченных из базы знаний.
Некоторые будут снабжаться короткими пояснениями и дополнительными математическими расчетами (в формате PDF).
Зеленым фоном выделяется ключевая статья из базы знаний, а желтым — ссылки на дополнительную информацию: библиографические, на внешние онлайн-курсы, вебинары и т. д.
Три демо-темы демонстрируют разные опции системы: 1. пример динамического курса по Фурье-преобразованию, принцип формирования которого вы найдете в описании системы УТЗ,
2. пример пользовательских знаний (расчетов по ГОСТ) и 3. демо дополнительного функционала системы (вывода картинок в оглавлении микрокурса).
д.
Три демо-темы демонстрируют разные опции системы: 1. пример динамического курса по Фурье-преобразованию, принцип формирования которого вы найдете в описании системы УТЗ,
2. пример пользовательских знаний (расчетов по ГОСТ) и 3. демо дополнительного функционала системы (вывода картинок в оглавлении микрокурса).
Для того, чтобы сформировать микрокурсы по другим темам, используйте поиск или выбор темы из иерархического списка база знаний.
Идея и разработка: Дмитрий Кирьянов.
Формула Эйлера — это… Что такое Формула Эйлера?
Геометрический смысл формулы ЭйлераФормула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.
Формула Эйлера утверждает, что для любого вещественного числа выполнено следующее равенство:
- ,
где — основание натурального логарифма,
- — мнимая единица.

История
Формула Эйлера впервые была приведена в книге «Гармония мер» английского математика Роджера Котса (помощника Ньютона), которая была издана в 1722 году, уже после смерти автора. Котс открыл формулу около 1714 года и выразил её в логарифмической форме:
- .
Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (1748), построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя (см. Г. Вессель).
Производные формулы
При помощи формулы Эйлера можно определить функции и следующим образом:
- ,
- .
Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть , тогда:
- ,
- .
Известное тождество Эйлера, связывающее пять фундаментальных математических констант:
является частным случаем формулы Эйлера при .
Применение в комплексном анализе
Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: .
Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: , . Геометрический смысл данной формулы следующий: при возведении числа в степень его расстояние до центра возводится в степень , а угол поворота относительно оси увеличивается в раз.
Формула возведения в степень верна не только для целых , но и для вещественных. В частности, комплексная запись числа позволяет находить корни любой степени из любого комплексного числа, что и используется при доказательстве основной теоремы алгебры: «Многочлен степени имеет ровно комплексных корней».
Взаимосвязь с тригонометрией
Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера :
с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения, результат выражения остается вещественным. Например:
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).
Доказательство
Доказательство формулы Эйлера можно провести с использованием рядов Тейлора. Разложим функцию в ряд Тейлора по степеням . Получим:
Разложим функцию в ряд Тейлора по степеням . Получим:
Но
Поэтому
ч. т. д.
Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.
Пусть комплексное число в тригонометрической форме имеет вид . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим:
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь ,.
См. также
Литература
ЕГЭ. Русский язык. ШПАРГАЛКА – подсказка. ВСЕ ТРУДНЫЕ СЛУЧАИ в одном месте.Задания № 2, 4,7,9,15.
Шпаргалка — подсказка.Данная шпаргалка поможет при выполнении заданий № 2,4,6,7,9,15.
Здесь собраны примеры трудных случаев, слов, которые нужно запомнить.
Почаще читайте данную книжку-шпаргалку, запоминайте слова.
| НАРЕЧИЯ. | ||||||||||
| Часто подходят в заданиях следующие наречия. Зачем. Затем. Отчего. Оттого. Почему. Потому. Посему. Поэтому. Наречий очень много: сейчас, здесь, тут, там, сегодня завтра и др.
Задание: найти частицу и местоименное наречие (пример: именно+ поэтому).
Местоименные наречия указывают на место, время, способ действия и пр. или спрашивают о них.
| ||||||||||
Сочинительные союзы. | ||||||||||
| И ,а, но, однако, тоже ,также, или, либо. Да=и, да= но.
Иногда в задании необходимо подобрать сочинительный союз определённого разряда. Приведём их здесь. Соединительные: и, да=и, ни-ни, тоже, также. Противительные: а, но, зато, однако, да=но. Разделительные: или, либо, не то-не то, то-то. | ||||||||||
| Подчинительные союзы. | ||||||||||
| ||||||||||
| Вводные слова. | ||||||||||
| Различные чувства говорящего в связи с сообщением: к счастью, к несчастью, к радости, к ужасу, к сожалению и др. Оценка степени реальности сообщения (уверенность, возможность, неуверенность): конечно, несомненно, вероятно, может быть, кажется и др. Источник сообщения: говорят, сообщают, по словам, по-моему, по мнению и др. Связь мыслей, последовательность изложения: итак, следовательно, во-первых, наконец, между прочим, … Оформление высказываемых мыслей: одним словом, вообще, иначе говоря, так сказать и др. Привлечение внимания: видишь (ли), понимаешь, пожалуйста, скажем, допустим и др. Указывают на степень обычности того, о чем говорится: бывает, бывало, как водится, как всегда, по обыкновению, по обычаю, случается, случалось.
Внимание!
Вводных слов очень много, приведены лишь наиболее распространённые.
Запомните слова, которые НЕ являются вводными. авось, будто, буквально; вдобавок, вдруг, ведь, в конечном счете, вряд ли, вроде бы, всё-таки, даже, едва ли, исключительно, именно, как будто (будто), как бы, как раз, к тому же, между тем, небось, по постановлению (чьему), по решению (чьему), почти, приблизительно, примерно, просто, решительно, якобы. | ||||||||||
| Частицы. | ||||||||||
| Отрицательные: не, ни, вовсе не, отнюдь не, далеко не. Вопросительные: неужели, разве, ли, ль. Указательные: вон, вот, это. Уточняющие: именно, как раз, прямо, точно, точь-в-точь. Ограничительные и выделительные: только, лишь, исключительно, почти, единственно. Усилительные: даже, же, ведь, уж, ну. Сомнительные: едва ли, вряд ли. Восклицательные: что за, ну и, как.
Как, что за – это частицы, если находятся в восклицательных предложениях. Что за прелесть эти сказки! Как прекрасен это мир!. | ||||||||||
| Задание: подобрать местоимение (и указан его разряд). Разряды местоимений. 1.Личные. Некто, нечто, некий, некоторый, несколько, кто-то, что-то, какой-то, чей-то, сколько-то, кое-кто, кое-что, кое-какой, кто-нибудь, что-нибудь, какой-нибудь, чей-нибудь, сколько-нибудь, кто- либо, что-либо, какой-либо, чей-либо | ||||||||||
| Задание: подберите сочетание производного предлога с местоимением.
Производные предлоги. В течение. В продолжение. В заключение. Вследствие. Благодаря, согласно, вопреки. Несмотря на. Невзирая на. Ввиду. Насчёт.
Навстречу, напротив, впереди, везде, вокруг, вдоль, вопреки, наперекор, наперерез, позади, внутри, мимо, посередине и др.
Вместо, вроде, ввиду, в виде, в отличие от, за счёт, насчёт (=о),по причине, по поводу, за исключением, в связи с и др.
| ||||||||||
| Задание: подберите союзное слово.
Союзное слово – это самостоятельные части речи, служащие средством связи придаточных предложений с главным и являющиеся одновременно членами предложения.
В роли союзных слов могут выступать: 1. Относительные местоимения: какой, который, кто, что, кем, чем, кого, сколько. 2. Местоименные наречия: где, куда, откуда, как, когда, зачем, почему, отчего. | ||||||||||
| Частица + указательное местоимение: Именно такая. | ||||||||||
СЛОВА, встречающиеся в ответах ФИПИ. С этой целью. Другие же. И всё-таки. Дело в том, что. Именно из-за. Именно так. Прежде чем. На самом деле. Другие же. С другой стороны. Несмотря на это. Иными словами. В конце концов. Помимо. Кроме. |
Задание № 4
| 1.анАлог | 1.аристокрАтия | 1.бАнты (бАнтов) |
| 2. анАтом | 2. асимметрИя | 2.бухгАлтеры (бухгАлтеров) |
| 3. апострОф | 3. баловАть | 3. вЕчеря |
| 4. валовОй | 4. вероисповЕдание | 4. включИшь (включИт) |
| 5. ветеринАрия | 5. ворожеЯ | 5. дипломИрованный |
| 6. гофрирОванный | 6. гЕнезис | 6. добелА |
| 7. диоптрИя | 7. граффИти | 7.забронИровать |
| 8. дОгмат | 8.диспансЕр (сэ) | 8. завИдно завИдно |
| 9. еретИк | 9. договОры | 9. инспЕкторы |
| 10. жалюзИ | 10. жерлО | 10.искрИться |
| 11.завсегдАтай | 11. заплЕсневеть | 11.кровоточИть |
| 12. закУпорив | 12. знАмение | 12. кУхонный |
| 13. зубчАтый | 13.исчЕрпать | 13.маркировАть |
| 14. Иконопись | 14. квартАл | 14.ободрИть |
| 15. инженЕрия | 15. красИвее | 15.освЕдомиться |
| 16.Искра | 16. лЕкторов | 16.тОрты (тОртов) |
| 17. каталОг | 17. мозаИчный | 17.трЕнеры |
| 18. кружевА | 18.мышлЕние | 18.увЕдомить |
| 19. мастерскИ | 19. недУг | 19.украИнский |
| 20.намЕрение | 20. начатА | 20.фенОмен |
| 21. новорождЁнный | 21.озорничАть | 21.фетИш |
22. обеспЕчение обеспЕчение | 22. Опрометью | 22.чЕрпать |
| 23. облегчИть | 23.ракУшка | 23.черствЕть |
| 24. Отрочество | 24. рефлЕксия | 24.шАрфы(шАрфов) |
| 25. пулОвер | 25.сосредотОчение | 25.щавЕль |
| 26. ретировАться | 26.тефтЕли | 26.щепОть |
| 27. свЁкла | 27.тУфля | 27.Экскурс |
| 28. слИвовый | 28.углубИть | 28.экспЕрт |
| 29.страхОвщик | 29.факсИмиле | 29.Ягодицы |
| 30.танцОвщица | 30.ходАтайствовать | 30.Ясли (яслей) |
| 1.агЕнт | 1.безУдержный | 1.взялА |
| 2. алкогОль | 2.боЯзнь | 2.вручИт,вручАт |
| 3. алфавИт | 3.бралАсь | 3.зАгодя |
| 4.берЁста | 4.дефИс | 4.зАговор |
| 5.балОванный | 5. двИжимый двИжимый | 5.зевОта |
| 6.бАрмен | 6.дОверху | 6.кАмфора |
| 7.бОчковое | 7.зАгодя | 7.квАшение |
| 8.бытиЕ | 8.заперлАсь | 8.кедрОвый |
| 9. взялА | 9.знАчимый | 9.киркА (орудие труда) |
| 10. вОзрасты (вОзрастов) | 10.манЯщий | 10.кИрка (лютеранская церковь) |
| 11.главЕнство | 11.клАла | 11.клАла |
| 12. гренадЕр | 12.нет кОнусов | 12.клЕщи (инструмент) |
| 13. добЫча | 13.кормЯщий | 13.клещИ (насекомое) |
| 14.дремОта | 14.крАны | 14.комбАйнер |
| 15.заИндеветь | 15.красИвейший | 15.костюмирОванный |
| 16. знАхарка | 16.наделИт | 16.мЕстностей |
| 17.издрЕвле | 17.накренИт | 17.надОлго |
| 18.инсУльт | 18.налитА | 18.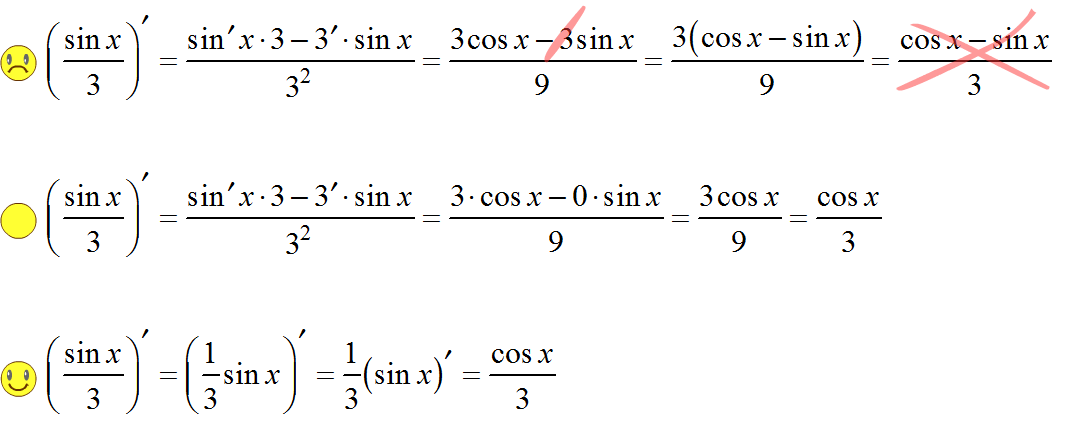 некролОг некролОг |
| 19.наращЁнные | 19.нарвалА | 19.новостЕй |
| 20.обеспЕчение | 20.начАвшись | 20.облилАсь |
| 21.Обнял | 21.обогналА | 21.ободрИть |
| 22. осЕдлый | 22.пЕрчить | 22.обострЁнный |
| 23. откУпорить | 23.повторЁнный | 23.опОшлить |
| 24.тОтчас | 24.понЯвший | 24.пОгнутый |
| 25.чЕрпать | 25.пОчестей | 25.прИнялись |
| 26. шассИ | 26.предпринЯв | 26.произвдЁн |
| 27. шелковИца | 27.прожИвший | 27.профессорОв |
| 28. щИколотка | 28.сверлИт | 28.снятА |
| 29.Экспорт | 29. цыгАн | 29.солгалА |
| 30.электропрОвод | 30. щИколотка | 30.экскОрт |
| 1.АльтЫ, альтОв | 1. блЁкнуть блЁкнуть | 1.быстрА |
| 2.анонИм | 2.ворОта, в ворОтах | 2.валИть, валИт (снег) |
| 3.асбЕст | 3.ломОть | 3.вАлит (деревья) |
| 4.афИнянин | 4.лубОчный | 4.ветлА |
| 5.баловнИца | 5.нЕнецкий | 5.вЫстрочить |
| 6.БальмОнт | 6.обгрЫзенный | 6.вЫстругать |
| 7.безнадЁжный | 7.Обнял | 7.децимЕтр |
| 8.бЕсишь | 8.озлОбленность | 8.добылА, добЫта |
| 9.бечевА | 9.отчАсти | 9.заглушИт |
| 10.бряцАть | 10.пАмятовать | 10.Из лесу, Из дому, Из носу, Из виду |
| 11.блЁклый | 11.партЕр (э) | 11. исповЕдание |
| 12.волкОв | 12.перИод | 12.крАла |
| 13.ворОв | 13.пепелИще | 13.лЕкторы |
| 14..воспринЯть | 14.пЕтля | 14.МеримЕ ПроспЕр |
15.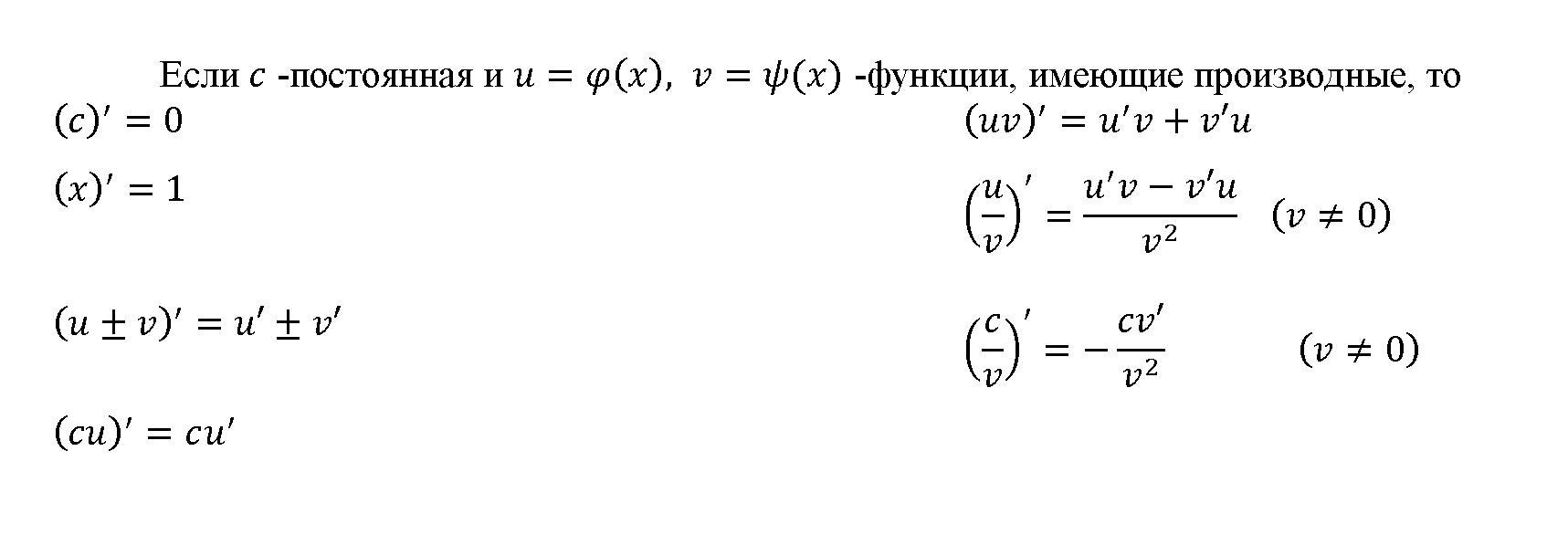 горА, зА гору, нА гору, горА, зА гору, нА гору,пОд гору | 15.плЕсневеть | 15.мИнуть, минУв |
| 16.дИптрих | 16.повАренный | 16.простолюдИн |
| 17.из двЕри, на двЕри | 17.поедОм | 17.расщепИт |
| 18.дЕбет | 18.полшагА | 18.рыкАть |
| 19.деньгАм, о деньгАх | 19.прИработок | 19.свАленный |
| 20.дефИс | 20.прОтивень | 20.сегмЕнт |
| 21.домЕн | 21.расклЁшенный | 21.сверлИт |
| 22.зА бороду, зА день | 22.расщепИт | 22.силОк |
| 23.заЁм | 23.убыстрИть | 23.сИлос |
| 24.ИешуА | 24.цемЕнт | 24.сорИт |
| 25.интервьюЕр (Э) | 25.часовщИк | 25.топОрщить |
| 26.крамОла | 26.чуднОй(странный) | 26.тошнотА |
| 27.лососЁвый | 27.чУдный (красивый) | 27.удилА |
28.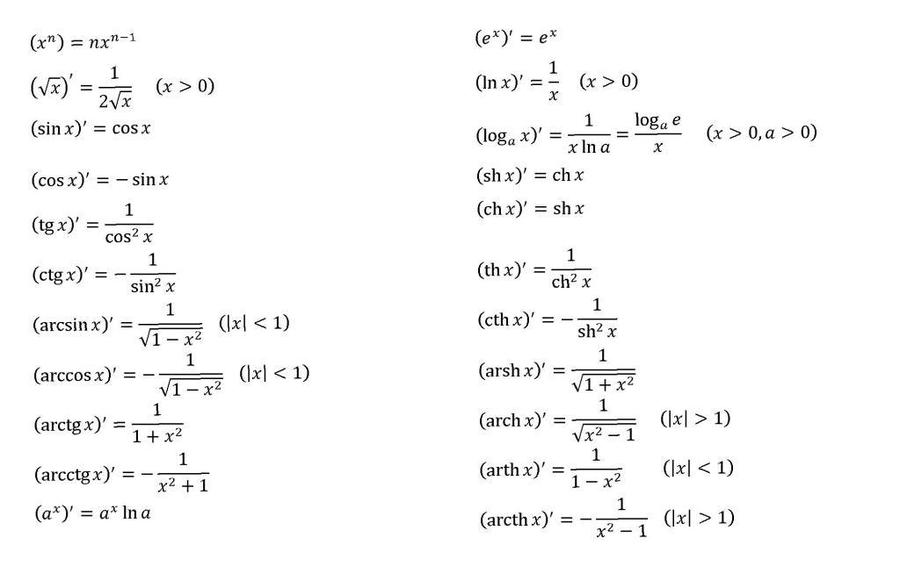 нАчал, начАть, начатА нАчал, начАть, начатА | 28.щемИт | 28.умнО |
| 29.нЕ дал, не далА, нЕ дало, нЕ дали | 29.экзальтирОванный | 29.усОвестить |
| 30. нет дУпел | 30.юрОдивый | 30.облилАсь 31. Углей |
Задание № 7.
| -а, -я | -ы, -и |
| борт-бОрты | бухгАлтер-бухгАлтеры |
| порт-пОрты | возраст-вОзрасты |
| торт-тОрты | грифель- грИфели |
| вексель- векселЯ | грунт- грУнты |
| вензель- вензелЯ | диспетчер-диспЕтчеры |
| директор-директорА | договОр-договОры |
| инспектор- инспекторА | дрАйвер- дрАйверы |
| катер- катерА | инженЕр- инженЕры |
| китель-кителЯ | констрУктор- констрУкторы |
| кузов-кузовА | лектор-лЕкторы |
| купол-куполА | лифт-лИфты |
| округ-округА | плЕйер-плЕйеры |
| ордер-ордерА | пиговОр- приговОры |
| паспорт-паспортА | прИнтер- прИнтеры |
| погреб-погребА | прожЕктор-прожЕкторы |
| профессор-профессорА | редАктор-редАкторы |
| сторож-сторожА | рЕктор-рЕкторы |
| тенор-тенорА | свИтер-свИтеры |
| флюгер-флюгерА | сЕктор- сЕкторы |
| фельдшер-фельдшерА | склад-склАды |
| хутор-хуторА | слЕсарь-слЕсари |
| штАбель- штабелЯ | снАйпер- снАйперы |
| штЕмпель- штемпелЯ | трЕнер-трЕнеры |
| шУлер-шулерА | флот- флОты |
| фронт- фронтЫ | |
| шофёр-шофЁры | |
| штаб-штабЫ | |
| штурман- штУрманы |
Родительный падеж множественного числа в названиях национальностей.

| казАхи-казахов | армяне-армЯн |
| калмЫки-калмЫков | башкИры-башкИр |
| киргИзы-киргИзов | болгАры-болгАр |
| монгОлы-монгОлов | бурЯты-бурЯт |
| таджИки- таджИков | грузИны-грузИн |
| тунгУсы-тунгУсов | лезгИны-лезгИн |
| узбЕки- узбЕков | осетИны-осетИн |
| хорвАты-хорвАтов | румЫны-румЫн |
| якУты-якУтов | татары-татАр |
| тУрки- тУрок | |
| туркмЕны-туркмЕн | |
| цыгАне-цыгАн |
Родительный падеж множественного числа существительных.
| Нулевое окончание | Нулевое окончание | Нулевое окончание | Окончание –ев (-ов) | Окончание -ей |
| НЕТ партизан | колен | барышень | платьев | ружей |
| солдат | плеч | боярышень | устьев | свечей |
| гусар | чисел | деревень | подмастерьев | кеглей |
| драгун | кресел | одеялец | носков | саклей |
| кирасир | брёвен | яблок | метров | распрей |
| валенок | полотенец | блюдец | граммов | пашей |
| сапог | волокон | вафель | килограммов | юношей |
| чулок | рёбер | туфель | гектаров | будней |
| ботинок | ядер | кровель | рельсов | яслей |
| погон | розог | оглобель | апельсинов | дрожжей |
| эполет | кухонь | свадеб | мандаринов | дровней |
| ампер | кочерёг | усадеб | помидоров | людей |
| ватт | ставен | нянь | томатов | отрубей |
| вольт | басен | дел | баклажанов | саней |
| ом | песен | брызг | лимонов | углей(мн. ч.) ч.) |
| аршин | сплетен | брюк | болотцев | |
| микрон | домен | бус | копытцев | |
| герц | черешен | каникул | кружевцев | |
| рентген | носилок | макарон | оконцев | |
| денег | потёмок | салазок | заморозков | |
| сумерек | брелоков |
Запомните: игра не стоит свеч.
Запомните: снадобий, захолустий, раздумий.
Количественные числительные (сколько?)
| И.п. | тысяча восемьсот двадцать пять |
| Р.п. | тысячи восьмисот двадцати пяти |
| Д.п. | тысяче восьмистам двадцати пяти |
| В.п | тысяча восемьсот двадцать пять |
| Т.п. | тысячей восьмьюстами двадцатью пятью( восемьюстами) |
П. п. п. | о тысяче восьмистах двадцати пяти |
Порядковые числительные ( какой?)
| И.п. | три седьмых |
| Р.п. | трёх седьмых |
| Д.п. | трём седьмым |
| В.п | три седьмых |
| Т.п. | тремя седьмыми |
| П.п. | о трёх седьмых |
| И.п. | шестеро |
| Р.п. | шестерых |
| Д.п. | шестерым |
| В.п | шестерых |
| Т.п. | шестерыми |
| П.п. | о шестерых |
Числительные ОБА,ОБЕ.
| И.п. | оба | обе |
| Р.п. | обоих | обеих |
Д. п. п. | обоим | обеим |
| В.п | оба, обоих | обе, обеих |
| Т.п. | обоими | обеими |
| П.п. | об обоих | об обеих |
| И.п. | тысяча | миллион | миллиард |
| Р.п. | тысячи | миллиона | миллиарда |
| Д.п. | тысяче | миллиону | миллиарду |
| В.п. | тысячу | миллион | миллиард |
| Т.п. | тысячей | миллионом | миллиардом |
| П.п. | о тысяче | о миллионе | о миллиарде |
ГЛАГОЛЫ.
Запомните трудные формы:
выздоровеют, опостылеют, опротивеют
чтить- чтут ( допускается – чтят)
стлать ( -ся)- доп. стелить(-ся)
ездить – ездит, ездят
мучить, мерить.
лазить – лазишь, лазим, лазят, лазь
чтить – чту, чтишь, чтит, чтим, чтите, чтят
жечь — жгу, жжём, жжёшь, жжёте, жжёт, жгут
(запомните, что неверно следующее: жгёшь, жгём, жгёт, жгёте)
Запомните формы настоящего и будущего времени:
внимать – внимают (внемлют- поэтич. )
)
глодать – гложет
дремать – дремлет
кликать –кличет
клокотать- клокочет
колыхать – колышет
кудахтать- кудахчет
махать – машет,
мурлыкать – мурлычет,
плескать- плещет,
полоскать- полощет
рыскать – рыщет
сыпать- сыплет
трепать – треплет
хлестать- хлещет
щипать — щиплет
лечь- лягу, ляжет, лягут
течь – теку, течёт, текут
беречь- берегу, бережёт, берегут
Исключение: ткать – тку, ткёт, ткут
возникнуть – возник
высохнуть – высох
исчезнуть – исчез
погибнуть- погиб
привыкнуть – привык
промокнуть – промок
проникнуть – проник
( то есть нельзя употреблять слова типа: возникнул, проникнул и т.д.!)
Запомните:
глохнуть – глох
достигнуть – достиг,
киснуть – кис,
пахнуть – пах,
подвергнуться- подвергся,
вянуть – вял.
Запомните некоторые формы повелительного наклонения:
лечь – ляг, лягте
сесть – сядь, сядьте
резать – режь, режьте
мазать – мажь, мажьте
ехать – поезжай, поезжайте (неверно: езжай, ехай, ехайте).
Но при отрицании : не езди, не ездите.
пойти – пойдёмте, пойдём
Запомните наиболее часто встречающиеся примеры в задании № 7.
| Существительные | Числительные |
| любимые профессора | в двухстах метрах |
| греческих богинь | в полутора часах |
| несколько ножниц | из полутора метров ткани |
| хорошие доктора | пять барышень |
| умелые повара | до тысяча восемьсот двенадцатого года |
| несколько яблок | в обеих руках |
| лежат на шкафу | обоих студентов |
| пять кочерёг | до тысяча девятьсот пятого года |
| пара туфель | шестьюстами учебниками |
| несколько пар туфель | с тремястами бойцами |
| домашняя туфля | о трёхстах участниках |
| несколько полотенец | в трёхстах метрах |
| новые выборы | на триста пятьдесят седьмой странице |
| косвенных падежей | четырьмястами студентами |
| здоровые дёсны | свыше четырёх тысяч метров |
| об аэропорте | в течение тридцати пяти минут |
| уважаемые директора | с пятьюдесятью рублями |
| спелых абрикосов | семьюдесятью процентами |
| несколько мандаринов | почти в ста странах |
| новых полотенец | с семьюстами метрами |
| много облаков | четырьмястами рублями |
| пара ботинок | четырьмястами рублями |
| ряд критериев | пятьюстами тридцатью тремя метрами |
| несколько яблок | в тысяча девятисотом году |
| новых джинсов | две седьмых |
| пачка макарон | более полутораста зрителей |
| сладких помидоров | о полутора часах |
| молодые бухгалтеры | Глаголы |
| пять граммов | быстро выздоровеет |
| пропуска на предприятия | выправь текст |
| согласно графику | мокла под дождём |
| в боку | поезжай побыстрее |
| благодаря решению | поезжай вперёд |
| две пары чулок | поезжайте в город |
| три пары носков | заезжай завтра |
| опытные шофёры | хорошо проповедует |
| пара ботинок | жжёт костёр |
| двух пар ботинок | зажжёт фейерверк |
| согласно тарифу | совсем озяб |
| часовые пояса | оденьтесь теплее |
| среди грузин | одень ребёнка |
| пять блюдец | высохла шапка |
| все возрасты | лягте на пол |
| ряд критериев | лажу по крышам |
| килограмм вафель | разожжёт костёр |
| почерк | прополощи бельё |
| много вишен | попробуем |
| опытные тренеры | пусть попробует |
| килограмм помидоров | попробует торт |
| около двух килограммов | мокла под дождём |
| лучшие парикмахеры | лягте на коврик |
| все возрасты | насмехаться |
| милых барышень | разъезжайтесь |
| современных кухонь | поскользнуться |
| пара варежек | посади дерево |
| модных серёг | надень перчатки |
| несколько сотен | зажжётся огонь |
| почётные титулы | поймать кошку |
| банка сардин | полощет рот |
| нет заморозков | полощет бельё |
| старых басен | клади на место |
| полки для кухонь | жаждет славы |
| новые компьютеры | насквозь промок |
| новый шампунь | помашите отъезжающим |
| дальние деревни | Степени сравнения |
| вместе с детьми | наиболее решительно поступил |
| тонкий тюль | наиболее уместно |
| летних каникул | богатейший выбор |
| без погон | пришёл более поздно |
| варка макарон | чудеснейшим образом |
| песни цыган | товары дешевле |
| взвод солдат | жёстче дерева |
| жареные тетерева | фильм интереснее |
| около трёх аршин | менее значительный |
| по приезде в город | более глубокий конфликт |
| горячие супы | петь ещё звонче |
| иностранные паспорта | самый молодой |
| все инженеры | более высоко прыгнуть |
| уборка яслей | серьёзнейшее замечание |
| несколько яблонь | эта работа более хорошая |
| Причастия | повеселее |
| обгрызенное яблоко | наисложнейший |
| обгрызенная груша | длиннее |
| полощущий бельё | более резкое движение |
| запрещающий игры | наиболее интересный |
| Деепричастия | торт менее сладкий |
| смотря вперёд | наилучших снимков |
| почитав рассказ | повеселее |
| не проронив ни слова | Местоимения |
| Наречие | на их территории |
| поделить напополам | их письма |
| по их указанию |
Степени сравнения качественных имён прилагательных и наречий.
| Прилагательные. | Наречия. |
| Красивый. | Красиво. |
| Красивее. | Красивее. |
| Более красивый. | Боле красиво. |
| Красивейший. | |
| Красивее всех. Самый красивый. | Красивее всех. |
Задание № 9
| Корни с чередующимися гласными. | ||
| О-А (11 корней) | Е-И (9 корней. | А , Я – ИМ, ИН |
| Без ударения — О. гар — гор твар — твор клан — клон
Без ударения А. зар- зор плав-плов
См. на конечную согласную в корне. лаг-лож раст-, ращ- рос- скак-скоч
кас — (есть суффикс А) кос- (нет)
См. равн-(одинаковый) ровн- (ровный)
мак-(окускать в жидкость), мок- (пропускать жидкость) | Правило: И- есть суффикс А Е- нет суффикса А.
бер-бир дер-дир мер-мир пер-пир тер-тир
блест- блист стел-стил
жег-жиг чет-чит
| занять- занимать начать -начинать пожать — пожинать понять – понимать примять -приминать проклясть- проклинать распять -распинать сжать – сжимать снять -снимать
|
Запомните слова- исключения.
| О-А | О-А | Е-И |
| зоревать зорянка
пригарь выгарки изгарь утварь полог
росток ростовщик Ростов Ростислав отрасль | скачок скачу
пловец пловчиха плывуны
уровень ровесник равнина равняйсь равнение(направо) | сочетать сочетание чета |
Задание № 10
| ПРЕ- | прелюдия |
| преамбула | премьера |
| пребывать | пренебречь |
| превалировать | преобладать |
| превентивный | преодолеть |
| превзойти | препарат |
| превозмочь | препинания (знак) |
| превратный | препираться |
| превращение | преподаватель |
| превосходство | преподобный |
| прегрешения | препона |
| предание | препроводить |
| преданность | препятствие |
| предатель | пререкаться |
| предать | прерогатива |
| предел | прервать |
| преемник | преследовать |
| презентабельный | пресловутый |
| презентация | пресмыкаться |
| президиум | преставиться |
| презирать | престиж |
| презумпция | престол |
| преимущество | преткновение |
| преисподняя | претворить |
| прейскурант | претендент |
| преклонный | претензия |
| преклоняться | префект |
| прекословить | преходящий |
| прекращение | преклонять |
| преломление | преступить |
| прельстить | прецедент |
| Приставка ПРИ- | приличия |
| прибаутка | примадонна |
| прибор | примат |
| приватизация | примета |
| приватный | примитивный |
| приведение | принадлежность |
| привилегия | принизить |
| привередливый | принцесса |
| приверженец | принципиальный |
| привет | принять |
| приветствие | приоритет |
| приволье | припев |
| привратник | природа |
| привыкать | прискорбное |
| приглашение | приспособить |
| пригодиться | пристойно |
| пригожий | присутствие |
| придать | присяга |
| придел (в церкви) | притворство |
| придирчивый | притворщица |
| приесться | притон |
| приёмник | притязание |
| призирать (заботиться) | приурочить |
| призвание | прицел |
| признание | причёска |
| приказ | причина |
| приключение | причиндалы |
| прикорнуть | причудливый |
| прилежание | приятель |
| приятный |
| Ъ | Ь |
| абъюрация | альтернатива |
| адъютант | арьергард |
| безъядерный | батальон |
| изъявительное (наклонение) | бильярд |
| изъять | бульон |
| инъекция | Вьетнам |
| дизъюнкция | вьюга |
| двухъярусный | вьюн |
| конръякобинский | вьючный |
| конъектура (восстановление испорченного текста) | дьяк |
| конъюнктивит | интерьер |
| конъюнктура (сложившаяся обстановка, например, на рынке) | интервьюировать |
| межъярусный | интервьюер |
| неотъемлемый | компаньон |
| объект | компьютер |
| объём | медальон |
| объявление | Нью-Йорк |
| объяснительная | Ньютон |
| объять | обезьяна |
| отъявленный | павильон |
| панъевропейский | пасьянс |
| подъезд | пеньюар |
| предъюбилейный | подьячий |
| предъявить | портьера |
| сверхъестественный | премьера |
| съезд | пьедестал |
| съёжился | пьеса |
| субъект | сеньор |
| суперъястребы | серьёзный |
| трансъевропейский | синьорина |
| трёхъязычный | фортепьяно |
| фельдъегерь | фельдмаршал |
| четырёхъярдовый | шампиньон |
| И | Ы |
| взимать | взыгравший |
| дезинформация | взыскать |
| дезинтегральный | возыметь |
| контригра | безыглый |
| контритог | безыдейный |
| контриск | безынвентарный |
| межигровой | безынициативный |
| межиздательский | безынтересный |
| межинститутский | безымянный |
| панисламизм | безыскровая |
| панисламский | безыскусный |
| постиндустриальный | безысходность |
| постимпрессионизм | изымать |
| постинфарктный | изыскать |
| сверхизысканный | небезызвестный |
| сверхиндивидуальный | обындеветь |
| сверхинтеллигентный | обыскать |
| сверхинтересный | подыгрывать |
| субинспектор | подыскать |
| суперигровой | подытожить |
| суперизящный | предыдущий |
| трансиорданский | предынфарктный |
| трансиндийский | предыстория |
Сложные слова. | разыскивать |
| двухигольный | розыгрыш |
| трёхимпульсный | сыгранный |
| четырёхигровой | сыздавна |
| Сложносокращённые слова. | сызмальства |
| мединститут | сымитировать |
| предисполкома | сымпровизировать |
| сельхозинвентарь | сыронизировать |
| специнстурмент | |
| спортинвентарь |
Задание № 15Исключения.
| -Н- | -НН- |
| Ветреный | Оловянный |
| Юный | Деревянный |
| Зелёный | Стеклянный |
| Синий | |
| Румяный | Нежданный |
| Пряный | Негаданный |
| Невиданный | |
| Посажёный отец | Неслыханный |
| Названый брат | Нечаянный |
| Прощёное воскресенье | Отчаянный |
| Приданое | Желанный |
| Смышлёный | Священный |
| Кованый | Медленный |
| Жёваный | Виденный |
| Клеваный | Жеманный |
| Раненый( кто? боец, зверь) Но: израненный, раненный в руку. | Недрёманноё око |
| читаный-перечитаный глаженый-переглаженый хоженый-перехоженый и др.
| Пеклеванный |
| Считанный | |
| Чеканный | |
| Чванный | |
| Деланный | |
| Ставленник | |
| Нетленный | |
| Обещанный | |
| Штукатуренный |
Материал подготовила: Мельникова Вера Александровна.
Вернутьсяк списку тестов по русскому языку ЕГЭ
Поиск производной квадратного корня от x — стенограмма видео и урока
Решение
Формула показывает, что производная квадратного корня из x равна (1/2) x -1/2. Это можно записать в нескольких разных формах:
Проверка вашей работы
Есть несколько различных способов, которыми мы можем проверить нашу работу при работе с деривативами. Первый касается определения производной с использованием лимитов.
Первый касается определения производной с использованием лимитов.
Мы можем использовать это определение для проверки нашей работы. При этом мы должны получить тот же результат, что и при использовании формулы. Мы начинаем с того, что позволяем f ( x ) = sqrt ( x ) и подключаемся соответственно.
Теперь мы хотим найти предел, так как h приближается к 0. Один из способов оценки предела — подставить число, которое приближается к h , на h .Однако в этом случае мы будем вставлять 0 для h . Вы понимаете, почему мы не можем этого сделать? Если вы думаете, что мы не можем подставить 0 для h , потому что это приведет к нулевому знаменателю, то вы правы! Следовательно, мы собираемся манипулировать лимитом, чтобы преобразовать его в форму, в которой мы можем вставить 0 для h без создания неопределенного выражения. Умножим все это на версию числа 1:
Умножим все это на версию числа 1:
Помните, мы не меняли предел, поскольку в конечном итоге мы просто умножили его на единицу.Также обратите внимание, что теперь мы можем подставить ноль для h без создания нулевого знаменателя или неопределенного выражения. Давайте сделаем это, чтобы найти предел и, в процессе, найти производную квадратного корня из x . Как только мы вставим 0 для ч , наше уравнение станет:
Видите ли, производная квадратного корня из x равна (1/2) x -1/2, и это именно то, что мы получили, когда использовали формулу.Уф! Это хорошие новости! Значит, мы сделали свою работу правильно.
Интегралы
Другой способ проверить нашу работу — использовать интегралы. Интегралы называются антипроизводными, и они в основном отменяют производные. То есть, если a является производной от b , то интеграл от a равен b + C , где C — константа.
Это говорит нам о том, что в нашем примере, поскольку производная sqrt ( x ) равна (1/2) x -1/2, то интеграл от (1/2) x -1/2 — это sqrt ( x ) + C , где C — постоянная.Возможно, вы еще не знакомы с интегралами, но это нормально. Нам посчастливилось иметь два простых факта, которые позволят нам найти интеграл от (1/2) x -1/2.
1.) Интеграл от постоянной, умноженной на функцию, равен этой константе, умноженной на интеграл функции.
2.) Формула для интеграла x n равна:
Используя эти два правила, мы можем найти интеграл (1/2) x -1/2 и проверить, что это sqrt ( x ) + C , где C — это постоянный.Это позволит нам проверить, правильно ли мы сделали свою работу.
Как мы и надеялись, мы видим, что интеграл от (1/2) x -1/2 равен sqrt ( x ) + C , где C — постоянная. Большой! И снова наша работа проходит проверку.
Большой! И снова наша работа проходит проверку.
При работе с производными функции производных с использованием пределов и интегралов чрезвычайно полезны для проверки правильности нашей работы.
Результаты обучения
Тщательно изучите урок и запомните достаточно информации, чтобы уверенно:
- Найдите производную квадратного корня x
- Использовать интегралы для проверки своей работы
Математическая сцена — Производные — Урок 3
Математическая сцена — Производные — Урок 3 — Корни, отрицательные степени, умноженные и разделенные функции2009 Rasmus ehf и Джанн Сак | Производные |
Урок 3
.Корни, отрицательные силы, умноженные и разделенные функции
Пример 1
Найдите производную от.
Используйте правило: |
Мы тоже можем написать так проверим, действует ли правило дифференцирования степеней целыми числами То, что использовалось в уроке 2, также применимо и в этом случае. Мы бы получили
.
Мы можем показать, что правило f (x) = nx n1 также применяется, когда n является дробь |
Пример 2
Используйте правило, чтобы различать следующие Например, сначала упростив корень и записав его в виде дроби с помощью обозначение.
Двигаться 7 / 6 вперед, затем уменьшите мощность на 1. |
Пример 3
Используйте определение производного инструмента для
дифференцировать f (x) = x 1 = 1 / х.
Сначала упростите числитель, затем упростите и отмените столько, сколько возможный. |
Это говорит о том, что мы можно использовать правило f (x) = nx n1 на отрицательных степенях |
Теперь докажем правило который показывает, как различать функцию, состоящую из двух функций, умноженных все вместе.
f (х) = и (х) v (х).
Мы знаем, что когда h мало
и
, что дает нам
ху (х) u (x + h) u (x) и, следовательно, u (x + h) ху (х) + и (х)
и hv (x) v (x + h) v (x) и, следовательно, v (x + h) hv (x) + v (x)
Ввод этих значений в приведенное выше уравнение, упрощая, отменяя и затем принимая предел, дает нам Правило нахождения производной при умножении двух функций:
(и (х) v (х)) = и (х) v (х) + и (х) v (х) |
Легче запомнить
правило, если мы опускаем x.
Пример 4
Проверим правило и убедитесь, что вы это понимаете, найдя производную от f (x) = x 3 x 2 .
Самый простой и очевидный способ состоит в том, чтобы сначала упростить, а затем найти производную: f (x) = x 5 и f (x) = 5x 4 .
Теперь воспользуйтесь правилом умножения:
Положим u = x 3 дает u = 3x 2 и v = x 2 дает v = 2x.
f (x) = (УФ) = УФ + УФ
= 3x 2 x 2 + x 3 2x
= 3x 4 + 2x 4 = 5x 4
, который соответствует нашему первому метод.
Теперь посложнее правило, правило дифференцирования рациональных функций u / v, где u и v являются функциями x:
Это можно доказать с помощью
определение производной так же, как правило умножения
доказано.Это также можно доказать с помощью правила, называемого цепным правилом, которое будет
представлен в 5 уроке.
Даем цепное правило доказательство здесь, вы можете вернуться к этому доказательству, когда закончите урок 5.
Мы используем цепное правило (v 1 ) = v 2 v и правило (uv) = uv + uv где u и v являются функциями от x.
Это правило:
Пример 5
Используйте правило деления на дифференцировать
u = x + 1, так что u = 1 и v = x 2 давая v = 2x.
Поместив их в формула выше дает нам
Попрактикуйтесь в этих методах, а затем пройдите тест 3 по производным.
л.с. Запомните свой контрольный список.
Если y = √sinx, найти dy / dx
В этой производной задаче задано, что $ y = \ sqrt {\ sin {x}} $.Итак, дифференцирование квадратного корня из $ \ sin {x} $ по $ x $ необходимо вычислить, чтобы найти производную $ y $ по $ x $. Это можно сделать двумя разными способами.
Это можно сделать двумя разными способами.
Метод дифференциации
Мы знаем, что $ y = \ sqrt {\ sin {x}} $, и берем производную с обеих сторон для нахождения дифференцирования $ y $ по $ x $.
$ \ подразумевает $ $ \ dfrac {d} {dx} {\, y} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {\ sin {x}}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {\ sin {x}}} $
В дифференциальном исчислении нет прямой формулы для нахождения производной квадратного корня из функции $ \ sin {x} $.Функция $ \ sqrt {\ sin {x}} $ представляет собой композицию двух функций $ \ sqrt {x} $ и $ \ sin {x} $. Следовательно, дифференцирование $ \ sqrt {\ sin {x}} $ можно вычислить по цепному правилу.
Возьмите $ u = \ sin {x} $, затем $ \ dfrac {d} {dx} {\, u} = \ dfrac {d} {dx} {\, \ sin {x}} $ согласно производной от Формула sinx. Следовательно, $ \ dfrac {du} {dx} = \ cos {x} $
.$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, \ sqrt {u}} $
Правую часть уравнения можно записать следующим образом согласно цепному правилу.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {du} {dx} \ times \ dfrac {d} {du} {\, \ sqrt {u}}
долл. СШАВычислено примерно, что $ \ dfrac {du} {dx} = \ cos {x} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ cos {x} \ times \ dfrac {d} {du} {\, \ sqrt {u}} $
Теперь найдите производную квадратного корня из $ u $ по $ u $ по производной формулы квадратного корня.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ cos {x} \ times \ dfrac {1} {2 \ sqrt {u}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {u}} $
На самом деле, в этом примере $ u = \ sin {x} $.Итак, замените $ u $ его фактическим значением.
$ \, \, \, \ следовательно \, \, \, \, \, \, $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {\ sin {x}}}
долларов СШАМетод пределов
Производная квадратного корня из $ \ sin {x} $ по $ x $ может быть вычислена из первого принципа. Согласно определению производной, дифференцирование $ \ sqrt {\ sin {x}} $ можно записать в предельной форме.
Возьмем $ y = f {(x)} $. Итак, $ f {(x)} = \ sqrt {\ sin {x}} $, тогда $ f {(x + \ Delta x)} = \ sqrt {\ sin {(x + \ Delta x)}} $
.$ \ dfrac {d} {dx} {\, f {(x)}} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {f {(x + \ Delta x)} — f {(x)}} {\ Delta x}}
долларов$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {d} {dx} {\, f {(x)}} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {f {(x + \ Delta x)} — f {(x)}} {\ Delta x}} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt { \ sin {(x + \ Delta x)}} — \ sqrt {\ sin {x}}} {\ Delta x}}
долларовВозьмите $ h = \ Delta x $ и выразите выражение через $ h $.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}}
долларовПопробуйте метод прямой замены
Попробуем вычислить дифференцирование квадратного корня из функции $ \ sin {x} $, вычислив предел тригонометрической функции методом прямой подстановки.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ sqrt {\ sin {(x + 0)}} — \ sqrt {\ sin {x}}} {0}
долларов США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ sqrt {\ sin {x}} — \ sqrt {\ sin {x}}} {0} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {0} {0} $
вычислено, что производная от $ \ sqrt {\ sin {x}} $ по $ x $ не определена.Таким образом, невозможно найти производную, оценивая предел методом прямой подстановки.
Использовать метод рационализации
Теперь попробуйте вычислить предел тригонометрической функции методом рационализации, чтобы найти производную функции $ \ sqrt {\ sin {x}} $ по $ x $.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}} $ $ \ times $ 1 \ Bigg] $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}}} {h}} $ $ \ times $ $ \ dfrac {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg]
долларов$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ Big (\ sqrt {\ sin {(x + h)}} — \ sqrt {\ sin {x}} \ Big) \ times \ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
Числитель представляет собой специальное произведение биномов, и их произведение может быть записано по формуле разности квадратов.2} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ sin {(x + h)} — \ sin {x}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долларовИспользуйте тригонометрическую идентичность преобразования разницы в произведении, чтобы объединить синусоидальные функции в числителе.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {2 \ cos {\ Bigg (\ dfrac {x + h + x} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {x + hx} {2} \ Bigg)}} {h \ times {\ Big ( \ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долларов США.$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ require {cancel} \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [ \ dfrac {2 \ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {\ cancel {x} + h- \ cancel {x}} {2} \ Bigg)}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]} $
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {2 \ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {h \ times {\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)}} \ Bigg]}
долларовТеперь разложите функцию на множители как произведение двух тригонометрических функций следующим образом.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)} \ times 2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {{\ Big (\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}} \ Big)} \ times h} \ Bigg]}
долларов$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ Bigg [\ Bigg (\ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg) \ times \ Bigg (\ dfrac {2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {h} \ Bigg) \ Bigg]}
долларов США.Теперь используйте правило пределов продукта, чтобы найти предел продукта на произведение их пределов.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {2 \ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} { h} \ Bigg)}
долларов$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ Bigg (\ dfrac {h} {2} \ Bigg)}} {\ dfrac {h} {2}} \ Bigg)}
долларов США$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim _ {\ frac {h} {2} \, \ to \, 0} {\ normalsize \ dfrac {\ sin {\ Bigg (\ dfrac {h} {2}) \ Bigg)}} {\ dfrac {h} {2}} \ Bigg)}
долларов США.Возьмите $ q = \ dfrac {h} {2} $ и замените $ \ dfrac {h} {2} $ на $ q $ только во втором множителе.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cos {\ Bigg (\ dfrac {2x + h} {2} \ Bigg)}} {\ sqrt {\ sin {(x + h)}} + \ sqrt {\ sin {x}}} \ Bigg)} $ \ раз $ $ \ Bigg (\ displaystyle \ large \ lim_ {q \, \ to \, 0} {\ normalsize \ dfrac {\ sin {q}} {q} \ Bigg)} $
Вычислить пределы функций
Найдите значение первого фактора, оценив предел тригонометрической функции методом прямой подстановки, а затем найдите значение второго фактора по пределу sinx / x, когда x приближается к 0 по формуле стандартной формы.
$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ Bigg (\ dfrac {\ cos {\ Bigg (\ dfrac {2x + 0} {2} \ Bigg)}} {\ sqrt {\ sin {(x + 0)}} + \ sqrt {\ sin {x}}} \ Bigg) $ $ \ times $ $ \ Bigg (1 \ Bigg) $
.$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {\ Bigg (\ dfrac {2x} {2} \ Bigg)}} {\ sqrt {\ sin {x}} + \ sqrt {\ sin {x}}}
долларов$ \ подразумевает $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ require {cancel} \ dfrac {\ cos {\ Bigg (\ dfrac {\ cancel {2} x} {\ cancel {2}} \ Bigg)}} {2 \ sqrt {\ sin {x}}}
долл. США$ \, \, \, \ следовательно \, \, \, \, \, \, $ $ \ dfrac {dy} {dx} $ $ \, = \, $ $ \ dfrac {\ cos {x}} {2 \ sqrt {\ sin {x}}}
долларов США3.2: Производная как функция
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке.Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная.Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \ (f \) — функция. Производная функция , обозначаемая \ (f ‘\), является функцией, область определения которой состоит из таких значений \ (x \), что существует следующий предел:
\ [f ‘(x) = \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h}. \ label {derdef} \]
Функция \ (f (x) \) называется дифференцируемой в точке \ (a \), если существует \ (f ‘(a) \). В более общем смысле, функция называется дифференцируемой на \ (S \), если она дифференцируема в каждой точке открытого множества \ (S \), а дифференцируемая функция — это функция, в которой \ (f ‘( x) \) существует в своем домене.
В следующих нескольких примерах мы используем уравнение \ ref {derdef}, чтобы найти производную функции.
Пример \ (\ PageIndex {1} \): поиск производной функции квадратного корня
Найдите производную от \ (f (x) = \ sqrt {x} \).
Решение
Начните непосредственно с определения производной функции.
Заменить \ (f (x + h) = \ sqrt {x + h} \) и \ (f (x) = \ sqrt {x} \) в \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \).
| \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} \) | ||
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h} ⋅ \ frac {\ sqrt {x + h} + \ sqrt { x}} {\ sqrt {x + h} + \ sqrt {x}} \) | Умножьте числитель и знаменатель на \ (\ sqrt {x + h} + \ sqrt {x} \) без распределения в знаменателе. | |
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {h} {h \ left (\ sqrt {x + h} + \ sqrt {x} \ right)} \) | Умножьте числители и упростите. 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \): \ (f ‘(x), \ quad \ dfrac {dy} {dx}, \ quad y’, \ quad \ dfrac {d} {dx} \ big (f (x) \ big) \). Вместо \ (f ‘(a) \) мы также можем использовать \ (\ dfrac {dy} {dx} \ Big | _ {x = a} \). Нотация \ (\ dfrac {dy} {dx} \) (называемая нотацией Лейбница) довольно распространена в технике и физике. Чтобы лучше понять это обозначение, напомним, что производная функции в точке — это предел наклона секущих линий, когда секущие линии приближаются к касательной.Наклоны этих секущих часто выражаются в виде \ (\ dfrac {Δy} {Δx} \), где \ (Δy \) — разность значений \ (y \), соответствующая разнице в \ (x \) значения, которые выражаются как \ (Δx \) (Рисунок \ (\ PageIndex {1} \)). Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как \ (\ Displaystyle \ frac {dy} {dx} = \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Рисунок \ (\ PageIndex {1} \): производная выражается как \ (\ dfrac {dy} {dx} = \ displaystyle \ lim_ {Δx → 0} \ frac {Δy} {Δx} \).График производнойМы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \ (f ‘(x) \) дает скорость изменения функции \ (f (x) \) (или наклон касательной линия к \ (f (x) \)). В примере \ (\ PageIndex {1} \) мы обнаружили, что для \ (f (x) = \ sqrt {x} \), \ (f ‘(x) = \ frac {1} {2 \ sqrt { Икс}}\).Если мы построим график этих функций на тех же осях, как на рисунке \ (\ PageIndex {2} \), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, а это означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f ‘(x)> 0 \) для всех значений x в его области определения. Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f ‘(x) \).2−2x, \; f ‘(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x <1 \). Для тех же значений \ (x \), \ (f '(x) <0 \). Для значений \ (x> 1 \), \ (f (x) \) увеличивается и \ (f ‘(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в \ (x = 1 \) и \ (f ‘(1) = 0 \). Рисунок \ (\ PageIndex {3} \): производная \ (f ‘(x) <0 \), где функция \ (f (x) \) убывает, и \ (f' (x)> 0 \), где \ (f (x) \) возрастает. Производная равна нулю, если функция имеет горизонтальную касательную.Пример \ (\ PageIndex {3} \): эскиз производной с использованием функции Используйте следующий график \ (f (x) \), чтобы нарисовать график \ (f ‘(x) \).2−4 \). На каком интервале находится график \ (f ‘(x) \) над осью \ (x \)?
Деривативы и непрерывностьТеперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью.Мы увидим, что если функция дифференцируема в точке, она должна быть непрерывной там; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость предполагает непрерывность Пусть \ (f (x) \) — функция и \ (a \) находится в ее области определения. Если \ (f (x) \) дифференцируема в \ (a \), то \ (f \) непрерывна в \ (a \). Проба Если \ (f (x) \) дифференцируемо в \ (a \), то \ (f ‘(a) \) существует и, если мы положим \ (h = x — a \), имеем \ (x = a + h \), и поскольку \ (h = xa \ to 0 \), мы можем видеть, что \ (x \ to a \). Затем \ [f ‘(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ nonumber \] можно переписать как \ (F ‘(a) = \ displaystyle \ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \). Мы хотим показать, что \ (f (x) \) непрерывно в \ (a \), показав, что \ (\ displaystyle \ lim_ {x → a} f (x) = f (a). \) Таким образом, \ (\ begin {align *} \ displaystyle \ lim_ {x → a} f (x) & = \ lim_ {x → a} \; \ big (f (x) −f (a) + f (a)) \ big) \\ [4pt] Следовательно, поскольку \ (f (a) \) определено и \ (\ displaystyle \ lim_ {x → a} f (x) = f (a) \), мы заключаем, что \ (f \) непрерывно в \ (а \). □ Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию \ (f (x) = | x | \).2}} = + ∞ \). Таким образом, \ (f ‘(0) \) не существует. Быстрый взгляд на график \ (f (x) = \ sqrt [3] {x} \) проясняет ситуацию. Функция имеет вертикальную касательную в точке \ (0 \) (рисунок \ (\ PageIndex {5} \)). Рисунок \ (\ PageIndex {5} \): функция \ (f (x) = \ sqrt [3] {x} \) имеет вертикальную касательную в точке \ (x = 0 \). Он непрерывен в \ (0 \), но не дифференцируем в \ (0 \).Функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) также имеет производную, которая демонстрирует интересное поведение в \ (0 \). Мы видим, что \ (е ‘(0) = \ displaystyle \ lim_ {x → 0} \ frac {x \ sin \ left (1 / x \ right) −0} {x − 0} = \ lim_ {x → 0} \ sin \ left (\ frac {1} {x} \ right) \). Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю (Рисунок \ (\ PageIndex {6} \)). Рисунок \ (\ PageIndex {6} \): функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) не дифференцируем в \ (0 \).Итого:
| Упростим числитель. |
| \ (= \ Displaystyle \ lim_ {h → 0} (4x + h − 3) \) | Выносим за скобки \ (h \) в числителе и сокращаем, добавляя \ (h \) в знаменатель. | |
| \ (= 4x − 3 \) | Возьми предел. |
Затем найдите \ (f » (x) \), взяв производную от \ (f ‘(x) = 4x − 3. \)
| \ (f » (x) = \ displaystyle \ lim_ {h → 0} \ frac {f ‘(x + h) −f’ (x)} {h} \) | Используйте \ (f ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) с \ (f’ (x) \) в место \ (f (x).3 \), найти \ (a (t). \)
Ключевые концепции
Ключевые уравнения\ (е ‘(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) Глоссарий
Авторы и авторство
|



 Отрицательные.
Отрицательные.
 на значение.
на значение.