Найти производную y x e x: Найти производную y=x^ascsinx — ответ на Uchi.ru

Производная параметрически и неявно заданных функций

Пусть x =  (t),y =  (t), t [a,b] — достаточно гладкие функции. Тогда говорят, что функция задана параметрически. Примером параметрически заданной функции является уравнение окружности: x = acos t,y = asin t, t [0,2]. Рассмотрим вопрос о нахождении производных y = y(x) по переменной x.

В силу свойства инвариантности формы первого дифференциала следует, что y’ = dy/dx, dy = '(t)dt, dx = '(t)dt. Поэтому

y’(x) = ‘(t)/‘(t).

Используя формулу для второго дифференциала, получим

y(2)(x) = d(y’(x))/dx = ( ‘(t)/ ‘(t))‘dt/ ‘(t)dt =

= ( »(t)  ‘(t)- »(t) ‘(t))/( ‘(t))³

.

Чтобы вычислить третью производную, запишем y»'(x) в следующем виде

y»’(x) = d(y»(x))/dx.

Пример 10. Функция задана параметрически

x = a(t-sin t), y = a(1-cos t).

Наити y»(x).

y’_t = asin t, x’_t = a(1-cos t).

Отсюда

y’(x) = (asin t)/(a(1-cos t)) = ctg (t/2), t 2 k.

y»(x) = d(ctg (t/2))/(a(1-cos t)) = -1/4sin⁴t/2.

Пусть функция задана неявно уравнением F(x,y) = 0. Для нахождения производной функции, заданной неявно, нужно продифференцировать обе части уравнения, считая y = y(x) функцией от x, а затем из полученного уравнения найти производную y’.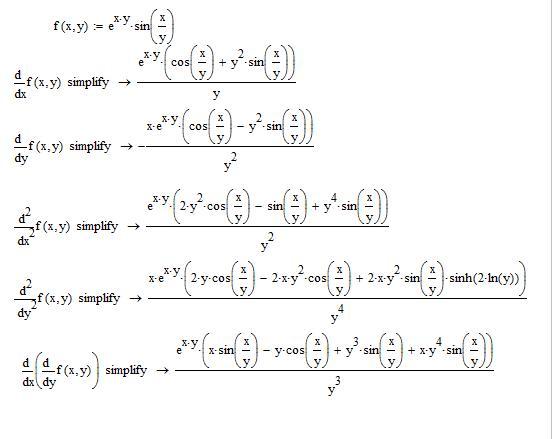

Чтобы найти производные высших порядков, нужно дифференцировать необходимое число раз уравнение F(x,y) = 0, и затем выразить нужную производную.

Пример 11. Найти y»(x), если :

x+y = e^x-y.

Дифференцируем данное уравнение по x, считая y функцией от x.

1+y’_x(x) = e^x-y(1-y’_x(x)),откуда y’_x = (e^x-y—1)/(1+e^x-y).

Дифференцируя уравнение еще раз, получим

y»_x(

x) = e^x-y(1-y’_x(x))²-e^x-yy»_x(x),

следовательно,

y»_x(x) = (1-y’_x)²e^x-y/(1+e^x-y) = 4e^x-y/(1+e^x-y)³.

43

Пусть даны два уравнения

x=x(t),y=y(t), где t  [T1, T2].

(1)

Каждому значению t из [T₁, T₂] соответствуют определенные значения 

x и y. Если рассматривать значения x и y как координаты точки на плоскости xOy, то каждому значению t будет соответствовать определенная точка плоскости. Когда tизменяется от T₁ до T₂, эта точка на плоскости описывает некоторую кривую. Уравнения (1) называютсяпараметрическими уравнениями этой кривой, t называется параметром, а способ задания кривой уравнениями (1) называется параметрическим.

Предположим, что функция x=x(t) имеет обратную t=t(x). Тогда, очевидно, у является функцией от x: y=y[t(x)]. Следовательно, уравнения (1) определяют y как функцию от x, и говорят, что функция y от x задается параметрически.

При рассмотрении функций, заданных параметрически, исключение параметра не всегда возможно. Во многих случаях удобнее задавать различные значения t и затем вычислять соответствующие значения аргумента x и функции y.

Пример. Пусть кривая задана параметрическими уравнениями:

Построим эту кривую на плоскости, придавая различные значения параметру t и находя соответствующие значения х и у.

При t =0 M(R, 0). 

Таким образом, получаем окружность с центром в начале координат, радиуса R. Здесь t обозначает угол, образованный радиусом, проведенным в некоторую точку окружности М(x, y), и осью Ox.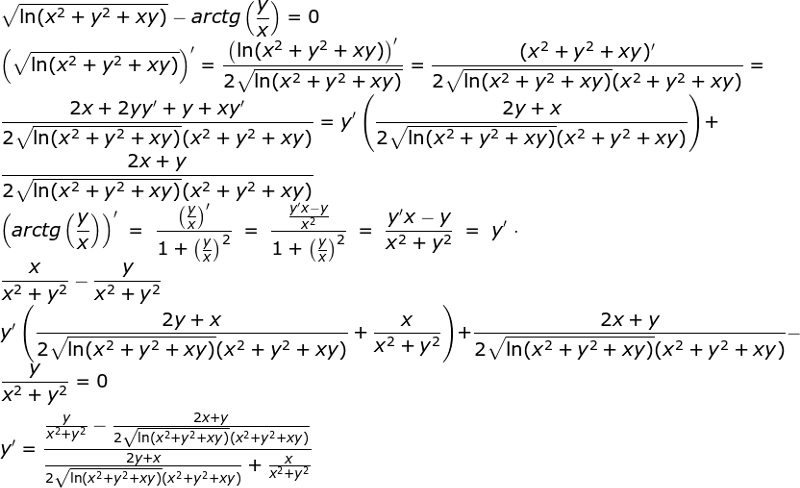

Если исключим из этих уравнений параметр t, то получим уравнение окружности, содержащее только x и y. Возводя в квадрат параметрические уравнения и складывая их, находим:

x²+ y²=R²(cos²t + sin²t) или x²+ y²=R².

Выведем правило нахождения производных функций, заданных параметрически. Пусть x=x(t), y=y(t), причем на некотором отрезке [T₁, T₂] функции x(t) и y(t) дифференцируемы и x‘ ≠ 0.

Т.к. у – функция, зависящая от переменной x, то будем считать, что функция x=x(t) имеет обратную t=t(x).

Будем обозначать: y_x‘ – производная функции по переменной 

x, y_t‘, x_t‘, t_x‘ – соответственно производные по t и х.

Воспользовавшись правилом дифференцирования сложной функции, получим . Производную t_x‘ найдем по правилу дифференцирования обратной функции .

Окончательно, .

Итак,

Полученную функцию  можно рассматривать как функцию, заданную параметрически: .

Используя эту формулу, можно находить и производные высших порядков функций, заданных параметрически. Найдем . По определению второй производной . Учитывая, что y_x‘ есть функция параметра t, y_x‘=f(t),получаем:

Примеры.

1. , y = arcsin (t–1). Найдем .

Следовательно, .

2. Найти угловой коэффициент касательной к циклоиде x = a·(t – sin t), y = a·(1 – cost)

в произвольной точке (0 ≤t≤ 2·π).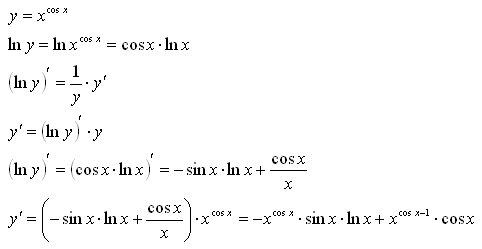

Угловой коэффициент касательной .

x‘ = a·(1 – cost) ,y‘ = a·sin t. Поэтому .

Найти .

44

Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве

. Точка, в которой достигается экстремум, называетсяточкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализевыделяют также понятие локальный экстремум (соответственно минимум или максимум).

Логарифмическая производная. Производная функции, заданной параметрическими уравнениями. (Семинар 9)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Семинар 9. Логарифмическая производная. Производная функции, заданной
параметрическими уравнениями
Понятие о логарифмической производной
Рассмотрим сложную функцию y ln z, z ( x)
Применяя правило дифференцирования сложной функции, получаем
y x’ (ln z ) ‘x (ln z ) ‘z z x’ y x’
1 ‘
z’
z x y ‘ (ln z ) ‘x
z
z
Производная от логарифмической функции называется логарифмической
производной функции.
2
Пример y ln( x 2 4 x 5) y’ ( x 2 4 x 5)’ 2 2 x 4
x 4x 5
x 4x 5
Производная функции, заданной параметрическими уравнениями
Зависимость между переменными x,y иногда удобно задавать двумя уравнениями
x (t ), y (t )
(1), где t – вспомогательная переменная, (параметр).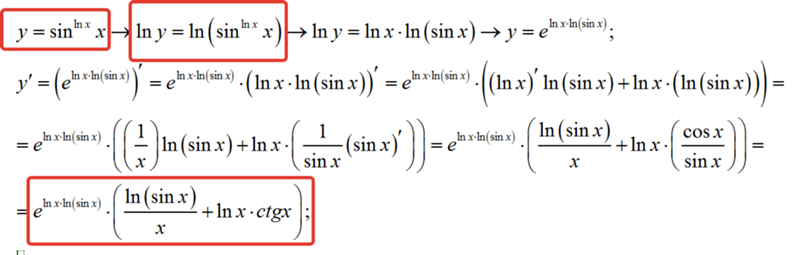 В общем
случае, уравнения (1) определяют y как сложную функцию относительно x.

Разрешив первое уравнение системы (1) относительно параметра t (если это
возможно), получимt (x), функция, обратная к функции Далее, исключая
из уравнений (1) параметр t, получаем y ( ( x)) (2). Пользуясь формулой (2) легко
найти производную y x’ как производную сложной функции. Кроме того, существует
правило для нахождения y x’ не требующее исключение параметра t (параметр
невозможно исключить).
Теорема
Если функция y аргумента x задана параметрическими уравнениями x (t ), y (t ) ,где
(t ), (t )- дифференцируемые функции и (t ) 0 производная этой функции есть
y t’
y ‘
xt
‘
x
(3).
Примеры с решениями.
1.Применяя логарифмическую производную вычислить производные следующих
функций:
Решение Здесь основание и показатель степени зависят от х.
1) y x x
Логарифмируя, получим y x 2 ln x
Продифференцируем обе части последнего равенства по х. 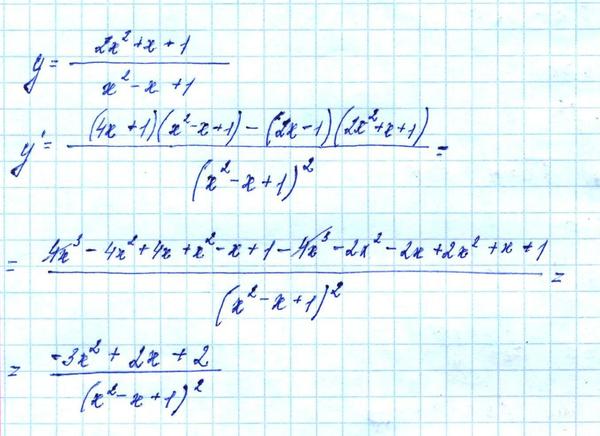Так как y является функцией
y’
от х, то lny есть сложная функция х и
Следовательно
(ln
y )’
2
y
2
2
y’
1
x 2 2 x ln x y’ yx(2 ln x) x x x(1 2 ln x) x x 1( 2 ln x )
y
x
2) y (sin x) tgx
Решение .Имеем ln y tgx ln sin x откуда
3) y
(2 x 1) 2 3x 2
(5x 4) 2 3 1 x
y ‘ ln sin x
cos x ln sin x
ln sin x
tgx
1 y ‘ (sin x) tgx (1
)
2
2
y cos x
sin x cos x
cos 2 x
Решение. Здесь заданную функцию также полезно предварительно
прологарифмировать
1
1
ln y 3(ln( 2 x 1) ln( 3x 2) 2 ln( 5 x 4) ln( 1 x)
2
3
y’
6
3
10
1
y 2 x 1 2(3x 2) 5 x 4 3(1 x)
Получаем
y’
(2 x 1) 2 3x 2
(5x 4) 2 3 1 x
(
6
3
10
1
)
2 x 1 2(3x 2) 5 x 4 3(1 x)
4) y x x 2 x x 2
Решение. заданную функцию также полезно предварительно прологарифмировать
ln y x ln x x ln 2 2 x ln 2 ln x x 3
y’
1
ln 2( x 3 3x 2 ln x) ln 2 x 2 (1 3 ln x)
y
x
следовательно y’ x x 2 x x 2 ( ln 2 x 2 (1 3 ln x))
2. 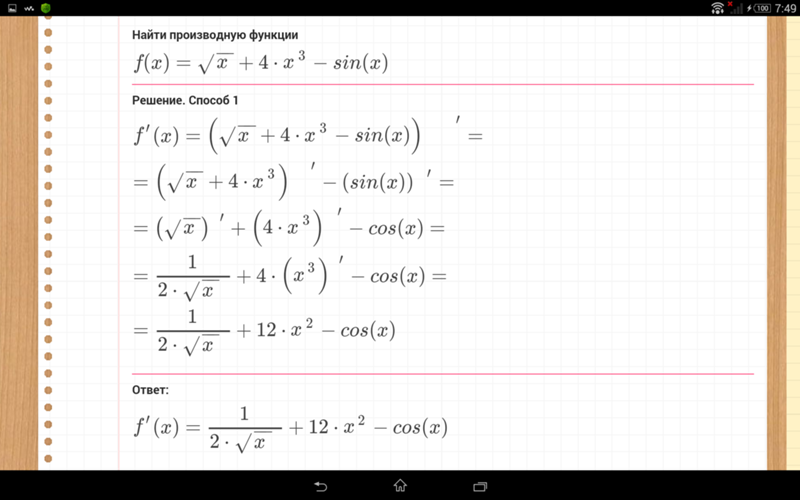Продифференцировать функции, заданные параметрическими уравнениями
‘
3
y
‘
t
1.Найти y x ‘ если x t 3t 1
xt
Решение
2.Найти
5
3
y 3t 5t 1
xt’ 3t 2 3; yt’ 15t 4 15t 2 y x’
y t’
y ‘
xt
‘
x
если x e t sin t
y e t cos t
15t 4 15t 2
5t 2
2
3t 3
Решение xt’ e t sin t e t cos t; yt’ e t cos t e t sin t y x’ e t(cos t sin t ) e 2t
e (cos t sin t )
‘
3. Найти ‘ y t
если x ln( t 2 1)
yx ‘
xt
y arctgt
t
Решение
1
2t
1
‘
‘
1 t 2 1
xt’
;
y
y
t
x
2t
2t
1 t2
1 t 2
2
1 t
Примеры для самостоятельного решения.
1.Применяя логарифмическую производную вычислить производные следующих
функций
x
x
ctg
x
2
sin x
1
thx
x
1. y 4
2. y (ln x) 3. y
4. y ( x 1)
5. y (tx2 x) 2
6. y 3
1 thx
x 5
5
x2 4
1 x
1
7. y 1 e x arctgx 2 ln x 1
2
x
2.