Вычисление ранга матрицы методом элементарных преобразований (алгоритм Гаусса).
Высшая математика » Матрицы и определители » Ранг матрицы » Вычисление ранга матрицы методом элементарных преобразований.
Под элементарными преобразованиями строк (столбцов) матрицы понимают следующие действия:
- Перемена мест двух строк (столбцов).
- Умножение всех элементов строки (столбца) на некоторое число $a\neq 0$.
- Суммирование всех элементов одной строки (столбца) с соответствующими элементами иной строки (столбца), умноженными на некое действительное число.
Если применить к строкам или столбцам матрицы $A$ некое элементарное преобразование, то получим новую матрицу $B$. В этом случае $\rang{A}=\rang{B}$, т.е. элементарные преобразования не изменяют ранг матрицы.
Если $\rang A=\rang B$, то матрицы $A$ и $B$ называются эквивалентными. Тот факт, что матрица $A$ эквивалентна матрице $B$, записывают так: $A\sim B$. T}$. Этим свойством в некоторых случаях удобно пользоваться (см. пример №3), так как при необходимости строки легко сделать столбцами и наоборот.
T}$. Этим свойством в некоторых случаях удобно пользоваться (см. пример №3), так как при необходимости строки легко сделать столбцами и наоборот.
Краткое описание алгоритма
Введём несколько терминов. Нулевая строка – строка, все элементы которой равны нулю. Ненулевая строка – строка, хоть один элемент которой отличен от нуля. Ведущим элементом ненулевой строки называется её первый (считая слева направо) отличный от нуля элемент. Например, в строке $(0;0;5;-9;0)$ ведущим будет третий элемент (он равен 5).
Ранг любой нулевой матрицы равен 0, поэтому станем рассматривать матрицы, отличные от нулевых. Конечная цель преобразований матрицы – сделать её ступенчатой. Ранг ступенчатой матрицы равен количеству ненулевых строк.
Рассматриваемый метод нахождения ранга матрицы состоит из нескольких шагов. На первом шаге используется первая строка, на втором шаге – вторая и так далее. Когда под той строкой, которую мы используем на текущем шаге, остаются лишь нулевые строки, или же не остаётся строк вовсе, то алгоритм прекращается, так как полученная матрица будет ступенчатой.
Теперь обратимся к тем преобразованиям над строками, которые выполняются на каждом шаге алгоритма. Пусть под текущей строкой, которую нам нужно использовать на данном шаге, имеются ненулевые строки, причём $k$ – номер ведущего элемента текущей строки, а $k_{\min}$ – наименьший из номеров ведущих элементов тех строк, которые лежат ниже текущей строки.
- Если $k\lt{k_{\min}}$, то переходим к следующему шагу алгоритма, т.е. к использованию следующей строки.
- Если $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Если появляются нулевые строки, то переносим их в низ матрицы. Затем переходим к следующему шагу алгоритма.
- Если $k\gt{k_{\min}}$, то меняем местами текущую строку с одной из тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. После этого производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$.

Как конкретно происходит обнуление ведущих элементов, рассмотрим на практике. Буквами $r$ (от слова «row») станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова «column») станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.
В примерах на данной странице буквой $k$ я стану обозначать номер ведущего элемента текущей строки, а запись $k_{\min}$ будет использована для обозначения наименьшего из номеров ведущих элементов строк, лежащих под текущей строкой.
Пример №1
Найти ранг матрицы $A=\left(\begin{array}{ccccc}
-2 & 3 & 1 & 0 & -4 \\
0 & 0 & 0 & 5 & -6 \\
4 & -11 & -5 & 12 & 18 \\
-9 & 6 & 0 & -2 & 21 \\
-5 & 5 & 1 & 1 & 1
\end{array} \right)$.
Решение
Данная матрица не является нулевой, а значит её ранг больше нуля. Перейдём к первому шагу алгоритма.
Первый шаг
На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является первый элемент, т.е. номер ведущего элемента первой строки $k=1$. Посмотрим на строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номера 4, 1, 1 и 1. Наименьшим из этих номеров есть $k_{\min}=1$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Иными словами, нужно обнулить ведущие элементы третьей, четвёртой и пятой строк.
В принципе, можно приступать к обнулению указанных выше элементов, однако для тех преобразований, которые выполняются для обнуления, удобно, когда ведущим элементом используемой строки является единица. Это не обязательно, но очень упрощает расчёты. У нас ведущим элементом первой строки есть число -2. Чтобы заменить «неудобное» число единицей (или числом (-1)) есть несколько вариантов. Можно, например, умножить первую строку на 2, а затем от первой строки вычесть пятую. А можно просто поменять местами первый и третий столбцы. После перестановки столбцов №1 и №3 получим новую матрицу, эквивалентную заданной матрице $A$:
Чтобы заменить «неудобное» число единицей (или числом (-1)) есть несколько вариантов. Можно, например, умножить первую строку на 2, а затем от первой строки вычесть пятую. А можно просто поменять местами первый и третий столбцы. После перестановки столбцов №1 и №3 получим новую матрицу, эквивалентную заданной матрице $A$:
$$ \left(\begin{array}{ccccc} -2 & 3 & 1 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 4 & -11 & -5 & 12 & 18 \\ -9 & 6 & 0 & -2 & 21 \\ -5 & 5 & 1 & 1 & 1 \end{array}\right)\overset{c_1\leftrightarrow{c_3}}{\sim} \left(\begin{array}{ccccc} \boldred{1} & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ \normblue{-5} & -11 & 4 & 12 & 18 \\ 0 & 6 & -9 & -2 & 21 \\ \normgreen{1} & 5 & -5 & 1 & 1 \end{array}\right) $$
Ведущим элементом первой строки стала единица. Номер ведущего элемента первой строки не поменялся: $k=1$. Номера ведущих элементов строк, расположенных ниже первой, таковы: 4, 1, 2, 1. Наименьший номер $k_{\min}=1$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и пятой строк. Эти элементы выделены синим и зелёным цветами.
Номер ведущего элемента первой строки не поменялся: $k=1$. Номера ведущих элементов строк, расположенных ниже первой, таковы: 4, 1, 2, 1. Наименьший номер $k_{\min}=1$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и пятой строк. Эти элементы выделены синим и зелёным цветами.
Чтобы обнулить нужные элементы, будем выполнять операции со строками матрицы. Запишу эти операции отдельно:
$$ \begin{aligned} &r_3-\frac{\normblue{-5}}{\boldred{1}}\cdot{r_1}=r_3+5r_1;\\ &r_5-\frac{\normgreen{1}}{\boldred{1}}\cdot{r_1}=r_5-r_1. \end{aligned} $$
Запись $r_3+5r_1$ означает, что к элементам третьей строки прибавили соответствующие элементы первой строки, умноженные на пять. Результат записывают на место третьей строки в новую матрицу. Если с устным выполнением такой операции возникают сложности, то это действие можно выполнить отдельно:
$$
r_3+5r_1
=(-5;\;-11;\;4;\;12;\;18)+5\cdot(1;\;3;\;-2;\;0;\;-4)=\\
=(-5;\;-11;\;4;\;12;\;18)+(5;\;15;\;-10;\;0;\;-20)
=(0;\;4;\;-6;\;12;\;-2).
Действие $r_5-r_1$ выполняется аналогично. В результате преобразований строк получим такую матрицу:
$$ \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ -5 & -11 & 4 & 12 & 18 \\ 0 & 6 & -9 & -2 & 21 \\ 1 & 5 & -5 & 1 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3+5r_1 \\ \phantom{0} \\ r_5-r_1 \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 4 & -6 & 12 & -2 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) $$
На этом первый шаг можно считать законченным. Так как под первой строкой остались ненулевые строки, то нужно продолжать работу. Единственный нюанс: в третьей строке полученной матрицы все элементы делятся нацело на 2. Чтобы уменьшить числа и упростить себе расчёты, умножим элементы третьей строки на $\frac{1}{2}$, а затем уже перейдём ко второму шагу:
Единственный нюанс: в третьей строке полученной матрицы все элементы делятся нацело на 2. Чтобы уменьшить числа и упростить себе расчёты, умножим элементы третьей строки на $\frac{1}{2}$, а затем уже перейдём ко второму шагу:
$$ \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 4 & -6 & 12 & -2 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ 1/2\cdot{r_3} \\ \phantom{0} \\ \phantom{0} \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 2 & -3 & 6 & -1 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) $$
Второй шаг
На втором шаге мы работаем с второй строкой.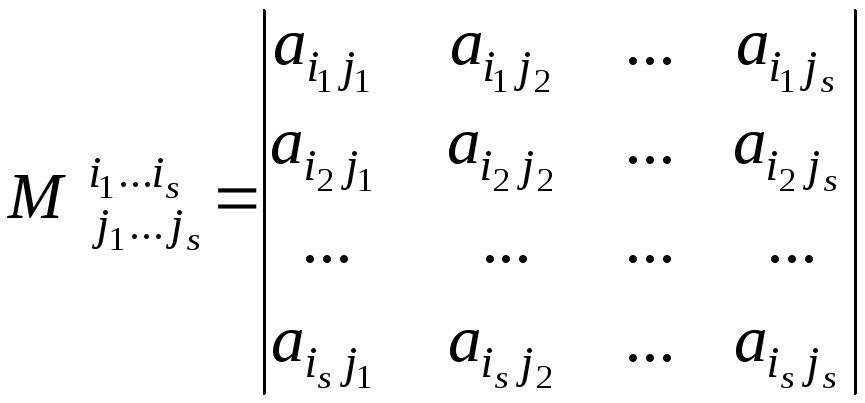 Во второй строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента второй строки $k=4$. Посмотрим на строки, расположенные под второй строкой. Ведущие элементы в этих строках имеют номера 2, 2 и 2. Наименьшим из этих номеров есть $k_{\min}=2$. Так как $k\gt{k_{\min}}$, то нужно поменять местами текущую вторую строку с одной из тех строк, у которых номер ведущего элемента равен $k_{\min}$. Иными словами, надо поменять вторую строку с третьей, четвёртой или пятой. Я выберу пятую строку (это позволит избежать появления дробей), т.е. поменяю местами пятую и вторую строки:
Во второй строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента второй строки $k=4$. Посмотрим на строки, расположенные под второй строкой. Ведущие элементы в этих строках имеют номера 2, 2 и 2. Наименьшим из этих номеров есть $k_{\min}=2$. Так как $k\gt{k_{\min}}$, то нужно поменять местами текущую вторую строку с одной из тех строк, у которых номер ведущего элемента равен $k_{\min}$. Иными словами, надо поменять вторую строку с третьей, четвёртой или пятой. Я выберу пятую строку (это позволит избежать появления дробей), т.е. поменяю местами пятую и вторую строки:
$$ \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 2 & -3 & 6 & -1 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) \overset{r_2\leftrightarrow{r_5}}{\sim} \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & \boldred{2} & -3 & 1 & 5 \\ 0 & \normblue{2} & -3 & 6 & -1 \\ 0 & \normgreen{6} & -9 & -2 & 21 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) $$
Опять обратимся ко второй строке. Теперь ведущим в ней является второй элемент (он выделен красным цветом), т.е. $k=2$. Наименьшим из номеров ведущих элементов нижележащих строк (т.е. из чисел 2, 2 и 4) будет $k_{\min}=2$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк. Эти элементы выделены синим и зелёным цветами.
Теперь ведущим в ней является второй элемент (он выделен красным цветом), т.е. $k=2$. Наименьшим из номеров ведущих элементов нижележащих строк (т.е. из чисел 2, 2 и 4) будет $k_{\min}=2$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк. Эти элементы выделены синим и зелёным цветами.
Отмечу, что на предыдущем шаге ведущим элементом текущей строки с помощью перестановки столбцов была сделана единица. Это было выполнено, чтобы избежать работы с дробями. Здесь тоже можно поставить единицу на место ведущего элемента второй строки: например, поменяв местами второй и четвёртый столбцы. Однако делать это мы не станем, так как дробей и так не возникнет. Действия со строками будут такими:
$$
\begin{aligned}
&r_3-\frac{\normblue{2}}{\boldred{2}}\cdot{r_2}=r_3-r_2;\\
&r_4-\frac{\normgreen{6}}{\boldred{2}}\cdot{r_2}=r_4-3r_2. \end{aligned}
$$
\end{aligned}
$$
Выполняя указанные операции, придём к такой матрице:
$$ \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 2 & -3 & 6 & -1 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3-r_2 \\ r_4-3r_2 \\ \phantom{0} \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 0 & 0 & -5 & 6 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) $$
Второй шаг закончен. Так как под второй строкой остались ненулевые строки, то переходим к третьему шагу.
Третий шаг
На третьем шаге мы работаем с третьей строкой. В третьей строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента третьей строки $k=4$. Посмотрим на строки, расположенные под третьей строкой. Ведущие элементы в этих строках имеют номера 4 и 4, наименьший из которых $k_{\min}=4$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы четвёртой и пятой строк. Преобразования, которые выполняются с этой целью, полностью аналогичны тем, что осуществлялись ранее:
В третьей строке матрицы ведущим является четвёртый элемент, т.е. номер ведущего элемента третьей строки $k=4$. Посмотрим на строки, расположенные под третьей строкой. Ведущие элементы в этих строках имеют номера 4 и 4, наименьший из которых $k_{\min}=4$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы четвёртой и пятой строк. Преобразования, которые выполняются с этой целью, полностью аналогичны тем, что осуществлялись ранее:
$$ \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 0 & 0 & -5 & 6 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ r_4+r_3 \\ r_5-r_3 \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right) $$
Под третьей строкой остались лишь нулевые строки. Это значит, что преобразования закончены. Мы привели матрицу к ступенчатому виду. Так как приведённая матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $\rang A=3$. Полное решение без пояснений таково:
Это значит, что преобразования закончены. Мы привели матрицу к ступенчатому виду. Так как приведённая матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $\rang A=3$. Полное решение без пояснений таково:
$$ \left(\begin{array}{ccccc} -2 & 3 & 1 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 4 & -11 & -5 & 12 & 18 \\ -9 & 6 & 0 & -2 & 21 \\ -5 & 5 & 1 & 1 & 1 \end{array}\right)\overset{c_1\leftrightarrow{c_3}}{\sim} \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ -5 & -11 & 4 & 12 & 18 \\ 0 & 6 & -9 & -2 & 21 \\ 1 & 5 & -5 & 1 & 1 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3+5r_1 \\ \phantom{0} \\ r_5-r_1 \end{array}\sim $$ $$ \sim\left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 4 & -6 & 12 & -2 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ 1/2\cdot{r_3} \\ \phantom{0} \\ \phantom{0} \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 2 & -3 & 6 & -1 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 2 & -3 & 1 & 5 \end{array}\right) \overset{r_2\leftrightarrow{r_5}}{\sim} \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 2 & -3 & 6 & -1 \\ 0 & 6 & -9 & -2 & 21 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3-r_2 \\ r_4-3r_2 \\ \phantom{0} \end{array}\sim $$ $$ \sim\left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 0 & 0 & -5 & 6 \\ 0 & 0 & 0 & 5 & -6 \end{array}\right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ \phantom{0} \\ r_4+r_3 \\ r_5-r_3 \end{array}\sim \left(\begin{array}{ccccc} 1 & 3 & -2 & 0 & -4 \\ 0 & 2 & -3 & 1 & 5 \\ 0 & 0 & 0 & 5 & -6 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right) $$
Ответ: $\rang A=3$.
Пример №2
Найти ранг матрицы $A=\left(\begin{array}{ccccc} 11 & -13 & 61 & 10 & -11\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right)$.
Решение
Данная матрица не является нулевой, а значит её ранг больше нуля. Перейдём к первому шагу алгоритма.
Первый шаг
На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является первый элемент, т.е. номер ведущего элемента первой строки $k=1$. Посмотрим на строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номер 1, т.е. наименьший из номеров ведущих элементов нижележащих строк есть $k_{\min}=1$. Так как $k=k_{\min}$, то нужно произвести обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Иными словами, нужно обнулить ведущие элементы второй, третьей и четвёртой строк.
Для удобства расчётов сделаем так, чтобы ведущим элементом первой строки стала единица. В предыдущем примере для этого мы меняли местами столбцы, однако с этой матрицей такое действие не пройдёт – в данной матрице нет элементов, равных единице. Выполним одно вспомогательное действие: $r_1-5r_2$. Тогда ведущий элемент первой строки станет равен 1.
$$ \left(\begin{array}{ccccc} 11 & -13 & 61 & 10 & -11\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right) \begin{array} {l} r_1-5r_2\\ \phantom{0}\\ \phantom{0} \\ \phantom{0} \end{array}\sim \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right) $$
Ведущим элементом первой строки стала единица. Обнулим ведущие элементы нижележащих строк:
Обнулим ведущие элементы нижележащих строк:
$$ \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right) \begin{array} {l} \phantom{0}\\ r_2-2r_1\\ r_3+3r_1 \\ r_4-4r_1 \end{array}\sim \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & -4 & 1 & -2 & 0\\ 0 & 12 & 0 & 7 & -4 \end{array} \right) $$
Первый шаг закончен. Так как под первой строкой остались ненулевые строки, то нужно продолжать работу.
Второй шаг
На втором шаге работаем с второй строкой. Во второй строке матрицы ведущим является второй элемент, т.е. номер ведущего элемента второй строки $k=2$. Ведущие элементы в нижележащих строках имеют тот же номер 2, поэтому $k_{\min}=2$. Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк.
Так как $k=k_{\min}$, то производим обнуление ведущих элементов тех нижележащих строк, у которых номер ведущего элемента равен $k_{\min}$. Это значит, что нужно обнулить ведущие элементы третьей и четвёртой строк.
$$ \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & -4 & 1 & -2 & 0\\ 0 & 12 & 0 & 7 & -4 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3+r_2 \\ r_4-3r_2 \end{array}\sim \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 3 & 1 & -4 \end{array} \right) $$
Появилась нулевая строка. Опустим её в низ матрицы:
$$ \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 3 & 1 & -4 \end{array} \right) \overset{r_3\leftrightarrow{r_4}}{\sim} \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & 0 & 3 & 1 & -4\\ 0 & 0 & 0 & 0 & 0 \end{array} \right) $$
Второй шаг закончен. Заметьте, что мы уже получили ступенчатую матрицу. Впрочем, мы можем формально закончить наш алгоритм. Так как под второй строкой остались ненулевые строки, то следует перейти к третьему шагу и работать с третьей строкой, однако под третьей строкой ненулевых строк нет. Следовательно, преобразования завершены.
Заметьте, что мы уже получили ступенчатую матрицу. Впрочем, мы можем формально закончить наш алгоритм. Так как под второй строкой остались ненулевые строки, то следует перейти к третьему шагу и работать с третьей строкой, однако под третьей строкой ненулевых строк нет. Следовательно, преобразования завершены.
К слову, полученная нами матрица является трапециевидной. Трапециевидная матрица – это частный случай ступенчатой матрицы.
Так как данная матрица содержит три ненулевых строки, то её ранг равен 3. Следовательно, и ранг исходной матрицы равен трём, т.е. $\rang{A}=3$. Полное решение без пояснений таково:
$$ \left(\begin{array}{ccccc} 11 & -13 & 61 & 10 & -11\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right) \begin{array} {l} r_1-5r_2\\ \phantom{0}\\ \phantom{0} \\ \phantom{0} \end{array}\sim \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 2 & -2 & 11 & 2 & -2\\ -3 & 5 & -17 & -2 & 3\\ 4 & 0 & 24 & 7 & -8 \end{array} \right) \begin{array} {l} \phantom{0}\\ r_2-2r_1\\ r_3+3r_1 \\ r_4-4r_1 \end{array}\sim $$ $$ \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & -4 & 1 & -2 & 0\\ 0 & 12 & 0 & 7 & -4 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3+r_2 \\ r_4-3r_2 \end{array}\sim \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 3 & 1 & -4 \end{array}\right)\overset{r_3\leftrightarrow{r_4}}{\sim} \left(\begin{array}{ccccc} 1 & -3 & 6 & 0 & -1\\ 0 & 4 & -1 & 2 & 0\\ 0 & 0 & 3 & 1 & -4\\ 0 & 0 & 0 & 0 & 0 \end{array} \right) $$
Ответ: $\rang A=3$.
Пример №3
Найти ранг матрицы $A=\left(\begin{array}{ccc} 0 & 2 & -4 \\ -1 & -4 & 5 \\ 3 & 1 & 7 \\ 0 & 5 & -10 \\ 2 & 3 & 0 \end{array} \right)$.
Решение
Иногда в процессе решения удобно транспонировать матрицу. Так как ранг транспонированной матрицы равен рангу исходной матрицы, то такая операция вполне допустима. В этом примере будет рассмотрен как раз такой случай. В ходе преобразований возникнут две одинаковые строки $(0;\;1;\;-2)$ (первая и четвёртая). В принципе, можно выполнить действие $r_4-r_1$, тогда четвёртая строка обнулится, однако это лишь удлинит решение на одну запись, поэтому выполнять обнуление четвёртой строки не станем.
$$ \left(\begin{array}{ccc} 0 & 2 & -4 \\ -1 & -4 & 5 \\ 3 & 1 & 7 \\ 0 & 5 & -10 \\ 2 & 3 & 0 \end{array} \right) \begin{array} {l} 1/2\cdot{r_1}\\ \phantom{0}\\ \phantom{0} \\ 1/5\cdot{r_4} \\\phantom{0} \end{array}\sim \left(\begin{array}{ccc} 0 & 1 & -2 \\ -1 & -4 & 5 \\ 3 & 1 & 7 \\ 0 & 1 & -2 \\ 2 & 3 & 0 \end{array} \right)\sim $$ $$ \sim\left(\begin{array}{ccccc} 0&-1&3&0&2\\ 1&-4&1&1&3\\ -2&5&7&-2&0 \end{array} \right) \overset{r_1\leftrightarrow{r_2}}{\sim} \left(\begin{array}{ccccc} 1&-4&1&1&3\\ 0&-1&3&0&2\\ -2&5&7&-2&0 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3+2r_1 \end{array}\sim $$ $$ \left(\begin{array}{ccccc} 1&-4&1&1&3\\ 0&-1&3&0&2\\ 0&-3&9&0&6 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3-3r_2 \end{array}\sim \left(\begin{array}{ccccc} 1&-4&1&1&3\\ 0&-1&3&0&2\\ 0&0&0&0&0 \end{array} \right) $$
Ранг преобразованной матрицы равен 2, поэтому и ранг исходной матрицы $\rang{A}=2$. В принципе, можно было найти ранг и без транспонирования матрицы: поменять местами первую строку с второй, третьей или пятой и продолжить обычные преобразования со строками. Метод сведения матрицы к ступенчатому виду допускает вариации процесса решения.
В принципе, можно было найти ранг и без транспонирования матрицы: поменять местами первую строку с второй, третьей или пятой и продолжить обычные преобразования со строками. Метод сведения матрицы к ступенчатому виду допускает вариации процесса решения.
Ответ: $\rang A=2$.
Пример №4
Найти ранг матрицы $A=\left(\begin{array}{cccccc} 0 & -1 & 2 & -4 & 0 & 5 \\ 0 & 0 &5 &0 &2 &3 \\ 0 & 0 & 10 & 0& -4&1 \end{array} \right)$.
Решение
Данная матрица не является нулевой, т.е. её ранг больше нуля. Перейдём к первому шагу алгоритма.
Первый шаг
На первом шаге мы работаем с первой строкой. В первой строке заданной нам матрицы ведущим является второй элемент, т.е. номер ведущего элемента первой строки $k=2$. Рассмотрим строки, расположенные под первой строкой. Ведущие элементы в этих строках имеют номер 3, т.е. наименьший из номеров ведущих элементов нижележащих строк есть $k_{\min}=3$. Так как $k\lt{k_{\min}}$, то переходим к следующему шагу алгоритма.
Так как $k\lt{k_{\min}}$, то переходим к следующему шагу алгоритма.
Второй шаг
На втором шаге мы работаем с второй строкой. Во второй строке ведущим является третий элемент, т.е. номер ведущего элемента второй строки $k=3$. Под второй строкой расположена лишь одна третья строка, номер ведущего элемента которой равен 3, поэтому $k_{\min}=3$. Так как $k=k_{\min}$, то производим обнуление ведущего элемента третьей строки:
$$ \left(\begin{array}{cccccc} 0 & -1 & 2 & -4 & 0 & 5 \\ 0 & 0 &5 &0 &2 &3 \\ 0 & 0 & 10 & 0& -4&1 \end{array} \right) \begin{array} {l} \phantom{0}\\ \phantom{0}\\ r_3-2r_2 \end{array}\sim \left(\begin{array}{cccccc} 0 & -1 & 2 & -4 & 0 & 5 \\ 0 & 0 &5 &0 &2 &3 \\ 0 & 0 & 0 & 0& -8&-5 \end{array} \right) $$
Получена ступенчатая матрица. Ранг преобразованной матрицы, а следовательно и ранг исходной матрицы, равен 3.
Ранг преобразованной матрицы, а следовательно и ранг исходной матрицы, равен 3.
Ответ: $\rang A=3$.
Пример №5
Найти ранг матрицы $A=\left(\begin{array}{ccccc} 0&0&0&0&6\\ 9&0&0&0&-11\\ 5&2&0&0&-5. \end{array} \right)$.
Решение
Иногда можно свести матрицу к ступенчатой с помощью одних лишь перестановок строк или столбцов. Это бывает, разумеется, крайне редко, однако удачная перестановка позволяет существенно упростить решение.
$$ \left(\begin{array}{ccccc} 0&0&0&0&6\\ 9&0&0&0&-11\\ 5&2&0&0&-5 \end{array} \right) \overset{r_1\leftrightarrow{r_3}}{\sim} \left(\begin{array}{ccccc} 5&2&0&0&-5\\ 9&0&0&0&-11\\ 0&0&0&0&6 \end{array} \right) \overset{с_1\leftrightarrow{с_4}}{\sim} \left(\begin{array}{ccccc} 0&2&0&5&-5\\ 0&0&0&9&-11\\ 0&0&0&0&6 \end{array} \right) $$
Матрица приведена к ступенчатой, $\rang{A}=3$.
Ответ: $\rang A=3$.
Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Решение высшей математики онлайн
‹— Назад
В этом разделе рассмотрим еще одну важную числовую характиристику матрицы, связанную с тем, насколько ее строки (столбцы) зависят друг от друга.
Определение 14.10 Пусть дана матрица размеров и число , не превосходящее наименьшего из чисел и : . Выберем произвольно строк матрицы и столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных строк и столбцов, называется минором порядка матрицы .
Пример 14.9 Пусть .
Минором первого порядка является любой элемент матрицы. Так 2, , — миноры первого порядка.
Так 2, , — миноры первого порядка.
Миноры второго порядка:
- возьмем строки 1, 2, столбцы 1, 2, получим минор ;
- возьмем строки 1, 3, столбцы 2, 4, получим минор ;
- возьмем строки 2, 3, столбцы 1, 4, получим минор
Миноры третьего порядка:
строки здесь можно выбрать только одним способом,
- возьмем столбцы 1, 3, 4, получим минор ;
- возьмем столбцы 1, 2, 3, получим минор .
Предложение 14.23 Если все миноры матрицы порядка равны нулю, то все миноры порядка , если такие существуют, тоже равны нулю.
Доказательство.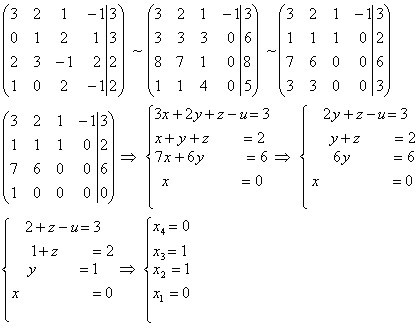 Возьмем произвольный минор порядка . Это определитель матрицы порядка . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка исходной матрицы. По условию миноры порядка равны нулю. Поэтому и минор порядка будет равен нулю.
Возьмем произвольный минор порядка . Это определитель матрицы порядка . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка исходной матрицы. По условию миноры порядка равны нулю. Поэтому и минор порядка будет равен нулю.
Определение 14.11 Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю.
Единое, стандартное, обозначение ранга матрицы отсутствует. Следуя учебнику [1], мы будем обозначать его .
Пример 14.10 Матрица примера 14.9 имеет ранг 3, так как есть минор третьего порядка, отличный от нуля, а миноров четвертого порядка нет.
Ранг матрицы равен 1, так как есть ненулевой минор первого порядка (элемент матрицы ), а все миноры второго порядка равны нулю.
Ранг невырожденной квадратной матрицы порядка равен , так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.
Предложение 14.24 При транспонировании матрицы ее ранг не меняется, то есть .
Доказательство. Транспонированный минор исходной матрицы будет являться минором транспонированной матрицы , и наоборот, любой минор является транспонированным минором исходной матрицы . При транспонировании определитель (минор) не меняется ( предложение 14.6). Поэтому если все миноры порядка в исходной матрице равны нулю, то все миноры того же порядка в тоже равны нулю. Если же минор порядка в исходной матрице отличен от нуля, то в есть минор того же порядка, отличный от нуля. Следовательно, .
Определение 14.12 Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором.
Пример 14. 11 Пусть . Определитель матрицы равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
11 Пусть . Определитель матрицы равен нулю, так как третья строка равна сумме первых двух. Минор второго порядка, расположенный в первых двух строках и первых двух столбцах, равен . Следовательно, ранг матрицы равен двум, и рассмотренный минор является базисным.
Базисным минором является также минор, расположенный, скажем, в первой и третьей строках, первом и третьем столбцах: . Базисным будет минор во второй и третьей строках, первом и третьем столбцах: .
Минор в первой и второй строках, втором и третьем столбцах равен нулю и поэтому не будет базисным. Читатель может самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.
Так как столбцы (строки) матрицы можно складывать, умножать на числа, образовывать линейные комбинации, то можно ввести определения линейной зависимости и линейной независимости системы столбцов (строк) матрицы. Эти определения аналогичны таким же определениям 10.14, 10.15 для векторов.
Эти определения аналогичны таким же определениям 10.14, 10.15 для векторов.
Определение 14.13 Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.
Определение 14.14 Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.
Верно также следующеее предложение, аналогичное предложению 10.6.
Предложение 14.25 Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.
Сформулируем теорему, которая называется теорема о базисном миноре.
Теорема 14. 2 Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.
2 Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.
Доказательство можно найти в учебниках по линейной алгебре, например, в [1], [3].
Предложение 14.26 Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.
Доказательство. Пусть ранг матрицы равен . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15 и 14.18 этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно .
Предположим, что столбцов образуют линейно независимую систему. Составим из них матрицу . Все миноры матрицы являются минорами матрицы . Поэтому базисный минор матрицы имеет порядок не больше . По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы , является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу . Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше . Значит, оно равно , что и утверждалось.
Предложение 14.27 Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему.
Доказательство. По предложению 14.24 ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы.
Предложение 14.28 Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Доказательство. Пусть порядок матрицы равен . Определитель является единственным минором квадратной матрицы, имеющим порядок . Так как он равен нулю, то . Следовательно, система из столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.
Результаты предложений 14.15, 14.18 и 14.28 дают следующую теорему.
Теорема 14.3 Определитель матрицы равен нулю тогда и только тогда, когда один из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).
Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка. ) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.
Определение 14.15 Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.
Предложение 14.29 При элементарных преобразованиях ранг матрицы не меняется.
Доказательство. Пусть ранг матрицы равен , — матрица, получившаяся в результате выполнения элементарного преобразования.
Рассмотрим перестановку строк. Пусть — минор матрицы , тогда в матрице есть минор , который или совпадает с , или отличается от него перестановкой строк. И наоборот, любому минору матрицы можно сопоставить минор матрицы или совпадающий с , или отличающийся от него порядком строк. Поэтому из того, что в матрице все миноры порядка равны нулю, следует, что в матрице тоже все миноры этого порядка равны нулю. И так как в матрице есть минор порядка , отличный от нуля, то и в матрице тоже есть минор порядка , отличный от нуля, то есть .
Поэтому из того, что в матрице все миноры порядка равны нулю, следует, что в матрице тоже все миноры этого порядка равны нулю. И так как в матрице есть минор порядка , отличный от нуля, то и в матрице тоже есть минор порядка , отличный от нуля, то есть .
Рассмотрим умножение строки на число , отличное от нуля. Минору из матрицы соответствует минор из матрицы или совпадающий с , или отличающийся от него только одной строкой, которая получается из строки минора умножением на число, отличное от нуля. В последнем случае . Во всех случаях или и одновременно равны нулю, или одновременно отличны от нуля. Следовательно, .
Пусть к -ой строке матрицы прибавлена ее -ая строка, умноженная на число . Рассмотрим миноры порядка в матрице . Если через минор не проходит -ая строка, то он совпадает с минором , расположенным в тех же строках и столбцах в матрице , и следовательно, равен нулю.
Если через минор проходят и -ая и -ая строки, то он получается из минора , расположенного в тех же строках и столбцах матрицы , прибавлением к -ой строке минора -ой строки, умноженной на . По свойству определителя . Следовательно, .
По свойству определителя . Следовательно, .
Пусть через минор проходит -ая строка и не проходит -ая. Тогда отличается от -ой строкой. Эта строка в является строкой , к которой добавлены элементы -ой строки, умноженные на . По свойствам определителей , где — минор порядка матрицы , стоящий в -ой строке и в тех же строках, что и минор , исключая -ую, а знак » » связан с возможным изменением порядка строк. Так как все миноры порядка в матрице равны нулю, то .
Итак, в матрице все миноры порядка равны нулю. Следовательно, , то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что , и . Тогда в матрице к -ой строке прибавим -ую строку, умноженную на число . В результате получим исходную матрицу . По только что доказанному . Получили противоречие: . Предположение не верно, следовательно, .
Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.
Алгоритм нахождения ранга матрицы.
Пусть требуется вычислить ранг матрицы размеров . Если матрица нулевая, то по определению . В противном случае с помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что .
Первую строку оставляем без изменений. Ко второй строке прибавляем первую, умноженную на число . В результате вторая строка принимает вид
Затем к третьей строке прибавляем первую строку, умноженную на число . В результате третья строка принимает вид
В результате третья строка принимает вид
Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке.
Преобразованная матрица имеет вид
Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как есть минор первого порядка, отличный от нуля . В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что .
Первую и вторую строки оставляем без изменений. К третьей строке прибавляем вторую, умноженную на число . В результате получим, что второй элемент третьей строки равен нулю. Затем к четвертой строке прибавляем вторую, умноженную на число , и т.д. В результате получаем матрицу
Если все строки, начиная с третьей, нулевые, то , так как минор . В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
На каком-то этапе мы придем к матрице, у которой все строки, начиная с -ой , равны нулю (или отсутствуют при ), а минор в первых строках и первых столбцах является определителем треугольной матрицы с ненулевыми элементами на диагонали. Ранг такой матрицы равен . Следовательно, .
Замечание 14.15 В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Замечание 14. 16 Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
16 Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
Пример 14.12 Найдите ранг матрицы .
Решение. Первую строку оставляем без изменений. Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2:
Первую строку умножим на и прибавим ко второй. Получим строку . Первую строку умножим на и прибавим к третьей. Получим строку . Первую строку умножим на и прибавим к четвертой. Получим строку . В итоге имеем матрицу
Вторую строку оставляем без изменений. К третьей строке прибавляем вторую, умноженную на 2. Получим строку . К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
К четвертой строке прибавляем вторую. Получим нулевую строку. Преобразованная матрица имеет вид
Поменяем местами третий и четвертый столбцы:
Базисный минор матрицы стоит в первых трех столбцах и первых трех строках, . Следовательно, .
Замечание 14.17 В приведенном примере вычисления были бы проще, если сначала четвертый столбец сделать первым и четвертую строку сделать первой. Но для того, чтобы догадаться об этом, нужно анализировать вопросы делимости чисел, что достаточно сложно описать в алгоритме, пригодном для всех случаев.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
понятие, как вычислить, методы нахождения, пример
Содержание:
- Что такое ранг матрицы — понятие, для чего используется
-
Как определить ранг матрицы, примеры
- Нахождение ранга матрицы по определению
- Нахождение ранга матрицы методом окаймляющих миноров
- Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Содержание
- Что такое ранг матрицы — понятие, для чего используется
-
Как определить ранг матрицы, примеры
- Нахождение ранга матрицы по определению
- Нахождение ранга матрицы методом окаймляющих миноров
- Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Что такое ранг матрицы — понятие, для чего используется
Возьмем случайную матрицу \(\underset{m\times n}A\) и натуральное число k, меньшее или равное числам m и n. k\) миноров k-го порядка.
k\) миноров k-го порядка.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Например, из \(\underset{3\times 4}A\) мы получим 12 миноров 1-го порядка, 18 — 2-го и 4 — 3-го.
Если среди матричных элементов \(a_{ij}\) (i = 1, 2 … m; j = 1, 2 … n) есть отличные от нуля, то существует натуральное число r, которое обладает следующими свойствами:
- У матрицы А есть ненулевой минор r-го порядка.
- Любой из миноров этой матрицы порядка r + 1 или выше будет нулевым.
Число r с такими характеристиками — ранг матрицы A.
Ранг матрицы — это наивысший порядок ее ненулевых миноров.
Устоявшегося обозначения ранга не существует, чаще всего его записывают как \(r (A)\) или rang A, где А — обозначение матрицы. Понятие ранга обычно используют в ситуациях, когда необходима проверка совместимости системы линейных уравнений.
В случае, когда базисный минор матрицы \(\underset{3\times 4}A\) имеет порядок r < m, то как минимум одна ее строка будет не базисной. Согласно теореме о базисном миноре, в таком случае строки рассматриваемой матрицы \(\underset{3\times 4}A\) линейно зависимы. В случае, когда r = m, все строки являются базисными и линейно независимыми.
Из этого можно сделать следующие выводы:
- Когда ранг матрицы A меньше числа ее строк, они линейно зависимы. В случае, когда он равен числу строк, все они линейно независимы.
- Всякие r + 1 строк матрицы A ранга r линейно зависимы.
- Ранг любой матрицы равняется максимальному числу ее линейно независимых строк.
Теорема 1
Максимальное число линейно независимых столбцов матрицы равно максимальному количеству ее линейно независимых строк и равно ее рангу.
Следствие
Ранг не меняется при транспонировании.
Как определить ранг матрицы, примеры
Нахождение ранга матрицы по определению
Определить ранг можно, перебрав все миноры.
Теорема 2
Если из элементов матрицы можно составить ненулевой минор n-го порядка, то ранг равен n.
С учетом данной теоремы перебор производится по следующему алгоритму:
- Перебрать миноры 1-го порядка. Если наличествует хоть один ненулевой минор 1-го порядка, ранг как минимум равен 1.
- Перебрать миноры 2-го порядка. Если все они нулевые, ранг — единичный. В противном случае переходим к пункту 3.
- Перебрать миноры 3-го порядка. Если все они нулевые, ранг — два. В противном случае переходим к минорам 4-го, 5-го порядков и т. д.
Нахождение ранга матрицы методом окаймляющих миноров
Этот метод дает возможность сократить вычисления.
Окаймляющий минор — минор (n+1)-го порядка матрицы А. Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.
Пример № 1
Вычислить ранг матрицы
\(\begin{pmatrix}2&3&7&11\\1&2&4&7\\5&0&10&5\end{pmatrix}.\)
Решение:
В матрице есть элементы, отличные от нуля, значит, ее ранг больше единицы.
\(М_2\;=\;\begin{pmatrix}2&3\\1&2\end{pmatrix}\;=\;4\;-\;3\;=\;1\; \neq 0. \)
Раз ранг больше двух, нужно рассмотреть миноры 3-го порядка, содержащие вышеприведенный минор \(М_2.\)
\(М_3\;=\;\begin{pmatrix}2&3&7\\1&2&4\\5&0&10\end{pmatrix}\;=\;5\;\times\;\begin{pmatrix}3&7\\2&4\end{pmatrix}\;+\;10\;\times\;\begin{pmatrix}2&3\\1&2\end{pmatrix}=\;5\;\times\;(12\;-\;14)\;+\;10\;\times\;(4\;-\;3)\;=\;-\;10\;+\;10\;=\;0. \)
\)
\(М_3\;=\;\begin{pmatrix}2&3&11\\1&2&7\\5&0&5\end{pmatrix}\;=\;5\;\times\;\begin{pmatrix}3&11\\2&7\end{pmatrix}\;+\;5\;\times\;\begin{pmatrix}2&3\\1&2\end{pmatrix}=\;5\;\times\;(21\;-\;22)\;+\;5\;\times\;(4\;-\;3)\;=\;-\;5\;+\;5\;=\;0.\)
Как мы видим, все миноры 3-го порядка нулевые, значит, наибольший ненулевой минор относится ко 2-му порядку.
Ответ: 2.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
В большинстве случаев нахождение ранга перебором миноров требует долгих вычислений. Более простой способ решения этой задачи базируется на элементарных преобразованиях по методу Гаусса, сохраняющих ранг исходной матрицы A и приводящих ее к ступенчатому виду. К таким преобразованиям относятся:
- Вычеркивание нулевой строки или столбца. Нулевая строка не может быть базисной строкой, ведь в таком случае базисные строки были бы линейно зависимы, а это противоречит теореме о базисном миноре.

- Перестановка двух строк между собой. Другие строки в этом случае не меняются. Это утверждение непосредственно следует из теоремы о базисном миноре, согласно которой ранг равняется максимальному числу линейно независимых строк.
- Умножение любой строки на число\( \lambda \neq 0\).
- Вычеркивание строки, которая является линейной комбинацией других строк.
- Прибавление к одной строке другой строки, умноженной на число \(\lambda \neq 0\).
- Транспонирование.
Проведем подробный разбор пункта 5. Представим, что к q-й строке прибавлена p-я строка, умноженная на \(\lambda \neq 0\). В итоге появится новая матрица A′. Если q-я и p-я строки — базисные, это преобразование не изменит значения базисного минора. В случае, когда только p-я строка — базисная, q-я строка является их линейной комбинацией. Умножение на \(\lambda\) это не изменит, и такую строку допустимо удалить при преобразовании.
Если q-я строка — базисная, а p-я — нет, то после преобразования \(r_{q} \rightarrow r_{q} + \lambda r_{p}\) базисный минор \(\triangle_{r}\) перейдет в минор \(\triangle’_{r}\) матрицы A′, который отличается от \(\triangle_{r}\) тем, что вместо элементов строки \(r_{q}\) содержит элементы строки\( r_{q} + \lambda r_{p}\).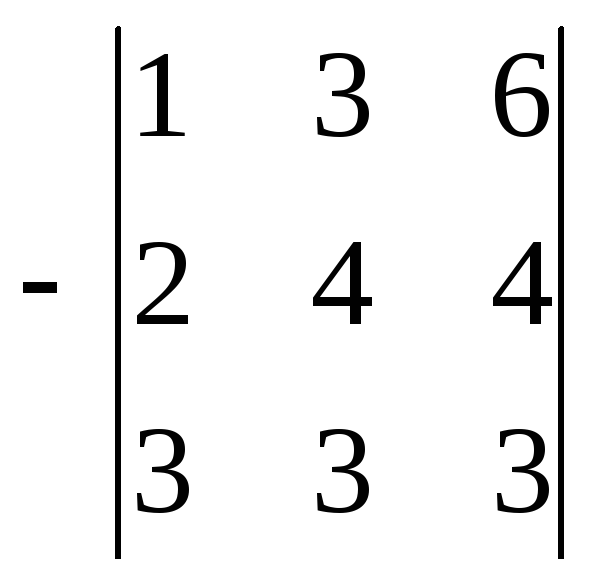 {(1)} = \triangle_r.\)
{(1)} = \triangle_r.\)
Как мы видим, при преобразовании\( r_{q} \rightarrow r_{q} + \lambda r_{p}\) базисный минор ни при каких условиях не изменяется. Из этого делаем вывод, что r (A) = r (A′).
Примечание
Матрицы A и B эквивалентны по рангу и обозначаются A ∼ B в том случае, когда B можно получить из A путем элементарных преобразований, перечисленных выше.
Пример № 2
Вычислить ранг матрицы
\(В\;=\;\begin{pmatrix}4&0&-1\\0&2&4\\4&4&1\end{pmatrix}.\)
Решение:
Прибавим первую строку матрицы B, умноженную на -1, к ее третьей строке. После произведения необходимых расчетов получим:
\(В\;\sim\;\begin{pmatrix}4&0&-1\\0&2&4\\0&4&2\end{pmatrix}.\)
Умножим вторую строку получившейся матрицы на -2 и прибавим результат умножения к третьей строке:
\(В\;\sim\;\begin{pmatrix}4&0&-1\\0&2&4\\0&0&-6\end{pmatrix}. \)
\)
Итак, исходная матрица 3-го порядка является невырожденной, поскольку ее определитель равен
\(4 \times 2 \times (-6) = -48 \neq 0.\)
Ответ: 3.
Насколько полезной была для вас статья?
Рейтинг: 1.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Найти ранг матрицы — Онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Под рангом матрицы понимают ее наивысший порядок, который не равен нулю. Чтобы определить ранг матрицы онлайн, воспользуйтесь нашим сервисом. Расчеты производятся без внесения оплаты за услуги неограниченное число раз. Автоматические вычисления помогут избежать ошибок и быстро получить ответ.
Автоматические вычисления помогут избежать ошибок и быстро получить ответ.
Помощь в нахождении ранга матрицы онлайн понадобится студентам в процессе подготовки к занятиям, школьникам при освоении усложненной программы по алгебре, специалистам для оптимизации рабочих расчетов. Заложенная в калькулятор формула не только показывает ответ, но и подробное решение примера. Как найти ранг матрицы онлайн Чтобы произвести расчет ранга матрицы онлайн-калькулятором необходимо:
- настроить количество строк и столбцов;
- ввести значения матрицы в соответствующие поля;
- нажать кнопку «Рассчитать».
Нахождение ранга матрицы
Как найти ранг матрицы с помощью онлайн-калькулятора:
- Задайте число строк и столбцов (до 7) в соответствующих полях:
Для наглядности вычислим ранг матрицы 3х3: - Задайте значения матрицы:
Для конкретного примера заданная матрица будет выглядеть следующим образом: - Нажмите «Рассчитать» и получите ответ с решением:
Материалы, которые помогут вам лучше разобраться в теме:
- Матрицы (раздел)
- Умножение матриц: примеры, алгоритм действий, свойства произведения
- Определитель матрицы: алгоритм и примеры вычисления определителя матрицы
- Равенство матриц: как доказать и проверить?
- Действия над матрицами.
 Сложение и вычитание
Сложение и вычитание - Нахождение ранга матрицы
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Найти определитель матрицы
- Найти обратную матрицу
- Возведение матрицы в степень
- Умножение матрицы на число
- Умножение матриц
- Транспонирование матрицы
- Сложение и вычитание матриц
Вы можете самостоятельно вычислить результат и свериться с ответом. Таким образом сервис Zaochnik влияет на повышение уровня образования. Во время подготовки к занятиям студент усваивает знания, видя способ вычислений. Благодаря подробной расшифровке учащийся сможет не только найти ранг матрицы онлайн-калькулятором, но и определить ответ в подобных задачах.
Таким образом сервис Zaochnik влияет на повышение уровня образования. Во время подготовки к занятиям студент усваивает знания, видя способ вычислений. Благодаря подробной расшифровке учащийся сможет не только найти ранг матрицы онлайн-калькулятором, но и определить ответ в подобных задачах.
Метод решения примера состоит в выполнении следующих действий:
- Осуществляется запись матрицы.
- Выбирается первый элемент из первого столбца. С помощью него элементы, находящиеся ниже данного, зануляются.
- Выбирается второй элемент из второго столбца. Далее до конца осуществляются те же операции.
- Число «ступеней» — количество линейно независимых уравнений соответствует рангу матрицы.
Если вычисления являются промежуточными и не ставят перед собой учебную задачу, вычислить ранг матрицы онлайн – оптимальный вариант. Так вы сэкономите время и получите проверенный результат. Этим пользуются преподаватели при проверке большого количества студенческих работ, работники инженерных специальностей для ускорения расчетов.
Если у вас остались вопросы или возникли проблемы при освоении темы, напишите консультанту в удобное для вас время. Оператор подберет квалифицированного исполнителя, который решит необходимые задачи. Опытный преподаватель сможет найти ранг расширенной матрицы онлайн и произвести другие расчеты по выгодной цене.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒
Рассмотрим прямоугольную матрицу Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m).
Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы. Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы : — замены строк столбцами, а столбцов соответствующими строками; — перестановки строк матрицы; — вычеркивания строки, все элементы которой равны нулю; — умножения строки на число, отличное от нуля; — прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.
Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится. Пример 1. Определить ранг матрицы Решение Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы равен единице. Пример 2. Определить ранг матрицы Решение Вычеркнув из этой матрицы вторую строку и выбрав первый и четвертый столбцы, получим минор Ранг матрицы равен 2.
Решение линейных систем уравнений методом Крамера, Гаусса, матричным методом. Метод Крамера Для системы n линейных уравнений с n неизвестными (над произвольным полем)
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn и x1,x2,…,xn, либо набор c1,c2,…,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
Пример Система линейных уравнений: Определители:
Решение: Пример: Определители:
Метод Гаусса Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных. Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.
Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.
Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно — предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.
Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования: Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему. Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.
Пример 1. Решить систему методом Гаусса.
Решение Определитель системы не равен нулю (см. пример из 2.2.1). Поэтому система совместна и определена (решение единственно). Выполним преобразования. Первое уравнение оставим без изменения. Для того, чтобы избавиться от первого неизвестного во втором и третьем уравнениях, к ним прибавим первое, умноженное на -2 в первом случае и на -1 — во втором
Теперь избавимся от второго неизвестного в третьем уравнении. Для этого второе уравнение умножим на -2 и прибавим к третьему. Получим эквивалентную заданной систему треугольного вида
Решаем систему снизу вверх. Из третьего уравнения имеем x3= 3 и, подставляя его во второе уравнение, находим x2= 2. Проверка: Получили три тождества. Пример 2. Решить систему
Решение В ней для исключения первого неизвестного во второй и третьей строках (уравнениях) умножим первую строку расширенной матрицы на -2 и -3 и сложим полученные результаты со второй и третьей строками соответственно. Следовательно, мы пришли к эквивалентной системе Ее третье уравнение получено в результате сложения двух последних уравнений (строк). Найдя , мы приходим к выводу, что система несовместна. Об этом же говорит и противоречие в третьем уравнении системы. Пример 2. Решить систему Решение В ней Умножим первую строку расширенной матрицы на 2 и -3, сложим полученные результаты со второй и третьей строками соответственно и получим Следовательно, мы пришли к эквивалентной системе которая может быть представлена в виде поскольку два последних уравнения — истинные равенства. Поскольку постольку система совместна, но имеет множество решений. Общее решение системы имеет вид Множество частных решений системы будет трехмерным, так как зависит от трех параметров. Выбрав t = 2, v = 1, s = -3, получим частное решение системы x1 = — 6, x2 = 2, x3 = 1, x4= -3. Матричный метод Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная). Из этих условий следует, что и, следовательно, система совместна и определена. Решение системы можно получить так: Используя свойства произведения матриц и свойство обратной матрицы Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов. Пример Решить систему матричным методом. Решение В соответствии с пунктом 1.5 найдем обратную матрицу для матрицы коэффициентов системы Вычислим определитель, раскладывая по первой строке: Поскольку Δ ≠ 0, то A-1 существует. Обратная матрица найдена верно. Найдем решение системы Следовательно, x1 = 1, x2 = 2, x3 = 3. Проверка: Система решена верно. Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.
⇐ Предыдущая12345678910Следующая ⇒ Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Matrix Rank Calculator
Предположим, что вы на свидании в модном ресторане, и ваш партнер вызывает вас на соревнование по вычислению матричного ранга . Судя по всему, это новый вирусный вызов TikTok, так что , что вы можете сделать?
Судя по всему, это новый вирусный вызов TikTok, так что , что вы можете сделать?
Вы просите джентльмена, борющегося со стейком на соседнем столе, привести пример матрицы. Очевидно, он с радостью обязывает .
| А | = |
|
Готов? Установлен? Идти!
К счастью, вы знаете веб-сайт Omni Calculator наизнанку и сразу же посещаете калькулятор ранга матрицы . Чтобы заставить его работать в вашу пользу, нам сначала нужно сообщить калькулятору, с чем мы имеем дело. Это матрица размера
Чтобы заставить его работать в вашу пользу, нам сначала нужно сообщить калькулятору, с чем мы имеем дело. Это матрица размера 4 × 3 , поэтому мы вводим 4 под количеством строк и 3 под номером столбца. Это покажет нам символический пример матрицы , похожей на нашу. Нам просто нужно дать ему правильные цифры.
Согласно рисунку в первой строке есть элементы a₁ , a₂ , и a₃ , поэтому оглядываемся назад на наш массив и помещаем его первую строку под эти символы:
a₁ = 0 , а₂ = 2 , а₃ = -1 .
Аналогично вводим остальные три строки:
b₁ = 1 , b₂ = 0 , b₃ = 1 ,
c₁ = 2 , c₂ = -1 , c₃ = 3 ,
d₁ = 1 , d₂ = 1 , d₃ = 4 .
Как только мы введем последнее число, калькулятор ранга матрицы выдаст ранг нашей матрицы . К сожалению, когда он собирался это сделать, ваша подруга заставляет вас положить трубку и указывает, что будет веселее посмотреть, сколько времени потребуется, чтобы сделать это без каких-либо причудливых инструментов. ну вроде нам все-таки придется вычислять вручную .
К сожалению, когда он собирался это сделать, ваша подруга заставляет вас положить трубку и указывает, что будет веселее посмотреть, сколько времени потребуется, чтобы сделать это без каких-либо причудливых инструментов. ну вроде нам все-таки придется вычислять вручную .
Прежде всего, мы видим, что первый элемент первой строки равен 0 . Нам не нравятся нули — мы не можем использовать их в методе исключения Гаусса-Жордана, чтобы избавиться от других чисел в этом столбце. Так почему бы нам не поменять местами первую строку со второй ?
|
Вот это больше похоже! Таким образом, мы можем позаботиться о 2 и 1 в двух нижних рядах. Для этого добавляем к этим строкам подходящее кратное первой единицы, так что получаем нули во всем первом столбце, кроме первой строки. Поскольку у нас есть
Для этого добавляем к этим строкам подходящее кратное первой единицы, так что получаем нули во всем первом столбце, кроме первой строки. Поскольку у нас есть 1 для работы и 2 + (-2)*1 = 0 и 1 + (-1)*1 = 0 , мы добавляем (-2) , кратное первой строке к третьему и (-1) кратно четвертому. Обратите внимание, что нам не нужно ничего делать со второй строкой , так как у нас уже есть 0 .
| = |
| = |
|
Хорошо, мы потеряли довольно много времени, пытаясь использовать калькулятор ранга матрицы, поэтому нам нужно немного ускорить .
Переходим ко второй колонке. Мы хотели бы использовать 2 во второй строке, чтобы исключить -1 и 1 из двух нижних строк. Как и раньше, мы добавляем подходящее кратное второй строки: на этот раз это будет 0,5 для третьей строки и -0,5 для последней.
| = |
| = |
|
Вы видите, как ваша партнерша нервно строчит на своем листе бумаги, а джентльмен за соседним столом подбадривает вас. Время для последнего шага.
Время для последнего шага.
Теперь мы хотим избавиться от 2,5 в четвертой строке, используя 0,5 из третьей. Складываем кратное (-5) , чтобы получить
| = |
| = |
|
Матрица имеет три ненулевых строки , что означает, что rank(A) = 3 . Вы торжествующе смотрите на свою пару и объявляете себя победителем . Джентльмен рядом с вами аплодирует, и вы решаете отпраздновать это кусочком шоколадного торта. Такое веселье заслуживает вкусного десерта и хороших чаевых, тебе так не кажется?
Вы торжествующе смотрите на свою пару и объявляете себя победителем . Джентльмен рядом с вами аплодирует, и вы решаете отпраздновать это кусочком шоколадного торта. Такое веселье заслуживает вкусного десерта и хороших чаевых, тебе так не кажется?
Метод наименьших квадратов
Цели
- Изучите примеры задач наилучшего соответствия.
- Научитесь превращать задачу наилучшего соответствия в задачу наименьших квадратов.
- Рецепт: найти решение методом наименьших квадратов (два способа).
- Рисунок: геометрия решения методом наименьших квадратов.
- Словарный запас: решение методом наименьших квадратов .
В этом разделе мы ответим на следующий важный вопрос:
Предположим, что Ax=b не имеет решения. Каково наилучшее приближенное решение?
Для наших целей наилучшее приближенное решение называется методом наименьших квадратов . Мы представим два метода нахождения решений методом наименьших квадратов и дадим несколько приложений к задачам наилучшего соответствия.
Мы представим два метода нахождения решений методом наименьших квадратов и дадим несколько приложений к задачам наилучшего соответствия.
Начнем с пояснения, что именно мы будем подразумевать под «наилучшим приближенным решением» несовместимого матричного уравнения Ax=b.
Определение
Пусть A — матрица размера m × n, а b — вектор в Rm. Решение методом наименьших квадратов матричного уравнения Ax=b есть вектор Kx в Rn такой, что
расстояние(b,AKx)≤расстояние(b,Ax)
для всех остальных векторов x в Rn.
Напомним, что dist(v,w)=Av−wA — это расстояние между векторами v и w. Термин «наименьшие квадраты» происходит от того факта, что dist(b,Ax)=Ab−AKxA — это квадратный корень из суммы квадратов элементов вектора b−AKx. Таким образом, решение методом наименьших квадратов минимизирует сумму квадратов разностей между элементами AKx и b. Другими словами, решение по методу наименьших квадратов максимально точно решает уравнение Ax=b в том смысле, что сумма квадратов разности b-Ax минимизируется.
Метод наименьших квадратов: изображение
Предположим, что уравнение Ax=b несовместно. Напомним из этого примечания в разделе 2.3, что пространство столбцов A — это множество всех других векторов c, таких что Ax=c непротиворечиво. Другими словами, Col(A) — это множество всех векторов вида Ax. Следовательно, ближайший к b вектор формы Ax является ортогональной проекцией b на Col(A). Это обозначено как bCol(A), следуя этим обозначениям в Разделе 6.3.
ColAAxAxAxAKx=bCol(A)bb−AKx=bCol(A)⊥0Решением уравнения Ax=b методом наименьших квадратов является решение Kx согласованного уравнения Ax=bCol(A)
Где Кх на этой картинке? Если v1,v2,…,vn — столбцы A, то
AKx=AEIIGKx1Kx2…KxnFJJH=Kx1v1+Kx2v2+···+Kxnvn.
Следовательно, элементы Kx являются «координатами» bCol(A) относительно остовного множества {v1,v2,…,vm} Col(A). (Они являются честными B-координатами, если столбцы A линейно независимы.)
ColAv1v2Kx1v1Kx2v2AKx=bCol(A)bb−AKx=bCol(A)⊥0 Рис. 4. Фиолетовая плоскость — Col(A). Ближайший вектор, который Ax может подобрать к b, — это ближайший к b вектор на Col(A), который является ортогональной проекцией bCol(A) (синий). Векторы v1,v2 — это столбцы A, а коэффициенты Kx — это длины зеленых линий. Нажмите и перетащите b, чтобы переместить его.
4. Фиолетовая плоскость — Col(A). Ближайший вектор, который Ax может подобрать к b, — это ближайший к b вектор на Col(A), который является ортогональной проекцией bCol(A) (синий). Векторы v1,v2 — это столбцы A, а коэффициенты Kx — это длины зеленых линий. Нажмите и перетащите b, чтобы переместить его.Мы научились решать такую задачу ортогональной проекции в разделе 6.3.
Теорема
Пусть A — матрица размера m × n, а b — вектор в Rm. Решения Ax=b методом наименьших квадратов являются решениями матричного уравнения
.ATAx=ATb
Доказательство
По этой теореме из раздела 6.3, если Kx является решением матричного уравнения ATAx=ATb, то AKx равно bCol(A). Выше мы утверждали, что решение Ax=b методом наименьших квадратов является решением Ax=bCol(A).
В частности, поиск решения методом наименьших квадратов означает решение непротиворечивой системы линейных уравнений. Мы можем перевести приведенную выше теорему в рецепт:
Рецепт 1.
 Вычисление решения методом наименьших квадратов
Вычисление решения методом наименьших квадратовПусть A — матрица размера m×n, а b — вектор в Rn. Вот метод вычисления решения по методу наименьших квадратов Ax=b:
.- Вычислить матрицу ATA и вектор ATb.
- Сформируйте расширенную матрицу для матричного уравнения ATAx=ATb и уменьшите количество строк.
- Это уравнение всегда непротиворечиво, и любое решение Kx является решением методом наименьших квадратов.
Повторяю: как только вы нашли решение методом наименьших квадратов Kx для Ax=b, тогда bCol(A) равно AKx.
Пример
Пример
Читатель, возможно, заметил, что мы постарались сказать «решение методом наименьших квадратов» во множественном числе, а «решение методом наименьших квадратов» — с неопределенным артиклем. Это связано с тем, что решение методом наименьших квадратов не обязательно должно быть уникальным: действительно, если столбцы A линейно зависимы, то Ax=bCol(A) имеет бесконечно много решений. Следующая теорема, дающая эквивалентные критерии единственности, является аналогом этого следствия из раздела 6.3.
Следующая теорема, дающая эквивалентные критерии единственности, является аналогом этого следствия из раздела 6.3.
Теорема
Пусть A — матрица размера m × n, а b — вектор в Rm. Следующие эквивалентны:
- Ax=b имеет единственное решение методом наименьших квадратов.
- Столбцы A линейно независимы.
- АТА является обратимым.
В этом случае решение методом наименьших квадратов равно
.Kx=(ATA)−1ATb.
Доказательство
Множество решений уравнения Ax=b методом наименьших квадратов является множеством решений согласованного уравнения ATAx=ATb, которое является преобразованием множества решений однородного уравнения ATAx=0. Поскольку ATA — квадратная матрица, эквивалентность 1 и 3 следует из теоремы об обратимой матрице в разделе 5.1. Множество решений методом наименьших квадратов также является множеством решений согласованного уравнения Ax=bCol(A), которое имеет единственное решение тогда и только тогда, когда столбцы A линейно независимы в соответствии с этим важным примечанием в разделе 2. 5.
5.
Пример (бесконечно много решений методом наименьших квадратов)
Как обычно, вычисления с проекциями становятся проще при наличии ортогонального множества. В самом деле, если A представляет собой матрицу размера m × n с 90 652 ортогональными 90 653 столбцами u1,u2,…,um, то мы можем использовать формулу проецирования в разделе 6.4, чтобы записать
bCol(A)=b·u1u1·u1u1+b·u2u2·u2u2+···+b·umum·umum=AEIIG(b·u1)/(u1·u1)(b·u2)/(u2·u2). ..(b·um)/(um·um)FJJH.Обратите внимание, что решение методом наименьших квадратов в этом случае единственно, поскольку ортогональное множество линейно независимо.
Рецепт 2. Вычисление решения методом наименьших квадратов
Пусть A — матрица размера m×n с ортогональными столбцами u1,u2,…,um, и пусть b — вектор в Rn. Тогда решением Ax=b методом наименьших квадратов является вектор
Kx=Lb·u1u1·u1,b·u2u2·u2,…,b·umum·umM. Эта формула особенно полезна в естественных науках, так как в природе часто возникают матрицы с ортогональными столбцами.
Пример
В этом подразделе мы даем применение метода наименьших квадратов к моделированию данных. Начнем с базового примера.
Пример (наиболее подходящая линия)
Предположим, что мы измерили три точки данных
(0,6),(1,0),(2,0),
и что наша модель для этих данных утверждает, что точки должны лежать на прямой. Конечно, эти три точки на самом деле не лежат на одной линии, но это может быть связано с ошибками в наших измерениях. Как мы можем предсказать, на какой линии они должны лежать?
(0,6)(1,0)(2,0)Общее уравнение для (невертикальной) линии:
у=Мх+В.
Если бы наши три точки данных лежали на этой прямой, то удовлетворялись бы следующие уравнения:
6=М·0+В0=М·1+В0=М·2+В.(6.5.1)
Чтобы найти наилучшую прямую, мы пытаемся решить приведенные выше уравнения с неизвестными M и B. Поскольку три точки на самом деле не лежат на прямой, фактического решения нет, поэтому вместо этого мы вычисляем наименьшую- решение квадратов.
Приведя наши линейные уравнения в матричный вид, мы пытаемся решить Ax=b для
.А=C011121Dx=LMBMb=C600D.
В этом примере мы решили эту задачу наименьших квадратов: единственное решение наименьших квадратов для Ax=b — это Kx=AMBB=A−35B, поэтому наиболее подходящая линия — это
.у=-3х+5.
(0,6)(1,0)(2,0)y=−3x+5Что именно минимизирует линия y=f(x)=−3x+5? Решение Kx методом наименьших квадратов минимизирует сумму квадратов элементов вектора b−AKx. Вектор b является левой частью (6.5.1), а
AL-35M=C-3(0)+5-3(1)+5-3(2)+5D=Cf(0)f(1)f(2)D.
Другими словами, AKx — это вектор, элементами которого являются y-координаты графика линии при значениях x, которые мы указали в наших точках данных, а b — вектор, элементами которого являются y-координаты этих точек данных. . Разница b−AKx представляет собой вертикальное расстояние графика от точек данных:
(0,6)(1,0)(2,0)−12−1y=−3x+5b−AKx=C600D−AL−35M=C−12−1D Линия наилучшего соответствия минимизирует сумму квадратов этих вертикальных расстояний.
Интерактив: оптимальная линия
Пример (парабола наилучшего соответствия)
Пример (наилучшая линейная функция)
Все приведенные выше примеры имеют следующий вид: указано некоторое количество точек данных (x,y), и мы хотим найти функцию
y=B1g1(x)+B2g2(x)+···+Bmgm(x)
, наилучшим образом аппроксимирующий эти точки, где g1,g2,…,gm — фиксированные функции от x. Действительно, в примере с наилучшей линией у нас было g1(x)=x и g2(x)=1; в примере с наилучшей параболой у нас было g1(x)=x2,g2(x)=x и g3(x)=1; и в примере наилучшей линейной функции у нас было g1(x1,x2)=x1,g2(x1,x2)=x2 и g3(x1,x2)=1 (в этом примере мы берем x как вектор с две записи). Мы оцениваем приведенное выше уравнение для заданных точек данных, чтобы получить систему линейных уравнений с неизвестными B1, B2,…, Bm — как только мы оцениваем gi, они просто становятся числами, поэтому не имеет значения, какие они — и находим решение методом наименьших квадратов. Полученная функция наилучшего соответствия минимизирует сумму квадратов вертикальных расстояний от графика y = f (x) до наших исходных точек данных.
Чтобы подчеркнуть, что природа функций gi на самом деле не имеет значения, рассмотрим следующий пример.
Пример (наилучшая тригонометрическая функция)
Следующий пример несколько отличается от предыдущих.
Пример (наиболее подходящий эллипс)
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Теорема о недействительности ранга | Brilliant Math & Science Wiki
Александр Кац, Кристофер Уильямс, а также Чимин Хим внес
Содержимое
- Примеры
- Доказательства
- Смотрите также
Рассмотрим матрицу
A=(31−6−2).A = \begin{pmatrix}3&1\\-6&-2\end{pmatrix}.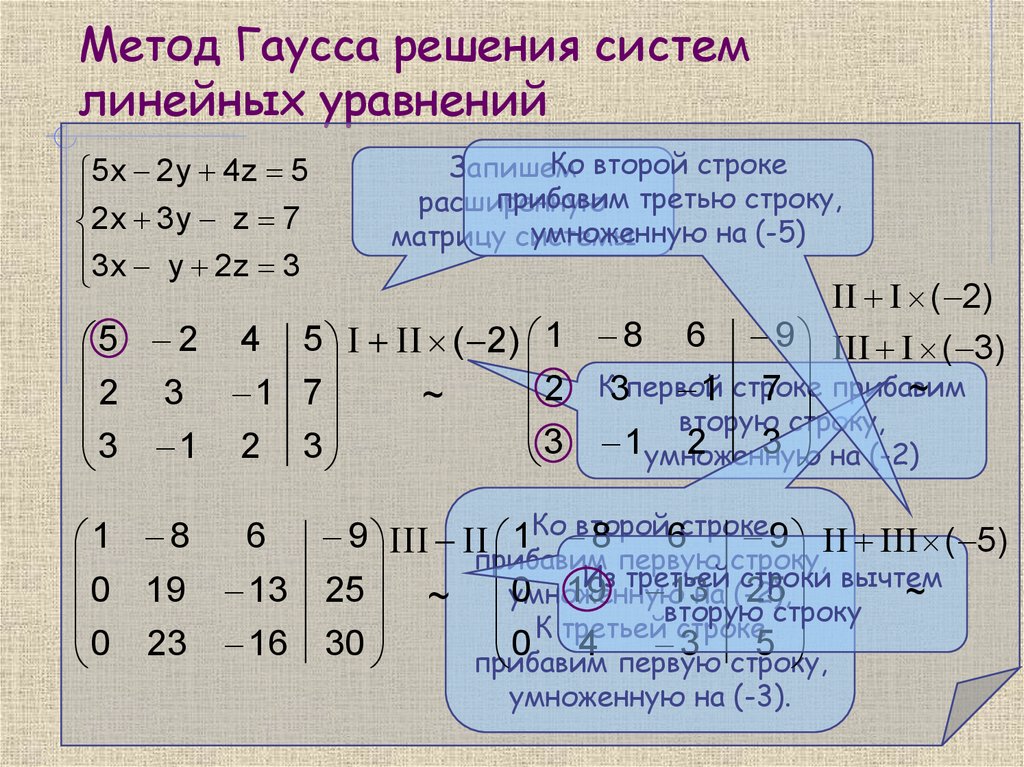 A=(3−61−2).
A=(3−61−2).
Здесь ранг равен 1, так как базис {(3−6),(1−2)}\left\{\begin{pmatrix}3\\-6\end{pmatrix},\begin{pmatrix} 1\\-2\end{pmatrix}\right\}{(3−6), (1−2)} можно сократить до {(1−2)}\left\{\begin{pmatrix}1 \\-2\end{pmatrix}\right\}{(1−2)}. Ядром ААА являются векторы, такие что Av=0Av = 0Av=0, то есть векторное пространство, натянутое на {(1−3)}\left\{\begin{pmatrix}1\\-3\end{pmatrix}\ right\}{(1−3)} и имеет размерность 1. Следовательно, и ранг, и недействительность равны 1, а их сумма равна 2, количеству столбцов в AAA.
Это применимо и к неквадратным матрицам. Например, в матрице
A=(25−3142),A = \begin{pmatrix}2&5&-3\\1&4&2\end{pmatrix},A=(2154−32),
ранг равен 2, натянутый на первые два столбца AAA, а ядро является векторным пространством, натянутым на {(22−73)}\left\{\begin{pmatrix}22\\-7\\3\end{pmatrix }\right\}⎩⎨⎧⎝⎛22−73⎠⎞⎭⎬⎫, которая, таким образом, имеет размерность 1. Как и ожидалось, сумма ранга и недействительности равна 3, количеству столбцов в AAA.
Ранг = 3, Недействительность = 3 Ранг = 2, Недействительность = 2 Ранг = 1, Недействительность = 3 Ранг = 2, Недействительность = 3 Ранг = 3, Недействительность = 1
Рассмотрим матрицу
A=(112334−12−1−254). A = \begin{pmatrix}1 & 1 & 2 & 3 \\ 3 & 4 & -1 & 2 \\ -1 & -2 & 5 & 4 \end{pmatrix}.A=⎝⎛13−1 14−22−15324⎠⎞.
Каковы ранг и ничтожность ААА?
Существует ряд доступных доказательств теоремы о ранге недействительности. В самом простом используется приведение матрицы к форме Гаусса-Жордана, так как ее гораздо легче анализировать. Таким образом, стратегия доказательства проста: показать, что теорема ранга-недействительность может быть сведена к случаю матрицы Гаусса-Жордана, путем анализа влияния операций со строками на ранг и недействительность, а затем показать, что теорема о ранг-недействительности верна. {-1}0 = 0Ax=M−1Bx=M−10=0, поэтому Null(A)=Null(B),\text{Null}(A) = \text{Null}(B),Null(A )=Null(B), по желанию.
{-1}0 = 0Ax=M−1Bx=M−10=0, поэтому Null(A)=Null(B),\text{Null}(A) = \text{Null}(B),Null(A )=Null(B), по желанию.
Ранг матрицы в форме Гаусса-Жордана — это число ведущих переменных. Недействительность матрицы в форме Гаусса-Жордана — это количество свободных переменных.
По определению форма матрицы Гаусса-Жордана состоит из матрицы, ненулевые строки которой имеют начальную единицу. Они не могут обращаться в нуль при операциях со строками, поэтому все ненулевые строки линейно независимы. Следовательно, ранг равен количеству ведущих единиц, что эквивалентно количеству ведущих переменных.Теперь предположим, что есть ведущие переменные mmm и свободные переменные nnn. Тогда векторы
v1=(00⋮10⋮0),v2=(00⋮01⋮0),…,vn=(00⋮00⋮1)v_1 = \begin{pmatrix}0\\0\\\vdots\\1 \\0\\\vdots\\0\end{pmatrix}, v_2 = \begin{pmatrix}0\\0\\\vdots\\0\\1\\\vdots\\0\end{pmatrix}, \ldots, v_n = \begin{pmatrix}0\\0\\\vdots\\0\\0\\\vdots\\1\end{pmatrix}v1=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ ⎛00⋮10⋮0⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞,v2=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮01⋮0⎠⎟⎟⎟⎟⎟ ⎟⎟⎟⎟⎟⎞,…,vn=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛00⋮00⋮1⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
образуют основу для нулевого пространства формы Гаусса-Жордана матрицы.
Очевидно, что эти векторы линейно независимы, и, следовательно, значение NULL равно nnn — числу свободных переменных.
Теорема о ранге недействительности является непосредственным следствием этих двух результатов. Ранг матрицы AAA и нулевое пространство матрицы AAA эквивалентны рангу и нулевому пространству формы Гаусса-Жордана матрицы AAA, поэтому достаточно доказать теорему ранга-недействительности для матриц уже в форме Гаусса-Жордана. Но количество столбцов в матрице формы Гаусса-Жордана в точности равно сумме числа ведущих переменных (которое, как было показано выше, является рангом) и количества свободных переменных (которое, как было показано выше, является нулем), как каждая переменная должна быть либо ведущей, либо свободной. Это завершает доказательство. □_\квадрат□
- Фундаментальные подпространства
- Ранг
- Ядро (нулевое пространство)
- Исключение Гаусса-Джордана
- Матрицы
Процитировать как: Теорема ранга-недействительности. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/rank-nullity-theorem/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/rank-nullity-theorem/
Online MBA, GMAT не требуется
Загрузка…
Какая программа вас интересует?
Выберите поле ввода Выберите программу Магистр делового администрирования (MBA) Магистр наук в области бизнес-аналитики (MSBA) Магистр наук в области маркетинга (МСМ) Магистр финансов (MSF) Магистр бухгалтерского учета (MAcc) Сертификат по основам бизнес-аналитики (FBA) Сертификат управления инвестициями Сертификат финансирования недвижимости Сертификат корпоративных финансов Для кого предназначена эта брошюра?Поле ввода текста
Адрес электронной почты*
Поле ввода номера телефона
Нажимая «Получить брошюру о программе», я соглашаюсь предоставить контактную информацию, указанную выше, для получения сообщений об образовательных программах и возможностях.
Спасибо за вашу заявку!
К сожалению, что-то пошло не так.
Главная МВА
Чтобы эффективно руководить современными организациями, нужен настоящий революционер. Сложные, глобальные проблемы, которые определяют современный бизнес, не поддаются традиционным решениям, и только самые гибко мыслящие и находчивые профессионалы могут подойти к ним так, чтобы подготовить свою команду к успеху.
Онлайн-программа MBA Школы бизнеса Рэймонда А. Мейсона дает необходимые бизнес-знания и формирует динамичное мышление, необходимое для лидерства в сегодняшней сложной и быстро меняющейся бизнес-среде. Неудивительно, что более 97% наших выпускников оценивают свою удовлетворенность программой как «высокую» или «очень высокую».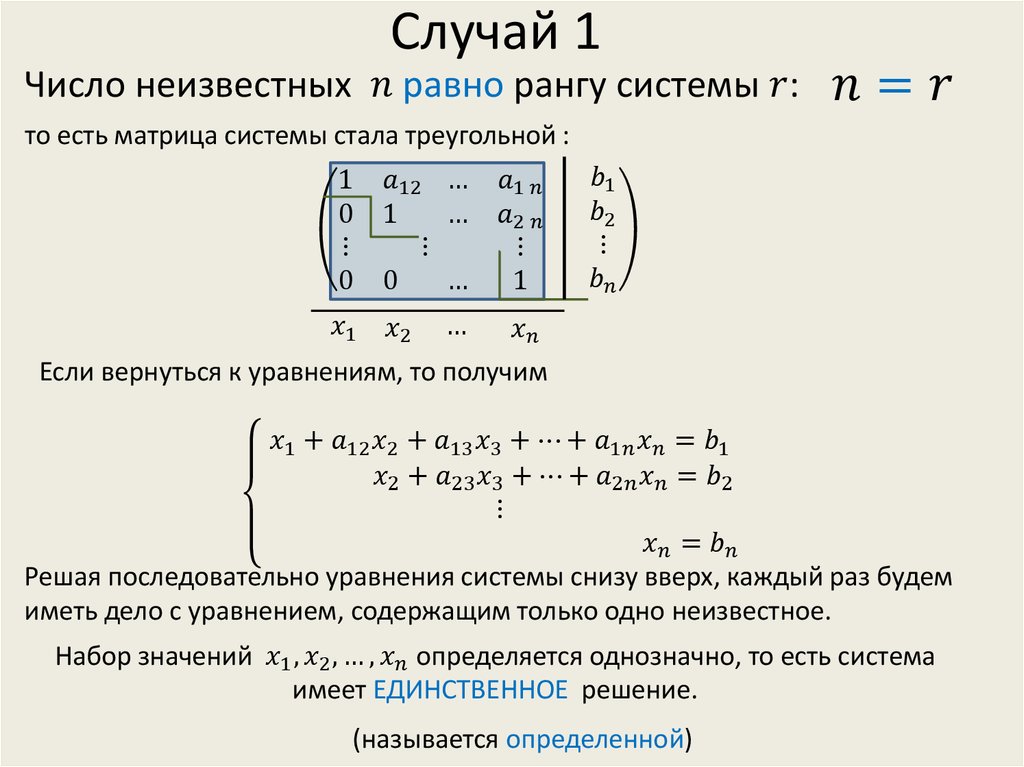 1
1
Лучшая онлайн-программа MBA без требований к GMAT
Посетите страницу с требованиями к заявкам , чтобы узнать, как наша приверженность комплексной оценке вдохновила нас предложить нашу известную онлайн-программу MBA без требований к GMAT.
ДИЗАЙН-МЫШЛЕНИЕ
ЗЛАЯ ПРОБЛЕМА
УЧЕБНАЯ ПРОГРАММА
ДИЗАЙН-МЫШЛЕНИЕ УЧЕБНАЯ ПРОБЛЕМА
Сделайте свой онлайн-MBA фокусом на аналитике
Мы понимаем, что сегодня многие целеустремленные профессионалы хотят приобрести набор технических навыков, которые выходят за рамки нашей стандартной учебной программы Online MBA.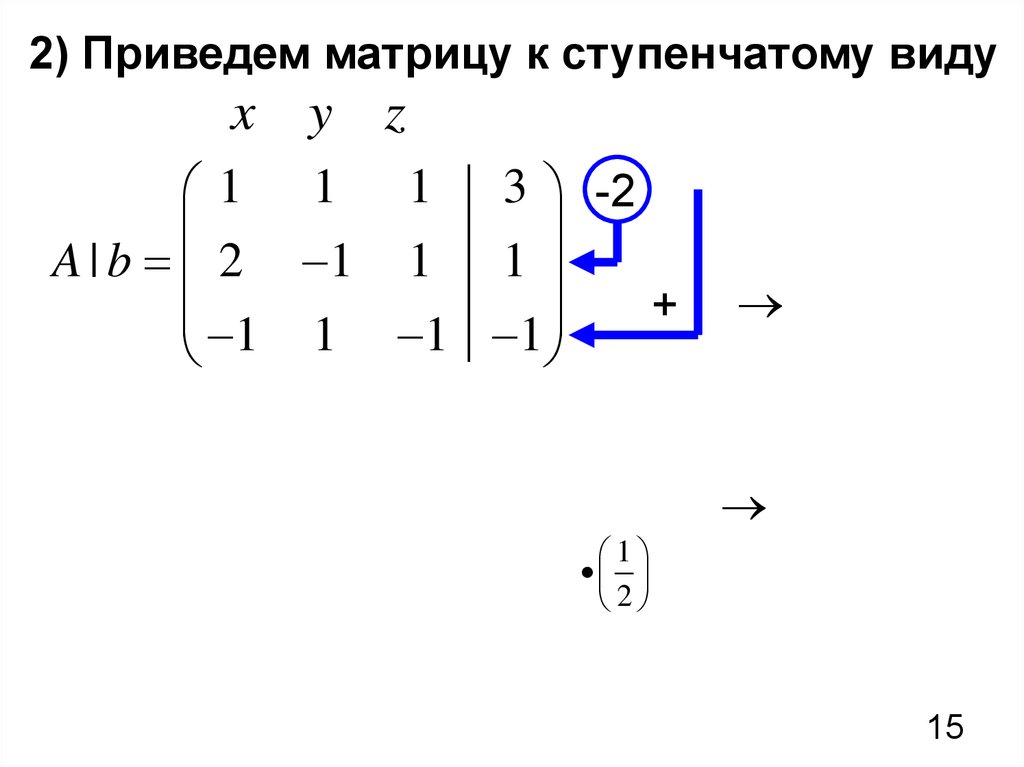 По этой причине мы рады предложить два варианта, чтобы удовлетворить спрос наших студентов на более надежные курсы по программированию и аналитике.
По этой причине мы рады предложить два варианта, чтобы удовлетворить спрос наших студентов на более надежные курсы по программированию и аналитике.
Будучи студентом онлайн-программы MBA, вы можете:
- Зарегистрироваться на курс BUAD 502B R Programming и/или BUAD 502C Python Programming из нашей онлайн-программы MSBA, чтобы дополнить свой онлайн-MBA знанием этих языков
- Дополнить онлайн-программу MBA с нашим сертификатом Online Foundations in Business Analytics Certificate , чтобы добавить практический технический опыт к вашему набору инструментов лидерства в рамках учебной программы из пяти курсов (12 кредитов)
Оба эти варианта могут быть легко интегрированы в вашу последовательность программ Online MBA, позволяя вам развивать эти дополнительные навыки, не увеличивая время на получение степени. Свяжитесь с консультантом по приему для получения дополнительной информации.
Не заинтересованы в нашей онлайн-MBA? Ознакомьтесь с другими нашими программами MBA.
Откройте для себя ценность разнообразия когорт
Наши когорты Online MBA исторически представляли более ста университетов бакалавриата и впечатляюще разнообразные этнические группы, области карьеры и профессиональный опыт. История, которую рассказывает эта статистика, заключается в том, что эта программа представляет собой программу, в которой самые разные голоса собираются вместе, чтобы развивать свои навыки, а также способствовать личному и профессиональному росту других.
Получите бесценное знакомство с разнообразной группой коллег с новыми и важными взглядами, и пусть их понимание поможет вам справиться с проблемами и возможностями, созданными коварными проблемами современного бизнеса.
ПРИМЕЧАНИЕ. Статистические данные основаны на кумулятивных данных профиля студента W&M Online MBA, собранных по всем группам в период с весны 2016 г. Поиск нейронной архитектуры с ограниченными ресурсами в наборах данных в виде таблиц ][bib] gcimpute: пакет для вменения отсутствующих данных NysADMM: более быстрая композитная выпуклая оптимизация с помощью низкоранговой аппроксимации bib] На пути к устойчивости группы при наличии меток частичной группы Как низко мы можем опуститься: обмен памяти на ошибку в низкоточном обучении Матричная факторизация для вменения пропущенных значений и Реконструкция разреженных данных Нормализация CDF для управления распределением активаций скрытого слоя Randomized Nystr\»om Preconditioning Can we globally оптимизировать потери при перекрестной проверке Квазивыпуклость в гребневой регрессии Privileged Zero-Shot AutoML Автоматическая система обнаружения эквивалентности итерационных алгоритмов TenIPS: выборка обратной склонности для завершения тензора Онлайн-вменение пропущенных значений и обнаружение изменений корреляции для данных смешанного типа с помощью гауссовой связки Надежная нелинейная матричная факторизация для изучения словарей, шумоподавления и кластеризации О простоте и обусловленности полуопределенных программ низкого ранга Масштабируемое полуопределенное программирование Рандомизированный Алгоритмы создания эскизов для динамической оптимизации с малым объемом памяти Оптимальное хранилище Подход к полуопределенному программированию с использованием приближенной дополнительности Влияние точности на интерпретацию моделей Регуляризация квазинормы Строгий подход к оценке погрешности и чувствительности решения конических программ Galaxy TSP: новый эталонный тест для TSP с миллиардом узлов Комбинаторные алгоритмы, 2020 Приблизительная перекрестная проверка с данными низкого ранга в больших размерностях Онлайн-вменение смешанного пропущенного значения с использованием гауссовой связки TenIPS: выборка обратной склонности для завершения тензора (семинар) Завершение матрицы с количественной неопределенностью с помощью гауссовской связки низкого ранга Обучение решению задач комбинаторной оптимизации на графах реального мира в линейном времени Эффективный конвейерный поиск AutoML с помощью матрицы и Tensor Factorization Zero-shot AutoML AutoML в реальном времени Постоянный мониторинг окружающей среды с помощью планирования и прогнозирования на основе моделей низкого ранга Выбор конвейера AutoML: эффективное перемещение в комбинаторном пространстве Завершение полиномиальной матрицы для вменения отсутствующих данных и трансдуктивного обучения Вменение пропущенных значений для смешанных данных с помощью гауссовой связки Низкоранговая аппроксимация тензора Такера из потоковых данных SysML: новый рубеж систем машинного обучения Регуляризация разреженной группы факторов для эффективного восстановления матриц низкого ранга AutoML с использованием языковых вложений метаданных OBOE: совместная фильтрация для выбора модели AutoML «Почему вы должны доверять моим объяснениям?» Понимание неопределенности в объяснениях LIME Аппроксимация потоковой низкоранговой матрицы с приложением к научному моделированию Большие данные имеют низкий ранг Завершение высокоранговой матрицы онлайн Оптимальный дизайн эффективных фотоэлектрических батарей на крыше Справедливость в условиях неосознанности: оценка неравенства, когда защищенный класс не наблюдается Почему матрицы больших данных имеют примерно низкий ранг? Tensor Random Projection for Low Memory Dimension Reduction Более практичные алгоритмы построения эскизов для аппроксимации матриц низкого ранга OBOE: совместная фильтрация для инициализации AutoML (версия для семинаров) Метод Келли с ограниченной памятью Составные выпуклые и субмодульные объективы Причинный вывод с зашумленными и отсутствующими ковариатами посредством матричной факторизации Алгоритмы стиля Франка-Вульфа для крупномасштабной оптимизации Аппроксимация фиксированного ранга положительно-полуопределенной матрицы из потоковых данных Граф-регуляризованные обобщенные модели низкого ранга Дисциплинированное мультивыпуклое программирование Практические алгоритмы построения эскизов для аппроксимации матриц низкого ранга Звук хлопка APALM: более быстрая негладкая невыпуклая оптимизация с помощью стохастической асинхронной PALM Выявление фенотипов пациентов с использованием обобщенных моделей низкого ранга Выявленные предпочтения в масштабе: изучение персонализированных предпочтений на основе выбора ассортимента Обобщенные модели низкого ранга Ограничивающий разрыв двойственности для разделимых задач с линейными ограничениями Обобщенные модели низкого ранга Максимизация доходов для поставщиков услуг широкополосного доступа, использующих потенциал доходов PCA on a Data Факторизация для умножения аналого-цифровых матриц Помимо анализа главных компонентов (PCA) Обобщенные модели низкого ранга Максимизация суммы сигмоидов Линейные бандиты, заполнение матриц и системы рекомендаций Использование лекарств в клинических заметках для безопасности пациентов Этот модуль содержит большое количество вероятностных распределений,
сводная и частотная статистика, корреляционные функции и статистические
тесты, маскированная статистика, оценка плотности ядра, квази-Монте-Карло
функциональность и многое другое. Статистика — это очень большая область, и есть темы, которые выходят за рамки
для SciPy и покрываются другими пакетами. Некоторые из наиболее важных
являются: статистические модели:
регрессия, линейные модели, анализ временных рядов, расширения тем
также покрывается Pandas: табличные данные, временные ряды
функциональность, интерфейсы к другим статистическим языкам. PyMC: байесовская статистическая
моделирование, вероятностное машинное обучение. scikit-learn: классификация, регрессия,
выбор модели. Сиборн: визуализация статистических данных. rpy2: мост между Python и R. Каждое одномерное распределение является экземпляром подкласса Общий класс непрерывных случайных величин, предназначенный для создания подклассов. Общий класс дискретных случайных величин, предназначенный для создания подклассов. Генерирует распределение в виде гистограммы. Альфа-непрерывная случайная величина. Непрерывная случайная величина угла. Непрерывная случайная величина с арксинусом. Распределение Argus Бета-непрерывная случайная величина. Бета-простая непрерывная случайная величина. Непрерывная случайная величина Брэдфорда. A Burr (Тип III) непрерывная случайная величина. A Burr (тип XII) непрерывная случайная величина. Непрерывная случайная величина Коши. Хи-непрерывная случайная величина. Непрерывная случайная величина хи-квадрат. Косинусно-непрерывная случайная величина. Распределение Crystalball Двойная гамма-непрерывная случайная величина. Двойная непрерывная случайная величина Вейбулла. Непрерывная случайная величина Эрланга. Экспоненциальная непрерывная случайная величина. Экспоненциально модифицированная нормальная непрерывная случайная величина. Экспоненциальная непрерывная случайная величина Вейбулла. Непрерывная случайная величина в экспоненциальной степени. Непрерывная случайная величина F. Непрерывная случайная величина усталостной долговечности (Бирнбаум-Сондерс). Непрерывная случайная величина Фиска. Свернутая непрерывная случайная величина Коши. Свернутая нормальная непрерывная случайная величина. Обобщенная логистическая непрерывная случайная величина. Обобщенная нормальная непрерывная случайная величина. Обобщенная случайная величина, непрерывная по Парето. Обобщенная экспоненциальная непрерывная случайная величина. Непрерывная случайная величина обобщенного экстремального значения. Гипергеометрическая непрерывная случайная величина Гаусса. Гамма-непрерывная случайная величина. Обобщенная гамма-непрерывная случайная величина. Обобщенная полулогистическая непрерывная случайная величина. Обобщенная гиперболическая непрерывная случайная величина. Обобщенная обратная гауссовская непрерывная случайная величина. Непрерывная случайная величина Gibrat. Непрерывная случайная величина Гомперца (или усеченного Гамбеля). Непрерывная случайная величина Гумбеля с асимметрией вправо. Непрерывная случайная величина Гамбеля с асимметрией влево. Непрерывная случайная величина полу-Коши. Полулогистическая непрерывная случайная величина. Полунормальная непрерывная случайная величина. Верхняя половина обобщенной нормальной непрерывной случайной величины. Гиперболическая секущая непрерывная случайная величина. Инвертированная гамма-непрерывная случайная величина. Обратная гауссовская непрерывная случайная величина. Инвертированная непрерывная случайная величина Вейбулла. Непрерывная случайная величина Johnson SB. Непрерывная случайная величина Джонсона SU. Каппа 4 распределения параметров. Каппа 3 распределения параметров. Односторонний критерий Колмогорова-Смирнова статистическое распределение. Двухсторонний критерий Колмогорова-Смирнова статистическое распределение. Предельное распределение масштабированной статистики двустороннего критерия Колмогорова-Смирнова. Непрерывная случайная величина Лапласа. Асимметричная непрерывная случайная величина Лапласа. Непрерывная случайная величина Леви. Непрерывная случайная величина Леви с асимметрией влево. Стабильная по Леви непрерывная случайная величина. Логистическая (или Sech-квадрат) непрерывная случайная величина. Логарифмическая гамма-непрерывная случайная величина. Логарифмическая непрерывная случайная величина Лапласа. Логнормальная непрерывная случайная величина. Логарифмическая или обратная непрерывная случайная величина. Ломакс (Парето второго рода) непрерывная случайная величина. Непрерывная случайная величина Максвелла. Непрерывная случайная величина Mielke Beta-Kappa / Dagum. Непрерывная случайная величина Мойала. Непрерывная случайная величина Накагами. Нецентральная непрерывная случайная величина хи-квадрат. Непрерывная случайная величина с нецентральным F-распределением. Нецентральная непрерывная случайная величина Стьюдента t. Нормальная непрерывная случайная величина. Нормальная обратная Гауссова непрерывная случайная величина. Парето-непрерывная случайная величина. Непрерывная случайная величина Пирсона типа III. Непрерывная случайная величина со степенной функцией. Логарифмически нормальная непрерывная случайная величина. Степенная нормальная непрерывная случайная величина. R-распределенная (симметричная бета) непрерывная случайная величина. Непрерывная случайная величина Рэлея. Непрерывная случайная величина Райса. Обратная обратная гауссовская непрерывная случайная величина. Полукруглая непрерывная случайная величина. Искаженная случайная величина Коши. Косонормальная случайная величина. Непрерывная случайная величина студенческого диапазона. Непрерывная случайная величина Стьюдента t. Трапециевидная непрерывная случайная величина. Треугольная непрерывная случайная величина. Усеченная экспоненциальная непрерывная случайная величина. Усеченная нормальная непрерывная случайная величина. Дважды усеченная минимальная непрерывная случайная величина Вейбулла. Непрерывная случайная величина Тьюки-Ламдба. Равномерная непрерывная случайная величина. Непрерывная случайная величина фон Мизеса. Непрерывная случайная величина фон Мизеса. Непрерывная случайная величина Вальда. Минимальная непрерывная случайная величина Вейбулла. Максимальная непрерывная случайная величина Вейбулла. Обернутая непрерывная случайная величина Коши. Многомерная нормальная случайная величина. Матричная нормальная случайная величина. Случайная величина Дирихле. Случайная величина Уишарта. Обратная случайная величина Уишарта. Полиномиальная случайная величина. Специальная ортогональная матрица (SO(N)) случайная величина. Ортогональная матричная (O(N)) случайная величина. Случайная величина U(N), принимающая матричное значение. Матрица случайной корреляции. Многомерная случайная величина с t-распределением. Многомерная гипергеометрическая случайная величина. Дискретная случайная величина Бернулли. Бета-биномиальная дискретная случайная величина. Биномиальная дискретная случайная величина. Случайная величина Больцмана (усеченная дискретная экспонента). Лапласова дискретная случайная величина. Геометрическая дискретная случайная величина. Гипергеометрическая дискретная случайная величина. Логарифмическая (логарифмическая серия, серия) дискретная случайная величина. Отрицательная биномиальная дискретная случайная величина. Нецентральная гипергеометрическая дискретная случайная величина Фишера. Нецентральная гипергеометрическая дискретная случайная величина Валлениуса. Отрицательная гипергеометрическая дискретная случайная величина. Планковская дискретная экспоненциальная случайная величина. Дискретная случайная величина Пуассона. Однородная дискретная случайная величина. Дискретная случайная величина Скеллама. Дискретная случайная величина Юла-Саймона. Дискретная случайная величина Zipf (Zeta). Дискретная случайная величина Ципфа. Ниже приводится обзор статистических функций. Многие из этих функций
есть аналогичная версия Вычислить несколько описательных статистик переданного массива. Вычислить взвешенное среднее геометрическое вдоль указанной оси. Вычислить взвешенное среднее гармоническое вдоль указанной оси. Вычислить средневзвешенное значение мощности вдоль указанной оси. Вычислить эксцесс (Фишер или Пирсон) набора данных. Возвращает массив модального (наиболее распространенного) значения в переданном массиве. Вычислить n-й момент относительно среднего для выборки. Вычислить выборочную асимметрию набора данных. Вернуть n-ю k-статистику (пока что 1<=n<=4). Возвращает несмещенную оценку дисперсии k-статистики. Вычислить усеченное среднее. Вычислите усеченную дисперсию. Вычислить усеченный минимум. Вычислить усеченный максимум. Вычислите стандартное отклонение усеченной выборки. Вычислить усеченную стандартную ошибку среднего. Вычислить коэффициент вариации. Поиск повторов и количество повторов. Возвращает среднее значение массива после обрезки распределения с обоих концов. Расчет стандартного геометрического отклонения массива. Вычислить межквартильный диапазон данных по указанной оси. Вычислить стандартную ошибку среднего. Байесовские доверительные интервалы для среднего, var и станд. «Замороженные» распределения для среднего значения, дисперсии и стандартного отклонения данных. Вычислить энтропию распределения для заданных значений вероятности. По выборке распределения оцените дифференциальную энтропию. Вычислить среднее абсолютное отклонение данных по заданной оси. Возвращает гистограмму совокупной частоты, используя функцию гистограммы. Вычислить процентильный ранг оценки относительно списка оценок. Вычислить оценку для заданного процентиля входной последовательности. Возвращает гистограмму относительной частоты, используя функцию гистограммы. Вычислить бинарную статистику для одного или нескольких наборов данных. Вычислить двумерную бинарную статистику для одного или нескольких наборов данных. Вычислить многомерную бинарную статистику для набора данных. Выполнение однофакторного дисперсионного анализа. Выполняет тест Александра Говерна. Коэффициент корреляции Пирсона и значение p для проверки отсутствия корреляции. Рассчитайте коэффициент корреляции Спирмена с соответствующим p-значением. Вычислите точечный бисериальный коэффициент корреляции и его p-значение. Рассчитайте тау Кендалла, меру корреляции для порядковых данных. Вычислите взвешенную версию Кендалла \(\tau\). Вычисляет D Сомерса, асимметричную меру порядковой ассоциации. Рассчитать линейную регрессию методом наименьших квадратов для двух наборов измерений. Вычисляет оценку Зигеля для набора точек (x, y). Вычисляет оценку Тейла-Сена для набора точек (x, y). Вычисляет статистику теста многомасштабной корреляции графов (MGC). Рассчитать Т-критерий для среднего значения ОДНОЙ группы баллов. Рассчитайте Т-критерий для средних двух независимых выборок оценок. Т-критерий для средних двух независимых выборок из описательной статистики. Рассчитайте t-критерий для ДВУХ СВЯЗАННЫХ выборок оценок, a и b. Вычислите односторонний критерий хи-квадрат. Выполните одновыборочный критерий Крамера-фон Мизеса для проверки соответствия. Выполните тест Крамера-фон Мизеса с двумя образцами для проверки соответствия. Кресси-Рид статистика расхождения мощности и критерий согласия. Выполняет (одновыборочный или двухвыборочный) тест Колмогорова-Смирнова на соответствие. Выполняет одновыборочный тест Колмогорова-Смирнова на соответствие. Выполняет двухвыборочный тест Колмогорова-Смирнова на качество соответствия. Вычислить статистику теста Эппса-Синглтона (ES). Выполните U-ранговый критерий Манна-Уитни на двух независимых выборках. Поправочный коэффициент на ничью для U-критерия Манна-Уитни и H-критерия Крускала-Уоллиса. Присваивайте ранги данным, соответствующим образом обрабатывая связи. Вычислить статистику суммы рангов Уилкоксона для двух выборок. Вычислить критерий знакового ранга Уилкоксона. Вычислите H-критерий Крускала-Уоллиса для независимых выборок. Вычислите критерий Фридмана для повторных выборок. Вычислите критерий Бруннера-Мюнцеля для выборок x и y. Объедините p-значения независимых тестов, основанных на одной и той же гипотезе. Выполнение критерия согласия Жака-Бера для выборочных данных. Проведите тест Пейджа, измеряющий тенденцию в наблюдениях между курсами лечения. Выполните тест Тьюки HSD на равенство средних при нескольких обработках. Выполните тест Ансари-Брэдли для параметров одинаковой шкалы. Выполнить тест Бартлетта на равные дисперсии. Выполнить тест Левена на равные дисперсии. Выполните тест Шапиро-Уилка на нормальность. Тест Андерсона-Дарлинга для данных, поступающих из определенного распределения. Критерий Андерсона-Дарлинга для k-выборок. Провести проверку, что вероятность успеха равна p. Провести проверку, что вероятность успеха равна p. Выполнить тест Флигнера-Киллина на равенство дисперсий. Проведите средний тест настроения. Выполнить тест настроения для одинаковых параметров шкалы. Проверить, отличается ли перекос от нормального распределения. Проверить, имеет ли набор данных нормальный эксцесс. Проверить, отличается ли выборка от нормального распределения. Вычисление двустороннего доверительного интервала начальной загрузки для статистики. Выполняет перестановочный тест заданной статистики на предоставленных данных. Проверка методом Монте-Карло выборки из заданного распределения. Возвращает набор данных, преобразованный степенным преобразованием Бокса-Кокса. Вычислить оптимальный параметр преобразования Бокса-Кокса для входных данных. Логарифмическая функция правдоподобия Бокскокса. Вернуть набор данных, преобразованный степенным преобразованием Йео-Джонсона. Вычислить оптимальный параметр преобразования Йео-Джонсона. Логарифмическая функция правдоподобия Йеджонсона. Вычислить преобразование О’Брайена для входных данных (любое количество массивов). Выполнить итеративное сигма-отсечение элементов массива. Отрежьте часть элементов с обоих концов массива. Отрезать пропорцию от ОДНОГО конца переданного распределения массива. Вычислить относительные z-значения. Вычислите значение z. Вычислите геометрическую стандартную оценку. Вычисление первого расстояния Вассерштейна между двумя одномерными распределениями. Вычислить энергетическое расстояние между двумя одномерными распределениями. Генерация случайных выборок из функции плотности вероятности с использованием метода соотношения однородностей. Подгонка дискретного или непрерывного распределения к данным Вычислить среднее круговое для выборок в диапазоне. Вычислить круговую дисперсию для выборок, которые, как предполагается, находятся в диапазоне. Вычислите круговое стандартное отклонение для выборок, которые, как предполагается, находятся в диапазоне [от низкого до высокого]. Хи-квадрат критерий независимости переменных в таблице непредвиденных обстоятельств. Возвращает таблицу количества для каждой возможной уникальной комбинации в Вычислите ожидаемые частоты из таблицы непредвиденных обстоятельств. Возвращает список предельных сумм массива a . Вычислите относительный риск (также известный как коэффициент риска). Вычисляет степень связи между двумя номинальными переменными. Выполните точный критерий Фишера для таблицы непредвиденных обстоятельств 2×2. Выполните точный тест Барнарда на таблице непредвиденных обстоятельств 2×2. Выполните точный тест Бошлоо на таблице непредвиденных обстоятельств 2×2. Рассчитайте параметр формы, который максимизирует PPCC. Расчет и, при необходимости, построение графика коэффициента корреляции вероятностного графика. Вычислить квантили для вероятностного графика и при необходимости отобразить график. Вычислите параметры для графика нормальности Бокса-Кокса, опционально отобразите его. Вычислите параметры графика нормальности Йео-Джонсона, опционально отобразите его. Представление оценки плотности ядра с использованием ядер Гаусса. по весну 2018 г.
по весну 2018 г. Бумаги
К. Чанг, Дж. Юн, С. Арик, М. Уделл и Т. Пфистер
препринт arXiv arXiv:2203.02034, 2022
[bib]
В. С. Локханде, К. Сон, Дж. Юн, М. Уделл, К. Ли и Т. Пфистер
С. Локханде, К. Сон, Дж. Юн, М. Уделл, К. Ли и Т. Пфистер
CoRR, 2022
[url][ bib]
C. Yang, Z. Wu, J. Chee, CD Sa и M. Udell
Международная конференция по представлениям обучения (ICLR), 2022
[arxiv][bib]
Н. Сенгупта, М. Уделл, Н. Сребро и Дж. Эванс
Принято в Sociological Methodology, 2022
[bib]
M. Ван Несс и М. Уделл
Я (все еще) не могу поверить, что это не лучше! NeurIPS 2021 Workshop, 2021
[bib]
Z. Frangella, J. A. Tropp, and M. Udell
Submitted, 2021
[arxiv][bib]
В. Т. Стивенсон, З. Франгелла, М. Уделл и Т. Бродерик
Т. Стивенсон, З. Франгелла, М. Уделл и Т. Бродерик
Достижения в системах обработки нейронной информации (NeurIPS), 2021 г.
[arxiv][bib]
Н. Сингх, Б. Кейтс, Дж. Ментч, А. Харкар, М. Уделл и И. Дрори
2021
[arxiv][bib] ]
С. Чжао, Л. Лессард и М. Уделл : Выбор признаков по разреженным лесам
Б. Лю, М. Се и М. Уделл
Конференция ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных (KDD), 2021 г.
[arxiv][slides][bib]
C. Yang, L. Ding, Z. Wu и М. Уделл
Международная конференция по искусственному интеллекту и статистике (AISTATS), 2021 г.
[arxiv][bib]
Ю. Чжао , Э. Ландгребе, Э. Шехтман, М. Уделл
Чжао , Э. Ландгребе, Э. Шехтман, М. Уделл
AAAI, 2021
[arxiv][bib]
Дж. Фан, К. Ян и М. Уделл
IEEE Trans. Signal Processing (TSP), 2021
[arxiv][pdf][url][bib]
L. Ding and M. Udell
SIAM Journal on Optimization (SIOPT) ), 2021
[arxiv][url][bib]
А. Юрцевер, Дж. Тропп, О. Феркок, М. Уделл и В. Чевхер
SIAM Journal on Mathematics of Data Science (SIMODS), 2021
[arxiv][pdf][bib]
Р. Мутукумар, Д. Коури и М. Уделл
SIAM Journal on Optimization (SIOPT), 2021
[pdf][url][bib]
Л. Динг, А. Юрцевер, В. Чевхер, Дж. Тропп и М. Уделл
Динг, А. Юрцевер, В. Чевхер, Дж. Тропп и М. Уделл
SIAM Journal on Optimization (SIOPT), 2021
Лауреат премии INFORMS Optimization Society 2017 года за студенческую работу
[arxiv][pdf][слайды ][bib]
Б. Лю и М. Уделл
2020
[arxiv][bib]
Дж. Фан, Л. Дин, К. Янг, М. Уделл
Представлено, 2020 г.
[arxiv][bib]
L. Ding and M. Udell
Представлено, 2020 г.
[arx9iv][bib]
[url][bib]
В. Стефенсон, М. Уделл и Т. Бродерик
Достижения в системах обработки нейронной информации (NeurIPS), 2020
[arxiv][url][ bib]
Э. Ландгребе, Ю. Чжао и М. Уделл
Ландгребе, Ю. Чжао и М. Уделл
ICML Workshop on the Art of Learning with Missing Values (Artemiss), 2020
[bib]
К. Ян, Л. Дин, З. Ву и М. Уделл
OPT2020: 12-й ежегодный семинар по оптимизации для машинного обучения, 2020 г. с более сильными оракулами подзадач
L. Ding, J. Fan, and M. Udell
Представлено, 2020
[arxiv][bib]
Y. , Udell
Достижения в области систем обработки нейронной информации (NeurIPS), 2020 г.
[arxiv][pdf][bib]
И. Дрори, А. Харкар, В. Р. Сикингер, Б. Кейтс, К. Ма, С. Ге, Э. Долев, Б. Дитрих, Д. П. Уильямсон и М. Уделл
Международная конференция IEEE по машинному обучению и приложениям (IEEE ICMLA), 2020 г.
[arxiv][bib]
C. Yang, J. Fan, Z. Wu, and M. Udell
2020
[arxiv][bib]
И. Дрори, Л. Лю, К. Ма, Б. Кейтс и М. Уделл
Ежегодный симпозиум по машинному обучению, 2020 г.
[нагрудник]
И. Дрори, Л. Лю, К. Ма, Дж. Дейкин, Б. Кейтс и М. Уделл
2020
[нагрудник]
Э. Риччи, М. Уделл и Р. Неппер
2020
[arxiv][bib]
C. Yang, J. Fan, Z. Wu и M. Udell
ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), 2020
[arxiv][url][bib]
Дж. Фан, Ю. Чжан и М. Уделл
Фан, Ю. Чжан и М. Уделл
Тридцать четвертая конференция AAAI по Искусственный интеллект, 2020
[arxiv][url][bib]
Ю. Чжао и М. Уделл
Конференция ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных (KDD), 2020
[arxiv ][pdf][slides][bib]
Ю. Сун, Ю. Го, К. Луо, Дж. Тропп и М. Уделл
SIAM Journal по математике науки о данных (SIMODS), 2020
[arxiv][pdf][url][slides][bib]
А. Ратнер, Д. Алистар, Г. Алонсо, Д. Г. Андерсен, П. Бейлис, С. Берд, Н. Карлини, Б. Катандзаро, Э. Чанг, Б. Далли, Дж. Дин, И. С. Диллон, А. Г. Димакис, П. Дубей, К. Элкан, Г. Фурсин, Г. Р. Гангер, Л. Гетур, П. Б. Гиббонс, Г. А. Гибсон, Дж. Э. Гонсалес, Дж. Готтшлих, С. Хан, К. М. Хейзелвуд, Ф. Хуан, М. Джагги, К. Г. Джеймисон, М. И. Джордан, Г. Джоши, Р. Халаф, Дж. Найт, Дж. Конечни, Т. Краска, А. Кумар, А. Кириллидис, Дж. Ли, С. Мэдден, Х. Б. МакМахан, Э. Мейер, И. Митлягкас, Р. Монга, Д. Г. Мюррей, Д. С. Папайлиопулос, Г. Пехименко, Т. Рекацинас, А. Ростамизаде, С. Р’э, С. Д. Са, Х. Седги, С. Сен, В. Смит, А. Смола, Д. Сонг, Э. Р. Спаркс, И. Стойка, В. Сзе, М. Уделл, Дж. Ваншорен, С. Венкатараман, Р. Винаяк, М. Веймер, А. Г. Уилсон, Э. П. Син, М. Захария, К. Чжан и А. Талвалкар
Г. Джеймисон, М. И. Джордан, Г. Джоши, Р. Халаф, Дж. Найт, Дж. Конечни, Т. Краска, А. Кумар, А. Кириллидис, Дж. Ли, С. Мэдден, Х. Б. МакМахан, Э. Мейер, И. Митлягкас, Р. Монга, Д. Г. Мюррей, Д. С. Папайлиопулос, Г. Пехименко, Т. Рекацинас, А. Ростамизаде, С. Р’э, С. Д. Са, Х. Седги, С. Сен, В. Смит, А. Смола, Д. Сонг, Э. Р. Спаркс, И. Стойка, В. Сзе, М. Уделл, Дж. Ваншорен, С. Венкатараман, Р. Винаяк, М. Веймер, А. Г. Уилсон, Э. П. Син, М. Захария, К. Чжан и А. Талвалкар
CoRR, 2019
[arxiv][url][bib]
Дж. Фан, Л. Дин, Ю. Чен и М. Уделл
Успехи в системах обработки нейронной информации (NeurIPS), 2019
[arxiv][pdf][bib]
И. Дрори, Л. Лю, С. Кооратхота, Н. Йи, Дж. Ли , А. Моретти, Дж. Фрейре и М. Уделл
Семинар NeurIPS по метаобучению, 2019 г.
[arxiv][pdf][bib]
C. Yang, Y. Akimoto, D. Kim и M. Udell
Yang, Y. Akimoto, D. Kim и M. Udell
ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), 2019
Устная презентация
[arxiv][pdf][url][bib]
Y. Zhang, K. Song , Ю. Сун, С. Тан и М. Уделл
ICML Workshop AI for Social Good, 2019 г.
[arxiv][bib]
Тропп Дж., Юрцевер А., Удел М., Чевхер В.
SIAM Scientific Computing (SISC), 2019
[arxiv][pdf][url][bib]
М. Уделл
SIAG/OPT Views and News, 2019
[pdf][url][слайды][bib][ видео]
Дж. Фан и М. Уделл
Компьютерное зрение и распознавание образов (CVPR), 2019
Устная презентация
[pdf][bib]
М. Уделл и О. Тул
Уделл и О. Тул
Журнал INFORMSInterfaces по прикладной аналитике (Журнал прикладной аналитики INFORMSInterfaces) , 2019
Второе место в конкурсе статей INFORMS Doing Good with Good OR Paper Competition
[pdf][url][bib]
Дж. Чен, Н. Каллус, X. Мао, Г. Свача, М. Уделл
FAT*: Конференция по справедливости, подотчетности и прозрачности, 2019 г.
[arxiv][pdf][slides][bib]
М. Уделл и А. Таунсенд
SIAM Journal on Mathematics of Data Science (SIMODS), 2019 г. Udell
Operations Research, 2019
[arxiv][url][bib]
Y. Sun, Y. Guo, J. Tropp, and M. Udell
NeurIPS Workshop on Relational Representation Learning, 2018
[arxiv][pdf][url][bib]
Дж. Тропп, А. Юрцевер, М. Уделл и В. Чевхер
Тропп, А. Юрцевер, М. Уделл и В. Чевхер
Калифорнийский технологический институт Технический отчет ACM 2018-01, 2018
]
К. Ян, Ю. Акимото, Д. Ким и М. Уделл
Семинар NeurIPS по автоматизированному машинному обучению, 2018 г.
[arxiv][pdf][url][bib]
С. Чжоу, С. Гупта и М. Уделл
Достижения в системах обработки нейронной информации, 2018 г.
Обзорная презентация
[arxiv][pdf][slides][bib]
Н. Каллус, X. Мао и М. Уделл
Достижения в системах обработки нейронной информации, 2018
[arxiv][code][bib]
L. Динг и М. Уделл
Крупномасштабная и распределенная оптимизация, 2018
[arxiv][pdf][bib]
Дж. Тропп, А. Юрцевер , М. Уделл и В. Чевхер
Тропп, А. Юрцевер , М. Уделл и В. Чевхер
Достижения в системах обработки нейронной информации, 2017 г.
[arxiv][pdf][url][bib]
М. Парадкар и М. Уделл
CVPR Workshop on Tensor Methods in Computer Vision, 2017
[pdf][bib ]. Презентация
[arxiv][pdf][url][слайды][нагрудник][видео]
X. Шен, С. Даймонд, М. Уделл, Ю. Гу и С. Бойд
Китайская конференция по управлению и принятию решений (CCDC), 2017 г.
Лучшая студенческая работа
[arxiv] [bib]
Дж. Тропп, А. Юрцевер, М. Уделл и В. Чевхер
SIAM Journal of Matrix Analysis and Applications (SIMAX), 2017
[arxiv ][pdf][url][bib]
Д. Дэвис, Б. Эдмундс и М. Уделл
Дэвис, Б. Эдмундс и М. Уделл
Достижения в системах обработки нейронной информации, 2016 г.
[arxiv][pdf][bib]
А. Шулер, В. Лю, Дж. Ван, А. Каллахан, М. Уделл, Д. Старк и Н. Шах
Тихоокеанский симпозиум по биокомпьютерам (PSB), 2016 г.
[pdf][url][нагрудник]
Н. Каллус и М. Уделл
Конференция ACM по экономике и вычислениям 2016 г., 2016 г.
[pdf][url][bib]
Н. Каллус и М. Уделл
Семинар ICML по вычислительным платформам для персонализации, 2016 г.
[arxiv][bib]
М. Уделл, К. Хорн, Р. Заде и С. Бойд
Основы и тенденции в машинном обучении, 2016
[arxiv][pdf][url][slides][code][bib]
М. Уделл и С. Бойд
Уделл и С. Бойд
Вычислительная оптимизация и приложения, 2016
[arxiv][pdf][url][bib]
M. Udell
Диссертация Стэнфордского университета, 2015
[pdf][code][bib]
H. Mehmood, M. Udell, and J. Cioffi
IEEE Global Communications Conference, 2015
[pdf][bib]
М. Уделл и С. Бойд
2015
[pdf][code][bib]
Э. Ли, М. Уделл и С. Вонг
Международный Конференция по акустике, речи и обработке сигналов (ICASSP), 2015 г.
[pdf][url][bib]
M. Udell and S. Boyd
Обзор биомедицинских вычислений, 2014
[pdf][url][bib]
Выпуклая оптимизация в Джулии
М. Уделл, К. Мохан, Д. Зенг, Дж. Хонг, С. Даймонд и С. Бойд
Уделл, К. Мохан, Д. Зенг, Дж. Хонг, С. Даймонд и С. Бойд
Семинар SC14 по высокопроизводительным техническим вычислениям на динамических языках, 2014 г.
[arxiv] [код] [нагрудник]
М. Уделл, К. Хорн, Р. Заде и С. Бойд
Семинар NeurIPS по распределенному машинному обучению и матричным вычислениям, 2014 г.
[pdf][code][bib]
М. Уделл и С. Бойд
2013
[pdf][code][ bib]
М. Уделл и Р. Такапуи
Семинар NeurIPS по крупномасштабному матричному анализу и выводу, 2013 г.
[pdf][bib]
P. LePendu, Y. Liu, S. Iyer, M. Udell, and N. Shah
Proceedings of the AMIA Summits on Translational Science, 2012
[pdf][url][bib] Статистические функции (scipy.
 stats) — SciPy v1.9.1 Manual
stats) — SciPy v1.9.1 Manual scipy.stats .
Распределения вероятностей
rv_continuous ( rv_discrete для дискретных дистрибутивов): rv_continuous ([momtype, a, b, xtol, …]) rv_discrete ([a, b, name, badvalue, …]) rv_histogram (гистограмма, *args, **kwargs) Непрерывное распределение
альфа 
угловой арксинус Аргус бета бета-прим Брэдфорд бор бор 12 Коши 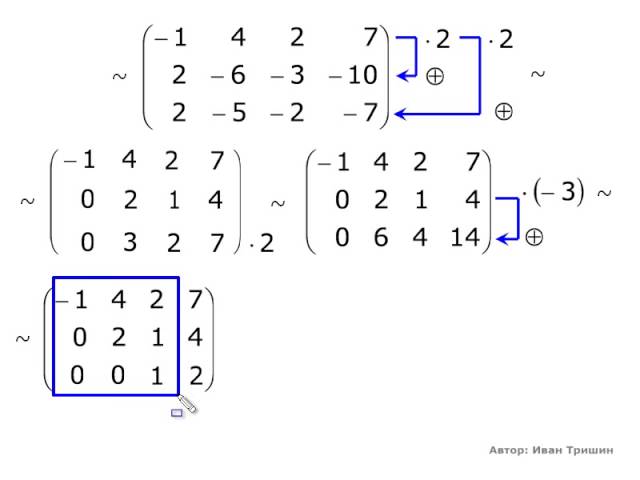
чи чи2 косинус хрустальный шар дгамма двейбулл Эрланг экспон экспоннорм 
экспонвейб экспонпоу ф срок службы фиск фолдкоши складная норма Генлогистика 
геннорм Генпарето генэкспон генестрим Гауссхайпер гамма генгамма Генхалфлогистика 
генгиперболический генинвгаусс гибрат гомперц гумбел_р гамбел_л полукоши полулогистика 
полунорма полугеннорм гипсекан инвгамма инвгаусс Инввейбулл Джонсонсб Джонсонсу 
каппа4 каппа3 ксоне кство кствобигн Лаплас лаплас_асимметричный сбор 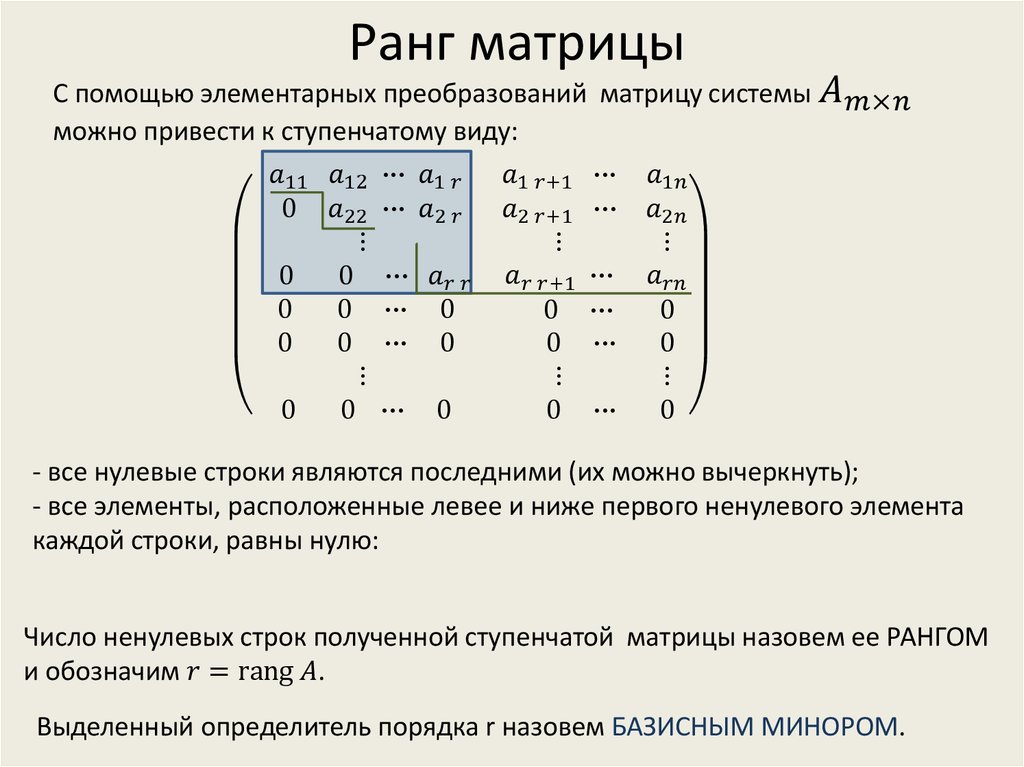
levy_l levy_stable логистика логгамма логлаплас логнорм Логуниформа ломакс 
Максвелл Мильке мойал накагами ncx2 НКФ нкт норма норминвгаусс 
Парето Пирсон3 степенной закон powerlognorm мощностьнорм рдист реле рис 
ресивергаусс полукруглая косой асимметрия студенческий_диапазон т трапециевидная треугольник 
транэкспон нормальная truncweibull_min тукейлямбда униформа вонмизес vonmises_line Вальд 
weibull_min weibull_max обертка Многомерные распределения
многомерный_нормальный матрица_нормальная Дирихле желание invwishart 
многочлен специальная_орто_группа орто_группа унитарная_группа случайная_корреляция multivariate_t multivariate_hypergeom Дискретные распределительные устройства
Бернулли 
бетабином бином Больцманн плаплас геом гипергеом регистратор нбином 
нчипергеом_фишер nchypergeom_wallenius нгипергеом планка Пуассон рэндинт Скеллам Юлесимон 
застежка-молния Зипфиан scipy.stats.mstats , которая работает для маскированных массивов. Сводная статистика
описать (a[ ось, ddof, смещение, nan_policy]) gmean (a[ ось, dtype, веса, nan_policy, …]) hmean (a[ ось, dtype, веса, nan_policy, …])
pmean (a, p, *[ ось, dtype, веса, …]) эксцесс (а[ ось, фишер, смещение, …]) режим (a[ ось, nan_policy, keepdims]) момент (a[ момент, ось, nan_policy, keepdims]) перекос (a[ ось, смещение, nan_policy, keepdims]) kstat (данные [ n, ось, nan_policy, keepdims])
kstatvar (данные [ n, ось, nan_policy, keepdims]) tmean (a[ пределы, включительно, ось]) tvar (a[пределы,включительно,ось,ddof]) tmin (a[ нижний предел, ось, включительно, …]) tmax (a[ верхний предел, ось, включительно, …]) tstd (a[ пределы, включительно, ось, ddof]) цем (а[ пределы, включительно, ось, ddof])
вариант (a[ ось, nan_policy, ddof, keepdims]) find_repeats (обр) уравновешивание_среднее (а, пропорциональный разрез [ ось]) gstd (a[ ось, ddof]) iqr (x[ ось, rng, масштаб, nan_policy, …]) sem (a[ ось, ddof, nan_policy]) bayes_mvs (данные [ альфа])
mvsdist (данные) энтропия (pk[ qk, основание, ось]) дифференциальная_энтропия (значения, *[ …]) median_abs_deviation (x[ ось, центр, …]) Частотная статистика
cumfreq (a[ numbins, defaultreallimits, Weights]) процентиль от оценки (a, оценка[ вид, nan_policy])
оценка в процентиле (a, на[ предел, …]) relfreq (a[ numbins, defaultreallimits, Weights]) binned_statistic (x, значения[ статистика, …]) binned_statistic_2d (x, y, values[ …]) binned_statistic_dd (выборка, значения[ …])
Корреляционные функции
f_oneway (*образцы[ ось]) александрговерн (*образцы[ nan_policy]) pearsonr (x, y, *[ альтернатива]) spearmanr (a[ b, ось, nan_policy, альтернатива]) точка бисериал (х, у) Кендаллтау (x, y[ initial_lexsort, . ..])
..]) weightedtau (x, y[ ранг, вес, добавка]) иногда (x[ y, альтернатива]) линейный регресс (x[ y, альтернатива]) уклоны зигеля (y[ x, метод]) склоны (у[ х, альфа, метод]) multiscale_graphcorr (x, y[ …])
Статистические тесты
ttest_1samp (a, popmean[ axis, nan_policy, …]) ttest_ind (a, b[ ось, equal_var, …]) ttest_ind_from_stats (mean1, std1, nobs1, …) ttest_rel (a, b[ ось, nan_policy, альтернатива]) хи-квадрат (f_obs[ f_exp, ddof, ось]) cramervonmises (rvs, cdf[ args])
cramervonmises_2samp (x, y[ метод]) power_divergence (f_obs[ f_exp, ddof, ось, …]) kstest (rvs, cdf[ args, N, альтернатива, метод]) ks_1samp (x, cdf[ args, альтернатива, метод]) ks_2samp (данные1, данные2[ альтернатива, метод]) epps_singleton_2samp (x, y[ t])
маннвитнею (x, y[ use_continuity, …]) tiecorrect (рангвалы) ранговые данные (a[ метод, ось]) ранговые суммы (x, y[ альтернатива, ось, …]) Уилкоксон (x[ y, zero_method, исправление, …]) kruskal (*samples[ nan_policy, ось, keepdims])
friedmanchisquare (*образцы) brunnermunzel (x, y[ альтернативный, …]) comb_pvalues (pvalues[ метод, веса]) jarque_bera (x) page_trend_test (данные[ рейтинг, …]) tukey_hsd (*аргументы)
ансари (x, y[ альтернатива]) Бартлетт (*образцы) levene (*образцы[ центр, пропорциональный разрез]) шапиро (х) Андерсон (x[ расст.]) anderson_ksamp (образцы [ средний ранг]) binom_test (x[ n, p, альтернатива])
биномтест (k, n[ p, альтернатива]) флюгер (*образцы[ центр, пропорциональный разрез]) median_test (*образцы[ связи, коррекция, …]) настроение (x, y[ ось, альтернатива]) skewtest (a[ ось, nan_policy, альтернатива]) kurtosistest (a[ ось, nan_policy, альтернатива]) normaltest (a[ ось, nan_policy])
Квази-Монте-Карло
scipy.stats.qmc ) Методы повторной выборки
начальная загрузка (данные, статистика, *[ n_resamples, …])
permutation_test (данные, статистика, *[ …]) monte_carlo_test (выборка, rvs, статистика, *) Функции скрытой статистики
scipy.stats.mstats ) mstats.plotting_positions
mstats.plotting_positions stats.mstats.linregress
stats.mstats.linregress stats.mstats.obriantransform
stats.mstats.obriantransform Другие статистические функции
Преобразования
boxcox (x[ lmbda, alpha, оптимизатор])
boxcox_normmax (x[ скобка, метод, оптимизатор]) boxcox_llf (lmb, данные) йоджонсон (x[ lmbda]) йеоджонсон_нормакс (x[ скобка]) yeojohnson_llf (lmb, данные) обриентрансформ (*образцы) сигмаклип (a[ низкий, высокий])
триммер (а, пропорциональный рез [ ось]) обрезка1 (а, пропорциональная обрезка [ хвост, ось]) змап (оценки, сравнение[ ось, ddof, nan_policy]) zscore (a[ ось, ddof, nan_policy]) gzscore (a, *[ ось, ddof, nan_policy]) Статистические расстояния
wasserstein_distance (u_values, v_values[ …])
energy_distance (u_values, v_values[ …]) Отбор проб
scipy.stats.sampling ) scipy.stats.sampling Генерация случайных переменных / инверсия CDF
rvs_ratio_uniforms (pdf, umax, vmin, vmax[ . ..])
..]) Распределительный фитинг
соответствие (расстояние, данные[ границы, предположение, оптимизатор]) Круговые статистические функции
среднеквадратичное (образцы [ высокий, низкий, ось, nan_policy]) circvar (образцы [ высокий, низкий, ось, nan_policy]) circstd (образцы [ высокий, низкий, ось, . ..])
..]) Функции таблицы непредвиденных обстоятельств
chi2_contingency (наблюдается[ коррекция, лямбда_]) contingency.crosstab (*args[ levels, sparse]) *args . contingency.expected_freq (наблюдается) непредвиденные расходы (a)
contingency.relative_risk (exposed_cases, …) contingency.association (наблюдаемый[ метод, …]) fisher_exact (таблица[ альтернатива]) barnard_exact (таблица[ альтернатива, пул, n]) boschloo_exact (таблица[ альтернатива, n]) Участковые тесты
ppcc_max (x[ скобка, расстояние])
ppcc_plot (x, a, b[ dist, plot, N]) probplot (x[ sparams, dist, fit, plot, rvalue]) boxcox_normplot (x, la, lb[ plot, N]) yeojohnson_normplot (x, la, lb[ plot, N]) Одномерная и многомерная оценка ядерной плотности
gaussian_kde (набор данных [ bw_method, веса])



 Сложение и вычитание
Сложение и вычитание Способы его нахождения. — КиберПедия
Способы его нахождения. — КиберПедия ..
.. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка.
Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка.



 Поставив найденные неизвестные в первое уравнение, получим x1= 1. Таким образом, получим решение системы: x1= 1, x2= 2, x3= 3.
Поставив найденные неизвестные в первое уравнение, получим x1= 1. Таким образом, получим решение системы: x1= 1, x2= 2, x3= 3.

 Очевидно, что эти векторы линейно независимы, и, следовательно, значение NULL равно nnn — числу свободных переменных.
Очевидно, что эти векторы линейно независимы, и, следовательно, значение NULL равно nnn — числу свободных переменных.