Чтобы привести дроби к общему знаменателю нужно. Записи с меткой «наименьший общий знаменатель»
Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.
Как найти наименьший общий знаменатель – понятие
Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Как найти наименьший общий знаменатель – примеры
Рассмотрим примеры нахождения НОЗ.
Вычислить: 3/5 + 2/15.
Решение (Последовательность действий):
- Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
- Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.

- Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель. Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
- Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
Ответ: 3/5 + 2/15 = 11/15.
Вычислить: 1/2 – 5/12 + 3/6
Решение (последовательность действий):
- Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
- Получим: 1/2 – 5/12 + 3/6 = ?/12.
- Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.

- Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.
Ответ: 1/2 – 5/12 + 3/6 = 7/12.
При сложении и вычитании алгебраический дробей с разными знаменателями сначала дроби приводят к общему знаменателю . Это значит, находят такой один знаменатель, который делится на исходный знаменатель каждой алгебраической дроби, входящей в состав данного выражения.
Как известно, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, отличное от нуля, то значение дроби не изменится. Это является основным свойством дроби. Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).
Например, дана такая сумма алгебраических дробей:
Требуется упростить выражение, т. е. сложить две алгебраические дроби. Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.
Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.
Для числовых коэффициентов и переменных НОК ищется отдельно. НОК(3, 2) = 6, а НОК(x, y) = xy. Далее найденные значения перемножаются: 6xy.
Теперь надо определить, на какой множитель надо умножить 3x, чтобы получить 6xy:
6xy ÷ 3x = 2y
Значит, при приведении первой алгебраической дроби к общему знаменателю ее числитель надо умножить на 2y (знаменатель уже был умножен при приведении к общему знаменателю). Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.
Таким образом, получаем:
Далее уже можно действовать как с дробями с одинаковыми знаменателями: складываются числители, а в знаменателе пишется один общий:
После преобразований получается упрощенное выражение, представляющее собой одну алгебраическую дробь, являющуюся суммой двух исходных:
Алгебраические дроби в исходном выражении могут содержать знаменатели, представляющие собой многочлены, а не одночлены (как в приведенном выше примере).
Здесь многочлен a 2 – b 2 можно представить как произведение (a – b)(a + b). Множитель 2a – 2b раскладывается как 2(a – b). Таким образом, общий знаменатель будет равен 2(a – b)(a + b).
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. ( см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (
Страница 1 из 1 1
Знаменателем арифметической дроби a / b называют число b, показывающее размеры долей единицы, из которых составлена дробь. Знаменателем алгебраической дроби A / B называют алгебраическое выражение B. Для выполнения арифметических действий с дробями их необходимо привести к наименьшему общему знаменателю.
Вам понадобится
- Для работы с алгебраическими дробями при нахождении наименьшего общего знаменателя необходимо знать методы разложения многочленов на множители.
Инструкция
Рассмотрим приведение к наименьшему общему знаменателю двух арифметических дробей n/m и s/t, где n, m, s, t – целые числа. Понятно, что эти две дроби можно привести к любому знаменателю, делящемуся на m и на t. Но стараются привести к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей m и t данных дробей. Наименьшее кратное (НОК) чисел – это наименьшее , делящееся одновременно на все заданные числа. Т.е. в нашем случае необходимо найти наименьшее общее кратное чисел m и t. Обозначается как НОК (m, t). Далее дроби умножаются на соответствующие : (n/m) * (НОК (m, t) / m), (s/t) * (НОК (m, t) / t).
Приведем нахождения наименьшего общего знаменателя трех дробей: 4/5, 7/8, 11/14. Для начала разложим знаменатели 5, 8, 14 : 5 = 1 * 5, 8 = 2 * 2 * 2 = 2^3, 14 = 2 * 7. 2. Для
2. Для
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п. 1.2. данного урока.
1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
Как легче найти общий знаменатель двух чисел. Способы нахождения наименьшего общего кратного, нок
Рассмотрим три способа нахождения наименьшего общего кратного.
Нахождение путём разложения на множители
Первый способ заключается в нахождении наименьшего общего кратного путём разложения данных чисел на простые множители.
Допустим, нам требуется найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:
Чтобы искомое число делилось на 99, на 30 и на 28, необходимо и достаточно, чтобы в него входили все простые множители этих делителей. Для этого нам необходимо взять все простые множители этих чисел в наибольшей встречающейся степени и перемножить их между собой:
2 2 · 3 2 · 5 · 7 · 11 = 13 860
Таким образом, НОК (99, 30, 28) = 13 860. Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Никакое другое число меньше 13 860 не делится нацело на 99, на 30 и на 28.
Чтобы найти наименьшее общее кратное данных чисел, нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с каким он встречается, и перемножить эти множители между собой.
Так как взаимно простые числа не имеют общих простых множителей, то их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 — взаимно простые. Поэтому
НОК (20, 49, 33) = 20 · 49 · 33 = 32 340.
Таким же образом надо поступать, когда отыскивается наименьшее общее кратное различных простых чисел. Например, НОК (3, 7, 11) = 3 · 7 · 11 = 231.
Нахождение путём подбора
Второй способ заключается в нахождении наименьшего общего кратного путём подбора.
Пример 1. Когда наибольшее из данных чисел делится нацело на другие данные числа, то НОК этих чисел равно большему из них. Например, дано четыре числа: 60, 30, 10 и 6. Каждое из них делится нацело на 60, следовательно:
НОК (60, 30, 10, 6) = 60
В остальных случаях, чтобы найти наименьшее общее кратное используется следующий порядок действий:
- Определяем наибольшее число из данных чисел.

- Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке их возрастания и проверяя делятся ли на полученное произведение остальные данные числа.
Пример 2. Дано три числа 24, 3 и 18. Определяем самое большое из них — это число 24. Далее находим числа кратные 24, проверяя делится ли каждое из них на 18 и на 3:
24 · 1 = 24 — делится на 3, но не делится на 18.
24 · 2 = 48 — делится на 3, но не делится на 18.
24 · 3 = 72 — делится на 3 и на 18.
Таким образом, НОК (24, 3, 18) = 72.
Нахождение путём последовательного нахождения НОК
Третий способ заключается в нахождении наименьшего общего кратного путём последовательного нахождения НОК.
НОК двух данных чисел равно произведению этих чисел, поделённого на их наибольший общий делитель.
Пример 1. Найдём НОК двух данных чисел: 12 и 8. Определяем их наибольший общий делитель: НОД (12, 8) = 4. Перемножаем данные числа:
Делим произведение на их НОД:
Таким образом, НОК (12, 8) = 24.
Чтобы найти НОК трёх и более чисел используется следующий порядок действий:
- Сначала находят НОК каких-нибудь двух из данных чисел.
- Потом, НОК найденного наименьшего общего кратного и третьего данного числа.
- Затем, НОК полученного наименьшего общего кратного и четвёртого числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример 2. Найдём НОК трёх данных чисел: 12, 8 и 9. НОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное числа 24 и третьего данного числа — 9. Определяем их наибольший общий делитель: НОД (24, 9) = 3. Перемножаем НОК с числом 9:
Делим произведение на их НОД:
Таким образом, НОК (12, 8, 9) = 72.
При сложении и вычитании алгебраический дробей с разными знаменателями сначала дроби приводят к общему знаменателю . Это значит, находят такой один знаменатель, который делится на исходный знаменатель каждой алгебраической дроби, входящей в состав данного выражения.
Как известно, если числитель и знаменатель дроби умножить (или разделить) на одно и то же число, отличное от нуля, то значение дроби не изменится. Это является основным свойством дроби. Поэтому, когда дроби приводят к общему знаменателю, по-сути умножают исходный знаменатель каждой дроби на недостающий множитель до общего знаменателя. При этом надо умножить на этот множитель и числитель дроби (для каждой дроби он свой).
Например, дана такая сумма алгебраических дробей:
Требуется упростить выражение, т. е. сложить две алгебраические дроби. Для этого в первую очередь надо привести слагаемые-дроби к общему знаменателю. Первым делом следует найти одночлен, который делится и на 3x и на 2y. При этом желательно, чтобы он был наименьший, т. е. найти наименьшее общее кратное (НОК) для 3x и 2y.
Для числовых коэффициентов и переменных НОК ищется отдельно. НОК(3, 2) = 6, а НОК(x, y) = xy. Далее найденные значения перемножаются: 6xy.
Теперь надо определить, на какой множитель надо умножить 3x, чтобы получить 6xy:
Значит, при приведении первой алгебраической дроби к общему знаменателю ее числитель надо умножить на 2y (знаменатель уже был умножен при приведении к общему знаменателю). Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.
Аналогично ищется множитель для числителя второй дроби. Он будет равен 3x.
Таким образом, получаем:
Далее уже можно действовать как с дробями с одинаковыми знаменателями: складываются числители, а в знаменателе пишется один общий:
После преобразований получается упрощенное выражение, представляющее собой одну алгебраическую дробь, являющуюся суммой двух исходных:
Алгебраические дроби в исходном выражении могут содержать знаменатели, представляющие собой многочлены, а не одночлены (как в приведенном выше примере). В таком случае, перед поиском общего знаменателя следует разложить знаменатели на множители (если это возможно). Далее общий знаменатель собирается из разных множителей. Если множитель есть в нескольких исходных знаменателях, то его берут единожды. Если множитель имеет разные степени в исходных знаменателях, то его берут с большей. Например:
Здесь многочлен a 2 – b 2 можно представить как произведение (a – b)(a + b). Множитель 2a – 2b раскладывается как 2(a – b). Таким образом, общий знаменатель будет равен 2(a – b)(a + b).
Таким образом, общий знаменатель будет равен 2(a – b)(a + b).
Для решения примеров с дробями необходимо уметь находить наименьший общий знаменатель. Ниже приведена подробная инструкция.
Как найти наименьший общий знаменатель – понятие
Наименьший общий знаменатель (НОЗ) простыми словами – это минимальное число, которое делится на знаменатели всех дробей данного примера. Другими словами его называют Наименьшим Общим Кратным (НОК). НОЗ используют только в том случае, если знаменатели у дробей различны.
Как найти наименьший общий знаменатель – примеры
Рассмотрим примеры нахождения НОЗ.
Вычислить: 3/5 + 2/15.
Решение (Последовательность действий):
- Смотрим на знаменатели дробей, убеждаемся, что они разные и выражения максимально сокращены.
- Находим наименьшее число, которое делится и на 5, и на 15. Таким числом будет 15. Таким образом, 3/5 + 2/15 = ?/15.
- Со знаменателем разобрались. Что будет в числителе? Помочь выяснить это нам поможет дополнительный множитель.
 Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1. - Выяснив дополнительный множитель, умножаем его на числители дробей и складываем получившиеся значения. 3/5 + 2/15 = (3*3+2*1)/15 = (9+2)/15 = 11/15.
Ответ: 3/5 + 2/15 = 11/15.
Если в примере складываются или вычитаются не 2, а 3 или больше дробей, то НОЗ нужно искать уже для стольких дробей, сколько дано.
Вычислить: 1/2 – 5/12 + 3/6
Решение (последовательность действий):
- Находим наименьший общий знаменатель. Минимальным числом, делящимся на 2, 12 и 6 будет 12.
- Получим: 1/2 – 5/12 + 3/6 = ?/12.
- Ищем дополнительные множители. Для 1/2 – 6; для 5/12 – 1; для 3/6 – 2.
- Умножаем на числители и приписываем соответствующие знаки: 1/2 – 5/12 + 3/6 = (1*6 – 5*1 + 2*3)/12 = 7/12.
Ответ: 1/2 – 5/12 + 3/6 = 7/12.
Умножение «крест-накрест»
Метод общих делителей
Задача. Найдите значения выражений:
Задача. Найдите значения выражений:
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест».
Общий знаменатель дробей
Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Смотрите также:
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.

- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Как найти наименьший общий знаменатель
Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю?
Общий знаменатель, понятие и определение.
Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты.
 Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей.
Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Смотрите также:
Приведение дробей к общему знаменателю
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется. А искомые числа, «выравнивающие» знаменатели, называются.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа.
Приведение дробей к общему знаменателю
Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.

- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20: 5=4). Для 2-й дроби дополнительный множитель равен 5 (20: 4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Мы привели данные дроби к наименьшему общему знаменателю (20 ).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8: 4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8 ).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей
). Находим НОК(16; 20)=2 4 · 5=16· 5=80. Дополнительный множитель для 1-й дроби равен 5 (80: 16=5). Дополнительный множитель для 2-й дроби равен 4 (80: 20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80 ).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30: 5=6), дополнительный множитель ко 2-й дроби равен 5 (30: 6=5), дополнительный множитель к 3-ей дроби равен 2 (30: 15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30 ).
Страница 1 из 1 1
Приведение дробей к общему знаменателю. Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
Материал этой статьи объясняет, как найти наименьший общий знаменатель и как привести дроби к общему знаменателю . Сначала даны определения общего знаменателя дробей и наименьшего общего знаменателя, а также показано, как найти общий знаменатель дробей. Дальше приведено правило приведения дробей к общему знаменателю и рассмотрены примеры применения этого правила. В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
В заключение разобраны примеры приведения трех и большего количества дробей к общему знаменателю.
Навигация по странице.
Что называют приведением дробей к общему знаменателю?
Теперь мы можем сказать, что такое приведение дробей к общему знаменателю. Приведение дробей к общему знаменателю – это умножение числителей и знаменателей данных дробей на такие дополнительные множители, что в результате получаются дроби с одинаковыми знаменателями.
Общий знаменатель, определение, примеры
Теперь пришло время дать определение общего знаменателя дробей.
Иными словами, общим знаменателем некоторого набора обыкновенных дробей является любое натуральное число, которое делится на все знаменатели данных дробей.
Из озвученного определения следует, что данный набор дробей имеет бесконечно много общих знаменателей, так как существует бесконечное множество общих кратных всех знаменателей исходного набора дробей.
Определение общего знаменателя дробей позволяет находить общие знаменатели данных дробей. Пусть, к примеру, даны дроби 1/4
и 5/6
, их знаменатели равны 4
и 6
соответственно. Положительными общими кратными чисел 4
и 6
являются числа 12
, 24
, 36
, 48
, … Любое из этих чисел является общим знаменателем дробей 1/4
и 5/6
.
Пусть, к примеру, даны дроби 1/4
и 5/6
, их знаменатели равны 4
и 6
соответственно. Положительными общими кратными чисел 4
и 6
являются числа 12
, 24
, 36
, 48
, … Любое из этих чисел является общим знаменателем дробей 1/4
и 5/6
.
Для закрепления материала рассмотрим решение следующего примера.
Пример.
Можно ли дроби 2/3 , 23/6 и 7/12 привести к общему знаменателю 150 ?
Решение.
Для ответа на поставленный вопрос нам нужно выяснить, является ли число 150 общим кратным знаменателей 3 , 6 и 12 . Для этого проверим, делится ли 150 нацело на каждое из этих чисел (при необходимости смотрите правила и примеры деления натуральных чисел , а также правила и примеры деления натуральных чисел с остатком): 150:3=50 , 150:6=25 , 150:12=12 (ост. 6) .
Итак, 150 не делится нацело на 12 , следовательно, 150 не является общим кратным чисел 3 , 6 и 12 . Следовательно, число 150 не может быть общим знаменателем исходных дробей.
Ответ:
Нельзя.
Наименьший общий знаменатель, как его найти?
В множестве чисел, являющихся общими знаменателями данных дробей, существует наименьшее натуральное число , которое называют наименьшим общим знаменателем. Сформулируем определение наименьшего общего знаменателя данных дробей.
Определение.
Наименьший общий знаменатель – это наименьшее число, из всех общих знаменателей данных дробей.
Осталось разобраться с вопросом, как найти наименьший общий делитель.
Так как является наименьшим положительным общим делителем данного набора чисел, то НОК знаменателей данных дробей представляет собой наименьший общий знаменатель данных дробей.
Таким образом, нахождение наименьшего общего знаменателя дробей сводится к знаменателей этих дробей. Разберем решение примера.
Пример.
Найдите наименьший общий знаменатель дробей 3/10 и 277/28 .
Решение.
Знаменатели данных дробей равны 10
и 28
. Искомый наименьший общий знаменатель находится как НОК чисел 10
и 28
. В нашем случае легко : так как 10=2·5
, а 28=2·2·7
, то НОК(15, 28)=2·2·5·7=140
.
В нашем случае легко : так как 10=2·5
, а 28=2·2·7
, то НОК(15, 28)=2·2·5·7=140
.
Ответ:
140 .
Как привести дроби к общему знаменателю? Правило, примеры, решения
Обычно обыкновенные дроби приводят к наименьшему общему знаменателю. Сейчас мы запишем правило, которое объясняет, как привести дроби к наименьшему общему знаменателю.
Правило приведения дробей к наименьшему общему знаменателю состоит из трех шагов:
- Во-первых, находится наименьший общий знаменатель дробей.
- Во-вторых, для каждой дроби вычисляется дополнительный множитель, для чего наименьший общий знаменатель делится на знаменатель каждой дроби.
- В-третьих, числитель и знаменатель каждой дроби умножается на ее дополнительный множитель.
Применим озвученное правило к решению следующего примера.
Пример.
Приведите дроби 5/14 и 7/18 к наименьшему общему знаменателю.
Решение.
Выполним все шаги алгоритма приведения дробей к наименьшему общему знаменателю.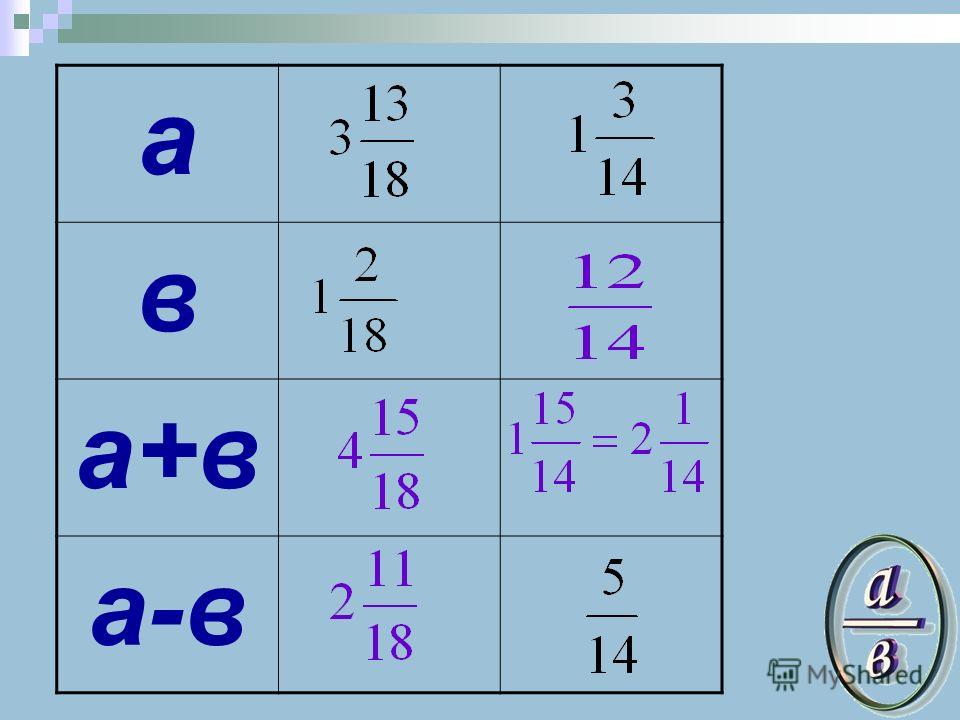
Сначала находим наименьший общий знаменатель, который равен наименьшему общему кратному чисел 14 и 18 . Так как 14=2·7 и 18=2·3·3 , то НОК(14, 18)=2·3·3·7=126 .
Теперь вычисляем дополнительные множители, с помощью которых дроби 5/14 и 7/18 будут приведены к знаменателю 126 . Для дроби 5/14 дополнительный множитель равен 126:14=9 , а для дроби 7/18 дополнительный множитель равен 126:18=7 .
Осталось умножить числители и знаменатели дробей 5/14 и 7/18 на дополнительные множители 9 и 7 соответственно. Имеем и .
Итак, приведение дробей 5/14 и 7/18 к наименьшему общему знаменателю завершено. В итоге получились дроби 45/126 и 49/126 .
Схема приведения к общему знаменателю
- Нужно определить, какое будет наименьшее общее кратное для знаменателей дробей. Если Вы имеете дело со смешанным или целым числом, то его нужно сначала превратить в дробь, а уже потом определять наименьшее общее кратное. Чтобы целое число превратить в дробь, нужно в числителе записать само это число, а в знаменателе — единицу.
 Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5. - После этого необходимо найти дополнительный множитель, который определяется делением НОЗ на знаменатель каждой дроби.
- Последний шаг — умножение дроби на дополнительный множитель.
Важно запомнить, что приведение к общему знаменателю нужно не только для сложения или вычитания. Для сравнения нескольких дробей с разными знаменателями также необходимо сначала привести каждую из них к общему знаменателю.
Приведение дробей к общему знаменателю
Для того чтобы понять, как привести к общему знаменателю дробь, необходимо разобраться в некоторых свойствах дробей. Так, важным свойством, используемым для приведения к НОЗ, является равенство дробей. Другими словами, если числитель и знаменатель дроби умножается на число, то в результате получает дробь, равная предыдущей.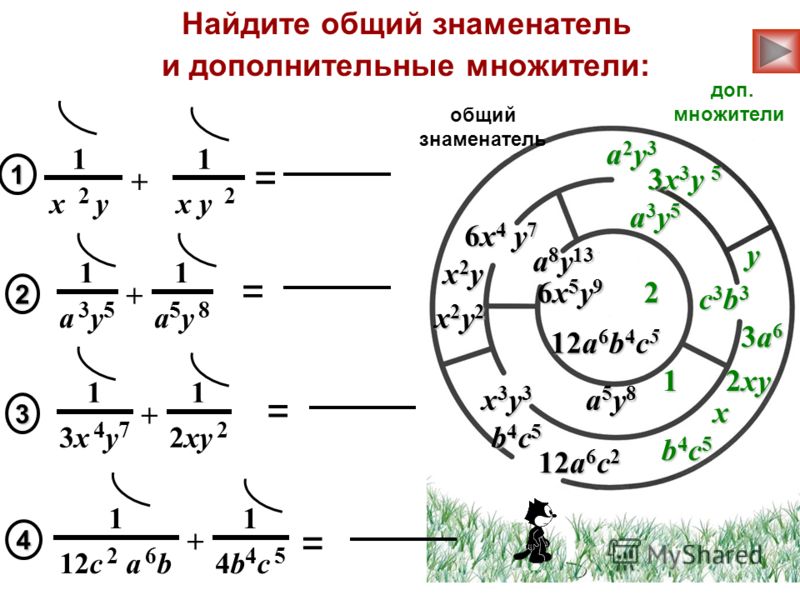 В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
В качестве примера приведём следующий пример. Для того чтобы привести дроби 5/9 и 5/6 к наименьшему общему знаменателю, нужно выполнить следующие действия:
- Сначала находим наименьшее общее кратное знаменателей. В данном случае для чисел 9 и 6 НОК будет равно 18.
- Определяем дополнительные множители для каждой из дробей. Делается это следующим образом. Делим НОК на знаменатель каждой из дробей, в результате получаем 18: 9 = 2, а 18: 6 = 3. Эти числа и будут дополнительными множителями.
- Приводим две дроби к НОЗ. Умножая дробь на число, нужно умножить и числитель, и знаменатель. Дробь 5/9 можно умножить на дополнительный множитель 2, в результате чего получится дробь, равная данной, — 10/18. То же самое делаем со второй дробью: 5/6 умножаем на 3, в результате чего получаем 15/18.
Как видим из представленного выше примера, обе дроби были приведены к наименьшему общему знаменателю. Чтобы окончательно разобраться в том, как найти общий знаменатель, необходимо освоить еще одно свойство дробей. Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
Оно заключается в том, что числитель и знаменатель дроби можно сократить на одно и то же число, которое называется общим делителем. Например, дробь 12/30 можно сократить до 2/5, если разделить ее на общий делитель — число 6.
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
Получим:
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:
Заметим, что 84: 21 = 4; 72: 12 = 6 . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2 . Это число намного меньше произведения 8 · 12 = 96 .
Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a ; b ) . Например, НОК(16; 24) = 48 ; НОК(8; 12) = 24 .
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3 . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4 . Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей.
 Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.
Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
На этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачи по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, вспомним о взаимно простых числах. Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .
Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три — это дополнительный множитель для первой дроби, а два — для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби — 4, для второй — 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель — 24. Дополнительные множители, соответственно, — 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. — ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
Наименьший общий знаменатель
Эта статья про математику. Для компьютеров см. Наименьший общий знаменатель (компьютеры).
Для компьютеров см. Наименьший общий знаменатель (компьютеры).
В математика, то наименьший общий знаменатель или наименьший общий знаменатель (сокращенно ЖК-дисплей) это наименьшее общее кратное из знаменатели набора фракции. Это упрощает сложение, вычитание и сравнение дробей.
Содержание
- 1 Описание
- 2 Роль в арифметике и алгебре
- 3 Практическое использование
- 4 Разговорное использование
- 5 Смотрите также
- 6 использованная литература
Описание
Самый низкий общий знаменатель набора фракции это наименьшее число, которое является множественный всех знаменателей: их наименьшее общее кратное. Произведение знаменателей всегда является общим знаменателем, например:
- 12+23=36+46=76{ displaystyle { frac {1} {2}} + { frac {2} {3}} ; = ; { frac {3} {6}} + { frac {4} {6}} ; = ; { frac {7} {6}}}
но это не всегда наименьший общий знаменатель, например:
- 512+1118=1536+2236=3736{ displaystyle { frac {5} {12}} + { frac {11} {18}} ; = ; { frac {15} {36}} + { frac {22} {36}} ; = ; { frac {37} {36}}}
Здесь 36 — наименьшее общее кратное 12 и 18. {2} cd}}}
{2} cd}}}
Некоторые методы расчета ЖКД приведены на Наименьшее общее кратное # Вычисление наименьшего общего кратного.
Роль в арифметике и алгебре
Одна и та же фракция может быть выражена в разных формах. Если соотношение числителя и знаменателя одинаково, дроби представляют собой одно и то же число. Например:
- 23=69=1218=144216=200,000300,000{ displaystyle { frac {2} {3}} = { frac {6} {9}} = { frac {12} {18}} = { frac {144} {216}} = { frac {200,000} {300,000}}}
потому что все они умножаются на 1 и записываются в виде дроби:
- 23=23×33=23×66=23×7272=23×100,000100,000.{ displaystyle { frac {2} {3}} = { frac {2} {3}} times { frac {3} {3}} = { frac {2} {3}} times { frac {6} {6}} = { frac {2} {3}} times { frac {72} {72}} = { frac {2} {3}} times { frac {100 000 } {100,000}}.}
Обычно проще всего складывать, вычитать или сравнивать дроби, когда каждая выражается с одним и тем же знаменателем, называемым «общим знаменателем». Например, числители дробей с общими знаменателями можно просто сложить, так что 512+612=1112{ displaystyle { frac {5} {12}} + { frac {6} {12}} = { frac {11} {12}}} и это 512<1112{ displaystyle { frac {5} {12}} , поскольку каждая дробь имеет общий знаменатель 12. Без вычисления общего знаменателя не очевидно, что 512+1118{ displaystyle { frac {5} {12}} + { frac {11} {18}}} равно, или 512{ displaystyle { frac {5} {12}}} больше или меньше чем 1118{ displaystyle { frac {11} {18}}}. Подойдет любой общий знаменатель, но обычно желателен наименьший общий знаменатель, поскольку он максимально упрощает остальные вычисления.[2]
Например, числители дробей с общими знаменателями можно просто сложить, так что 512+612=1112{ displaystyle { frac {5} {12}} + { frac {6} {12}} = { frac {11} {12}}} и это 512<1112{ displaystyle { frac {5} {12}} , поскольку каждая дробь имеет общий знаменатель 12. Без вычисления общего знаменателя не очевидно, что 512+1118{ displaystyle { frac {5} {12}} + { frac {11} {18}}} равно, или 512{ displaystyle { frac {5} {12}}} больше или меньше чем 1118{ displaystyle { frac {11} {18}}}. Подойдет любой общий знаменатель, но обычно желателен наименьший общий знаменатель, поскольку он максимально упрощает остальные вычисления.[2]
Практическое использование
ЖК-дисплей имеет множество практических применений, таких как определение количества объектов двух разной длины, необходимых для выравнивания их в ряд, который начинается и заканчивается в одном месте, например, в кирпичная кладка, черепица, и мозаика. Это также полезно при планировании графики работы с сотрудниками с у выходные каждые Икс дней. «наименьший общий знаменатель», Словарь английского языка Коллинза (по состоянию на 21 февраля 2018 г.)
«наименьший общий знаменатель», Словарь английского языка Коллинза (по состоянию на 21 февраля 2018 г.)
Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя — верхней части, и знаменателя — нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34 умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.
Приведение дробей к общему знаменателюПриведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменательОбщий знаменатель дробей — это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменательМожно ди дроби 13, 216, 512 привести к общему знаменателю, который равен 150?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12. Другими словами, число 150 должно без остатка делиться на 3, 6, 12. Проверим:
150÷3=50, 150÷6=25, 150÷12=12,5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменательНужно найти наименьший общий знаменатель для дробей 110 и 12728.
Ищем НОК чисел 10 и 28. Разложим их на простые множители и получим:
10=2·528=2·2·7НОК(15, 28)=2·2·5·7=140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель.
 Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби. - Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателюЕсть дроби 314 и 518. Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14=2·718=2·3·3НОК(14, 18)=2·3·3·7=126
Вычисляем дополнительные множители для каждой дроби. Для 314 дополнительный множитель находится как 126÷14=9, а для дроби 518 дополнительный множитель будет равен 126÷18=7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3·914·9=27126, 5·718·7=35126.
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателюПривести дроби 32, 56,38 и 1718 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
НОК(2, 6)=6НОК(6, 8)=24НОК(24, 18)=72НОК(2, 6, 8, 18)=72
Далее вычислим дополнительные множители для каждой дроби.
Для 32 дополнительный множитель равен 72÷2= 36, для 56 дополнительный множитель равен 72÷6= 12, для 38 дополнительный множитель равен 72÷8= 9, наконец, для 1718 дополнительный множитель равен 72÷18= 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
32·36=1087256·12=607238·9=27721718·4=6872
Как привести дробь к наименьшему общему знаменателю (пример)
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
ЖК-калькулятор.
 Найти наименьший общий знаменатель
Найти наименьший общий знаменательСоздано Ханной Памула, кандидатом наук
Отредактировано Домиником Черниа, кандидатом наук и Джеком Боуотером
Последнее обновление: 06 апреля 2022 г.
Содержание:- Какой наименьший общий знаменатель? ЖК по математике
- Как найти наименьший общий знаменатель?
- Способ 1. Список кратных
- Способ 2. Использование простой факторизации
- Метод 3. Использование наибольшего общего делителя (множителя)
- Метод 4. Чертежная таблица/сетка/лестница/торт
- Наименьший общий знаменатель на практике
- Как пользоваться ЖК-калькулятором?
- Реальные приложения для поиска наименьшего общего знаменателя
Добро пожаловать в ЖК-калькулятор — интуитивно понятный инструмент, который поможет вам найти наименьший общий знаменатель. Все, что вам нужно сделать, это ввести до пяти дробей и мы рассчитаем LCD и эквивалентные дроби с этим знаменателем.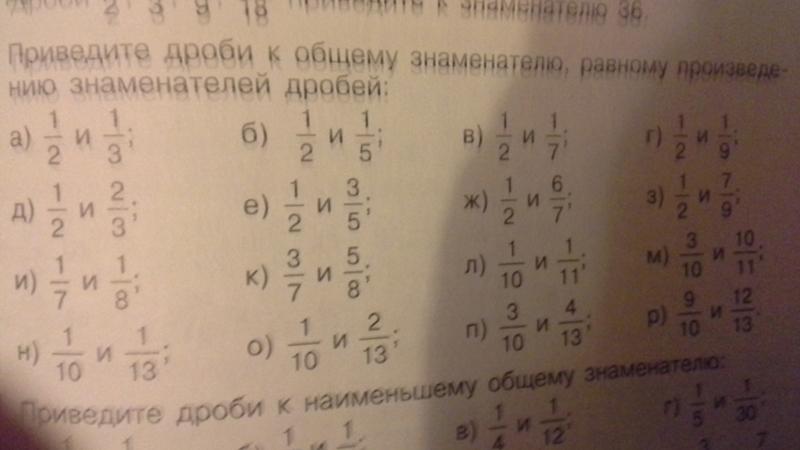 Довольно просто, да? 😉
Довольно просто, да? 😉
Однако, если вы хотите сначала узнать , что такое наименьший общий знаменатель или , как найти наименьший общий знаменатель вручную ✍️ — мы тоже здесь для вас. Прокрутите вниз и прочитайте нашу короткую и информативную статью о наименьшем общем знаменателе!
Какой наименьший общий знаменатель? LCD в математике
Наименьший общий знаменатель, также известный как наименьший общий знаменатель, равен наименьшему общему кратному знаменателей данного набора .
Обычно мы ищем наименьший общий знаменатель, когда хотим выполнить операцию над дробями, например, сложить дроби (и вычесть) или сравнить дроби. Например:
- ЖК-дисплей 1 / 2 и 1 / 3 равен 6, поскольку НОК(2, 3) = 6;
- Зная ЖК, можно найти дроби эквивалентные вашим 1 / 2 и 1 / 3 , при этом знаменатель равен найденному ЖК:
1 / 2 = 3 / 6
1 / 3 = 2 / 6 .
- Теперь легко складывать дроби, вычитать их или сравнивать:
- 3 / 6 + 2 / 6 = 5 / 6
- 3 / 6 — 2 / 6 = 1 / 6
- 3 / 6 > 2 / 6
Однако, если вы только что загуглили вопрос « Что такое LCD? » и искали определение с наименьшим общим знаменателем, результаты поиска могут вас немного удивить 😮. Аббревиатура LCD также означает жидкокристаллический дисплей — тип дисплея, который мы используем в наших компьютерах 💻, экранах телевизоров 📺, цифровых камерах 📽️, часах ⌚ и смартфонах 📱. Так что в следующий раз попробуй « Что такое ЖК-дисплей по математике? » вместо этого 😉
Как найти наименьший общий знаменатель?
Ну, самый простой и простой способ — использовать наш ЖК-калькулятор — именно поэтому вы здесь, верно? 😉
Шутки в сторону — мы очень ценим это вы хотели бы узнать как найти наименьший общий знаменатель . Есть несколько методов, и мы опишем четыре из них здесь. Итак, давайте представим их на относительно простом примере:
Есть несколько методов, и мы опишем четыре из них здесь. Итак, давайте представим их на относительно простом примере:
Предположим, что у нас есть три фракции: 1 / 2 , 3 / 8 и / 12 707070707070707070707070707070707070707070707070707070707070707070707070707070707070707070. и / 12 . Какова стоимость ЖК? Какие равные дроби имеют одинаковые знаменатели?
Во-первых, нам нужно найти наименьший общий знаменатель наших дробей. Прочитайте о четырех методах ниже и выберите тот, который вам больше нравится.
Способ 1. Список кратных
Список кратных — это метод грубой силы. Это может быть полезно в особых случаях, например, если числа относительно малы. Итак, как найти наименьший общий знаменатель? Составьте список кратных каждого числа, пока не найдете первое общее кратное всех чисел :
- кратное 2:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 , 26, 28.
..
- Кратность 12:
12, 24 , 36, 48, 60…
- Кратность 8:
8, 16, 24 , 32, 40, 48 …
Обычно это не рекомендуемый метод, представьте себе перечисление общих знаменателей 2 и 1000 — это не имеет особого смысла, не так ли? 🙂
Метод 2. Использование простой факторизации
Еще один способ найти наименьший общий знаменатель — метод простой факторизации:
#1 Запишите все числа как произведение их простых множителей :
- Простая факторизация 2:
2 = 2¹
- Разложение числа 12 на простые множители:
2 * 2 * 3 = 2² * 3¹
- Разложение 8 на простые множители:
2 * 2 * 2 = 2³
#2 Найдите максимальную степень каждого простого числа:
2³,3¹
#3 Умножьте эти значения вместе:
2³ * 3¹ = 24
Метод 3.
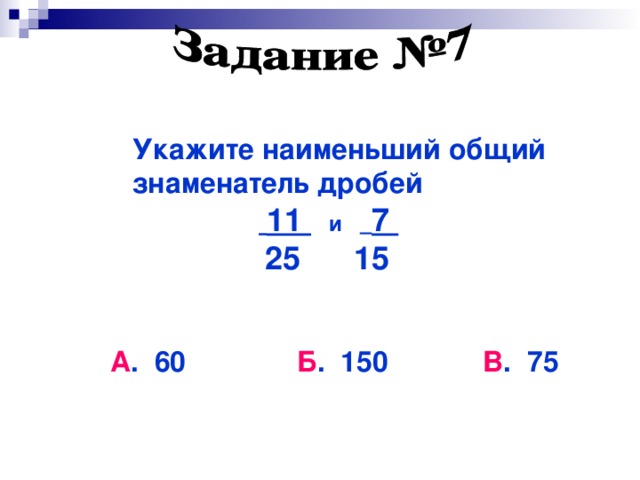 Использование наибольшего общего делителя (множителя)
Использование наибольшего общего делителя (множителя)Вы можете рассчитать НОД по значению наибольшего общего делителя (НОД):
НЦП(a,b) = |a * b| / GCF(a,b)
, где |a * b| является абсолютным значением a * b .
#1 Подставляем первые два числа (2 и 8) в формулу:
LCD(2, 8) = |2 * 8| / GCF(2, 8)
мы знаем, что GCF(2, 8) = 2 поэтому:
LCD(2, 8) = 16 / 2 = 8
#2 Найдите LCD результата предыдущего шага (т. е. 8) и следующего числа в списке, 12:
LCD(12, 8) = |12 * 8| / GCF(12, 8)
вычисляем, что GCF(12, 8) = 4 поэтому:
LCD(12, 8) = 96 / 4 = 24
Метод 4. Таблица для рисования/ сетка/лесенка/торт
Последний метод — метод лестницы. Многим учащимся нравится этот прием, поэтому попробуйте его, и, возможно, у вас появится новый фаворит:
#1 Начните с написания всех ваших чисел рядом друг с другом:
| 2 | 8 | 12 |
#2 Найдите простое число, на которое можно разделить не менее двух ваших чисел (без остатка).
Запишите это простое число слева:
| 2 | 2 | 8 | 12 |
#3 Разделите свои исходные номера на основные и напишите целые по исходным номерам. Если ваш номер не является равномерным делительным, просто запишите это число снова:
| 2 | 2 | 8 | 12 | ||||
| 9000 4000 | 4000 4 | ||||||
| 9000 9000 | |||||||
| 9000 9000 | |||||||
| 9000 9000 | |||||||
| 9000 9000 | |||||||
| .0004 6 |
#4 Repeat until the whole table is complete:
| 2 | 2 | 8 | 12 |
| 2 | 1 | 4 | 6 |
| 2 | 1 | 2 | 3 |
| 1 | 1 | 3 |
#5 Найдите ЖК-дисплей, умножив все значения в оранжевой букве «L» вокруг вашего стола/торта:
2 * 2 * 2 * 1 * 1 * 3 = 24 910
Воспользуйтесь нашим калькулятором LCM, где калькулятор показывает, как найти наименьший общий знаменатель - A. K.A. наименьшее общее кратное. Потому что, в общем, найти LCM и LCD — это почти то же самое, что и !
K.A. наименьшее общее кратное. Потому что, в общем, найти LCM и LCD — это почти то же самое, что и !
Наименьший общий знаменатель на практике
Теперь, когда вы знаете значение LCD, вы можете перейти ко второму шагу - найти дроби , эквивалентные вашим основным дробям, но с тем же знаменателем - 24 в нашем случае:
-
1 / 2 = ? / 24, чтобы получить 24 в знаменателе, умножьте дробь на 12 / 12 (потому что 24 / 2 = 12):
1 / 2 = 1 / 2 ⋅ 12 / 12 = 12 / 249
-
3 / 8 = ? / 24, умножьте на 3 / 3 , чтобы получить 24 в качестве нижнего числа:
3 / 8 = 3 / 8 ⋅ 3 / 3 = 9 / 20960
-
11 / 12 = ? / 24, так как 24 / 12 = 2, умножьте дробь на 2 / 2 :
11 / 12 = 11 / 12 ⋅ 2 / 2 = 22 / 24
И все! После прочтения вы (надеюсь) поняли, что такое наименьший общий знаменатель, и узнали о четырех методах, которые могут помочь вам найти НОК в математике. И что теперь? Пришло время проверить, как работает ЖК-калькулятор!
И что теперь? Пришло время проверить, как работает ЖК-калькулятор!
Как пользоваться ЖК-калькулятором?
Ознакомьтесь с этим пошаговым руководством, если у вас есть какие-либо сомнения относительно того, как использовать наш инструмент:
- Выберите тип дроби . Если вам нужны простые дроби, оставьте как есть. Если хотя бы один из ваших номеров является смешанным числом (или целым числом), выберите вариант «смешанный номер».
- Введите дроби . Допустим, мы хотим найти ЖК дробей 1 / 4 и 11 / 14 . Для первой дроби введите 1 в качестве числителя и 4 в качестве знаменателя; для второго числитель равен 11, а знаменатель равен 14.
- Успокойся, расслабься и прочитай результат - ЖК-калькулятор сделал свое дело и нашел наименьший общий знаменатель ! Это 28.
Кроме того, инструмент отображает эквивалентные дроби со значением на ЖК-дисплее в качестве знаменателя:
- 1 / 4 = 7 / 28 ; и
- 11 / 14 = 22 / 28 .
- При желании можно даже выбрать вариант "пошаговое решение" . Из него вы узнаете некоторые подробности о том, как найти LCD по математике!
Применение наименьшего общего знаменателя в реальной жизни
Теперь, когда вы знаете, что такое наименьший общий знаменатель и как его найти, давайте поговорим о некоторых ЖК-приложения . Мы почти слышим, как вы стонете "Но где я когда-либо буду использовать его?" Не беспокойтесь - наименьший общий знаменатель полезен во многих жизненных ситуациях. Вы можете использовать его в любое время, когда хотите «выровнять» две или более вещи разной длины, например:
- В строительстве 🏗️, например. при возведении стены из кирпича или работе с плиткой разной длины;
- В музыке 🎵 - при вычислении наименьшего количества долей для комбинированного ритма; и
- При организации графиков работы 📅 - например, в ситуации, когда у одного сотрудника выходной каждые 6 дней, а у другого каждые 4 дня, можно рассчитать, когда оба они отсутствуют.

Hanna Pamuła, PhD candidate
Fraction form
Values (enter up to 5 fractions)
1 st fraction
Numerator (n₁)
Denominator (d₁)
2 nd fraction
Числитель (n₂)
Знаменатель (d₂)
Наименьший общий знаменатель
Пошаговое решение?
Посмотрите 17 похожих калькуляторов дробей 🍕
Складывание дробейСравнение дробейДесятичная дробь… Еще 14
Что такое наибольший общий делитель и наименьшее общее кратное?
TranscriptFAQsFact SheetPractice
Привет! Добро пожаловать в это видео, посвященное наименьшему общему кратному и наибольшему общему множителю!
Как вы знаете, бывают случаи, когда нам приходится алгебраически «настраивать» то, как выглядит число или уравнение, чтобы продолжить нашу математическую работу. Для этого мы можем использовать наибольший общий делитель и наименьшее общее кратное. наибольший общий делитель (НОК) — это наибольшее число, являющееся делителем двух или более чисел, а наименьшее общее кратное (НОК) — это наименьшее число, кратное двум или более числам.
Для этого мы можем использовать наибольший общий делитель и наименьшее общее кратное. наибольший общий делитель (НОК) — это наибольшее число, являющееся делителем двух или более чисел, а наименьшее общее кратное (НОК) — это наименьшее число, кратное двум или более числам.
Чтобы понять, насколько полезны эти понятия, давайте рассмотрим сложение дробей. Прежде чем мы сможем складывать дроби, мы должны убедиться, что знаменатели одинаковы, создав эквивалентную дробь:
\(\frac{2}{3}+\frac{1}{6} \rightarrow \frac{2 }{3} \times \frac{2}{2}\)\(+\frac{1}{6} \rightarrow \frac{4}{6} +\frac{1}{6}=\frac{ 5}{6}\)
В этом примере необходимо определить наименьшее общее кратное 3 и 6. Другими словами, «Каково наименьшее число, на которое можно разделить без остатка и 3, и 6?» Немного подумав, мы понимаем, что 6 является наименьшим общим кратным, потому что 6, деленное на 3, равно 2, а 6, деленное на 6, равно 1. Затем дробь \(\frac{2}{3}\) приводится к эквиваленту дробь \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2. Теперь можно сложить две дроби с общими знаменателями, чтобы получить окончательное значение \(\frac{5}{6}\) .
Затем дробь \(\frac{2}{3}\) приводится к эквиваленту дробь \(\frac{4}{6}\) путем умножения числителя и знаменателя на 2. Теперь можно сложить две дроби с общими знаменателями, чтобы получить окончательное значение \(\frac{5}{6}\) .
Найдите наименьшее общее кратное
В контексте сложения или вычитания дробей наименьшее общее кратное называется наименьшим общим знаменателем .
Как правило, вам нужно определить число, большее или равное двум или более числам, чтобы найти их наименьшее общее кратное.
Важно отметить, что существует несколько способов определения наименьшего общего кратного. Один из способов — просто перечислить все кратные рассматриваемых значений и выбрать наименьшее общее значение, как показано здесь:
Наименьшее общее кратное чисел 8, 4, 6
\(8\стрелка вправо 8,16,24,32,40,48\)
\(4\стрелка вправо 4,8,12,16,20,24, 28,32\)
\(6\стрелка вправо 6,12,18,24,30,36\)
Это показывает, что наименьшее общее кратное чисел 8, 4 и 6 равно 24, поскольку оно является наименьшим число, на которое можно поровну разделить 8, 4 и 6.
Другой распространенный метод включает первичную факторизацию каждого значения. Помните, что простое число делится только на 1 и само на себя.
После определения простых множителей перечислите общие множители один раз, а затем умножьте их на остальные оставшиеся простые множители. Результатом является наименьшее общее кратное:
\(30=2\умножить на 2\умножить на 3\умножить на 3\)
\(90=2\умножить на 3\умножить на 3\умножить на 5\)\(\text {НОК}=2\умножить на 3\умножить на 3\умножить на 2\умножить на 5\)
Наименьшее общее кратное также можно найти с помощью общего (или повторного) деления. Этот метод иногда считают более быстрым и эффективным, чем листинг 9.0933 умножить на и найти простые множители. Вот пример нахождения наименьшего общего кратного 3, 6 и 9 с помощью этого метода:
Разделите числа на множители любого из трех чисел. 6 имеет коэффициент 2, поэтому давайте использовать 2. Девять и 3 не могут делиться на 2, поэтому мы просто перепишем здесь 9 и 3. Повторяйте этот процесс, пока все числа не будут уменьшены до 1. Затем перемножьте все множители вместе, чтобы получить наименьшее общее кратное.
Девять и 3 не могут делиться на 2, поэтому мы просто перепишем здесь 9 и 3. Повторяйте этот процесс, пока все числа не будут уменьшены до 1. Затем перемножьте все множители вместе, чтобы получить наименьшее общее кратное.
| 2 | 3 | 6 | 9 |
| 3 | 3 | 3 | 9 |
| 3 | 1 | 1 | 3 |
| 1 | 1 | 1 |
НОК \(=2\умножить на 3\умножить на 3=18\)
Теперь, когда были введены методы нахождения наименьших общих кратных, нам нужно изменить свое мышление, чтобы найти наибольший общий множитель двух или более числа. Мы будем определять значение, меньшее или равное рассматриваемым числам. Другими словами, спросите себя: «Какое наибольшее число делит оба этих числа?» Понимание этой концепции необходимо для деления и факторизации многочленов.
Какой наибольший общий делитель?
Разложение на простые множители также можно использовать для определения наибольшего общего делителя. Однако вместо того, чтобы умножать все простые множители, как мы это делали для наименьшего общего кратного, мы будем умножать только те простые множители, которые являются общими для чисел. Полученное произведение является наибольшим общим множителем.
Однако вместо того, чтобы умножать все простые множители, как мы это делали для наименьшего общего кратного, мы будем умножать только те простые множители, которые являются общими для чисел. Полученное произведение является наибольшим общим множителем.
Обзор
Давайте завершим парой вопросов, верных или неверных:
1. Наименьшее общее кратное 45 и 60 равно 15,9.0907
2. Наименьшим общим кратным является число, большее или равное рассматриваемым числам.
Спасибо за просмотр и приятного изучения!
Часто задаваемые вопросы
Q
Как найти LCM и GCF?
A
Существует множество методов определения LCM и GCF. Две наиболее распространенные стратегии включают составление списка или использование простой факторизации.
Например, НОК 5 и 6 можно найти, просто перечислив кратные \(5\) и \(6\), а затем указав наименьшее кратное, общее для обоих чисел.
\(5, 10, 15, 20, 25, \mathbf{30}, 35…\)
\(6, 12, 18, 24, \mathbf{30}, 36…\)
\(\mathbf{ 30}\) — LCM.
Аналогичным образом, GCF можно найти, перечислив факторы каждого числа, а затем указав наибольший общий фактор. Например, GCF для \(40\) и \(32\) можно найти, перечислив множители каждого числа.
\(40\): \(1, 2, 4, 5, \mathbf8, 10, 20, 40\)
\(32\): \(1, 2, 4, \mathbf8, 16, 32\ )
\(\mathbf8\) — это GCF.
Для больших чисел будет нереально составить список факторов или множителей для определения GCF или LCM. Для больших чисел наиболее эффективно использовать метод простой факторизации.
Например, при нахождении НОК начните с нахождения разложения каждого числа на простые множители (это можно сделать, создав дерево факторов). Простая факторизация \(20\) равна \(2\times2\times5\), а простая факторизация \(32\) - это \(2\times2\times2\times2\times2\). Обведите общие факторы и посчитайте эти только один раз .
Теперь умножьте все множители (помните, что не нужно дважды считать обведенные \(2\)). Это становится \(2\times2\times5\times2\times2\times2\), что равняется \(160\). LCM \(20\) и \(32\) равен \(160\).
LCM \(20\) и \(32\) равен \(160\).
При нахождении GCF начните с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Например, простая факторизация \(45\) равна \(5\times3\times3\), а простая факторизация \(120\) равна \(5\times3\times2\times2\times2\). Теперь просто умножьте все факторы, которые являются общими для обоих чисел. В этом случае мы умножим \(5\times3\), что равно \(15\). GCF \(45\) и \(120\) равен \(15\).
Подход с простой факторизацией может показаться довольно длительным процессом, но при работе с большими числами он гарантированно сэкономит время.
Q
Как узнать GCF?
A
Существует две основные стратегии нахождения GCF: перечисление факторов или использование простой факторизации.
Первая стратегия состоит в том, чтобы просто перечислить множители каждого числа, а затем найти наибольший множитель, общий для обоих чисел. Например, если мы ищем GCF для \(36\) и \(45\), мы можем перечислить множители обоих чисел и определить наибольшее общее число.
\(36\): \(1,2,3,4,6,\mathbf9,12,18,36\)
\(45\): \(1,3,5,\mathbf9,15,45 \)
GCF для \(36\) и \(45\) равен \(\mathbf9\).
Список делителей каждого числа, а затем определение наибольшего общего делителя хорошо работает для небольших чисел. Однако при нахождении GCF очень больших чисел более эффективно использовать метод простой факторизации.
Например, при нахождении GCF чисел \(180\) и \(162\) мы начинаем с перечисления простой факторизации каждого числа (это можно сделать, создав дерево факторов). Простая факторизация \(180\) равна \(2\times2\times3\times3\times5\), а простая факторизация \(162\) - это \(2\times3\times3\times3\times3\). Теперь найдите факторы, которые являются общими для обоих чисел. В этом случае оба числа имеют одну общую \(2\) и две \(3\)s, или \(2\times3\times3\). Результатом \(2\times3\times3\) является \(18\), что является GCF! Эта стратегия часто более эффективна при нахождении GCF действительно больших чисел.
Q
Что означает GCF?
A
GCF означает «наибольший общий делитель». GCF определяется как наибольшее число, являющееся множителем двух или более чисел. Например, GCF для \(24\) и \(36\) равен \(12\), потому что наибольший делитель, общий для \(24\) и \(36\), равен \(12\). \(24\) и \(36\) имеют другие общие факторы, но \(12\) является самым большим.
GCF определяется как наибольшее число, являющееся множителем двух или более чисел. Например, GCF для \(24\) и \(36\) равен \(12\), потому что наибольший делитель, общий для \(24\) и \(36\), равен \(12\). \(24\) и \(36\) имеют другие общие факторы, но \(12\) является самым большим.
Q
Как найти наименьшее общее кратное?
A
Существует множество методов нахождения наименьшего общего кратного. Двумя распространенными подходами являются перечисление кратных и использование простой факторизации. Список кратных так же, как это звучит, просто перечислите кратные каждого числа, а затем найдите наименьшее кратное, общее для обоих чисел. Например, при нахождении наименьшего общего кратного чисел \(3\) и \(4\) перечислите кратные:
\(3\): \(3,6,9,\mathbf{12},15,18 …\)
\(4\): \(4,8,\mathbf{12},16,20…\)
\(\mathbf{12}\) — наименьшее кратное, совместно используемое \(3\) и \(4\).
Перечисление кратных — отличная стратегия, когда числа довольно малы. Когда числа большие, такие как \(38\) и \(42\), мы должны использовать метод простой факторизации. Начните с перечисления простой факторизации каждого числа (это можно сделать с помощью факторного дерева).
Когда числа большие, такие как \(38\) и \(42\), мы должны использовать метод простой факторизации. Начните с перечисления простой факторизации каждого числа (это можно сделать с помощью факторного дерева).
\(38\): \(2\times19\)
\(42\): \(2\times3\times7\)
Теперь обведите общие множители (считайте эти только один раз ).
Теперь умножьте все множители (не забудьте подсчитать \(2\) только один раз). Это становится \(2\times19\times3\times7\), что равняется \(798\). LCM \(38\) и \(42\) равен \(798\).
Q
Как вынуть LCM?
A
Извлечение НОК полезно при сложении или вычитании дробей. При определении наименьшего общего кратного получается знаменатель, одинаковый для обеих дробей. Например, общий знаменатель для \(\frac{2}{7}+\frac{3}{5}\) будет равен \(35\), потому что \(35\) является НОК для \(7\ ) и \(5\). Новые дроби становятся \(\frac{10}{35}+\frac{21}{35}\), что равняется \(\frac{31}{35}\).
Информационные бюллетени
Загрузить Информационные бюллетени
Загрузить Информационные бюллетени
Практические вопросы
Вопрос №1:
Каков наибольший общий делитель чисел 16 и 42? Используйте его, чтобы уменьшить дробь \(\frac{16}{42}\).
GCF равно 8, и мы уменьшаем его до \(\frac{2}{5}\).
GCF равен 1, и мы не можем больше уменьшать.
GCF равно 4, и мы уменьшаем его до \(\frac{4}{11}\).
GCF равно 2, и мы уменьшаем его до \(\frac{8}{21}\).
Показать ответ
Ответ:
Правильный ответ D: GCF равен 2, и мы уменьшаем до \(\frac{8}{21}\).
Давайте подойдем к этой задаче, перечислив простые множители как числителя, так и знаменателя.
\(16=2×2×2×2\)
\(42=2×3×7\)
Здесь мы видим, что 2 — единственный общий делитель чисел 16 и 42 и, следовательно, их наибольший общий делитель. Затем мы можем разделить оба числа на 2, чтобы уменьшить дробь:
\(\frac{16\div2}{42\div2}=\frac{8}{21}\)
Hide Answer
Question #2:
Find the least common multiple of 2, 6, and 8.
16
18
24
48
Show Answer
Answer:
Правильный ответ C: 24.
Для этой задачи перечислим простые множители каждого числа.
\(2=2\) (обратите внимание, что мы могли написать \(2\times1\), но 1 понимается или подразумевается, и обычно его не нужно писать)
\(6=2\times3\)
\(8=2\times2\times2\)
Помните, что при вычислении НОК двух или более чисел мы перечисляем каждый простой множитель один раз, который является общим для всех чисел. Поскольку каждое из наших чисел имеет 2 в качестве простого множителя, наш LCM также будет иметь 2 в качестве одного из своих простых множителей.
LCM \(=2\times\) _______
Теперь из 6 у нас осталась 3, а из 8 осталось две двойки. Мы умножаем их, чтобы получить
LCM \(=2\times3\times2\times2=24\)
Обратите внимание, что хотя 2, 6 и 8 являются делителями 48, решение не D, потому что 48 не является наименьшее общее кратное.
Скрыть ответ
Вопрос № 3:
Перечислите первые несколько кратных 3, 5 и 6, чтобы найти наименьшее общее кратное.
LCM - 15
LCM 30
LCM - 18
LCM 75
Показать Ответ
Ответ:
Ответ:
. : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
Первые несколько кратных 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Первые несколько кратных 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Как мы см. выше, 30 – это первое (наименьшее) число, которое является общим среди кратных чисел 3, 5 и 6, поэтому наименьшее общее кратное равно 30.
Скрыть ответ
54 конфеты, а у Триш 36. Они хотят приготовить мешочки с конфетами на день рождения своей подруги Ким, но в каждом мешочке должно быть равное количество конфет. Чтобы в каждом пакете было как можно больше конфет, когда Кортни и Триш работают отдельно, сколько пакетов они могут сделать и сколько конфет будет в каждом пакете?
Они хотят приготовить мешочки с конфетами на день рождения своей подруги Ким, но в каждом мешочке должно быть равное количество конфет. Чтобы в каждом пакете было как можно больше конфет, когда Кортни и Триш работают отдельно, сколько пакетов они могут сделать и сколько конфет будет в каждом пакете?
10 пакетов по 9 конфет
9 пакетов по 10 конфет
15 пакетов по 6 конфет
5 пакетов по 18 конфет
Показать Ответ
Ответ:
Правильный ответ D: 5 пакетов по 18 конфет в каждом.
Для начала перечислите простые множители чисел 54 и 36:
\(54=2\times3\times3\times3\)
\(36=2\times2\times3\times3\)
Обратите внимание, что они оба разделяют двойка и две тройки. Произведение этих общих простых множителей равно \(2\times3\times3=18\). Теперь мы знаем, что GCF равен 18, а это значит, что в каждом пакете будет 18 конфет. Из 54 частей Кортни получится 3 сумки, а из 36 частей Триш получится 2 сумки. Вместе они сделают 5 пакетов по 18 конфет в каждом.
Вместе они сделают 5 пакетов по 18 конфет в каждом.
Скрыть ответ
Вопрос № 5:
Сара покупает фрукты для обеда в офисе, и ей нужно равное количество яблок и бананов. Однако яблоки продаются в мешках по 4 штуки, а бананы — в связках по 6 штук. Какое наименьшее количество яблок и бананов может купить Сара?
24 яблока и 24 банана
18 яблок и 18 бананов
12 яблок и 12 бананов
16 яблок и 16 бананов
Показать ответ
Ответ:
Правильный ответ C: 12 яблок и 12 бананов.
В этой задаче мы хотим узнать наименьшее общее кратное чисел 4 и 6. Используя метод простых множителей, мы видим, что
\(4=2\times2\)
\(6=2\times3\)
LCM \(=2\times2\times3=12\)
Сара купит три пакета яблок и две связки бананов, чтобы получить по 12 каждого фрукта.
Скрыть ответ
Вернуться к предварительным алгебраическим видео
83869924
20269946579
LCM 5, 12 и 15
Калькуляторы Учебные ресурсы по математике
- Домашняя страница
- Математические функции
- Калькулятор LCM
- LCM из 5, 12 и 15
LCM из 5, 12 и 15 равно 60. Как найти, дает больше информации о том, что можно найти это lcm 5, 12 и 15 с использованием простых множителей и специальных методов деления, а также пример использования математики и реальных задач.
что такое lcm 5, 12 и 15?
lcm (5 12 15) = (?)
5 => 5
12 => 2 x 2 x 3
15 => 3 x 5
= 3 x 5 x 2 x 2
= 60
lcm (5 , 12 и 15) = 60
60 — lcm чисел 5, 12 и 15.
, где
5 — целое положительное число,
12 — целое положительное число,
60 — lcm чисел 5, 12. и 15,
и 15,
{3, 5} в {5, 2 x 2 x 3, 3 x 5} являются наиболее повторяющимися факторами 5, 12 и 15,
{2, 2} в {5, 2 x 2 x 3 , 3 x 5} — остальные оставшиеся множители 5, 12 и 15.
Использование в математике: НОК 5, 12 и 15
Ниже приведены некоторые математические приложения, в которых можно использовать МОК 5, 12 и 15:
- найти наименьшее число, которое точно делится на 5, 12 и 15.
- , чтобы найти общие знаменатели для дробей, имеющих 5, 12 и 15 в знаменателях при сложении или вычитании разнородных дробей.
Использование в реальных задачах: 5, 12 и 15 lcm
В контексте задач реального мира lcm, lcm 5, 12 и 15 помогает найти точное время, когда три одинаковых и повторяющихся с разным графиком времени происходят вместе в одно и то же время. Например, задачи реального мира включают lcm в ситуациях, когда нужно определить, в какое время все колокола A, B и C звонят вместе, если колокол A звонит через 5 секунд, B звонит через 12 секунд и C звонит через 15 секунд несколько раз. Ответ заключается в том, что все колокола A, B и C звонят вместе через 60 секунд в первый раз, через 120 секунд во второй раз, через 180 секунд в третий раз и так далее.
Ответ заключается в том, что все колокола A, B и C звонят вместе через 60 секунд в первый раз, через 120 секунд во второй раз, через 180 секунд в третий раз и так далее.
Важные примечания: 5, 12 и 15 lcm
Ниже приведены важные примечания, которые следует помнить при решении lcm из 5, 12 и 15:
- Повторяющиеся и неповторяющиеся простые множители 5, 12 и 15 следует умножить, чтобы найти наименьшее общее кратное 5, 12 и 15 при решении lcm методом простых множителей.
- Результаты lcm 5, 12 и 15 идентичны, даже если мы изменим порядок заданных чисел в вычислении lcm, это означает, что порядок заданных чисел в вычислении lcm не повлияет на результаты.
Для значений, отличных от 5, 12 и 15, используйте этот инструмент ниже:
В приведенном ниже решенном примере с пошаговой работой показано, как найти lcm числа 5, 12 и 15, используя либо метод простых множителей, либо специальный метод деления. .
.
Пример решения с использованием метода простых множителей:
Что такое НОК 5, 12 и 15?
шаг 1
Обратитесь к входным параметрам, значениям и посмотрите, что будет найдено:
Входные параметры и значения:
A = 5
B = 12
C = 15
Что нужно найти:
найти lcm чисел 5, 12 и 15
шаг 2, 5: 2 и 5
Простые множители 5 = 5
Простые множители 12 = 2 x 2 x 3
Простые множители 15 = 3 x 5
Шаг 3 Определите повторяющиеся и неповторяющиеся простые множители чисел 5, 12 и 15:
{3 , 5} — наиболее повторяющиеся множители, а {2, 2} — неповторяющиеся множители 5, 12 и 15.
шаг 4 Найдите произведение повторяющихся и неповторяющихся простых множителей 5, 12 и 15:
= 3 x 5 x 2 x 2
= 60
lcm(20 и 30) = 60
Следовательно,
lcm числа 5 , 12 и 15 равно 60
Пример решения с использованием специального метода деления:
Этот специальный метод деления является самым простым способом понять весь расчет того, что такое lcm для 5, 12 и 15.
шаг 1 Обратитесь к входным параметрам, значениям и посмотрите, что нужно найти:
Входные параметры и значения:
Целые числа: 5, 12 и 15
Что нужно найти:
lcm (5, 12, 15) = ?
шаг 2 Расположите заданные целые числа по горизонтали, разделяя их пробелами или запятыми. Формат:
5, 12 и 15
шаг 3 Выберите делитель, который делит каждое или большинство заданных целых чисел (5, 12 и 15), разделите каждое целое число отдельно и запишите частное в следующей строке прямо под соответствующими целыми числами. Перенесите целое число на следующую строку, если какое-либо целое число в числах 5, 12 и 15 не делится на выбранный делитель; повторяйте тот же процесс, пока все целые числа не будут равны 1, как показано ниже:
| 2 | 5 | 12 | 15 |
| 2 | 5 | 6 | 15 |
| 3 | 5 | 3 | 15 |
| 5 | 5 | 1 | 5 |
| 1 | 1 | 1 |
Шаг 4 Умножение дивизоров, чтобы найти LCM 5, 12 и 15:
= 2 x 2 x 3 x 5
= 60
НОК(5, 12, 15) = 60
Наименьшее общее кратное для трех чисел 5, 12 и 15 равно 60
Наименьший общий знаменатель
Наименьший общий знаменатель двух или более ненулевых знаменателей на самом деле наименьшее целое число , то есть делится на каждое знаменателя. Существует два широко используемых метода нахождения наименьшего общего знаменателя.
Существует два широко используемых метода нахождения наименьшего общего знаменателя.
На самом деле, это та же основная идея, что и при нахождении наименьшего общего кратного (НОК) для целых чисел (без дробных частей).
Примечание : В приведенных ниже примерах мы будем добавлять три дроби вместо обычного два , потому что принципы те же. Это даст вам лучшее понимание процесса. А в разделе « Собираем все вместе » мы добавим четыре дроби .
Метод 1:
Чтобы найти наименьший общий знаменатель, просто перечислите числа, кратные каждого знаменателя (обычно работает умножение на 2, 3, 4 и т. д. до 6 или 7), затем найдите наименьшее число , которое появляется в каждом списке.
Пример : Предположим, мы хотим добавить 1/5 + 1/6 + 1/15. Мы найдем наименьший общий знаменатель следующим образом…
- Сначала мы перечислим кратных каждого знаменателя.

Кратные числа 5 равны 10, 15, 20, 25, 30 , 35, 40,… из 15 есть 30 , 45, 60, 75, 90,…. - Теперь, когда вы посмотрите на список кратных чисел, вы увидите, что 30 — это наименьшее число, встречающееся в каждом списке.
- Следовательно, наименьший общий знаменатель чисел 1/5 , 1/6 и 1/15 равен 30 .
Этот метод работает очень хорошо. Но, складывая дроби с большими числами в знаменателях, может получиться довольно грязно.
Итак, задержите эту мысль на мгновение, пока мы смотрим на другим способом найти наименьший общий знаменатель для сложения этих самых дробей.
Метод 2:
Чтобы найти наименьший общий знаменатель с помощью этого метода, разложите каждый из знаменателей на простых числа . Затем для каждого различных простых чисел во всех факторизациях выполните следующее…
Затем для каждого различных простых чисел во всех факторизациях выполните следующее…
- Подсчитайте количество раз, когда каждое простое число встречается в каждой из факторизаций.
- Для каждого простого числа возьмите крупнейших из этих подсчетов.
- Запишите это простое число столько раз, сколько вы насчитали для него на шаге 2.
- Наименьший общий знаменатель равен произведению всех записанных простых чисел.
Пример : Мы будем использовать те же дроби, что и выше: 1/5 , 1/6 и 1/15 .
Разложите на простые числа (Нажмите здесь, чтобы увидеть нашу таблицу простых чисел.)
- Разложение числа на простые множители 5 равно 5 ( 5 — простое число)
- Разложение числа 6 на простые множители равно 2 x 3
- Разложение числа на простые множители 15 равно 3 x 5
- Обратите внимание, что разные простые числа — это 2, 3 и 5.

- Теперь делаем Шаг #1 – Подсчитаем число раз каждое простое число встречается в каждом факторизации…
- Количество простых чисел в 5 равно единице 5
- Количество простых чисел в 6 равно 1 2 и 1 3
- Количество простых чисел в 15 равно один 3 и один 5
- Шаг #2 – Для каждого простого числа возьмите наибольших из этих подсчетов. Итак, у нас есть…
- Наибольшее число 2s равно единице
- Наибольшее количество троек равно единице
- Наибольшее число 5s равно единице
- Шаг № 3 — Поскольку теперь мы знаем количество каждого простого числа, вы просто — запишите это простое число как столько раз, сколько вы насчитали для него на шаге № 2.
 Вот числа… 2, 3, 5
Вот числа… 2, 3, 5 - Шаг #4 – Наименьший общий знаменатель равен произведению всех записанных простых чисел.
2 x 3 x 5 = 30
// Следовательно, наименьший общий знаменатель чисел 1/5, 1/6 и 1/15 равен 30 .
Как видите, оба метода дают одинаковые результаты .
Причина, по которой мы можем захотеть использовать разные методы, заключается в том, что Метод #1 прекрасно работает для небольших чисел . Но когда число становится больше , Метод № 2 является ЕДИНСТВЕННЫМ способом.
Теперь давайте сделаем сложную часть, очень простую — преобразуем каждую дробь в эквивалентную дробь, используя только что найденный наименьший общий знаменатель , который равен 30 .
Помните нашу задачу: Сложите: 1/5 +1/6 + 1/15
Шаг № 2 для сложения дробей с разными знаменателями гласит: «Перепишите каждую эквивалентную дробь , используя наименьший общий знаменатель в качестве знаменателя. ” Итак, давайте сделаем это!
” Итак, давайте сделаем это!
Это будет немного подробно, так что держись !
Переписать каждую дробь в виде эквивалентной дроби
Правило для перезаписи дроби в виде эквивалентной дроби с использованием наименьшего общего знаменателя гласит…
- Разделить наименьший общий знаменатель на знаменатель дроби.
- Умножьте ответ на числитель дроби.
- Перепишите дробь, используя в качестве знаменателя наименьший общий знаменатель.
Итак, если мы запишем 1/5 как эквивалентную дробь, используя 30 в качестве знаменателя , мы разделим 30 на знаменатель «5» , что равно 6 . Затем мы умножаем это 6 на числитель «1» , что дает нам новый числитель 6 .
Наконец, мы перепишем эквивалентную дробь, используя 30 в качестве знаменателя, поэтому наша эквивалентная дробь равна 9. 0933 30/6 .
0933 30/6 .
Правило на самом деле выглядит так…
Новый Числитель = (LCD ÷ Знаменатель) x Числитель
Новый Знаменатель = LCD
и повторяем процессИспользуя 1/6 далее, (30 ÷ 6 = 5, и 5 x 1 = 5) , поэтому 1/6 эквивалентно 5/30
И для 1/15, ( 30 ÷ 15 = 2, и 2 x 1=2) , поэтому 1/15 эквивалентно 2/30
Теперь, наконец, мы можем сложить наши дроби…
1/5 + 1/6 + 1/15 = 6/30 + 5/30 + 2/ 30 = 13/30
Собираем все вместе
Мы собираемся использовать , немного более сложную задачу на сложение дробей с разными знаменателями, чтобы показать, что вы МОЖЕТЕ это сделать. Кроме того, мы будем использовать метод #2 , чтобы найти наименьший общий знаменатель, потому что он работает лучше всего почти во всех случаях.
Если у вас возникли проблемы с какой-либо частью этого упражнения, перечитайте раздел выше, посвященный этому. Мы собираемся рассказать о каждом шаге сложения этих дробей, не цитируя точно правила, как в «реальном мире».
Посмотрите на как у все работает и все будет хорошо!
Мы сложим эти дроби...
1/9 + 1/8 + 5/12 + 7/18
Поскольку наши знаменателя это 9, 8, 12 и 18, нам нужно найти наименьший общий знаменатель . Итак, мы делим каждое число на простые.
- Факторизация числа 9 равно 3 x 3
- Факторизация числа 8 равна 2 x 2 x 2
- Факторизация числа 12 равна 2 x 2 x 3
- Простая факторизация числа 18 равна 2 x 3 x 3
Когда мы делаем самых больших подсчета простых чисел, мы находим тройки двойки и две тройки (вы их видите?) , поэтому переписываем количество и находим произведение.
Вот так…
2 x 2 x 2 x 3 x 3 = 72
Теперь у нас есть наименьший общий знаменатель 72
Далее… преобразуем 72 в эквивалентную дробь. наш новый знаменатель . Итак, переведем... 1/9 + 1/8 + 5/12 + 7/18
- 1/9 = 8/72
- 1/8 = 9/72
- 5/12 = 30/72
- 7/18 = 28/72
Миссия выполнена... все наши знаменатели равны и , так что мы можем просто сложить числители.
Наши новые эквивалентные дроби — это 8/72, 9/72, 30/72 и 28/72
Вот что меняет нашу задачу на… 30/72 + 28/72
Теперь складываем все числители и помещаем результаты в наш общий знаменатель , ответ равен…
8/72 + 9/72 + 30/72 + 28/72 = 75/72
Поскольку наш ответ — неправильная дробь (числитель на больше знаменателя на ), теперь у нас есть три варианта .
- Покажите ответ как есть, с наименьшим общим знаменателем.
75/72 - Сократите дробь и отобразите ее как наименьший уменьшенный эквивалент.
25/24 - Упростите ответ и покажите его как смешанное число.
1 1/24
Помните, всегда указывайте свой ответ в форме , которая запрашивается для в ваших инструкциях.
Таблица факторизации простых чисел
Обзор LCM
Таблицы дробей для печати
Факторы и простые числа
Общий знаменатель
Общий знаменательПО МАТЕМАТИКЕ: 1. н. знаменатель (делитель, нижнее число), общий для двух или более дробей. БЫВШИЙ. Для сложения дробей нужны общие знаменатели.
Обычный демониматор — это не просто произведение факторов, общих для дробей, но,
ОБЩИЕ ФАКТОРЫ И ФАКТОРЫ, ДЕЛАЮЩИЕ КАЖДУЮ ФРАКЦИЮ ОТЛИЧНОЙ.
Общий демониматор включает в себя все факторы из каждой дроби, и есть много общих знаменателей.
Наименьший общий знаменатель – это наименьшее произведение множителей каждой дроби.
Вот два метода нахождения наименьшего общего знаменателя, наименьшего произведения коэффициенты каждой фракции.
- Первый метод общих факторов.
- Фактор каждого демониматора -- обычно фактор как простые множители.
- Перечислите общие множители, множители, общие для каждой дроби, написав этот множитель только один раз.
- Добавьте в список факторы, которые не являются общими для каждой фракции, перечислив только один раз те, которые у них есть общего с некоторыми другими фракциями.
- Список факторов является общим знаменателем. Перемножьте коэффициенты, если это необходимо.
- Метод «одна фракция за раз».
- Фактор каждого демониматора -- обычно фактор как простые множители.
- Перечислите каждый множитель первой дроби.
- Добавить в список факторы второй дроби, которые еще не были перечислены.
- Повторите шаг 3 для каждой фракции.

- Список факторов является общим знаменателем. Перемножьте коэффициенты, если это необходимо.
В приведенных ниже примерах строки, начинающиеся в верхней части примера, показывают первый шаг в работе.
Пример. 1. Найдите общий знаменатель для 5/12 и 3/4.| Сначала общие делители Общие делители равны 2 и 2. В первом знаменателе также есть 3. Общий знаменатель равно 2·2·3 или 12. | Одна дробь за один раз Первый знаменатель имеет делители 2, 2 и 3. Второй знаменатель имеет множители 2 и 2, и они уже перечислены. Нет необходимости перечислять новые факторы. |
Пример. 2. Найдите общий знаменатель для 2/3 и 3/4.
| Общие факторы Первые Общих факторов нет. Перечислите факторы каждой дроби. Общий знаменатель равен 2·2·3 или 12. | Одна дробь за один раз Единственным простым делителем числа 3 является число 3. Затем перечислите делители числа 4.  Общий знаменатель равен 2·2·3 или 12. Общий знаменатель равен 2·2·3 или 12. |
Пример. 3. Найдите общий знаменатель для 1/6, 1/2, 5/12, 2/15.
| Сначала общие множители Нет общего множителя 6, 2, 12 и 15. Следующими наиболее распространенными являются 2 и 3, поэтому перечислите их, избегая дублирование. Требуются дополнительные 2 и дополнительные 5. Общий знаменатель равен 2·2·3·5 или 60. | Одна дробь за раз Простые множители числа 6 равны 2 и 3, поэтому перечислите их. Простой множитель 2 равен 2, но это уже было перечислено. Простые множители числа 12 — это 2, 2 и 3. 2 и 3 являются дубликатами, поэтому просто напишите еще одну 2. простые делители числа 15 — это 3 и 5. Укажите 5, но не дублируйте 3, которые уже перечислены. Общий знаменатель равен 2·2·3·5 или 60. |
Пример. 4. Найдите общий знаменатель для 3/10 и 4/25.
| Общие делители сначала Десять и 25 имеют общий делитель 5, поэтому перечислите его.  Требуются дополнительные множители 2 и 5.
Общий знаменатель равен 2·5·5 или 50. Требуются дополнительные множители 2 и 5.
Общий знаменатель равен 2·5·5 или 50. | Одна дробь за один раз Перечислите множители 2 и 5 для знаменателя 10. Не указывайте повторяющийся множитель 5, но укажите дополнительный множитель 5 для множителей 25. Общий знаменатель равен 2·5·5 или 50. |
Пример 5 очень похож на пример 4. В одном есть арифметические факторы, в другом — алгебраические. Прокуратура такая же.
Пример. 5. Найдите общий знаменатель для 2/x 2 и -3/(xy).| Сначала общие множители Каждый знаменатель имеет множитель x. Перечислите его только один раз. Затем перечислите два необходимых фактора x и y. Общий знаменатель равен x·x·y или x 2 y. | Одна фракция за раз Знаменатель первой дроби равен x и x. Перечислите каждого. Следующая дробь имеет множители x и y. Не дублируйте x. Перечислите у. Общий знаменатель равен x·x·y или x 2 y.  |
Пример. 6. Найдите общий знаменатель для 2x/(4x+4y) и -3/(2x-2y).
| Сначала общие факторы биномы 4x+4y и 2x-2y имеют только 2 в качестве Общий делитель. Перечислите это. Другими необходимыми уникальными факторами являются x+y, x-y и 2. Перечислите каждый. Общий знаменатель равно 2·2·(x+y)·(x-y) или 4x 2 -4 года 2 . | Одна дробь за раз Первая дробь имеет простые множители в знаменателе. 2, 2 и х+у. Перечислите это. Второй знаменатель имеет повторяющийся множитель 2 и уникальный множитель x-y. Список только х-у. Общий знаменатель равен 2·2·(x+y)·(x-y) или 4x 2 -4y 2 . |
Пример. 7. Найдите общий знаменатель для 5/(x 2 -1) и 3/(x 2 +4x+3).
| Общие множители Первые Дроби имеют общий знаменатель x+1. Перечислите это. У них есть уникальные факторы x-1 и x+3. Перечислите их.  Общий знаменатель равен (x+1)(x-1)(x+3). Общий знаменатель равен (x+1)(x-1)(x+3). | Одна дробь за один раз Первая дробь как множители знаменателя x+1 и x-1. Перечислите их. В знаменателе второй дроби x+1 является дубликатом. Не перечисляйте это. Х+3 нужен. Перечислите это. Общий знаменатель равен (x+1)(x-1)(x+3). |
Пример. 8. Найдите общий знаменатель для 5/(2x + 8) и 4/(x 2 -16).
| Первые общие множители Знаменатели имеют общий множитель x+4. Перечислите это. Также необходимы уникальные коэффициенты 2 и x-4. Перечислите их. Общий знаменатель равен 2(x+4)(x-4). | Одна дробь за один раз Первая дробь имеет множители знаменателя 2 и x+4. Перечислите их. Вторая фракция имеет дублирующий фактор x+4. Не перечисляйте это. Он имеет уникальный коэффициент x-4. Перечислите это. Общий знаменатель равен 2(x+4)(x-4). |
Пример. 9. Найдите общий знаменатель для 4/(9ab 2 ) и (a+1)/(12a 2 b 3 ).
| Общие множители Первые Общие множители: 3, a, b и b. Перечислите их. Существуют уникальные факторы 2, 2, a, 3 и b. Перечислите их также. Общий знаменатель равен 2·2·3·3·a·a·b·b·b или 36a 2 b 3 . | Одна дробь за раз Первый знаменатель имеет делители 3, 3, a, b и b. Перечислите их. Следующая дробь имеет дубликат коэффициенты 3, а, b и b. Не перечисляйте их. Перечислите уникальные факторы 2, 2 и b. Общий знаменатель равно 2·2·3·3·a·a·b·b·b или 36a 2 б 3 . |
|
НА АНГЛИЙСКОМ ЯЗЫКЕ: 1. н. характеристика, присущая двум или более вещам или людям. БЫВШИЙ. Их общим знаменателем была любовь к математике.
ПРИМЕНЕНИЕ: См. список 40.
- Найдите общий знаменатель для:
- 1.




 Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
Дополнительный множитель – это число, получившееся при делении НОЗ на знаменатель конкретной дроби. Для 3/5 дополнительный множитель равен 3, так как 15/5 = 3. Для второй дроби дополнительным множителем будет 1, так как 15/15 = 1.
 Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

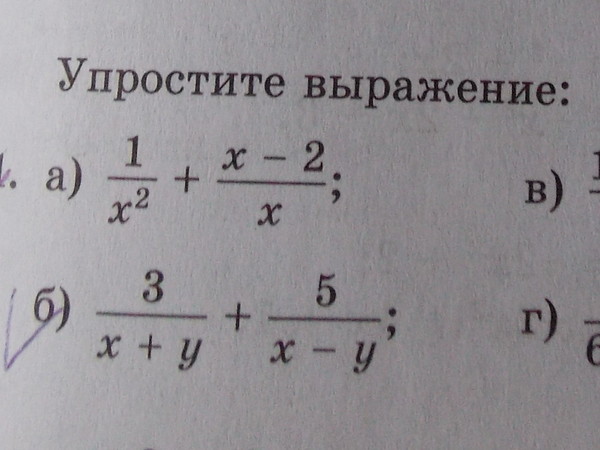 Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
Например, число 5 в виде дроби будет выглядеть так: 5/1. Чтобы смешанное число превратить в дробь, нужно целое число умножить на знаменатель и прибавить к нему числитель. Пример: 8 целых и 3/5 в виде дроби = 8×5+3/5 = 43/5.
 Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.
Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
 ..
..

