Квадратный сантиметр. 3-й класс
Тип урока: комбинированный.
Дидактические цели:
- Формирование новых знаний о единице площади – квадратном сантиметре и ценностного отношения к этим знаниям.
- Формирование позитивного опыта применения ранее сформированных знаний о площади фигур и действий по сравнению площадей фигур на основе их переноса в новые условия в ситуациях неопределенности.
- Формирование предметных и универсальных учебных действий на основе применения ранее сформированных знаний о площади фигур, табличных случаях умножения и соответствующих случаях деления, порядка выполнения действий в выражениях, решения составных задач и задач на увеличения числа в несколько раз.
ХОД УРОКА
I. Адаптационный этап
Задачи:
- адаптировать учащихся к деятельности на уроке;
- выявить предварительные знания учащихся и определить их границы: интеллектуальное затруднение (создание проблемной ситуации)
Учитель: Сегодня мы отправимся на
рыбалку, но не простую, а математическую.
– Зачем ходят на рыбалку? (Ловить рыбу,
отдохнуть, получать удовольствие).
– Вот и мы будем ловить «математическую» рыбу и
получать удовольствие.
Учитель: Отгадайте ребус («Квадратный сантиметр»). Это тема нашего урока. Определите цель урока.
Учитель: К рыбалке нужно подготовиться и запастись некоторыми предметами.
Устный счет
Цель:
- повторить табличные случаи умножения и соответствующие случаи деления;
- повторить порядок выполнения действий в выражениях.
На доске:
3 – 2 : 1 = [ ]
- (83 – 48) : 5 = 7
- 18 : 9 + (100 – 39) = 63
- 7 х 5 + 7 х 7 = 84
84 – 63 : 7 = 75
Учитель: На карточках записана
формула. Её нужно расшифровать, выполнив
вычисления. Результаты примеров являются
данными, которые нужно подставить в формулу и
решить пример, который получится. Расшифровав
формулу, мы получим то, что нам пригодиться на
рыбалке. (1-й и 2-й примеры ученики решают
у доски, 3 – коллективно)
Результаты примеров являются
данными, которые нужно подставить в формулу и
решить пример, который получится. Расшифровав
формулу, мы получим то, что нам пригодиться на
рыбалке. (1-й и 2-й примеры ученики решают
у доски, 3 – коллективно)
– Что получилось? (Наживка)
– Что это такое? (Червяки, мотыль, хлеб)
(Учитель к доске прикрепляет иллюстрацию)
Цель:
- закрепить представление о площади;
- закрепить умение сравнивать площади разных фигур разными способами
1 слайд
– Сравните площади фигур
– Как узнали? (На глаз)
2 слайд
– Сравните площади фигур.
(Трудно определить, площадь какой фигуры
больше. Нужно наложить одну фигуру на
другую. Площадь восьмиугольника больше, т.к.
квадрат полностью поместился в нем, площадь
квадрата меньше.)
Площадь восьмиугольника больше, т.к.
квадрат полностью поместился в нем, площадь
квадрата меньше.)
3 слайд
– Сравните площади фигур.
(Площадь 1 фигуры больше площади второй фигуры, т.к. 1 фигура состоит из 8 квадратов, а 2 – из 7 квадратов).
– Каким способом сравнили? (Посчитали квадраты)
4 слайд
– Сделайте вывод: как узнать, площадь какой фигуры больше, а какой меньше?
- На глаз
- Наложением
- Подсчитать квадраты с одинаковой площадью
Учитель: Мы удачно выполнили задание и то, что получаем для рыбалки, отгадайте:
С утра сижу я на реке,
Подъёмный кран держу в руке. (Удочка)
(Прикрепляется иллюстрация)
II. Основной этап
Задачи:
- формирование знаний, отношений, действий, опыта.

- разрешение интеллектуального затруднения – находится ответ на проблемный вопрос.
1. Работа в группах
Учитель: Сейчас мы разделимся на 3 группы по рядам. Каждой группе я даю по 2 фигуры.
Задание: В своих группах вы должны выяснить, какова площадь этих фигур. (2 одинаковых прямоугольника, но разного цвета, разделены на квадраты со стороной 1 см и меньше).
Учитель: Проверяем:
– Каковы площади фигур? (48 и 12)
– Площадь какой фигуры больше? (Одинаковые)
– А почему результаты разные? (Разные
результаты измерения)
– На каком прямоугольнике было легче подсчитать
квадраты?
– Чему равна длина стороны такого квадрата?
Учитель: Итак, мы измеряли площади
прямоугольников одинаковыми квадратами. Каждый
такой квадрат со стороной 1 см – это квадратный
сантиметр – единица измерения площади. И сколько
таких квадратных сантиметров содержится в
фигуре, такова и площадь фигуры.
Каждый
такой квадрат со стороной 1 см – это квадратный
сантиметр – единица измерения площади. И сколько
таких квадратных сантиметров содержится в
фигуре, такова и площадь фигуры.
2. Работа по учебнику
Учитель: Откройте учебник на с.52.
Прочитайте сведения за красной линией (правило).
– Что такое квадратный сантиметр? (Это квадрат
со стороной 1 см – единица площади)
– Начертите в тетради квадрат со стороной 1 см,
как в учебнике. Чему равна его площадь? (1 кв.см)
Подпишите.
III. Творческий этап
Задачи:
- первичное закрепление знаний, действий, отношений, опыта на основе их применения
- повышение уровня формируемых знаний на основе
применения разноуровневых и творческих заданий.

1. Устно. Прочитайте задание.
– Сосчитайте. Сколько квадратных сантиметров в каждой фигуре? Сравните площади. (Площадь 1 фигуры – 8 кв.см, площадь 2 фигуры – 7 кв.см, значит площадь 1 фигуры > площади 2 фигуры)
Учитель: За верно выполненное задание мы получаем… Отгадайте загадку:
За водой идёт – песни звонкие поёт,
А назад идет – слезы льёт. (Ведро)
Физкультминутка
Рыбки
Рыбки весело плескались
Столько мы подпрыгнем раз.
В чистой свеженькой воде.
То согнутся, разогнутся,
То зароются в песке.
Приседаем столько раз,
Сколько рыбок здесь у нас.
Сколько чаек у нас,
Учитель: Все готово для рыбалки: и
наживка, и удочка, и ведро.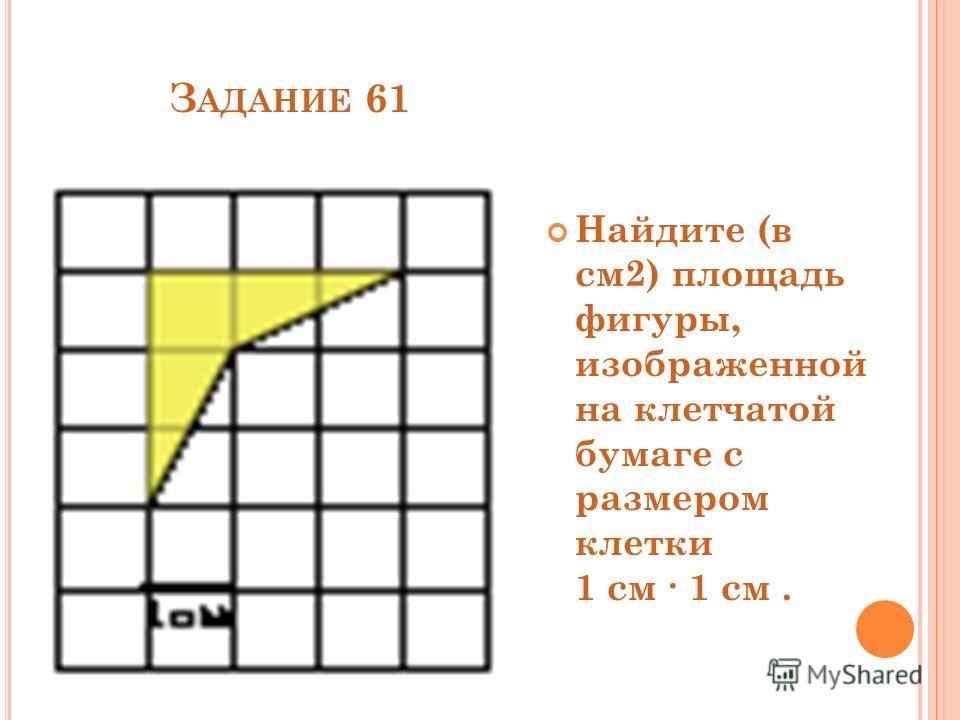 Осталось выбрать
только место для ловли.
Осталось выбрать
только место для ловли.
2. Интерактивная доска
Цель: закрепить умение решать составные задачи, на уменьшение в несколько раз.
Задача: От автобусной остановки до луга рыбаки шли 42 м, а по лугу до озера в 6 раз меньше. Какое расстояние прошли рыбаки от автобусной остановки до озера?
Учитель: О чем говорится в задаче?
– Что известно?
– Что нужно узнать?
– Для решения задачи выполним чертеж.
3. Самостоятельная работа в парах и группах
Учитель: Место для рыбалки выбрано . Можно ловить рыбу
– С последних парт каждого ряда я пускаю листы,
на которых записаны примеры. Каждая парта
совместно решает свои примеры и передает лист
вперед. Выполнив свое задание, нужно прикрепить
рыбку на ведро. Ребятам, сидящим за 1 партой, нужно
будет расшифровать слово.
| 24 : 8 = 6 х 9 = |
C Т |
| 15 : 3 = 7 х 2 = |
А Р |
| 45 : 9 = 10 х 2 = |
А Н |
| 18 : 3 = 4 х 3 = |
И Е |
| С | Е | А | Т | И | Р | Н |
| 3 | 12 | 5 | 54 | 6 | 14 | 20 |
| 24 : 8 = 6 х 3 = |
Т Е |
| 15 : 3 = 7 х 2 = |
Р П |
| 9 х 2 = 10 х 2 = |
Е Н |
| 12 х 4 = 3 х 6 = | И Е |
| П | Е | Т | И | Р | Н |
| 14 | 18 | 3 | 48 | 5 | 20 |
| 24 : 8 = 6 х 3 = |
Т И |
| 15 : 3 = 9 х 2 = |
Ш И |
| 6 х 9 = 42 : 7 = |
Н А |
| 4 х 9 = 21 : 3 = |
– – |
| Ш | А | Т | И | Н |
| 5 | 6 | 3 | 18 | 54 |
Учитель: Проверяем. Что
потребовалось вам, чтобы выполнить задание? (Старание,
терпение, тишина). Все это нужно соблюдать и на
рыбалке, чтобы получить вот такой улов!
Что
потребовалось вам, чтобы выполнить задание? (Старание,
терпение, тишина). Все это нужно соблюдать и на
рыбалке, чтобы получить вот такой улов!
(На доске ведро с рыбками).
– Что будем дальше делать с уловом? (Варить уху).
(Прикрепляется иллюстрация с костром)
Итог
Учитель: Пока рыба готовится…
– Какие новые знания вы сегодня усвоили?
– С какой единицей площади познакомились?
– Что такое квадратный сантиметр?
Оценки и рефлексия
– Как вы оцениваете свою работу?
– Что получилось, что нет?
– Что для этого нужно?
– Я ставлю…
Домашнее задание: с.53 №6
– Прошу вас отразить свое отношение к уроку с помощью стикеров на экране.
Учитель: Вот наше блюдо и готово. (Дети кушают бутерброды с рыбой).
Страница не найдена — Центр развития «Ступени Роста»
Страница не найдена — Центр развития «Ступени Роста»Наверх
К сожалению мы не можем показать то, что вы искали. Может быть, попробуете поиск по сайту или одну из приведенных ниже ссылок?
Может быть, попробуете поиск по сайту или одну из приведенных ниже ссылок?
Архивы
Архивы Выберите месяц Март 2021Рубрики
РубрикиВыберите рубрикуАнонсыСтраницы
- «Объединяя опыт, воплощаем мечты»
- «Основы проектной деятельности»
- «Педагог года Удмуртии 2018»
- «Цифровое образование»
- ⇨ Конкурсы для обучающихся
- ⇨ Конкурсы для педагогов
- 1 этап
- 10
- 11
- 2
- 5
- 6
- 6
- 7
- 8
- 9
- Cеминар для руководителей музейных формирований
- I городская научно-практическая конференция «ПИРАМИДА»
- I городская научно-практическая конференция «ПИРАМИДА»
- iTeacher
- IV Межрегиональная очно-заочная научно-практическая конференция «Историко-культурное наследие славянских народов волго-камского региона»
- PRо дополнительное образование
- PRо дополнительное образование
- VIII межрегиональный конкурс «Перевод в поле многоязычия»
- XV всероссийский конкурс молодежных авторских проектов и проектов «Моя страна — моя Россия»
- Августовская конференция
- Английский язык
- Английский язык
- Английский язык — Олимпиады, конкурсы
- Английский язык — План работ на месяц
- Английский язык — Методические рекомендации
- Анонсы стажировок на 2020-2021 учебный год
- Астрономия
- Астрономия
- Астрономия — Олимпиады, конкурсы
- Астрономия — План работ на месяц
- Астрономия — Методические рекомендации
- Аттестация
- Биоинженерные классы
- Биология
- Биология
- Биология — Методические рекомендации
- Биология — Олимпиады, конкурсы
- Биология — План работ на месяц
- Вебинары
- ВЗАИМООБУЧЕНИЕ ГОРОДОВ
- Видеоматериалы и статьи
- Виртуальный методический кабинет
- Вопрос-ответ
- Всероссийская олимпиада для школьников «13 элемент.
 ALхимия будущего»
ALхимия будущего» - ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ
- Заключительный этап
- Муниципальный этап
- Региональный этап
- Школьный этап
- Всероссийская олимпиада школьников
- ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ
- ВСЕРОССИЙСКИЙ КОНКУРС «Призвание — воспитатель»
- Всероссийский конкурс «Открытое образование в открытой среде»
- Всероссийский конкурс «Читаем Солженицына»
- Всероссийский конкурс «Читаем Солженицына» — 2018
- Всероссийский конкурс сочинений 2018 года
- ВсОШ
- География
- География
- География — Олимпиады, конкурсы
- География — План работ на месяц
- География — Методические рекомендации
- Главная
- Главная
- Городская интеллектуальная игра для старшеклассников по химии «Путешествие химических элементов — 2018»
- Городская научно-практическая конференция по русскому языку и литературе «Русское слово»
- Городская олимпиада по удмуртскому языку для обучающихся 2-7 классов
- Городской конкурс «Жила – была (удмуртская, татарская) сказка…»
- Городской конкурс мультимедийных историй на иностранном языке «Digital storytelling» Городской конкурс мультимедийных историй на иностранном языке «Digital storytelling»
- Городской конкурс мультимедийных историй на иностранном языке «Digital storytelling» Городской конкурс мультимедийных историй на иностранном языке «Digital storytelling»
- Городской конкурс на лучшее эссе «Мой будущий президент»
- Городской конкурс статей «Методическая копилка»
- Грантовый конкурс «Музейный десант»
- Грантовый конкурс «Новый театр»
- Грантовый конкурс Русского географического общества 2018 года
- Гранты
- Гранты 2018 года за подготовку программистов и мероприятия в IT
- ГРАНТЫ СТД РФ НА РЕАЛИЗАЦИЮ ПРОЕКТОВ ДЛЯ ДЕТЕЙ И ПОДРОСТКОВ
- Двенадцатая Олимпиада Эйлера учителей математики Санкт-Петербурга
- Действующие НПК, в которых могут принять участие все желающие
- День 1
- День 2
- День 3
- День 4
- День 5
- ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
- Домашний час
- Дополнительное образование
- Завучу на заметку
- Зал 1
- Зал 2
- Зал 3.
 Практики дополнительного образования
Практики дополнительного образования - Зал 4. Воспитательные практики
- Зал 5. Кадетское движение
- Зал 6
- Зал 7
- Зал 7
- Зал № 4
- Зал №1
- Зал №2
- Зал №3
- Заместителю директора
- Завучу на заметку
- Нормативно-правовая документация
- Изобразительное искусство
- Изобразительное искусство — Олимпиады, конкурсы
- Изобразительное искусство — План работ на месяц
- Изобразительное искусство — Методические рекомендации
- Инженерно-технологические классы
- Инженерные классы
- Инженерный класс
- Иностранные языки
- Интеграция разных уровней образования для достижения высоких образовательных результатов
- Информатика
- Информатика
- Информатика — Олимпиады, конкурсы
- Информатика — План работ на месяц
- Информатика — Методические рекомендации
- Искусство
- Искусство
- Испанский язык
- Испанский язык
- Испанский язык — Методические рекомендации
- Испанский язык — Олимпиады, конкурсы
- Испанский язык — План работ на месяц
- История
- История
- История — Олимпиады, конкурсы
- История — План работ на месяц
- История — Методические рекомендации
- Итальянский язык
- Итальянский язык
- Итальянский язык — Методические рекомендации
- Итальянский язык — Олимпиады, конкурсы
- Итальянский язык — План работ на месяц
- Итоги конкурса «Красота родникового края»
- Итоги конкурса «Красота родникового края»
- Итоги конкурса «Красота родникового края»
- Календарь мероприятий
- КиВО — Конкурс инноваций в образовании
- Кинозал
- Китайский язык
- Классы «Бизнес-РостОК!»
- Ключи к заданиям муниципального этапа ВсОШ, 2020г.

- Ключи к заданиям муниципального этапа ВсОШ, 2020г.
- Ключи к экологии
- Ключи по китайскому языку
- Конкурс «Be My Valentine!»
- Конкурс «Будущий учитель столицы»
- Конкурс «Мелодии наших школьников»
- Конкурс «Городской пейзаж. Город вчера, сегодня, завтра»
- Конкурс «Городской пейзаж. Город вчера, сегодня, завтра»
- Конкурс «Мой лучший предметно-ориентированный урок немецкого языка»
- Конкурс «Современный урок русского языка и литературы в контексте требований ФГОС»
- Конкурс 2018 года «Самый умный абитуриент Сибири»
- Конкурс 2018 года «Самый умный абитуриент Сибири»
- Конкурс для преподавателей иностранного языка «Мой любимый кабинет иностранного языка»
- Конкурс для преподавателей иностранного языка «Мой любимый кабинет иностранного языка»
- Конкурс методических разработок «IT-учитель»
- Конкурс на получение денежного поощрения лучшим учителям в 2018 году
- Конкурс на получение денежного поощрения лучшими педагогическими работниками УР в 2018 году
- Конкурс на получение денежного поощрения лучшими педагогическими работниками УР в 2018 году
- Конкурс на получение денежного поощрения лучшими учителями 2018 года
- Конкурс на создание Центров социальных инноваций в сфере культуры
- Конкурс на участие в Осенней школе для педагогов
- конкурс по обж
- конкурс по обж
- Конкурс по программе «Поддержка ЦМИТ» (4-я очередь)
- Конкурс по финансовой грамотности и безопасности «Международный онлайн-конкурс Фоксфорда — Финансовый баттл»
- Конкурсы
- Конкурсы в рамках городского инновационного проекта «Столичный учитель»
- Конкурсы в рамках проекта «Столичный учитель»
- Конкурсы и гранты
- Конкурсы, видеоконкурсы
- Контакты
- Литература
- Личностно-профессиональная навигация педагога XXI века
- Математика
- Математика
- Математика — Олимпиады, конкурсы
- Математика — План работ на месяц
- Математика — Методические рекомендации
- Материалы с мероприятий
- Медицинский класс
- Международная Scratch-Олимпиада по креативному программированию 2018
- Международная Scratch-Олимпиада по креативному программированию 2018
- Международный технологический конкурс проектов «Imagine Cup»
- Межрегиональная образовательная онлайн-олимпиада по английскому языку Skyeng Super Cup Winter 2018
- Мероприятия
- Методическая копилка
- Методические рекомендации
- Методические рекомендации
- Молодому педагогу
- Музыка
- Музыка — Олимпиады, конкурсы
- Музыка — План работ на месяц
- Музыка — Методические рекомендации
- Муниципальная олимпиада
- Муниципальная олимпиада
- Муниципальная олимпиада по математике и русскому языку среди обучающихся 3-4 классов
- Муниципальный конкурс исследовательских работ «Кристалл-2018»
- Муниципальный конкурс исследовательских работ «Кристалл-2018»
- Муниципальный конкурс исследовательских работ «Кристалл-2018»
- Муниципальный конкурс исследовательских работ «Кристалл-2018»
- Муниципальный конкурс проектных работ школьников «Мой русский язык»
- Муниципальный конкурс творческих работ «Городской пейзаж: город вчера, сегодня, завтра»
- МУНИЦИПАЛЬНЫЙ ЭТАП
- Муниципальный этап
- МХК
- МХК — Олимпиады, конкурсы
- МХК — План работ на месяц
- МХК — Методические рекомендации
- Начальная школа
- Начальная школа
- Начальная школа — Олимпиады, конкурсы
- Начальная школа — План работ на месяц
- Начальная школа — Методические рекомендации
- Начальные классы
- Наша команда
- Наши ветераны
- Наши сборники, публикации
- Немецкий язык
- Немецкий язык
- Немецкий язык
- Немецкий язык — Олимпиады, конкурсы
- Немецкий язык — План работ на месяц
- Немецкий язык — Методические рекомендации
- Новости, мероприятия
- Нормативно-правовая документация
- НПК
- О нас
- ОБЖ
- ОБЖ
- ОБЖ — Олимпиады, конкурсы
- ОБЖ — План работ на месяц
- ОБЖ — Методические рекомендации
- Образ нового директора
- Образовательные события
- Образцы ДИПЛОМОВ в рамках муниципальной олимпиады по математике и русскому языку (3-4 классы)
- Обществознание
- Обществознание
- Обществознание — Олимпиады, конкурсы
- Обществознание — План работ на месяц
- Обществознание — Методические рекомендации
- Олимпиада НТИ
- Олимпиады для школьников на 2017-2018 учебный год
- Олимпиады, конкурсы
- Онлайн — турнир знатоков русского языка «Самый умный»
- ОРКСЭ
- ОРКСЭ — Олимпиады, конкурсы
- ОРКСЭ — План работ на месяц
- ОРКСЭ — Методические рекомендации
- Особому ученику качественное образование
- Особый ребенок в обычной школе: «Гибкие классы»
- Отчеты
- План и положения
- План работ на месяц
- План работ на месяц
- План работы
- Платные услуги
- Повышение качества образования в школах с низкими результатами обучения
- Подборка полезных сайтов
- Подборка полезных сайтов
- Право
- Право
- Право — Олимпиады, конкурсы
- Право — План работ на месяц
- Право — Методические рекомендации
- Предварительные результаты муниципального этапа, 2020 г.

- Предварительные результаты МЭ ВсОШ по экологии, 2020 г.
- про
- Проект «УРОКИ НАСТОЯЩЕГО»
- Проект “Образ нового директора. Трансформация”
- Проектный офис
- Протоколы по китайскому языку
- Профессиональные консультации: вы спрашивайте — мы отвечаем
- Профессиональные сообщества (Учителя — предметники)
- Публикации
- Региональный конкурс Челябинского университетского образовательного конкурса
- РЕГИОНАЛЬНЫЙ ЭТАП
- Республиканский конкурс «Педагог года Удмуртии 2018»
- Республиканский конкурс «Педагог года Удмуртии 2018»
- Республиканский конкурс «Учитель здоровья Удмуртии — 2018»
- Робототехника
- Родные языки
- Руководителю методической службы
- Русский язык
- Русский язык, литература
- Русский язык, литература — Олимпиады, конкурсы, конференции
- Русский язык, литература — План работ на месяц
- Русский язык, литература — Методические рекомендации
- Сведения об организации
- Семинар «Школьная библиотека 2.
 0 как ресурс индивидуализации обучения»
0 как ресурс индивидуализации обучения» - Сетевая конференция проектных работ
- СМИ о нас
- Создание системы воспитательной и внеурочной деятельности в муниципальной социальной системе
- Социальный
- Стипендия Хорнби 2018-2019 года для преподавателей английского языка
- Столичный учитель
- Татарский язык
- Татарский язык
- Татарский язык — Методические рекомендации
- Татарский язык — Олимпиады, конкурсы
- Татарский язык — План работ на месяц
- Технология
- Технология
- Технология — Олимпиады, конкурсы
- Технология — План работ на месяц
- Технология — Методические рекомендации
- Удмуртский язык
- Удмуртский язык
- Удмуртский язык — Методические рекомендации
- Удмуртский язык — Олимпиады, конкурсы
- Удмуртский язык — План работ на месяц
- Урок в музее
- Урок в школьном музее
- Участники Муниципального этапа от районов
- Участники Муниципального этапа от районов
- Учителю МКОУ— Олимпиады, конкурсы
- Физика
- Физика
- Физика — Олимпиады, конкурсы
- Физика — План работ на месяц
- Физика — Методические рекомендации
- Физическая культура
- Физическая культура — Олимпиады, конкурсы
- Физическая культура — План работ на месяц
- Физическая культура — Методические рекомендации
- Физкультура
- Финансовая грамотность
- Финансовая грамотность — Методические рекомендации
- Финансовая грамотность — Олимпиады, конкурсы
- Финансовая грамотность — План работ на месяц
- Формула успеха
- Фотоконкурс по Периодической Системе Элементов имени Д.
 И.Менделеева
И.Менделеева - Фотоконкурс по Периодической Системе Элементов имени Д.И.Менделеева
- Французский язык
- Французский язык
- Французский язык — Олимпиады, конкурсы
- Французский язык — План работ на месяц
- Французский язык — Методические рекомендации
- ХIV Республиканская конференция школьников по русскому языку и литературе «Лишь слову жизнь дана…»
- Химия
- Химия
- Химия
- Химия — Олимпиады, конкурсы
- Химия — План работ на месяц
- Химия — Методические рекомендации
- Хочу быть директором
- Школьному библиотекарю
- Школьный этап
- ШКОЛЬНЫЙ ЭТАП
- Экология
- Экология
- Экология — Олимпиады, конкурсы
- Экология — План работ на месяц
- Экология — Методические рекомендации
- Экономика
- Экономика
- Экономика — Олимпиады, конкурсы
- Экономика — План работ на месяц
- Экономика — Методические рекомендации
- Эффективная начальная школа
Контрольные работы по математике по программе развивающего обучения Л.
 В. Занкова (авторы учебника И И Аргинская, Е И. Ивановская.и др.) 4 класс. | Учебно-методический материал по математике (4 класс) по теме:
В. Занкова (авторы учебника И И Аргинская, Е И. Ивановская.и др.) 4 класс. | Учебно-методический материал по математике (4 класс) по теме:Контрольные работы по математике по программе развивающего обучения Л. В. Занкова (авторы учебника И И Аргинская, Е И. Ивановская.и др.) 4 класс.
Данная подборка содержит 13 контрольных работ, каждая из которых имеет 1и2 варианты
Для составления контрольных работ были использованы методические издания:
1.Математика «Поурочные планы» по учебнику И. И. Аргинской.
Издательство «Учитель» г. Волгоград 2010 г.
2.Учебник «Математика» автор Аргинская И. И. ( Издательский дом «Фёдоров») 2012 г
3.Контрольные и проверочные работы по системе Л. В. Занкова . ( Издательский дом «Фёдоров») 2014г.
4. И. И. Аргинская «Сборник заданий по математике «Издательский дом «Фёдоров») 2009г.
5. Журнал «Начальная школа» октябрь 2013г.. декабрь 2012г., апрель 2013г.
6.О. В. Узорова, Е. А. Нефёдова «2500 задач по математике» (Издательство . »Астрель» 2010 г.
»Астрель» 2010 г.
ВХОДНАЯ КОНТРОЛЬНАЯ РАБОТА 1
Цель: проверка остаточных знаний :
1) вычислительных приемов сложения, вычитания, умножения и деления в пределах 1000;
2) правил порядка выполнения действий в выражениях;
3) единиц длины, площади; 4) умения решать задачи.
I в а р и а н т
1 А). Решите задачу.
С одного участка школьники собрали 160 кг моркови, а с другого – в 2 раза больше. Четвертую часть всей моркови они израсходовали на корм кроликам. Сколько килограммов моркови израсходовали на корм кроликам?
Б).Измени вопрос, чтобы решение задачи было длиннее.
2. А). Найдите значения выражений.
18 + 36 : 9 + 6 · 8 – 50
400 – (80 + 180 : 3) + 60
Б). Во втором выражении удали скобки и реши новое выражение.
3. Решите примеры столбиком.
138 + 567 152 · 6
447 – 189 867 : 3
4. Переведите.
125 см = …м …дм …см 7 м 3 см = …см
847 дм = …м …дм 700 см2 = …дм2
5. Начертите прямоугольник со сторонами 5 см и 3 см. Найдите его площадь и периметр.
Начертите прямоугольник со сторонами 5 см и 3 см. Найдите его площадь и периметр.
II в а р и а н т
1. А).Решите задачу.
На одном участке школьники вырастили 240 кг капусты, на другом – в 2 раза меньше. Четвертую часть всей капусты израсходовали на корм кроликам. Сколько килограммов капусты израсходовали на корм кроликам?
Б).Измени вопрос, чтобы решение задачи было длиннее
2. А). Найдите значения выражений.
(18 + 36) : 9 + 6 · 8 – 50
720 : (2 + 7) + (140 – 90)
Б). Во втором выражении удали скобки и реши новое выражение.
3. Решите примеры столбиком.
523 + 197 279 · 3
831 – 369 792 : 2
4. Переведите.
8 м 4 см = …см 275 см = …м …дм …см
900 см2 = …дм 631 дм = …м …дм
5. Начертите прямоугольник со сторонами 6 см и 2 см. Найдите площадь и периметр этого прямоугольника.
ПРОВЕРОЧНАЯ РАБОТА №2 ПО ТЕМЕ «НУМЕРАЦИЯ»
Цели:
– проверить умения записывать многозначное число в пределах класса тысяч;
– определять место каждого из них в натуральном ряду;
– устанавливать отношения между изученными натуральными числами и записывать при помощи знаков;
– определять количество десятков и сотен.
В а р и а н т I
З а д а н и е 1.
а) Запишите числа, которые стоят в натуральном ряду между числами:
3495 и 3508;
997 и 10009;
183989 и 184003.
б) С данными числами составь как можно больше верных неравенств.
З а д а н и е 2.
а) Расположи в порядке возрастания числа:
2649, 2651, 2645, 2655, 2658, 2644, 2647, 2643;
4789, 4792, 4804, 4795, 4807, 4798, 4803, 4790.
б) Запиши пропущенные между ними числа.
З а д а н и е 3.
а) Напиши, чем похожи числа:
137245, 132745, 532741, 714352.
б) Запиши еще 5 чисел, используя подмеченное сходство.
З а д а н и е 4.
а) Какие цифры можно поставить вместо звездочек, чтобы неравенство было верным:
2967 > 296* 748*
53*8 47*9?
б) Запиши все возможные неравенства.
З а д а н и е 5.
а) Запиши цифрами числа:
десять тысяч сто девять;
двести пять тысяч сорок четыре;
семьсот тысяч двести девяносто два;
тридцать пять тысяч девяносто два;
пятьдесят тысяч пятьсот семьдесят.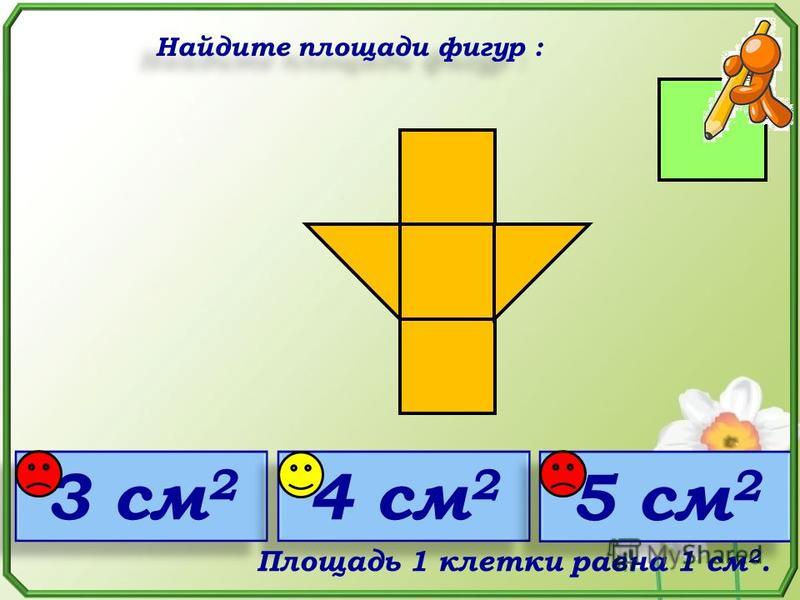
б) Данные числа представь в виде суммы разрядных слагаемых.
В а р и а н т II
З а д а н и е 1.
а) Запишите числа, которые стоят в натуральном ряду между числами:
7857 и 7865;
53995 и 54006;
412991 и 413005.
б) С данными числами составь как можно больше верных неравенств.
З а д а н и е 2.
а) Расположи в порядке убывания числа:
3649, 3651, 3645, 3655, 3658, 3644, 3647, 3643;
5689, 5692, 5704, 5695, 5707, 5698, 5703, 5690.
б) Запиши пропущенные между ними числа.
З а д а н и е 3.
а) Напиши, чем похожи числа:
967834, 679384, 436789, 876439.
б) Запиши еще 5 чисел, используя подмеченное сходство.
З а д а н и е 4.
а) Какие цифры можно поставить вместо звездочек, чтобы неравенство было верным:
2967 7488
53*8 > 53*6 47*5
б) Запиши все возможные неравенства.
З а д а н и е 5.
а) Запиши цифрами числа:
десять тысяч сто пять;
триста шесть тысяч пятьсот семь;
пятьсот тысяч сто тридцать два;
сорок шесть тысяч восемьдесят восемь;
двадцать тысяч восемьсот пятьдесят.
б) Данные числа представь в виде суммы разрядных слагаемых.
ПРОВЕРОЧНАЯ РАБОТА №3 ПО ТЕМЕ
«ПЛОЩАДЬ, ПЕРИМЕТР»
Цели:
– проверить умения определять площадь прямоугольного треугольника;
– решать составные задачи на нахождение площади и периметра фигур;
– выражать изученные величины, используя разные меры их измерения.
В а р и а н т I
З а д а н и е 1.
а) Реши задачу.
Периметр прямоугольника 32 см. Длина одной его стороны на 2 см меньше длины другой. Найдите площадь прямоугольника.
б) Запишите длину сторон других прямоугольников с таким же периметром.
З а д а н и е 2.
а) Реши задачу.
Стороны прямоугольника равны 10 см и 8 см. Определи его периметр и площадь.
б) Как изменятся периметр и площадь прямоугольника, если каждую его сторону увеличить на 2 см? (Постарайся найти ответ, не вычисляя периметр и площадь нового прямоугольника.)
З а д а н и е 3.
а) Начерти прямоугольный треугольник с двумя сторонами, равными 5 см и 7 см, и определи его площадь. (Постарайся найти не одно решение.)
(Постарайся найти не одно решение.)
б) Как изменится площадь данного треугольника, если одну сторону увеличить на 2 см?
З а д а н и е 4.
Заполни пропуски так, чтобы получились верные равенства:
3 м2 86 см2 = … см2
4 дм2 5 мм2 = … мм2
6 м2 7 дм2 = … дм2
8 см2 24 мм2 = … мм2
З а д а н и е 5.
а) Площадь прямоугольного треугольника равна 16 см2. Определи длины сторон, образующих прямой угол.
б) Из четырех прямоугольных треугольников составили четырехугольник. Чему равна площадь данного четырехугольника?
З а д а н и е 6. а) Вычисли площадь четырехугольника АВСD разными способами. б) Подчеркни рациональный способ. |
В а р и а н т II
З а д а н и е 1.
а) Реши задачу.
Периметр прямоугольника 48 мм. Длина одной его стороны на 3 мм больше длины другой. Найди площадь прямоугольника.
Найди площадь прямоугольника.
б) Запиши длину сторон других прямоугольников с таким же периметром.
З а д а н и е 2.
а) Реши задачу.
Стороны прямоугольника равны 9 дм и 10 дм. Определи его периметр и площадь.
б) Как изменятся периметр и площадь прямоугольника, если каждую его сторону увеличить на 4 см? (Постарайся найти ответ, не вычисляя периметр и площадь нового прямоугольника.)
З а д а н и е 3.
а) Начерти прямоугольный треугольник с двумя сторонами, равными 6 см и 4 см, и определи его площадь. (Постарайся найти не одно решение.)
б) Как изменится площадь данного треугольника, если одну сторону увеличить на 2 см?
З а д а н и е 4.
Заполни пропуски так, чтобы получились верные равенства:
4 м2 74 см2 = … см2
3 дм2 6 мм2 = … мм2
7 м2 8 дм2 = … дм2
9 см2 36 мм2 = … мм2
З а д а н и е 5.
а) Площадь прямоугольного треугольника равна 36 см2. Определи длины сторон, образующих прямой угол.
б) Из трех данных прямоугольных треугольников составили четырехугольник.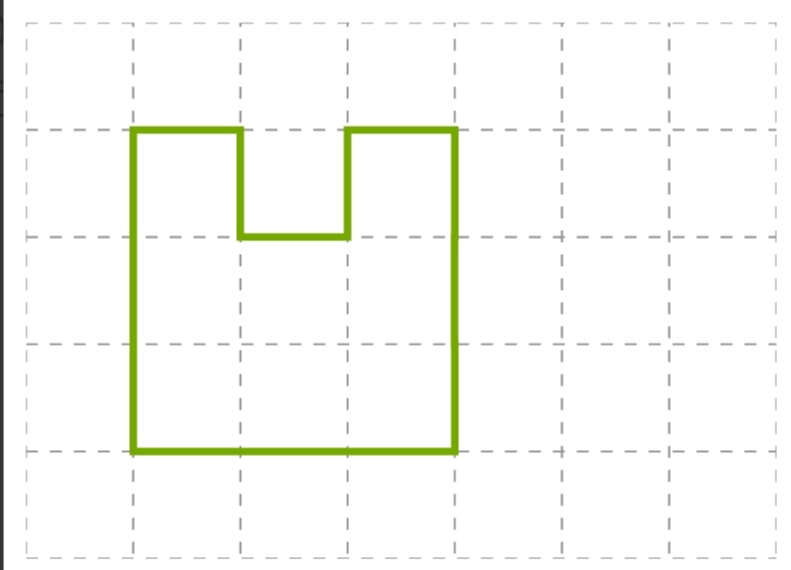 Чему равна площадь данного четырехугольника?
Чему равна площадь данного четырехугольника?
З а д а н и е 6. а) Вычисли площадь четырехугольника АВСD разными способами. б) Подчеркни рациональный способ. |
КОНТРОЛЬНАЯ РАБОТА №4. ПО ИТОГАМ I ЧЕТВЕРТИ
Цели:
– проверить навыки и умения решать задачи, сложные выражения, задачи на вычисление площади прямоугольного треугольника;
– контролировать знание нумерации многозначных чисел;
– выявить умения составлять и решать простые уравнения и преобразовывать их в более сложные.
I в а р и а н т
Задание 1. Решите задачу.
Для школьной столовой засолили огурцы. В первый день засолили огурцы в 5 бочонках, по 18 кг в каждом. Во второй день огурцов засолили на 105 кг больше, чем в первый день. Сколько кг огурцов засолили за два дня?
Задание 2. Решите примеры.
(210 – 30) : 9 · (999 + 1)
70 + 350 : 7 · (10 + 990)
Задание 3. Сравните.
Сравните.
48 м 9 см … 48 м 9 дм 3 т 5 ц … 3 т 240 кг
43 000 м … 4 км 300 м 400 ц … 4 т
З а д а н и е 4.
а) Составь, запиши и реши уравнение, для решения которого нужно выполнить одно действие первой ступени (постарайся найти все возможные варианты таких уравнений).
б) Преобразуй свое уравнение так, чтобы для его решения нужно было выполнить 2 действия первой ступени.
З а д а н и е 5.
а) Найди площадь прямоугольного треугольника, у которого стороны, образующие прямой угол, равны 4 см и 5 см.
б) Начерти две фигуры, которые можно сложить из трех таких треугольников, и определи их площадь.
Вариант-2.
Задание 1. Решите задачу.
С одного опытного участка школьники собрали 4 мешка картофеля, по 50 кг в каждом, а со второго на 110 кг больше, чем с первого. Сколько кг картофеля школьники собрали с двух участков?
Задание 2. Решите примеры.
(480 + 320) : 8 · (9 + 91)
7200 : (2 + 7) + (140 – 90)
Задание 3.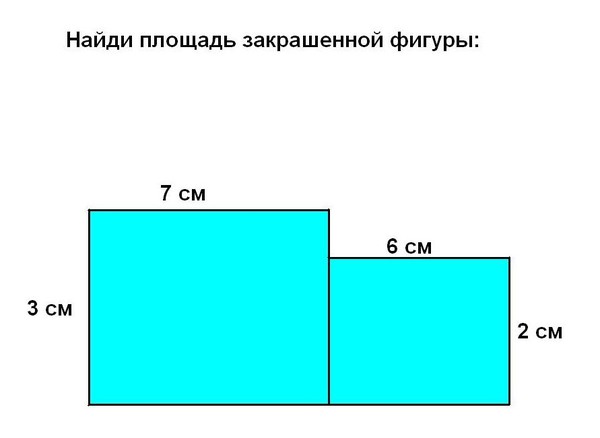 Сравните.
Сравните.
6 м 7 см … 6 м 7 дм 3 т … 300 ц
9 км 3 м … 9 030 м 4 т 6 ц … 4 т 550 кг
40 а … 4 000 м2 8 ц 2 кг … 82 кг
З а д а н и е 4.
а) Составь, запиши и реши уравнение, для решения которого нужно выполнить одно действие второй ступени (постарайся найти все возможные варианты таких уравнений).
б) Преобразуй свое уравнение так, чтобы для его решения нужно было выполнить два действия второй ступени.
З а д а н и е 5.
а) Найди площадь прямоугольного треугольника, у которого стороны, образующие прямой угол, равны 3 см и 6 см.
б) Начерти две фигуры, которые можно сложить из четырех таких треугольников, и определи их площадь.
ПРОВЕРОЧНАЯ РАБОТА №5 ПО ТЕМЕ
«ДЕЙСТВИЯ С МНОГОЗНАЧНЫМИ ЧИСЛАМИ»
Цели: проверить навыки вычислений, умение устанавливать порядок действий в сложных выражениях.
В а р и а н т I
З а д а н и е 1.
а) Выполни сложение и запиши признак сходства всех данных сумм:
1) 347 + 431 472 + 415 644 + 253 112 + 247 | 2) 347 + 435 678 + 315 546 + 240 118 + 247 | 3) 365 + 572 475 + 451 265 + 353 741 + 186 |
б) Допиши три подходящие суммы и найди их значения.
З а д а н и е 2.
а) Выполни вычитание и запиши признак сходства всех данных разностей:
1) 347 – 225 793 – 450 876 – 432 956 – 423 | 2) 785 – 569 770 – 644 583 – 469 946 – 718 | 3) 979 – 791 856 – 374 238 – 175 546 – 492 |
б) Допиши три подходящих разности и найди их значения.
З а д а н и е 3.
а) Найди значения сумм разными способами и подчеркни самый рациональный из них:
37 + 12 + 63 + 88
76 + 124 + 11 + 89
997 + 838 + 1162 + 1003
б) Составь и запиши свои три суммы, значения которых можно найти таким же рациональным способом.
З а д а н и е 4.
а) Раздели на группы выражения, связанные между собой:
80 · 3 448 : 8 236 : 4 56 · 8 240 : 3 | 240 : 80 236 : 59 448 : 56 59 · 4 |
б) Найди значения выражений каждой группы.
в) Дополни каждую группу недостающим выражением.
З а д а н и е 5.
а) Выпиши частные, в значениях которых цифр меньше, чем в делимых:
7*** : 3 6** : 4 5***** : 8 | 3**** : 5 3**** : 6 8*** : 4 |
б) В любом из выписанных частных замени звездочки цифрами так, чтобы можно было выполнить деление без остатка.
З а д а н и е 6.
а) Выполни деление в столбик:
972 : 9 864 : 8 37112 : 2 612 : 2 | 945 : 9 3216 : 4 8376 : 4 735 : 7 |
б) Раздели данные равенства на группы.
В а р и а н т II
З а д а н и е 1.
а) Выполни сложение и запиши признак сходства всех данных сумм:
1) 227 + 632 505 + 492 513 + 457 701 + 213 | 2) 257 + 439 405 + 367 718 + 146 108 + 513 | 3) 272 + 362 538 + 391 284 + 593 384 + 343 |
б) Допиши три подходящие суммы и найди их значения.
З а д а н и е 2.
а) Выполни вычитание и запиши признак сходства всех данных сумм:
1) 649 – 346 463 – 333 586 – 172 285 – 73 | 2) 563 – 248 891 – 679 672 – 415 462 – 153 | 3) 408 – 234 647 – 382 307 – 183 757 – 463 |
б) Допиши три подходящие разности и найди их значения.
З а д а н и е 3.
а) Найди значения сумм разными способами и подчеркни самый рациональный из них:
164 + 79 + 921 + 236
95 + 75 + 905 + 125
25 + 666 + 334 + 275
б) Составь и запиши свои три суммы, значения которых можно найти таким же рациональным способом.
З а д а н и е 4.
а) Раздели на группы выражения, связанные между собой:
364 : 7 228 : 3 3 · 76 104 · 7 728 : 4 | 7 · 52 76 · 3 7 · 104 364 : 52 |
б) Найди значения выражений каждой группы.
в) Дополни каждую группу недостающим выражением.
З а д а н и е 5.
а) Выпиши частные, в значениях которых цифр меньше, чем в делимых:
1***** : 2 5**** : 3 6** : 7 | 3**** : 5 34*** : 6 8*** : 4 |
б) В любом из выписанных частных замени звездочки цифрами так, чтобы можно было выполнить деление без остатка.
З а д а н и е 6.
а) Выполни деление в столбик:
627 : 3 545 : 5 63828 : 9 856 : 8 | 816 : 4 9448 : 8 6315 : 5 832 : 4 |
б) Раздели данные равенства на группы.
КОНТРОЛЬНАЯ РАБОТА №6 ПО ТЕМЕ
«ЗАДАЧИ НА ДВИЖЕНИЕ»
Цели: проверить умения решать задачи на движение и выражать меры длины, используя разные единицы измерения.
В а р и а н т I
З а д а н и е 1.
а) Реши задачу арифметически двумя способами.
Два пешехода одновременно вышли навстречу друг другу из двух поселков и встретились через 3 ч. Определи расстояние между поселками, если один пешеход двигался со скоростью 5 км/ч, а другой – 6 км/ч.
б) Подчеркни способ, который больше нравится.
З а д а н и е 2.
а) Реши задачу.
Самолет проделал путь в 6590 км. 4 часа он летел со скоростью 920 км/ч, а остальной путь – со скоростью 970 км/ч. Сколько часов самолет был в пути?
б) Измени условие задачи так, чтобы ее решение стало короче. Реши эту задачу.
З а д а н и е 3.
Найди все возможные решения задачи.
Два поезда вышли одновременно с одной станции. Скорость одного поезда – 75 км/ч, а другого – 82 км/ч. На каком расстоянии друг от друга они будут через 3 часа?
З а д а н и е 4.
а) Реши задачу.
Турист проехал на машине 16 часов со скоростью 92 км/ч, а остальную часть пути на поезде со скоростью 56 км/ч. Весь путь равен 2424 км. Сколько всего часов турист был в пути?
Весь путь равен 2424 км. Сколько всего часов турист был в пути?
б) Измени условие задачи так, чтобы нужно было узнать весь путь, который проехал турист..
З а д а н и е 5.
Запиши верные равенства или неравенства:
36 дм 3 мм … 36003 мм
240 км 47 м … 24047 м
106 км 9 м … 106009 м
14 см 3 мм … 134 мм
85 м 4 дм … 8540 дм
1 км 206 м … 12060 м
В а р и а н т II
З а д а н и е 1.
а) Реши задачу арифметически двумя способами.
Две улитки начали одновременно ползти по одной ветке навстречу друг другу и встретились через 3 минуты. Скорость одной улитки 3 м/мин, а другой – 2 м/мин. На каком расстоянии друг от друга были улитки до начала движения?
б) Подчеркни способ, который больше нравится.
З а д а н и е 2.
а) Реши задачу.
Поезд проехал 704 км. 9 часов он шел со скоростью 52 км/ч, а остальной путь – со скоростью 48 км/ч. Сколько часов поезд был в пути?
б) Измени условие задачи так, чтобы ее решение стало короче. Реши эту задачу.
Реши эту задачу.
З а д а н и е 3.
Найди все возможные решения задачи.
Два катера вышли одновременно с одной пристани. Скорость одного катера 25 км/ч, а другого – 28 км/ч. На каком расстоянии друг от друга они будут через 5 часов
З а д а н и е 4.
а) Реши задачу.
Турист проехал на поезде 9 часов со скоростью 83 км/ч, а остальную часть пути на самолете со скоростью 950 км/ч. Весь путь равен 4547 км. Сколько всего часов турист был в пути?
б) Измени условие задачи так, чтобы нужно было узнать весь путь, который проехал турист.
З а д а н и е 5.
Запиши верные равенства или неравенства:
42 дм 4 мм … 42004 мм
360 км 54 м … 36054 м
207 км 9 м … 207009 м
73 м 5 дм … 7350 дм
27 см 4 мм … 274 мм
5 км 602 м … 50602 м
КОНТРОЛЬНАЯ РАБОТА №7 ПО ИТОГАМ II ЧЕТВЕРТИ
Цель: проверить навыки и умения решать задачи на вычисление периметра и площади геометрических фигур, сложные уравнения; знание нумерации многозначных чисел; умения решать сложные уравнения и выполнять проверку.
В а р и а н т I
З а д а н и е 1.
а) Реши задачу арифметически двумя способами.
В книге 128 страниц. Юра прочитал всех страниц. Сколько страниц ему осталось прочитать?
б) Подчеркни способ, который тебе больше нравится.
в) Измени вопрос задачи так, чтобы ее решение стало короче.
З а д а н и е 2.
а) Запиши число, у которого:
375 единиц второго класса и 79 единиц первого класса;
500 единиц второго класса и на 103 единицы меньше первого класса;
81 единица второго класса и в 3 раза меньше единиц первого класса.
б) Запиши несколько других чисел, которые можно составить из классов данных чисел.
З а д а н и е 3.
а) Укажи порядок выполнения действий и найди значение выражения:
128 · 19 – 675 + 34125 : 5.
б) Не изменяя чисел и знаков действий, измени выражение так, чтобы его значение изменилось.
З а д а н и е 4.
Реши уравнения и сделай проверку.
7у + 9 – 5у = 13
(k + 2958) : 87 = 134
З а д а н и е 5.
а) Начерти прямоугольник, периметр которого равен периметру треугольника со сторонами 1 дм, 4 см, 8 см.
б) Постарайся найти не одно решение.
в) Найди площадь одного найденного прямоугольника.
З а д а н и е 6*.
Сумма цифр двузначного числа равна наименьшему двузначному числу. Цифры в разряде десятков обозначают число, в четыре раза больше, чем цифры в разряде единиц. Какое это двузначное число?
В а р и а н т II
З а д а н и е 1.
а) Реши задачу арифметически двумя способами.
В школьном хоре 150 человек. из них составляют девочки. Сколько в хоре мальчиков?
б) Подчеркни способ, который тебе больше нравится
З а д а н и е 2.
а) Запиши число, у которого:
209 единиц второго класса и 79 единиц первого класса;
705 единиц второго класса и на 109 единиц больше первого класса;
180 единиц второго класса и в 3 раза больше единиц первого класса.
б) Запиши несколько других чисел, которые можно составить из классов данных чисел.
З а д а н и е 3.
а) Укажи порядок выполнения действий и найди значение выражения:
1000 – 31518 : 6 + 706 · 18.
б) Не изменяя чисел и знаков действий, измени выражение так, чтобы его значение изменилось.
З а д а н и е 4.
Реши уравнения и сделай проверку.
10х + 3 – х = 39
(у – 72) : 84 = 204
З а д а н и е 5.
а) Начертите прямоугольник, периметр которого равен периметру четырехугольника со сторонами длиной 9 см, 6 см, 8 см и 7 см.
б) Постарайся найти не одно решение.
в) Найди площадь одного найденного прямоугольника.
З а д а н и е 6*.
Сумма цифр двузначного числа равна наименьшему двузначному числу. Цифры в разряде десятков обозначают число, в четыре раза меньше, чем цифры в разряде единиц. Какое это двузначное число?
КОНТРОЛЬНАЯ РАБОТА №8 ПО ТЕМЕ «УРАВНЕНИЯ.
РЕШЕНИЕ ЗАДАЧ АЛГЕБРАИЧЕСКИМ СПОСОБОМ»
Цель: проверка умения решать уравнения и задачи с помощью составления уравнения.
В а р и а н т I
З а д а н и е 1.
а) Запиши уравнения в порядке увеличения сложности их решения:
х + 6 · 8 = 427 – 389
у : 7 = 94
2 · n – 391 = 73 · 5 + 109
е · 8 + 267 = 1755
б) Реши уравнения и напиши, сколько для каждого из них потребовалось действий.
З а д а н и е 2.
Будут ли в уравнениях равные корни? Напиши ответ и объясни его:
6 · (х – 3) + 2 · (х + 2) = 10;
6 · (х – 3) = 10 – 2 · (х + 2).
З а д а н и е 3.
Составь уравнение по тексту задачи и реши его.
Купили 12 пачек фруктового сока по 7 р. за пачку и 5 пачек томатного сока. Сколько стоит пачка томатного сока, если за весь сок заплатили 129 р.?
З а д а н и е 4.
а) Вставь пропущенные числа, чтобы все уравнения имели одинаковые корни:
□ + х = □;
□ : х + х = □ + □;
(□ + □) : □ + х = □ : □ + □.
б) Найди корень уравнений.
З а д а н и е 5.
а) Используя данную схему, составь уравнение:
б) Реши уравнение.
В а р и а н т II
З а д а н и е 1.
а) Запиши уравнения в порядке увеличения сложности их решения:
6 · р – (468 + 9 · 7) = 405
875 : n + 194 = 219
16 + b = 32
(537 – 129 · 4) · t = 15414
б) Реши уравнения и напиши, сколько для каждого из них потребовалось действий.
З а д а н и е 2.
Будут ли в уравнениях равные корни? Напиши ответ и объясни его:
8 · (у + 3) + 4 · (у – 2) = 30;
6 · (у + 3) = 30 – 4 · (у – 2).
З а д а н и е 3.
Составь уравнение по тексту задачи и реши его.
В школьный буфет привезли 6 коробок конфет по 9 кг в каждой и 5 коробок зефира. Какова масса коробки зефира, если всего в школьный буфет привезли 84 кг сладостей?
З а д а н и е 4.
а) Вставь пропущенные числа, чтобы все уравнения имели одинаковые корни:
х – □ = □;
х – □ : = □ + □;
х – (□ + □) : □ = □ : □ + □.
б) Найди корень уравнений.
З а д а н и е 5.
а) Используя данную схему, составь уравнение:
б) Реши уравнение.
КОНТРОЛЬНАЯ РАБОТА №9 ПО ТЕМЕ
«ОБЪЕМ И ЕГО ИЗМЕРЕНИЕ»
Цели: проверить умения находить периметр, площадь и объем; решать составные задачи.
В а р и а н т I
З а д а н и е 1.
Длина прямоугольного листа бумаги – 8 см, а ширина на 4 см меньше. Определи периметр и площадь этого листа.
З а д а н и е 2.
Высота комнаты – 2 м, длина комнаты в 5 раз больше высоты, а ширина на 3 м меньше длины. Найди объем комнаты.
З а д а н и е 3.
Заполни пропуски.
3 см3 = … мм3 3 м3 = … см3 | 4 дм3 15 см3 = … см3 7 м3 114 см3 = … см3 |
В а р и а н т II
З а д а н и е 1.
Длина участка 10 м, а ширина на 3 см меньше. Определи периметр и площадь этого участка.
З а д а н и е 2.
Высота коробки – 3 дм, длина коробки в 6 раз больше высоты, а ширина на 2 дм меньше длины. Найди объем комнаты.
Найди объем комнаты.
З а д а н и е 3.
Заполни пропуски.
6 дм3 = … см3 7 м3 = … дм3 | 8 дм3 34 см3 = … см3 2 м3 297 см3 = … см3 |
ПРОВЕРОЧНАЯ РАБОТА №10 . ПО ТЕМЕ
«ДЕЙСТВИЯ С ИМЕНОВАННЫМИ ЧИСЛАМИ»
Цели: проверить знания алгоритма письменного выполнения действий с величинами, алгоритма письменного умножения и деления на двузначное и трехзначное число, умение решать задачи с именованными числами.
В а р и а н т I
З а д а н и е 1.
На сколько килограммов 35 т 74 кг больше 19 т 186 кг?
Во сколько раз 243 м 32 см больше 3 м 8 см?
Во сколько раз 7 ц 84 кг меньше 477 т 456 кг?
З а д а н и е 2.
Поставьте знаки >,
3 м 8 мм + 2 м 7 мм … 8 км 400 м : 8
4 кг 800 г : 6 … 34 кг – 33 кг 200 г
402 м 64 см : 56 … 183 см 7 мм · 4.
З а д а н и е 3.
Вставьте пропущенные числа, чтобы получились верные записи:
3057 м 24 см : □ = 876 см
6 ц 34 кг · □ = 29 т 7 ц 98 кг
□ ч – □ ч = 5 сут.
З а д а н и е 4.
Разгадайте правило, по которому связаны между собой тройки величин, и заполните пустые клетки.
7 км | 69930 дм | 7 м | 7 дм | 7 см | ||
7 т | 630 кг | 7 ц | 7 ц | 7 кг | ||
7 м | 630 см | 7 дм | 7 ч | 7 мин |
З а д а н и е 5.
а) Решите задачу.
С одного участка собрали 11 ц 80 кг моркови, что на 790 кг меньше, чем со второго, а с третьего – в 3 раза больше, чем с первого. На сколько больше килограммов моркови собрали с третьего участка, чем со второго?
б) Измените вопрос так, чтобы последнее действие было сложнее.
З а д а н и е 6.
а) Найдите значение выражения:
200823 : 917 · 84 + 47432 : 52 · 213.
б) Преобразуйте выражение так, чтобы его значение не изменилось.
В а р и а н т II
З а д а н и е 1.
На сколько килограммов 42 т 15 кг больше 39 т 289 кг?
Во сколько раз 181 м 72 см больше 3 м 8 см?
Во сколько раз 13 г меньше 2 кг 28 г?
З а д а н и е 2.
Поставьте знаки >,
6 дм 9 мм + 2 дм 5 мм … 6 м 3 дм : 9
4 кг 200 г : 6 … 23 кг – 22 кг 300 г
228 м 15 см : 27 … 203 см 8 мм · 4
З а д а н и е 3.
Вставьте пропущенные числа, чтобы получились верные записи:
30457 м 12 см : □ = 793 см
9 ц 34 кг · □ = 79 т 3 ц 90 кг
□ с – □ с = 2 ч
З а д а н и е 4.
Разгадайте правило, по которому связаны между собой тройки величин, и заполните пустые клетки.
8 м | 720 см | 8 дм | 8 ц | 8 кг | ||
8 км | 79920 дм | 8 м | 8 дм | 8 см | ||
8 т | 7200 кг | 8 ц | 8 ч | 8 мин |
З а д а н и е 5.
а) Решите задачу.
В зоопарке для животных заготавливают 12 ц 30 кг мяса, что на 950 кг меньше, чем рыбы, а овощей – в 4 раза больше, чем мяса. На сколько килограммов больше заготавливают в зоопарке овощей, чем рыбы?
б) Измените вопрос так, чтобы последнее действие было сложнее.
З а д а н и е 6.
а) Найдите значение выражения:
344442 : 417 · 93 + 60768 : 72 · 123
б) Преобразуйте выражение так, чтобы его значение не изменилось.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА №11. (3-Я ЧЕТВЕРТЬ)
Цели:
– проверить знания алгоритма письменного умножения и деления на двузначное число, умение применять эти знания при решении текстовых задач, производить действия с величинами.
В а р и а н т I
З а д а н и е 1.
а) Найди корни уравнений и сделай проверку:
5х – 4х + 7 = 10;
9 + 6у – 5 – 5у = 5;
11р + 42 – 2р + 9р = 100 – 32.
б) Напиши, какими знаниями ты при этом воспользовался.
З а д а н и е 2.
а) Найди рационально значение выражения:
4 т 150 кг · 69 – 4 т 15 кг · 69 + 7 т 900 кг · 69.
б) Запиши два выражения с другими величинами, значения которых удобно найти тем же способом.
в) Найди значения записанных выражений.
З а д а н и е 3.
Запиши пропущенные единицы величин, используя разные варианты:
891… = 7… 9 …. 1…
786… = 7… 8… 6…
З а д а н и е 4.
Вставь пропущенные числа, чтобы получились верные равенства:
□ : 43 = 178 54027 : □ = 69 □ · 184 = 118496 | □ : 29 = 198 52668 : □ = 84 □ · 186 = 141918 |
З а д а н и е 5.
а) Расположи выражения в порядке возрастания их значений, не выполняя деления:
15048 : 418 7618 : 586 | 9528 : 397 12816 : 267 |
б) Составь сложное выражение, используя данные частные.
в) Найди его значение.
З а д а н и е 6.
а) Реши задачу.
Косяк журавлей в первый день пролетел 318 км, во второй день – 424 км. На весь этот путь он затратил 14 ч. Сколько часов был в пути косяк журавлей каждый день, если он летел с одинаковой скоростью?
б) Измени задачу так, чтобы ее решение стало короче.
В а р и а н т II
З а д а н и е 1.
а) Найди корни уравнений и сделай проверку:
8а – 3 – 7а = 11;
15t + 30 – 12t = 42;
3b – 2 + 6b – 8b = 20 – 10.
б) Напиши, какими знаниями ты при этом воспользовался.
З а д а н и е 2.
а) Найди рационально значение выражения:
5 км 240 м · 84 – 5 км 24 м · 84 + 8 км 600 м · 84
б) Запиши два выражения с другими величинами, значения которых удобно найти тем же способом.
в) Найди значения записанных выражений.
З а д а н и е 3.
Запиши пропущенные единицы величин, используя разные варианты:
354… = 3… 5…. 4…
987… = 9… 8… 7…
З а д а н и е 4.
Вставь пропущенные числа, чтобы получились верные равенства:
□ : 36 = 179 63802 : □ = 73 □ · 162 = 119718 | □ : 48 = 159 66804 : □ = 76 □ · 179 = 149644 |
З а д а н и е 5.
а) Расположи выражения в порядке убывания их значения, не выполняя деления:
8294 : 319 8208 : 456 | 4773 : 129 9062 : 197 |
б) Составь сложное выражение, используя данные частные.
в) Найди его значение.
З а д а н и е 6.
а) Реши задачу.
Планер в первый день пролетел 430 км, во второй день – 516 км. На весь этот путь он затратил 11 ч. Сколько часов был в пути планер каждый день, если он летел с одинаковой скоростью?
б) Измени задачу так, чтобы ее решение стало короче.
КОНТРОЛЬНАЯ РАБОТА №12 ПО ТЕМЕ «РЕШЕНИЕ ЗАДАЧ»
Цель: проверить умение решать задачи разных типов алгебраическим способом, преобразовывать задачи.
В а р и а н т I
З а д а н и е 1.
а) Реши задачу сначала арифметически, а потом алгебраически.
С двух участков собрали 24 т свеклы. Со второго участка собрали на 8 кг меньше, чем с первого. Сколько свеклы собрали с каждого участка?
б) Подчеркни более удобный способ решения.
З а д а н и е 2.
а) Реши задачу.
В бассейн емкостью 2000 ведер накачивают воду 2 насоса. Первый накачивает в минуту 8 ведер, а второй – 12. За какое время наполнится бассейн?
б) Какой мощности нужно подключить третий насос, чтобы время наполнения бассейна сократилось вдвое?
в) Что произойдет с уровнем воды в бассейне, если после его заполнения первый и второй насосы будут накачивать воду, а третий – откачивать?
З а д а н и е 3.
а) Реши задачу.
От двух пристаней А и В, расстояние между которыми 120 км, в одном и том же направлении отплыли одновременно катер и теплоход: от пристани А – катер, а от пристани В – теплоход. Скорость теплохода 35 км/ч. Какова скорость катера, если он догнал теплоход через 5 часов?
Скорость теплохода 35 км/ч. Какова скорость катера, если он догнал теплоход через 5 часов?
б) С этими же данными и вопросом составь задачу на встречное движение.
в) Реши новую задачу.
В а р и а н т II
З а д а н и е 1.
а) Реши задачу сначала арифметически, а потом алгебраически.
Участок в 262 га вспахали за 2 дня. В первый день вспахали на 40 га больше, чем во второй. Сколько гектаров вспахали в первый день?
б) Подчеркни более удобный способ решения.
З а д а н и е 2.
а) Реши задачу.
В бассейн емкостью 3000 ведер накачивают воду 2 насоса. Первый накачивает в минуту 16 ведер, а второй – 14. За какое время наполнится бассейн?
б) Какой мощности нужно подключить третий насос, чтобы время наполнения бассейна сократилось вдвое?
в) Что произойдет с уровнем воды в бассейне, если после его заполнения первый и второй насосы будут накачивать воду, а третий – откачивать?
З а д а н и е 3.
а) Реши задачу.
Из Владимира и Москвы в Санкт-Петербург по одному и тому же шоссе выехали одновременно автобус и джип: из Владимира – джип, а из Москвы – автобус. Скорость автобуса 55 км/ч. Какова скорость джипа, если он догнал автобус через 4 ч после выезда, а расстояние между Москвой и Владимиром – 184 км?
Скорость автобуса 55 км/ч. Какова скорость джипа, если он догнал автобус через 4 ч после выезда, а расстояние между Москвой и Владимиром – 184 км?
б) С этими же данными и вопросом составь задачу на встречное движение.
в) Реши новую задачу.
ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА
Цели: проверить уровень сформированности знаний, умений, навыков при решении задач, чтении и записи многозначных чисел в пределах класса миллионов; при решении сложных уравнений; нахождении значения сложных выражений с величинами и с отвлеченными числами; при решении задач геометрического содержания.
В а р и а н т I
З а д а н и е 1.
а) Реши задачу.
Из двух поселков одновременно навстречу друг другу выехали два автомобиля. Один ехал со скоростью 53 км/ч и проехал до встречи 212 км. Определи расстояние между поселками, если скорость второго была 48 км/ч.
б) Измени условие решенной задачи так, чтобы решение новой задачи было длиннее или короче решения данной.
З а д а н и е 2.
а) Запиши цифрами и словами числа, которые содержат:
648 единиц 2-го класса и 27 единиц 1-го класса;
6 единиц 1-го класса, 14 единиц 2-го класса и 7 единиц 3-го класса;
120 единиц 3-го класса, 9 единиц 2-го класса и 60 единиц 1-го класса.
б) Каждое записанное число увеличь на 15 единиц третьего класса и столько же единиц первого класса; уменьши на 999 единиц первого класса и 45 единиц второго класса; увеличь в 6 раз; уменьши в 3 раза.
З а д а н и е 3.
Укажи порядок выполнения действий и найди значения выражений.
86 · (727216 : 604 + 2018) – 181708
33 кг 120 г : (41 кг 120 г – 39 кг 280 г)
(189 р. 12 к. + 16 р. 50 к.) · 18
З а д а н и е 4.
Реши уравнения и выполни проверку.
45 · х + 72 = 207
600 –156 : у = 574
(а – 7) : 184 = 46
З а д а н и е 5.
Площадь прямоугольного треугольника 16 см2. Какой длины могут быть его стороны, образующие прямой угол?
В а р и а н т II
З а д а н и е 1.
а) Реши задачу.
Два поезда отошли одновременно от одной станции в противоположных направлениях со скоростями 57 км/ч и 54 км/ч. Первый из них проехал 342 км. На каком расстоянии друг от друга в этот момент находились поезда?
б) Измени условие решенной задачи так, чтобы решение новой задачи было длиннее или короче решения данной.
З а д а н и е 2.
а) Запиши цифрами и словами числа, которые содержат:
805 единиц 2-го класса и 45 единиц 1-го класса;
70 единиц 1-го класса, 300 единиц 2-го класса и 60 единиц 3-го класса;
8 единиц 3-го класса, 80 единиц 2-го класса и 0 единиц 1-го класса.
б) Каждое записанное число увеличь на 215 единиц третьего класса и столько же единиц первого класса; уменьши на 598 единиц второго класса и 40 единиц первого класса; увеличь в 7 раз; уменьши в 5 раз.
З а д а н и е 3.
Укажи порядок выполнения действий и найди значения выражений.
(479484 + 113796) : 72 – 146 · 18
(156 т 104 кг : 52 – 19 ц 48 кг) · 720 + 5 т 364 кг
8 ч 36 мин · 475 – 364 ч 48 мин : 24
З а д а н и е 4.
Реши уравнения и выполни проверку.
576 : х + 79 = 127
8 · (е – 97) = 136
(1293 – m) : 19 = 57
З а д а н и е 5.
Ширина прямоугольника 7 см, а длина на 2 см больше. Найди периметр и площадь прямоугольника. Найди площадь квадрата, имеющего такой же периметр.
Геометрия. Задачи на клетчатой бумаге и площади фигур
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где и — диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Площадь пересечения двух окружностей
спросил
Изменено 3 года, 9 месяцев назад
Просмотрено 160 тысяч раз
$\begingroup$
Предположим, у вас есть 2 окружности, которые пересекаются друг с другом таким образом, что каждая окружность проходит через центр другой. Какова площадь между кругом (или общей площадью), т.е. площадь между центрами кругов?
Какова площадь между кругом (или общей площадью), т.е. площадь между центрами кругов?
- круги
$\endgroup$
4
$\begingroup$
Обозначьте центр первого круга $C$ и центр второго круга $C’$. Обозначьте одну из точек пересечения двух окружностей $A$, а другую — $B$. Пусть радиус окружностей равен $r>0$. Должно быть ясно, что все следующие длины равны $r$. $AC$, $AC’$, $BC$, $BC’$, $CC’$. Несложным применением теоремы Пифагора получаем, что длина отрезка $AB$ равна $\sqrt{3}r$. 92\left(\frac{2\pi}{3}-\frac{\sqrt{3}}{2}\right)$$
$S$ — общая рассматриваемая площадь
$\endgroup$
1
$\begingroup$
Я использую симметрию задачи
$\endgroup$
$\begingroup$
Мы можем найти ответ, используя эту формулу 92 \cdot \left( \frac{\pi}{3} — \frac{\sqrt{3}}{2} \right) $$
$\endgroup$
5
Объем прямоугольной призмы – объяснение и примеры
Объем прямоугольной призмы – это мера пространства, которое ее заполняет. В этой статье вы узнаете , как найти объем прямоугольной призмы, используя формулу объема прямоугольной призмы . Мы также обсудим объем сферического цилиндра.
В этой статье вы узнаете , как найти объем прямоугольной призмы, используя формулу объема прямоугольной призмы . Мы также обсудим объем сферического цилиндра.
Как найти объем прямоугольной призмы?
Прямоугольная призма – это трехмерный объект с шестью прямоугольными гранями . Прямоугольная призма также называется кубоидом, прямоугольным шестигранником, прямоугольной призмой или прямоугольным параллелепипедом.
Чтобы найти объем прямоугольной призмы, умножьте длину, ширину и высоту. Единицей измерения объема прямоугольной призмы являются кубические единицы, т. е. см 3 , мм 3 , дюймов 3 , м 3, и т. д.
Объем прямоугольной призмы Формула
Формула объема прямоугольной призмы дается как: прямоугольная призма = (длина х ширина х высота) кубических единиц.
V = (д x ш x в) кубических единиц
В прямоугольной призме произведение длины и ширины называется площадью основания. Следовательно, мы также можем представить объем прямоугольной призмы формулой как:
Следовательно, мы также можем представить объем прямоугольной призмы формулой как:
Объем прямоугольной призмы = площадь основания x высота
Давайте попробуем формулу, решив несколько примеров задач.
Пример 1
Длина, ширина и высота прямоугольной призмы равны 15 см, 10 см и 5 см соответственно. Каков объем призмы?
Раствор
Дано, длина = 15 см,
ширина = 10 см,
высота = 5 см.
По объему прямоугольной призмы имеем
Объем = Д x Ш x В
= (15 x 10 x 5) см 3
= 750 см 3 .
Пример 2
Объем прямоугольной призмы 192 см 3 . Найдите размеры прямоугольной призмы, если длина призмы в два раза больше высоты и ширины 6 см.
Решение
Дано,
Пусть высота равна x.
Длина = 2x
Ширина = 6 см.
Объем = 192.
По объему прямоугольной призмы,
⇒ 192 = x(2x) (6)
⇒ 192 = 12x 2
. 2
2
⇒ x = 4, -4
Замена
Длина = 2x ⇒ 2x 4 =8 см
Высота = x ⇒ 4 см см.
Пример 3
Длина и ширина прямоугольного аквариума 800 мм и 350 мм. При заселении рыб в аквариум уровень воды поднимается на 150 мм. Найдите объем рыбы.
Решение
Объем рыбы = объем вытесненной воды.
Объем рыбы = 800 x 350 x 150 мм 3
= 4,2 x 10 7 мм 3
Пример 4
Прямоугольный бак 80 м. 4014 М. 50 м. в ширину и 60 м в высоту. Если глубина воды в баке 45 м, найдите объем воды, необходимый для заполнения бака?
Раствор
Чтобы найти объем воды, необходимый для заполнения бака, вычтите доступный объем воды из объема воды, когда бак полный.
Объем воды при полном баке = 80 x 50 x 60
= 240 000 м 3
Объем доступной воды = 80 x 50 x 45
= 180 000 м 1
03 3 Объем необходимое количество воды = (240 000 – 180 000) м 3
= 60 000 м 3
Пример 5
Объем и площадь основания прямоугольного грузового контейнера составляют 778 м 3 и 120 м 2 . Найдите высоту контейнера?
Найдите высоту контейнера?
Раствор
Объем прямоугольной призмы = площадь основания x высота
778 = 120 x высота
Разделите 120 на обе стороны.
778/120 = высота
высота = 6,48 м
Итак, высота контейнера 6,48 м.
Пример 6
Небольшие коробки размером 1 м x 4 м x 5 м должны быть упакованы в большую прямоугольную тару размерами 8 м x 10 м x 5 м. Найдите максимальное количество маленьких коробок, которые можно упаковать в контейнер?
Решение
Чтобы найти количество упаковываемых коробок, разделите объем контейнера на объем коробки.
Объем контейнера = 8 x 10 x 5
= 400 м 3 .
Объем коробки = 1 x 4 x 5
= 20 м 3
Количество ящиков = 400 м 3 /20 м 3 .
= 20 коробок.
Пример 7
Внешние размеры деревянного ящика, открытого сверху, составляют 12 см в длину, 10 см в ширину и 5 см в высоту. Если толщина стенок ящика 1 см, найдите объем ящика
Если толщина стенок ящика 1 см, найдите объем ящика
Решение
Найдите внутренние размеры ящика
Длина = 12 – (1 x 2)
= 10 см
Ширина = 10 – (1 x 2)
= 8 см
Высота = 5 см – 1 …… (открыт сверху)
= 4 см
Объем = 10 x 8 x 4
= 320 см 3 .
Пример 8
Каковы размеры куба того же объема, что и прямоугольная призма с размерами 8 м на 6 м на 3 м?
Раствор
Объем прямоугольной призмы = 8 x 6 x 3
= 144 см 3
Итак, куб тоже будет иметь объем 144 см 3
Так как мы знаем, что объем куба = а 3
где а длина куба.
144 = A 3
3 √ A 3 = 3 √144
A = 5,24
Следовательно, размеры куба будут 5,24 C -54 CM.
Пример 9
Вычислите объем сплошной прямоугольной призмы, площадь основания которой составляет 18 дюймов 2 и высота 4 дюйма.
Решение
Объем прямоугольной призмы = длина x ширина x высота
= площадь основания x высота
Пример 10
Найдите площадь основания прямоугольной призмы, объем которой равен 625 см 3 , а высота равна 18 см.
Решение
Объем = площадь основания x высота
625 = площадь основания x 18
, деляя обе стороны на 18, мы получаем
базовую площадь = 34,72 см 2
12.1 Скорость потока и его связь с велосией — Физика колледжа: OpenSax
Глава и медицинские приложения
Сводка
- Рассчитать скорость потока.
- Определить единицы объема.
- Опишите несжимаемые жидкости.
 3\textbf{/s}},[/latex],но ряд других единиц для [латекс]\boldsymbol{Q}[/ латекс] широко используются. Например, сердце покоящегося взрослого человека перекачивает кровь со скоростью 5,00 литров в минуту (л/мин). Обратите внимание, что 93}[/латекс]). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации. Рис. 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P в однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .
3\textbf{/s}},[/latex],но ряд других единиц для [латекс]\boldsymbol{Q}[/ латекс] широко используются. Например, сердце покоящегося взрослого человека перекачивает кровь со скоростью 5,00 литров в минуту (л/мин). Обратите внимание, что 93}[/латекс]). В этом тексте мы будем использовать любые метрические единицы, наиболее удобные для данной ситуации. Рис. 1. Расход – это объем жидкости в единицу времени, протекающий через точку через площадь A . Здесь заштрихованный цилиндр жидкости течет мимо точки P в однородной трубе за время t . Объем цилиндра равен Ad , а средняя скорость равна v̄=d/t , так что расход равен Q=Ad/t=Av̄ .Пример 1. Расчет объема по скорости кровотока: сердце перекачивает много крови за всю жизнь
Сколько кубических метров крови перекачивает сердце за 75 лет жизни, если предположить, что средняя скорость кровотока составляет 5,00 л/мин?
Стратегия
Время и скорость потока[latex]\boldsymbol{Q}[/latex] даны, поэтому объем[latex]\boldsymbol{V}[/latex]может быть рассчитан из определения потока оценивать.

Решение 93.} \end{array}[/latex]
Обсуждение
Это количество составляет около 200 000 тонн крови. Для сравнения, это значение примерно в 200 раз превышает объем воды, содержащейся в 50-метровом плавательном бассейне с 6 дорожками.
Расход и скорость являются связанными, но совершенно разными физическими величинами. Чтобы прояснить различие, подумайте о скорости течения реки. Чем больше скорость воды, тем больше расход реки. Но скорость течения также зависит от размера реки. Быстрый горный поток несет гораздо меньше воды, чем, например, река Амазонка в Бразилии. Точное соотношение между скоростью потока[латекс]\жирныйсимвол{Q}[/латекс]и скоростью[латекс]\жирныйсимвол{\бар{в}}[/латекс] равно 9.0005
[латекс]\boldsymbol{Q=A\bar{v}},[/латекс]
, где[латекс]\жирныйсимвол{А}[/латекс]– площадь поперечного сечения, а[латекс]\жирныйсимвол{\бар{в}}[/латекс]– средняя скорость. Это уравнение кажется достаточно логичным. Соотношение говорит нам, что скорость потока прямо пропорциональна как величине средней скорости (далее называемой скоростью), так и размеру реки, трубы или другого водовода.
 Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем
Чем больше трубопровод, тем больше его площадь поперечного сечения. Рисунок 1 иллюстрирует, как получается это соотношение. Заштрихованный цилиндр имеет объем[латекс]\boldsymbol{V=Ad},[/латекс]
, который проходит мимо точки[latex]\textbf{P}[/latex]за время[latex]\boldsymbol{t}.[/latex]Разделив обе стороны этого отношения на[latex]\boldsymbol{t}[ /латекс] дает
[латекс]\boldsymbol{\frac{V}{t}}[/latex][латекс]\boldsymbol{=}[/latex][латекс]\boldsymbol{\frac{Ad}{t}}.[/ латекс]
Заметим, что [латекс]\boldsymbol{Q=V/t}[/latex]и средняя скорость равна[латекс]\boldsymbol{v\bar{v}=d/t}.[/latex] Таким образом, уравнение становится [латекс]\boldsymbol{Q=A\bar{v}}.[/латекс]
На рис. 2 показано течение несжимаемой жидкости по трубе с уменьшающимся радиусом. Поскольку жидкость несжимаема, через любую точку трубки за заданное время должно пройти одинаковое количество жидкости, чтобы обеспечить непрерывность потока. В этом случае, поскольку площадь поперечного сечения трубы уменьшается, скорость обязательно должна увеличиваться.
 Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2
Эту логику можно расширить, чтобы сказать, что скорость потока должна быть одинаковой во всех точках трубы. В частности, по пунктам 1 и 2[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2.} \end{array}[/latex] [латекс]\rbrace[/латекс]
Это называется уравнением неразрывности и справедливо для любой несжимаемой жидкости. Следствия уравнения неразрывности можно наблюдать, когда вода течет из шланга в узкую форсунку: она выходит с большой скоростью — в этом назначение форсунки. И наоборот, когда река впадает в один конец водохранилища, вода значительно замедляется и, возможно, снова набирает скорость, когда выходит из другого конца водохранилища. Другими словами, скорость увеличивается, когда площадь поперечного сечения уменьшается, и скорость уменьшается, когда площадь поперечного сечения увеличивается.
Рисунок 2. Когда трубка сужается, тот же объем занимает большую длину. Чтобы один и тот же объем прошел точки 1 и 2 за заданное время, скорость должна быть больше в точке 2. Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)
Процесс точно обратим. Если жидкость течет в противоположном направлении, ее скорость будет уменьшаться при расширении трубы. (Обратите внимание, что относительные объемы двух цилиндров и соответствующие стрелки вектора скорости нарисованы не в масштабе.)Поскольку жидкости практически несжимаемы, уравнение неразрывности справедливо для всех жидкостей. Однако газы сжимаемы, поэтому уравнение следует применять с осторожностью к газам, если они подвергаются сжатию или расширению.
Пример 2. Расчет скорости жидкости: скорость увеличивается при сужении трубы
Насадка с радиусом 0,250 см прикреплена к садовому шлангу с радиусом 0,900 см. Скорость потока через шланг и сопло составляет 0,500 л/с. Рассчитайте скорость воды (а) в шланге и (б) в насадке.
Стратегия
Мы можем использовать соотношение между расходом и скоростью, чтобы найти обе скорости. Мы будем использовать нижний индекс 1 для шланга и 2 для насадки. 92}}[/latex][latex]\boldsymbol{=\:1.
 2}[/latex]вместо площади поперечного сечения, получим 92}}[/latex][latex]\boldsymbol{1,96\textbf{ м/с}=25,5\textbf{ м/с}}.[/latex]
2}[/latex]вместо площади поперечного сечения, получим 92}}[/latex][latex]\boldsymbol{1,96\textbf{ м/с}=25,5\textbf{ м/с}}.[/latex]Обсуждение
Скорость 1,96 м/с примерно подходит для воды, вытекающей из шланга без насадок. Форсунка создает значительно более быстрый поток, просто сужая поток в более узкую трубку.
Решение последней части примера показывает, что скорость обратно пропорциональна квадрату радиуса трубы, что приводит к большим эффектам при изменении радиуса. Мы можем задуть свечу на довольно большом расстоянии, например, сжав губы, тогда как задувание свечи с широко открытым ртом совершенно неэффективно.
Во многих ситуациях, в том числе в сердечно-сосудистой системе, происходит разветвление потока. Кровь перекачивается из сердца в артерии, которые подразделяются на более мелкие артерии (артериолы), которые разветвляются на очень тонкие сосуды, называемые капиллярами. В этой ситуации непрерывность потока сохраняется, но сохраняется сумма расходов в каждой из ветвей на любом участке вдоль трубы.
 Уравнение неразрывности в более общем виде принимает вид
Уравнение неразрывности в более общем виде принимает вид[латекс]\boldsymbol{n_1A_1\бар{v}_1=n_2A_2\бар{v}_2},[/латекс]
где[latex]\boldsymbol{n_1}[/latex]и[latex]\boldsymbol{n_2}[/latex]количество ответвлений на каждом из участков вдоль трубы.
Пример 3: расчет скорости кровотока и диаметра сосуда: разветвления в сердечно-сосудистой системе
Аорта является основным кровеносным сосудом, по которому кровь покидает сердце, чтобы циркулировать по всему телу. а) Рассчитайте среднюю скорость движения крови в аорте при скорости потока 5,0 л/мин. Аорта имеет радиус 10 мм. (б) Кровь также течет через более мелкие кровеносные сосуды, известные как капилляры. При скорости кровотока в аорте 5,0 л/мин скорость крови в капиллярах составляет около 0,33 мм/с. Учитывая, что средний диаметр капилляра составляет[latex]\boldsymbol{8.0\:\mu},[/latex]рассчитайте количество капилляров в системе кровообращения. 92}}[/latex][latex]\boldsymbol{=\:0.27\textbf{ м/с.}}[/latex]
Решение для (b)
Использование[latex]\boldsymbol{n_1A_1\ bar{v}_1=n_2A_2\bar{v}_1},[/latex]присваивая индекс 1 аорте и 2 капиллярам и находя[latex]\boldsymbol{n_2}[/latex](число капилляров) дает[latex]\boldsymbol{n_2=\frac{n_1A_1\bar{v}_1}{A_2\bar{v}_2}}.
 93}.[/латекс]
93}.[/латекс] - Расход и скорость связаны соотношением[latex]\boldsymbol{Q=A\bar{v}}[/latex],где[latex]\boldsymbol{A}[/latex]является площадью поперечного сечения потока и [латекс]\boldsymbol{\bar{v}}[/латекс] — его средняя скорость.
- Для несжимаемых жидкостей скорость потока в различных точках постоянна. То есть,
[латекс]\begin{array}{c} \boldsymbol{Q_1=Q_2} \\ \boldsymbol{A_1\bar{v}_1=A_2\bar{v}_2} \\ \boldsymbol{n_1A_1\bar{v }_1=n_2A_2\bar{v}_2.} \end{массив}[/latex][latex]\rbrace[/latex]
- расход
- , сокращенно Q , это объем V , протекающий через определенную точку за время t , или Q = V/t
- литр
- единица объема, равная 10 −3 м 3
Площадь поверхности пирамиды
Горячая математика боковой площадь поверхности регулярного пирамида
есть сумма площадей его боковых граней.
общая площадь правильной пирамиды есть сумма площадей его боковых граней и основания.
Общая формула для площадь боковой поверхности правильной пирамиды л . С . А . знак равно 1 2 п л куда п представляет собой периметр основания и л наклонная высота.
Пример 1:
Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждое ребро основания равно 8 дюймов, а наклонная высота 5 дюймы.
Периметр основания равен сумме сторон.
п знак равно 3 ( 8 ) знак равно 24 дюймы
л . С . А . знак равно 1 2 ( 24 ) ( 5 ) знак равно 60 дюймы 2
Общая формула для общая площадь поверхности правильной пирамиды
Т
. С
.
А
.
знак равно
1
2
п
л
+
Б
куда
п
представляет собой периметр основания,
л
наклонная высота и
Б
площадь базы.
С
.
А
.
знак равно
1
2
п
л
+
Б
куда
п
представляет собой периметр основания,
л
наклонная высота и
Б
площадь базы.
Пример 2:
Найдите площадь полной поверхности правильной пирамиды с квадратным основанием, если каждое ребро основания равно 16 дюймов, наклонная высота стороны равна 17 дюймов, а высота 15 дюймы.
Периметр основания равен
4
с
так как это квадрат.
п знак равно 4 ( 16 ) знак равно 64 дюймы
Площадь базы составляет с 2 .
Б знак равно 16 2 знак равно 256 дюймы 2
Т . С . А . знак равно 1 2 ( 64 ) ( 17 ) + 256 знак равно 544 + 256 знак равно 800 дюймы 2
Формулы площади поверхности неправильных пирамид не существует, так как наклонная высота не определена. Чтобы найти
площадь, найдите площадь каждой грани и площадь основания и сложите их.
Чтобы найти
площадь, найдите площадь каждой грани и площадь основания и сложите их.
Решения NCERT для области математики класса 5 и ее границы
Решения NCERT для области математики класса 5 и ее границ Решения книги доступны в формате PDF для бесплатной загрузки. Эти мудрые вопросы и ответы, посвященные главам книги, очень полезны для экзамена CBSE. CBSE рекомендует книги NCERT, и большинство вопросов на экзамене CBSE задаются из учебников NCERT. Решение NCERT по математике для класса 5 по математике для книги по математике, все главы можно бесплатно загрузить с нашего веб-сайта и мобильного приложения myCBSEguide.
ГЛАВА-11
ТЕРРИТОРИЯ И ЕЕ ОГРАНИЧЕНИЯ
1. (a) Арбаз планирует выложить на полу своей кухни зеленую квадратную плитку. Каждая сторона плитки равна 10 см. Его кухня 220 см в длину и 180 см в ширину. Сколько плиток ему понадобится? Ответ. (a) Мы знаем, что
(a) Мы знаем, что
Площадь прямоугольника = Длина Ширина
Площадь пола кухни = (Длина Ширина)
= (220 180) квадратных см.
Также мы знаем, что
Площадь квадрата = Сторона Сторона
Площадь одной плитки = (10 10) квадратных см
Количество необходимых плиток
=
=
= 22 18 = 396
15 б) Ограждение квадратного сада имеет длину 20 м. Какова длина одной стороны сада?
Ответ. (b) Имеем Периметр = 20 м
Сторона = Периметр
Сторона = = 5 м
(c) Тонкая проволока длиной 20 сантиметров сформирована в виде прямоугольника. Если ширина этого прямоугольника 4 сантиметра, то какова его длина?Ответ. (c) Периметр = 20 см и Ширина = 4 см
Длина = Периметр – Ширина
Длина = 20 см – 4 см = 6 см
= 10 см – 4 см = 6 см г) периметр квадратной доски для карамболя равен 320 см. Сколько его площадь?
Сколько его площадь?
Ответ. (d) У нас есть Периметр = 320 см
Сторона = Периметр
Сторона = 320 см = 80 см
Площадь = Сторона Сторона
= (80 80) квадратных см = 6400 квадратных см
(e) Сколько плиток, подобных приведенному здесь треугольнику, поместится в белый узор?Область дизайна = …………………. Площадь см
Анс. (e) Площадь рисунка = 1 полный квадрат + 4 полуквадрата
= (1 + 2) полный квадрат
= 3 полных квадрата
= 3 1 квадратный см = 3 квадратных см
Площадь одной плитки = половина квадратного см
= квадратный см
Количество плиток =
= = 3 = 6
(f) Санья, Аруши, Манав и Кабир сделали поздравительные открытки. Complete the table for their cards:| Whose card | Length | Width | Perimeter | Area |
| Sanya | 10 cm | 8 см | ||
| Манав | 11 cm | 44 cm | ||
| Aarushi | 8 cm | 80 square cm | ||
| Kabir | 40 cm | 100 square cm |
Ответ. (f)
(f)
В случае Саньи:
Длина = 10 см, ширина = 8 см
Периметр = 2 (длина + ширина)
= 2 (10+8) см
= 2 18 см = 36 см
Площадь = длина ширина
= 10 8 квадратных см Манав:
У нас есть, Длина = 11 см, Периметр = 44 см
2 (Длина + Ширина) = 44 см
Длина + Ширина = 22 см
11 см + Ширина = 22 см
2 см- 11 см = 11 см
А, площадь = длина ширина
= 11 11 квадратных см
= 121 кв. см
В случае Aarushi:
Ширина = 8 см
Площадь = 80 кв. см
Длина Ширина = 80 кв. Длина = см = 10 см
И, периметр = 2 (длина + ширина)
= 2 (10 + 8) см
= 2 18 см = 36 см
В случае Кабира:
5
2 , Периметр = 40 см
Площадь = 100 квадратных см
2 (Длина+Ширина) = 40 см
И, Длина + Ширина = Длина и Ширина
т.е. Длина + Ширина = 20
Ширина = 20 – Длина ……. .(1)
.(1)
Длина Ширина = 100
0 Длина (
) 2 (длина) – (длина)= 100Длина – 20 Длина +100 = 0
(Длина – 10) = 0 Длина-10 = 0
Длина = 10
Ширина = 20 – Длина = 20 -10 = 10
т. е. длина = 10 см и ширина = 10 см
Таким образом, полная таблица выглядит следующим образом:
| Whose card | Length | Width | Perimeter | Area |
| Sanya | 10 cm | 8 cm | 36 cm | 80 square cm |
| Manav | 11 cm | 11 cm | 44 cm | 121 square cm |
| Aarushi | 10 cm | 8 cm | 36 cm | 80 square cm |
| Kabir | 10 cm | 10 cm | 40 cm | 100 square cm |
NCERT Solutions for Class 5 Maths Area and its Boundary
2. Возьмите лист плотной бумаги длиной 14 см и шириной 9 см. Также можно использовать старую открытку. а) Какова его площадь? Каков его периметр?
Возьмите лист плотной бумаги длиной 14 см и шириной 9 см. Также можно использовать старую открытку. а) Какова его площадь? Каков его периметр? Ответ. (а) Мы это знаем,
Площадь прямоугольника = Длина Ширина
Площадь листа толстой бумаги = (Длина Ширина)
= (149) квадратных см = 126 квадратных см
Периметр прямоугольного листа
= 2(Длина + Ширина)
= 2(14 + 9) см
= 2 23 см = 46 см
(б) Теперь вырежьте из него полоски одинакового размера.Ответ. (b) Нарежем полоски одинакового размера из данного листа бумаги длиной 14 см и шириной 9 см.
(c) Какой длины твой ремень?
Ответ. (c) Полоски шириной 1 см:
Будет 9 полосок шириной 1 см и длиной 14 см. Соединим эти полоски встык, используя ленту, чтобы получился пояс.
Его длина
= (14+14+14+14+14+14+14+14+14)
= 9 14 см = 126 см
Его периметр = 2(126+1) см = 2 127 см = 254 см
(г) Каков его периметр?
Ответ. (d) Полоски длиной см:
(d) Полоски длиной см:
Будет 6 полос шириной см и длиной 14 см. Соединим эти полоски встык, используя ленту, чтобы получился пояс.
Его длина = (14+14+14+14+14+14) см
= 6 14 см = 84 см
Его периметр = 2 (84 + 1,5) см = 2 85 – 5 см = 171 см
(e) Чей пояс самый длинный в классе?
Ответ. (e) Полоски шириной 3 см:
Будет 3 полоски шириной 3 см и длиной 14 см.
Соединим эти полоски встык с помощью скотча, чтобы получился пояс.
Его длина = (14+14+14) см = 3 14 см = 42 см
Его периметр = 2(42+3) см = 2 45 см = 90 см
Очевидно, что пояс с наименьшей шириной является и самым длинным. Таким образом, ремень шириной 1 см является самым длинным в классе. Итак, мой пояс самый длинный.
Решения NCERT для области математики 5-го класса и ее границ
3. Давайте обсудим:(a) Почему у некоторых из ваших друзей ремень длиннее, чем у других?
Ответ. (a) У некоторых моих друзей ремни длиннее, чем у других, поскольку ширина их ремней короче, чем у других.
(a) У некоторых моих друзей ремни длиннее, чем у других, поскольку ширина их ремней короче, чем у других.
(b) Совпадает ли площадь вашего пояса с площадью открытки? Почему или почему нет?
Ответ. (b) Площадь ремня такая же, как площадь открытки, потому что он сделан из открытки без потерь.
(c) Что вы сделаете, чтобы получить более длинный ремень в следующий раз?
Ответ. (c) В следующий раз я получу более длинный ремень, если позабочусь о том, чтобы ширина моего ремня была короче, чем у другого.
Решения NCERT для области математики класса 5 и ее границы
4. Люди Люди повсюду:(A) В эту игру можно играть на земле.
Сделайте два квадрата по одному квадратному метру каждый.
Разделите свой класс на две команды. Готов играть!
Попробуйте в своих командах:
(a) Сколько из вас может уместиться на одном квадратном метре?
Ответ. (a) Трое из нас могут сидеть на одном квадратном метре.
(a) Трое из нас могут сидеть на одном квадратном метре.
(b) Сколько из вас может в нем стоять?
Ответ. (b) В нем могут стоять четверо.
(c) Какая команда может заставить детей встать на своем квадрате? Как много?
Ответ. (c) Команда А может заставить больше детей стоять на своем квадрате. Их пять штук.
(d) Какая команда может заставить больше детей сидеть на своем квадрате? Как много?
Ответ. (d) Команда А может рассадить больше детей на своем квадрате. Их четыре числом.
(B) Измерьте длину пола ваших детей в метрах. Также измерьте ширину.
(a) Какова площадь пола ваших детей в квадратных метрах?
Ответ. (a) Измерим пол классной комнаты в метрах.
Находим, что его длина = 10 метров, а ширина = 6 метров
Его площадь = (длина ширина)
= (106) квадратных метров
= 60 квадратных метров.
(b) Сколько детей в вашем классе?
Ответ. (b) В моем классе 60 детей.
(c) Итак, сколько детей может поместиться на одном квадратном метре?
Ответ. (c) Количество детей, которые могут сидеть на одном квадратном метре =
= =1
Таким образом, один ребенок может сидеть на одном квадратном метре.
(d) Если вы хотите легко передвигаться, то как вы думаете, сколько детей должно быть на одном квадратном метре?
Ответ. (d) Чтобы легко передвигаться, я думаю, что 2 ребенка могут сидеть на площади 3 квадратных метра.
Решения NCERT для области математики класса 5 и ее границы
5. Разделите землю: Насрина — фермер, которая хочет разделить свою землю поровну между тремя своими детьми, Чамки, Джумри и Имраном. Она хочет разделить землю так, чтобы на каждом участке земли было по одному дереву. Ее земля выглядит так.
Ее земля выглядит так.
(а) Можете ли вы разделить землю поровну? Покажите, как вы будете его делить. Помните, что каждый человек должен получить дерево. Раскрасьте участок земли каждого человека по-своему.
Ответ. (a) Да, я могу поровну разделить землю между тремя детьми Насрины. Чумки, Джумри и Имран такие, что каждому достается по одному дереву. Участок земли каждого человека окрашен по-разному, как показано на рисунке.
(b) Если каждый квадрат на этой странице равен 1 квадратному метру земли, сколько земли получит каждый из ее детей? … кв. м
Отв. (b) Пусть земля Чумки будет ABCDEF, земля Джумри будет BGHIJC, а земля Имрана будет DJIHKE.
Общая площадь земли = 10 9 м = 90 квадратных метров
Так как каждый человек получает равную землю.
Каждая доля = кв. м = 30 кв. м
Таким образом, каждому чолду достается 30 кв. м земли.
(c) Чумки Джумри и Имрану нужна проволока, чтобы сделать забор.
Ответ. (c) Для ограждения:
Периметр участка Чумки ABCDEF = AB + BC + CD + DE + EF + FA
= (4 + 6 +2 + 3+ 2+ 9) м = 26 м
Периметр участка Земля Джумри BGHIJC = BG + GH + HI + IJ + JC + CB
= (6 + 4+ 3 + 2 + 3+ 6) м = 24 м
Периметр земли Имрана DJIHKE = DJ + JI + IH + HK + KE + ED
= (5 + 2 + 3 + 5 + 8 +3) м = 26 м
(г) Кому понадобится самая длинная проволока для ограждения?
Ответ. (d) Понятно, что для забора Чумки и Имрану нужны самые длинные, но одинаковые провода.
(e) Сколько всего провода понадобится троим?
Ответ. (e) Необходимое количество проволоки = (26 + 24 + 26) м = 76 м
Решения NCERT для математики класса 5 Площадь и ее границы
6. Ответьте на эти вопросы:(a) Периметр квадрата A равен .. см.
Ответ. (a) Периметр квадрата A равен 4 3 см = 12 см.
(a) Периметр квадрата A равен 4 3 см = 12 см.
(b) Сторона квадрата B равна .. см.
Ответ. (b) Сторона квадрата B равна 2 3 см = 6 см.
(c) Площадь квадрата B равна .. квадратных см.
Ответ. (с) Площадь квадрата B равна 6 см 6 см = 36 кв. см.
(d) Площадь квадрата B равна .. умноженной на площадь квадрата A.
Ответ. (d) Площадь квадрата B в четыре раза больше площади квадрата A.
(e) Периметр квадрата B равен .. см.
Ответ. (e) Периметр квадрата B равен 46 см = 24 см.
(f) Периметр квадрата B в .. раз больше периметра квадрата A.
Ответ. (е) Периметр квадрата B в два раза больше периметра квадрата A.
Решения NCERT для 5-го класса по математике Площадь и ее границы
7. Thread and Play(A) Какая фигура имеет наибольшую площадь? Сколько?
Ответ. (A) Чтобы найти площадь фигуры A
(A) Чтобы найти площадь фигуры A
Рисунок A содержит 9 полных квадратов, 2 полуквадрата, 7 больше половины квадратов и 8 меньше половины квадратов. Пренебрегая менее чем половиной квадратов и считая более половины квадрата полными квадратами. Следовательно, примерная площадь фигуры А.
= квадратный см = (9+1+7) квадратный см = 17 квадратных см
Аналогично, площадь фигуры B будет приблизительно равна
квадратный см = 10 квадратных см.
А, площадь фигуры C = квадратный см
= кв. см
Очевидно, что форма А имеет наибольшую площадь.
Это (17 – 10) т.е. на 7 кв.см больше, чем у формы В и т.е. на кв.см больше, чем у уклона.
(B) Какая фигура имеет наименьшую площадь? Сколько? Чему равен периметр фигуры?
Также сделайте треугольник, квадрат, прямоугольник и круг. Найдите, какая фигура имеет наибольшую площадь, а какая наименьшую?
Ответ. (B) Форма B имеет наименьшую площадь.
(B) Форма B имеет наименьшую площадь.
На (17-10) т.е. на 2 см меньше, чем у формы А и т.е. на 1 см2 меньше, чем у формы С.
Периметр этой формы равен 15 см.
Сплетем также треугольник, квадрат, прямоугольник и круг из той же нити 15 см.
Площадь треугольника = кв.см = 12 кв.см (прибл.)
Площадь квадрата = кв.см = 16 кв.см (прибл.)
Площадь треугольника = кв.см = кв.см см (прибл.)
Площадь круга = кв.см = 16 кв.см (прибл.)
Круг и квадрат имеют наибольшую площадь, а треугольник имеет наименьшую площадь.
Решения NCERT для области математики 5 класса и ее границы
8. Save the Birds: Рядом с деревней есть два красивых озера. Люди приезжают покататься на лодках и устроить пикник на обоих озерах. Деревня Панчаят обеспокоена тем, что с шумом лодок перестанут прилетать птицы. Панчаяту нужны моторные лодки только на одном озере. Другое озеро будет сохранено для птиц, чтобы вить свои гнезда.
(a) Сколько см длины границы озера А на рисунке?
Ответ. (a) Длина границы озера А на рисунке равна 33 см.
(b) Какова длина границы озера B на рисунке?
Ответ. (b) Длина границы озера B на рисунке равна 26 см.
(c) Более длинная граница вокруг озера поможет большему количеству птиц отложить яйца. Так какое озеро оставить для птиц? Какое озеро следует использовать для лодок?
Ответ. (c) Поскольку 1 см на чертеже = 1 км на местности
33 см соответствует 33 1 км, т. е. 33 км.
(d) Найдите площадь озера B на чертеже в квадратных см. Какова реальная площадь в квадратных километрах?
Ответ. (d) Озеро B содержит 15 полных квадратов, 3 полуквадрата, 8 больше половины квадратов и 2 меньше половины квадратов. Пренебрегая менее чем половиной квадратов и учитывая более половины квадратов примерную площадь озера B на чертеже.
= квадратный см = квадратный см
Фактическая площадь озера B = квадратный километр
Решения NCERT для математики класса 5 Площадь и ее границы
Чаггу и Анар. Для него сделали очень большую и красивую кровать. Итак, в качестве даров царь хотел дать немного земли Чаггу и немного золота Анару.Чаггу был счастлив. Он взял 100 метров проволоки и попытался сделать разные прямоугольники. Он сделал прямоугольник 10 м 40 м. Его площадь составляла 400 квадратных метров. Затем он сделал прямоугольник 30 м 20 м.
(а) Какова его площадь? Это больше, чем первый прямоугольник?
Ответ. (a) Площадь этого прямоугольника = 30 м 20 м = 600 квадратных метров.
Да, его площадь больше площади первого прямоугольника.
(б) Какой еще прямоугольник он может сделать из 100 метров проволоки? Обсудите, какой из этих прямоугольников будет иметь наибольшую площадь.
Ответ. (b) Многие другие прямоугольники можно сделать из 100 метров проволоки. Например,
5 м 45 м, площадью 225 квадратных метров.
15 м 35 м площадью 525 квадратных метров.
20 м 30 м площадью 600 квадратных метров.
25 м 25 м, площадью 625 квадратных метров.
Длина прямоугольника = ширине, т.е. квадрат будет иметь наибольшую площадь.
Решения NCERT для области математики класса 5 и ее границы
10. Таким образом, Анар также испробовал много разных способов сделать границу для 800 квадратных метров земли.(а) Он сделал прямоугольники А, В, С разных размеров. Найдите длину границы каждого. Сколько золотой проволоки он получит за эти прямоугольники?
Ответ. (a) Граница прямоугольника = 2 (Длина + Ширина)
Граница для А = 2(40+20) м = 260 м = 120 м
Золотая проволока для А = 120 метров
Граница для В = 2 (80+10) м = 2 90 м = 180 м
Золотая проволока для B = 180 м
Граница для C = 2(800+1) м = 2 801 м = 1602 м
Золотая проволока для C = 1602 метра
Граница для D = 2(8000+0,1) м = 2 8000,1 м = 16000,2 м
Таким образом, он получит 16000,2 метра золотой проволоки.
Решения NCERT для области математики 5 класса и ее границы
(b) Можете ли вы сделать прямоугольник с еще более длинной границей? Я сделал прямоугольник шириной 1 см и длиной 80000 м. Представьте, какой длины будет эта граница!! С таким количеством золотой проволоки я могу стать королем!
Ответ. (b) Да, можно сделать прямоугольник с еще более длинной границей.
Граница прямоугольника шириной 1 см и длиной 80000 м.
= 2(0,01+80000) m = 2 80000,01 m = 160000,02 m
NCERT Solutions Class 5 Maths PDF (скачать) Бесплатно в приложении myCBSEguide и на веб-сайте myCBSEguide. Ncert Solution Class 5 Maths включает в себя решения учебников из Class 5 Maths Book. Решения NCERT для математики класса 5 CBSE состоят всего из 14 глав. 5 Maths NCERT Solutions в PDF для бесплатного скачивания на нашем сайте. Решения Ncert Maths class 5 PDF и Maths ncert class 5 PDF-решения с последними изменениями и в соответствии с последней программой CBSE доступны только в myCBSEguide.


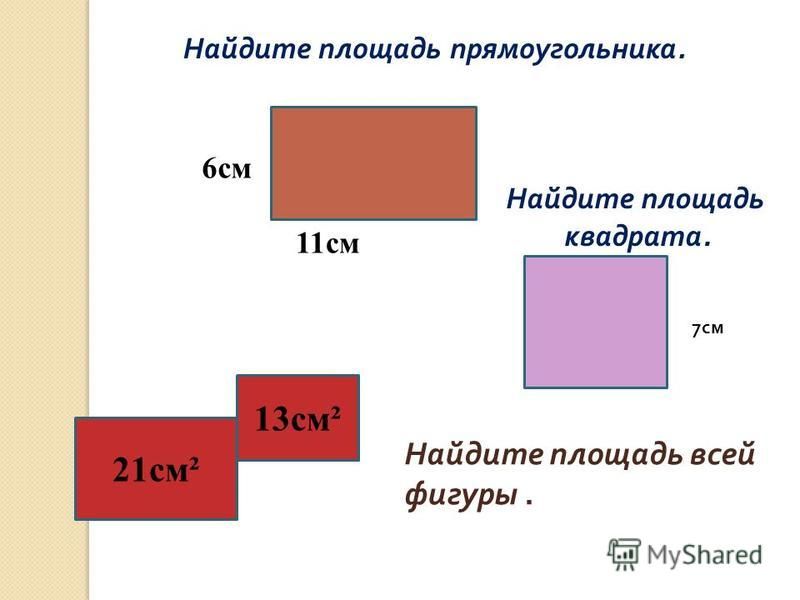 ALхимия будущего»
ALхимия будущего» Практики дополнительного образования
Практики дополнительного образования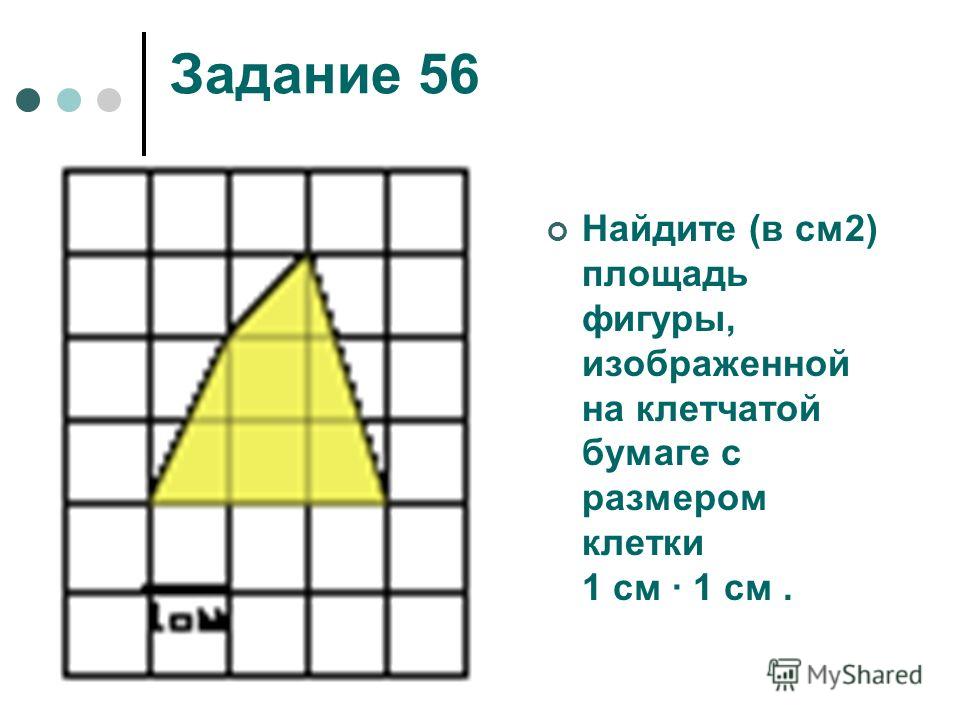
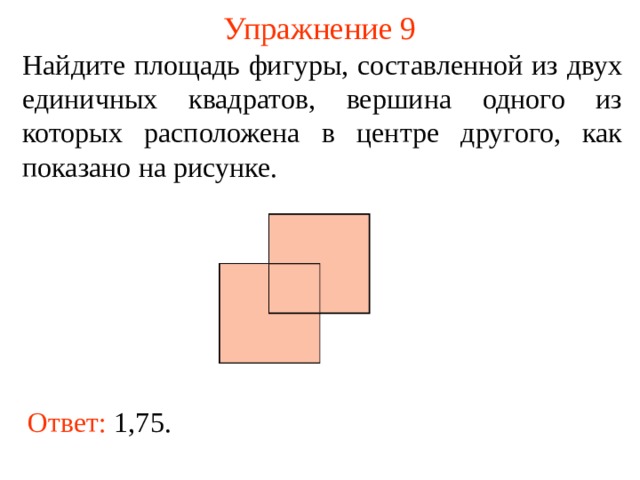 0 как ресурс индивидуализации обучения»
0 как ресурс индивидуализации обучения» И.Менделеева
И.Менделеева