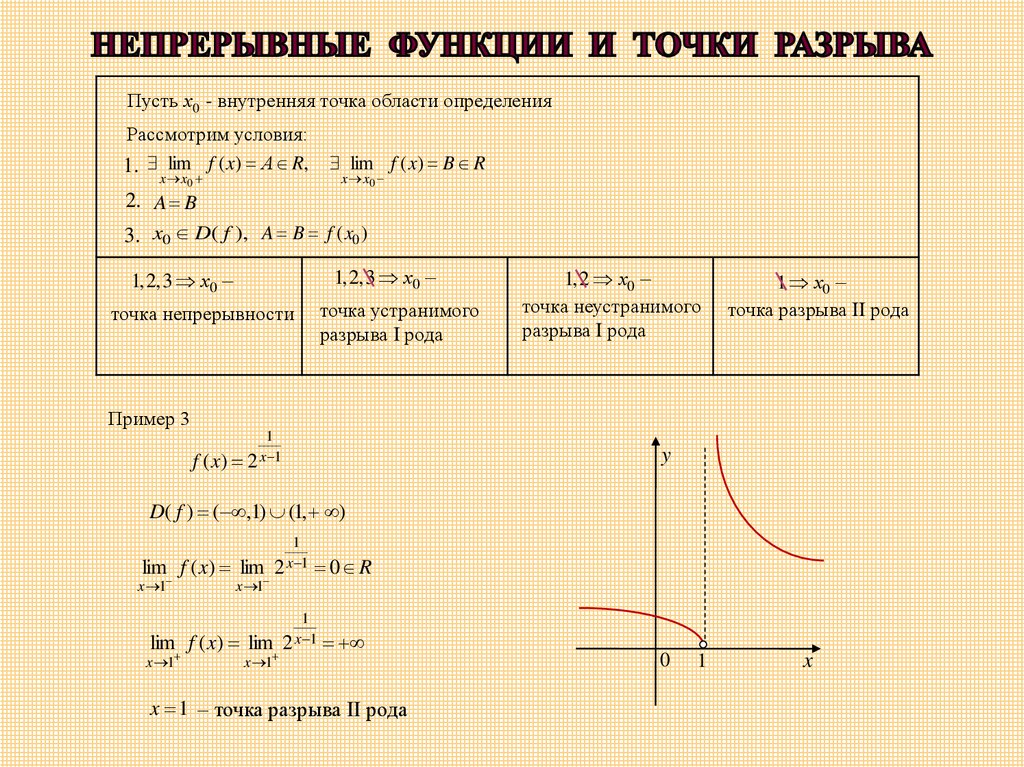
Функция y 3 2×2 x4 имеет в точке x 0
Обновлено: 10.10.2022
Данный калькулятор предназначен для построения графиков функций онлайн.
Графики функций – это множество всех точек, представляющих геометрический вид функции; при этом x – любая точка из области определения функции, а все y — точки, равные соответствующим значениям функции. Другими словами, график функции y=f(x) является множеством всех точек, абсциссы и ординаты которых соответствуют уравнению y=f(x).
Изобразить график функции абсолютно точно в большинстве случаев невозможно, так как точек бесконечно много, трудно найти все точки графика функции. В таких случаях можно построить приблизительный график функции. Чем больше точек берется в расчет, тем график более точный.
Данный сервис дает возможность провести исследование графика функции наиболее точно, так как программа строит график функции онлайн в прямоугольной системе координат на определенном интервале значений с учетом максимального количества точек.
Сервис поддерживает возможность построения графиков функций как вида , так и вида . Для того, чтобы построить график функции на отрезке \right]» />
нужно написать в строке: f[x],. Если Вы хотите, чтобы диапазон изменения ординаты был конкретным, например \right]» />
, нужно ввести: f[x],,.
Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:f[x]&&g[x]&&h[x]&&…&&t[x],.
Для того, чтобы построить график функции на прямоугольнике \right],y \in \left[ \right]» />
, нужно написать в строке: f[x, y],,. К сожалению, диапазон изменения аппликаты пока что нельзя сделать конкретным. Тем не менее, интересно отметить, что при построении графика функции Вы получите не только поверхность, которую она определяет, но и «контурную карту» поверхности (линии уровня).
Юля метала дротики. После выполнения всех бросков 10 очков она заработала один раз, 14 очков — раза, а 22 очк(-ов, -а), 4 очк(-ов, -) и 17 очков — каж … дое по три раза. Два а) Расположи все полученные очки в порядке возрастания: б) Вычисли среднее число очков, полученных в одном броске: (Ответ округли до сотых).
Какова линейная ск-ть тела, движущегося по окружности радиусам 40м центр ускорение 1,5 м/с Помогите пожалуйста срочно срочно срочно
петя в магазине виберал себе бассейн причём консультант ему сказал что объём всех трёх бассейнов равен 276см3 причём объём первого босейна на 50см3 бо … льше чем второго а объём третьего на 70 см3 меньше чем объём первого условие надо записать словами)
Данный калькулятор предназначен для нахождения точек разрыва функции онлайн.
Существует определенная классификация точек разрыва функции.
 Точки разрыва функции (нули знаменателя) делятся на точки разрыва первого рода и точки разрыва второго рода.
Точки разрыва функции (нули знаменателя) делятся на точки разрыва первого рода и точки разрыва второго рода.Точки разрыва первого рода при x=a имеют место быть, если существуют левосторонний и правосторонний пределы: lim(x→a-0)f(x) и lim(x→a+0)f(x). Эти пределы должны быть конечны. Если хотя бы один из односторонних пределов равен нулю или бесконечности, то в таком случае функция имеет точки разрыва второго рода.
Для того чтобы найти точки разрыва функции онлайн, необходимо указать функцию и значение аргумента.
Для получения полного хода решения нажимаем в ответе Step-by-step.
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.

- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
Воспользуемся методом построения линейных функций «по точкам».
| x | y |
| 0 | -1 |
| 1 | 2 |
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
| x | y |
| 0 | 2 |
| 1 | 1 |
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x — a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Читайте также:
- Полное имя соупа из call of duty
- Арканум сбор налогов
- Разрушитель заклинаний skyrim id
- Слив сакуры и ино
- Решите уравнение 2 sin 2 x
Точки разрыва функции — алгоритмы и примеры решения » Kupuk.net
Нахождение точек разрыва функции является одним из важнейших элементов исследования в математическом анализе. Многие студенты используют для пополнения своих знаний информацию из интернета, однако даже не подозревают, что она может быть недостоверной. Чтобы избежать неприятных последствий, следует решать по методике, которую рекомендуют специалисты, а также обладать определенными базовыми знаниям.
Общие сведения
Функцией называется зависимость одной переменной от другой. Если записать ее в виде равенства w = f (p), то величина «w» зависит от «р». Первая называется значением функциональной зависимости, а вторая — ее аргументом.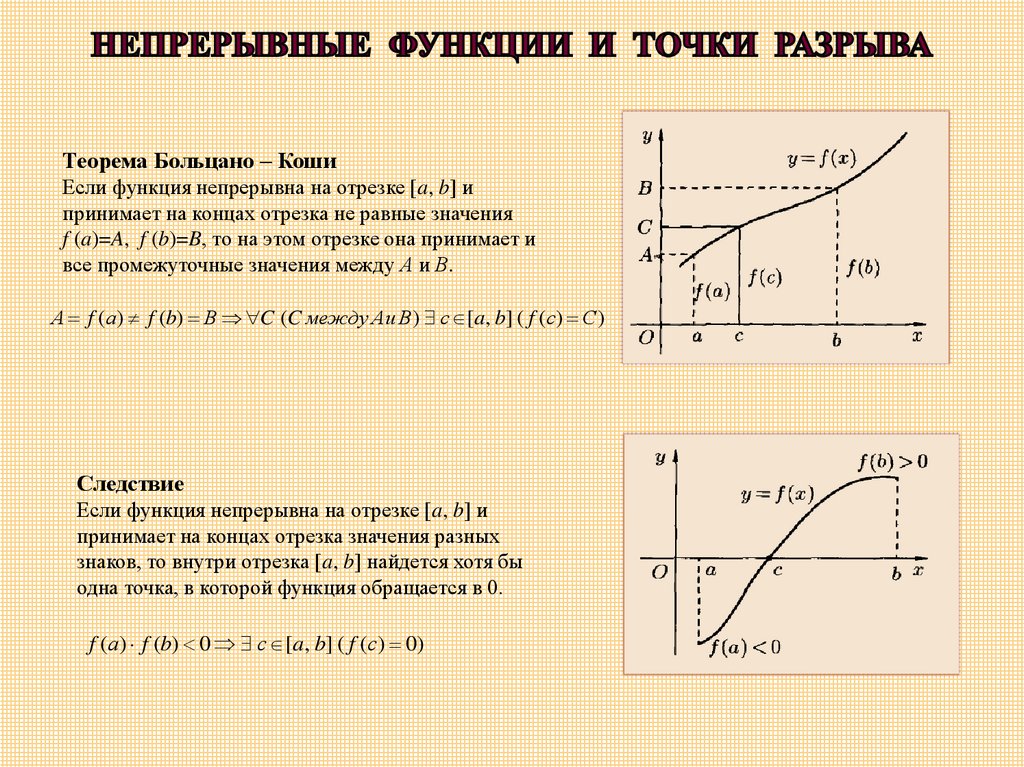 Последний может принимать любые значения, кроме превращающих «w» в пустое множество. Примером является выражение w = [(p — 2)(p + 7)] / (p 2 — 1). При значениях р1 = -1 и р2 = 1 получается пустое множество, поскольку на нуль делить нельзя.
Последний может принимать любые значения, кроме превращающих «w» в пустое множество. Примером является выражение w = [(p — 2)(p + 7)] / (p 2 — 1). При значениях р1 = -1 и р2 = 1 получается пустое множество, поскольку на нуль делить нельзя.
Когда математики говорят, что нужно произвести исследование функции на непрерывность, т. е. необходимо найти точки разрыва первого и второго рода. Если же таковых нет, то данное утверждение следует доказать математическим методом.
Непрерывной называется функция, которая не имеет точек разрыва, и меняется без существенных скачков в некоторых точках или промежутках, т. е. обладает определенным знакопостоянством. Это свойство определяется при помощи метода, представляющего совокупность математических преобразований. Последние основываются на теоремах. Они позволяют доказать существование или отсутствие точек и интервалов разрыва графика функции.
com/embed/fa7kuQajmU4″/>Базовые знания
Базовые знания — совокупность навыков, необходимых для решения какой-либо задачи. Для нахождения точек разрыва необходимы такие знания:
- Область определения — D.
- Решение уравнений.
- Нахождение пределов при известных значениях левосторонней и правосторонней границ.
- Классификация точек разрыва.
Когда список сформирован, тогда необходимо приступать к изучению материала. После полного понимания первого пункта необходимо переходить к последующему. Все пять элементов связаны между собой. Специалисты рекомендуют не заучивать наизусть понятия и термины, а понимать их.
Область определения
Областью определения некоторой функции w = f (p) называется интервал или числовой промежуток всех значений аргумента «р», при которых существует эта функция. Величину следует обозначать литерой «D». Конечная запись для вышеописанного тождества имеет такой вид: D (w) или D (f (р)).
Следует отметить, что D (w) зависит от ее вида. В алгебре бывают только простые и составные. К первым нужно отнести следующие подтипы:
- Алгебраические: рациональные (целые и дробные) и иррациональные (знак радикала).
- Тригонометрические (sin, cos, tg, ctg и производные от них).
- Трансцендентные (степенные, показательные и логарифмические).
К рациональным равенствам целого типа относятся любые выражения без корней, степеней, дробей, логарифмов, а также тождества, не содержащие каких-либо тригонометрических функций. В этом случае D соответствует всему интервалу действительных, которые обозначаются литерой «Z».
Для дробных D (w) зависит от знаменателя. В этом случае нужно решить уравнение, приравняв знаменатель к нулю. Например, чтобы найти D у функции вида w = [(p — 2)(p + 7)] / (p 2 — 1), нужно приравнять знаменатель дроби к 0.
Когда выражение является иррациональным, тогда нужно обратить внимание на степень корня и подкоренное выражение. (½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».
(½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».
Выражение под натуральным логарифмом должно быть всегда больше 0. В этом случае решается также неравенство, состоящее из тождества, находящегося под его знаком. Интервал для косинуса и синуса — все Z. Однако для tg (x) рекомендуется исключить значения аргумента (Pi / 2) + Pi * k, а для и ctg (x) — Pi * k (к принадлежит множеству Z).
Решение уравнений
Уравнения бывают нескольких видов: линейными, квадратными, кубическими и биквадратными. Первые являются самыми простыми, и решаются при помощи такой методики:
- Выполнение математических преобразований, упрощающих выражение.
- Перенос неизвестных в одну, а известных — в другую часть.

- Определение неизвестной.
К квадратным относятся равенства вида ap 2 + bp + c = 0. Математики их классифицируют на неполные и полные. К первым относятся только равенства, которые не содержат второй или третий член. Квадрат при первом коэффициенте должен быть всегда. Существует 4 метода решения:
- Если а = 1, то решается по теореме Виета.
- Использование дискриминанта.
- Разложение на множители.
- Построение графика.
- Использование программного обеспечения.
В первом случае нахождение корней осуществляется с помощью двух формул: р1 + р2 = -b и р1 * р2 = с. Однако при а > 1 нужно воспользоваться формулой для расчета некоторого вспомогательного параметра. Он называется дискриминантом (D). Для решения уравнения по второй методике рекомендуется применять такой алгоритм:
При с = 0 применяется методика разложения на множители. Нужно вынести р за скобку: р * (ар + b) = 0. В этом случае будут получены два линейных уравнения: р1 = 0 и а * р2 + b = 0.
Графический метод — построение графика параболы. Точки пересечения с осью ОХ и будут корнями уравнения. Можно также воспользоваться дополнительным программным обеспечением — онлайн-калькулятором. Этот метод позволит существенно сэкономить время решения задачи, и избежать ошибок. Однако им специалисты рекомендуют пользоваться только для проверки результата.
Решение кубических и биквадратных уравнений осуществляется при помощи введения замены переменной на другую. В этом случае происходит простое понижение степени до квадрата. Затем решается квадратное уравнение, а его корни подставляются в выражение замены.
Нахождение пределов
Нахождение предела функции — основа математического анализа. В некоторых источниках описаны разнообразные формулы и теоремы. Предел состоит из трех элементов:
- Знака «lim».

- Запись «t->a», которая означает, что аргумент «t» стремится к некоторой величине «а».
- Функция.
Для примера следует рассмотреть функцию w = [(t — 2)(t + 7)] / (t 2 — 1). Ее предел записывается в таком виде: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> 2). Читается запись следующим образом: предел функции w = [(t — 2)(t + 7)] / (t 2 — 1) с аргументом t, значение которого стремится к 2. Данный предел является простым, и решение сводится к подстановке аргумента в функцию: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> 2) = [((2 — 2)(2 + 7)) / (2 2 — 1)] = 0.
Существует еще один тип пределов, в которых необходимо делить на 0 или бесконечность (inf). Найти решение очень просто: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (p -> 1) = бесконечность и lim [7 / (t 2 — 1)] | (t -> +inf) = lim [7 / бесконечность] | (t -> +inf) = 0.
Более сложные пределы не решаются первым способом (подстановкой).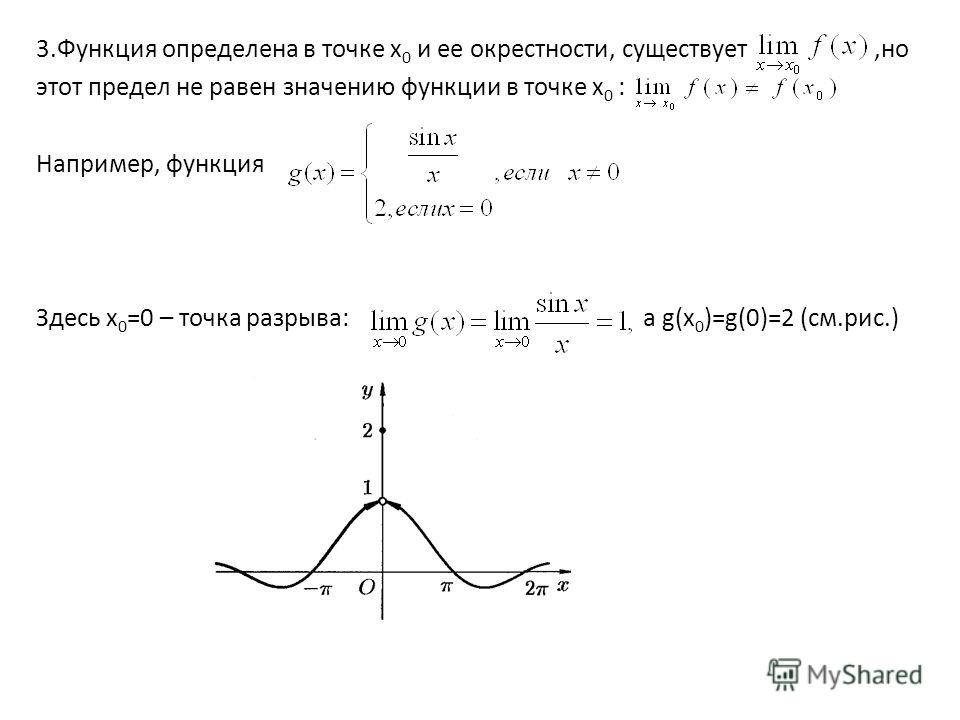 Если ее произвести, то может получиться соотношение inf/inf. В этом случае нужно разделить числитель и знаменатель на старшую степень, а затем выполнить подстановку. Процедуру можно выполнять неограниченное количество раз до получения необходимого результата. Для нахождения значения предела lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> +inf) нужно воспользоваться таким алгоритмом:
Если ее произвести, то может получиться соотношение inf/inf. В этом случае нужно разделить числитель и знаменатель на старшую степень, а затем выполнить подстановку. Процедуру можно выполнять неограниченное количество раз до получения необходимого результата. Для нахождения значения предела lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> +inf) нужно воспользоваться таким алгоритмом:
При «0/0» рекомендуется упростить числитель и знаменатель. Например, следует вычислить lim [(2t 2 — 3t — 5) / (t + 1)] | (t -> -1). Для упрощения числителя нужно решить уравнение 2t 2 — 3t — 5 = 0. 2 — 4 * 2 * (-5) = 49 > 0.
2 — 4 * 2 * (-5) = 49 > 0.
Следовательно, 2t 2 — 3t — 5 = (t + 1) * (2t — 5). После разложения нужно вычислить предел: lim [((t + 1) * (2t — 5)) / (t + 1)] | (t -> -1) = lim [2t — 5] | (t -> -1) = [2* (-1) — 5] = -2 — 5 = -7. Уравнения могут объединяться в системы.
Виды разрывов
Чтобы исследовать функцию на непрерывность, нужно уметь определять характер разрыва. Он классифицируется следующим образом: первого и второго рода. Первые бывают двух типов: устранимые и неустранимые.
Разрыв I рода существует в том случае, когда оба предела (левосторонний и правосторонний) являются конечными, т. е. не равны inf. Когда оба предела равны, то это точка устранимого разрыва. В противном случае (при неравенстве односторонних пределов) — разрыв является неустранимым, и называется «скачком».
Возможен вариант, когда один из пределов эквивалентен бесконечности. В этом случае говорят, что это разрыв II рода. Запись левого и правого пределов имеет такой вид: p -> -5 — 0 и p -> -5 + 0 соответственно.
Решения задач
После получения базовых знаний необходимо разобрать примеры решения. Точки разрыва функции следует искать по следующему алгоритму:
Однако для начала нужно найти область определения, которая играет важную роль в решении. Если она является множеством всех действительных чисел, то искать разрыв не имеет смысла. Он не существует. Если указанная функция содержит неизвестную, которая может превратить ее значение в неопределенность, то нужно вычислить правосторонний и левосторонний пределы (пункт 1). После этого их нужно сравнить, и сделать выводы о принадлежности точки к какому-нибудь виду.
Простые варианты
Нужно исследовать функцию w = (r 2 — 1) / (r — 2) на непрерывность или доказать, что она разрывная. Область определения D (w) = (-inf;2) U (2;+inf). (½) — 1 — 0) — 2].
(½) — 1 — 0) — 2].
Выполнять вычисления для двух точек необязательно, поскольку пределы будут равны и в этом случае. Следовательно, это устранимый разрыв I рода.
Таким образом, для нахождения разрывов необходимо знать некоторые особенности и методику, позволяющую правильно классифицировать их характер.
Точки разрыва функции — алгоритмы и примеры решения
Нахождение точек разрыва функции является одним из важнейших элементов исследования в математическом анализе. Многие студенты используют для пополнения своих знаний информацию из интернета, однако даже не подозревают, что она может быть недостоверной. Чтобы избежать неприятных последствий, следует решать по методике, которую рекомендуют специалисты, а также обладать определенными базовыми знаниям.
Содержание
- Общие сведения
- Базовые знания
- Область определения
- Решение уравнений
- Нахождение пределов
- Виды разрывов
- Решения задач
- Простые варианты
- Сложное задание
Общие сведения
Функцией называется зависимость одной переменной от другой. Если записать ее в виде равенства w = f (p), то величина «w» зависит от «р». Первая называется значением функциональной зависимости, а вторая — ее аргументом. Последний может принимать любые значения, кроме превращающих «w» в пустое множество. Примером является выражение w = [(p — 2)(p + 7)] / (p 2 — 1). При значениях р1 = -1 и р2 = 1 получается пустое множество, поскольку на нуль делить нельзя.
Когда математики говорят, что нужно произвести исследование функции на непрерывность, т. е. необходимо найти точки разрыва первого и второго рода. Если же таковых нет, то данное утверждение следует доказать математическим методом.
Непрерывной называется функция, которая не имеет точек разрыва, и меняется без существенных скачков в некоторых точках или промежутках, т. е. обладает определенным знакопостоянством. Это свойство определяется при помощи метода, представляющего совокупность математических преобразований. Последние основываются на теоремах. Они позволяют доказать существование или отсутствие точек и интервалов разрыва графика функции.
Базовые знания
Базовые знания — совокупность навыков, необходимых для решения какой-либо задачи. Для нахождения точек разрыва необходимы такие знания:
- Область определения — D.
- Решение уравнений.
- Нахождение пределов при известных значениях левосторонней и правосторонней границ.
- Классификация точек разрыва.
Когда список сформирован, тогда необходимо приступать к изучению материала.
После полного понимания первого пункта необходимо переходить к последующему. Все пять элементов связаны между собой. Специалисты рекомендуют не заучивать наизусть понятия и термины, а понимать их.
Область определения
Областью определения некоторой функции w = f (p) называется интервал или числовой промежуток всех значений аргумента «р», при которых существует эта функция. Величину следует обозначать литерой «D». Конечная запись для вышеописанного тождества имеет такой вид: D (w) или D (f (р)).
Следует отметить, что D (w) зависит от ее вида. В алгебре бывают только простые и составные. К первым нужно отнести следующие подтипы:
- Алгебраические: рациональные (целые и дробные) и иррациональные (знак радикала).
- Тригонометрические (sin, cos, tg, ctg и производные от них).
- Трансцендентные (степенные, показательные и логарифмические).
К рациональным равенствам целого типа относятся любые выражения без корней, степеней, дробей, логарифмов, а также тождества, не содержащие каких-либо тригонометрических функций. (½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».
(½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».
Выражение под натуральным логарифмом должно быть всегда больше 0. В этом случае решается также неравенство, состоящее из тождества, находящегося под его знаком. Интервал для косинуса и синуса — все Z. Однако для tg (x) рекомендуется исключить значения аргумента (Pi / 2) + Pi * k, а для и ctg (x) — Pi * k (к принадлежит множеству Z).
Решение уравнений
Уравнения бывают нескольких видов: линейными, квадратными, кубическими и биквадратными. Первые являются самыми простыми, и решаются при помощи такой методики:
- Выполнение математических преобразований, упрощающих выражение.
- Перенос неизвестных в одну, а известных — в другую часть.

- Определение неизвестной.
К квадратным относятся равенства вида ap 2 + bp + c = 0. Математики их классифицируют на неполные и полные. К первым относятся только равенства, которые не содержат второй или третий член. Квадрат при первом коэффициенте должен быть всегда. Существует 4 метода решения:
- Если а = 1, то решается по теореме Виета.
- Использование дискриминанта.
- Разложение на множители.
- Построение графика.
- Использование программного обеспечения.
В первом случае нахождение корней осуществляется с помощью двух формул: р1 + р2 = -b и р1 * р2 = с. Однако при а > 1 нужно воспользоваться формулой для расчета некоторого вспомогательного параметра. Он называется дискриминантом (D). Для решения уравнения по второй методике рекомендуется применять такой алгоритм:
При с = 0 применяется методика разложения на множители. Нужно вынести р за скобку: р * (ар + b) = 0.
В этом случае будут получены два линейных уравнения: р1 = 0 и а * р2 + b = 0.
Графический метод — построение графика параболы. Точки пересечения с осью ОХ и будут корнями уравнения. Можно также воспользоваться дополнительным программным обеспечением — онлайн-калькулятором. Этот метод позволит существенно сэкономить время решения задачи, и избежать ошибок. Однако им специалисты рекомендуют пользоваться только для проверки результата.
Решение кубических и биквадратных уравнений осуществляется при помощи введения замены переменной на другую. В этом случае происходит простое понижение степени до квадрата. Затем решается квадратное уравнение, а его корни подставляются в выражение замены.
Нахождение пределов
Нахождение предела функции — основа математического анализа. В некоторых источниках описаны разнообразные формулы и теоремы. Предел состоит из трех элементов:
- Знака «lim».

- Запись «t->a», которая означает, что аргумент «t» стремится к некоторой величине «а».
- Функция.
Для примера следует рассмотреть функцию w = [(t — 2)(t + 7)] / (t 2 — 1). Ее предел записывается в таком виде: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> 2). Читается запись следующим образом: предел функции w = [(t — 2)(t + 7)] / (t 2 — 1) с аргументом t, значение которого стремится к 2. Данный предел является простым, и решение сводится к подстановке аргумента в функцию: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> 2) = [((2 — 2)(2 + 7)) / (2 2 — 1)] = 0.
Существует еще один тип пределов, в которых необходимо делить на 0 или бесконечность (inf). Найти решение очень просто: lim [((t — 2)(t + 7)) / (t 2 — 1)] | (p -> 1) = бесконечность и lim [7 / (t 2 — 1)] | (t -> +inf) = lim [7 / бесконечность] | (t -> +inf) = 0.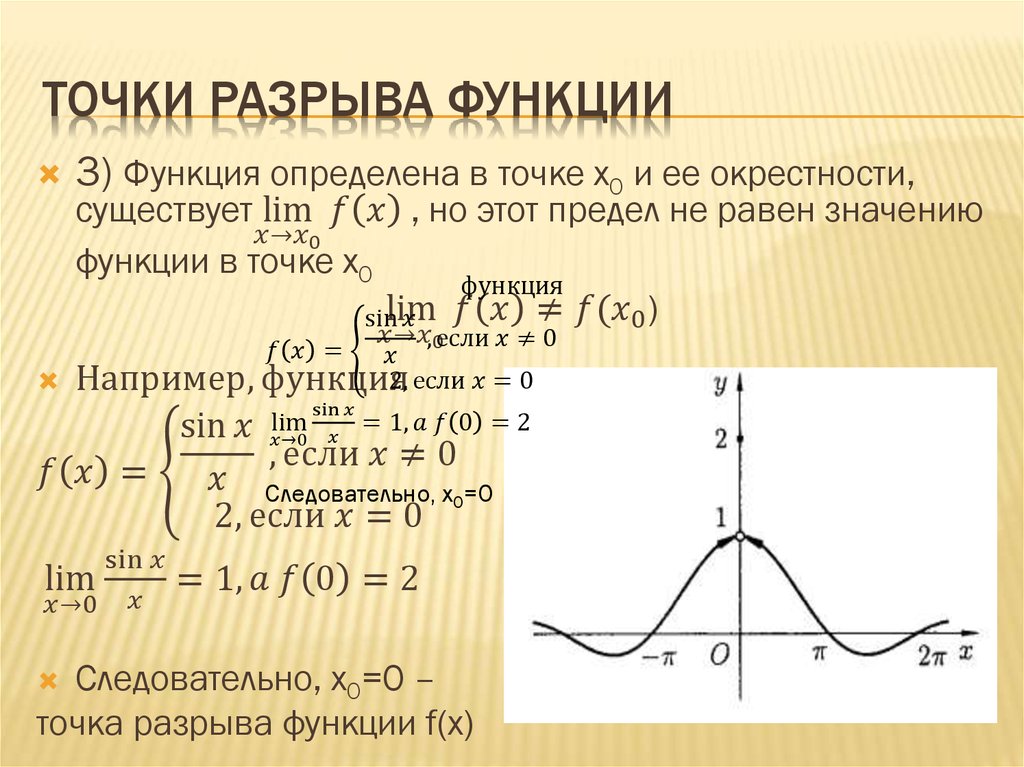
Более сложные пределы не решаются первым способом (подстановкой). Если ее произвести, то может получиться соотношение inf/inf. В этом случае нужно разделить числитель и знаменатель на старшую степень, а затем выполнить подстановку. Процедуру можно выполнять неограниченное количество раз до получения необходимого результата. Для нахождения значения предела lim [((t — 2)(t + 7)) / (t 2 — 1)] | (t -> +inf) нужно воспользоваться таким алгоритмом:
 2 — 4 * 2 * (-5) = 49 > 0.
2 — 4 * 2 * (-5) = 49 > 0.Следовательно, 2t 2 — 3t — 5 = (t + 1) * (2t — 5). После разложения нужно вычислить предел: lim [((t + 1) * (2t — 5)) / (t + 1)] | (t -> -1) = lim [2t — 5] | (t -> -1) = [2* (-1) — 5] = -2 — 5 = -7. Уравнения могут объединяться в системы.
Виды разрывов
Чтобы исследовать функцию на непрерывность, нужно уметь определять характер разрыва. Он классифицируется следующим образом: первого и второго рода. Первые бывают двух типов: устранимые и неустранимые.
Разрыв I рода существует в том случае, когда оба предела (левосторонний и правосторонний) являются конечными, т. е. не равны inf. Когда оба предела равны, то это точка устранимого разрыва. В противном случае (при неравенстве односторонних пределов) — разрыв является неустранимым, и называется «скачком».
Возможен вариант, когда один из пределов эквивалентен бесконечности. В этом случае говорят, что это разрыв II рода. Запись левого и правого пределов имеет такой вид: p -> -5 — 0 и p -> -5 + 0 соответственно.
Запись левого и правого пределов имеет такой вид: p -> -5 — 0 и p -> -5 + 0 соответственно.
Решения задач
После получения базовых знаний необходимо разобрать примеры решения. Точки разрыва функции следует искать по следующему алгоритму:
Однако для начала нужно найти область определения, которая играет важную роль в решении. Если она является множеством всех действительных чисел, то искать разрыв не имеет смысла. Он не существует. Если указанная функция содержит неизвестную, которая может превратить ее значение в неопределенность, то нужно вычислить правосторонний и левосторонний пределы (пункт 1). После этого их нужно сравнить, и сделать выводы о принадлежности точки к какому-нибудь виду.
Простые варианты
Нужно исследовать функцию w = (r 2 — 1) / (r — 2) на непрерывность или доказать, что она разрывная. (½) — 1 — 0) — 2].
(½) — 1 — 0) — 2].
Выполнять вычисления для двух точек необязательно, поскольку пределы будут равны и в этом случае. Следовательно, это устранимый разрыв I рода.
Таким образом, для нахождения разрывов необходимо знать некоторые особенности и методику, позволяющую правильно классифицировать их характер.
Предыдущая
МатематикаКак решать пропорции — правила, методы и примеры вычислений
Следующая
МатематикаДоверительный интервал — формула и примеры определения вероятности
Калькулятор точки безубыточности— MathCracker.com
Финансы Решатели
Инструкции: Используйте этот калькулятор точки безубыточности для расчета точки безубыточности (\(BEP\)), указав фиксированную стоимость (\(FC\)), переменную стоимость единицы продукции (\(VC\)) и цену продажи.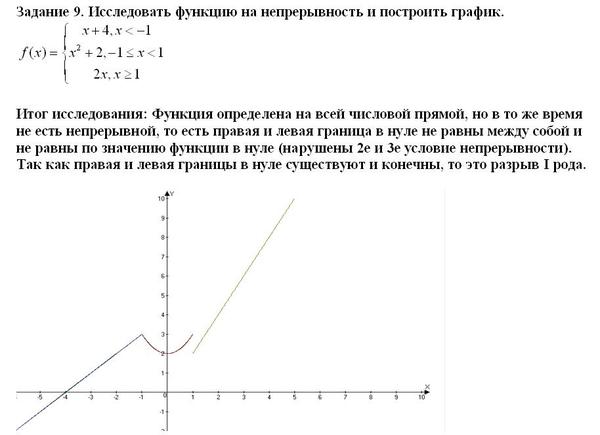 (\(П\)):
(\(П\)):
Фиксированная стоимость \((FC)\) =
Переменная стоимость за единицу \((VC)\) =
Цена продажи \((P)\) =
Подробнее о калькуляторе безубыточности, чтобы лучше понять, как им пользоваться. Сначала начнем с определения безубыточности: Точка безубыточности — это объем производства, при котором прибыль будет равна нулю.
Прежде всего, что такое точка останова?
В финансах точка разрыва наступает тогда, когда выручка равняется затратам, поэтому компания «безубыточна» (именно здесь наступает «прорыв»). из).
Обычно точка останова измеряется либо в единицах, либо в долларах. Так, например, вы находите количество единиц, которые
необходимо, чтобы выручка покрывала расходы. Вы также можете найти стоимость продаж в долларах, необходимую для безубыточности.
Так, например, вы находите количество единиц, которые
необходимо, чтобы выручка покрывала расходы. Вы также можете найти стоимость продаж в долларах, необходимую для безубыточности.
Как рассчитать точку безубыточности?
Расчет довольно прост. Вам нужно использовать следующую формулу:
\[ BEP = \displaystyle \frac{FC}{P — VC} \]
Часто, когда дело доходит до концепции точки безубыточности в бухгалтерском учете, вместо точки безубыточности рассматриваются продажи за наличные, связанные с уровнем продаж в точке безубыточности.
Обратите внимание на формулу цены безубыточности, что знаменатель имеет \(P — VC\). Так что же происходит, когда \(P = VC\)? В этом случае точка безубыточности равна бесконечности, и в этом случае вывод состоит в том, что, когда цена равна переменным затратам на единицу, точка безубыточности отсутствует.
Так что же происходит, когда \(P = VC\)? В этом случае точка безубыточности равна бесконечности, и в этом случае вывод состоит в том, что, когда цена равна переменным затратам на единицу, точка безубыточности отсутствует.
Что такое анализ безубыточности?
Идея безубыточности в реальной жизни заключается в том, что я не проигрываю и не выигрываю. И именно в этом заключается идея анализа безубыточности: вам нужно определить, сколько единиц продукции вам нужно произвести, чтобы ваша прибыль была равна нулю, так что не проигрывайте и не выигрывайте, вы просто безубыточны.
Таким образом, точка безубыточности соответствует количеству единиц, которые вам нужно продать, чтобы выйти на уровень безубыточности. Если вы продаете меньше, чем это, вы получаете убыток, а если вы продаете больше, вы получаете прибыль.
Пример точки безубыточности
Предположим, вы владеете фирмой с фиксированными затратами в размере 10 000 долларов США (включая аренду, интернет и т. д.). Вы продаете виджет, производство которого обходится вам в 1,25 доллара, и вы можете продать его за 2,50 доллара. Какова будет ваша точка безубыточности?
В этом случае постоянные затраты равны \(FC = 10 000\), переменные затраты на единицу продукции равны \(VC = 1,25\), а цена продажи равна \(P = 2,50\). Нам нужно подставить эти числа в следующую формулу:
\[ \text{Точка безубыточности} = \displaystyle \frac{FC}{P — VC} = \displaystyle \frac{10,000}{2,50 — 1,25} = \displaystyle \frac{10,000}{1,25} = 8,000 \text {единицы} \]
Следовательно, чтобы выйти в безубыток, вам нужно будет продать 8000 единиц. Если вы продадите менее 8000 единиц, вы
есть убыток, и если вы продадите более 8000 единиц, вы получите положительную прибыль.
Если вы продадите менее 8000 единиц, вы
есть убыток, и если вы продадите более 8000 единиц, вы получите положительную прибыль.
Другие связанные финансовые калькуляторы
Другие финансовые калькуляторы, которые могут вас заинтересовать, это калькулятор чистой приведенной стоимости и калькулятор внутренней нормы прибыли.
Базовый финансовый пакет Калькулятор точки безубыточности Калькулятор безубыточности Финансовый калькулятор Финансовый решатель
Аппроксимация функции с помощью регрессионного анализа
Проблема аппроксимации функции заключается в том, как выбрать функцию из четко определенного класса, которая точно соответствует («аппроксимирует») целевой неизвестной функции.
Этот калькулятор использует предоставленные данные таблицы целевых функций в виде точек {x, f(x)} для построения нескольких моделей регрессии, а именно: линейной регрессии, квадратичной регрессии, кубической регрессии, степенной регрессии, логарифмической регрессии, гиперболической регрессии, ab -экспоненциальная регрессия и экспоненциальная регрессия. Результаты можно сравнивать по коэффициенту корреляции, коэффициенту детерминации, средней относительной ошибке (стандартной ошибке регрессии) и визуально, на графике. Теория и формулы, как обычно, даны под калькулятором.
Функция приближения с регрессионным анализом
83 71 64 69 69 64 68 59 81 91 57 65 58 62
x Значения, разделенные пространством
183 168 171 178 176 172 165 183 182 163 175 164 175
9000 29000 2
9000 2
9000 2
9000 2
9000 2
9000 2 9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 298 172 Значения Y, разделенные пробелом
Линейная регрессия
Квадратичная регрессия
Кубическая регрессия
Степенная регрессия
ab-Экспоненциальная регрессия
Логарифмическая регрессия
Гиперболическая регрессия
Экспоненциальная регрессия
Точность расчета
цифры после десятичной точки: 4
Линейная регрессия
Коэффициент линейной корреляции
Коэффициент определения
Относительная ошибка, %
.
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Cubic regression
Correlation coefficient
Coefficient of determination
Average relative error, %
Power regression
Correlation coefficient
Coefficient of determination
Средняя относительная ошибка, %
ab-Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент определения
Средняя относительная ошибка, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент
Altrication Shortication Shortive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive Oltive.
Коэффициент корреляции
Коэффициент детерминации
Средняя относительная ошибка, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент определения
Средняя относительная ошибка, %
. Во время загрузки и создания может происходить замедление работы браузера.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и в случае квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же формулы, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – то же.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии — те же, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.
Коэффициент корреляции, коэффициент детерминации, стандартная ошибка регрессии – те же, что и выше.
Начнем с задачи:
Имеем неизвестную функцию y=f(x), заданную в виде табличных данных (например, таких, как полученные из экспериментов).
Нам нужно найти функцию с известным типом (линейная, квадратичная и т.д.) y=F(x), эти значения должны быть как можно ближе к табличным значениям в тех же точках. На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.
В результате мы должны получить формулу y=F(x), называемую эмпирической формулой (уравнение регрессии, функция аппроксимации), которая позволяет вычислить y для x, не представленных в таблице. Таким образом, эмпирическая формула «сглаживает» значения y.
Мы используем метод наименьших квадратов , чтобы получить параметры F для наилучшего соответствия. Наилучшее соответствие по методу наименьших квадратов минимизирует сумму квадратов невязок, причем невязка представляет собой разницу между наблюдаемым значением и подобранным значением, предоставленным моделью.
Таким образом, когда нам нужно найти функцию F, такую как сумма квадратов невязок, S будет минимальным
Опишем решение этой задачи на примере линейной регрессии F=ax+b.
Нам нужно найти наилучшее соответствие для коэффициентов a и b, таким образом, S является функцией a и b. Для нахождения минимума найдем точки экстремума, в которых частные производные равны нулю.
Используя формулу для производной комплексной функции, получим следующие уравнения:
Разложив первые формулы с частными производными, получим следующие уравнения:
Из этих уравнений можно получить формулы для a и b , что будет соответствовать приведенным выше формулам.
| Загрузка: SegReg стандарт Загрузка: Перейти к: Программное обеспечение Общие статьи Artículos Опубликованные Частные Часто задаваемые вопросы Домашняя страница | ||||||
| Альтернативы (1) — Приложение усиления SegReg
калькулятор, позволяющий выразить
предпочтение определенному виду
сегментации или желания исключить
определенного типа, можно скачать с
СегРегА. | |||||||
| См. также Дополнительные примеры см.
сегментированная регрессия
статья на стр. 13 и далее,
бумага допуска на
устойчивость сельскохозяйственных культур к засолению почвы или
чувствительная бумага на
чувствительность культур к мелководью. | |||||||
| Часть 1 иллюстраций для 1 иждивенца и одного
переменная (Y и X соответственно). | |||||||
| (Часть 2 для полиномиального случая 1 зависимого переменная (Y) и 2 независимые переменные (X и Z) можно увидеть ниже) | |||||||
| Вводный экран программы калькулятора SegReg: Модель поставляется с различными пояснениями, такими как запрограммированные типы функций, методы расчета и применение критериев значимости.  Пример Тип 3: Пример Тип 3 с удлиненной горизонтальной линией (плато)
используя те же данные, что и выше, в
Программное обеспечение PartReg
приложение вместо SegReg. Пример Тип 4: Культура допускает глубину грунтовых вод
7 дм. Пример Тип 5: В 9 году (1976) построена плотина в р.
река | |||||||
Часть 2 для полиномиального случая 1 зависимого переменная (Y) и 2 независимые переменные (X и Z) Скриншот меню ввода для многочлена
случай (1 зависимая переменная (Y) и 2 независимые
переменные (X и Z). |







 В этом случае будут получены два линейных уравнения: р1 = 0 и а * р2 + b = 0.
В этом случае будут получены два линейных уравнения: р1 = 0 и а * р2 + b = 0.
 е.
факторы роста сельскохозяйственных культур, такие как глубина грунтовых вод и
засоленность почвы. Его также можно рассматривать как
регрессионный калькулятор.
е.
факторы роста сельскохозяйственных культур, такие как глубина грунтовых вод и
засоленность почвы. Его также можно рассматривать как
регрессионный калькулятор. Хотя это может привести к манипуляциям,
доступен для запроса.
Хотя это может привести к манипуляциям,
доступен для запроса. 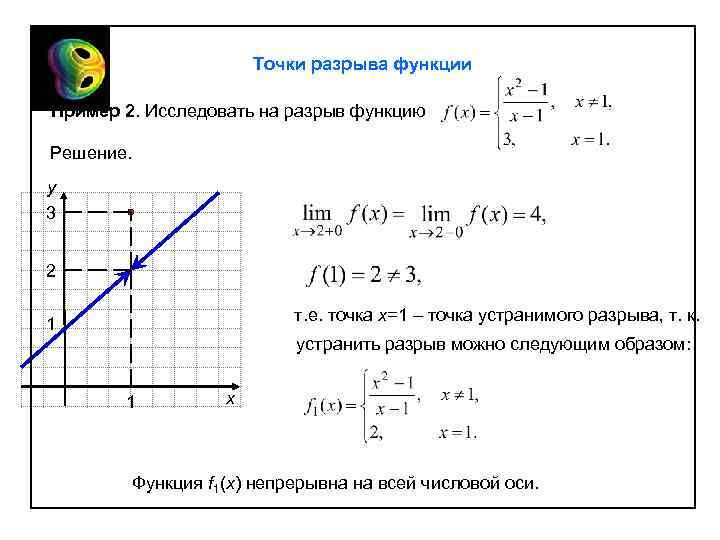 t-распределение, см.
программа t-тест.
t-распределение, см.
программа t-тест. 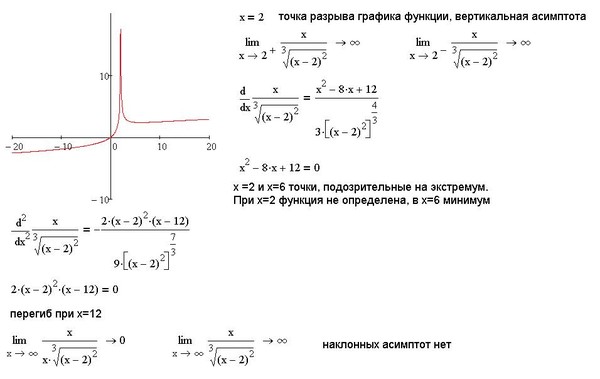
 Описание математики
участие, с примерами, можно увидеть в этом
бумага о доверии.
Эти изменения были мотивированы предложениями, внесенными
вперед Дон Норен и Вэньхуай Ли.
Описание математики
участие, с примерами, можно увидеть в этом
бумага о доверии.
Эти изменения были мотивированы предложениями, внесенными
вперед Дон Норен и Вэньхуай Ли. 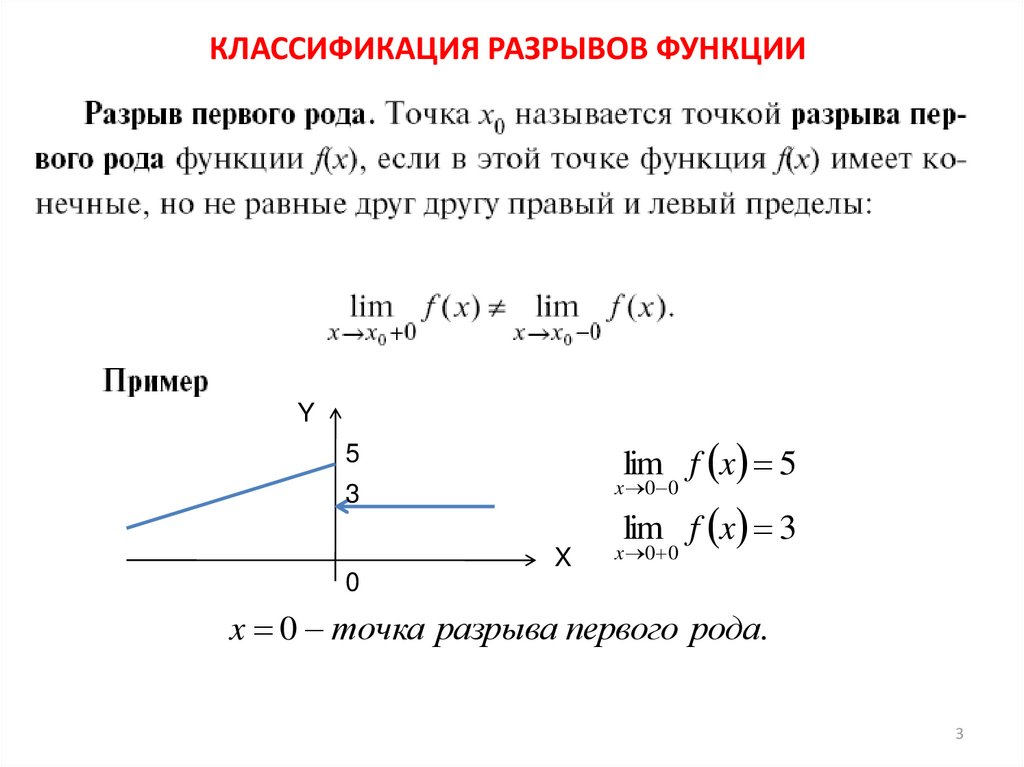 Это также дает возможность выбрать S-образную кривую,
степенная функция, или обобщенная третья степень
полином, см.:
S-кривые,
кубический,
Мощность или,
Полином.
Это также дает возможность выбрать S-образную кривую,
степенная функция, или обобщенная третья степень
полином, см.:
S-кривые,
кубический,
Мощность или,
Полином. 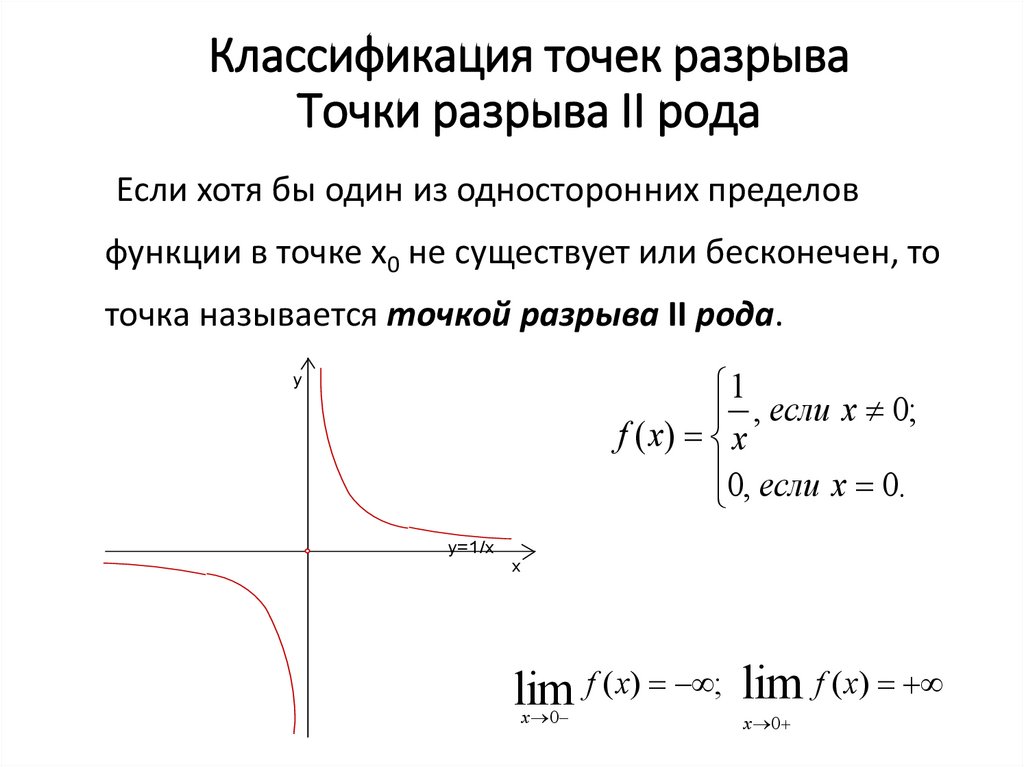 сначала минимизирует отклонения модели
значений от наблюдаемых на протяжении всего
домен, тогда как второй вычисляет
максимальная часть (диапазон) домена по
коэффициент регрессии (т.е.
наклон линии регрессии) может быть
принимается равным нулю.
сначала минимизирует отклонения модели
значений от наблюдаемых на протяжении всего
домен, тогда как второй вычисляет
максимальная часть (диапазон) домена по
коэффициент регрессии (т.е.
наклон линии регрессии) может быть
принимается равным нулю.  Немного
результаты также показаны там.
Немного
результаты также показаны там.