Урок для 10 класса по теме: «Функция y=sin x ее свойства и график»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 47 с углубленным изучением отдельных предметов
городского округа Тольятти
Урок алгебры и начала анализа
Учитель математики МБУ СОШ № 47 Автозаводского района г.о. Тольятти
Дьячкова Светлана Николаевна
Класс: 10 «А»
Тип урока: объяснение нового материала.
Модель урока: интегрированный с информатикой и ИКТ
Технология: личностно-ориентированная с применением ИКТ технологий.
Тема: Функция y=sin x ее свойства и график.
Цель урока: изучить построение графика функции y=sinx, рассмотреть построение графиков тригонометрических функций, задаваемых формулами вида y=sinx+n, y=Аsinx , y=sin(x-m ), y=sinkx с помощью программы Microsoft Office Excel.
Задачи урока:
Обучающая: познакомить с основными свойствами функции y=sin x, отработать алгоритм работы с таблицей и диаграммой в программе Microsoft Office Excel при построении тригонометрической функции, повторить основные свойства изученных функций.
Развивающая: уметь соотносить изучаемые функции с конкретной и жизненной ситуацией, развивать наглядно-образное и наглядно – действенное мышление, уметь работать по инструкции.
Воспитательная: ориентировать на профессиональный выбор, профессию.
Оборудование: компьютерный класс, проектор, операционная система Windows, пакет Microsoft Office.
Ход урока.
Организационно-мотивационный момент-7 минут
Приветствие. Сообщение цели урока. Инструктаж по технике безопасности при работе с компьютером.
Цель этапа: постановка задачи и мотивация на дальнейшую деятельность обучающихся на уроке.
1.1. Слово учителя математики:
-Здравствуйте ребята, сегодня мы повторим все известные вам функции и изучим новую функцию y=sin x, построим график ее с помощью программы Microsoft Office Excel. Но для начала вспомним правила работы за компьютером в школе (проведение инструктажа по технике безопасности).
1.2. Стартовая презентация учителя математики в программе Microsoft Office PowerPoint и постановка проблемных вопросов для обучающихся:
Какие кривые существуют вокруг нас?
Какая кривая называется линией жизни. Какие свойства у линии жизни?
Гармоническое колебание линии жизни.
Расчет биоритмов человека с помощью ИКТ технологий.

Цель: повторить основные свойства изученных функций, обобщить знания ребят по теме «Функция» и ввести в новую тему урока, развивать умение соотносить изучаемые функции с конкретной и жизненной ситуацией.
Беседа сопровождается наглядным материалом презентации. На экране всевозможные фотографии из жизни «Кривые вокруг нас», ученик должен увидеть на график какой функцию похоже изображение вспомнить ее свойства, перечислить и ответить на вопрос:
-Какие кривые существуют вокруг нас?
В конце показа приходим к функции y=sin x, мы видим на фото хребет гор и кардиограмму сердца больного с учащенным биением ритма. И задаем вопрос, какую функцию вы видите здесь- «Линия жизни», и мы переходим к следующему этапу изучение новой темы, а, именно, задаем новый вопрос: Какая кривая называется линией жизни. Какие свойства у линии жизни?
Объяснение нового материал-10 минут.

Цель: познакомить с основными свойствами функции y=sin x, отработать алгоритм работы с таблицей и диаграммой в программе Microsoft Office Excel при построении тригонометрической функции.
Слово учителя математики. Практическая работа обучающихся.
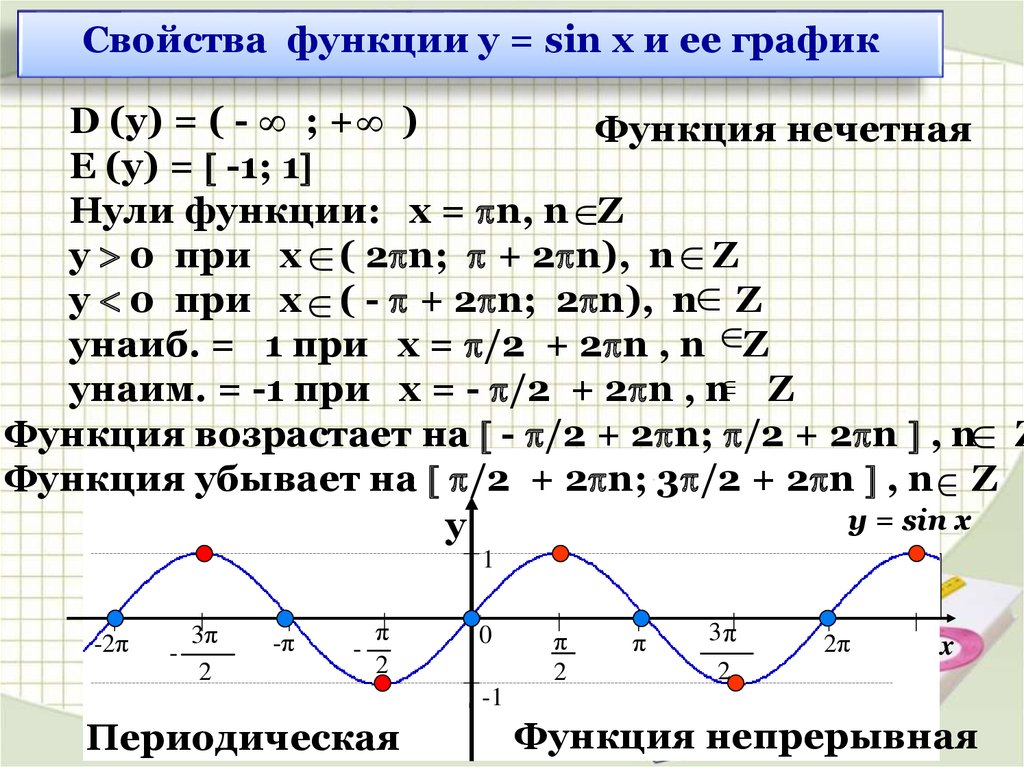
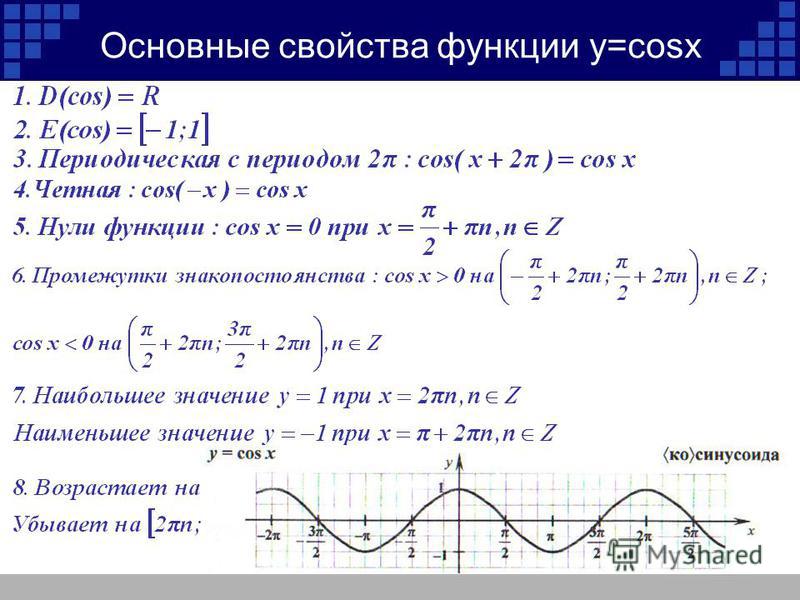
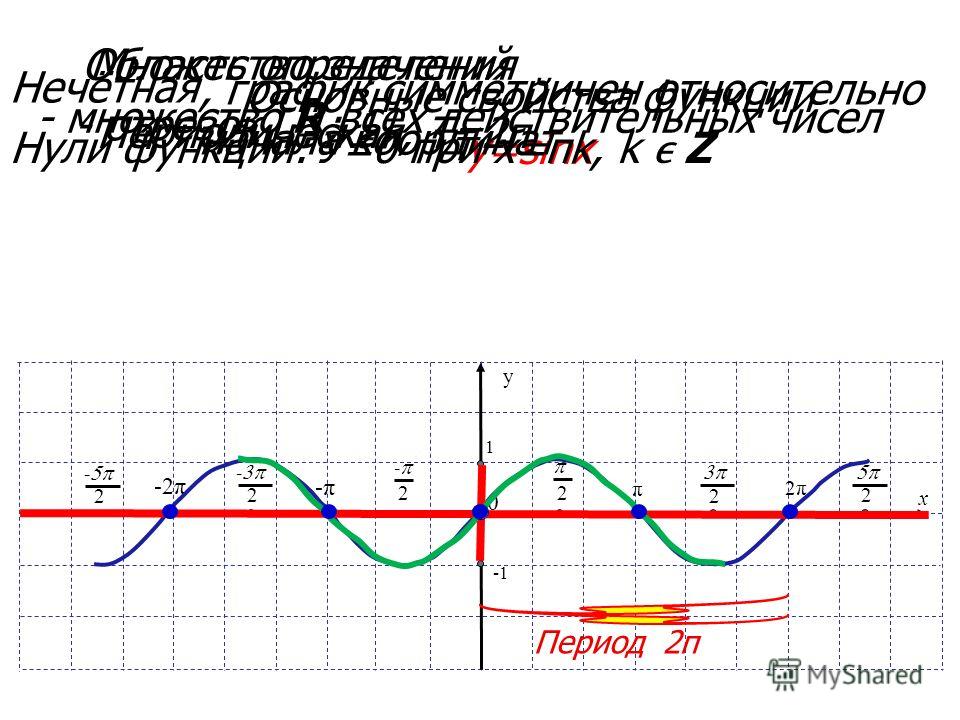
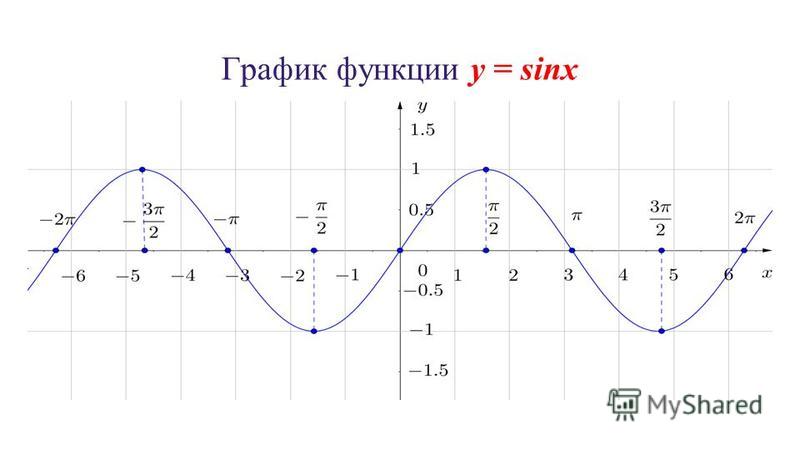
Кривая линия жизни очень похожа на график функции у=sin x. Определение: числовая функция, заданная формулой у=sin x, называется синусом. График такой функции является синусойда. Используя единичную окружность и таблицу значений синуса, построим в тетради график данной функции.
-Но для начала подумаем, а какова будет область определения данной функции?
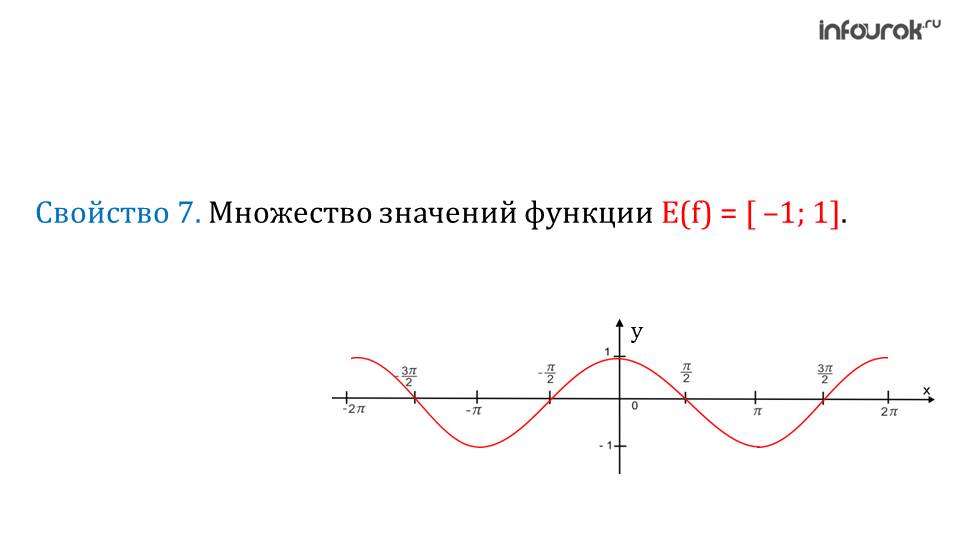
-Область значений?
-Установите четность, нечетность функции?
В тетради постройте систему координат. Учитывая, что область определения синуса промежуток от -1 до 1, ось y разместим на 10 клетках. Ось х растянем на ширину тетрадного листа.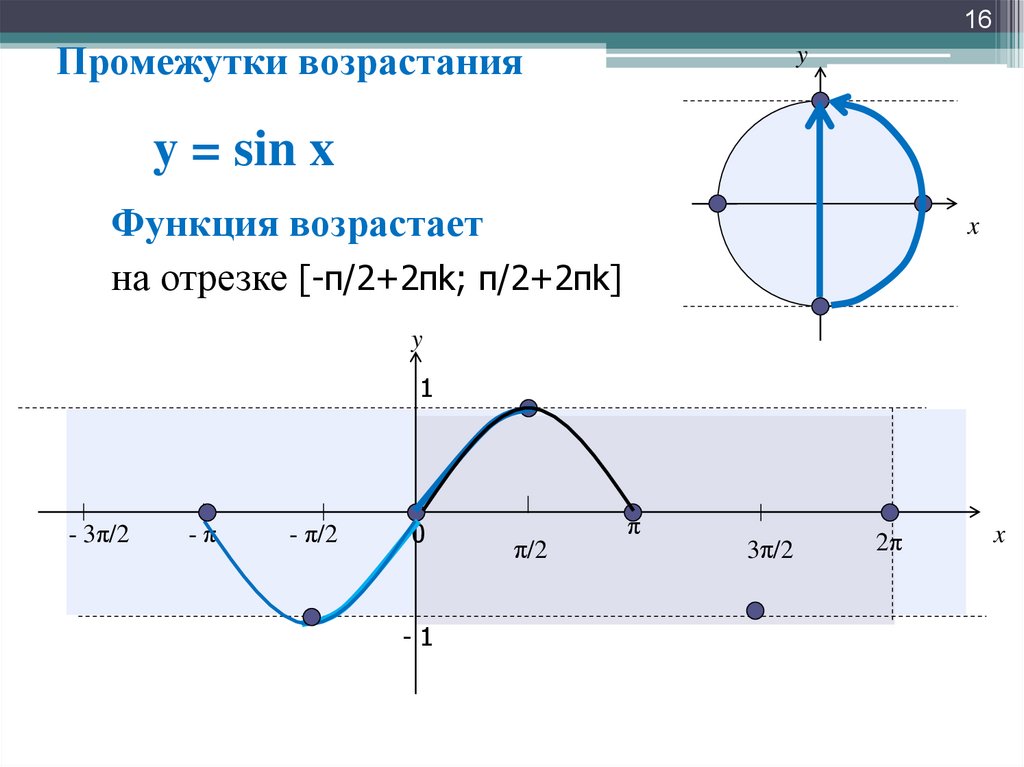 За единичный отрезок по оси х возьмем 1 см. Учитывая, что p»3,14, и округляя это число до целых, на оси х за p возьмем 6 клеток. Отметим узловые точки и табличные значения синуса. Выполним преобразование симметрии относительно прямой x=p/2, относительно точки (p, 0). Соединим полученные точки и продолжим график с учетом периодичности функции, учитывая что sin (x+2пn)=sin x.
За единичный отрезок по оси х возьмем 1 см. Учитывая, что p»3,14, и округляя это число до целых, на оси х за p возьмем 6 клеток. Отметим узловые точки и табличные значения синуса. Выполним преобразование симметрии относительно прямой x=p/2, относительно точки (p, 0). Соединим полученные точки и продолжим график с учетом периодичности функции, учитывая что sin (x+2пn)=sin x.
Оперирование полученными знаниями в новой ситуации-13 минут.
Цель этапа: рассмотреть построение графиков тригонометрических функций, задаваемых формулами вида y=sinx+n, y=Аsinx , y=sin(x-m ), y=sinkx с помощью программы Microsoft Office Excel, формировать умение действовать по инструкции.
3.1.Слово учителя математики. Актуализация ранее полученных знаний по теме «Движение функции».
А теперь ответим на вопрос: «Гармоническое колебание линии жизни».
Учитель: Сколько и какие существуют преобразования графика функции y=f(x)?
y=f(x)+b, b–число. Параллельный перенос графика вдоль оси ординат на вектор
(0;b). Если b>0 – перенос вверх, by=kf(x). Расширение графика вдоль оси ординат в. Если |k| раз.
y=f(x–a). Параллельный перенос графика вдоль оси ординат на вектор
(a;0).Если а>0 – перенос вправо, аy=f(). Растяжение графика вдоль абсцисс. Если |k| раз.
y=–f(x). Симметрия графика относительно оси ординат.
y=f(–x). График симметричен относительно оси абсцисс.
y=|f(x) |. Часть графика при y0 сохраняется, а часть графика при y
y=f(|x|). Часть графика при x0 сохраняется, часть при x
Учитель: Какая команда меню позволяет строить диаграммы и графики в табличном процессоре Ехсе1? Ответ учеников: Мастер диаграмм.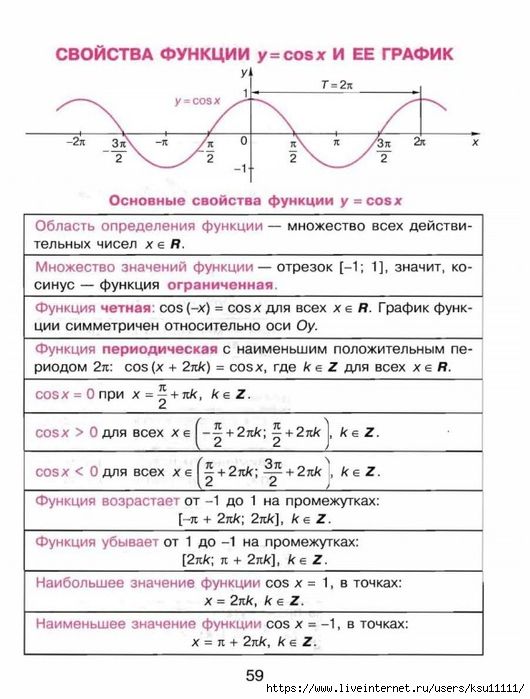
Учитель: Как задается вычисление в таблице значений ячеек по формуле? Ответ учеников: Ввести знака «=», активизация нужной ячейки, содержимое которой будет являться аргументом, ввод соответствующих функций и знаков арифметических операций. Ввод формулы можно контролировать с помощью окна ввода формулы.
Учитель: Как можно скопировать формулу в несколько ячеек? Ответ учеников: С помощью маркера автозаполнения в правом нижнем углу курсора или с помощью команды Правка – Копировать и Правка – Вставить.
Учитель: Как сделать ссылку абсолютной для того, чтобы при копировании она не изменялась? Ответ учеников: Необходимо установить перед именем столбца и строки знак «$».
3.2 Самостоятельная работа обучающихся за компьютером. Действие по инструкции.
Класс делится на четыре варианта и каждый получает задание. Получившиеся графики отражаются на экране.
Получившиеся графики отражаются на экране.
Построить график функции y=кsin x,
Построить график функции y=sin x+в,
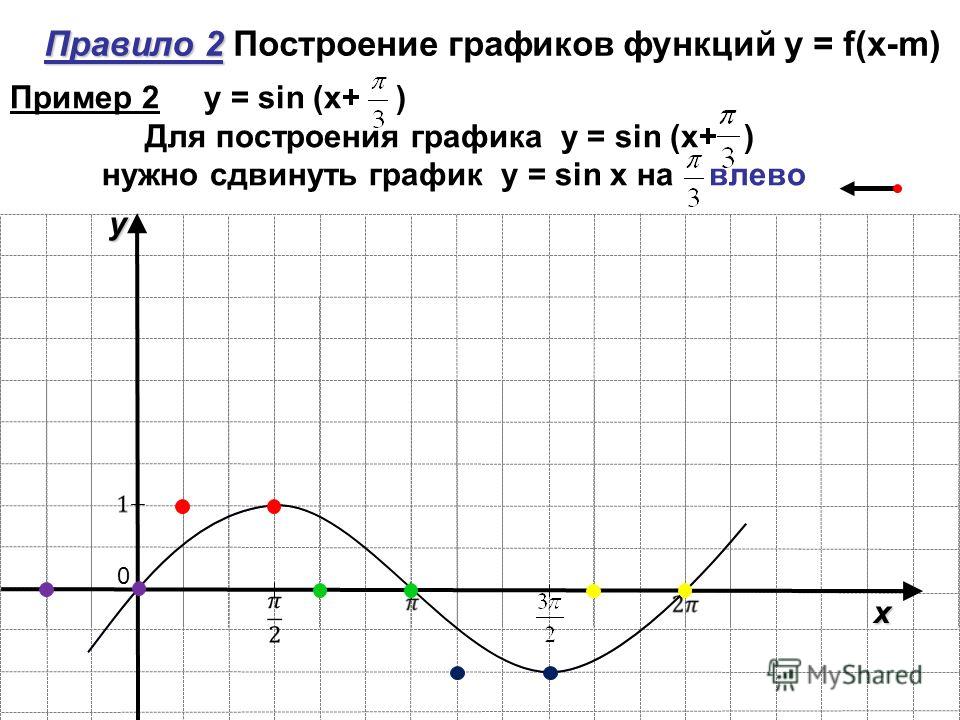
Построить график функции y=sin (x+с),
Построить график функции y=sin (x+с)+в,
Инструкционная карта для построения y=sin x:
Заполнение таблицы зависимости y(x)
1. Запустите среду MS Excel. Выполните команду Файл-Открыть… Выберите в окне файлера Windows файл «График тригонометрической функции.xlt» из папки Общие документы.
2. Занесите исходные числовые данные в следующие ячейки:
D10 – левая граница области построения (введите -12)
D11 – правая граница области построения (введите 12)
D12 –число столбцов (20 штук)
D13-шаг=0,4
3.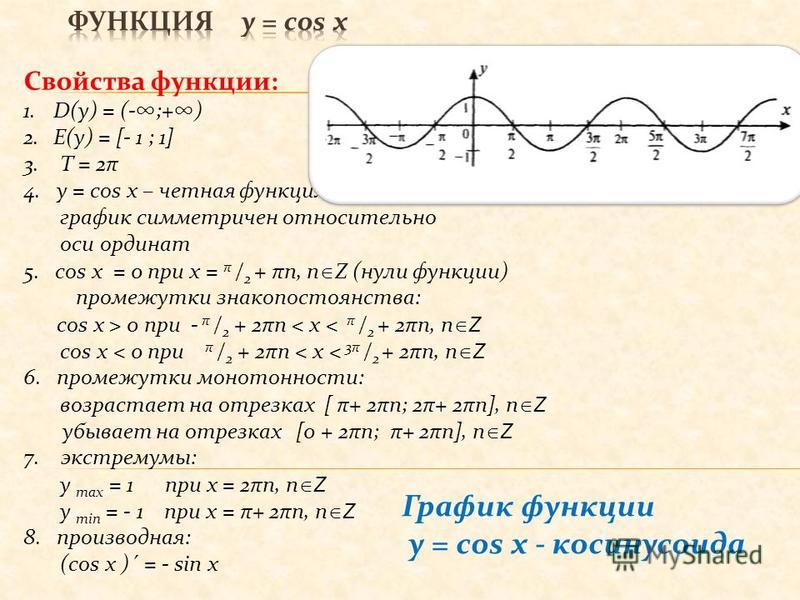 Таблица данных содержит пару колонок Абсцисса (F5) и Ордината G(5). Заполним таблицу:
Таблица данных содержит пару колонок Абсцисса (F5) и Ордината G(5). Заполним таблицу:
скопируйте в ячейку F5 содержимое ячейки D10 (левая граница области построения): введите формулу в ячейку F5: =D10;
в ячейке F6 произведите расчет следующего значения абсциссы. Ввести формулу в ячейку F6: =F5+$D$13;
скопируйте формулу из ячейки F6 в диапазон ячеек F7:F40. Колонка Абсцисса заполнена.
в диапазон ячеек G5:G40 занесите формулы, позволяющие рассчитать значение функции в каждой точке: введите формулу в ячейку G5: =sin(F5), скопируйте формулу в ячейки G5:G40;
Измените имя листа на Тригонометрическая функция.

Построение графика зависимости y(x)
Таблица данных содержит один ряд данных F5:G40 для построения графика вида y=f(x).
1. Выделите диапазон ячеек F5:G40, содержащий данные для построения графика. 2. Выберите команду Вставка-Диаграмма…
Шаг 1. В диалоговом окне Тип диаграммы выберите тип диаграммы Точечная, вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров», нажмите кнопку Далее.
Шаг 2. В окне Источник данных диаграммы на вкладке Диапазон данных проверьте, что диапазон выбран правильно и установлен флажок опции «Ряды в столбцах».
Шаг 3. Задайте параметры диаграммы (окно Параметры диаграммы): на вкладке Заголовки введите:
– в поле Название диаграммы – «График показательной функции»
– в поле Ось Х (категорий) – «x»;
– в поле Ось Y (значений) – «y»;
На вкладке Линии сетки отключите основные и промежуточные линии сетки по каждой из осей. На вкладке Легенда уберите флажок Добавить легенду. Нажмите кнопку Далее.
На вкладке Легенда уберите флажок Добавить легенду. Нажмите кнопку Далее.
Шаг 4. Выберите расположение диаграммы на отдельном листе и введите имя листа График в соответствующем поле. После этого нажмите кнопку Готово.
Инструкционная карта «Преобразование графика тригонометрической функции»:
Для построения графика функции y=кsin x, в диапазон ячеек G5:G40 занесите формулы, позволяющие рассчитать значение функции в каждой точке: введите формулу в ячейку (в зависимости от задания) G5: =к*sin(F5) или G5: =sin(F5+с) или G5: =(sin(F5)) +в или G5: =(к*sin(F5+с))+в где к, с, в действительные числа, скопируйте формулу в ячейки G5:G40.

Далее по инструкции «Построение графика зависимости y(x)» проделайте те же шаги.
Презентация групп. Описание свойств функции по каждому графику.
Вывод: график функции y=sin x совершает гармонические колебания: движения по осям координат.
Пронаблюдав движение графика с помощью компьютерной программы, ребята строят графики функций y=2sin x, =sin x+2, y=sin (x-п/3) в тетради, учитывая, что п=6 клеток. п/2=3 клетки, п/3=2 клетки и правила движения функции по осям координат.
4.Первичное закрепление полученных знаний-7 минут.
Цель этапа: уметь соотносить изучаемые функции с конкретной и жизненной ситуацией, развивать наглядно-образное и наглядно – действенное мышление, ориентировать на профессиональный выбор, профессию.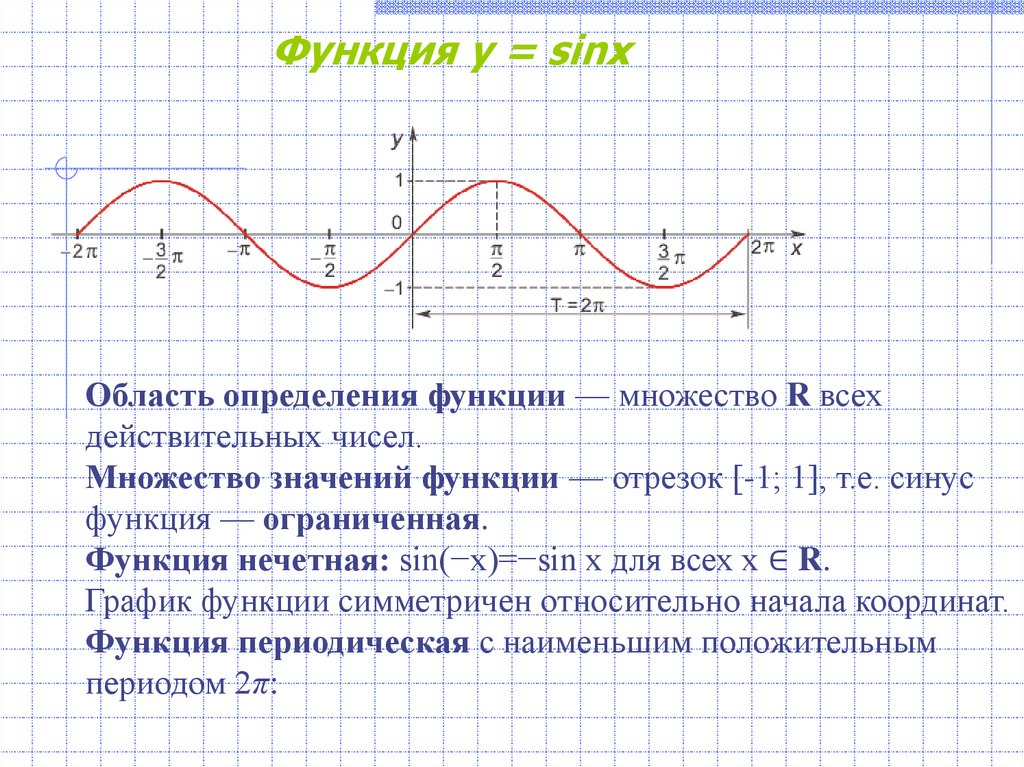
Слово учителю математики:
Синусоида была первым графиком тригонометрических функций. Этот график был вычерчен в конце 30-х годов XVII в. французским математиком Жюлем Робельвалем . Где же в жизни мы встречаемся с такими функциями и существуют ли вообще их применение? По закону синуса происходят гармонические колебания. Примером таких колебаний является движение маятника или шарика, подвешенного на пружинке, частота звука также описывается законом синуса. Гармонические колебания – это колебания, при которых изменение смещения во времени происходит по закону функции синус. Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII Леонардом Эйлером. Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д.. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики и для других наук. Итак давайте ответим на вопрос последний сегодняшнего урока: Расчет биоритмов человека с помощью ИКТ технологий
д.. Поэтому тригонометрические функции всесторонне и глубоко исследовались и приобрели важное значение для всей математики и для других наук. Итак давайте ответим на вопрос последний сегодняшнего урока: Расчет биоритмов человека с помощью ИКТ технологий
Китайский ученый Кай Цун разработал в 19 веке формулу подсчета собственных биоритмов человека. Каждый человек ежемесячно выстраивать с помощью тригонометрической функции y=sin x свой график интеллектуальной, эмоциональной и физической кривой. Увидеть когда у человека «взрыв» деятельности, а когда спад. Предлагается каждому учащемуся выстроить свои кривые на данный месяц с помощью компьютера.
Самостоятельная работа обучающихся, ориентированная на закрепление полученных знаний о построении функции и ее свойств.
Формула y=аsin (х+Т)/n+3,1, где a –число месяца, х- число лет человеку, Т- количество дней в данном месяце, п –календарный год.
Тетрадь ученика.
Подведение итогов урока. Оценочная часть- 3 минуты.
Беседа
Какие свойства у линии жизни?
Как происходит гармоническое колебание линии жизни?
Каково практическое применение тригонометрической функции?
Выставление оценок обучающимися проявивших себя в умении читать и строить график функции y=sin x с учетом движения и помощью программы Microsoft Office Excel. Рефлексия.
Домашнее задание:
на оценку «3» выполнить задание по учебнику № 36, (а,б), 37 (а,б) № 33 (а)
на оценку «4» дополнительно построить график функции y=2 sin(0,5x–p/6)+1 с помощью компьютера, сохранить данные на листе и выполнить скриншет данной странице, показать его учителю.

на оценку «5» выполнить данные задания и сделать подбор физических или химических, экономических задач, где используется функция y=sin x.
Функция y = Sinx, её свойства и график. доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экономика
Презентация на тему Функция y = Sinx, её свойства и график. , предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 21 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Тема урока:
«Функция y = Sinx, её свойства и график»
Выполнила: Иманова Людмила Алексеевна
учитель математики МОБУ «СОШ № 73»
г.Оренбург
Алгебра и начала анализа 10 класс
Цели урока:
Обучающая: изучить функцию y = Sinx; научить строить график функции y = Sinx.
Развивающая: развивать графические навыки учащихся, развитие наблюдательности, умение рассуждать и аргументировать свои действия.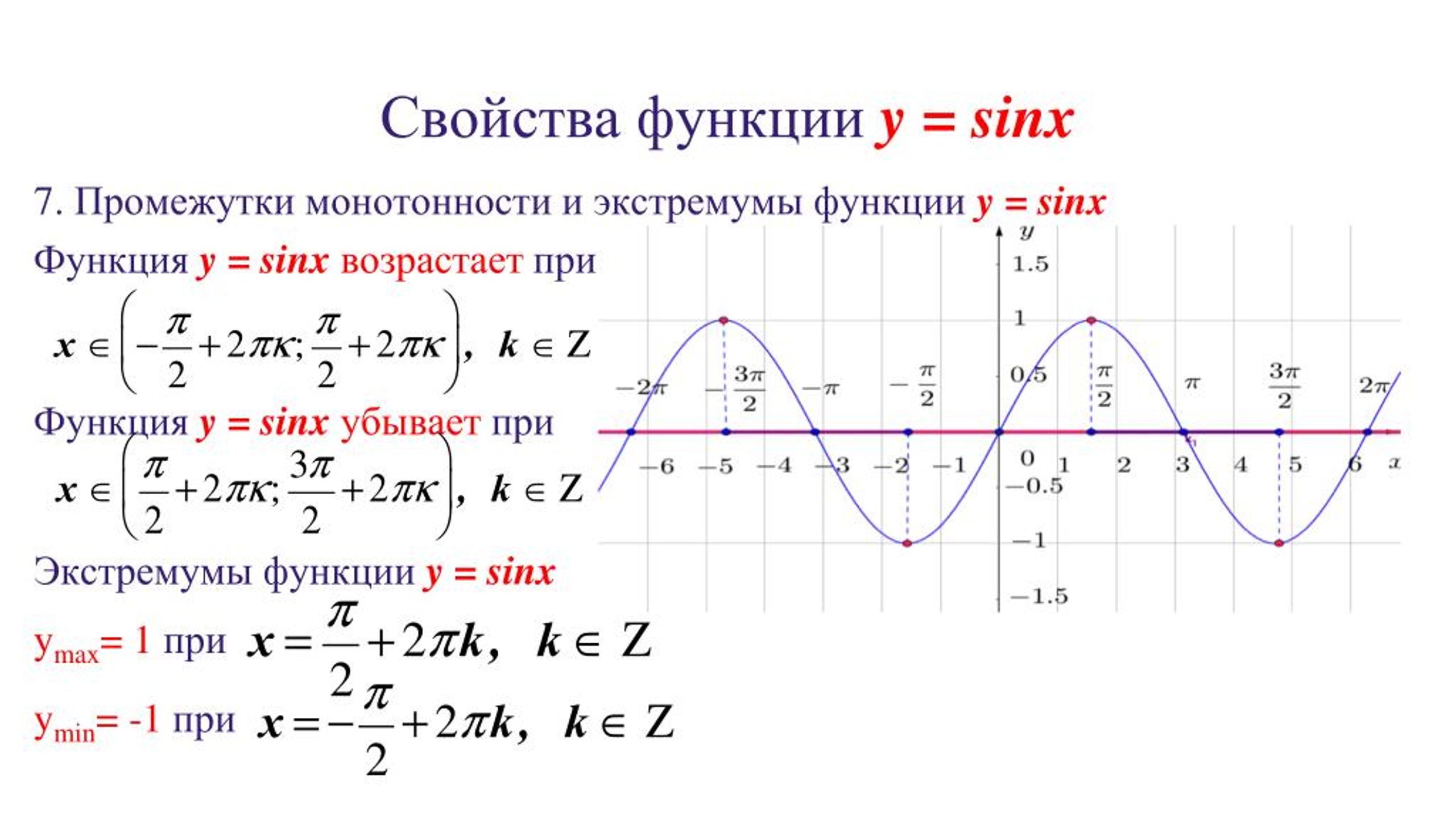
Воспитательная: воспитание требовотельного отношения к себе при самостоятельном изучении нового материала.
Прочитать графики функций
Найдите значения синуса для следующих углов поворота:
x
Y
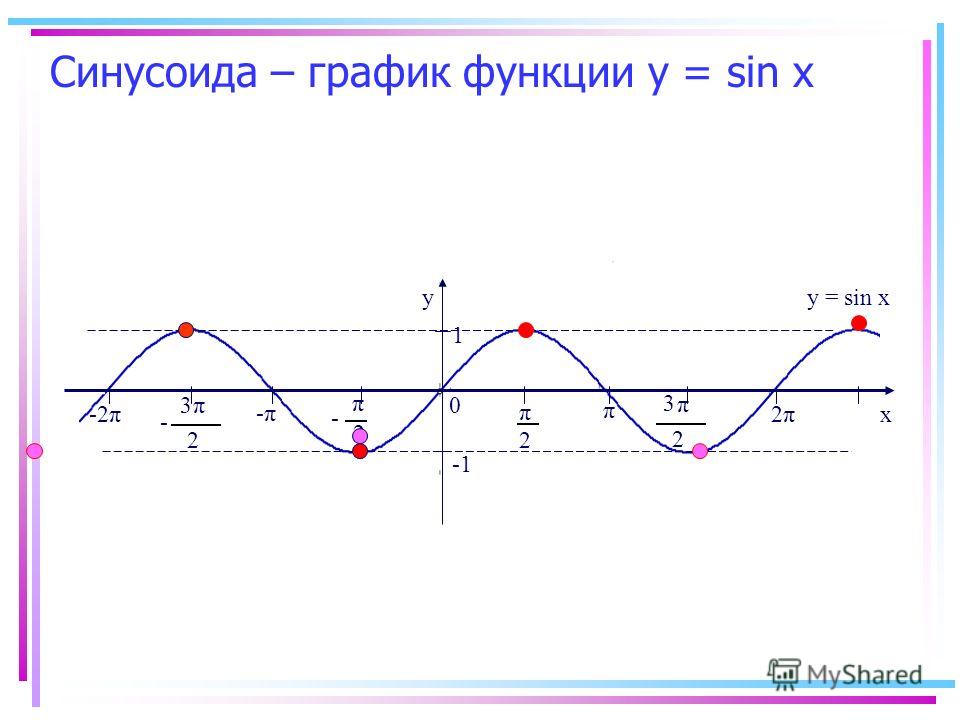
График y = Sinx — cинусоида
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Область определения
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Область значений
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Нули функции
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Монотонность функции
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Функция возрастает
Монотонность функции
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Функция убывает
Функция отрицательна
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
х
y
Функция положительна
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
х
y
Чётность функции
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Функция y = Sinx нечётная, т.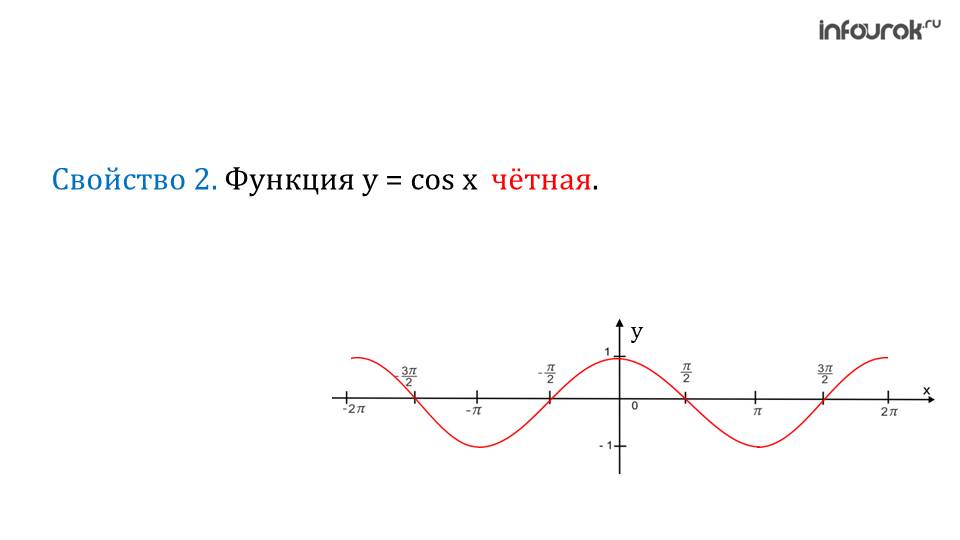 к Sin(-x) = — Sinx
к Sin(-x) = — Sinx
Периодичность функции
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Функция периодическая, с главным периодом 2π, sin ( α + 2π ) = sin α
x
y
Построить график фунции y = Sin(x + a)
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Построить график функции y = Sinx + a
y = sin x — 1
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
y = sin x — 1
Построение графика функции y = Sin(x + a) + k
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
Построение графиков y =k Sinx
π
π/2
-π/2
2π
-π
-3π/2
3π/2
5π/2
3π
1
-1
y = 1,5Sinx
y = 1,5Sinx
Сравнить числа Sin2 и Sin3
= 3,14
на отрезке функция y = Sinx убывает.
Значит Sin2 > Sin3
Сравнить:
и
и
и
и
Домашнее задание:
подготовить творческое задание на выбор:
подготовить задания на преобразование графиков
кроссворд на тему «Функция y = Sinx»
презентация на тему «Функция y = Sinx»
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.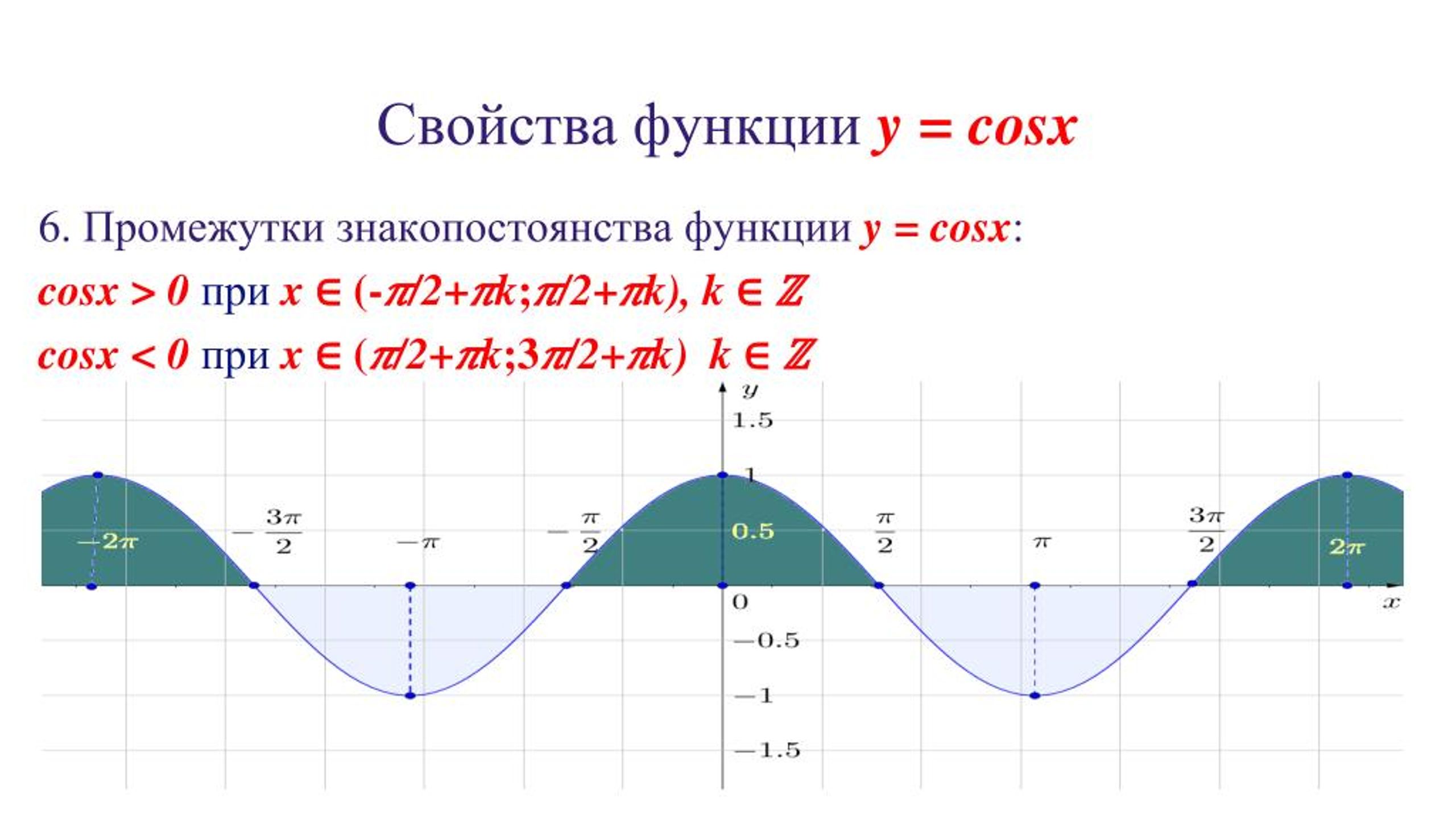 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.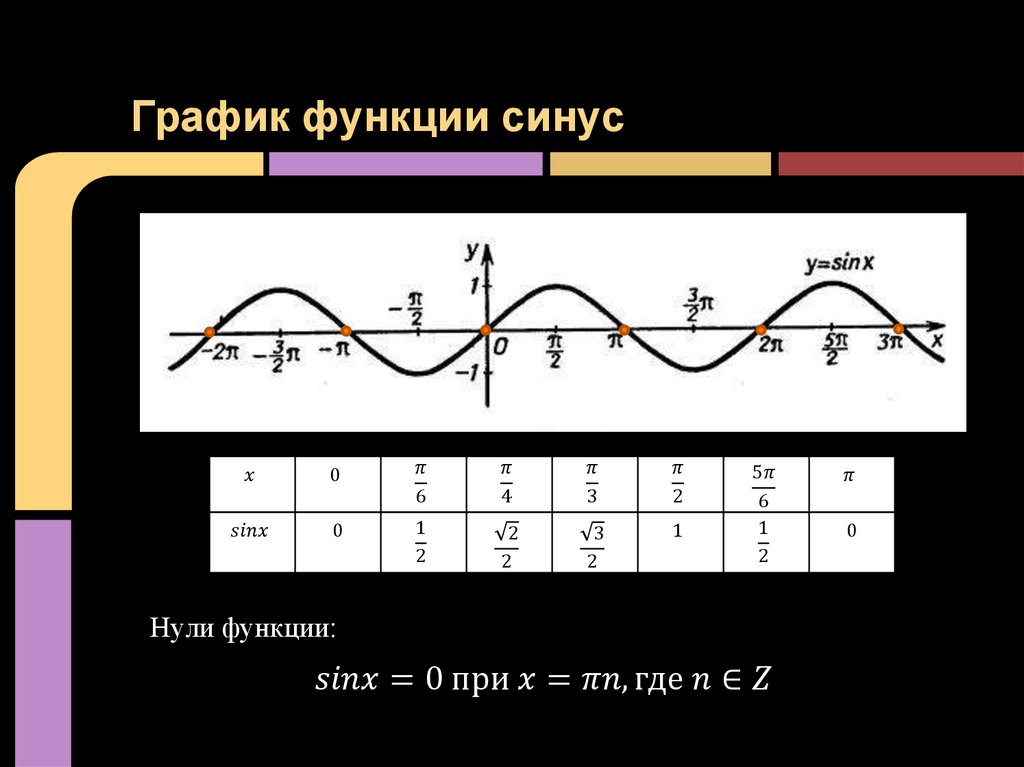 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
sin, свойства cos
sin, свойства cos| Свойства графиков синусов и косинусов |
Периодические функции
Некоторые математические функции повторяются в своей области.
Значения y повторяются в определенном диапазоне снова и снова.
Такие функции называются периодическими или циклическими функциями .
Вот графики двух периодических функций.
Как мы видим, оба графика повторяют свои значения y каждые 4 единицы оси x .
Мы говорим, что период этих графов составляет 4 единицы .
Диапазон f ( x ) слева равен и
диапазон г ( x ) справа .
| A периодическая функция f обладает тем свойством, что y-значения одинаковы для x 1 и x 2 (в домене).  Интервал x 2 x 1 называется периодом функции f . |
Все тригонометрические функции являются периодическими функциями.
| интро | основной синус | преобразованный синус | практика | решения |
Свойства графиков синусов и косинусов :
Основная синусоида: f ( x ) = sin x .
Поскольку мера радиана представляет длину, а также вращение (углы),
мы выражаем наши x -значения в радианах и наши y -значения в sin x значений.
Используя этот подход, мы можем построить графики триггерных функций.
Из значений x и y единичного круга мы знаем:
| грех 0 = 0 |
Здесь мы видим два цикла f ( x ) = sin x .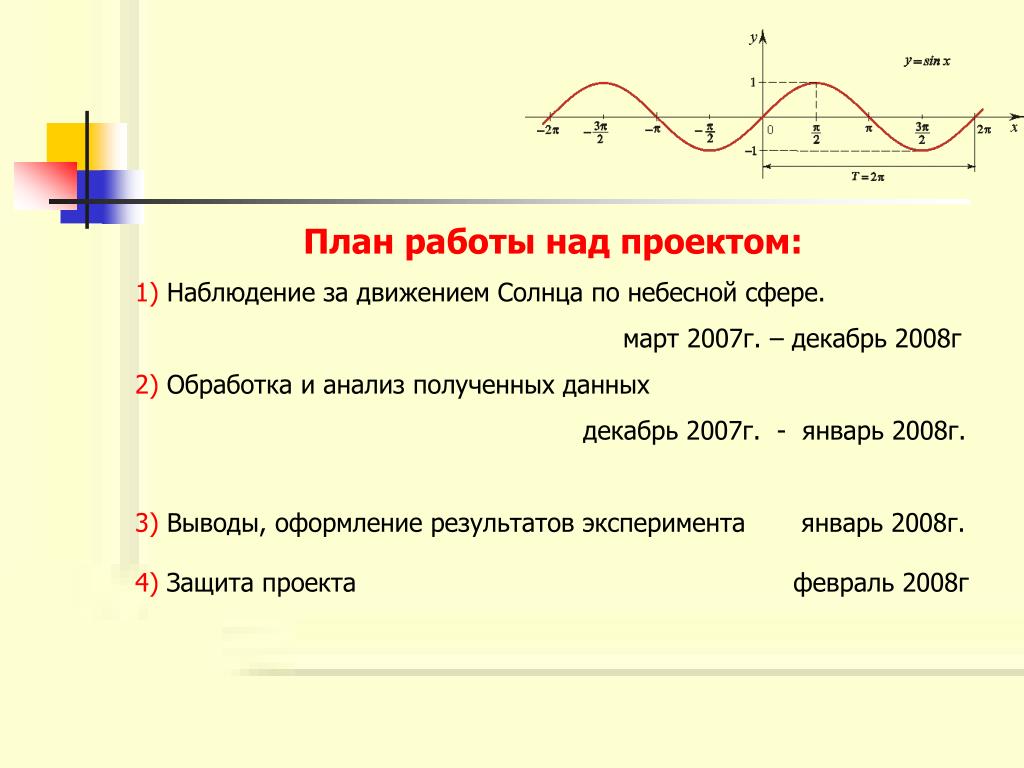
Этот шаблон будет бесконечно повторяться вправо и влево.
Как видите, домен — это R , диапазон — это [ 1, 1].
Существует бесконечно много нулей , каждый из которых расположен в середине
между ближайшим максимумом и минимумом .
Свойства циклических триггерных графов по-прежнему включают в себя все элементы прежнего списка (то есть: домен, диапазон, максимум, минимум, возрастание, убывание и знаки), но также включают:
амплитуда, период, частота, фазовый сдвиг и вертикальное смещение.
| интро | основной синус | преобразованный синус | практика | решения |
.
T Он преобразовал синус.
амплитуда : амплитуда синусоиды или косинусоидальной кривой является мерой расстояния на ней
перемещается выше или ниже своей горизонтальной оси.
Его можно найти, взяв 1/2 (y max — y min ). На приведенной выше базовой кривой амплитуда равна 1.
| амплитуда = | а | | a > 0 кривая движется вверх (примечание) | a < 0 кривая смещается вниз (примечание) |
период : период синусоидальной или косинусоидальной кривой равен интервал домена одного цикла .
На приведенной выше базовой кривой период равен , так как значения y достигнут
каждое значение между 1 и 1.
| период = | | | , если b < 0, тот же эффект, что и a < 0.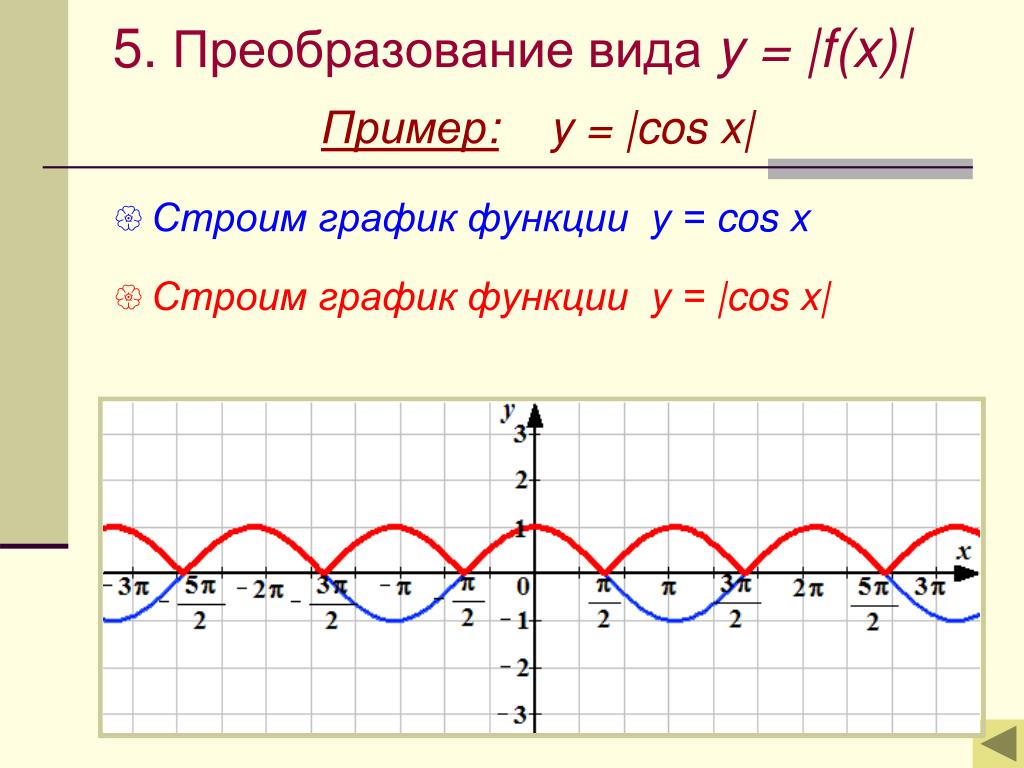 (примечание) (примечание) |
частота : частота синусоидальной или косинусоидальной кривой определяется как обратная величина периода .
На приведенной выше базовой кривой частота равна .
частота = .
фазовый сдвиг : фазовый сдвиг кривой синуса, косинуса или косинуса — причудливое имя
для горизонтального перевода , выполненного h .
фазовый сдвиг = ч .
вертикальный перевод : вертикальный перевод — это движение вверх или вниз по горизонтальной оси кривой. Как обычно, вертикальный перевод k .
| вертикальное перемещение = к | максимум: k + | и | | минимум: к | и | |
Теперь давайте изучим простой способ построения преобразованной синусоиды.
Как видно из приведенной выше основной синусоиды, кривая делится на 4 равных частей:
от нуля до максимума , от максимума до нуля , от нуля до минимума и от минимума до нуля .
Это верно для всех синусоидальных кривых.
Итак, устанавливаем нашу точку старта ( ч , к ), добавляем период к ч , находим конечную точку
затем, используя средние точки, мы делим этот интервал на 4 равные части, чтобы найти максимум , минимум и на оси точек.
Примечание1 : если или a или b отрицательны (< 0 ), кривая мин.0006 в начале цикла, а не наоборот.
Так, если бы мы наметили Y = SIN x или y = SIN ( x ) , Curve был бы инициированным вниз
.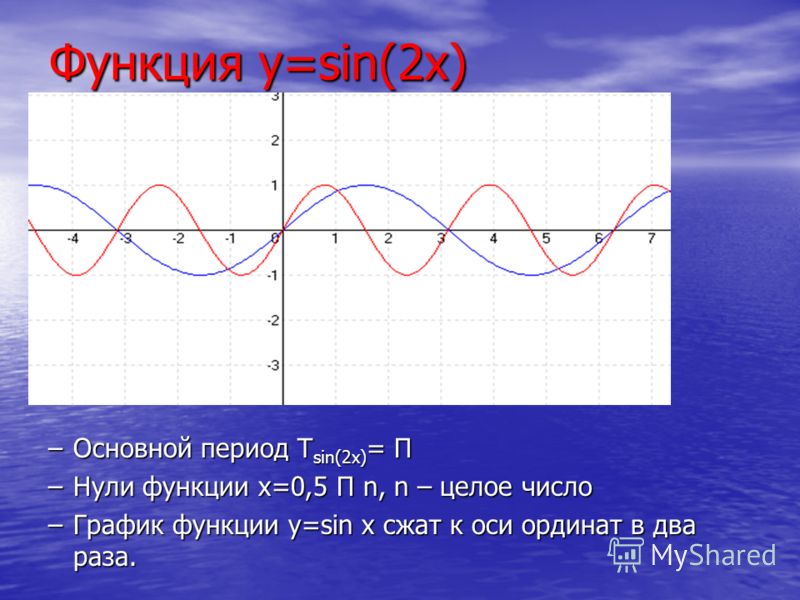 до вместо повышения до .
до вместо повышения до .
Если и , и b отрицательны, кривая ведет себя так, как если бы они оба были положительными.
В каком-то смысле они компенсируют друг друга.
Примечание2 : Для кривые косинуса , a и b работают по-разному, поскольку косинус угла в 4-м квадре положителен, поэтому, если b отрицательный знак косинус.
Для косинусных кривых знак a определяет, начинается ли кривая с максимального или минимального , поскольку косинусных кривых начинаются с крайнего значения , а не с горизонтальной оси, как синусоидальные кривые.
Примечание3 : Косинусоидальная кривая — это всего лишь синусоидальная кривая , оттянутая назад на четверть периода.
Обратите внимание, что синяя кривая косинуса начинается с (0, 1), максимум
.
вместо (0, 0) « значение по оси », как красная синусоида.
.
.
Пример
Список всех свойств функций для:
| а) | b) | ||
| начальное направление: a < 0 перемещается вниз до мин. | начальное направление: a > 0 начинается с максимума | ||
| амплитуда: | и | = 5 | амплитуда: | и | = 4 | ||
| период: | период: | ||
| фазовый сдвиг: | фазовый сдвиг: | ||
| начало: ( начинается на оси ) | начало: ( начинается с макс.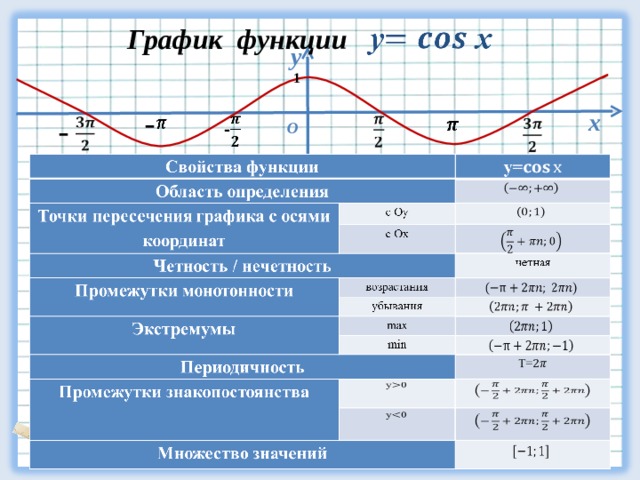 ) ) | ||
| конец: | конец: | ||
| ¼ точек цикла: | ¼ точек цикла: | ||
| вертикальное перемещение: k = 3 | вертикальное перемещение: k = 1 | ||
| мин.: k a = 2 | макс: к + a = 8 | мин: к a = 5 | макс: к + a = 3 |
.
| интро | основной синус | преобразованный синус | практика | решения |
Практика
Представим эти функциональные правила в стандартной форме f ( x ) = a sin b ( x h ) + k
Скопируйте список свойств из таблицы и найдите значения для этих функций.
- 1/
- 2/
| интро | основной синус | преобразованный синус | практика | решения |
Решения
| 1/ | 2/ | ||
| начальное направление: a > 0, b < 0 до мин. | начальное направление: a < 0 начинается с мин. | ||
| амплитуда: | и | = 14 | амплитуда: | и | = 3 | ||
| период: | период: | ||
| фазовый сдвиг: | фазовый сдвиг: | ||
| начало: ( начало по оси ) | начало: ( начинается с мин. ) ) | ||
| конец: | конец: | ||
| ¼ точек цикла: | ¼ точек цикла: | ||
| вертикальное перемещение: k = 12 | вертикальное перемещение: k = 7 | ||
| мин.: k a = 26 | макс.: к + a = 2 | мин: к a = 4 | макс.: к + a = 10 |
Дополнительную информацию по этой теме см.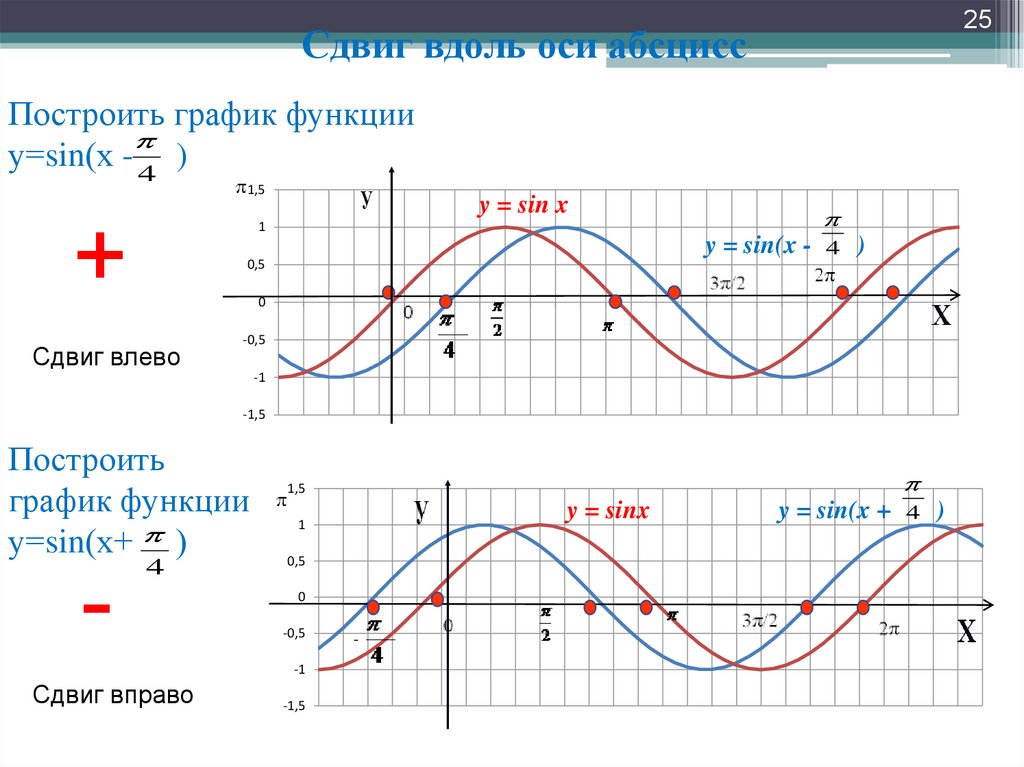 в уроке Trig MathRoom Графики синусоидальных и косинусоидальных кривых .
в уроке Trig MathRoom Графики синусоидальных и косинусоидальных кривых .
| интро | основной синус | преобразованный синус | практика | решения |
Trig Индекс MathRoom
(все содержание уроков MathRoom © Tammy the Tutor; 2004 — ).
Синусоидальные функции | bartleby
Что такое синусоидальная функция?
Семейство синусоидальных функций применимо либо к синусоидальным, либо к косинусоидальным волнам, поскольку они одинаковы, за исключением горизонтального изменения.
Набор координат X единичной окружности представляет собой функцию косинуса , , а набор координат Y представляет собой функцию синуса 05 .
ПРИМЕЧАНИЕ. Все функции синуса и косинуса являются периодическими.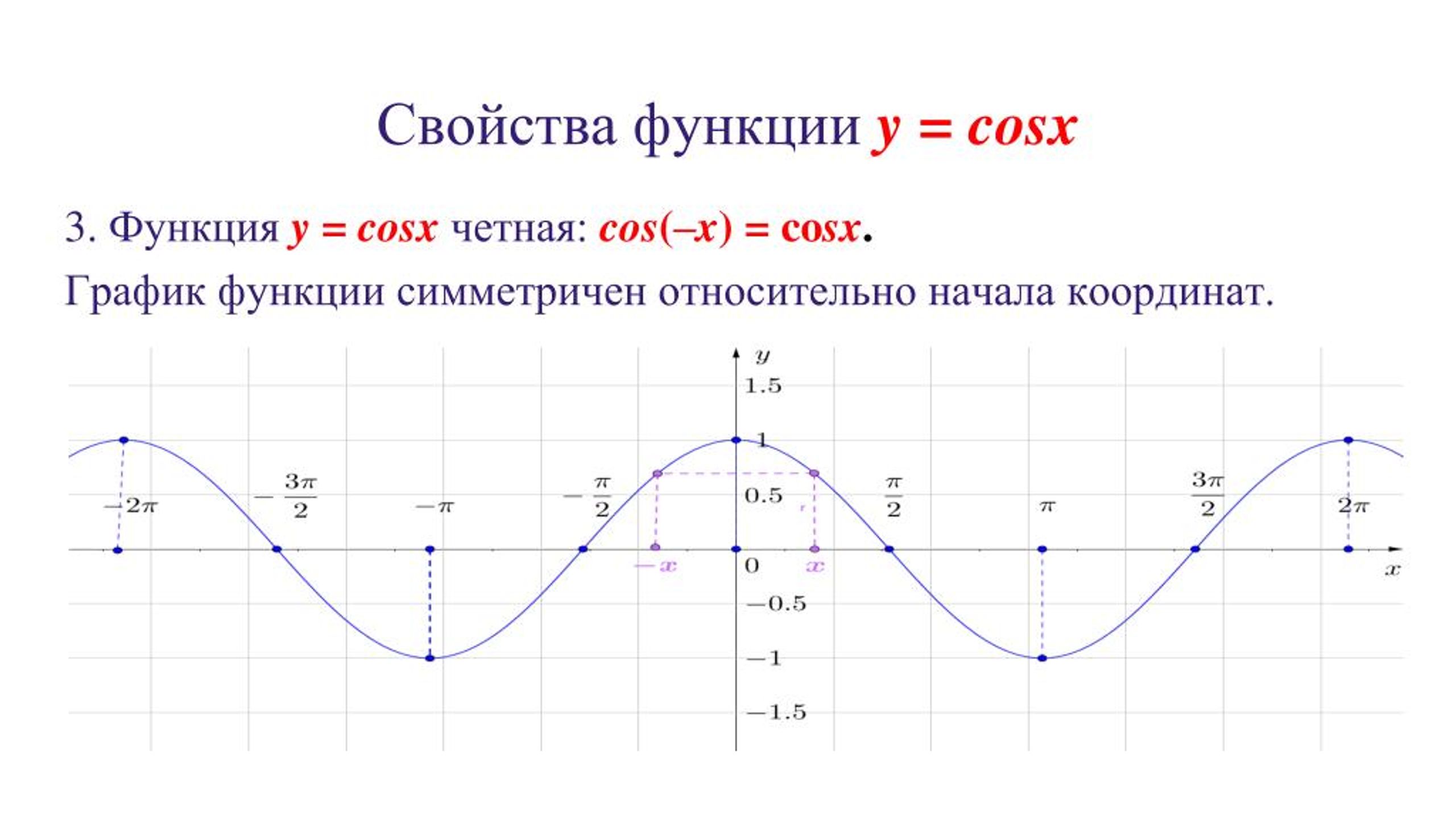 Периодическая функция может быть синусоидой. Это связано с тем, что периодическая функция включает в себя sin, cosec, cos, sec, tan и cot, тогда как синусоидальные функции включают только sin или cos.
Периодическая функция может быть синусоидой. Это связано с тем, что периодическая функция включает в себя sin, cosec, cos, sec, tan и cot, тогда как синусоидальные функции включают только sin или cos.
Синусоидальная волна
График функции «синус» или «косинус» называется синусоидальной волной.
Стандартное уравнение для нахождения синусоиды:
y = D + A sin [B (x — C)] или
y = D + A cos [B (x — C)]
где,
- A = Амплитуда
- B = Число циклов от 0 до 2π или 360 градусов
- C = Фазовый сдвиг (горизонтальный сдвиг)
- D = Синусоидальная ось
- Период = 2π/B
Свойства синусоиды Условия)
- Период: период синусоидальной волны – это длина всего цикла.
- Частота: количество полных циклов, происходящих каждую секунду.
- Амплитуда: расстояние по вертикали между синусоидальной осью и максимальным или минимальным значением функции.
- Фазовый сдвиг: Обозначает разницу во времени между двумя похожими сигналами.

- Синусоидальная ось: горизонтальная линия, лежащая между гребнями и впадинами графика функции.
Характеристики функций синуса и косинуса
Функции синуса и косинуса имеют несколько различных характеристик:
- Это периодические функции с периодом 2π.
- Область определения каждой функции — (−∞, ∞), а диапазон — [−1,1].
- График y = sin x симметричен относительно начала координат, потому что это нечетная функция.
- График y = cos x симметричен относительно y -ось, потому что это четная функция.
Период, амплитуда и средняя линия
- Средняя линия: Горизонтальная линия проходит точно между максимальной и минимальной точками графика в середине.
- Амплитуда: Это расстояние по вертикали между одной из крайних точек и средней линией.
- Период: Разница между двумя последовательными максимальными точками или двумя последовательными минимальными точками (эти расстояния должны быть равными).

Как рассчитать период синусоидальной функции?
Общее уравнение функции синуса,
y = D + A sin [B (x — C)]
Уравнение, показывающее отношение B к периоду, имеет вид P = 2π|B|. Если |B|>1, то период меньше 2π и функция подвергается горизонтальному сжатию, а если |B| < 1, то период больше 2π и функция испытывает горизонтальное растяжение.
Например,
- f ( x ) = sin ( x ), B = 1, поэтому период равен 2π, что мы знали.
- Если f ( x ) = sin (2 x ), то B = 2, поэтому период равен π, а график сжат.
- Если f(x)=sinx2, то B=12, поэтому период равен 4π и график растянут. Обратите внимание на рисунок ниже, как период косвенно связан с |B|.
Как определить амплитуду синусоидальной функции?
Для синусоидальной функции, возвращаясь к общей формуле,
y = D + A sin [B (x — C)]
Мы узнали, как переменная B относится к периоду. Теперь давайте переключимся на переменную A, чтобы оценить, как связана амплитуда или наиболее значимое расстояние от других.
Теперь давайте переключимся на переменную A, чтобы оценить, как связана амплитуда или наиболее значимое расстояние от других.
A представляет собой коэффициент вертикального растяжения, а амплитуда — его абсолютное значение |A|. Таким образом, локальные максимумы будут на расстоянии | А | выше вертикали средняя линия графика, которая представляет собой линию x = D ; поскольку в этом случае D = 0, средней линией является ось x .
Локальные минимумы будут на одинаковом расстоянии ниже средней линии.
Если | А | > 1, график растянут.
Например, амплитуда f ( x ) = 4 sin x в два раза больше амплитуды f ( x ) = 2 sin x .
Если | А | < 1, граф сжимается.
Поиск функций на графике
Мы можем проанализировать его, чтобы найти срединную линию, амплитуду и время на графике синусоидальной функции. Рассмотрим, например, следующий график.
Рассмотрим, например, следующий график.
Синусоида на графике имеет точку максимума (1,7), затем точку минимума (3,3) и еще одну точку максимума (5,7).
Горизонтальная линия, которая проходит точно между Y=7 (максимальное значение) и Y=3 (минимальное значение), равна Y=5, так что это средняя линия.
Расстояние по вертикали между средней линией и каждой из точек экстремума равно 2, поэтому амплитуда равна 2.
Интервал между двумя максимальными точками подряд равен 4, так что это период.
Мы знаем, что, не меняя своей формы, распространяется синусоидальная волна. Для изучения распространения волн в распределенном линейном методе используются синусоидальные волны.
Частота
Понятие частоты используется в некоторых приложениях периодических явлений вместо периода.
Количество периодов (или циклов) в единицу времени — это частота синусоидальной функции.
Поскольку частота — это количество циклов в единицу времени, а количество времени, необходимое для завершения одного цикла, — это период, уравнение, показывающее взаимосвязь между частотой и временем, выглядит следующим образом:
частота = 1/период
Формулы
Если уравнением синусоидальной функции является y = D + A sin [B (x — C)], то справедливы следующие формулы:
- Период = 2π|B|
- Амплитуда = |A|
- Частота = 1/период = | B | 2π
- синусоидальная ось: y = D
- Горизонтальный сдвиг = C -единицы
Общие ошибки
- 9 39083 9083 9083 9083 9083 9083 9083 9083 9083 9083.
- Sin(x) не является умножением
- Sin (x+y) ≠ Sin (x) + Sin(y)
- Sin 3x ≠ 3 * Sin(x)
- Степени функций синуса
- Sin(x n) 0 910 x) n
- Функция обратного синуса
- Sin -1 (x) ≠ 1/Sin(x)
- Измерение высоты высокого здания или горы.
- Разработка видеоигр.
- Строительная промышленность.
- Археологические раскопки.
- Косинус
- Тригонометрия
График повторяется каждые 2𝞹 или 360 °
Минимальное значение для синуса -1
Максимальное значение для синуса равно 1
Это означает, что амплитуда графика равна 1, а его период равен 2𝞹 (или 360 °)
График пересекает ось y в точке 0, и через каждые 𝞹 радиан до и после этого.
Синусоидальная функция достигает своего максимального значения в 𝞹 / 2 и каждые 2 𝞹 до и после этого.

Синусоидальная функция достигает своего минимального значения при 3𝞹 / 2 и каждые 2𝞹 до и после этого.
График повторяется каждые 2𝞹 или 360° 1
Максимальное значение косинуса 1
Это означает, что амплитуда графика равна 1, а его период равен 2𝞹 (или 360 °)
График пересекает ось y в точке 2𝞹 / , и каждые 𝞹 радиан до и после этого.

Функция косинуса достигает своего максимального значения в 0 и каждые 2𝞹 до и после этого.
Функция косинуса достигает своего минимального значения в 𝞹 и каждые 2 𝞹 до и после этого.
График повторяется каждые 𝞹 или 180 °
Минимальное значение для тангенса равно -бесконечности тангенс равен бесконечности
Это означает, что функция тангенса не имеет амплитуды и ее период равен 𝞹 (или 180°)
График пересекает ось y в точке 0 и через каждые 𝞹 радиан до и после этого
График касательной имеет асимптоты, то есть значения, при которых функция приближается к бесконечности.

Эти асимптоты находятся в 𝞹 / 2 и каждые 𝞹 до и после этого.
 тригонометрические расчеты выполняются с учетом того, что углы указаны в радианах, а не в градусах.
тригонометрические расчеты выполняются с учетом того, что углы указаны в радианах, а не в градусах., аспиранты и многие инженерные отрасли.
Тригонометрия может применяться в:
Мы предоставим вам пошаговые решения для миллионов задач из учебников, круглосуточную помощь экспертов в данной области, когда вы запутались, и многое другое.
Ознакомьтесь с примером решения вопросов и ответов по тригонометрии здесь!
*Время ответа зависит от темы и сложности вопроса. Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Среднее время отклика составляет 34 минуты для платных подписчиков и может быть больше для рекламных предложений.
Тригонометрические функции: определение, формулы и графики
Давайте рассмотрим все, что связано с тригонометрическими функциями – функции синуса, косинуса и тангенса и их соответствующие графики. Затем давайте рассмотрим функции секанса, косеканса, котангенса, арксинуса, арккосинуса и арктангенса.
Что такое тригонометрические функции?
Тригонометрические функции — это функции, относящиеся к углам и длинам в треугольнике. Наиболее распространенными тригонометрическими функциями являются синус, косинус и тангенс. Однако есть обратные тригонометрические функции, такие как косеканс, секанс, котангенс и обратные тригонометрические функции, такие как арксинус, арккосинус и арктангенс, которые мы также рассмотрим в этой статье.
SOH CAH TOA Простой способ запомнить функции синуса, косинуса и тангенса и сторонам, которым они соответствуют в прямоугольном треугольнике, — использовать SOH CAH TOA. Если у нас есть прямоугольный треугольник, как показано ниже, и мы обозначили один угол 𝞱, мы должны обозначить три противоположные стороны треугольника (для единственной стороны, которая противоположна углу 𝞱 и не соприкасается с этим углом), гипотенуза ( для самой длинной стороны, которая всегда находится напротив 90° угол) и смежные (для последней стороны).
Если у нас есть прямоугольный треугольник, как показано ниже, и мы обозначили один угол 𝞱, мы должны обозначить три противоположные стороны треугольника (для единственной стороны, которая противоположна углу 𝞱 и не соприкасается с этим углом), гипотенуза ( для самой длинной стороны, которая всегда находится напротив 90° угол) и смежные (для последней стороны).
Обозначение сторон прямоугольного треугольника
Функции синуса, косинуса и тангенса связывают отношение двух сторон прямоугольного треугольника к одному из его углов. Чтобы запомнить, какие функции включают какие стороны треугольника, мы используем аббревиатуру SOH CAH TOA. S, C и T обозначают синус, косинус и тангенс соответственно, а O, A и H обозначают противоположность, смежность и гипотенузу. Таким образом, функция синуса включает в себя противоположность, гипотенузу и так далее.
SOH CAH TOA Треугольники для запоминания тригонометрических функций
Все функции синуса, косинуса и тангенса равны количеству сторон, в которые они входят, деленным друг на друга.
Что такое функция синуса?
Как показано выше, вы можете вычислить синус угла в прямоугольном треугольнике, разделив противоположное значение на гипотенузу. График синусоидальной функции выглядит следующим образом (красная кривая):
Графическая иллюстрация синусоидальной функции
На этом графике мы можем наблюдать ключевые особенности функции синуса:
Запоминание значений синуса
Вам нужно будет запомнить значения синуса для часто используемых углов наизусть, и хотя это может показаться сложным, есть способ облегчить запоминание. Вам нужно будет знать значения синусов для углов 0, 𝞹/6 (30°), 𝞹/4 (45°), 𝞹/3 (60°) и 𝞹/2 (90°). Для этого проще всего начать строить таблицу для угла, 𝞱 и sin𝞱:
| θ | 0 | ||||
| SINθ |
| θ | 0 | ||||
| sin θ | 0 | 1 | 2 | 3 | 4 |
The next step is to add a square root to all these numbers and divide them by 2:
| θ | 0 | ||||
| SIN θ |
Теперь все, что мы оставили для того, чтобы сделать, — это упростить то, что мы можем:
| θ | |||||
. 0007 0007 | |||||
| SIN θ | 0 | 1 |
и это!
Что такое функция косинуса?
Значение косинуса угла прямоугольного треугольника можно найти, разделив прилежащий угол на гипотенузу. График значения косинуса выглядит точно так же, как график синуса, за исключением того, что он сдвинут влево на 𝞹 / 2 радиана (синяя кривая):
Графическая иллюстрация функции косинуса
Наблюдая за этим графиком, мы можем определить ключевые особенности функции косинуса:
Вам также потребуется запомнить значения косинуса для часто используемых углов наизусть, и хотя это может показаться сложным, есть способ облегчить запоминание. Вам потребуется знать значения синусов для углов 0, 𝞹/6 (30°), 𝞹/4 (45°), 𝞹/3 (60°) и 𝞹/2 (90°). For this, we will use the same method as for sin and start constructing a table for the angle, 𝞱 and cos𝞱:
| θ | 0 | ||||
| cos θ |
Теперь мы заполним числа от 0 до 4, но на этот раз мы будем делать это справа налево:0007
and divide it by 2, and we simplify:
| θ | 0 | ||||
| cos θ | 1 | 0 |
Как видите, значения синуса и косинуса для обычных углов одинаковы, только наоборот.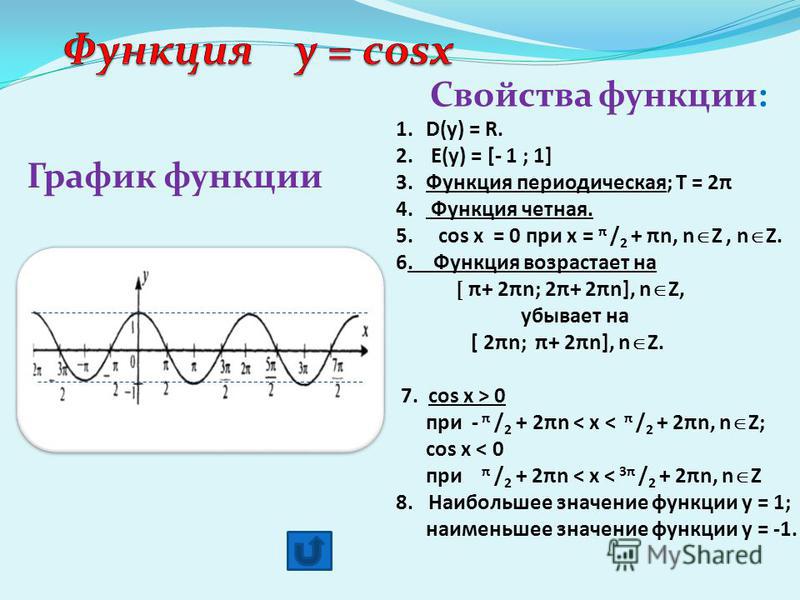
Что такое функция касательной?
Тангенс угла можно найти, разделив противоположный угол на прилежащий в прямоугольном треугольнике. Однако функция тангенса немного отличается от функций косинуса и синуса. Это не волна, а прерывистая функция с асимптотами:
Графическая иллюстрация функции тангенса
Наблюдая за этим графиком, мы можем определить ключевые особенности функции тангенса:
Тангенс угла также можно найти по этой формуле:
tan𝞱 = sin𝞱 / cos𝞱
Запоминание значений тангенса 0, 𝞹/6 (30°), 𝞹/4 (45°), 𝞹/3 (60°) и 𝞹/2 (90°). Для этого мы будем использовать приведенную выше формулу и таблицы, которые мы уже построили для синуса и косинуса, и использовать тот факт, что tan = sin/cos для определения значений tan𝞱: Обратите внимание, что значение для загара (𝞹 / 2) не может быть определено, поскольку оно равное 1/0, которое не может быть обработано. вне. Это приведет к асимптоте при 𝞹 / 2.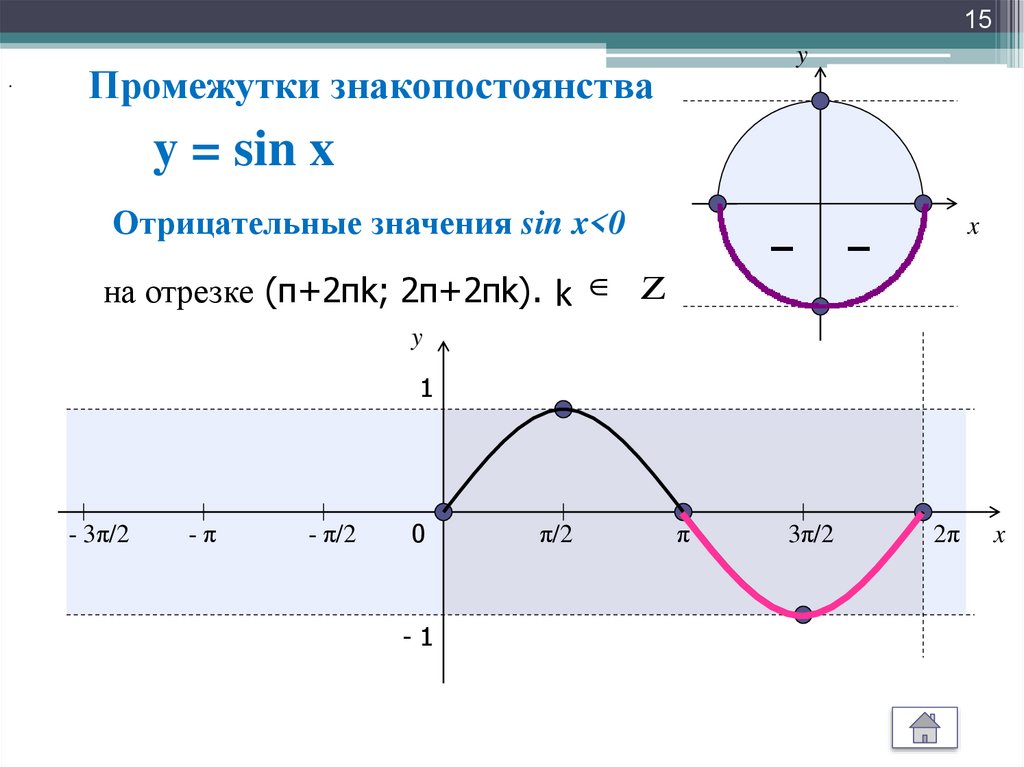
Обратные тригонометрические функции
Обратные тригонометрические функции относятся к функциям arcsin, arccos и arctan, которые также могут быть записаны как , , и . Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan.
Иллюстрация взаимосвязи между тригонометрическими функциями и их соответствующими обратными функциями
Графики для этих функций сильно отличаются от графиков sin, cos и tan:
Иллюстрация arcsin, arccos и arctan на x и y ось
Что такое обратные тригонометрические функции?
Обратные тригонометрические функции относятся к функциям косеканса, секанса и котангенса, сокращенно обозначаемым как csc, sec и cot соответственно. Нам нужно оглянуться назад на наш прямоугольный треугольник, чтобы понять, что представляют собой эти функции.
Обозначение сторон прямоугольного треугольника
Ранее мы определили sin, cos и tan на основе отношений сторон этого треугольника.