Найти точки разрыва: Точки разрыва функции онлайн

Примеры решений задач по математике

Построить график функции Точки разрыва функции Построение графика методом дифференциального исчисления Упростить выражение

Примеры решенийРанг матрицы Умножение матриц Метод Гаусса Найти производную Найти интегралРешение СЛАУ методом Крамера Диф уравнения онлайнОпределитель матрицы Точки разрыва функции

На этой странице собраны лишь некоторые примеры, решение которых были получены с помощью калькуляторов по высшей математике

Аналитическая геометрия

• Площадь грани пирамиды
• Найти точку M₁, симметричную точке M относительно плоскости P.
• В задачах 1 — 20 даны вершины треугольника АВС. Уравнение высоты треугольника. Уравнение окружности, для которой высота CD есть диаметр.

Пределы

• Примеры нахождения пределов
• Раскрытие неопределенности типа 0/0 и бесконечность/бесконечность. Правило Лопиталя.

Дифференциальное исчисление

• Вычисление приближенно с помощью дифференциала
• Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R

Интегральное исчисление

• Кратные и криволинейные интегралы

Примеры решений однородных дифференциальных уравнений

1. Сборник решений линейных дифференциальных уравнений с постоянными коэффициентами
2. Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть cos(x),sin(x)
3. Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть e^x*(Ax + B)
4. Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть exp(x),cos(x),sin(x)
5. Линейные дифференциальные уравнения с постоянными коэффициентами. Специальная часть Ax + B

Примеры решений задач методом Лагранжа

1. Метод множителей Лагранжа
2. Угол между градиентами скалярных полей

Ряды

• Признаки сходимости ряда
• Сходимость степенного ряда

Комплексные числа

• Решение уравнений с комплексными числами

Лекции по высшей математике

• Помощь в решении
• Поиск
• Поддержать проект

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.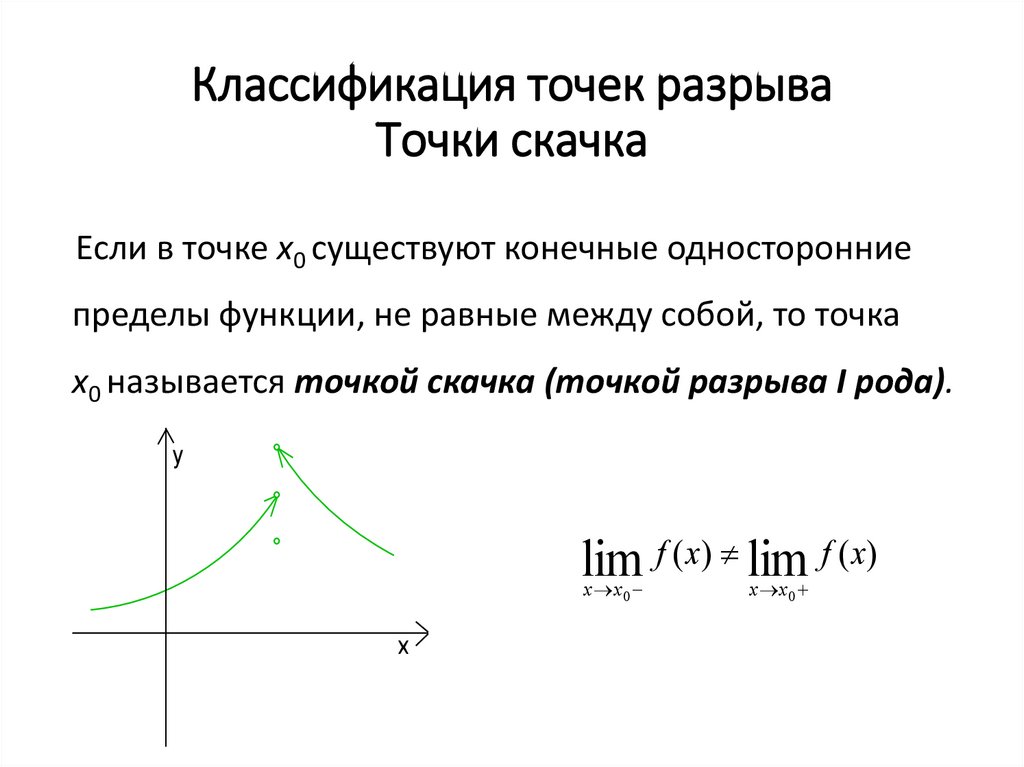
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Точки разрыва функции первого и второго рода

Функция f(x) называется непрерывной в точке х = а если:
1) она определена в этой точке;
2) существует предел функции в этой точке

3) значение предела равно значению функции в точке х = а, т.е.

Если одно из условий нарушается то функция называется разрывной в точке х = а, а сама точка х = а называется точкой разрыва. Все элементарные функции являются непрерывными на интервалах определенности.

Точка х0 называется точкой разрыва первого рода функции у = f(x) если существуют конечные односторонние пределы справа

и слева
.

Если, кроме этого, выполняется хотя бы одно из условий

то функция в точке х = а имеет неустранимый разрыв первого рода.

Если пределы равны, однако функция не существует

то имеем устранимый разрыв первого рода.

Точка х0 называется точкой разрыва второго рода функции у= f(x) если граница справа или слева не существует или бесконечна.

Скачком функции в точке разрыва х = х0 называется разность ее односторонних границ

если они разные и не равны бесконечности.

При нахождении точек разрыва функции можно руководствоваться следующими правилами:

1) элементарная функция может иметь разрыв только в отдельных точках, но не может быть разрывной на определенном интервале.
2) элементарная функция может иметь разрыв в точке где она не определена при условии, что она будет определена хотя бы с одной стороны от этой точки.
3) Неэлементарные функция может иметь разрывы как в точках где она определена, так и в тех где она определена.
Например, если функция задана несколькими различными аналитическими выражениями (формулами) для различных интервалов, то на границе стыка может быть разрывной.

Рассмотрим несколько задач по данной теме.

Задача 1.
Найти точки разрыва функции
а)

Решение:
Функция определена во всех точках кроме тех где знаменатель обращается в нуль x = 1, x = 1. Область определения функции следующая

Найдем односторонние пределы в точках разрыва

При нахождении односторонних границ подобного вида достаточно убедиться в знаке функции и в том, что знаменатель стремится к нулю. В результате получим границу равную бесконечности или минус бесконечности.

Поскольку в точках x = 1, x = -1 функция имеет бесконечные односторонние пределы, то аргументы являются точками разрыва второго рода. График функции приведен на рисунке ниже

——————————————————-

б)

Решение:
Задача достаточно простая. В первую очередь находим нули знаменателя

Таким образом функция определена на всей действительной оси за исключением точек , которые являются точками разрыва. Вычислим односторонние пределы справа и слева

Пределы бесконечны поэтому, по определению, имеем точки разрыва второго рода.

Из графиков приведенных функций видим что для ряда из них отыскания точек разрыва сводится до нахождения вертикальных асимптот. Но бывают функции которые и без вертикальных асимптот имеют разрывы первого или второго рода.

——————————————————-

в)

Решение:
Заданная функция непрерывна на всей числовой оси кроме точки x = -3. Вычислим односторонние границы в этой точке

Они различаются по значениям, однако есть конечными. Итак точка x = -3 является неустранимой точкой разрыва І рода.

——————————————————-

Задача 2.
Найти точки разрыва функции если они существуют. Вычислить скачок функции в точке разрыва. Построить график функции.

а)

Решение:
Для заданной функции точка x = 2 является точкой разрыва.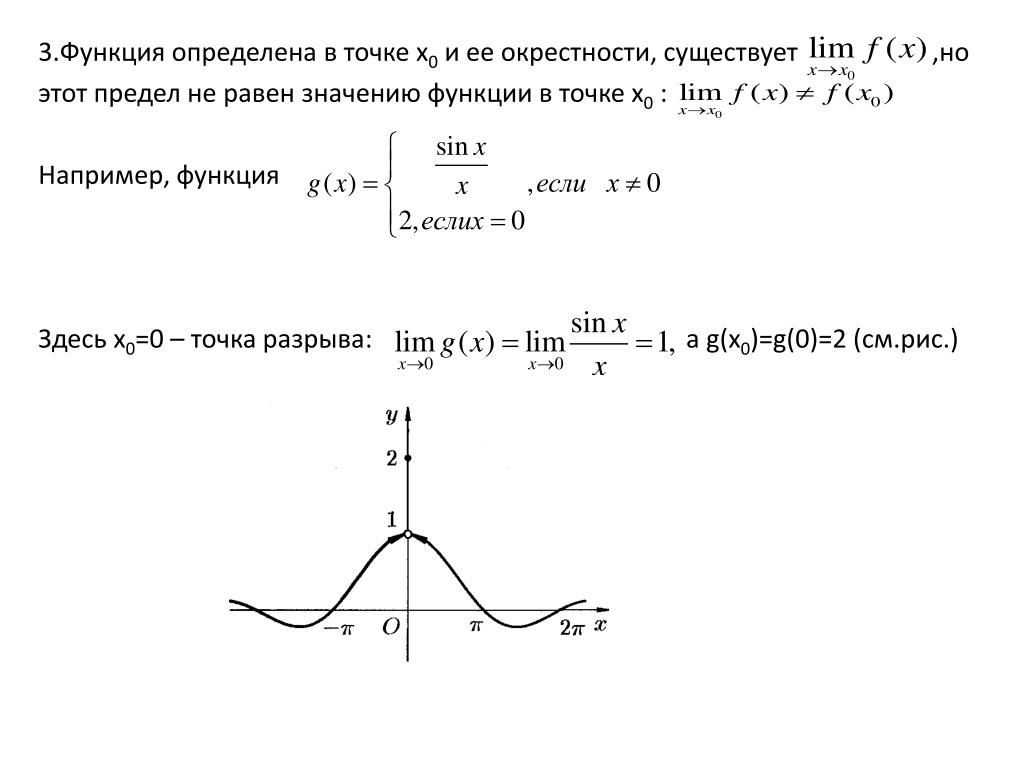 Найдем предел функции , чтобы определить характер разрыва

По определению, точка x = 2 является неустранимой точкой разрыва первого рода. Вычислим скачок функции при x=2

График функции на интервале который нас интересует приведен далее

——————————————————-

б)

Решение:
Неэлементарная функция y (x) определена для всех положительных значений аргумента. Точки которые разбивают функцию на интервалы могут быть разрывами. Для проверки найдем соответствующие пределы

Поскольку предел функции в точке x = 2 равен значению функции в этой точке то функция — непрерывная.

Отсюда также следует, что для непрерывной функции скачок равен 6-6 = 0.

Исследуем на непрерывность вторую точку

По определению функция в точке x = 2 имеет неустранимый разрыв І рода.

Прыжок функции равен 29 — (- 3) = 31.

По условию задания построим график функции.

Из приведенного материала Вы должны научиться находить разрывы первого и второго рода, а также различать их. Для этого подобрано немного примеров, которые в полной мере раскрывают все важные вопросы темы. Все остальное сводится к нахождению простых односторонних пределов и не должно быть для Вас сложным.

D2R MF Breakpoints Guide — Magic Find Breakpoints для уникальных персонажей в Diablo 2 Resurrected 2.5

В этом руководстве по D2R 2.5 MF Breakpoints мы собираемся ответить на некоторые из самых популярных вопросов, которые мы получаем о Magic Find и, самое главное, о контрольных точках MF в Diablo 2 Resurrected.

Diablo 2 Resurrected Руководство по контрольным точкам MF

Давайте разберем контрольные точки D2R MF, выяснив эти часто задаваемые вопросы о Magic Find в Diablo 2 Resurrected:

Сколько MF я должен получать или когда мне следует прекратить добавлять MF?

Это действительно зависит от того, вы хотите иметь довольно высокий MF, но вы не хотите жертвовать скоростью убийства, вы хотите убить как можно больше монстров за наименьшее количество времени, и чем больше убитых монстров, тем больше шанс бросать предметы. Например, вы не хотите тратить 10 минут на пит-ран для 7 игроков с 800 MF, когда вы можете использовать гораздо более низкий MF, убивая гораздо больше монстров. Кроме того, вы можете сделать сознательный выбор в отношении того, где вы занимаетесь фармом, какое снаряжение D2R вы хотите носить, сколько MF вы хотите. Общее правило в сообществе Diablo 2 — получить от 200 до 300 MF, а затем работать над скоростью убийства. В тот момент, когда у вас будет приличная скорость зачистки, вы начнете добавлять немного больше MF, речь идет о том, чтобы эффективно использовать свое время, но также иметь как можно больше магических находок, сохраняя при этом эту скорость убийства.

Выпадают ли магические руны с эффектом поиска в Diablo 2 Resurrected?

Нет, единственное, что влияет на выпадение рун, это настройка игрока, например, игрок 1 по сравнению с игроком 7, и убийство определенных типов монстров, у которых выше шанс выпадения рун. Например, обычные призраки или души не могут сбрасывать предметы, единственные вещи, которые они могут сбросить, — это амулеты, драгоценные камни, украшения и руны, что дает им более высокий шанс выпадения рун Diablo 2 по сравнению с другими монстрами.

Существуют ли контрольные точки Magic Find, и если да, то какие?

Да, в Diablo 2 Resurrected есть контрольные точки MF, но не в традиционном понимании контрольных точек, когда вы думаете о FCR и FHR, основанных на кадрах. Например, чем выше и выше точки останова, которые вы достигаете, тем меньше кадров требуется для выполнения этого действия. Теперь Magic Find, очевидно, не имеет ничего общего с рамками, но идея та же. Например, если у вас есть друид и у вас 99 FCR, вы находитесь в этой точке останова, и вы добавляете еще 20 FCR, что дает вам 119, вы по-прежнему фактически только на 99 FCR, потому что следующая точка останова до 163.

Идея, лежащая в основе этого, также как работает NF , будут определенные моменты, когда вы добавляете немного MF, но на самом деле это не дает вам никакой пользы.

Как рассчитать контрольную точку поиска магии в Diablo 2 Resurrected?

Мы можем убедиться в этом, взглянув на формулу и поняв, как на самом деле рассчитывается ваша эффективная магическая находка, так что давайте начнем.

D2R Magic Find Breakpoint Formula 

Это формула, которая используется для расчета эффективной магической находки в коде игры:

• X = (MF x Y) / (MF + Y)

• 90 002 X = эффективный магический поиск (это одно из чисел, которое игра использует в процессе выпадения предмета для определения редкости выпадающего предмета)

• MF = магический поиск из всего снаряжения и амулетов (ваша фактическая магическая находка волшебная находка складывается из всего вашего снаряжения)

• Y = множитель предметов (уникальные = 250, наборы = 500, редкие = 600)

Для магических предметов эффективная магическая находка равна сумме магической находки из всего вашего снаряжения

Теперь давайте сделаем некоторые примеры расчетов, чтобы помочь прояснить это немного дальше:

Пример 1:

Допустим, у нас есть 445 MF, это MF, сложенный из всех наших снастей и амулетов, это идет вместо MF в формула:

МФ (МФ от снаряжения/шармов) = 445

Y (Коэффициент предмета) = 250

X = (445 X 250) / (445 + 250)

X = 160,7

После усечения X = 160

Коэффициент предмета для уникальных предметов равен 25 0, это входит поместите Y, найдите X, и мы получим 160,7 эффективного магического поиска. .

Пример 2:

Теперь давайте сделаем это для другого количества магических находок, скажем, у нас есть 453 магических прайма из всего нашего снаряжения и амулетов, на этот раз это снова пойдет вместо Эффективного магического поиска. Мы по-прежнему будем искать уникальные предметы, поэтому коэффициент предмета по-прежнему равен 250, выполняем расчет и получаем 161,09.., как и в предыдущем примере, .09 усекается, и мы получаем общее количество эффективных магических находок, равное 161.

MF (MF от снаряжения/амулетов) = 453

Y (фактор предмета) = 250

X = (453 X 250) / (453 + 250)

X = 161,09

После усечения X = 161

Некоторые из вас, возможно, уже поняли, почему создаются эти волшебные контрольные точки поиска, и это из-за усечения после десятичных точек. Поскольку мы можем добавлять магические находки только целыми числами, например, добавляя пять, шесть или семь MF за раз, мы максимально приблизились к тому, чтобы эффективный магический поиск был целым числом.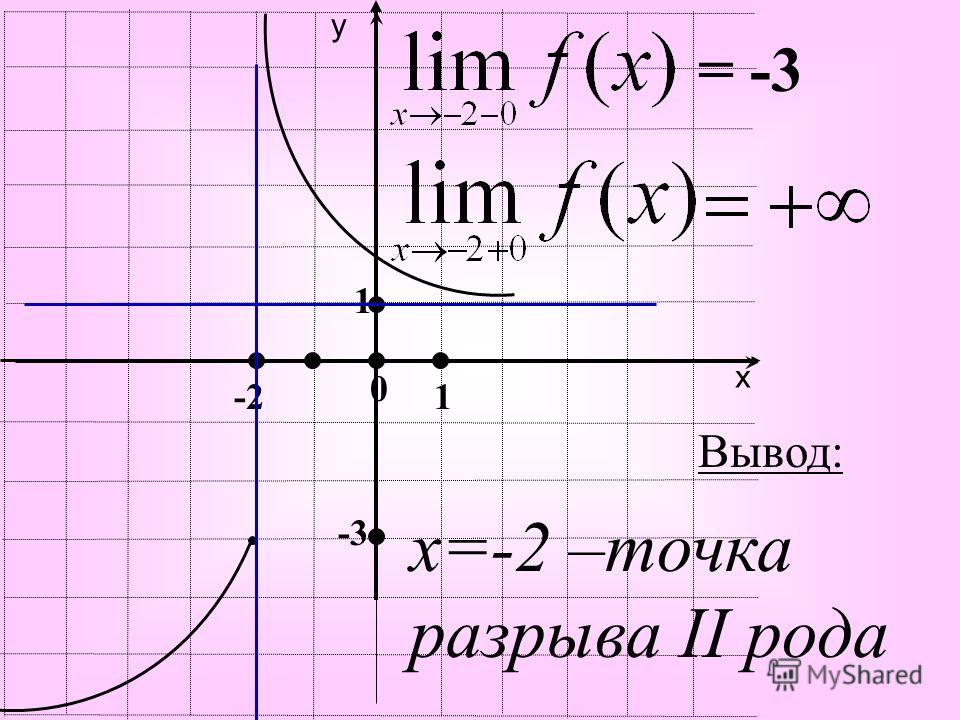 В примере 1 160,07 максимально близко к 160, насколько это возможно при одновременном добавлении нескольких волшебных находок, то же самое касается и второго примера.

Пример 3:

Чтобы было немного понятнее, если бы мы использовали 444,5 MF, что всего на половину MF меньше, чем в первом примере, наше значение EMF было бы 160,00 до его усечения. Как мы уже говорили ранее, мы можем добавлять значения только одной магической находки за раз, поэтому иметь 444,5 mf невозможно. Поэтому мы можем иметь либо 444 и 445 МП в первом случае, либо 452 и 453 МП во втором случае.

MF (MF от механизма/амулетов) = 444,5

Y (коэффициент предмета) = 250

X = 444,5 X 250) / 444,5 + 250)

X = 160,00, до усечения

Некоторые из вас, возможно, уже видели, как создаются эти точки останова, и это из-за этого усечения после десятичной точки.

Пример 4:

На этот раз давайте воспользуемся 452 MF и снова подставим значения для всех переменных, и мы получим 160,96 EMF:

MF (MF от механизма/амулетов) = 452

Y (коэффициент элемента) = 2 50

Х = 452 Х 250) / 452 + 250)

Х = 160,96

После усечения X = 160

Вы, наверное, думаете, что это так близко к 161, оно просто округляется, верно? Нет, то, чему вас учили в начальной школе, не применимо к Diablo, как и в предыдущих расчетах, этот ничем не отличается, 0,96 усечено, и наша результирующая ЭДС составляет всего 160.

Теперь, что мы можем вынести из всех этих вычислений. , хотя в предыдущем случае мы работали с 452 MF, мы пришли к выводу, что фактически получаем такое же значение ЭДС, как если бы мы работали только с 445 magic find? Проще говоря, добавление дополнительных семи магических находок к нашему персонажу все равно приведет к тому же ЭДС, равному 160.

Diablo 2 Resurrected Magic Find Breakpoints

Уникальная ЭДС (MF Breakpoint)  / Magic Find (From Gear)

0 / 0

1 / 2

2 / 3 9000 3

3 / 4

4 / 5

5 / 6

6 / 7

7 / 8

8 / 9

9 / 10

10 / 11

11 / 12

12/13

13/14

14/15

15/16

16/18

17/19

18 / 20

19 / 21

20 / 22

21 / 23

22 / 25

23 / 26

24 / 27

25 / 28

26 / 30

27 / 31

28 / 32

29 / 33

30 / 35

31 / 36

32 / 37

33 / 39

3 4/40

35/41

36/43

37/44

38/45

39/47

40/48

41/50

42 / 51

43 / 52

44 / 54

45 / 55

46 / 57

47 / 58

48 / 60

49 / 61

50 / 63

51 / 65

52 / 66

53 / 68

54 / 69

55 / 71

56 / 73

57 / 74

5 8/76

59/78

60/79

61/81

62/83

63/85

64/87

65/88

66 / 90

67 / 92

68 / 94

69 / 96

70 / 98

71 / 100

7 2/102

73/104

74/106

75/108

76 / 110

77 / 112

78 / 114

79 / 116

80 / 118

81 / 120

9 0002 82/123

83/125

84/127

85/129

86 / 132

87 / 134

88 / 136

89 / 139

90 / 141

91 / 144

92 / 146

93 / 149

94 / 151

90 002 95/154

96/156

97/159

98/162

99/164

100/167

101/170

102/173

103/176

104/179 90 003

105/182

106/185

107/188

108/191

109/194

110/197

111/200

112 / 203

113 / 207

114 / 210

115 / 213

116 / 217

117 / 220

118 / 224

119 / 228

120 / 231

121 / 235

122 / 239

123 / 243

124 / 247

125 / 250

126 / 255

127 / 259

128 / 263

129 / 267

130 / 271

131 / 276

132 / 280

133 / 285

134 / 289

135 / 294

136 / 299

137 / 304

138 / 309

139 / 314

140/319

141/324

142/329

143/335

144 / 340

145 / 346

146 / 351

147 / 357

148 / 363

149 / 369

150 / 375

151 / 382

152 / 388

153 / 395

154/402

155/408

156 / 415

157 / 423

158 / 430

159 / 437

160 / 445

161 / 453

162 / 461

163 / 469

164 / 477

165 / 486

166 / 495

167 / 504

168 / 513

169 / 522

170 / 532

171 / 542

172 / 552

173 / 562

174 / 573

175 / 584

176 / 595

177 / 607

178 / 619

179 / 631

180 / 643

181 / 656

182 / 670

183 / 683

184 / 697

185 / 712

186 / 727

187 / 743

188 / 759

189 / 775

190 / 792

191 / 810

192 / 828

193 / 847

194 / 867

195 / 887

196 / 908

197 / 930

198/952

199/976

200 / 1000

201 / 1026

202 / 1053

203 / 1080

204 / 1109

90 002 205 / 1139

206 / 1171

Когда люди говорят о магии, находят контрольные точки, это то, что они говоришь о. В некоторых случаях, таких как то, что мы только что видели, вы можете добавить 6 или 7 MF small charm, и это на самом деле не даст вам никакой пользы, это может показаться тривиальным, но когда мы говорим о реальной оптимизации сборки, это имеет значение. Это маленькое очарование 7 MF может быть вместо этого очарованием rs или аром максимального урона, все сводится к тому, чтобы получить максимальную отдачу от вашей сборки, насколько это возможно.

Reddit — Погрузитесь во что угодно

Перейти на slashdiablo р/слэшдиабло

р/слэшдиабло

Официальный сабреддит фантастического сервера сообщества Diablo II.

---

Члены Онлайн

от [удалено] 268Z»/>

---

Я подумал, что для тех, кто любит MF, это может быть интересно и полезно. Для волшебных предметов (синие) количество MF, которое у вас есть, равно количеству дополнительных волшебных предметов, которые вы получаете. Однако для редких, наборов и уникальных предметов все по-другому.

Формула для этих трех предметов следующая: X = (MF*Y)/(MF+Y), где MF — это ваша волшебная находка, X — ваша истинная волшебная находка, которую вы получаете, а Y — коэффициент предмета. Для редких предметов Y=600, для наборов Y=500 и для уникальных предметов Y=250. А так как Diablo 2 работает с целыми числами, а не с десятичными, всегда есть округление. Фактически это означает наличие точек останова MF, как и многих других свойств.

Поскольку наиболее востребованными предметами являются уникальные предметы, вот список контрольных точек уникальной магии. Я сделал это, просто обратив формулу к MF = -(X*250)/(X-250). И конечно, 250 недостижимо.

(Форматирование могло бы быть лучше, но все равно нормально)

Уникальная МФ / Волшебная находка

0 0

1 2

2 3

3 4

4 5

5 6

6 7

7 8

8 9

9 10

10 11

11 12

12 13

13 14

14 15

15 16

16 18

17 19

18 20

19 21

20 22

21 23

22 25

23 26

24 27

25 28

26 30

27 31

28 32

29 33

30 35

31 36

32 37

33 39

34 40

35 41

36 43

37 44

38 45

39 47

40 48

41 50

42 51

43 52

44 54

45 55

46 57

47 58

48 60

49 61

50 63

51 65

52 66

53 68

54 69

55 71

56 73

57 74

58 76

59 78

60 79

61 81

62 83

63 85

64 87

65 88

66 90

67 92

68 94

69 96

70 98

71 100

72 102

73 104

74 106

75 108

76 110

77 112

78 114

79 116

80 118

81 120

82 123

83 125

84 127

85 129

86 132

87 134

88 136

89 139

90 141

91 144

92 146

93 149

94 151

95 154

96 156

97 159

98 162

99 164

100 167

101 170

102 173

103 176

104 179

105 182

106 185

107 188

108 191

109 194

110 197

111 200

112 203

113 207

114 210

115 213

116 217

117 220

118 224

119 228

120 231

121 235

122 239

123 243

124 247

125 250

126 255

127 259

128 263

129 267

130 271

131 276

132 280

133 285

134 289

135 294

136 299

137 304

138 309

139 314

140 319

141 324

142 329

143 335

144 340

145 346

146 351

147 357

148 363

149 369

150 375

151 382

152 388

153 395

154 402

155 408

156 415

157 423

158 430

159 437

160 445

161 453

162 461

163 469

164 477

165 486

166 495

167 504

168 513

169522

170 532

171 542

172 552

173 562

174 573

175 584

176 595

177 607

178 619

179 631

180 643

181 656

182 670

183 683

184 697

185 712

186 727

187 743

188 759

189 775

190 792

191 810

192 828

193 847

194 867

195 887

196 908

197 930

198 952

199 976

200 1000

201 1026

202 1053

203 1080

204 1109

205 1139

206 1171

Здесь и далее недостижимо

207 1204

208 1239

209 1275

210 1313

211 1353

212 1395

213 1440

214 1487

215 1536

216 1589

217 1644

218 1704

219 1767

220 1834

221 1906

222 1983 г.