Найти угол между плоскостями онлайн калькулятор: Онлайн калькулятор. Угол между плоскостями

Угол между прямой и плоскостью.

Навигация по странице:

• Определение угла между прямой и плоскостью
• Формула для вычисления угла между прямой и плоскостью
• Вывод формулы вычисления угла между прямой и плоскостью
• Примеры задач на вычисление угла между прямой и плоскостью

Онлайн калькулятор. Угол между прямой и плоскостью.

Определение.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.

Формула вычисления угла между прямой и плоскостью

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	| A · l + B · m + C · n |
	√A2 + B2 + C2 · √l2 + m2 + n2

Вывод формулы для вычисления угла между прямой и плоскостью

Из уравнения прямой можно найти направляющий вектор прямой

s = {l; m; n}

Из уравнения плоскости вектор нормали плоскости имеет вид

q = {A; B; C}

Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой

cos ψ =	| q · s |
	| s | · |q |

Так как φ = 90° — ψ, то синус угла между прямой и плоскостью sin φ = cos ψ.

Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.

Пример вычисления угла между прямой и плоскостью

Пример 1.

Найти угол между прямой

x — 4	=	y + 2	= —	z — 6
2		6		3

и плоскостью x — 2y + 3z + 4 = 0.

Решение.

Из уравнения прямой найдем направляющий вектор прямой

s = {2; 6; -3}

Из уравнения плоскости найдем вектор нормали плоскости

q = {1; -2; 3}

Воспользовавшись формулой, найдем угол между прямой и плоскостью

sin φ =	| 2 · 1 + 6 · (-2) + (-3) · 3 |	=
	√22 + 62 + (-3)2 · √12 + (-2)2 + 32

sin φ =	| 2 — 12 — 9 |	=	19	=	19
	√4 + 36 + 9 · √1 + 4 + 9		√49 · √14		7√14

Ответ:

sin φ =  19 7√14

Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точками. Середина отрезка. Координаты середины отрезка.Уравнение прямой.Уравнение плоскости.Расстояние от точки до плоскости.Расстояние между плоскостями.Расстояние от точки до прямой на плоскости.Расстояние от точки до прямой в пространстве.Угол между плоскостями.Угол между прямой и плоскостью.

Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

2 угол между плоскостями

Вы искали 2 угол между плоскостями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и двугранный угол между плоскостями как найти, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 угол между плоскостями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 2 угол между плоскостями,двугранный угол между плоскостями как найти,как найти двугранный угол между плоскостями,как найти угол между двумя плоскостями,как найти угол между плоскостями,как найти угол между плоскостями методом координат,калькулятор онлайн найти угол между плоскостями,координатный метод угол между плоскостями,косинус угла между плоскостями,метод координат угол между плоскостями,найти косинус острого угла между плоскостями,найти косинус угла между плоскостями,найти угол между плоскостями,найти угол между плоскостями калькулятор онлайн,найти угол между плоскостями онлайн калькулятор,онлайн калькулятор найти угол между плоскостями,онлайн угол между плоскостями,определение угол между плоскостями,определить двугранные углы образованные пересечением двух плоскостей,определить двугранные углы образованные пересечением пар плоскостей,угол между двумя плоскостями,угол между двумя плоскостями как найти,угол между двумя плоскостями координатный метод,угол между плоскостями,угол между плоскостями как найти,угол между плоскостями координатный метод,угол между плоскостями онлайн,угол между плоскостями определение,угол между плоскостями формула,угол между плоскостями это.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 2 угол между плоскостями. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти двугранный угол между плоскостями).

Решить задачу 2 угол между плоскостями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор угла между двумя векторами. 2D и 3D векторы

С помощью этого калькулятора угла между двумя векторами вы быстро научитесь находить угол между двумя векторами. Неважно, находятся ли ваши векторы в 2D или 3D , и являются ли их представления координатами или начальными и конечными точками — наш инструмент является безопасным выбором в любом случае. Поиграйте с калькулятором и проверьте определения и пояснения ниже; если вы ищете формулу угла между двумя векторами, вы обязательно найдете их там.

Раз уж вы здесь, ищете решения своих векторных задач, можем ли мы предположить, что вы также интересуетесь векторными операциями? Проверьте другие инструменты Omni в разделе координатной геометрии.

Формулы угла между двумя векторами

В этом параграфе вы найдете формулы для угла между двумя векторами – и только формул. Если вы хотите понять, как мы их получаем, перейдите непосредственно к следующему параграфу, Как найти угол между двумя векторами .

Угол между двумя двумерными векторами

1. Векторы, представленные координатами (стандартное обозначение упорядоченного набора, форма компонента):

Для вектора a\boldsymbol aa:

a=(xa,ya)\qquad\scriptsize \boldsymbol a = (x_a,y_a)a=(xa​,ya​)

И b\boldsymbol bb:

b=(xb,yb)\qquad\scriptsize \boldsymbol b = (x_b,y_b)b=(xb​,yb​)

Угол:

angle=arccos((xa⋅xb+ya⋅yb) /((xa2+ya2)12⋅(xb2+yb2)12))\qquad\scriptsize\begin{split} \mathrm{угол} &= \mathrm{arccos}\bigg(\Big(x_a\cdot x_b +y_a \cdot y_b\Big)\\ &\!\!\!\!\!\!\!\!\!/\Большой(\большой(x_a^2+y_a^2\big)^{\frac{1}{2}}\cdot\ ! \ большой (x_b ^ 2 + y_b ^ 2 \ большой) ^ {\ гидроразрыва {1} {2}} \ большой) \ большой) \end{split}angle​=arccos((xa​⋅xb​+ya​⋅yb​)/((xa2​+ya2​)21​⋅(xb2​+yb2​)21​))​

2. Векторы между начальной и конечной точкой:

Для вектора a\boldsymbol aa:

A=(x1,y1,z1)\qquad\scriptsize A =(x_1,y_1,z_1)A=(x1​,y1​,z1​)

And:

B=(x2,y2,z2)\qquad\scriptsize B =(x_2,y_2,z_2)B=(x2​,y2​,z2​)

Итак, вектор a\boldsymbol aa равен:

a=( x2−x1,y2,y1)\qquad\scriptsize\boldsymbol a = (x_2-x_1,y_2,y_1)a=(x2​−x1​,y2​,y1​)

Для вектора b\boldsymbol bb:

C=(x3,y3,z3)\qquad\scriptsize C=(x_3,y_3,z_3)C=(x3​,y3​,z3​)

And:

D=(x4,y4,z4)\qquad\scriptsize D =(x_4,y_4,z_4)D=(x4​,y4​,z4​)

Итак, вектор b\boldsymbol bb равен:

b=(x4−x3,y4−y3)\qquad\scriptsize\boldsymbol{b}=(x_4-x_3,y_4-y_3)b=(x4​−x3​,y4​−y3​)

И :

угол=arccos(((x2−x1)⋅(x4−x3)+(y2−y1)⋅(y4−y3))/((((x2−x1)2+(y2−y1)2)12 ⋅((x4−x3)2+(y4−y3)2)12))\quad\scriptsize\begin{split} \mathrm{угол} &= \mathrm{arccos}\bigg(\Big((x_2-x_1)\cdot(x_4-x_3)\\ &\!\!\!\!\!\!\!\!\!+(y_2-y_1)\cdot(y_4-y_3)\Big)\\ &\!\!\!\!\!\!\!\!\!/\Big(\big((x_2-x_1)^2+(y_2-y_1)^2\big)^{\frac{1 {2}}\\ &\!\!\!\!\!\!\!\!\!\cdot\!\big((x_4-x_3)^2+(y_4-y_3)^2\big)^{\frac{1 }{2}}\Большой)\Большой) \end{split}angle​=arccos(((x2​−x1​)⋅(x4​−x3​)+(y2​−y1​)⋅(y4​−y3​))/(((x2​− x1​)2+(y2​−y1​)2)21​⋅((x4​−x3​)2+(y4​−y3​)2)21​))​

Угол между двумя трехмерными векторами

1. Векторы, представленные координатами:

a=(xa,ya,za)\qquad\scriptsize\boldsymbol a = (x_a,y_a,z_a)a=(xa​,ya​,za​)

And:

b=(xb,yb ,zb)\qquad\scriptsize\boldsymbol b = (x_b,y_b,z_b)b=(xb​,yb​,zb​)

Тогда:

angle=arccos((xa⋅xb+ya⋅yb+za ⋅zb)/((xa2+ya2+za2)12⋅(xb2+yb2+zb2)12))\scriptsize \начать{разделить} &\mathrm{угол} \!=\! \mathrm{arccos}\bigg((x_a\cdot x_b+y_a\cdot y_b+z_a\cdot z_b)\\ &\!\!/\Большой(\большой(x_a^2+y_a^2+z_a^2\big)^{\frac{1}{2}}\cdot\big(x_b^2+y_b^2+ z_b ^ 2 \ большой) ^ {\ гидроразрыва {1} {2}} \ большой) \ большой) \end{split}​angle=arccos((xa​⋅xb​+ya​⋅yb​+za​⋅zb​)/((xa2​+ya2​+za2​)21​⋅(xb2​+yb2​ +zb2​)21​))​

2. Векторы между начальной и конечной точкой:

Для вектора a\boldsymbol{a}a:

A=(x1,y1,z1)\qquad\scriptsize A = (x_1,y_1,z_1)A=(x1​,y1​,z1​)

И:

B=(x2,y2,z2)\qquad\scriptsize B =(x_2,y_2,z_2)B=(x2​,y2​,z2​)

Итак:

a=(x2−x1 ,y2−y1,z2−z1)\qquad\scriptsize\boldsymbol{a} = (x_2-x_1,y_2-y_1,z_2-z_1)a=(x2​−x1​,y2​−y1​,z2​− z1​)

Для вектора b\boldsymbol{b}b:

C=(x3,y3,z3)\qquad\scriptsize C = (x_3,y_3,z_3)C=(x3​,y3​,z3​ )

And:

D=(x4,y4,z4)\qquad\scriptsize D =(x_4,y_4,z_4)D=(x4​,y4​,z4​)

Итак:

b=(x4 −x3,y4−y3,z4−z3)\qquad\scriptsize\boldsymbol{b}=(x_4-x_3,y_4-y_3,z_4-z_3)b=(x4​−x3​,y4​−y3​,z4 ​−z3​)

Найдите окончательную формулу аналогично 2D версии:

angle=arccos(((x2−x1)⋅(x4−x3)+(y2−y1)⋅(y4−y3)+(z2 −z1)⋅(z4−z3))/(((x2−x1)2+(y2−y1)2+(z2−z1)2)12⋅((x4−x3)2+(y4−y3)2 +(z4−z3)2)12))\scriptsize\begin{split} \mathrm{угол} &= \mathrm{arccos}\bigg(\Big((x_2-x_1)\cdot(x_4-x_3)\\ &\!\!\!\!\!\!\!\!+(y_2-y_1)\cdot(y_4-y_3)+(z_2-z_1)\\ &\!\!\!\!\!\!\!\!\cdot(z_4-z_3)\Big)/\Big(\big((x_2-x_1)^2+(y_2-y_1)^2\ \ &\!\!\!\!\!\!\!\!+(z_2-z_1)^2\big)^{\frac{1}{2}}\!\cdot\!\big((x_4 -x_3)^2+(y_4-y_3)^2\\ &\!\!\!\!\!\!\!\!+(z_4-z_3)^2\big)^{\frac{1}{2}}\Big)\bigg) \end{split}angle​=arccos(((x2​-x1​)⋅(x4​-x3​)+(y2​-y1​)⋅(y4​-y3​)+(z2​-z1​) ⋅(z4​−z3​))/(((x2​−x1​)2+(y2​−y1​)2+(z2​−z1​)2)21​⋅((x4​−x3​) 2+(y4​−y3​)2+(z4​−z3​)2)21​))​

Также можно иметь один угол, определяемый координатами, а другой определяемый начальной и конечной точками, но мы не позволим этому еще больше запутать этот раздел.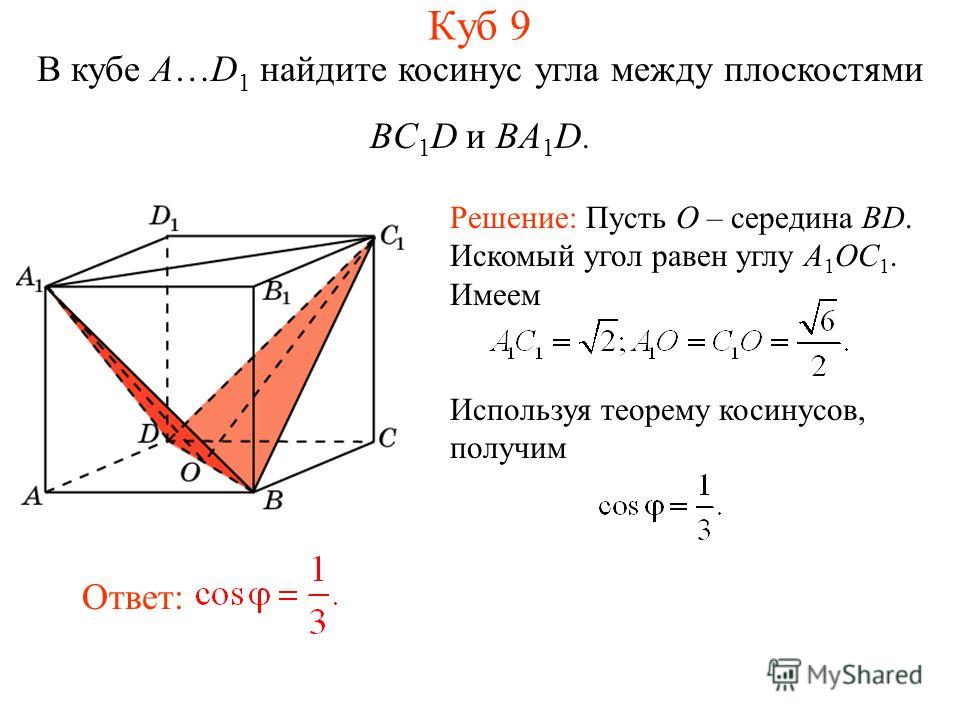 Все, что имеет значение, это то, что наш калькулятор угла между двумя векторами имеет все возможные комбинации, доступные для вас.

Как найти угол между двумя векторами?

Хорошо, вышеприведенный абзац был чем-то вроде TL;DR . Чтобы лучше понять формулы для угла между двумя векторами, давайте проверим, откуда они берутся:

1. Начните с базовой геометрической формулы для расчета скалярного произведения:

   Скалярное произведение определяется как произведение модулей векторов, умноженное на косинус угла между ними (здесь обозначается α\alphaα):

a⋅b=∣a∣×∣b∣×cos⁡(α)\qquad\boldsymbol{a}\cdot\boldsymbol{b} = |\boldsymbol{a}|\times|\boldsymbol{b}| \times \cos(\alpha)a⋅b=∣a∣×∣b∣×cos(α)

🙋 Наш калькулятор векторной величины здесь, чтобы помочь, если вам нужно обновить эту другую важную векторную величину!

2. Затем, сделайте угол предметом уравнения :

   Разделить на произведение величин векторов:

cos⁡(α)=(a⋅b∣a∣×∣b∣)\qquad\scriptsize\cos(\alpha) = \left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}} {|\boldsymbol{a}|\times|\boldsymbol{b}|}\right)cos(α)=(∣a∣×∣b∣a⋅b​)

Найдите арккосинус обеих сторон:

α=arccos(a⋅b∣a∣×∣b∣)\qquad\scriptsize\alpha = \mathrm{arccos}\left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{|\ boldsymbol{a}|\times|\boldsymbol{b}|}\right)α=arccos(∣a∣×∣b∣a⋅b​)

3. После этого нам нужно освежить определение величины векторов :

   . {\ гидроразрыва {1} {2}} \ большой) \ большой) \end{split}​α=arccos((xa​⋅xb​+ya​⋅yb​+za​⋅zb​)/((xa2​+ya2​+za2​)21​⋅(xb2​+yb2​ +zb2​)21​))​

   И все!

   Кроме того, если ваши векторы имеют другую форму (вы знаете их начальную и конечную точки), вам необходимо заранее выполнить некоторые вычисления. Цель состоит в том, чтобы привести их к стандартной векторной записи.

   Если вектор вашего примера описывается начальной точкой B=(x1,y1)B=(x_1, y_1)B=(x1​,y1​) и конечной точкой B=(x2,y2)B=(x_2 , y_2)B=(x2​,y2​), то vectora\boldsymbol{a}a может быть выражен как:

   a=(x2−x1,y2−y1)\scriptsize\boldsymbol{a} = (x_2- x_1,y_2-y_1)a=(x2​−x1​,y2​−y1​)

   Все еще не понятно? Не беспокойся! Мы подготовили несколько примерных расчетов, чтобы убедиться, что все предельно ясно.

   Угол между двумя трехмерными векторами – пример

   Предположим, что мы хотим найти угол между двумя векторами:

   a=(3,6,1)\scriptsize\boldsymbol{a} = (3, 6, 1)a =(3,6,1)

   и b\boldsymbol{b}b определяется как вектор между точками A=(1,1,2)A = (1, 1, 2)A=(1,1, 2) и B=(-4,-8,6)B=(-4,-8,6)B=(-4,-8,6) .

   Что нам нужно сделать?

   1. Сначала вычислить вектор b\boldsymbol{b}b , учитывая начальную и конечную точки:

   b=(−4−1,−8−1,6−2)=(−5,−9,4)\qquad\scriptsize \начать{разделить} \boldsymbol{b} &= (-4-1,-8-1,6-2)\\ &= (-5,-9,4) \end{split}b​=(−4−1,−8−1,6−2)=(−5,−9,4)​

   2. Тогда найдите скалярное произведение векторов a\boldsymbol {а}а и б\boldsymbol{b}б:

     a⋅b=(3×−5)+(6×−9)+(1×4)=−15−54+4=−65\quad\ \ \scriptsize \начать{разделить} \boldsymbol{a}\cdot\boldsymbol{b}&= (3 \times -5) + (6 \times-92}\\ &=\sqrt{122}\приблизительно11.045 \end{split}∣b∣​=(−5)2+(−9)2+42

   ​=122

   ​≈11,045​

   4. Наконец, используйте преобразованное уравнение скалярного произведения :

   α=arccos(a⋅b∣a∣×∣b∣)=arccos(−656,782×11,045)=arccos(−0,86767)=150,189°≈150,2°\qquad\scriptsize\begin{split} \alpha &= \mathrm{arccos}\left(\frac{\boldsymbol{a}\cdot\boldsymbol{b}}{|\boldsymbol{a}|\times|\boldsymbol{b}|}\right) \\[1em] &=\mathrm{arccos}\left(\frac{-65}{6,782\times11,045}\right) \\[1em] &=\mathrm{arccos}(-0,86767) \\[1em] &=150,189\градус\приблизительно150,2\градус \end{split}α​=arccos(∣a∣×∣b∣a⋅b​)=arccos(6,782×11,045−65​)=arccos(−0,86767)=150,189°≈150,2°​

   И вот вы идти! Вы только что вычислили угол между двумя трехмерными векторами. Поздравляем!

   Если вы хотите узнать больше о понятиях координатной геометрии, мы рекомендуем воспользоваться калькулятором средней скорости изменения.

   Как использовать калькулятор угла между двумя векторами?

   Итак, как работает наш калькулятор угла между двумя векторами? Следуйте этим пошаговым инструкциям:

   1. Выберите векторное пространство . Рассмотрим тот же пример, что и в предыдущем пункте. Наши векторы и точки имеют три координаты, поэтому нам нужно выбрать опцию 3D .

   2. Выберите представление первого вектора . Первый вектор имеет стандартную запись, поэтому мы оставляем значение по умолчанию: представление координат .

   3. Введите первый вектор . Введите x=3x = 3x=3, y=6y = 6y=6, z=1z = 1z=1.

   4. Выберите представление второго вектора . На этот раз нам нужно изменить его на точечное представление .

   5. Введите значения второго вектора . Входные данные A=(1,1,2)\boldsymbol A = (1,1,2)A=(1,1,2) и B=(−4,−8,6)\boldsymbol B = (-4, -8,6)B=(−4,−8,6) в соответствующие поля.

   6. Инструмент нашел угол между двумя 3D-векторами в момент заполнения последнего поля. В нашем случае это 150,2°150,2\градус 150,2° — это, конечно, тот же результат, который мы получили при ручных вычислениях.

   Часто задаваемые вопросы

   Что такое вектор?

   Вектор — это представление физической величины, которое имеет как величину, так и направление.

   Как определить угол, образованный двумя векторами?

   Угол между двумя векторами определяется с помощью арккосинуса скалярных произведений двух векторов и произведения их модулей.

   Как рассчитать угол между двумя векторами в 2D?

   Чтобы вычислить угол между двумя векторами в 2D-пространстве:

   1. Найдите скалярное произведение векторов.
   2. Разделите скалярное произведение на величину первого вектора.
   3. Разделите полученное число на величину второго вектора.

   Математически угол α между двумя векторами может быть записан как:

   α = arccos[(xa · xb + ya · yb) / (√(xa² + ya²) · √(xb² + yb²))]

   Как рассчитать угол между двумя векторами в 3D?

   Чтобы вычислить угол между двумя векторами в трехмерном пространстве:

   1. Найдите скалярное произведение векторов.
   2. Разделите скалярное произведение на величину первого вектора.
   3. Разделите полученное число на величину второго вектора.

   Математически угол α между двумя векторами может быть записан как:

   α = arccos[(xa · xb + ya · yb + za · zb) / (√(xa² + ya² + za²) · √(xb² + yb² + zb² ))]

   Угол между двумя плоскостями — формула, векторная форма, примеры, декартова форма, часто задаваемые вопросы

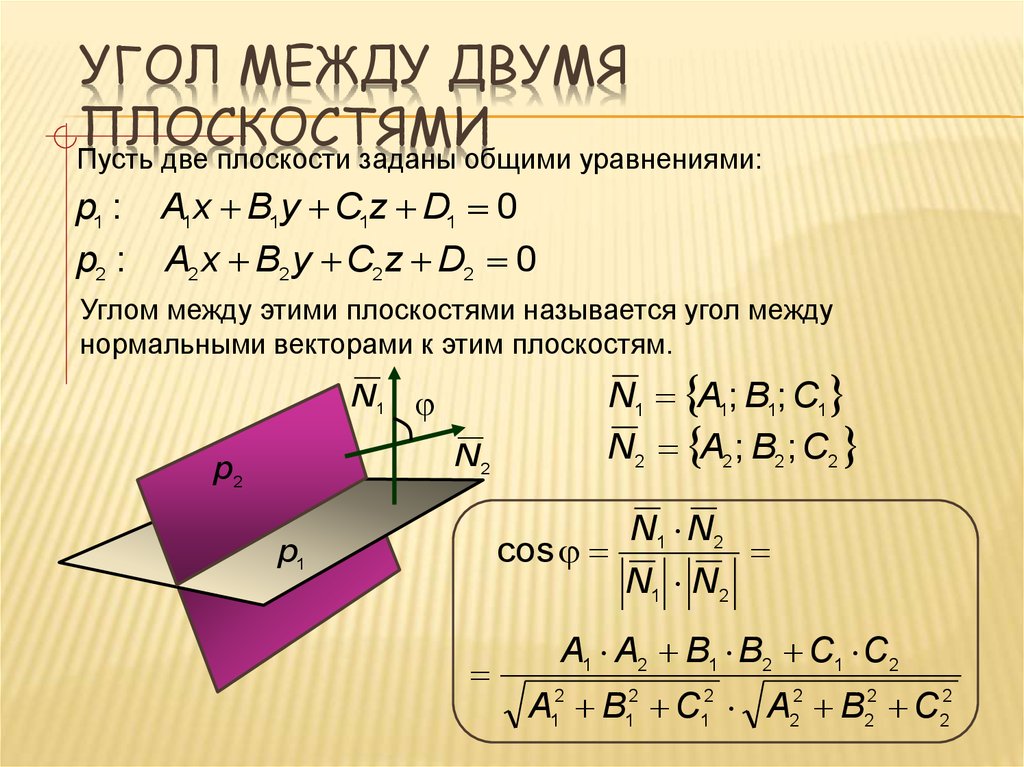
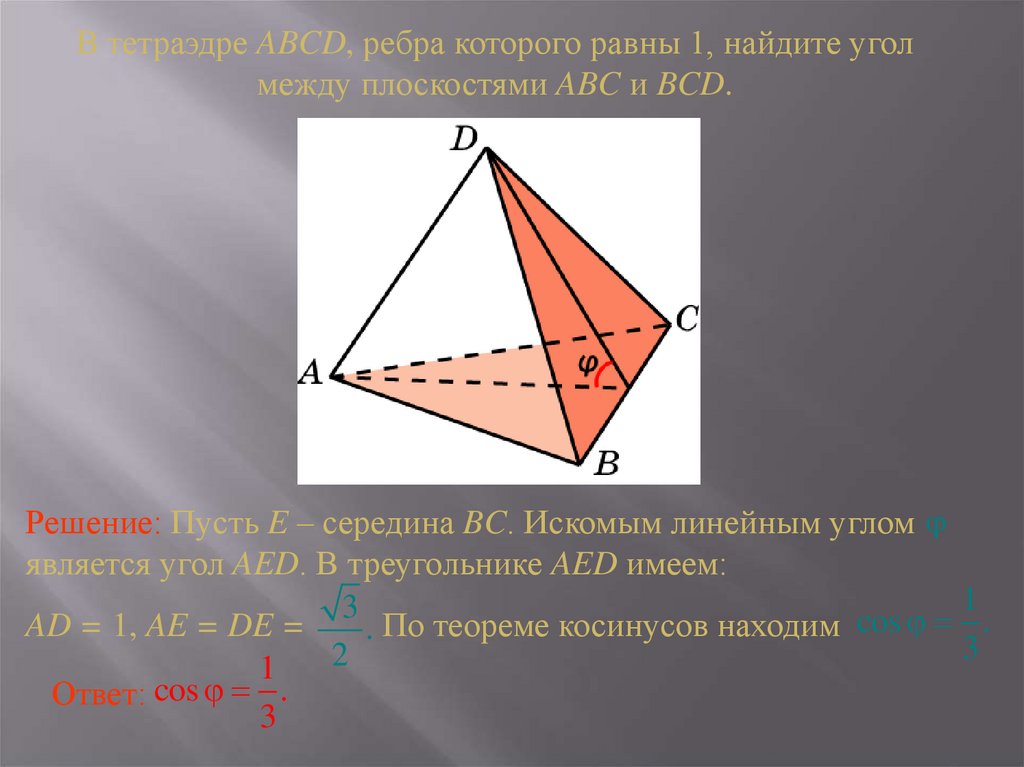
   Угол между двумя плоскостями определяется углом между нормалями двух плоскостей. Его можно определить с помощью векторной формы и декартовой формы уравнения плоскости. Угол между двумя плоскостями в векторной форме можно определить с помощью скалярного произведения векторов нормалей к двум плоскостям. Мы можем определить угол между двумя плоскостями в векторной форме и декартовой форме, и он равен углу между нормалью к двум плоскостям.

   Угол между двумя плоскостями также называется двугранным углом. В этой статье мы рассмотрим понятие угла между двумя плоскостями и его формулу в векторной и декартовой формах. Мы решим несколько примеров на основе этих формул для лучшего понимания концепции.

   1.	Что такое угол между двумя плоскостями?
   2.	Угол между двумя плоскостями Формула
   3.	Угол между двумя плоскостями в векторной форме
   4.	Угол между двумя плоскостями в декартовой форме
   5.	Часто задаваемые вопросы об угле между двумя плоскостями

   Что такое угол между двумя плоскостями?

   Угол между двумя плоскостями равен углу между векторами нормали к двум плоскостям. Мы можем определить угол между двумя плоскостями, используя декартово уравнение плоскости и векторное уравнение плоскости. Поскольку угол между двумя плоскостями определяется углом между нормалями к этим двум плоскостям, поэтому мы используем скалярное произведение и величины векторов нормалей в формуле, чтобы найти угол между ними. В векторной форме уравнение плоскости задается как rn = d, а его декартово уравнение задается как Ax + By + Cz + D = 0. Теперь давайте пройдемся по формулам, чтобы найти угол между двумя плоскостями.

   Угол между двумя плоскостями Формула

   Теперь есть две формулы для нахождения угла между двумя плоскостями. Формулы существуют в векторной форме и в декартовой форме. Рассмотрим две плоскости P ₁ и P ₂ , угол между которыми равен θ.

   Уравнения двух плоскостей в векторной форме имеют вид r.n ₁ = d ₁ и r.n ₂ = d ₂ , а уравнения двух плоскостей в декартовой форме имеют вид A ₁ х + В ₁ у + С ₁ z + D ₁ = 0 и А ₂ х + В ₂ у + С ₂ 4 41 + 2 90 Тогда , формулы для нахождения угла между двумя плоскостями:
   • cos θ = |(n ₁ . n ₂ )/|(|n ₁ |.|n ₂ |)
   • cos θ = |(А ₁ А ₂ + В ₁ В ₂ + С ₁ С ₂ )|/[√(А 9 9 9 2 ₁ 0441 1 ² + C ₁ ² )√(A ₂ ² + B ₂ ² + C ₂ ² )]

   Используя приведенные выше формулы, мы можем определить значение cos θ и взять cos, обратное с обеих сторон, чтобы найти значение θ и, следовательно, угол между двумя плоскостями.

   Угол между двумя плоскостями в векторной форме

   Теперь решим пример на основе формулы угла между двумя плоскостями в векторной форме. Для самолетов, р.н ₁ = d ₁ и r.n ₂ = d ₂ , будем использовать формулу cos θ = |(n ₁ . n ₂ )/(|n | ₂ |), где n ₁ и n ₂ — векторы нормали к двум плоскостям, а θ — угол между двумя плоскостями.

   Пример: Определите угол между двумя плоскостями, векторные уравнения которых представлены в виде r.(2i + 2j — 3k) = 4 и r.(3i — 3j + 5k) = 3.

   Решение: Уравнения плоскостей представлены в векторной форме . Теперь, чтобы найти угол между плоскостями r.(2i + 2j — 3k) = 4 и r.(3i — 3j + 5k) = 3, воспользуемся формулой cos θ = |(n ₁ . n ₂ )|/(|n ₁ |.|n ₂ |). Имеем

   n ₁ = 2i + 2j — 3k, n ₂ = 3i — 3j + 5k

   |n ₁ | = √(2 ² + 2 ² + (-3) ² ) = √(4 + 4 + 9) = √17

   |n ₂ | = √(3 ² + (-3) ² + 5 ² ) = √(9 + 9 + 15) = √43

   Скалярное произведение векторов нормалей определяется выражением n ₁ . n ₂ = (2i + 2j — 3k) . (3i — 3j + 5k) = 2 × 3 + 2 × (-3) + (-3) × 5 = 6 — 6 — 15 = -15

   Подставляя эти значения в формулу, имеем

   cos θ = |(-15)|/(√17 . √43)

   = 15/√731

   ⇒ θ = cos ^-1 (15/√731) [взяв арккосинус с обеих сторон]

   = 0,983

   Следовательно, угол между двумя плоскостями r.(2i + 2j — 3k) = 4 и r.(3i — 3j + 5k) = 3 равен cos ^-1 (15/√731) = 0,983 радиан .

   Угол между двумя плоскостями в декартовой форме

   В этом разделе мы решим пример и найдем угол между двумя плоскостями с уравнениями в декартовой форме. Для самолетов A ₁ x + B ₁ y + C ₁ z + D ₁ = 0 и A ₂ x + B ₂ y + C ₂ z + D ₂ = 0, воспользуемся формулой cos θ = |(A ₁ A ₂ + B ₁ B ₂ + C _{1 C 2 2 | /[√ (A 1 ² + B 1 ² + C 1 ² ) √ (A 2 ² + B44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444449. ² )], где A 1 i + B 1 j + C 1 k и A 2 i + B 2 j + C 2 k — векторы нормали к двум плоскостям, а θ — угол между двумя плоскостями.}

   Решение: Поскольку уравнения двух плоскостей заданы в декартовой форме, определим угол между двумя плоскостями в декартовой форме по формуле cos θ = |(A ₁ A ₂ + B ₁ В ₂ + С ₁ С ₂ ) |/[√ (A ₁ ² + B ₁ ² + C ₁ ² ) √ (A ₂ ² ) √ (A ₂ ^{2 2 2 ) √ (A ₂ 2 ) √ (A ₂ 2 ). + С ₂ 2 )]. Уравнения плоскостей: 2x + y — 2z = 5 и 3x — 6y — 2z = 7. Здесь A ₁ = 2, B ₁ = 1, C ₁ = -2, A ₂ = 3, В ₂ = -6, С ₂ = -2. Подставив эти значения в формулу, мы получим}

   cos θ = (2×3 + 1×(-6) + (-2)×(-2))/[√(2 ² + 1 ² + (-2) ² )√(3 ² + (-6) ² + (-2) ² )]

   ) + 4)/[√(4 + 1 + 4)√(9 + 36 + 4)]

   = 4/(√9 √49)

   = 4/(3×7)

   = 4/21

   ⇒ θ = cos ^-1 (4/21) [взяв арккосинус с обеих сторон]

   Следовательно, угол между двумя плоскостями 2x + y — 2z = 5 и 3x — 6y — 2z = 7 равен cos ^-1 (4/21).

   Важные замечания по углу между двумя плоскостями

   • Угол между двумя плоскостями равен углу между векторами нормалей к двум плоскостям и называется двугранным углом.
   • Для плоскостей, r.n ₁ = d ₁ и r.n ₂ = d ₂ , угол между ними равен, cos θ = |(n ₁ . n 2 ) п ₁ |.|п ₂ |)
   • Для самолетов, A ₁ x + B ₁ y + C ₁ z + D ₁ = 0 и A ₂ x + B ₂ y + C ₂ z + D ₂ = 0, угол между двумя плоскостями в декартовой форме определяется выражением, cos θ = |(A ₁ A ₂ + B ₁ B ₂ + C ₁ C ₂ ) |/[√ (A ₁ ² + B ₁ ² + C _{94441 94441 94441 94441 94441 9497 9497 + C 1 + C 9497 + C 2 ² + В 2 ² + С 2 ² )]}

   ☛ Похожие темы:

   • Векторы
   • Расстояние между двумя плоскостями
   • Расстояние между точкой и плоскостью

   Часто задаваемые вопросы об угле между двумя плоскостями

   Что означает угол между двумя плоскостями?

   Угол между двумя плоскостями равен углу между векторами нормали к двум плоскостям. Мы можем определить угол между двумя плоскостями в векторной форме и декартовой форме, и он равен углу между нормалью к двум плоскостям.

   Как называется угол между двумя плоскостями?

   Угол между двумя пересекающимися плоскостями называется двугранным углом. Другими словами, можно сказать, что угол между векторами нормалей двух плоскостей называется двугранным углом.

   Как найти угол между двумя плоскостями?

   Мы можем найти угол между двумя плоскостями, определив угол между векторами нормалей к двум плоскостям. Мы можем использовать следующие формулы, чтобы найти угол между двумя плоскостями. Уравнения двух плоскостей в векторной форме имеют вид r.n ₁ = d ₁ и р.н ₂ = d ₂ и уравнения двух плоскостей в декартовой форме имеют вид 1 = 0 и A ₂ x + B ₂ y + C ₂ z + D ₂ = 0. Тогда формулы для нахождения угла θ между двумя плоскостями:

   • cos θ = |(n ₁ . n ₂ )/|(|n ₁ |.|n ₂ |)
   • потому что θ = |(A ₁ A ₂ + B ₁ B ₂ + C ₁ C ₂ )|/[√(A ₁ ² + B ₁ ² + C ₁ ² )√(А ₂ ² + Б ₂ ² + С ₂ ² )]

   Что такое двугранный угол между двумя плоскостями?

   Двугранный угол между двумя плоскостями — это угол между двумя пересекающимися плоскостями. Простыми словами можно сказать, что угол между векторами нормалей двух плоскостей называется двугранным углом.

   Как найти косинус угла между двумя плоскостями?

   Чтобы найти косинус угла между двумя плоскостями A ₁ x + B ₁ y + C ₁ z + D ₁ = 0 и A ₂ x + B _{2 2 904 2 z + D 2 = 0 в декартовой форме и r.}

   No related posts.