Как найти угол между векторами в координатах?
Теперь у нас есть полная информация, чтобы ранее выведенную формулу косинуса угла между векторами выразить через координаты векторов :
Косинус угла между векторами плоскости и ,
заданными в ортонормированном базисе , выражается формулой:
.
Косинус угла между векторами пространства , заданными в ортонормированном базисе , выражается формулой:
Возвращаемся к нашим треугольникам:
Задача 31
Даны три вершины треугольника . Найти .
Решение: по условию чертёж выполнять не требуется, но всё-таки:
Из чертежа совершенно очевидно, что угол треугольника совпадает с углом между векторами и , иными словами: , и дальнейшее понятно. Найдём векторы и их длины:
Вычислим скалярное произведение:
Таким образом:
Именно такой порядок выполнения задания рекомендую «чайникам».
Более подготовленные читатели могут записать вычисления
«одной строкой»:
Косинус получился «плохим» (не табличным), однако, это не окончательный ответ задачи, и поэтому, к слову, не имеет особого смысла избавляться от корня в знаменателе.
Найдём сам угол:
Если посмотреть на чертёж, то результат вполне правдоподобен. Для проверки можно использовать Алгебраический Калькулятор (см. Приложения) или даже измерить угол транспортиром (у кого он есть). Только не повредите покрытие монитора =)
Ответ:
В ответе не забываем, что спрашивалось про угол треугольника (а не про угол между векторами), не забываем
указать точный ответ: и приближенное значение
угла: , найденное с помощью
калькулятора.
Задача 32
В пространстве задан треугольник координатами своих вершин , .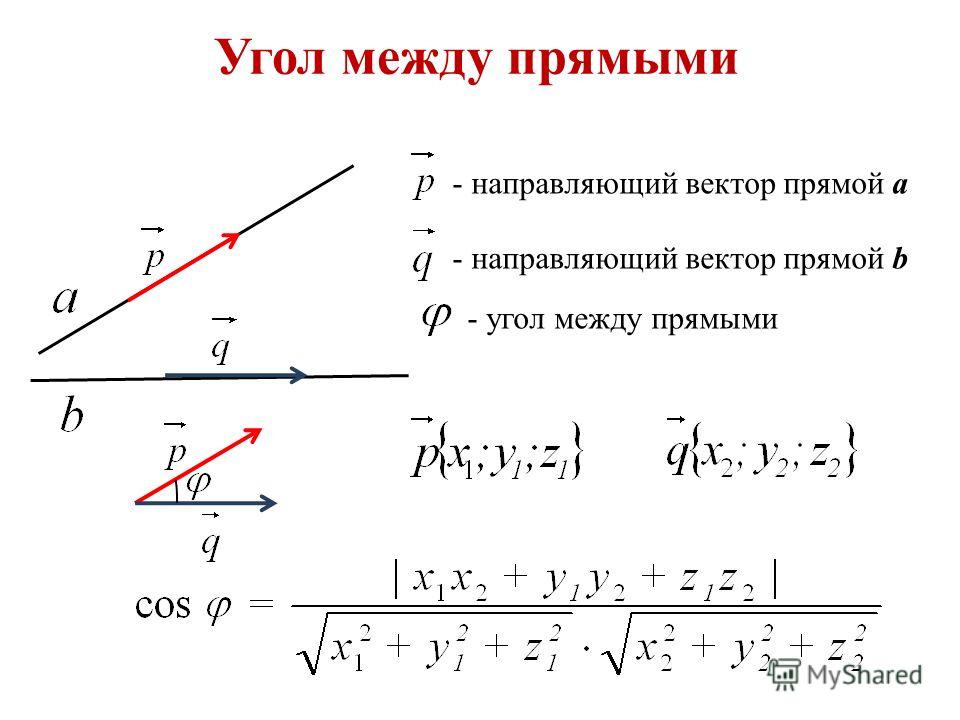
Найти угол между сторонами и
Это пример для самостоятельного решения, и, конечно же, задачка творческая, повторяем взаимосвязь между углом и знаком скалярного произведения:
Задача 33
При каком значении угол между векторами будет: а) острым, б) прямым, в) тупым?
Решение и ответ в конце книги.
Следующий небольшой параграф будет посвящен ортогональным проекциям векторов, в которых тоже «замешано» скалярное произведение:
1.7.1. Как найти проекцию вектора на вектор?
1.6.8. Если векторы заданы суммами векторов с известными координатами
| Оглавление |
Автор: Aлeксaндр Eмeлин
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |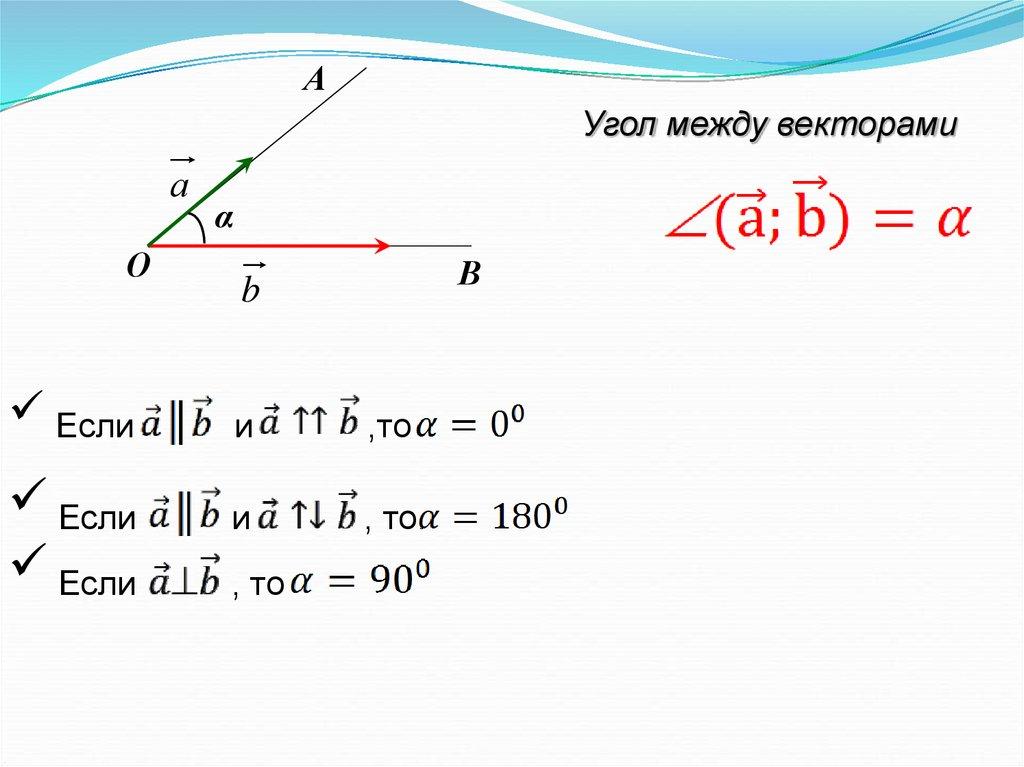
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | cos(30 град. ) | ||
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |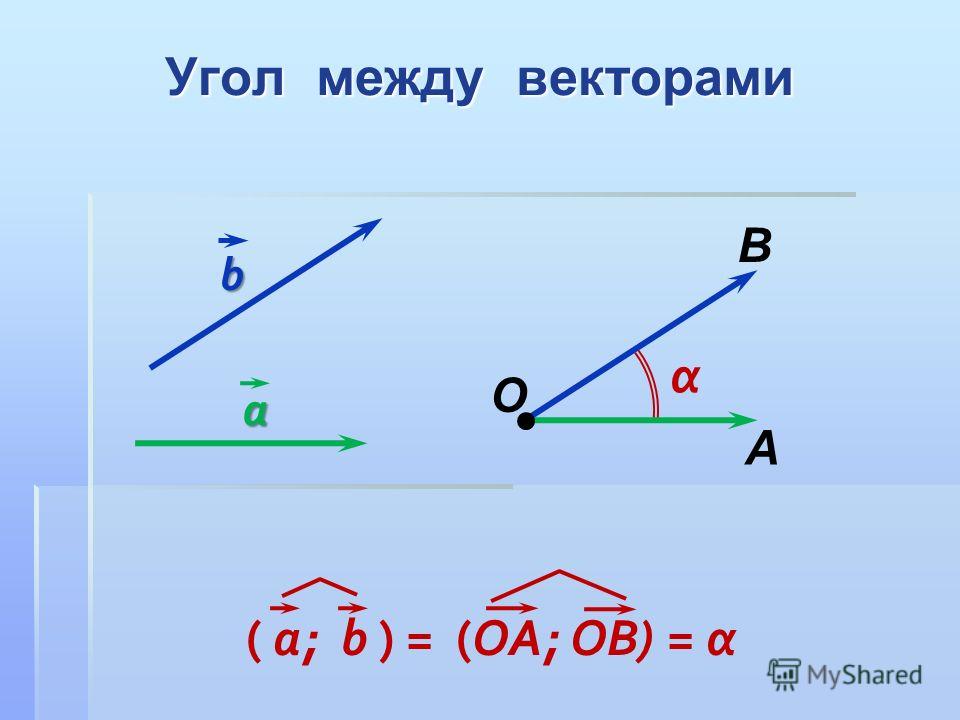
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |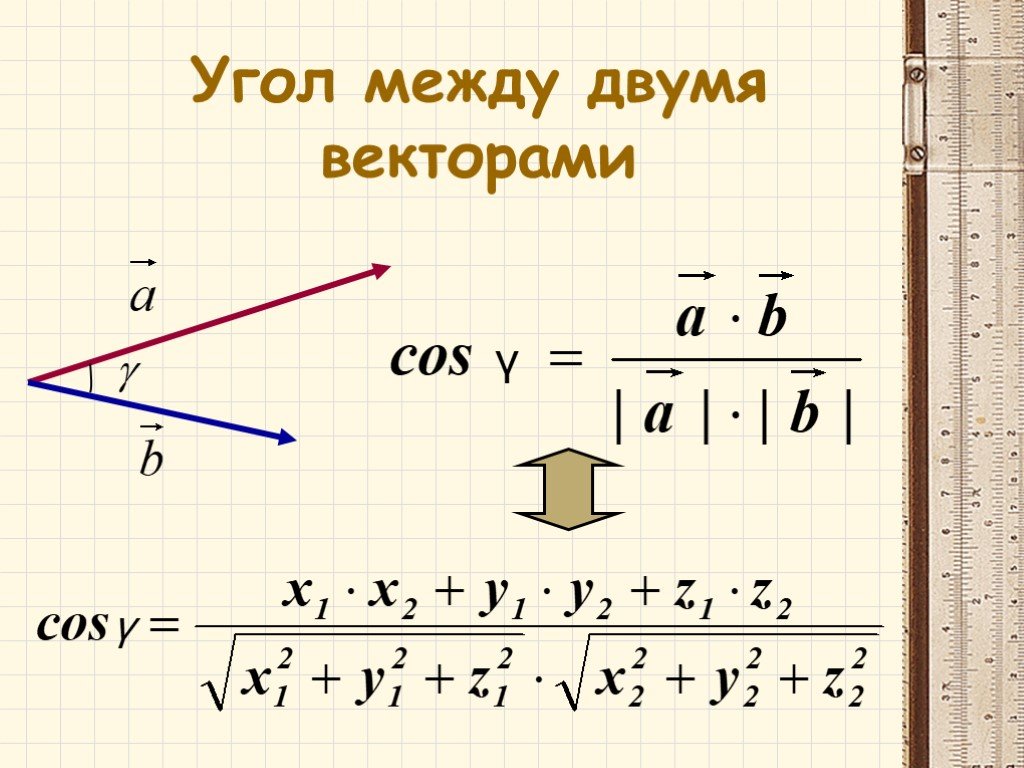
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |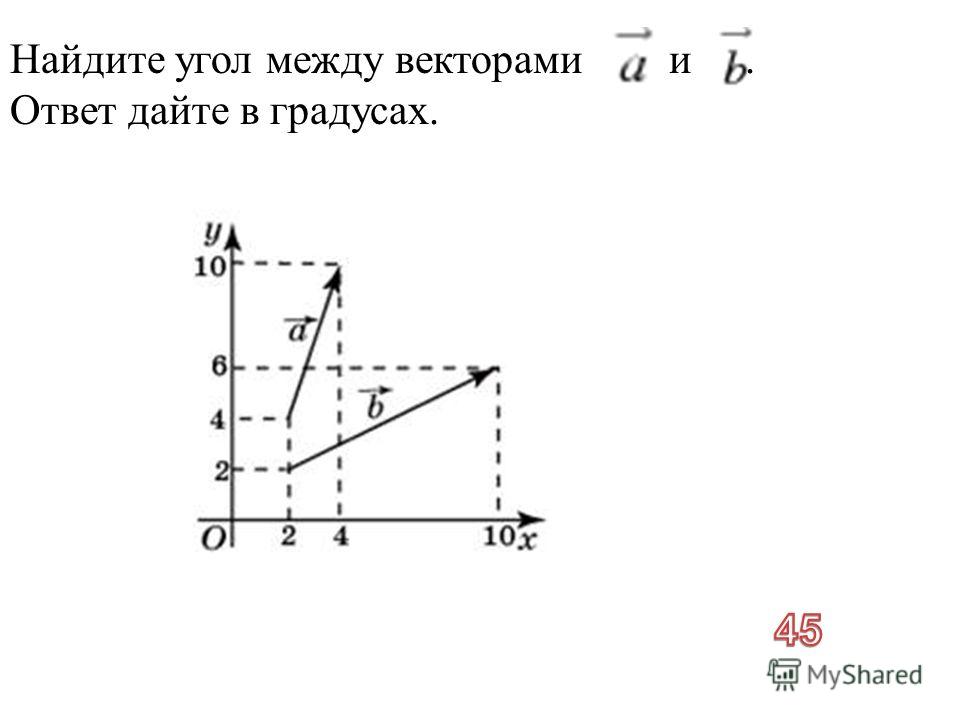
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Вопрос Видео: Нахождение угла между двумя заданными векторами
Стенограмма видео
Найдите угол 𝜃 между векторами 𝐕 пять, один, минус два и 𝐖 четыре, минус четыре, три. Дайте правильный ответ с точностью до двух знаков после запятой.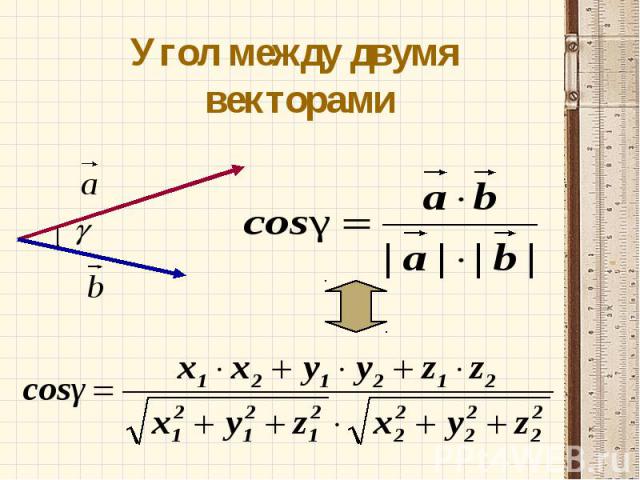
В этом вопросе нас просят определить угол 𝜃 между двумя векторами, вектором 𝐕 и вектором 𝐖, заданными в компонентной форме. Нам нужно указать наше значение 𝜃 с точностью до двух знаков после запятой. Чтобы помочь нам ответить на этот вопрос, стоит вспомнить, как мы находим угол между двумя векторами. Напомним, что если 𝜃 — это угол между двумя векторами 𝐀 и 𝐁, то косинус угла 𝜃 будет равен скалярному произведению векторов 𝐀 и 𝐁, деленному на величину вектора 𝐀, умноженную на величину вектора 𝐁. И стоит отметить, что то же самое верно и в обратном порядке. Если 𝜃 удовлетворяет этому уравнению, то можно сказать, что 𝜃 — это угол между векторами 𝐀 и 𝐁.
Однако по соглашению, когда мы говорим угол между двумя векторами, мы имеем в виду наименьший неотрицательный угол между этими двумя векторами. В этом случае мы можем найти это, взяв арккосинус обеих частей уравнения. На самом деле это означает, что для нахождения угла между двумя векторами нам нужно знать их скалярное произведение и величину двух векторов 𝐀 и 𝐁.
Следовательно, чтобы найти угол 𝜃 между нашими двумя векторами 𝐕 и 𝐖, нам нужно найти скалярное произведение между 𝐕 и 𝐖, величину вектора 𝐕 и величину вектора 𝐖. Начнем с нахождения скалярного произведения между вектором 𝐕 и вектором 𝐖.
Для этого нам нужно вспомнить, чтобы найти скалярное произведение между двумя векторами, нам нужно найти сумму произведений соответствующих компонентов двух векторов. В данном случае это пять, умноженное на четыре, плюс один, умноженный на минус четыре, плюс минус два, умноженный на три, и если мы оценим это выражение, мы получим, что оно равно 10. Далее нам нужно вычислить величину векторов 𝐕 и 𝐖 . Для этого напомним, что величина вектора равна квадратному корню из суммы квадратов его составляющих. Другими словами, величина вектора 𝑎, 𝑏, 𝑐 будет равна квадратному корню из 𝑎 в квадрате плюс 𝑏 в квадрате плюс 𝑐 в квадрате.
Мы можем использовать это, чтобы найти величину вектора 𝐕. Это величина вектора пять, один, минус два. Величина вектора 𝐕 будет квадратным корнем суммы квадратов его компонентов.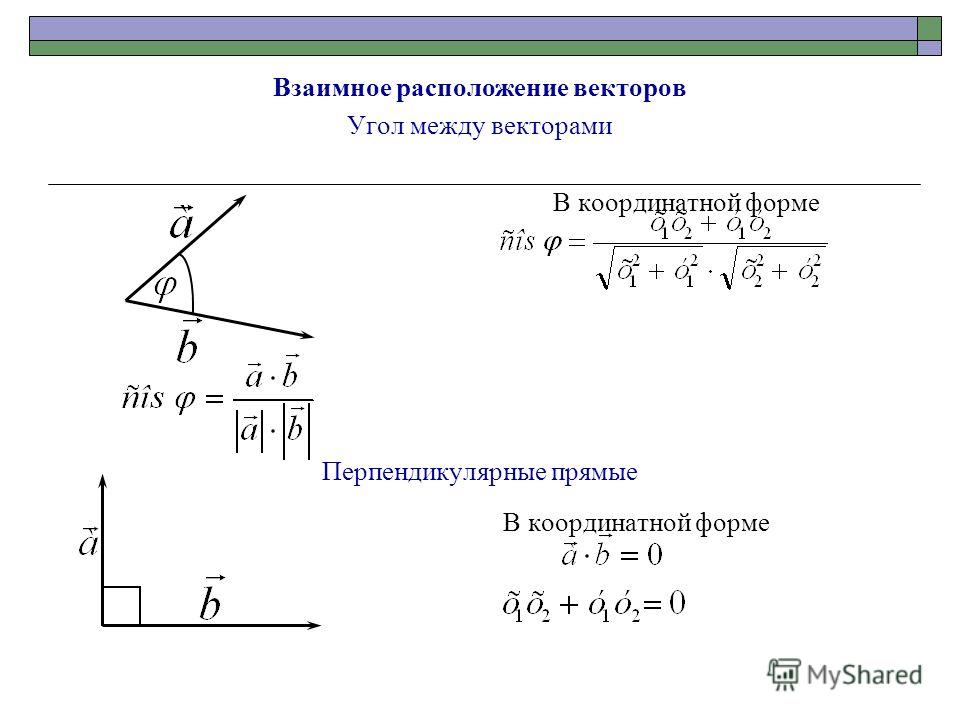
Величина 𝐕 представляет собой квадратный корень из пяти в квадрате плюс один в квадрате плюс минус два, все в квадрате, и если мы вычислим выражение внутри нашего символа квадратного корня, мы получим квадратный корень из 30. Затем мы можем сделать то же самое, чтобы найти величина вектора 𝐖. Оно равно квадратному корню из четырех в квадрате плюс отрицательные четыре в квадрате плюс три в квадрате, которые мы можем упростить, чтобы получить квадратный корень из 41. Теперь мы готовы найти выражение для нашего значения 𝜃.
Во-первых, мы знаем, что, поскольку 𝜃 — это угол между векторами 𝐕 и 𝐖, косинус 𝜃 будет равен скалярному произведению между вектором 𝐕 и вектором 𝐖, деленному на величину вектора 𝐕, умноженную на величину вектора 𝐖. Затем мы можем заменить найденные нами значения скалярного произведения между вектором 𝐕 и вектором 𝐖 и величиной вектора 𝐕 и вектора 𝐖. Мы получаем, что cos 𝜃 будет равен 10, деленному на корень 30, умноженный на корень 41. Затем мы можем найти значение 𝜃, взяв арккосинус обеих частей этого уравнения.
Помните, это даст нам наименьший неотрицательный угол между двумя векторами 𝐕 и 𝐖. Получаем, что 𝜃 будет равно обратному косинусу числа 10, деленному на корень 30, умноженному на корень 41.
Наконец, мы можем вычислить это значение в градусах. Мы получаем, что 𝜃 равно 73,433, и это продолжается в градусах. Но помните, вопрос требует, чтобы мы давали ответ с точностью до двух знаков после запятой. Для этого смотрим на третий десятичный знак, который равен трем. Поскольку это меньше пяти, это означает, что нам нужно округлить в меньшую сторону. И это дает нам окончательный ответ. Угол 𝜃 между вектором 𝐕 пять, один, минус два и вектором 𝐖 четыре, минус четыре, три до двух знаков после запятой составляет 73,43 градуса.
Найти угол между векторами a и b
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 467 раз
$\begingroup$
Если заданы векторы $\mathbf{a}$ и $\mathbf{b}$ и $|\mathbf{a}|=|\mathbf{b}| = 1$, найдите угол между $\mathbf{a}$ и $\mathbf{b}$ так, чтобы векторы $\mathbf{p}=\sqrt{3}\, \mathbf{a}-\mathbf{b }$ и $\mathbf{q}=-\mathbf{a}+\sqrt{3}\, \mathbf{b}$ перпендикулярны.