Найти вторую производную онлайн: Вторая и третья производные функции

(n-1)

Записаться на занятие к этому репетитору

Задайте свой вопрос!

Наши репетиторы максимально быстро дадут на него развёрнутый ответ. Это бесплатно!

Задать вопрос

Новые вопросы

Геометрия8 класс

27 сентября 2022

М

Матвей

Найдите основания прямоугольной трапеции с тупымуглом 120°, если ее меньшая диагональ и большая боковаясторона равны 10 см.

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

Вода в работающем электрическом чайнике получила в процессе теплообмена от горячей спирали чайника количество теплоты Q1=400 Дж и одновременно отдала окружающей среде количество теплоты Q2=100 Дж. Как изменилась за это время внутренняя энергия воды?

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

Внутренняя энергия тела равняется 1200 Дж. Тело отдало 400Дж тепла и совершило работу 300 Дж. Чему стала равна внутренняя энергия тела? Запишите первый закон термодинамики для этого случая с учётом правила знаков.

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

В комнате объёмом 75 м3 заполнена воздухом плотностью 𝜌 = 1,2 кг/м3, при этом среднее значение модуля скорости хаотического движения молекул 𝑣 = 500 м/с. Оцените значение внутренней энергии воздуха в комнате. Взаимодействием молекул воздуха друг с другом можно пренебречь. 

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

Водитель автомобиля, увидев препятствие на дороге, начал тормозить. На сколько изменилась внутренняя энергия автомобиля и дороги при торможении автомобиля до его полной остановки? Масса автомобиля m=2 т, его начальная скорость 𝑣 = 72 км/ч.

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

Определите какое количество теплоты получает газ, если еговнутренняя энергия увеличилась на 70 кДж. Работа в данномпроцессе не совершалась.

Ответ данЕлена Александровна

Предметы: Подготовка к ЕГЭ, Физика, Подготовка к ОГЭ

Физика8 класс

24 сентября 2022

М

Матвей

Металлический шар массой 𝑚 = 400 г падает на пол с высотыℎ = 2 м. Определите, на сколько изменится в процессе удара опол внутренняя энергия термодинамической системы,состоящей из шара и пола.

Ответ данДарья Александровна

Предметы: Химия

Биология11 класс

24 сентября 2022

У

Ученик

опишите пожалуйста взаимодействие нервной и мышечной ткани

Ответ данИрина Сергеевна

Предметы: Подготовка к ЕГЭ, Химия, Подготовка к ОГЭ, Биология

Алгебра11 класс

22 сентября 2022

У

Ученик

В стройотряде 70% первокурсников и 30% второкурсников. Среди первокурсников 10% девушек, среди второкурсников 5% девушек. Все студенты по очереди дежурят на кухне. Найти вероятность того, что в случайно выбранный день дежурит девушка. В случайно выбранный день дежурит девушка. Найти вероятность, что…

Ответ дан

Оксана Валентиновна

Алгебра9 класс

21 сентября 2022

У

Ученик

Как вычислить корень степени с нечетным показателем? Например, если показатель чëтный, то все делается очень просто: √9⁴=9^(1/2×4) =9²=81 А вот в случае с нечëтным показателем ничего не получается: √9³=9^(1/2×3)=9¹, 5=?  В общем, ерунда какая-то. Ответ — 27, но как его получить? 

Ответ данДарья Александровна

Предметы: Химия

Дифференцирование обобщённых функций : Анализ-II

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

DFooz	Дифференцирование обобщённых функций 16.10.2010, 01:05
15/03/07 35	Помогите пожалуйста с дифференцированием обоб. ф. Ответ По определению из Владимирова , где -классическая производная функции при , не определена в Как получают эту классическую производную? Для неё получается система В ответе Каким образом они получили это . Смотрели на график и пробовали подогнать с помощью ф-ии Хевисайда? Далее вторая производная: Но ведь по правилам классич дифференцирования вроде должно быть Куда дели ?

Alexey1	Re: Дифференцирование обобщённых функций 16.10.2010, 02:23
Заслуженный участник 08/09/07 841	Обобщённые функции дифференцируют следующим образом. Пусть , то есть тест функция со всеми непрерывными производными и с ограниченным носителем. Тогда производная обобщённой функции вычисляется по правилу: . С учётом того, что . Например, для производная равна . Отсюда получаем, что . В Вашем случае .

ewert	Re: Дифференцирование обобщённых функций 16.10.2010, 07:15
Заслуженный участник 11/05/08 32104	DFooz в сообщении #362632 писал(а): Куда дели ? А это превращается в парочку удвоенных дельта-функций. Другое дело, что неверно найдена самая первая производная (там дельта-функции должны идти с разными знаками).

DFooz	Re: Дифференцирование обобщённых функций 17.10.2010, 01:08
15/03/07 35	Спасибо за пояснения, начинаю понимать. Получается для первой произв. для второй? А куда делись? Я правильно понимаю, произведение ф-ии из или на дельта-фун. даёт дельта-фун.?

Alexey1	Re: Дифференцирование обобщённых функций 17.10.2010, 04:03
Заслуженный участник 08/09/07 841	Одним из свойств дельта-функции является . Что касается дифференцирования, то .

DFooz	Re: Дифференцирование обобщённых функций 17.10.2010, 16:46
15/03/07 35	спасибо

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 6 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

11.

Производные высших порядков. Формула Тейлора

Если функция имеет производную в каждой точке своей области определения, то ее производная есть функция от . Функция , в свою очередь, может иметь производную, которую называют производной второго порядка функции (или второй производной) и обозначают символом . Таким образом

Пример

Задание. Найти вторую производную функции 

Решение. Для начала найдем первую производную:

Для нахождения второй производной продифференцируем выражение для первой производной еще раз:

Ответ. 

Больше примеров решенийРешение производных онлайн

Производные более высоких порядков определяются аналогично. То есть производная -го порядка функции есть первая производная от производной -го порядка этой функции:

Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.

Формула Тейлора

, где R_n(x) — остаточный член формулы Тейлора.

Остаточный член формулы Тейлора

В форме Лагранжа:

В форме Коши:

12.Неопределенный и определенный интегралы

Неопределённый интеграл.

Определение. Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b) (конечном или бесконечном), если в каждой точке этого интервала f(x) является производной дляF(x), т.е. . Из этого определения следует, что задача нахождения первообразной обратна задаче дифференцирования: по заданной функции f(x ) требуется найти функцию F(x), производная которой равна f(x). Первообразная определена неоднозначно: для функции первообразными будут и функция arctg x, и функция arctg x-10: . Для того, чтобы описать все множество первообразных функции f(x), рассмотрим Свойства первообразной.

1. Если функция F(x) — первообразная для функции f(x) на интервале X, то функция f(x) + C, где C — произвольная постоянная, тоже будет первообразной для f(x) на этом интервале. (Док-во: ).

2. Если функция F(x) — некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C — постоянная на X функция.

Из этих свойств следует, что если F(x) — некоторая первообразная функции f(x) на интервале X, то всё множество первообразных функции f(x) (т.е. функций, имеющих производную f(x) и дифференциал f(x) dx) на этом интервале описывается выражением F(x) + C, где C — произвольная постоянная.

Неопределённый интеграл и его свойства. Определение. Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом . Как следует из изложенного выше, если F(x) — некоторая первообразная функции f(x), то , где C — произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx — подынтегральным выражением. Свойства неопределённого интеграла, непосредственно следующие из определения:

1. .

2.  (или ).

Таблица неопределённых интегралов.

1	.	11	.
2	.	12	.
3	().	13	.
4	.	14	.
5	; .	15	.
6	.	16
7	.	17	.
8	.	18	.
9	.	19	.
10	.	20	; .

В формулах 14, 15, 16, 19 предполагается, что a>0. Каждая из формул таблицы справедлива на любом интервале, на котором непрерывна подынтегральная функция. Все эти формулы можно доказать дифференцированием правой части. Докажем, например, формулу 4: если x > 0, то ; если x < 0, то . Простейшие правила интегрирования.

1.  ()

Решение высшей математики онлайн

‹— Назад

В предыдущих примерах мы видели, что хотя необходимое условие не гарантировало наличие экстремума в критической точке, мы смогли исследовать поведение функции в окрестности этой точки и выяснить, имеется ли в ней экстремум и если да, то какого рода. Однако для выяснения этого нам пришлось иной раз прибегать к искусственным преобразованиям функции, которые во общем случае могут быть не очевидны или затруднительны. В данном разделе мы рассмотрим несколько общих теорем, позволяющих исследовать поведение функции в критической точке.

        Теорема 7.5   Пусть  — критическая точка функции . Если функция не убывает в некоторой левой окрестности точки и не возрастает в некоторой её правой окрестности , то точка  — точка локального максимума.

Если же функция не возрастает в некоторой левой окрестности и не убывает в некоторой правой окрестности , то точка  — точка локального минимума.

        Доказательство.     Если не убывает в , то при всех , поскольку из непрерывности . Точно так же, при всех . Выберем из чисел и наименьшее: и рассмотрим симметричную окрестность . При , очевидно, , то есть  — точка локального максимума.

Вторая половина утверждения теоремы сводится к первой, если положить и заметить, что функция не убывает в и не возрастает в ; локальный максимум функции соответствует локальному минимуму функции .     

        Замечание 7.4   Найденное достаточное условие локального экстремума гарантирует наличие экстремума в точке . Однако оно не является необходимым: можно найти такую функцию , которая имеет экстремум (например, минимум) в некоторой точке , однако не монотонна ни в какой левой окрестности и ни в какой правой окрестности этой точки. Примером может служить функция

График этой функции зажат между двумя параболами и и в окрестности точки 0 имеет бесконечно много промежутков монотонности, разделённых стационарными точками, так что не монотонна ни на каком интервале вида или . В точке 0 функция непрерывна (по теореме «о двух милиционерах») и имеет минимум, так как при всех .

Заметим кстати, что производная этой функции равна

Эта производная имеет в точке разрыв второго рода.     

        Теорема 7.6   Пусть  — критическая точка функции , и у этой функции существует производная в некоторой проколотой окрестности . Если при этом в левой окрестности имеет место неравенство , а в правой окрестности  — неравенство , то точка  — точка локального максимума; если же в левой окрестности выполнено неравенство , а в правой окрестности — неравенство , то точка  — точка локального минимума. Наконец, если производная в левой и в правой окрестности имеет один и тот же знак, то точка не является точкой локального экстремума.

        Доказательство.     Доказательство первых двух утверждений теоремы сразу же следует из предыдущей теоремы и теоремы 7.2 о связи знака производной с возрастанием и убыванием функции: из неравенства следует неубывание функции , а из неравенства  — её невозрастание. Последнее утверждение теоремы также очевидно.     

Рис.7.25.Связь смены знака производной с локальными экстремумами

Доказанную теорему можно сформулировать следующим образом:

если производная меняет знак с на при переходе через критическую точку , то в этой точке — локальный максимум функции ; если знак производной меняется с на , то в точке  — локальный минимум; если же знак производной при переходе через не изменяется, то локального экстремума в точке функция не имеет.

Следующая теорема позволяет обойтись для обнаружения экстремума исследованием функции только в точке (а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной.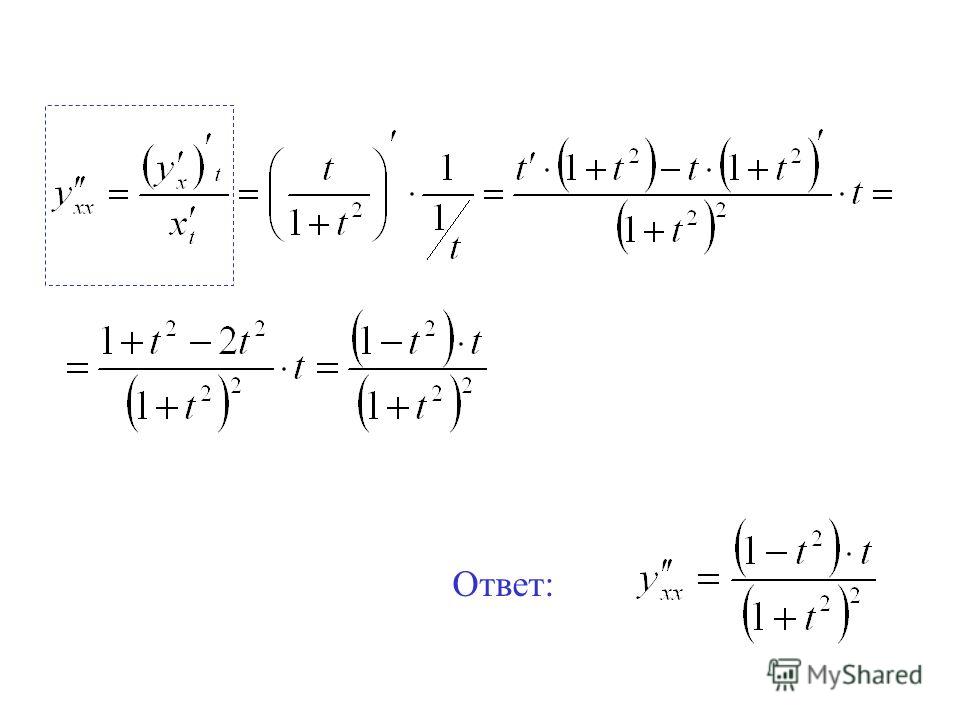

        Теорема 7.7   Пусть  — стационарная точка функции , и в этой точке существует вторая производная , причём . Тогда при точка есть точка локального максимума, а при  — локального минимума.

        Доказательство.     Поскольку , то по определению производной

Пусть . Тогда из существования предела следует, что для любого из некоторой достаточно малой проколотой окрестности точки выполняется то же неравенство для допредельного выражения, то есть

при . Поскольку, по предположению теоремы,  — стационарная точка, то , откуда , то есть имеет знак, противоположный знаку : при и при . Остаётся лишь применить теперь предыдущую теорему, из которой следует, что  — точка локального максимума.

Доказательство для случая совершенно аналогично.     

        Пример 7.24   Рассмотрим функцию . Её производная равна ; решая уравнение , находим стационарные точки функции : это . Чтобы определить поведение функции в этих стационарных точках, найдём вторую производную и выясним, какой она имеет знак в каждой из этих трёх точек. Имеем: . Отсюда , следовательно, в точке функция имеет локальный минимум; то же в точке , поскольку также равняется 8. В каждой из этих двух точек значение функции равно .

В точке получаем , поэтому в точке 0 функция имеет локальный максимум. Значение в этой точке равно 0.     

Рис.7.26. Три локальных экстремума функции

        Замечание 7.5   В последней теореме ничего не говорится о том, что происходит в стационарной точке в случае, когда . В этом случае в точке может быть как локальный экстремум (возможен и максимум, и минимум), так и не быть экстремума. В этом нас убеждают следующие три примера.     

        Пример 7.25   Функция имеет единственную стационарную точку . Вторая производная принимает в этой точке значение 0, сама же функция не имеет экстремума в точке 0.     

Рис.7.27.Функция не имеет экстремума в стационарной точке 0

        Пример 7.26   Функция также имеет единственную стационарную точку . Вторая производная принимает в этой точке значение 0, сама же функция имеет в точке 0 минимум.     

Рис. 7.28.Функция имеет минимум в стационарной точке 0, в которой

        Пример 7.27   Функция также имеет единственную стационарную точку . Её вторая производная принимает в стационарной точке значение 0, а сама функция имеет в этой точке максимум.     

Рис.7.29.Функция имеет максимум в стационарной точке 0, в которой

Для того, чтобы разобраться в поведении функции в такой стационарной точке , в которой , можно применить такую теорему:

        Теорема 7.8   Пусть функция имеет -ю производную в некоторой окрестности точки и эта производная непрерывна в точке . Предположим, что

Тогда, если число  — нечётное, то в точке функция не имеет локального экстремума; если же число  — чётное, то при в точке функция имеет локальный максимум, а при  — локальный минимум.

        Доказательство.     Для доказательства заметим, что если разложить по формуле Тейлора в точке с остаточным членом в форме Лагранжа, то получим

(где лежит между и ), поскольку слагаемые со степенями бинома , меньшими , имеют, по предположению, нулевые коэффициенты. Следовательно, приращение функции можно представить в виде

Поскольку и непрерывна в точке , то в некоторой окрестности точки она сохраняет тот же знак, что у числа , в частности, знак числа при , близких к , — тот же, что у числа .

Мы видим, что при нечётном приращение меняет знак при переходе через точку , поскольку меняет знак множитель в правой части. Значит, в этом случае локального экстремума в точке нет.

При чётном этот множитель положителен при всех , следовательно, приращение (при малых ) имеет тот же знак, что и : при (неравенство означает, что  — точка локального максимума) и при (неравенство означает, что  — точка локального минимума).     

        Замечание 7.6   Даже в этом усиленном виде ( теорема 7.8) достаточный признак экстремума, связанный со значениями производных высших порядков, не всегда отвечает на вопрос о том, есть ли локальный экстремум в стационарной точке. Дело в том, что, как мы видели выше, существуют такие функции, у которых все производные в некоторой точке обращаются в 0, и тем не менее функция отлична от 0 всюду, кроме этой точки. Примером может служить функция, которую мы рассматривали в главе 6 (замечание 6.2):

Эта функция имеет стационарную точку , характер которой нельзя распознать, применив теорему 7. 8, поскольку при всех . Однако очевидно, что при всех , так что  — точка минимума функции .

Кроме того, заметим, что может быть не выполнено предположение о непрерывности производной -го порядка в точке , даже если эта производная существует при всех . В качестве примера рассмотрите самостоятельно функцию

Эта функция имеет минимум (равный 0) в точке . Производная этой функции существует при всех и равна

Найдите и исследуйте вторую производную этой функции.     

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Калькулятор онлайн.

Найти (с решением) производную функции. Правила вычисления производных

Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$

Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) . 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.

Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .

Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.

Правила дифференцирования

Операция нахождения производной называется дифференцированием . При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. 2} $$

Представлено доказательство и вывод формулы для производной синуса — sin(x). Примеры вычисления производных от sin 2x, синуса в квадрате и кубе. Вывод формулы для производной синуса n-го порядка.

Производная по переменной x от синуса x равна косинусу x:
(sin x)′ = cos x .

Доказательство

Для вывода формулы производной синуса, мы воспользуемся определением производной:
.

Чтобы найти этот предел, нам нужно преобразовать выражение таким образом, чтобы свести его к известным законам, свойствам и правилам. Для этого нам нужно знать четыре свойства.
1) Значение первого замечательного предела:
(1) ;
2) Непрерывность функции косинус:
(2) ;
3) Тригонометрические формулы . Нам понадобится следующая формула:
(3) ;
4) Свойство пределов:
Если и , то
(4) .

Применяем эти правила к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(3) .
В нашем случае
; . Тогда
;
;
;
.

Теперь сделаем подстановку . При , . Применим первый замечательный предел (1):
.

Сделаем такую же подстановку и используем свойство непрерывности (2):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Формула производной синуса доказана.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих синус. Мы найдем производные от следующих функций:
y = sin 2x; y = sin 2 x и y = sin 3 x .

Пример 1

Найти производную от sin 2x .

Решение

Сначала найдем производную от самой простой части:
(2x)′ = 2(x)′ = 2 · 1 = 2.
Применяем .
.
Здесь .

Ответ

(sin 2x)′ = 2 cos 2x.

Пример 2

Найти производную от синуса в квадрате:
y = sin 2 x .

Решение

Перепишем исходную функцию в более понятном виде:
.
Найдем производную от самой простой части:
.
Применяем формулу производной сложной функции.

.
Здесь .

Можно применить одну из формул тригонометрии. Тогда
.

Ответ

Пример 3

Найти производную от синуса в кубе:
y = sin 3 x .

Производные высших порядков

Заметим, что производную от sin x первого порядка можно выразить через синус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции :

.
Здесь .

Теперь мы можем заметить, что дифференцирование sin x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5) .

Докажем это, применяя метод математической индукции.

Мы уже проверили, что при , формула (5) справедлива.

Предположим, что формула (5) справедлива при некотором значении . Докажем, что из этого следует, что формула (5) выполняется для .

Выпишем формулу (5) при :
.
Дифференцируем это уравнение, применяя правило дифференцирования сложной функции:

.
Здесь .
Итак, мы нашли:
.
Если подставить , то эта формула примет вид (5).

Формула доказана.

Производная Несмотря на то, что в предыдущих параграфах были рассмотрены два различных примера, между ними есть нечто общее. Для того чтобы это выяснить, нужно стать на функциональную точку зрения. Пусть дана функция y=f(x). Чтобы получить задачу о скорости, будем считать, что независимое переменное х есть время, а у- расстояние точки, движущейся по прямой, от начала координат. Уравне- у ние y-f(x) в этом случае называется законом движения. Чтобы получить задачу о касательной, будем счи- в Рис. 47. тать, что х-абсцисса и у — ордината точки, лежащей на кривой линии, определяемой уравнением у = /(х). Будем производить над функцией у = /(х) некоторые операции и одновременно выяснять, что эти операции означают в задаче о скорости и в задаче о касательной. 1. Дадим х определенное числовое значение и вычислим соответствующее значение У» fix). (1) В задаче о скорости это значит, что для определенного момента времени х мы нашли расстояние у движущейся точки от начала координат (рис, 47). В задаче о касательной это означает, что мы определили координаты точки Р, лежащей на кривой, определенной уравнением у=/(х) (рис. 48). 2. Дадим х приращение h и вычислим соответствующее приращенное значение уу которое отличается от первоначального на величину А у (приращение функции) (см. гл. V, § 4): у + Ьy=f(x+h). В задаче о скорости тем самым мы определяли положение Р, движущейся точки в момент времени x + h* В задаче о касательной получена новая точка М. Здесь АВ= PQ= h, OB = x + h, BM = f(x + h). 3. Найдем приращение функции Ду; для этого вычтем почленно из равенства (2) равенство (1): + h)-f»=/(*) + Ф»(*), (IV) т. е. производная суммы двух функций равна сумме их производных. V. Производная произведения двух функций. Предположим, что нам известны производные функций f{x) и представим ее в виде цепочки функций (см. гл. V, § 3): Рассмотрим уравнения (*) и (#*) независимо друг от друга. 1. Представим функцию у в виде цепочки: и-хг + 1, у~еа. Так как (х8 + 1)»= Зх2, (то » = = —

Калькулятор второй производной с шагами, формулой и решением

Калькулятор второй производной

Определение скорости изменения функции с точки зрения ее переменных определяется как производная. Калькулятор второй производной с шагами — это бесплатный онлайн-инструмент, который вычисляет производную функции второго порядка. Калькулятор второй производной поможет вам быстро и точно вычислить вторую производную.

Производные имеют дело с такими переменными, как x и y, функциями, такими как f(x), и изменениями переменных x и y. Производная функции обозначается символом f'(x). Это означает, что функция является производной по у по х. Дифференциалы имеют символы dy и dx. Вторая производная также известна как двойное дифференцирование, потому что это производная от производной функции.

Как пользоваться калькулятором второй производной?

Выполните следующие простые шаги, чтобы использовать калькулятор производной второго порядка:

Шаг 1: В заданном поле ввода введите функцию. {(\frac{1}{3})} \right) \;=\; \left[ — \frac{2}{9{\frac{5}{3}}} \right] $$

Связанные :Вы также можете вычислить частную производную по одной переменной, сделав другую переменную постоянной в уравнении второй производной. Для этого используйте калькулятор первой частной производной. Пользователю нужно только ввести функцию, переменную для дифференциации для расчета. Частная производная будет отображаться как результат автоматически.

Часто задаваемые вопросы:

Что такое производная второго порядка?

Производная первой производной данной функции является производной второго порядка. Кривизну или вогнутость графика обычно представляют второй производной функции. График функции вогнут вверх, если значение производной второго порядка положительно.

Каковы преимущества онлайн-калькулятора второй производной?

Этот калькулятор производных высших порядков экономит ваше время и усилия. Вы должны поставить только свои уравнения, и результат будет показан в секундах. Он также отображает все пошаговые расчеты конкретной функции.

В чем разница между дифференциальными уравнениями первого порядка и дифференциальными уравнениями второго порядка?

Решение разностного уравнения второго порядка можно найти тем же методом, что и разностную задачу первого порядка. Единственное отличие состоит в том, что нам нужны значения x для двух значений t вместо одного, чтобы начать процесс с уравнения второго порядка.

О чем говорит двойная производная?

Вторая производная функции измеряет мгновенную скорость изменения ее первой производной, которая уже вычислена. Знак второй производной также говорит вам, увеличивается или уменьшается наклон касательной.

Для измерения наклона касательной калькулятор двойной производной является одним из бесплатных и точных ресурсов.

Что такое тест второй производной?

Второй тест производной включает вычисление производной функции два раза. Это способ вычисления абсолютного максимума и минимального значения функции с действительным знаком, которая определена на замкнутом или ограниченном интервале. Калькулятор теста второй производной расскажет нам, как увеличивается или уменьшается мгновенная скорость изменения на граничном интервале. 9{3x} \; грех⁡2x $$

Таким образом, вы можете вычислить двойную производную функции этого типа. Кроме того, калькулятор двойного дифференцирования также предоставляет этот тип подробных результатов со всеми возможными шагами.

Как найти вторую производную функции?

Вторую производную функции можно вычислить вручную, выполнив следующие шаги. Однако вы также можете найти калькулятор второй производной для этой цели.

1. Найдите первую производную данной функции и при необходимости упростите ее.
2. Снова примените производную к первой производной функции.
3. Упростите решение, чтобы получить точное значение второй производной.

Онлайн-калькулятор деривативов предоставляет все онлайн-инструменты, связанные с деривацией. Например, калькулятор неявной производной и калькулятор дифференцирования по направлениям бесплатно.

Алан Уокер

Последнее обновление 20 сентября, 2022

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Калькулятор производных с шагами | Калькулятор дифференцирования

Определение калькулятора производных с шагами

В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания.

Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши.

Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию.

Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами.

Формулы, используемые калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$ 9{n-1} $$

Постоянное множественное правило:

$$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

Здесь c = реальное число

Правило суммы и разности:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d}{dx}g(x) $$

Правило продукта:

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{d }{dx}[f(x)] $$

или

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференциации позволяет пользователям вводить данные в виде уравнения.

Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами.

Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты.

Как найти калькулятор производных?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

1. Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
2. Выберите переменную, которую вы хотите дифференцировать.
3. Выберите, сколько раз вы хотите различать.
4. Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для закрепления ваших расчетов относительно нормальной линии уравнения, вам нужно попробовать уравнение нормальной прямой калькулятор, предлагаемый этим сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

• Калькулятор производной в точке
• Калькулятор n-ой производной
• Калькулятор крайних точек
• Калькулятор уклона криволинейной линии
• Калькулятор производных графиков

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5,4x+2,4 $$

Дифференцирование с обеих сторон по «х»

$$f'(x) \;=\; д/дх(5,4х+2,4)$$

У нас есть,

$$ f'(x) \;=\; д/дх(5,4х)+д/дх(2,4) $$ $$ f'(x) \;=\; 5. 4(1)+0 \;=\; 5,4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

1. Помните, что производная – это вычисление скорости изменения функции.
2. Применить производную к функции по независимой переменной, входящей в функцию.
3. Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x ?

Поскольку производная экспоненциальной функции с основанием «e» равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (e ^х ) = е ^х .

Это может оцениваться в дифференцирующем решателе для перекрестной проверки ответа и его шагов онлайн.

Алан Уокер

Последнее обновление 19 сентября, 2022

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Калькулятор производных с шагами | Дифференциальный калькулятор

Определение калькулятора производных с шагами

В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания.

Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши.

Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию.

Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами.

Формулы, используемые калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$ 9{n-1} $$

Постоянное множественное правило:

$$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

Здесь c = реальное число

Правило суммы и разности:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d}{dx}g(x) $$

Правило продукта:

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{d }{dx}[f(x)] $$

или

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференциации позволяет пользователям вводить данные в виде уравнения.

Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами.

Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты.

Как найти калькулятор производных?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

1. Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
2. Выберите переменную, которую вы хотите дифференцировать.
3. Выберите, сколько раз вы хотите различать.
4. Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для закрепления ваших расчетов относительно нормальной линии уравнения, вам нужно попробовать уравнение нормальной прямой калькулятор, предлагаемый этим сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

• Калькулятор производной в точке
• Калькулятор n-ой производной
• Калькулятор крайних точек
• Калькулятор уклона криволинейной линии
• Калькулятор производных графиков

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5,4x+2,4 $$

Дифференцирование с обеих сторон по «х»

$$f'(x) \;=\; д/дх(5,4х+2,4)$$

У нас есть,

$$ f'(x) \;=\; д/дх(5,4х)+д/дх(2,4) $$ $$ f'(x) \;=\; 5. 4(1)+0 \;=\; 5,4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

1. Помните, что производная – это вычисление скорости изменения функции.
2. Применить производную к функции по независимой переменной, входящей в функцию.
3. Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x ?

Поскольку производная экспоненциальной функции с основанием «e» равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (e ^х ) = е ^х .

Это может оцениваться в дифференцирующем решателе для перекрестной проверки ответа и его шагов онлайн.

Алан Уокер

Последнее обновление 19 сентября, 2022

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Калькулятор производных с шагами | Дифференциальный калькулятор

Определение калькулятора производных с шагами

В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания.

Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши.

Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию.

Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами.

Формулы, используемые калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$ 9{n-1} $$

Постоянное множественное правило:

$$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

Здесь c = реальное число

Правило суммы и разности:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d}{dx}g(x) $$

Правило продукта:

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{d }{dx}[f(x)] $$

или

$$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференциации позволяет пользователям вводить данные в виде уравнения.

Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами.

Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты.

Как найти калькулятор производных?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

1. Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
2. Выберите переменную, которую вы хотите дифференцировать.
3. Выберите, сколько раз вы хотите различать.
4. Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для закрепления ваших расчетов относительно нормальной линии уравнения, вам нужно попробовать уравнение нормальной прямой калькулятор, предлагаемый этим сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

• Калькулятор производной в точке
• Калькулятор n-ой производной
• Калькулятор крайних точек
• Калькулятор уклона криволинейной линии
• Калькулятор производных графиков

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5,4x+2,4 $$

Дифференцирование с обеих сторон по «х»

$$f'(x) \;=\; д/дх(5,4х+2,4)$$

У нас есть,

$$ f'(x) \;=\; д/дх(5,4х)+д/дх(2,4) $$ $$ f'(x) \;=\; 5. 4(1)+0 \;=\; 5,4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

1. Помните, что производная – это вычисление скорости изменения функции.
2. Применить производную к функции по независимой переменной, входящей в функцию.
3. Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x ?

Поскольку производная экспоненциальной функции с основанием «e» равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x. Математически это записывается как d/dx (e ^х ) = е ^х .

Это может оцениваться в дифференцирующем решателе для перекрестной проверки ответа и его шагов онлайн.

Алан Уокер

Последнее обновление 19 сентября, 2022

Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу.

Касательные линии

Касательные линии

Производная параметрического уравнения

Предположим, что

х = х(т) и     г = у(т) 

тогда пока dx/dt отлично от нуля

Пример:  

Найти dy/dx для 

х(т)  = 2 стоимость t     и     y(t) =  2 sin t

Решение:

У нас есть

дх/дт = -2 sin t     и     dy/dt = 2 стоимость т

отсюда

dy             dy / дт
=                     
дх дх/дт

2 стоимость т
знак равно = -кроватка т
-2 грех т

---

Вторая производная параметрического уравнения

Чтобы вычислить вторую производную, мы дважды используем цепное правило.

Следовательно, чтобы найти вторую производную, мы находим производную по к t первой производной, а затем разделить на производную от х с уважение к т.

Пример

Пусть

х(т) = т ³ у(т) = т ⁴  

затем

dy             4 т ³ 4
знак равно =          t
дх 3t ²            3

Отсюда       

д ² г д/дт (4/3 т) 4/3             4
знак равно знак равно =            
дх ² дх/дт 3т ² 9t ²

---

Длина дуги

Мы можем найти длину дуги кривой, разрезав ее на крошечные части и суммируя длину каждой из частей. Если кусочки маленькие и кривая дифференцируема, то каждый кусок будет примерно линейный.

Мы можем использовать формулу расстояния, чтобы найти длину каждого шт

Умножение и деление на D дает

Складывая все длины и принимая предел как Dt приближение к 0 дает формулу

Пример

Найдите длину дуги кривой, заданной параметрически с помощью

х(т) = т ² + 4т, у (т) = 1 — t ² ,     0 < t < 2

Раствор

Рассчитываем

х ‘  =  2t + 4, у ‘  =  -2t

Отсюда

Интеграл этого

Это довольно сложно (но не невозможно) сделать вручную. Либо вручную, либо на компьютере получаем

12,74

---

Площадь вращения

Если мы вращаем кривую вокруг оси x, какова площадь поверхности область, которая образуется? Если мы разрежем кривую на маленькие кусочки, то каждый кусок приблизительно представляет собой отрезок прямой, который при вращении вокруг оси X будет иметь площадь

2р (радиус) (длина)  =  2p y(t) Дт

Точно так же, если часть кривой вращается вокруг оси Y, то результирующая поверхность составляет

2р (радиус) (длина)  =  2p x (t) Дт

Складывая все части и принимая предел как Dt приближается к 0 дает

Определение площади поверхности

Пример

Установите интеграл, который дает площадь поверхности твердого тела, образованного вращающаяся кривая

х(т) = т ² ,    y(t) = t ³

Об оси Y

Решение

Вычисляем

х’ = 2т,    у’ = 3т ²

Формула дает

---

---

Назад на страницу полярных и параметрических уравнений

Назад на домашнюю страницу Math 107

Назад на домашнюю страницу математического факультета

электронная почта Вопросы и предложения

Исчисление I.

Форма графика, часть II

Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Форма графика, часть II

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-6: Форма графика, часть II

В предыдущем разделе мы видели, как можно использовать первую производную функции, чтобы получить некоторую информацию о графике функции. В этом разделе мы рассмотрим информацию, которую вторая производная функции может дать нам о графике функции.

Прежде чем мы это сделаем, нам понадобится пара определений. Основная концепция, которую мы будем обсуждать в этом разделе, — вогнутость. Вогнутость легче всего увидеть на графике (чуть позже мы дадим математическое определение).

Итак, функция вогнута вверх , если она «открывается» вверх, и функция вогнута вниз , если она «открывается» вниз. Заметьте также, что вогнутость не имеет ничего общего с увеличением или уменьшением. Функция может быть вогнутой и либо возрастающей, либо убывающей. Точно так же функция может быть вогнутой вниз и либо возрастающей, либо убывающей.

Вероятно, это не лучший способ определить вогнутость, указав, каким образом она «открывается», поскольку это несколько расплывчатое определение. Вот математическое определение вогнутости.

Определение 1

Если задана функция \(f\left( x \right)\), то

1. \(f\left( x \right)\) равно вогнутой вверх на интервале \(I\) если все касательные к кривой на \(I\) находятся ниже графика \(f\left( x \right)\).
2. \(f\left( x \right)\) равно вогнутой вниз на отрезке \(I\), если все касательные к кривой на \(I\) находятся над графиком \(f\left ( х \справа)\).

Чтобы показать, что приведенные выше графики действительно имеют заявленную выше вогнутость, вот снова график (немного увеличенный, чтобы было понятнее).

Итак, как вы можете видеть, на двух верхних графиках все нарисованные касательные линии находятся под графиком функции и вогнуты вверх. На двух нижних графиках все касательные находятся над графиком функции и вогнуты вниз.

Опять же, обратите внимание, что вогнутость и аспект возрастания/убывания функции полностью разделены и не имеют ничего общего друг с другом. Это важно отметить, потому что учащиеся часто смешивают эти два понятия и используют информацию об одном для получения информации о другом.

Есть еще одно определение, от которого нам нужно избавиться.

Определение 2

Точка \(x = c\) называется точкой перегиба , если функция в этой точке непрерывна и вогнутость графика изменяется в этой точке.

Теперь, когда у нас есть все определения вогнутости, нам нужно добавить вторую производную. В конце концов, мы начали этот раздел с того, что собираемся использовать вторую производную для получения информации о графике. Следующий факт связывает вторую производную функции с ее вогнутостью. Доказательство этого факта находится в разделе «Доказательства производных приложений» главы «Дополнительно».

Факт

Учитывая функцию \(f\left( x \right)\), то

1. Если \(f»\left( x \right) > 0\) для всех \(x\) в некоторый интервал \(I\), тогда \(f\left( x \right)\) вогнут вверх на \(I\).
2. Если \(f»\left( x \right) < 0\) для всех \(x\) в некотором интервале \(I\), то \(f\left( x \right)\) вогнуто вниз на \(Я\).

Итак, этот факт говорит нам о том, что точками перегиба будут все точки, где вторая производная меняет знак. В предыдущей главе мы видели, что функция может менять знак, если она либо равна нулю, либо не существует. Обратите внимание, что в предыдущем разделе мы работали с первой производной, но тот факт, что функция, которая может менять знак там, где она равна нулю или не существует, не имеет ничего общего с первой производной. Это просто факт, который применим ко всем функциям, независимо от того, являются ли они производными или нет.

Это, в свою очередь, говорит нам о том, что список возможных точек перегиба будет состоять из тех точек, где вторая производная равна нулю или не существует, поскольку это единственные точки, где вторая производная может изменить знак.

Будьте осторожны, однако не делайте предположения, что только потому, что вторая производная равна нулю или не существует, точка будет точкой перегиба. 3} + 3\] 92} — 1} \справа)\конец{выравнивание*}\]

Давайте начнем с увеличения/уменьшения информации, так как мы должны быть достаточно довольны этим после последнего раздела.

У этой функции есть три критические точки: \(x = — 1\), \(x = 0\) и \(x = 1\). Ниже находится числовая строка для увеличения/уменьшения информации.

Итак, у нас получились следующие интервалы возрастания и убывания.

\[\begin{align*}{\mbox{По возрастанию: }} & — \infty < x < - 1{\mbox{и}}1 < x <\infty \\ {\mbox{По убыванию: }} & - 1 < х < 0, \, \, \, 0 < х < 1 \ конец {выравнивание *} \]

Обратите внимание, что из теста первой производной мы также можем сказать, что \(x = — 1\) является относительным максимумом, а \(x = 1\) — относительным минимумом. Также \(x = 0\) не является ни относительным минимумом, ни максимумом.

Теперь давайте получим интервалы, где функция вогнута вверх и вогнута вниз. Если подумать, этот процесс почти идентичен процессу, который мы используем для определения интервалов возрастания и убывания. Единственное отличие состоит в том, что мы будем использовать вторую производную вместо первой.

Первое, что нам нужно сделать, это определить возможные точки перегиба. Это будут случаи, когда вторая производная равна нулю или не существует. Вторая производная в этом случае является многочленом и поэтому будет существовать везде. В следующих точках он будет равен нулю.

\[x = 0,\,\,x = \pm \frac{1}{{\sqrt 2}} = \pm \,0,7071\]

Как и в случае с возрастающей и убывающей частью, мы можем нарисовать числовую линию вверх и использовать эти точки, чтобы разделить числовую линию на области. Мы знаем, что в этих областях вторая производная всегда будет иметь один и тот же знак, поскольку эти три точки являются единственными местами, где функция май сменить знак. Поэтому все, что нам нужно сделать, это выбрать точку из каждой области и подставить ее во вторую производную. Тогда вторая производная будет иметь этот знак во всей области, из которой исходит точка

Вот числовая линия для этой второй производной.

Итак, у нас получились следующие интервалы вогнутости.

\[\begin{align*}{\mbox{Вогнутый вверх: }} & — \frac{1}{{\sqrt 2}} < x < 0{\mbox{and}}\frac{1}{{\ sqrt 2 }} < x < \infty \\ {\mbox{Вогнутый вниз: }} & - \infty < x < - \frac{1}{{\sqrt 2}}{\mbox{ и }}0 < x < \ frac {1} {{\ sqrt 2}} \ end {align *} \]

Это также означает, что

\[x = 0,\,\,x = \pm \frac{1}{{\sqrt 2}} = \pm 0,7071\]

— все точки перегиба.

Вся эта информация может быть немного ошеломляющей при построении графика. Первое, что мы должны сделать, это получить некоторые отправные точки. Критические точки и точки перегиба являются хорошими отправными точками. Итак, сначала нарисуйте эти точки.

С этого момента есть несколько способов приступить к рисованию графика. Способ, который мы считаем самым простым (хотя вы можете и не делать этого, и это совершенно нормально….), состоит в том, чтобы начать с увеличения/уменьшения информации и начать рисовать график только с этой информации, как мы делали в предыдущем разделе. Однако, в отличие от предыдущего раздела, на этот раз, когда мы рисуем возрастающую или убывающую часть кривой, мы также будем обращать внимание на вогнутость кривой.

Итак, если мы начнем с \(x < - 1\), мы знаем, что у нас есть возрастающая функция. В то же время мы знаем, что мы также должны быть вогнутыми в этом диапазоне. Итак, мы можем начать с рисования возрастающей кривой, которая также вогнута вниз, пока мы не достигнем \(x = - 1\).

В этот момент график начинает уменьшаться и будет продолжать уменьшаться, пока мы не достигнем \(x = 1\). Однако по мере того, как мы уменьшаем вогнутость, необходимо переключиться на вогнутость вверх при \(x \приблизительно — 0,707\), а затем снова переключиться на вогнутость вниз при \(x = 0\) с окончательным переключением на вогнутость вверх при \(x \ примерно 0,707\).

Как только мы достигаем \(x = 1\), график начинает увеличиваться и все еще остается вогнутым, и оба эти поведения сохраняются для остальной части графика.

Объединив всю эту информацию, мы получим следующий график функции.

Мы можем использовать предыдущий пример, чтобы проиллюстрировать другой способ классификации некоторых критических точек функции как относительных максимумов или относительных минимумов.

Обратите внимание, что \(x = — 1\) является относительным максимумом и что в этой точке функция вогнута вниз. Это означает, что \(f»\left( { — 1} \right)\) должно быть отрицательным. Точно так же \(x = 1\) является относительным минимумом, и в этой точке функция вогнута вверх. Это означает, что \(f»\left( 1 \right)\) должно быть положительным.

Как мы вскоре увидим, нужно быть очень осторожным с \(x = 0\). В этом случае вторая производная равна нулю, но на самом деле это не будет означать, что \(x = 0\) не является относительным минимумом или максимумом. Чуть позже мы увидим некоторые примеры этого, но сначала нам нужно позаботиться о другой информации.

Здесь также важно отметить, что все критические точки в этом примере были критическими точками, в которых первая производная была равна нулю, и это необходимо для того, чтобы это работало. Мы не сможем использовать этот тест в критических точках, где производная не существует.

Вот тест, который можно использовать для классификации некоторых критических точек функции. Доказательство этого теста находится в разделе «Доказательства производных приложений» главы «Дополнительно».

Тест второй производной

Предположим, что \(x = c\) является критической точкой \(f\left( x \right)\) такой, что \(f’\left( c \right) = 0\) и что \(f»\left( x \right)\) непрерывно в области вокруг \(x = c\). Тогда

1. Если \(f»\left( c \right) < 0\), то \(x = c\) является относительным максимумом.
2. Если \(f»\left( c \right) > 0\), то \(x = c\) является относительным минимумом.
3. Если \(f»\left( c \right) = 0\), то \(x = c\) может быть относительным максимумом, относительным минимумом или ни тем, ни другим.

Важно отметить третью часть теста второй производной. Если вторая производная равна нулю, критическая точка может быть любой. Ниже приведены графики трех функций, каждая из которых имеет критическую точку при \(x = 0\), вторая производная всех функций равна нулю при \(x = 0\), и все же показаны все три возможности. 93}\), и этот график не имел ни относительного минимума, ни относительного максимума в точке \(x = 0\).

Итак, мы видим, что нужно быть осторожным, если попадем в третий случай. В тех случаях, когда мы попадаем в этот случай, нам придется прибегнуть к другим методам классификации критической точки. Обычно это делается с помощью теста первой производной.

Давайте вернемся назад и посмотрим на критические точки из первого примера и применим к ним тест второй производной, если это возможно.

93} — 30х\]

Три критические точки (\(x = — 1\), \(x = 0\) и \(x = 1\)) этой функции являются критическими точками, где первая производная равна нулю, поэтому мы знаем, что у нас, по крайней мере, есть шанс, что Второй Производный Тест сработает. Значение второй производной для каждого из них равно

. \[h»\left( { — 1} \right) = — 30\hspace{0.5in}h»\left( 0 \right) = 0\hspace{0.5in}h»\left( 1 \ справа) = 30\]

Вторая производная в точке \(x = — 1\) отрицательна, так что согласно тесту второй производной эта критическая точка является относительным максимумом, как мы видели в первом примере. Вторая производная в точке \(x = 1\) положительна, поэтому мы имеем здесь относительный минимум по тесту второй производной, как мы также видели в первом примере.

В случае \(x = 0\) вторая производная равна нулю, поэтому мы не можем использовать критерий второй производной для классификации этой критической точки. Обратите внимание, однако, что мы знаем из теста первой производной, который мы использовали в первом примере, что 9{\ гидроразрыва {4} {3}}}}} \]

Критические точки,

\[t = \frac{{18}}{5} = 3,6\hspace{0,5 дюйма}t = 6\]

Также обратите внимание, что мы не сможем использовать критерий второй производной для \(t = 6\) для классификации этой критической точки, поскольку в этой точке производная не существует. Чтобы классифицировать это, нам понадобится информация о возрастании/убывании, которую мы получим, чтобы набросать график.

Однако мы можем использовать тест второй производной, чтобы классифицировать другую критическую точку, так что давайте сделаем это, прежде чем мы приступим к работе над эскизом. Вот значение второй производной при \(t = 3,6\).

\[f»\влево( {3,6} \вправо) = — 1,245 < 0\]

Итак, согласно тесту второй производной \(t = 3,6\) является относительным максимумом.

Теперь давайте продолжим работу, чтобы получить набросок графика и заметить, что когда у нас будет информация о возрастании/убывании, мы сможем классифицировать \(t = 6\).

Вот числовой ряд для первой производной.

Итак, в соответствии с тестом на первую производную мы можем убедиться, что \(t = 3,6\) на самом деле является относительным максимумом. Мы также можем видеть, что \(t = 6\) является относительным минимумом.

Будьте внимательны и не думайте, что критическая точка, которую нельзя использовать в тесте второй производной, не будет относительным экстремумом. Теперь мы ясно видим, как на этом примере, так и в обсуждении после того, как у нас есть тест, что только потому, что мы не можем использовать тест второй производной или тест второй производной ничего не говорит нам о критической точке, не означает что критическая точка не будет относительным экстремумом.