Решить систему уравнений методом обратной матрицы онлайн калькулятор: Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Содержание

Решение методом обратной матрицы. Решение систем линейных уравнений с помощью обратной матрицы. Решение матричных уравнений

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Предупреждение

Очистить все ячейки?

Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

Учитывая определение обратной матрицы, имеем A −1 A =E , где E — единичная матрица. Следовательно (4) можно записать так:

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к

A матрицу на вектор ограничений b .

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

Матричный вид записи системы линейных уравнений: Ax=b , где

Вычислим все алгебраические дополнения матрицы A :

Обратная матрица вычисляется из следующего выражения.

Метод обратной матрицы – эточастный случай матричного уравнения

Решить систему с матричным методом

Решение : Запишем систему в матричной форме.Решение системы найдем по формуле (см.последнюю формулу)

Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решаетсяметодом исключение неизвестных (методом Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:

То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.

Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).

Таким образом:

– матрица миноров соответствующих элементов матрицы .

– матрица алгебраических дополнений.

– транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?

Теперь записываем обратную матрицу:

Ни в коем случае не вносимв матрицу, это серьезно затруднит дальнейшие вычисления . Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение. Умножать матрицы можно научиться на урокеДействия с матрицами . Кстати, там разобран точно такой же пример.

Обратите внимание, что деление на 60 выполняется в последнюю очередь .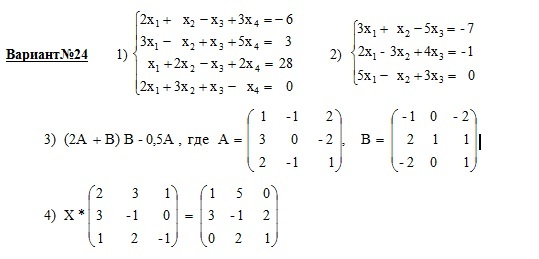

Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.

Ответ :

Пример 12

Решить систему с помощью обратной матрицы.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса) . Доступно объяснить алгоритм не так-то просто, но я старался!.

Желаю успехов!

Ответы:

Пример 3:

Пример 6:

Пример 8: , . Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).

Примеры 10, 12:

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если Вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.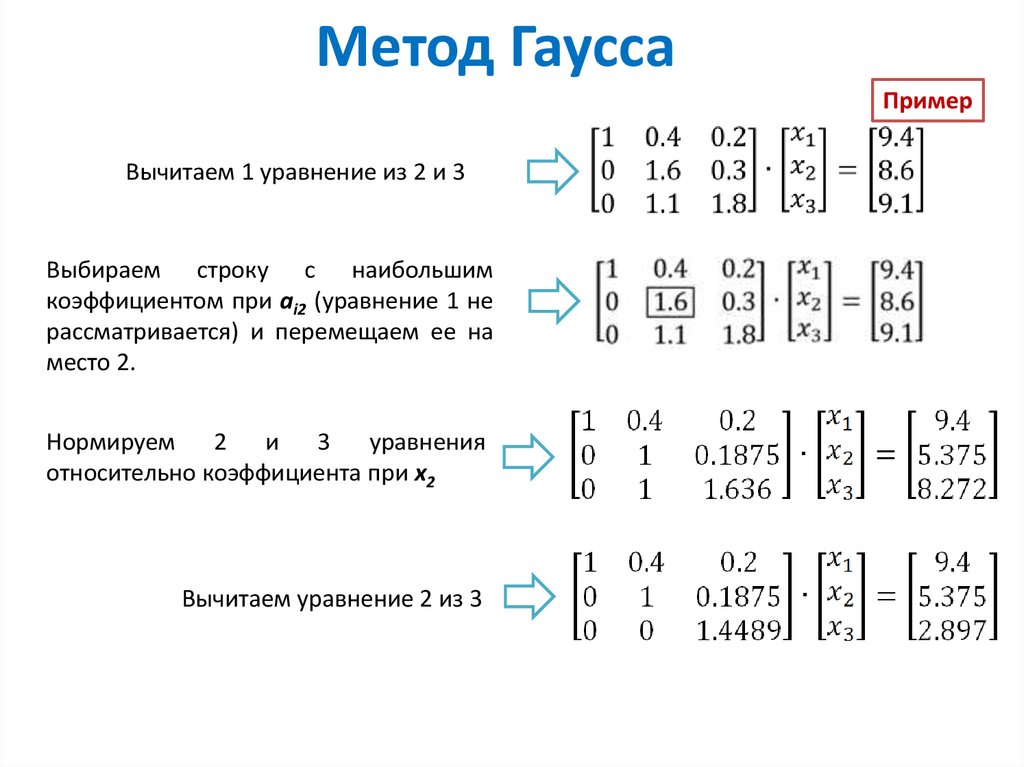

Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:

. Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует

удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯ

ЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе . Она уже почти решена.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :

(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :

А мысленный ход самих расчётов я уже рассмотрел выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ:

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх:
Да тут подарок получился:

Ответ: .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ: .

Пример 4: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена .
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83. .Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, ; .Если свободные члены

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.

Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A -1 · B , где A -1 — обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными:

Её можно переписать в матричной форме: AX = B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A -1 — матрицу, обратную к матрице A : A -1 (AX ) = A -1 B

Так как A -1 A = E , получаем X = A -1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0 , действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений .

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.

Пусть имеется квадратная матрица n-го порядка

Матрица А -1 называется обратной матрицей по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.

Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.

Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной , если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.

Алгоритм нахождения обратной матрицы

Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.

Пример 1

Для матрицы А найти обратную матрицу А -1

Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .

В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.

Ответ:

Решение матричных уравнений

Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.

Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.

Аналогично решаются другие уравнения.

Пример 2

Решить уравнение АХ = В, если

Решение : Так как обратная матрица равняется (см. пример 1)

Матричный метод в экономическом анализе

Наряду с другими в находят применение также матричные методы . Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.

В процессе применения матричных методов анализа можно выделить несколько этапов.

На первом этапе осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n) , а по вертикальным графам — номера показателей (j = 1,2,….,m) .

На втором этапе по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.

После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .

На третьем этапе все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k . Величина последнего определяется экспертным путем.

На последнем, четвертом этапе найденные величины рейтинговых оценок R j группируются в порядке их увеличения или уменьшения.

Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.

Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.

Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.

Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:

Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):

Значит, её легко перевести в матричную форму:

AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.

Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :

detA≠0.

Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.

Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .

Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.

Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.

Пример решения неоднородной СЛАУ.

Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.

Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.

Подставляем переменные в формулу:

Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.

Итак, x=2; y=1; z=4.

При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :

НЕЛЬЗЯ записать как:

Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:

Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :

в матричной форме записываем так:

Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.

решаем системы линейных алгебраических уравнений (слау)

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т. е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
—

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы — (2; -1; 1).

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.

Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид

Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1. 5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,

. (1.6)

Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:

(j = 1, 2, …, n ). (1.7)

Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:

(1.8)

Пример 1.5. Методом Крамера решить систему уравнений

Вычислим главный определитель системы:

Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):

Таким образом,

Действия над матрицами

1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.

2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть

. (1.9)

Пример 1.6. .

Сложение матриц.

Данная операция вводится только для матриц одного и того же порядка.

Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:

(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.

Пример 1.7. .

Умножение матриц.

Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:

Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:

Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :

Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :

2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .

Обратная матрица. Решение систем линейных уравнений матричным способом

Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:

где через I обозначается единичная матрица того же порядка, что и матрица А :

Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:

, (1.13)

где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).

Пример 1.9. Найти обратную матрицу A — 1 к матрице

Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:

Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.

1) Найдем алгебраические дополнения A ij :

Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.

Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:

Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:

где

Умножая обе части равенства (1.14) слева на A — 1 , мы получим решение системы:

, откуда

Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.

Задача 1.10. Решить систему линейных уравнений

с помощью обратной матрицы.

Решение. Запишем систему в матричном виде: ,

где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :

Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:

Решение системы находим по формуле (1.15):

Таким образом,

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:

(1.16)

Требуется найти решение системы, т. е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.

При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.

Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.

Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.

В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.

Пример 1.11.

После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:

Запомним второе уравнение, а из первого найдем z :

Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :

Затем подставим и в первое запомненное уравнение , откуда найдем x :

Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:

. (1.17)

Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение

В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.

Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.

Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.

Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:

. (1.18)

Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:

Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.

В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда

Подставим y и z в первое запомненное равенство и найдем x :

Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :

(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).

В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.

Пусть дана система линейных форм (уравнений):

, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.

Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.

Мы получим следующую систему:

. (1.21)

Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.

Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:

Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:

(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):

После приведения подобных членов, получим:

(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1. 21) (за исключением r -го уравнения):

(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».

Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:

Таблица 1.1

	x 1	x 2	…	x j	…	x s	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i =	a i 1	a i 2		a ij		a is		a in
…………………………………………………………………..
y r =	a r 1	a r 2		a rj		a rs		a rn
………………………………………………………………….
y n =	a m 1	a m 2		a mj		a ms		a mn

Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.

Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:

Таблица 1.2

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………. .
y i =	b i 1	b i 2		b ij		b is		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		b rn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		b ms		b mn

Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.

Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).

1. Разрешающий элемент заменяется обратным числом:

2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:

3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:

4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:

Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:

-21-26-13-37

Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.

Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1.4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).

Таблица 1.5 Таблица 1.6

Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .

Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:

Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:

x 1 = — 3 + 2t

x 2 = — 1 — 3t

x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!

Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.

Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.

Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .

Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.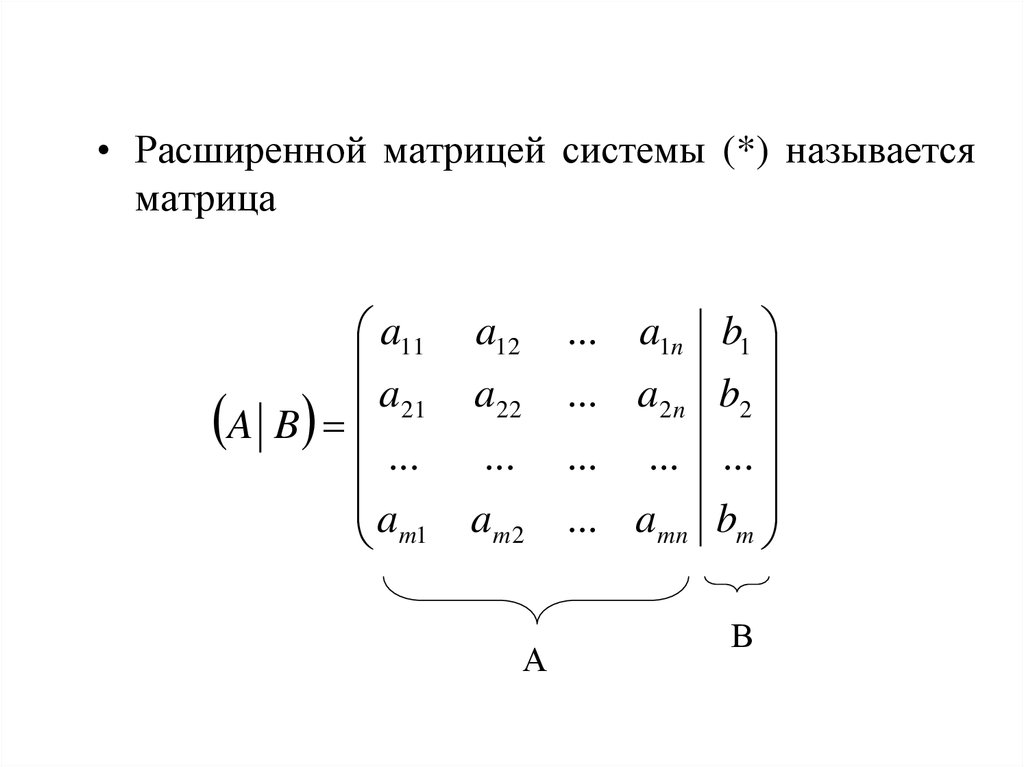

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.

Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:

1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).

2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.

Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.

Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:

Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.

Решение системы с помощью обратной матрицы

Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).

Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.

Решение СЛАУ методом Крамера

Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.

Согласно методу Крамера, решение находится по формулам:

Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.

В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:

Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .

А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Решение систем дифференциальных уравнений матричным способом — справочник студента

Матричный метод может применяться в решении систем линейных уравнений, в которых число неизвестных равно числу уравнений, то есть систем линейных уравнений с квадратной матрицей коэффициентов при неизвестных.

Другое условие применимости матричного метода — невырожденность матрицы коэффициентов при неизвестных, то есть неравенство нулю определителя этой матрицы.

Систему линейных уравнений, при выполнении вышеназванных условий, можно представить в матричном виде, а затем решить её путём отыскания обратной матрицы к матрице системы.

Решение систем линейных уравнений матричным методом основано на следующем свойстве обратной матрицы: произведение обратной матрицы и исходной матрицы равно единичной матрице. Обратная матрица обозначается символом .

Пусть нужно решить систему линейных уравнений:

Запишем эту систему уравнений в матричном виде:

Обозначим отдельно как A матрицу коэффициентов при неизвестных и как B матрицу неизвестных и матрицу свободных членов

Тогда

То есть, для нахождения решений системы нужно обе части уравнения умножить на матрицу, обратную матрице коэффициентов при неизвестных и приравнять соответствующие элементы полученных матриц.

Алгоритм решения системы линейных уравнений матричным методом разберём на следующем примере системы линейных уравнений второго порядка.

Пример 1. Решить матричным методом систему линейных уравнений:
Решение состоит из следующих шагов.

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Это сделано для того, чтобы применить в решении уже записанные закономерности, основанные на свойстве обратной матрицы:

По выведенному выше последнему равенству и будем вычислять решения данной системы.

Но сначала проверим, не является ли матрица коэффициентов при неизвестных вырожденной, то есть можем ли вообще применять матричный метод:

Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.

Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:

Шаг 3. Находим матрицу неизвестных:

Итак, получили решение:

Сделаем проверку:

Следовательно, ответ правильный.

Для второго примера выберем систему линейных уравнений третьего порядка.

Пример 2. Решить матричным методом систему линейных уравнений:

Шаг 1. Составляем следующие матрицы.

Матрица коэффициентов при неизвестных:
Матрица неизвестных:
Матрица свободных членов:
Проверим, не является ли матрица коэффициентов при неизвестных вырожденной:
.
Определитель этой матрицы не равен нулю, следовательно, можем применять матричный метод.
Шаг 2. Находим матрицу, обратную матрице коэффициентов при неизвестных:
.
Шаг 3. Находим матрицу неизвестных:
Итак, получили решение:
.
Сделаем проверку:
Следовательно, ответ правильный.

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Нет времени вникать в решение? Можно заказать работу! Пройти тест по теме Системы линейных уравнений

Всё по теме «Системы уравнений и неравенств»

Решение систем линейных уравнений методом подстановки и методом сложения Решение систем линейных уравнений методом Крамера Решение систем линейных уравнений методом Гаусса Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли Решение систем линейных уравнений матричным методом (обратной матрицы) Системы линейных неравенств и выпуклые множества точек

Начало темы «Линейная алгебра»

Поделиться с друзьями

Источник: https://function-x.ru/systems_matrix_method.html

Матричный метод онлайн

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

где

(3)

Мы будем предполагать, что матрица A имеет обратное, т. е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда
Учитывая определение обратной матрицы, имеем A−1A=E, где E— единичная матрица. Следовательно (4) можно записать так:
или, учитывая, что Ex=x:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Ответ:

Пример 2. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

Вычислим все алгебраические дополнения матрицы A:

Обратная матрица вычисляется из следующего выражения:

где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Ответ:

Источник: https://matworld.ru/calculator/matrix-method-online.php

Глава 4. Матрицы и дифференциальные уравнения

где – постоянный коэффициент; – непрерывная функция времени, определенная на некотором интервале . Решением уравнения является функция , подстановка которой в это уравнение обращает его в тождество. При уравнение называется однородным и его общее решение выражается как , где – произвольная постоянная. Общее решение исходного неоднородного уравнения ( ) выражается формулой 

Это решение представляет собой сумму общего решения однородного и частного решения неоднородного дифференциальных уравнений. Оно удовлетворяет начальному условию при , т. е.

.
Переходя к системам дифференциальных уравнений, рассмотрим их представление в нормальной форме:
,
к которой, как известно, можно привести любую систему линейных дифференциальных уравнений. В матричной записи эта система представляется одним уравнением
,
где – вектор (столбец) неизвестных функций ; – вектор (столбец) задающих функций и – квадратная матрица постоянных коэффициентов :
; ; .

Задачу об отыскании решения системы дифференциальных уравнений, удовлетворяющих заданным начальным значениям скаляра и вектора , называют задачей Коши. По аналогии с дифференциальным уравнением первого порядка можно записать искомое решение для вектора неизвестных функций в виде: .

Необходимо установить допустимость такого представления решения, а также выяснить смысл и способы определения входящей в него матрицы .

В матричной форме нормальная однородная система дифференциальных уравнений ( ) имеет вид: . Будем искать ее решение в виде где вектор (столбец) произвольных постоянных. Подставляя в исходное уравнение, получаем или после сокращения на скаляр и перенесения в левую часть равенства: .

Заметим, что сокращать на вектор нельзя, так как операция деления на вектор в общем случае не имеет смысла. Вынося за скобки вектор , необходимо умножить предварительно на единичную матрицу . Уравнение имеет нетривиальные решения при условии, что определитель матрицы обращается в нуль, т. е.

или

Так как порядок матрицы равен , то является многочленом -й степени относительно , т. е. . Корни уравнения (нули многочлена ), число которых равно , дадут значения при которых исходная система имеет нетривиальные решения.

Рассмотрим наиболее простой случай, когда все корни уравнения простые (попарно различные). Тогда при имеем однородное уравнение , из которого можно определить вектор . Таким образом, решение нормальной системы дифференциальных уравнений, соответствующее корню , будет .

Всего получим таких решений, соответствующих корням .

Для любой квадратной матрицы по установившейся терминологии называется характеристической матрицей, а – характеристическим уравнением. Корни уравнения называются собственными значениями (характеристическими числами), а векторы собственными векторами матрицы . Совокупность собственных значений называется спектром матрицы .

Множество всех решений однородной системы дифференциальных уравнений образует -мерное линейное пространство с базисом . Общее решение имеет следующий вид:
.
Это выражение может быть представлено в матричной форме
.
В свою очередь матрица выражается следующим образом
.
Здесь через обозначена матрица -го порядка, называемая модальной и состоящая из столбцов , а элементами диагональной матрицы являются экспоненциальные функции .

Итак, решение нормальной однородной системы линейных дифференциальных уравнений представляется в виде .

При матрица равна единичной матрице, следовательно, начальное условие , откуда . Подставляя это значение в общее решение, получаем . Матрица -го порядка называется фундаментальной матрицей. Ее вычисление сводится к определению собственных значений и собственных векторов матрицы системы дифференциальных уравнений.

Рассмотрим в качестве примера однородную систему дифференциальных уравнений:
.
Для этой системы
; .
Поскольку для вычисления необходимы алгебраические дополнения какой-либо строки матрицы , то определитель этой матрицы удобно получать разложением по элементам той же строки.
Алгебраические дополнения элементов первой строки:
;
;
.
Характеристический многочлен и собственные значения:
;
; ; .
Собственные векторы : ; ; .
Принимая (эти значения произвольны и выбираются по соображениям удобства), получаем модальную матрицу, а также обратную к ней:
;
Фундаментальная матрица
,
что после перемножения матриц приводит к следующему результату
.
Таким образом, в соответствии с соотношением общее решение рассматриваемой однородной системы дифференциальных уравнений:
,
где элементы вектора , равные начальным значениям соответствующих переменных при .
Выясним характер фундаментальной матрицы . Подставляя решение в однородное дифференциальное уравнение , получаем тождества:
; .

Так как в этих тождествах – вектор начальных значений не зависящий от времени, то , т. е. – это такая матрица, производная которой по времени равна произведению матрицы на саму матрицу. Аналогичными свойствами обладает единственная скалярная функция , поэтому по аналогии можно записать следующие соотношения:

.
Через экспоненциальную функцию выражаются также другие функции от матриц:
Следует иметь в виду, что , а соотношение имеет смысл только в случаях, когда и – перестановочные матрицы.
Решение неоднородной системы дифференциальных уравнений может быть записано в матричной форме , где – векторная функция времени, подлежащая определению. Подставляя выражение для и ее производной в исходное уравнение, имеем:
или после очевидных упрощений
.
При начальных условиях начальное значение искомой функции . Интегрированием получаем
.
Используя это выражение, находим решение неоднородного уравнения, удовлетворяющее начальному условию :
,

которое называется формулой Коши. Его можно рассматривать как сумму решения соответствующего однородного уравнения (при ) и решения неоднородного уравнения при нулевых начальных условиях ( ).

Пусть дана неоднородная система дифференциальных уравнений в нормальной форме:
.
Для этой системы:
; ; ;
;
.
Полагая для удобства , находим модальную матрицу и обратную к ней матрицу :
,
после чего определяется фундаментальная матрица:
.
Решение задачи Коши для однородной системы:
.
Найдем интеграл в выражении для частного решения неоднородной системы при :
Частное решение неоднородной системы:
.
Таким образом, решение неоднородной системы, удовлетворяющей начальным условиям , запишется следующим образом:
.
Контрольные вопросы к лекции 12

12-1. Как записывается система уравнений в матричном виде?

12-2. Как решается матричное уравнение ?

12-3. Что представляет собой определитель матрицы?

12-4. Как вычисляется определитель второго порядка?

12-5. Как вычисляется определитель третьего порядка?

12-6. В чем состоит свойство антисимметрии определителя?

12-7. В каком случае определитель равен нулю?

12-8. Как изменяется определитель матрицы -го порядка при умножении ее на скаляр?

12-9. Как вычисляется алгебраическое дополнение?

12-10. Как вычисляется обратная матрица?

12-11. Опишите алгоритм вычисления обратной матрицы методом исключения.

12-12. Какие матрицы называются особенными?

12-13. Для каких матриц существуют обратные матрицы?

12-14. Какая матрица называется инволютивной?

12-15. Что называется рангом матрицы?

12-16. Что называется дефектом матрицы?

12-17. Какая система уравнений называется совместной?

12-18. В чем состоит суть теоремы Кронекера – Капелли?

12-19. Какая система уравнений называется неопределенной?

12-20. Опишите алгоритм Гаусса для решения неоднородных систем линейных уравнений -го порядка?

12-21. Опишите алгоритм Гаусса – Жордана для решения неоднородных систем линейных уравнений -го порядка?

12-22. Какая система уравнений называется однородной?

12-23. Как определяется характеристическая матрица для квадратной матрицы ?

12-24. Как определяется характеристическое уравнение?

12-25. Что называется характеристическими числами квадратной матрицы ?

12-26. Что называется спектром квадратной матрицы ?

12-27. Какая матрица называется модальной?

12-28. Какая матрица называется фундаментальной?

12-29. Что представляет собой решение неоднородного дифференциального уравнения в форме Коши?

Дата добавления: 2016-09-06; просмотров: 5982;

Источник: https://poznayka.org/s59823t1.html

Исследование методов решения системы дифференциальных уравнений с постоянной матрицей (стр. 1 из 3)

Содержание
1. Введение
2. Постановка задачи

3. Нахождение собственных чисел и построение ФСР

6. Построение общего решения матричным методом

7. Задача Коши для матричного метода

8. Решение неоднородной системы

Графики

Заключение

1. Введение

Рассмотрим систему линейных уравнений первого порядка, записанную в нормальной форме:

(1)

где коэффициенты аij, i=1,2,…..,n, к=1,2,…,n, являются постоянными величинами;

yi=yi(t), i=1,2,…,n — неизвестные функции переменной t.
Если все bi(t) (i=1,2,…,n) положить равным нулю (bi(t)=0), то получится однородная система, соответствующая неоднородной системе (1).
Обозначая матрицу системы через А(х), а вектор

через тогда систему (1) можем переписать в матричной форме (1а)

Если
Всякая совокупность n функций
определенных и непрерывно дифференцируемых в интервале (a;b), называется решением системы (1) в этом интервале, если она обращает все уравнения системы (1) в тождества:

, то получаем соответствующую систему однородных уравнений . (2)

справедливые при всех значениях x из интервала (a, b). Общее решение неоднородной системы представляет собой сумму общего решения соответствующей однородной системы и частного решения неоднородной.

2. Постановка задачи

Цель работы: исследование методов решения системы дифференциальных уравнений с постоянной матрицей:

; ;

1. Найти собственные числа и построить фундаментальную систему решений (ФСР).

2. Построить фундаментальную матрицу методом Эйлера.

3. Найти приближенное решение в виде матричного ряда.

4. Построить общее решение матричным методом. Исследовать зависимость Жордановой формы матрицы А от ее собственных чисел.

5. Решить задачу Коши.

Начальные условия:
Вектор начальных условий: [1, 2, 3, 4]
t = 0

Однородной линейной системой дифференциальных уравнений называется система уравнений вида:

(3)

Если в матрице системы

все =const, то данная система называется системой с постоянными коэффициентами или с постоянной матрицей.

Фундаментальной системой решений однородной линейной системы уравнений называется базис линейного пространства решений a, т. е. n линейно независимых решений этой системы.

Для построения фундаментальной системы решений дифференциального уравнения необходимо найти собственные числа характеристического полинома, так как в зависимости от их вида (характеристические числа могут быть действительными разными, кратными, комплексными) строится фундаментальная система решений.

Для того чтобы эта система n линейных однородных уравнений с n неизвестными имела нетривиальное решение, необходимо и достаточно, чтобы определитель системы (вронскиан) был равен нулю:

(4)

Из этого уравнения степени n определяется значение k, при которых система имеет нетривиальные решения. Уравнение (4) называется характеристическим.

Запишем характеристический полином, для этого воспользуемся функцией CHARPOLY

Для нахождения собственных чисел воспользуемся функцией SOLVE(U, l), которая возвращает характеристические числа матрицы А в вектор l. Получим:
Получилось два действительно корня
Матрицу y(x), столбцами которой являются решения, образующие фундаментальную систему, называют фундаментальной матрицей.
И общее решение системы будет выглядеть следующим образом:
Найдем решение данной системы с помощью метода Эйлера.

и два комплексно-сопряженных корня . Следовательно, вектора, образующие фундаментальную матрицу, для данного типа корней будут находиться отдельно для и отдельно для . Запишем ФСР для данных для полученных характеристических чисел:

4. Построение фундаментальной матрицы решений методом Эйлера

Метод Эйлера заключается в следующем.
Решение системы (1) находится в виде:
Функция (5) является решением системы (1), если

(5) – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу .

Если собственные значения 1, 2, … , n матрицы А попарно различны и a1, a2, …, anсоответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :

где С1, С2, … , Сn – произвольные числа.
Для случая кратных корней решение системы принимает вид

(6)

где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них.

Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.

Если для кратного собственного значения
Если для собственного значения
Чтобы найти векторы
Для данного задания были найдены следующие собственные значения:
Построили фундаментальную систему решений:
Найдем 1 строку фундаментальной матрицы решений для характеристического числа

матрицы А имеется столько линейно независимых собственных векторов , какова его кратность, то ему соответствует k независимых решений исходной системы: кратности k имеется только m (m

Источник: https://mirznanii.com/a/313656/issledovanie-metodov-resheniya-sistemy-differentsialnykh-uravneniy-s-postoyannoy-matritsey

Решение алгебраических уравнений методом крамера.

Решить систему уравнений методами Крамера, Гаусса и с помощью обратной матрицы

Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений – система уравнений вида:

Итак, пусть система состоит из n уравнений с n неизвестными.

Такую систему можно переписать в матричном виде

Решение СЛАУ методом Крамера

Согласно методу Крамера, решение находится по формулам:

С количеством уравнений одинаковым с количеством неизвестных с главным определителем матрицы, который не равен нулю, коэффициентов системы (для подобных уравнений решение есть и оно только одно).

Теорема Крамера.

Когда определитель матрицы квадратной системы ненулевой, значит, система совместна и у нее есть одно решение и его можно найти по формулам Крамера :

где Δ — определитель матрицы системы ,

Δ i — определитель матрицы системы, в котором вместо i -го столбца находится столбец правых частей.

Когда определитель системы нулевой, значит, система может стать совместной или несовместной.

Этот способ обычно применяют для небольших систем с объемными вычислениями и если когда необходимо определить 1-ну из неизвестных. Сложность метода в том, что нужно вычислять много определителей.

Описание метода Крамера.

Есть система уравнений:

Систему 3-х уравнений можно решить методом Крамера, который рассмотрен выше для системы 2-х уравнений.

Составляем определитель из коэффициентов у неизвестных:

Это будет определитель системы . Когда D≠0 , значит, система совместна. Теперь составим 3 дополнительных определителя:

Решаем систему по формулам Крамера :

Примеры решения систем уравнений методом Крамера.

Пример 1 .

Дана система:

Решим ее методом Крамера.

Сначала нужно вычислить определитель матрицы системы:

Т.к. Δ≠0, значит, из теоремы Крамера система совместна и у нее есть одно решение. Вычисляем дополнительные определители. Определитель Δ 1 получаем из определителя Δ, заменяя его первый столбец столбцом свободных коэффициентов. Получаем:

Таким же путем получаем определитель Δ 2 из определителя матрицы системы заменяя второй столбец столбцом свободных коэффициентов:

Рассмотрим систему уравнений

На первом шаге вычислим определитель , его называют главным определителем системы .

метод Гаусса .

На практике вышеуказанные определители также могут обозначаться латинской буквой .

Корни уравнения находим по формулам:
,

Пример 7

Решить систему линейных уравнений

Что делать? В подобных случаях и приходят на помощь формулы Крамера.

;

Ответ : ,

Пример 8

Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

И, наконец, ответ рассчитывается по формулам:

Пример 9

Решить систему по формулам Крамера.

Решение : Решим систему по формулам Крамера.

, значит, система имеет единственное решение.

Ответ : .

Пример 10

Решить систему по формулам Крамера.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение : Запишем систему в матричной форме:
, где

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

2. Решение систем уравнений матричным методом (при помощи обратной матрицы).
3. Метод Гаусса решения систем уравнений.

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ ).

Формулы на примере системы из двух уравнений с двумя переменными.
Дано: Решить методом Крамера систему

Относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы Вычисление определителей. :

Применим формулы Крамера и найдем значения переменных:
и .
Пример 1:
Решить систему уравнений:

относительно переменных х и у .
Решение:

Заменим в этом определителе первый столбец столбцом коэффициентов из правой части системы и найдем его значение:

Сделаем аналогичное действие, заменив в первом определителе второй столбец:

Применим формулы Крамера и найдем значения переменных:
и .
Ответ:
Замечание: Этим методом можно решать системы и большей размерности.

Замечание: Если получается, что , а делить на ноль нельзя, то говорят, что система не имеет единственного решения. В этом случае система имеет или бесконечно много решений или не имеет решений вообще.

Пример 2 (бесконечное количество решений):

Решить систему уравнений:

относительно переменных х и у .
Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Решение систем методом подстановки.

Первое из уравнений системы — равенство, верное при любых значениях переменных (потому что 4 всегда равно 4). Значит, остается только одно уравнение. Это уравнение связи между переменными .
Получили, решением системы являются любые пары значений переменных, связанных между собой равенством .
Общее решение запишется так:
Частные решения можно определять выбирая произвольное значение у и вычисляя х по этому равенству связи.

и т.д.
Таких решений бесконечно много.
Ответ: общее решение
Частные решения:

Пример 3 (решений нет, система несовместна):

Решить систему уравнений:

Решение:
Найдем определитель матрицы, составленный из коэффициентов системы:

Применять формулы Крамера нельзя. Решим эту систему методом подстановки

Второе уравнение системы — равенство, неверное ни при каких значениях переменных (конечно же, так как -15 не равно 2). Если одно из уравнений системы не верно ни при каких значениях переменных, то и вся системы не имеет решений.
Ответ: решений нет

5.Обратная матрица.Способы нахождения. Достаточное условие существования обратной матрицы.

Обратная матрица — это матрица, обратная к данной.

Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.

Нахождение обратной матрицы

Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.

Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.

Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.

Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.

Пример 1

Для матрицы А найти обратную матрицу А-1

Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1.

Ответ:

Теорема условия существования обратной матрицы

Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.

Матрица А = (А1, А2,…Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.

Матричная форма записи систем линейных уравнений

В матричной записи система линейных уравнений может быть записана следующим образом:

AX=B

Пример 2: Записать в матричном виде систему из предыдущего примера

Решение системы с помощью обратной матрицы

Пример 11

Решить систему с матричным методом

Решение: Запишем систему в матричной форме: , где

Обратную матрицу найдем по формуле .

Я не буду приводить вывод этой формулы, так как его практически никогда не требуют в оформлении данной задачи. Согласно формуле нам нужно найти обратную матрицу и выполнить матричное умножение . Алгоритм нахождения обратной матрицы подробно разобран на уроке Как найти обратную матрицу?

Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Сначала разбираемся с определителем:

Здесь определитель раскрыт по первой строке.

Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключение неизвестных (методом Гаусса).

Теперь нужно вычислить 9 миноров и записать их в матрицу миноров

Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент: То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце

Таким образом:

– матрица миноров соответствующих элементов матрицы .

– матрица алгебраических дополнений.

– транспонированная матрица алгебраических дополнений.

Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?

Теперь записываем обратную матрицу:

Ни в коем случае не вносим в матрицу, это серьезно затруднит дальнейшие вычисления. Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.

Осталось провести матричное умножение. Умножать матрицы можно научиться на уроке Действия с матрицами. Кстати, там разобран точно такой же пример.

Обратите внимание, что деление на 60 выполняется в последнюю очередь. Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.

Ответ:

Пример 12

Решить систему с помощью обратной матрицы.

Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).

Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса). Доступно объяснить алгоритм не так-то просто, но я старался!.

Желаю успехов!

Ответы:

Пример 3:

Пример 6:

Пример 8: , . Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).

Примеры 10, 12:

3.4: Решающие системы с инверсиями

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 40128

OpenStax
OpenStax

Цели обучения

Найдите обратную матрицу.
Решите систему линейных уравнений с помощью обратной матрицы

Необходимые навыки

Прежде чем начать, пройдите этот обязательный тест.

1. С помощью калькулятора найдите $A \cdot B$, если $A=\begin{bmatrix} 2 & 1 \\5 & 3 \end{bmatrix} $, $B=\begin{ bmatrix} 3 & -1\\-5 & 2 \end{bmatrix} $.

Нажмите здесь, чтобы проверить свой ответ

$\begin{bmatrix} 1 & 0\\0 & 1 \end{bmatrix} $

Если вы пропустили какую-либо часть этой проблемы, просмотрите Раздел 3.2 . (Обратите внимание, что это откроется в новом окне.)

2. Упростите $5 \cdot \dfrac{1}{5}$ без использования калькулятора.

Нажмите здесь, чтобы проверить свой ответ

$1$

Если вы пропустили эту проблему, просмотрите здесь . (Обратите внимание, что это откроет другой учебник в новом окне.)

3. Упростите $\dfrac{3}{2} \cdot \dfrac{2}{3}$ без использования калькулятора.

Нажмите здесь, чтобы проверить свой ответ

$1$

4. Решите $-\dfrac{3}{2}x=\dfrac{5}{8}$, сначала выделив $x$. (Не умножайте обе стороны на ЖК-дисплей.)

Нажмите здесь, чтобы проверить свой ответ

$x=-\dfrac{5}{12}$

Нэнси планирует инвестировать $$10 500$ в две разные облигации, чтобы распределить свой риск. Первая облигация имеет годовой доход $10%$, а вторая облигация имеет годовой доход $6%$. Чтобы получить $8,5%$ доход от двух облигаций, сколько Нэнси должна инвестировать в каждую облигацию? Каков наилучший метод решения этой проблемы? Есть несколько способов решить эту проблему. Как мы видели в предыдущих разделах, системы уравнений и матриц полезны при решении реальных проблем, связанных с финансами. После изучения этого раздела у нас будут инструменты для решения проблемы связи с использованием обратной матрицы.

Матрица идентичности

Матрица идентичности представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем матрицы идентичности $I_n$, где $n$ представляет размерность матрицы. Единичные матрицы для матрицы $2×2$ и матрицы $3×3$ соответственно:

\[I_2=\begin{bmatrix}1&0 \\ 0&1 \end{bmatrix} \nonumber \ ]

\[I_3=\begin{bmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1\end{bmatrix} \nonumber \]

Единичная матрица действует как $1$ в матричной алгебре. Например,

\[AI=IA=A\nonumber\]

Определение: ИДЕНТИЧНАЯ МАТРИЦА

Единичная матрица , $I_n$, представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули везде. еще.

\[I_2=\begin{bmatrix}1&0 \nonumber \\ 0&1\end{bmatrix}\]

как для единичной матрицы $2 × 2$

\[I_3=\begin{bmatrix}1&0&0 \не число \\ 0&1&0 \не число \\ 0&0&1\end{bmatrix}\]

как для единичной матрицы $3 × 3$

Пример $\PageIndex{1}$: демонстрация того, что единичная матрица действует как 1

Для данной матрицы $A$, покажите, что $ АИ=ИА=А$.

\[A=\begin{bmatrix}3&4 \nonumber \\ −2&5\end{bmatrix}\]

Решение

Используйте умножение матриц, чтобы показать, что произведение $A$ и единичной матрицы равно произведению единичной матрицы на $A$.

\[\begin{align*} AI&=\begin{bmatrix}3&4 \nonumber \\ −2&5\end{bmatrix}\begin{bmatrix}1&0 \nonumber \\ 0&1\end{bmatrix} \nonumber \\[ 4pt] &=\begin{bmatrix}3⋅1+4⋅0&3⋅0+4⋅1 \nonumber \\ −2⋅1+5⋅0&−2⋅0+5⋅1\end{bmatrix} \nonumber \ \[4pt] &= \begin{bmatrix}3&4 \nonumber \\ −2&5\end{bmatrix} \end{align*}\]

\[\begin{align*} AI&=\begin{bmatrix}1&0 \nonumber \\ 0&1\end{bmatrix}\begin{bmatrix}3&4 \nonumber \\ −2&5\end{bmatrix} \nonumber \\[ 4pt] &=\begin{bmatrix}1⋅3+0⋅(−2)&1⋅4+0⋅5 \nonumber \\ 0⋅3+1⋅(−2)&0⋅4+1⋅5\end{ bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}3&4 \nonumber \\ −2&5\end{bmatrix} \end{align*}\]

Мы знаем, что мультипликативная обратная величина действительного числа такова: которое умножается, чтобы создать мультипликативную идентичность, которая равна 1. {-1 }\) мультипликативно обратны друг другу. 9{−1}\).

Пример $\PageIndex{2}$: демонстрация того, что матрица $A$ является мультипликативно обратной к матрице $B$

Показать, что данные матрицы являются мультипликативными обратными по отношению друг к другу.

\[A=\begin{bmatrix}1&5 \nonumber \\ −2&−9\end{bmatrix}\]

\[B=\begin{bmatrix}−9&−5 \nonumber \\ 2&1 \end{bmatrix}\]

Решение

Умножьте $AB$ и $BA$. Если оба произведения равны единице, то две матрицы являются обратными друг другу.

\[\begin{align*} AB &= \begin{bmatrix}1&5 \nonumber \\ −2&−9\end{bmatrix}·\begin{bmatrix}−9&−5 \nonumber \\ 2&1\end{ bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1(−9)+5(2)&1(−5)+5(1) \nonumber \\ −2(−9)−9(2 )&−2(−5)−9(1)\end{bmatrix} \nonumber \\[4pt] &=\begin{bmatrix}1&0 \nonumber \\ 0&1\end{bmatrix} \end{align*}\ ]

\[\begin{align*} BA &= \begin{bmatrix}−9&−5 \nonumber \\ 2&1\end{bmatrix}·\begin{bmatrix}1&5 \nonumber \\ −2&− 9\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−9(1)−5(−2)&−9(5)−5(−9) \nonumber \\ 2(1) +1(−2)&2(−5)+1(−9)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}1&0 \nonumber \\0&1\end{bmatrix} \end{ align*}\]

Поскольку и $AB$, и $BA$ равны единичной матрице, $A$ и $B$ являются обратными друг другу.

Упражнение $\PageIndex{1}$

Покажите, что следующие две матрицы являются обратными друг другу.

\[A=\begin{bmatrix}1&4 \nonumber \\[4pt] −1&−3\end{bmatrix}\]

\[B=\begin{bmatrix}−3&−4 \nonumber \\[4pt] 1&1\end{bmatrix}\]

Ответ

$\begin{align*} AB&=\begin{bmatrix}1&4 \nonumber \\[4pt] −1&−3\end{bmatrix}\begin{bmatrix}−3&−4 \nonumber \\[4pt] 1&1 \end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}1(−3)+4(1)&1(−4)+4(1) \nonumber \\[4pt] −1(− 3)+−3(1)&−1(−4)+−3(1)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}1&0 \nonumber \\[4pt] 0&1\ конец{bmatrix} \конец{выравнивание*}$

$\begin{align*} BA&=\begin{bmatrix}−3&−4 \nonumber \\[4pt] 1&1\end{bmatrix}\begin{bmatrix}1&4 \nonumber \\[4pt] −1&−3 \end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}−3(1)+−4(−1)&−3(4)+−4(−3) \nonumber \\[4pt ] 1(1)+1(-1)&1(4)+1(-3)\end{bmatrix} \nonumber \\[4pt] &= \begin{bmatrix}1&0 \nonumber \\[4pt] 0&1\ конец {bmatrix} \ конец {выравнивание *} $

Нахождение мультипликативного обратного путем увеличения тождества

9{−1}\).

Например, при заданном

$A=\begin{bmatrix}2&1 \nonumber \\[4pt] 5&3\end{bmatrix}$

дополнить $A$ идентификатором

$\left [ \begin{array}{cc|cc} 2&1&1&0 \\ 5&3&0&1\end{array} \right]$

Выполнение операций над строками с целью превратить A в тождество.

Поменяйте местами ряд 1 и ряд 2.
$\left[ \begin{array}{cc|cc} 5&3&0&1 \nonumber \\[4pt] 2&1&1&0\end{array} \right]$
Умножить строку 2 на -2 и прибавить к строке 1.
$\left[ \begin{array}{cc|cc} 1&1&-2&1 \nonumber \\[4pt] 2&1&1&0\end{массив} \right]$
Умножить строку 1 на -2 и прибавить к строке 2.
$\left[ \begin{array}{cc|cc} 1&1&-2&1 \nonumber \\[4pt] 0&-1&5&-2\end{массив} \right]$

Добавить строку 2 к строке 1.

$\left[ \begin{array}{cc|cc} 1&0&3&-1 \nonumber \\[4pt] 0&-1&5&-2\end{массив} \right]$ 9{−1}=\begin{bmatrix}3&−1 \nonumber \\[4pt] −5&2\end{bmatrix}\)

Нахождение мультипликативной обратной матрицы $2×2$ с использованием формулы

Когда нам нужно найти мультипликативное обратное матрицы $2 × 2$, мы можем использовать специальную формулу вместо матричного умножения или увеличения на единицу.

Если $A$ является матрицей $2×2$, например

$A=\begin{bmatrix}a&b \nonumber \\[4pt] c&d\end{bmatrix}$

мультипликативная обратная $A$ задается формулой 9{−1}=\dfrac{1}{ad-bc}\begin{bmatrix}d&-b \nonumber \\[4pt] -c&a\end{bmatrix}\)

, где $ad-bc≠0\ ). Если \(ad−bc=0$, то $A$ не имеет обратного.

Пример $\PageIndex{4}$: Использование формулы для нахождения мультипликативной обратной матрицы $A$

Использование формулы для нахождения мультипликативной обратной матрицы

\[A=\begin{bmatrix} 1&−2 \nonumber \\[4pt] 2&−3\end{bmatrix}\]

Решение

Мы можем проверить, что наша формула работает, используя один из других методов для вычисления обратной. Дополним $A$ тождеством.

$\left[ \begin{array}{cc|cc} 1&-2&1&0 \nonumber \\[4pt] 2&-3&0&1\end{array}\right]$

Выполнить рядовые операции с целью поворота $A$ в тождество.

Умножьте строку 1 на $−2$ и добавьте к строке 2.
$\left[ \begin{array}{cc|cc} 1&-2&1&0 \nonumber \\[4pt] 0&1&-2&1\end{массив} \right]$

Умножить строку 1 на $2$ и прибавить к строке 1.

$\left[ \begin{array}{cc|cc} 1&0&-3&2 \nonumber \\[4pt] 0&1&-2&1\end{массив} \right]$ 9{−1}=\begin{bmatrix}\dfrac{3}{5}&\dfrac{1}{5} \nonumber \\[4pt] −\dfrac{2}{5}&\dfrac{1}{ 5}\конец{bmatrix}\)

Нахождение обратной мультипликативной матрицы с помощью калькулятора

Для целей этого курса мы можем использовать калькулятор для нахождения обратной матрицы.

Как найти обратную матрицу с помощью калькулятора

Введите исходную матрицу в калькулятор с помощью экрана MATRIX EDIT.
Нажмите 2 ^nd MATRIX и используйте клавишу со стрелкой вниз, чтобы выбрать правильное имя матрицы из ИМЕНА меню.
Нажмите клавишу x ^— ¹ (для обратного). Нажмите Ввод.
На экране отображается такая команда, как [A] ^— ¹ . Нажмите Ввод.
Если матрица имеет обратную, калькулятор отобразит ее. Если матрица не имеет обратной, калькулятор выдаст ошибку.

Упражнение $\PageIndex{3}$

9{−1}=\begin{bmatrix}1&1&2 \nonumber \\[4pt] 2&4&−3 \nonumber \\[4pt] 3&6&−5\end{bmatrix}\)

Решение системы линейных уравнений с использованием обратной матрицы

Решение системы линейных уравнений с помощью обратной матрицы требует определения новых матриц: пусть $A$ будет матрицей коэффициентов, пусть $X$ — переменная матрица, а $B$ — постоянная матрица. При условии, что система уравнений имеет столько же уравнений, сколько и переменных, матричное умножение позволяет нам определить систему уравнений как новое матричное уравнение,

$AX=B$

Затем мы умножим обе части уравнения на обратную $A$, чтобы получить решение для $X$.

Например, посмотрите на следующую систему уравнений.

$a_1x+b_1y=c_1$

$a_2x+b_2y=c_2$

Из этой системы матрица коэффициентов равна

$A=\begin{bmatrix}a_1&b_1 \nonumber \\[4pt ] a_2&b_2\end{bmatrix}$

Переменная матрица

$X=\begin{bmatrix}x \nonumber \\[4pt] y\end{bmatrix}$ 9{-1}\right)b \end{align*}\]

Единственная разница между решением линейного уравнения и системы уравнений, записанной в матричной форме, состоит в том, что найти обратную матрицу сложнее, а матрицу умножение — более длительный процесс. Однако цель та же — изолировать переменную.

РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ОБРАТНОЙ МАТРИЦЫ

Для данной системы уравнений запишите матрицу коэффициентов $A$, матрицу переменных $X$ и матрицу констант $B$. Затем 9{-1}\right)B \end{align*}\]

Q&A: Если матрица коэффициентов не имеет обратной, означает ли это, что система не имеет решения?

Нет, если матрица коэффициентов необратима, система может быть несовместной и не иметь решения, или быть зависимой и иметь бесконечно много решений.

Пример $\PageIndex{7}$: Решение системы $2 × 2$ с помощью обратной матрицы

Решите данную систему уравнений с помощью обратной матрицы.

\[\begin{align*} 3x+8y&= 5\\ 4x+11y&= 7 \end{align*}\]

Решение

Запишите систему в терминах матрицы коэффициентов, переменной матрицы и постоянная матрица.

$A=\begin{bmatrix}3&8 \nonumber \\[4pt] 4&11\end{bmatrix}$, $X=\begin{bmatrix}x \nonumber \\[4pt] y\end{bmatrix }$, $B=\begin{bmatrix}5 \nonumber \\[4pt] 7\end{bmatrix}$

Затем

$\begin{bmatrix}3&8 \nonumber \\[4pt] 4&11 \end{bmatrix}\begin{bmatrix}x \nonumber \\[4pt] y\end{bmatrix}=\begin{bmatrix}5 \nonumber \\[4pt] 7\end{bmatrix}$ 9{−1}\) находился слева от $A$ с левой стороны и слева от $B$ с правой стороны. Поскольку умножение матриц не является коммутативным, порядок имеет значение.

Упражнение $\PageIndex{4}$

Решите систему, используя обратную матрицу коэффициентов.

\[\begin{align*} 2x-17y+11z&= 0\\ -x+11y-7z&= 8\\ 3y-2z&= -2 \end{align*}\]

Ответ: $X=\begin{bmatrix}4 \nonumber \\[4pt] 38 \nonumber \\[4pt] 58\end{bmatrix}$

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики решения систем с обратными значениями.

Матрица идентичности
Определение обратных матриц
Использование матричного уравнения для решения системы уравнений

Ключевые уравнения

Единичная матрица для матрицы $2 × 2$

$I_2=\begin{bmatrix}1&0 \nonumber \\[4pt] 0&1\end{bmatrix}$ 9{−1}А=I\).

См. пример $\PageIndex{2}$.

Используйте умножение матриц и тождество, чтобы найти обратную матрицу $2×2$. См. пример $\PageIndex{3}$.

Обратный мультипликатив можно найти по формуле. См. пример $\PageIndex{4}$.

Другой метод нахождения обратного числа — добавление к тождеству. См. пример $\PageIndex{5}$.

Мы можем дополнить матрицу $3×3$ единицей справа и использовать операции со строками, чтобы превратить исходную матрицу в единицу, а матрица справа станет обратной. См. пример $\PageIndex{6}$. 9{−1}В\). См. Пример $\PageIndex{7}$ и Пример $\PageIndex{8}$.

Мы также можем использовать калькулятор для решения системы уравнений с обратными матрицами. См. пример $\PageIndex{9}$.

Авторы и авторство

Эта страница под названием 3.4: Solving Systems with Inverses распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Показать страницу TOC
нет
Теги
1. идентификационная матрица
2. обратная матрица
3. Умножение матриц
4. источник@https://openstax. org/details/books/precalculus
5. источник[1]-math-15093
6. источник[2]-math-3102
7. источник[3]-math-15093

Как решать системы с использованием обратных матриц — Криста Кинг Математика

Мы знаем, как решать системы уравнений, но теперь мы посмотрим, как это сделать, используя обратную матрицу

Мы уже знаем, как решать системы линейных уравнений с помощью замены, исключения и построения графика. На этот раз мы хотим поговорить о том, как решать системы с использованием обратных матриц. Чтобы пройти через это, давайте воспользуемся простой системой.

???3x-4y=6???

???-2x+y=-9???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

И для наглядности давайте сравним это с общей системой

???ax+by=f???

???cx+dy=g???

Мы всегда можем представить такую линейную систему как матрицу коэффициентов, умноженную на вектор-столбец ???(x,y)???, равный вектору-столбцу констант ???(f,g) ???. 9{-1}\vec{b}??? даст нам немедленный набор решений для ???(x,y)???.

Прямо сейчас это не обязательно кажется очень полезным, но по мере того, как вы будете использовать матрицы более продвинутыми способами, станет чрезвычайно полезной возможность изменять значения, составляющие ???\vec{b}??? , и немедленно получите набор решений для ???(x,y)??? это происходит от ???\vec{a}???.

Как использовать обратные матрицы для решения систем уравнений

Пройти курс

Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂

Использование обратной матрицы для решения системы

Пример

Использование обратной матрицы для решения системы.

???3x-4y=6???

???-2x+y=-9???

Начните с преобразования системы в матричное уравнение.

???M\vec{a}=\vec{b}???

Найдите обратную матрицу коэффициентов. 9{-1}\vec{b}???

???\vec{a}=\begin{bmatrix}-\frac15(6)-\frac45(-9)\\ -\frac25(6)-\frac35(-9)\end{bmatrix}?? ?

???\vec{a}=\begin{bmatrix}-\frac65+\frac{36}{5}\\ -\frac{12}{5}+\frac{27}{5}\end{ бматрица}???

???\vec{a}=\begin{bmatrix}\frac{30}{5}\\ \frac{15}{5}\end{bmatrix}???

???\vec{a}=\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}6\\ 3\end{bmatrix}???

Используя этот процесс с обратной матрицей, мы заключаем, что решение системы ???\vec{a}=(x,y)=(6,3)???. 9(-1) на вектор-столбец (f,g)!

Графическое представление системы

Мы также можем выразить ту же систему из примера,

???3x-4y=6???

???-2x+y=-9???

как это матричное уравнение:

???\begin{bmatrix}3\\ -2\end{bmatrix}x+\begin{bmatrix}-4\\ 1\end{bmatrix}y=\begin{bmatrix} 6\\ -9\end{bmatrix}???

Графически это уравнение можно представить как вектор ???\vec{s}=(3,-2)??? за ???х??? и вектор ???\vec{t}=(-4,1)??? для ???y???, и результирующий вектор ???\vec{u}=(6,-9)???. Если мы поместим эти векторы в одну координатную плоскость, то получим

Мы уже знаем из примера, что ???x=6??? и ???y=3???. Что это решение говорит нам графически, так это то, что нам нужно поставить ???6??? из ???х??? векторы ???\vec{s}=(3,-2)??? и ???3??? из ???y??? векторы ???\vec{t}=(-4,1)??? вместе, и мы окажемся в том же месте, что и результирующий вектор ???\vec{u}=(6,-9)???.

Получите доступ к полному курсу линейной алгебры

Learn mathKrista King 1 февраля 2021 математика, выучить онлайн, онлайн курс, онлайн математика, линейная алгебра, обратные матрицы, обратная матрица, решение систем, системы уравнений, решение систем уравнений, решение систем с обратными матрицами, обратные матрицы для решающих систем

0 лайков

Решение системы линейных уравнений с использованием обратной матрицы | Колледж Алгебра |

Решение системы линейных уравнений с помощью обратной матрицы требует определения двух новых матриц:

XXX

— матрица, представляющая переменные системы, и

BBB

— матрица, представляющая константы. Используя матричное умножение , мы можем определить систему уравнений с тем же количеством уравнений в качестве переменных, что и

AX=BAX=BAX=B

Чтобы решить систему линейных уравнений с помощью обратная матрица , пусть

AAA

будет матрицей коэффициентов , пусть

XXX

будет переменной матрицей, и пусть

BBB

будет постоянной матрицей. Таким образом, мы хотим решить систему

AX=BAX=BAX=B

. Например, посмотрите на следующую систему уравнений.

a1x+b1y=c1a2x+b2y=c2\begin{array}{c}{a}_{1}x+{b}_{1}y={c}_{1}\\ {a}_{ 2}x+{b}_{2}y={c}_{2}\end{массив}a1x+b1y=c1a2x+b2y=c2

Из этой системы матрица коэффициентов равна

A=[a1b1a2b2]A=\left[\begin{array}{cc}{a}_{1}& {b}_{1}\\ {a}_{ 2}& {b}_{2}\end{массив}\right]A=[a1a2b1b2]

Матрица переменных:

X=[xy]X=\left[\begin{array}{c}x\\ y\end{array}\right]X=[xy]

А постоянная матрица равна

B=[c1c2]B=\left[\begin{array}{c}{c}_{1}\\ {c}_{2}\end{array}\right]B =[c1c2]

Тогда

AX=BAX=BAX=B

выглядит как 9{-1}\right)2=\left(\frac{1}{2}\right)2=1(2−1)2=(21)2=1

. {-1}\right)b\end{массив} ax=b (a1)ax= (a1)b(a−1)ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1)b x=(a−1)b

Единственная разница между решением линейного уравнения и системы уравнений , записанной в матричной форме, заключается в том, что нахождение обратной матрицы является более сложным, а умножение матриц является более длительным процессом. Однако цель та же — изолировать переменную.

Мы подробно изучим эту идею, но лучше начать с системы

2×22\times 22×2

, а затем перейти к системе

3×33×3

Общее примечание. Решение системы уравнений с использованием обратной матрицы

Дана система уравнений, запишите матрицу коэффициентов

AAA

, матрицу переменных

XXX

и матрицу констант

BBB

. {-1}\right)B\end{массив}(A−1)AX=(A−1)B[(A−1)A]X=(A −1)BIX=(A−1)BX=(A−1)B

Вопросы и ответы

Если матрица коэффициентов не имеет обратной, означает ли это, что система не имеет решения?

Нет, если матрица коэффициентов необратима, то система может быть несовместной и не иметь решения или быть зависимой и иметь бесконечно много решений.

Пример 7. Решение системы 2 × 2 с использованием обратной матрицы

Решите данную систему уравнений, используя обратную матрицу.

3x+8y=54x+11y=7\begin{array}{r}\qquad 3x+8y=5\\ \qquad 4x+11y=7\end{array}3x+8y=54x+11y=7

Решение

Запишите систему в терминах матрицы коэффициентов, переменной матрицы и постоянной матрицы.

A=[38411],X=[xy],B=[57]A=\left[\begin{массив}{cc}3& 8\\ 4& 11\end{массив}\right],X=\ влево[\begin{массив}{c}x\\ y\end{массив}\right],B=\left[\begin{массив}{c}5\\ 7\end{массив}\right]A= [34811],X=[xy],B=[57]

Затем

[38411] [xy]=[57]\left[\begin{array}{cc}3& 8\\ 4& 11\end{array}\right]\text{ }\left[\begin{array} {c}x\\ y\end{массив}\right]=\left[\begin{массив}{c}5\\ 7\end{массив}\right][34811] [xy]= [57] 9{-1}\right)B\qquad \\ \left[\begin{array}{rr}\qquad 11& \qquad -8\\ \qquad -4& \qquad 3\end{array}\right]\text{ }\left[\begin{array}{cc}3& 8\\ 4& 11\end{array}\right]\text{ }\left[\begin{array}{c}x\\ y\end{array} \right]=\left[\begin{array}{rr}\qquad 11& \qquad -8\\ \qquad -4& \qquad 3\end{array}\right]\text{ }\left[\begin{array }{c}5\\ 7\end{массив}\right]\qquad \\ \left[\begin{array}{cc}1& 0\\ 0& 1\end{массив}\right]\text{ }\ left[\begin{array}{c}x\\ y\end{массив}\right]=\left[\begin{array}{r}\qquad 11\left(5\right)+\left(-8 \right)7\\ \qquad -4\left(5\right)+3\left(7\right)\end{массив}\right]\qquad \\ \left[\begin{array}{c}x \\ y\end{массив}\right]=\left[\begin{array}{r}\qquad -1\\ \qquad 1\end{массив}\right]\qquad \end{массив}(A− 1)AX=(A−1)B[11−4−83] [34811] [xy]=[11–4−83] [57][1001] [ xy]=[11(5)+(−8)7−4(5)+3(7)][xy]=[−11] 9{-1}A−1

находился слева от

AAA

с левой стороны и слева от

BBB

с правой стороны.

Поскольку умножение матриц не является коммутативным, порядок имеет значение.

Пример 8. Решение системы 3 × 3 с использованием обратной матрицы

Решите следующую систему, используя обратную матрицу.

5x+15y+56z=35−4x−11y−41z=−26−x−3y−11z=−7\begin{array}{r}\qquad 5x+15y+56z=35\\ \qquad -4x — 11y — 41z=-26\\ \qquad -x — 3y — 11z=-7\end{array}5x+15y+56z=35−4x−11y−41z=−26−x−3y−11z=−7

Решение

Напишите уравнение

AX=BAX=BAX=B

[51556−4−11−41−1−3−11] [xyz]=[35−26−7]\left[\begin{array}{ccc}5& 15& 56\\ -4& -11& -41 \\ -1& -3& -11\end{массив}\right]\text{ }\left[\begin{array}{c}x\\ y\\ z\end{массив}\right]=\left[ \begin{массив}{r}\qquad 35\\ \qquad -26\\ \qquad -7\end{массив}\right]⎣

⎡5−4−115−11−356− 41−11⎦

⎤ ⎣

⎡xyz⎦

⎤=⎣

⎡35−26−7⎦

⎤

Во-первых, мы найдем обратное число

AAA

путем увеличения тождества.

[51556−4−11−41−1−3−11∣100010001]\left[\begin{array}{rrr}\qquad 5& \qquad 15& \qquad 56\\ \qquad -4& \qquad -11& \ qquad -41\\ \qquad -1& \qquad -3& \qquad -11\end{массив}|\begin{массив}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{массив}\ right]⎣

⎡5−4−115−11−356−41−11∣100010001⎦

⎤

Умножьте строку 1 на

15\frac{1}{5}51

[13565−4−11−41−1−3−11∣1500010001]\left[\begin{array}{ccc}1& 3& \frac{56}{5}\\ -4& -11& -41\\ -1& -3& -11\end{массив}|\begin{массив}{ccc}\frac{1}{5}& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{массив}\right]⎣

⎡1−4−13−11−3556−41−11∣5100010001⎦

⎤

Умножьте строку 1 на 4 и прибавьте ко второй строке. гидроразрыв{19{5}\\ -1& -3& -11\end{массив}|\begin{массив}{ccc}\frac{1}{5}& 0& 0\\ \frac{4}{5}& 1& 0 \\ 0& 0& 1\end{массив}\right]⎣

⎡10−131−3556519−11∣51540010001⎦

⎤

Добавьте строку 1 к строке 3.

[13565011950015∣150045101501]\left[\begin{array}{ccc}1& 3& \frac{56}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& \frac{1}{5}\end{массив}|\begin{array}{ccc}\frac{1}{5}& 0& 0\\ \frac{4}{5}& 1& 0\\ \ frac{1}{5}& 0& 1\end{массив}\right]⎣

⎡10031055651951∣515451010001⎦

⎤

Умножьте строку 2 на −3 и прибавьте к строке 1.

[10−15011950015∣−115−3045101501]\left[\begin{array}{ccc}1& 0& -\frac{1}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& \frac{1}{5}\end{массив}|\begin{массив}{ccc}-\frac{11}{5}& -3& 0\\ \ frac{4}{5}& 1& 0\\ \frac{1}{5}& 0& 1\end{массив}\right]⎣

⎡100010−5151951∣− 5115451−310001⎦

⎤

Умножьте строку 3 на 5.

[10−1501195001∣−115−304510105]\left[\begin{array}{ccc}1& 0& -\frac{1}{5}\\ 0& 1& \frac{19}{5}\\ 0& 0& 1\end{массив}|\begin{массив}{ccc}-\frac{11}{5}& -3& 0\\ \frac{4}{5}& 1& 0\\ 1& 0& 5\end{массив }\right]⎣

⎡100010−515191∣−511541−310005⎦

⎤

Умножьте строку 3 на

15\frac{1}{5}51

и добавьте к строке 1.

[10001195001∣−2−314510105]\left[\begin{array}{ccc}1& 0& 0\ \ 0& 1& \ гидроразрыв{19{5}\\ 0& 0& 1\end{массив}|\begin{массив}{ccc}-2& -3& 1\\ \frac{4}{5}& 1& 0\\ 1& 0& 5\end{массив }\right]⎣

⎡10001005191∣−2541−310105⎦

⎤

Умножьте строку 3 на

−195-\frac{19}{5}−519

и добавьте к строке 2.

[100010001∣−2−31−31−19105]\left[\begin{array} {ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}|\begin{array}{ccc}-2&-3&1\\-3&1&-19\\ 1&0&5\end{ массив}\справа]⎣ 9{-1}B:A-1AX=A-1B:

[-2-31-31-19105] [51556-4-11-41-1-3-11] [xyz]=[-2-31 −31−19105] [35−26−7]\left[\begin{array}{rrr}\qquad -2& \qquad -3& \qquad 1\\ \qquad -3& \qquad 1& \qquad -19\\ \ qquad 1& \qquad 0& \qquad 5\end{массив}\right]\text{ }\left[\begin{array}{rrr}\qquad 5& \qquad 15& \qquad 56\\ \qquad -4& \qquad -11& \qquad -41\\ \qquad -1& \qquad -3& \qquad -11\end{массив}\right]\text{ }\left[\begin{массив}{c}x\\ y\\ z\end {массив}\right]=\left[\begin{массив}{rrr}\qquad -2& \qquad -3& \qquad 1\\ \qquad -3& \qquad 1& \qquad -19{-1}B=\left[\begin{array}{r}\qquad -70+78 — 7\\ \qquad -105 — 26+133\\ \qquad 35+0 — 35\end{array}\ right]=\left[\begin{array}{c}1\\ 2\\ 0\end{массив}\right]A−1B=⎣

⎡−70+78−7−105−26+13335 +0−35⎦

⎤=⎣

⎡120⎦

⎤

Решение:

(1,2,0)\влево(1,2,0\вправо)(1,2,0)

Попробуйте 4

Решите систему, используя обратную матрицу коэффициентов.

2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2\begin{array}{l}\text{ }2x — 17y+11z=0\qquad \\ \text{ } -x+11y — 7z=8\qquad \\ \text{ }3y — 2z=-2\qquad \end{array} 2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2

Решение

Как сделать: Имея систему уравнений, решите с помощью калькулятора обратные матрицы.

Сохраните матрицу коэффициентов и матрицу констант как матричные переменные
[A]\left[A\right][A]
и
[B]\left[B\right][B]
.
Введите умножение в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
Если матрица коэффициентов обратима, калькулятор представит матрицу решения; если матрица коэффициентов необратима, калькулятор выдаст сообщение об ошибке.

Пример 9. Использование калькулятора для решения системы уравнений с обратными матрицами

Решить систему уравнений с обратными матрицами с помощью калькулятора

2x+3y+z=323x+3y+z=−272x+4y+z=−2\begin{array}{l}2x+3y+z=32\ qquad \\ 3x+3y+z=-27\qquad \\ 2x+4y+z=-2\qquad \end{массив}2x+3y+z=323x+3y+z=-272x+4y+z=- 2

Решение

На странице матрицы калькулятора введите матрицу коэффициентов в качестве переменной матрицы

[A]\left[A\right][A]

, и введите матрицу констант как переменную матрицы

[B]\left[B\right][B]

[A]=[231331241], [B]=[32−27−2]\left[A\right]=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{массив}\right],\text{ }\left[B\right]=\left[\begin{массив}{c}32\\ -27\\ -2\end{массив}\ right][A]=⎣

⎡232334111⎦

⎤, [B]=⎣

⎡32−27−2⎦

⎤

На главном экране калькулятора введите умножение, чтобы получить 9.{-1}\times \left[B\right][A]−1×[B]

Оцените выражение.

[−59−34252]\left[\begin{array}{c}-59\\ -34\\ 252\end{array}\right]⎣

⎡−59−34252⎦

⎤

Лицензии и атрибуты

Лицензионный контент CC, Конкретное авторство

Precalculus. Автор : Колледж OpenStax. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]:1/Preface. Лицензия : CC BY: Attribution

Курсы PDF, Упражнения, Документы pdf, ppt, бесплатно PDF

Курсы PDF, Упражнения, Документы pdf, ppt, бесплатно PDF | PDFprof.com

Титр

Корпус

ОШИБКА 404 Файл не найден

Администрация
Администрация
Общественная администрация
Общественная администрация
Агролесоводство
Агролесоводство
Аллеманд
Аллеманд
Бак ST2S
Андрагогия
Андрагогия
Драматическое искусство
Драматическое искусство
Художественные визуалы
Художественные визуалы
Астрономия
Астрономия
Бак
БАК Математика
BAC Physique Chimie
БАК СЭС
БАК СВТ
Биохимия
Биохимия
Биографии
Fiche de Cours
Fiches de Revision
География и история L
Исторический антиквариат
Современная история
Европейский союз
Ла Герр Фройд
La Premiere Guerre Mondiale
эпоха Возрождения
Биология
Биология
Биология и физиопатология человека
Бак ST2S
Биотехнология
Биотехнология
Чими
Чими
Курсы и упражнения
IP адрес
Алгоритм
Андроид
годовые
Bases des données
Бюротик
коммерция
Коммуникация
Совместимость
Comptabilité Analytique
Comptabilité générale
Концепция и анализ
курс 3ds max
Курс Ада
курс адрес ip
алгоритм курса
курс андроид
курс ассемблера
Кур Бак-сес
курс баз де донне
курс до-диез
Курс коммерции
Cours comptabilité
курс друпал
затмение
Курс эконом-класса
Курс Электрисите
Курс Электроник
курс эргономики
курсы и упражнения 5e
курсы и упражнения 6eme бесплатно
курсы и упражнения html css
курс и упражнения 1ère stmg
курсы и упражнения 5eme
Английский курс и упражнения
Курсы и упражнения Excel 2010 бесплатно
курсы и упражнения excel pdf
большая секция курсов и упражнений
курс превосходит
Курс финансов
курс фьюжн
Курс Гестион
курс канитель
курс jquery
курс labview
курс языка c
шепелявит
Управление курсами
Курсы маркетинга
Курс Математики
курс матлаб
Кур Оберон
цель курса c
курс паскаль
Курс PDF
Курс телосложения
курс pl sql
кур питон
курс qtcreator
курс рубин
Cours seconde
Cours sixieme
курс весна
курс sql
Статистика курса
Курс статистики
Терминал S
Тройская улица
курс unix linux
курс вба
курс визуальный базовый
курс визуальной студии
Курс Виндев
курс слово
Кутюр
Криптография
Дайверы
Эконом
Экономика pdf
социальная экономия
Электричество
электроника
эмс
Этюд функции
Совместимость экзаменов
Экзамены по информатике
маршрут упражнений
Упражнения коммерции
Совместимые упражнения
Упражнения эконом
упражнения
Упражнения Финансы
Упражнения
Управление упражнениями
Упражнения Маркетинг
Упражнения по математике
Упражнения pdf
Упражнения телосложения
Статистика упражнений
слово упражнения
Финансы
Фискалите
Гастрономия
геополитика
Жестион
гуманитарии
Информатика pdf
Комбинация логики
язык sql
Усилители
Les compteurs
Конденсаторы
диоды
Фильтры
английский язык
Управление распределением и т. д.
Управление человеческими ресурсами
Управление рисками
Управление pdf
Стратегическое управление
Цифровой маркетинг
Маркетинговая часть
Маркетинг pdf
Маркетинговая стратегия
Математика
Математика 1эр S
Терминал математики S
микроэкономика
модель отношений
оракул
Расходы по управлению
телосложение
Вероятности и статистика
Программирование
вопросник ле монд
наук
сэс
сес бак
Статистика
Системы эксплуатации
Тригонометрия
учебник язык с
учебник линукс
учебник excel
обучающая вспышка
сервер виндовс 2003
Курсы и упражнения PDF
Achats et approvisionnement
Рекламное действие
Научная деятельность
Актуальная экономика
Администрация информационных систем
Аэроспасьяль Эт Дефанс
Агенты экономики
Сельское хозяйство и лесное хозяйство
Аллеманд
Финансовый анализ
Английский
Anglais En Seconde Langue
Анналы Бак эс
анналес бак л
анналы бак с
Антропологические исследования автохтонов
Антропология
Apprendre Une Langue
Ардуино
Автоматизация
бак финансы
задний план
бакалавриат
залог рекламный
Коммерческий баланс
Биоинформатика
Биоэтика
ЧИМИ
Амбулатория торговли
Коммуникация и политика
Коммуникации и реклама
Comptabilité Et D’Audit
курс xml
Cours 2ème Bac
Кур Араб
курс назад
Кур-бак-Л
Cours bac s
Кур Бэк ST2DA
Курс бак STD2S
Cours bac STI2D
Cours bac STL
Cours bac STMG
Кур Банк
Кур Шими
Кур Компани
курсы css
Курс Эколь
Cours École Primaire
Cours École Secondaire
Кур Экология
Курс Энерги
Изготовление курсов
курс финансов
Кур Фискалите
Кур Геология
Курс истории
Кур Инженьери
Cours L’Informatique
Кур-ла-Физик
Курс Логистик
курс математики
кур мериз
Курс Метео
Курс MPSI
курс mysql
трассировщик пакетов
Курс PCSI
курс философии
Курсы физики
программа курса
Курс PSI
Курс ПТ
Курс ПТСИ
схема курса
Курс наук
курс Tronc Commun
курс веб-мастера
Курсансе
Круассан эконом
Демография
Демография и география
Демография и статистика
Devoirs Mathématiques
Диплом по дисциплине
экономика
экономика
экономия
коммерческая экономия
ECONOMIE CONCOMMATION ET épargne
экономия образования
экономия на строительстве
экономия удовольствия и удовольствия
Экономика и политика
географическая экономия
промышленная экономика
экономическая институция
мировая экономика
денежная экономика
сельская экономия
Écriture de scénario et creation li
Образование художественное
Исламское образование
образование телосложение образование»’
Коммерческий эффект
ЭЛЕКТРИЧЕСТВО
электрический батимент
электрический CAP
электрический колледж
электрический дебютант
электрисите женераль
электрическая промышленность
электрический лицей
электрическая первичная
электрическое веселье
ENA Национальные школы архитектуры
ENAM Национальная школа сельского хозяйства
ENCG Национальные школы торговли
Энергия
электрическая энергия
ENSA Национальные школы наук
Высшие национальные школы ENSAM
испанский
Статистика оценки
этюды аллеманды
Études allemandes et histoire
Английские этюды
арабские исследования
Азиатские исследования языка и культуры
Азиатские исследования
Этюды автохтонов
Каталанские этюды
Классические этюды
Классические и антропологические исследования
маршевые этюды
видео этюды игры
Азиатские этюды
Феминистские этюды
Испанские этюды
Международные исследования
Итальянские этюды
Латино-американские этюды
Средневековые этюды
Неоэллинские этюды
Квебекские этюды
Études religieuses (науки о ре
экзамены бак с
Упражнения
доступ к упражнениям
Упражнения для спины ES
Упражнения на спину L
Упражнения на спину
Упражнения бак ST2DA
Упражнения bac STD2S
Упражнения bac STI2D
Упражнения bac STL
Упражнения бак СТМГ
Упражнения де comptabilité analytiqu
Exercices de comptabilité financière
осуществляет финансы
Упражнения
Математические упражнения
Упражнения МП
Упражнения МПСИ
Упражнения ПК
Упражнения ПКСИ
Философия упражнений
программа упражнений
Упражнения пси
Упражнения ФТ
Упражнения наук
Упражнения СФЭ
Упражнения SUP
Упражнения ТСИ
окна упражнений
Факультет искусств и социальных наук
Факультет наук
Коммерческие финансы
Банковские финансы
Финансовый дебютант
Финансы и совместимость
Финансы количественные
Финансовый солидер
Финансирование проекта
Факультеты медицины и фармакологии FMP
Фонд коммерции
французский
Français langue seconde avancé
Джин генерал
география
Экологическая география
геополитика и политические науки
Геостатистический
Gestion de l’information numérique
Прием серв. де санте
Партизанский маркетинг
история
История экономики
История искусства
Историческая география
Гиперперсонализация
IAV Institut Agronomique et Vétérin
Входящий исходящий
Индустри Химик
информатика
Информационная аппликация
Психообразовательное вмешательство
Инвестор
ISEM Institut Supérieur d’Etudes Ma
ISIC Высший институт информации
ISPM Institut Supérieur des Pêches
Высший институт науки ISSS
Кинезиология и образование. физ.
Язык и культура allemandes
Английский язык и культура
Арабский язык и культура
Каталанский язык и культура
Китайский язык и культура
Язык и культура
Греческий язык и культура
Испанский язык и культура
Японский язык и культура
Латинский язык и культура
Язык и культура португалоязычный
Португальский язык и культура lusuph
Английские языки и культуры
Арабские языки и культуры
Каталанские языки и культуры
Греческие языки и культуры
Испанские языки и культуры
Неоэллинские языки и культуры
Языки и культуры русские
Letters et Sciences Humanes
Письма, языки и культуры
Littératures de langue française
Littératures de langue française et
Littératures et langues modernes
Logiciels D’Entreprise
Логистика и транспорт
Макроэкономика
Совместное управление
Культура управления
Менеджмент d’équipe
Управление инновациями
Управление знаниями
Управление операциями
Управление изменениями
Этика управления
Оперативное управление
Участие в управлении
Марж коммерческая
Маркетинговый агропродовольственный
Маркетинговая альтернатива
Маркетинговая аналитика
Маркетинг B2B
Маркетинговый банк
Маркетинговое сотрудничество
Маркетинговая реклама
Культура маркетинга
Контент-маркетинг
Массовый маркетинг
Маркетинговые ассоциации
Маркетинговая этика
Маркетинговая этника
Маркетинговые мероприятия
Маркетинговый опыт
Маркетинговая сенсорика
Маркетинг территориальный
математика
Математика и информатика
Математика здесь S
МЕХАНИКА
Мет. де ледук. физ. спорт.
Микробиология и иммунология
Микроменеджмент
Мобильная коммерция
Статистика моделирования
Мультидисциплинарный
Музыкальное образование
Нейромаркетинг
Когнитивная неврология
Ондес
ОПТИКА
Ориентация и консультирование
колебания
Техническая логистика
Рекламный спектакль
философия
Философия и классические исследования
php курсы и упражнения pdf бесплатно
телосложение
Телосложение и информатика
Physique-Chimie
Коммерческая перспектива
Психообразование,
Психология и социология
Реклама и маркетинг
Recrutement et Gestion des Carrière
Этнические отношения
Промышленные отношения
Природные ресурсы
Ресурсы Pédagogiques Et En Class
Ретаргетинг
Агрономические науки
биологические науки
Когнитивные науки
Науки о коммуникации
наук о жизни
инженерные науки
Экономика и управление науками
Науки экономические и социальные
Науки и технологии Механика
Математические науки
Математические науки A
Математические науки B
Науки естественные и прикладные
Религиозные науки
Sécurité et études policières
СЭС
Социология Отношения Этники
Статистика Зондажа
Статистическая аппликация
Статистический дебютант
исчерпывающая статистика
Неверная статистика
Статистическая психология
Коммерческая стратегия
Стратегия предприятия
Уличный маркетинг
Субвенции, Des Bourses et Des Aid
СВТ
Tableau de bord et management de pe
Электрик
Промышленная технология
Технологии
Коммерческая реклама
Курс Упражнения
аргументация
Бак де Франсэ 2013
Бодлер
Камю
искренний
диссертация
дом Хуан
описание изобретения
принцесса де Клев
цветочки зла
мадам Бовари
поэзия
Упражнения на курсе PDF
диссертация фр
экспертная совместимость
Недвижимость
Информатика
Ла Финанс
мастер говядина
Норм Ванкувер
норм апа
изнасилование
раппорт де этап
эти докторские
Курс телосложения
Курсы и упражнения
Криминология
Криминология
Дизайн интерьера
Дизайн интерьера
Первая дидактика
Первая дидактика
Право
Право
Эконом
Курсы и упражнения
экономическая политика
социальная экономия
Экономика и поведение
Бак про
Образование
Образование
Éducation physActivité phys
Éducation physActivité phys
образование телосложение
образование телосложение
ЭЛЕКТРИЧЕСТВО
Курсы и упражнения PDF
электроника
Алгебр де Буля
Электромагнетизм
Les Circuits RLC
Предприятие
Предприятие
Управление
Экологические исследования
Экологические исследования
Семейные исследования
Семейные исследования
Финансы
Финансы
Лесничество
Лесничество
французский
Бак генерал
Бак про
Кур Франсэ
французский
Второй французский язык
Второй французский язык
Джин гражданский
Джин гражданский
Джин Электрик
Джин Электрик
Джин механический
Джин механический
География
География
Геронтология
Геронтология
Gestion de l’information
Gestion de l\’information
Gestion de l\’information
Gestion de l’information
Управление операциями
Управление операциями
Прием серв. де санте
Прием серв. де санте
Gestion intégrée zone cotière
Gestion intégrée zone cotière
История
Антиквариат
История
История Европы
Histoire des États-Unis
Глобальная история
Гуманитарные науки
Писание
Наука о религиях
Информациякоммуникация
Информациякоммуникация
информатика
информатика
инженерия
Аэрокосмическая техника
Электротехника
информатика
инженерия
Промышленная техника
Кинезиология и образование. физ.
Кинезиология и образование. физ.
Язык по номиналу платит
Язык по номиналу платит
лингвистика
лингвистика
Литература
Литература
Управление
Бак СТМГ
Управление
Управление рисками
Маркетинг
Маркетинг
математический
Этюд функции
Математика
Бак ST2S
Бак СТИ2Д
Курсы и упражнения PDF
Enseignement des mathématiques
Элементарная математика
Мир труда
Этика
Пример де Plaidoirie
Финансы и экономика
Техника прогресса
Синдикаты
Музыка
Музыка
Питание и семейные исследования
Питание и семейные исследования
питаниепитание
питаниепитание
ofppt
курс ppt
PDF-документы
Ноты для альт-саксофона
Бас Ноты
Барабаны и перкуссия для начинающих
Пианино для начинающих
Скрипка для начинающих
Bien-être
Ноты для блюза для гитары
Блюз Ноты
Ноты для виолончели
курсы и упражнения Excel
курсы и упражнения python
Персонал по развитию
Этническая принадлежность, раса и жанр
Фантазия
Историческая фантастика
Ноты для флейты и пикколо
Ноты для гитары
Старая история
История Мойен-Востока
Европейская история
Мировая история
Ноты для гитары в стиле джаз и блюз
Ноты для джазовой гитары
Ноты для джазового фортепиано
Коран и священные писания
Классическая литература
Мода и красота
Ноты для гитары из фильмов и мюзиклов
Питание и Вин
Паранормальный
Разделы поп и рок
Перегородки для фортепиано
Политика и актуальная информация
Поп- и рок-бас-ноты
Популярная культура
Ноты для гитары R&B
Отношения и родители
Религиозные и праздничные ноты для гитары Mu
Вегетарианские и веганские блюда
Исторический роман
Научная фантастика
Ноты
Ноты для трубы
Ноты для укулеле
Городское планирование и землепользование
Ноты для скрипки
Философия
Отруи
Курсы и упражнения PDF
Искусство
L’Inconscient et la Conscience
Ла Либерте
Религия
Ле Бонёр
детерминизм
Ле Маль
Le réel et la raison
Ле Респект
Ле Рир
Труд и техника
Телосложение
Телосложение
Физико-химия и математика
Бак СТИ2Д
Политика и интернационал
военный
Психология
Фрейд
Истерия
Ла Восприятие
La Perfectibilite
Психология
Психология Когнитивная
Se Connaitre Soi Мем
стресс
Радиология
Радиология
Связи со сценой
Force et Faiblesse
Письмо о мотивации
Религия и духовность
атеизм
буддизм
христианство
индуизм
ислам
иудаизм
Религия
Богословие
Гуманитарные ресурсы
Гуманитарные ресурсы
Здоровье и культура
Альтернатива медицине
Научный лазарет
Научный лазарет
Наука политическая
Наука политическая
наук
Астрономия
Биология
Чими
Медицина
Наука об окружающей среде
наук де ла Терре
наук о здоровье
наук о здоровье
Экономические и социальные науки
Генеалогия
социальные науки
Антропология
Психология
Наука политическая
социальные науки
Социология
Общество
Помощник Суаньанте
Ситуаеннете
Поколение
Иммиграция
Liens Familiaux
Социология
Социология
Статистика
Статистика
СВТ
Бак генерал
Сист. информация. организационные элементы
Сист. д \ ‘информация. организационные элементы
Сист. д \ ‘информация. организационные элементы
Сист. информация. организационные элементы
Тех. медицинская лаборатория
Тех. медицинская лаборатория
Респираторная терапия
Респираторная терапия
токсикомания
токсикомания
перевод
перевод
Путешествие в соц.
Путешествие в соц.
Администрация
Бак
Бревет
Конкурсы
Дайверы
Трудоустройство
Формирование фише
Fiche metier
История
Письмо о мотивации
Ливр Блан
Рапорт де стадии
питание
Архитектура
Кинотеатр искусств
Искусство ддд пластики
Художественная литература
Искусство Музыка
Художественная фотография
Художественная пластика
Base de données
Биология
бюрократический
Коммерческий коучинг
Коммерческое общение
Коммерция ддд интернэшнл
Коммерческие дайверы
Коммерция Экономика
Коммерческий электронный маркетинг
Коммерческий этюд на марше
Коммерческие Финансы
Международная коммерция
Коммерческая логистика
Управление торговлей
Коммерческий маркетинг
Коммерческие СМИ
Коммерческая стратегия
Коммерческий туризм и услуги
Коммуникация
курс 3ds max
Курс 4D
доступ к курсу
Курс Аякс
алгоритм курса
курс андроид
курс апертура
Cours Architecture des ordinateurs
курс жерех
курс ассемблера
Cours assembleur Cours informatique
дерзость
Курс аудита
Автоматический курс
курс баз де донне
Курс биологии
Курский мост
курс с
курс до-диез
Курсы С/С++
Курс Сиэль Компта
Cours Ciel Devis фактура
Cours Ciel Gestion Commerciale
Курсы Cisco
Кур Коболь
Курс коммерции
курс аналитической совместимости
Cours comptabilite approfondie
Cours comptabilité des entreprises
Cours comptabilité des sociétés
Общий курс совместимости
Курсы криптографии
курсы css
Курс Дельфы
Кур Друа
курс друпал
затмение
Курс эконометри
Курс эконом-класса
Cours électricité автомобиль
Cours électricité de base
Электромеканская улица
Электронный курс
курс эргономики
курс превосходит
курс final cut pro
Cours Finance de Marché
Cours финансирует общественность
Курс фискальных услуг
курс фьюжн
курс гаражной группы
Cours Genie Civil
курс
Курсы управления проектами
Cours gestion des approvvisionnements
Cours gestion des entreprises
Cours gestion des ressources humanes
Cours gestion des risques
курс канитель
Бесплатные курсы
курс html
Курс гидравлики
Курс Имови
Курс информатики
курс iphoto
курс j2ee
Кур Ява
Курсы JAVA/J2EE
курс javascript
курс джумла
курс jquery
курс labview
курс языка c
Курс Лазаря
Курсы Linux
Курс ЛУА
курс обслуживания ПК
курс менеджмент
Стратегия управления курсами
курс маркетинга
Курс маркетинговой стратегии
Математический курс
курс матлаб
Курс медицины
кур мериз
Курс микроэкономики
курс mysql
цель курса c
трассировщик пакетов
курс паскаль
курс перл
Курс фотошоп
курс php
Cours physique chimie
Курсы PL/SQL
Курсы PowerPoint
Курс вероятностей
кур питон
курс qtcreator
Справочник по курсу
Курс Резо
Cours réseaux informatiques
схема курса
Cours Sécurité Informatique
курс
Курс звуковой кузницы
Курсы SQL
Статистика курса
Cours système d’exploitation
курс умл
Курсы Unix
курс unix linux
курс вб нетто
Курс VB/VB. NET
курс вба
курс визуальный базовый
курс визуальной студии
курс веб-мастера
Курс Виндев
Курсы Windows
курс windows server
курс слово
Курсы XHTML
курс xml
курс xsl
Право
Право дел
Конституционное право
Droit Contrats типы
Право ддд
Европейское право
Фискальное право
Право недвижимости
Международное право
Уголовное право
Право человеческих ресурсов
Права общества
Право труда
Образование
Совместимые упражнения
Упражнения и исправления
французский
Французская аналитика
Франсэ Биография
Франсез Комментарий
Общая французская культура
французский ддд
Французская диссертация
Лекция Франсе Фиша
Ревизия Francais Fiche bac
Французская литература
Французская философия
Изобретение Francais Sujet d
Совместимость с Gestion
Gestion Controle de gestion
Гестион Финанс
Программирование жестов
Gestion Ressources Humanes
Высокие технологии
Histoire geographie Droit
Histoire geographie Fiche revision bac
Историческая география
Историческая география
Индустри
информатика
Администрация информатики
Информатический анализ объекта uml merise
Информационная архитектура
Информатик Бдд
Информатика ддд
Informatique Genie Logiciel
Informatique Gestion de projet
Информатическое программирование
Informatique Reseaux информатики
Информационная безопасность информационных систем
Информатика Технологии
Ланге Алеманд
Английский язык
Арабский язык
Китайский язык
Langue ddds des signes
Испанский язык
Язык итальянский
Латинский язык
Языки знаков
логические
Математика
Медицина
Администрация методологии
Английская методология
Методологический комментарий
Методология коммуникации
Общая методология культуры
Методология Резюме
Испанская методология
Пересмотр методологии Fiche bac
Методология Письмо о мотивации
Математическая методология
Мемуар методологии
Методология анализа
Методология Отчет о стадии
Методология поддержки
Методология Технология
Музыка
Фотография
Physique-Chimie
Программирование
Рапорт де стадии
Резо информатики
Санте
Английские науки
наук Чими
Электронные науки
Управление науками
Математические науки
наук механика
Науки Медицина
Аптека наук
Науки Телосложение
наук Свт
Социальная философия
Социальная политика
Социальная психология
Гуманитарные социальные ресурсы
Социальные науки
Социальная социология
Спорт
Trucs et Astuces

Сайт использует файлы cookie для персонализации PUB, Si vous continuez à utiliser ce site, nousceptrons que vous en êtes satisfait. Савуар плюс

Политика конфиденциальности — Политика конфиденциальности

7.7 Решение систем с инверсиями — Алгебра колледжа

Цели обучения

В этом разделе вы:

Найдите обратную матрицу.
Решите систему линейных уравнений, используя обратную матрицу.

Нэнси планирует инвестировать 10 500 долларов в две разные облигации, чтобы распределить свой риск. Первая облигация имеет годовой доход 10%, а вторая облигация имеет годовой доход 6%. Сколько Нэнси должна инвестировать в каждую облигацию, чтобы получить доход в размере 8,5% от двух облигаций? Каков наилучший метод решения этой проблемы?

Есть несколько способов решить эту проблему. Как мы видели в предыдущих разделах, системы уравнений и матриц полезны при решении реальных проблем, связанных с финансами. После изучения этого раздела у нас будут инструменты для решения проблемы связи с использованием обратной матрицы.

Нахождение обратной матрицы

Мы знаем, что мультипликативная обратная величина действительного числа aa равна a−1,a−1, и aa−1=a−1a=(1a)a=1. aa−1=a−1a=(1a)a= 1. Например, 2−1=122−1=12 и (12)2=1.(12)2=1. Мультипликативная обратная матрица аналогична по своей концепции, за исключением того, что произведение матрицы AA и ее обратной матрицы A-1A-1 равно единичной матрице. Единичная матрица представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем матрицы идентичности по InIn, где nn представляет размерность матрицы. [ссылка] и следующие уравнения.

I2=[1001]I2=[1001]

I3=[100010001]I3=[100010001]

Единичная матрица действует как 1 в матричной алгебре. Например, AI=IA=A.AI=IA=A.

Матрица с мультипликативной обратной имеет свойства

АА-1=ИА-1А=ИАА-1=ИА-1А=I

Матрица, имеющая мультипликативную обратную, называется обратимой матрицей. Только квадратная матрица может иметь мультипликативную обратную, поскольку обратимость AA-1=A-1A=I, AA-1=A-1A=I является требованием. Не все квадратные матрицы имеют обратную, но если AA обратима, то A−1A−1 уникальна. Мы рассмотрим два метода нахождения обратной матрицы 2 × 22 × 2 и третий метод, который можно использовать как для матриц 2 × 22 × 2, так и для матриц 3 × 33 × 3.

Матрица тождества и мультипликативная обратная

Единичная матрица In,In представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах.

I2=[1001]I3=[100010001] 2×2 3×3I2=[1001]I3=[100010001] 2×2 матрица, а BB — это n×nn×n матрица такая, что AB=BA=In,AB=BA=In, тогда B=A−1,B=A−1, мультипликативная обратная матрица A.A.

Пример 1

Показывая, что матрица идентичности действует как 1

Учитывая матрицу A , покажите, что AI=IA=A.AI=IA=A.

А=[34−25]А=[34−25]

Решение

Используйте умножение матриц, чтобы показать, что произведение AA и идентичности равно произведению идентичности и A.

AI=[34−25][1001]=[3⋅1+4⋅03⋅0 +4⋅1−2⋅1+5⋅0−2⋅0+5⋅1]=[34−25]AI=[34−25][1001]=[3⋅1+4⋅03⋅0+4 ⋅1−2⋅1+5⋅0−2⋅0+5⋅1]=[34−25]

IA=[1001][34−25]=[1⋅3+0⋅(−2)1 ⋅4+0⋅50⋅3+1⋅(−2)0⋅4+1⋅5]=[34−25]IA=[1001][34−25]=[1⋅3+0⋅(−2) )1⋅4+0⋅50⋅3+1⋅(−2)0⋅4+1⋅5]=[34−25]

Как

Имея две матрицы, покажите, что одна из них мультипликативно обратна другой.

Даны матрица AA порядка n×nn×n и матрица BB порядка n×nn×n, умножить AB.AB.
Если AB=I,AB=I, то найти произведение BA.BA. Если BA=I, BA=I, то B=A-1B=A-1 и A=B-1.A=B-1.

Пример 2

Демонстрация того, что матрица

A является мультипликативной обратной матрицей B

Показать, что данные матрицы мультипликативно обратны друг другу.

A=[15−2−9],B=[−9−521]A=[15−2−9],B=[−9−521]

Решение

Умножить ABAB и BA. BA. Если оба произведения равны единице, то две матрицы являются обратными друг другу.

AB=[15−2−9]·[−9−521]=[1(−9)+5(2)1(−5)+5(1)−2(−9)−9(2 )−2(−5)−9(1)]=[1001]AB=[15−2−9]·[−9−521]=[1(−9)+5(2)1(−5) +5(1)−2(−9)−9(2)−2(−5)−9(1)]=[1001]

BA=[−9−521]·[15−2−9]=[−9(1)−5(−2)−9(5)−5(−9)2(1)+1(−2)2(5)+1(−9)]=[1001] BA=[−9−521]·[15−2−9]=[−9(1)−5(−2)−9(5)−5(−9)2(1)+1(−2) 2(5)+1(−9)]=[1001]

AA и BB обратны друг другу.

Попытайся #1

Покажите, что следующие две матрицы являются обратными друг другу.

А=[14-1-3],В=[-3-411]А=[14-1-3],В=[-3-411]

Нахождение мультипликативного обратного с помощью умножения матриц

Теперь мы можем определить, являются ли две матрицы обратными, но как нам найти обратную заданную матрицу? Поскольку мы знаем, что произведение матрицы и ее обратной является единичной матрицей, мы можем найти обратную матрицу, составив уравнение, используя матричное умножение.

Пример 3

Нахождение обратной мультипликативной матрицы с помощью умножения матриц

Используйте умножение матриц, чтобы найти обратную заданную матрицу.

А=[1-22-3]А=[1-22-3]

Решение

Для этого метода мы умножаем AA на матрицу, содержащую неизвестные константы, и приравниваем ее к единице.

[1−22−3] [abcd]=[1001][1−22−3] [abcd]=[1001]

Найдите произведение двух матриц слева от знака равенства.

[1-22-3] [abcd]=[1a-2c1b-2d2a-3c2b-3d][1-22-3] [abcd]=[1a-2c1b-2d2a-3c2b-3d]

Далее, составить систему уравнений с записью в строке 1, столбце 1 новой матрицы, равной первой записи тождества, 1. Установить запись в строке 2, столбце 1 новой матрицы, равной соответствующей записи тождество, которое равно 0.

1a-2c=1 R12a-3c=0 R21a-2c=1 R12a-3c=0 R2

Используя операции со строками, умножьте и сложите следующим образом: (−2)R1+R2→R2 . (−2)R1+R2→R2. Сложите уравнения и решите для c.c.

1a-2c=10+1c=-2c=-21a-2c=10+1c=-2c=-2

Обратная подстановка для решения а.о.

a−2(−2)=1a+4=1a=−3a−2(−2)=1a+4=1a=−3

Напишите другую систему уравнений, задав запись в строке 1, столбце 2 новая матрица равна соответствующей записи идентификатора, 0. Установите запись в строке 2, столбце 2, равной соответствующей записи идентификатора.

1b-2d=0R12b-3d=1R21b-2d=0R12b-3d=1R2

Используя операции со строками, умножьте и сложите следующим образом: (-2)R1+R2=R2.(-2)R1+R2=R2 . Сложите два уравнения и решите для d.d.

1b−2d=00+1d=1d=11b−2d=00+1d=1d=1

Еще раз подставим обратно и найдем b.b.

b-2(1)=0b-2=0b=2b-2(1)=0b-2=0b=2

A-1=[-32-21]A-1=[-32-21 ]

Нахождение мультипликативного обратного путем увеличения с тождеством

Другой способ найти мультипликативное обратное — путем увеличения с тождеством. Когда матрица AA преобразуется в I,I, расширенная матрица II преобразуется в A-1. A-1.

Например, учитывая

A=[2153]A=[2153]

дополнить AA идентификатором

[2153|1001][2153|1001]

Выполнение операций над строками с целью превращения AA в личность.

Поменяйте местами ряд 1 и ряд 2.
[5321|0110][5321|0110]
Умножить строку 2 на −2−2 и прибавить к строке 1.
[1121|-2110][1121|-2110]
Умножить строку 1 на −2−2 и прибавить к строке 2.
[110−1|−215−2][110−1|−215−2]
Добавить строку 2 к строке 1.
[100−1|3−15−2][100−1|3−15−2]
Умножить строку 2 на -1,-1.
[1001|3−1−52][1001|3−1−52]

Мы нашли матрицу A−1.A−1.

A−1=[3−1−52]A−1=[3−1−52]

Нахождение мультипликативной обратной матрицы 2×2 с помощью формулы

Когда нам нужно найти мультипликативную обратную матрицу Матрица 2×22×2, мы можем использовать специальную формулу вместо умножения матриц или увеличения на единицу.

Если AA представляет собой матрицу 2×22×2, например

A=[abcd]A=[abcd]

мультипликативная обратная AA задается формулой

A-1=1ad-bc[d-b-ca]A-1=1ad-bc[d-b-ca]

, где ad-bc≠0.ad-bc≠0. Если ad-bc=0,ad-bc=0, то AA не имеет обратного.

Пример 4

Использование формулы для нахождения мультипликативной обратной матрицы

A=[1−22−3]A=[1−22−3]

Решение

Используя формулу, мы имеем

A−1=1(1)(−3)−(−2)(2)[−32−21]=1−3+4[−32−21]=[− 32−21]A−1=1(1)(−3)−(−2)(2)[−32−21]=1−3+4[−32−21]=[−32−21]

Анализ

Мы можем проверить, что наша формула работает, используя один из других методов для вычисления обратного. Давайте дополним AA личностью.

[1−22−3|1001][1−22−3|1001]

Выполнение операций над строками с целью превращения AA в тождество.

Умножить строку 1 на −2−2 и прибавить к строке 2.
[1-201|10-21][1-201|10-21]
Умножить строку 1 на 2 и прибавить к строке 1.
[1001|−32−21][1001|−32−21]

Итак, мы проверили исходное решение.

А-1=[-32-21]А-1=[-32-21]

Попытайся #2

Используйте формулу, чтобы найти обратную матрицу A.A. Проверьте свой ответ, дополнив единичную матрицу.

А=[1-123]А=[1-123]

Пример 5

Нахождение обратной матрицы, если она существует

Найдите обратную матрицу, если она существует, данной матрицы.

А=[3612]А=[3612]

Решение

Воспользуемся методом пополнения тождеством.

[3612|1001][3612|1001]

Поменять местами ряд 1 и ряд 2.
[1332|0110][1332|0110]
Умножьте строку 1 на -3 и добавьте ее к строке 2.
[1200|10−31][1200|10−31]
Больше мы ничего сделать не можем. Нули в строке 2 означают, что эта матрица не имеет обратной.

Нахождение мультипликативной обратной матрицы 3×3

К сожалению, у нас нет формулы, аналогичной формуле для матрицы 2×22×2, для нахождения обратной матрицы 3×33×3. Вместо этого мы дополним исходную матрицу единичной матрицей и используем операции со строками, чтобы получить обратную.

Дано 3×33×3 матрица

А=[231331241]А=[231331241]

дополнить AA идентификационной матрицей

А|Я=[231331241 | 100010001]A|I=[231331241 | 100010001]

Для начала напишем расширенную матрицу с единицей справа и AA слева. Выполняя элементарные операции над строками так, чтобы единичная матрица оказалась слева, мы получим обратную матрицу справа. Мы найдем обратную этой матрице в следующем примере.

Как

Для заданной матрицы 3×33×3 найдите обратную

Запишите исходную матрицу, дополненную единичной матрицей справа.
Используйте элементарные операции со строками, чтобы идентификатор отображался слева.
Справа получается обратная исходная матрица.
Используйте умножение матриц, чтобы показать, что AA-1=IAA-1=I и A-1A=IA.A-1A=I.

Пример 6

Нахождение обратной матрицы 3 × 3

По заданной матрице 3 × 33 × 3 A, A найти обратную.

А=[231331241]А=[231331241]

Решение

Дополните AA единичной матрицей, а затем начните операции со строками, пока единичная матрица не заменит A.A. Матрица справа будет обратной матрице А.А.

[231331241|100010001]→Развязка R2 и R1[331231241|010100001][231331241|100010001]→Развязка R2 и R1[331231241|010100001]

−R2+R1=R1→[100231241|−110100001]−R2+R1=R1→[100231241|−110100001]

−R2+R3=R3→[100231010|−110100−101]−R2+R3= R3→[100231010|−110100−101]

R3↔ R2→[100010231|−110−101100]R3↔ R2→[100010231|−110−101100]

−2R1+R3=R030[030 −1013−20]−2R1+R3=R3→[100010031|−110−1013−20]

−3R2+R3=R3→[100010001|−110−1016−2−3]−3R2+R3=R3→ [100010001|−110−1016−2−3]

Таким образом,

A−1=B=[−110−1016−2−3]A−1=B=[−110−1016−2−3]

Анализ

Чтобы доказать, что B=A-1,B=A-1, давайте перемножим две матрицы вместе, чтобы увидеть, равно ли произведение единице, если AA-1=IAA-1=I и A-1A=I. A-1A = Я.

AA−1=[231331241] [−110−1016−2−3]=[2(−1)+3(−1)+1(6)2(1)+3(0)+1(− 2)2(0)+3(1)+1(-3)3(-1)+3(-1)+1(6)3(1)+3(0)+1(-2)3( 0)+3(1)+1(-3)2(-1)+4(-1)+1(6)2(1)+4(0)+1(-2)2(0)+4 (1)+1(−3)]=[100010001]AA−1=[231331241] [−110−1016−2−3]=[2(−1)+3(−1)+1(6)2 (1)+3(0)+1(-2)2(0)+3(1)+1(-3)3(-1)+3(-1)+1(6)3(1)+ 3(0)+1(-2)3(0)+3(1)+1(-3)2(-1)+4(-1)+1(6)2(1)+4(0) +1(−2)2(0)+4(1)+1(−3)]=[100010001]

A−1A=[−110−1016−2−3] [231331241]=[−1(2)+1(3)+0(2)−1(3)+1(3)+0(4) )−1(1)+1(1)+0(1)−1(2)+0(3)+1(2)−1(3)+0(3)+1(4)−1(1 )+0(1)+1(1)6(2)+−2(3)+−3(2)6(3)+−2(3)+−3(4)6(1)+−2 (1)+−3(1)]=[100010001]A−1A=[−110−1016−2−3] [231331241]=[−1(2)+1(3)+0(2)−1 (3)+1(3)+0(4)−1(1)+1(1)+0(1)−1(2)+0(3)+1(2)−1(3)+0 (3)+1(4)−1(1)+0(1)+1(1)6(2)+−2(3)+−3(2)6(3)+−2(3)+ −3(4)6(1)+−2(1)+−3(1)]=[100010001]

Попытайся #3

Найдите обратную матрицу 3×33×3.

А=[2-1711-111-703-2]А=[2-1711-111-703-2]

Решение системы линейных уравнений с использованием обратной матрицы

Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: XX — матрица, представляющая переменные системы, и BB — это матрица, представляющая константы. Используя умножение матриц, мы можем определить систему уравнений с тем же количеством уравнений в качестве переменных, что и

АКС=ВАХ=В

Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть AA будет матрицей коэффициентов, пусть XX будет переменной матрицей, а пусть BB будет постоянной матрицей. Таким образом, мы хотим решить систему AX=B.AX=B. Например, посмотрите на следующую систему уравнений.

a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2

Из этой системы матрица коэффициентов равна

А=[a1b1a2b2]А=[a1b1a2b2]

Переменная матрица

Х=[ху]Х=[ху]

А постоянная матрица

Б=[с1с2]Б=[с1с2]

Тогда AX=BAX=B выглядит как

[a1b1a2b2] [xy]=[c1c2][a1b1a2b2] [xy]=[c1c2]

Вспомните ранее в этом разделе обсуждение умножения действительного числа на его обратное, (2−1)2=(12)2 =1.(2−1)2=(12)2=1. Чтобы решить одно линейное уравнение ax=bax=b относительно x,x, мы должны просто умножить обе части уравнения на мультипликативную обратную (обратную) а. а. Таким образом,

ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1) b x=(a−1)b ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1)b x=(a−1)b

Единственная разница между решением линейного уравнения и системы уравнений, записанной в матричной форме, заключается в том, что найти обратную матрицу сложнее, а матрицу умножение — более длительный процесс. Однако цель та же — изолировать переменную.

Мы подробно изучим эту идею, но лучше начать с системы 2×22×2, а затем перейти к системе 3×33×3.

Решение системы уравнений с использованием обратной матрицы

Для данной системы уравнений запишите матрицу коэффициентов A,A, переменную матрицу X,X и постоянную матрицу B.B. Затем

AX=BAX=B

Умножьте обе части на обратную AA, чтобы получить решение .

(A-1)AX=(A-1)B[(A-1)A]X=(A-1)BIX=(A-1)BX=(A-1)B(A-1) AX=(A-1)B[(A-1)A]X=(A-1)BIX=(A-1)BX=(A-1)B

вопросы и ответы

Если матрица коэффициентов не имеет обратной, означает ли это, что система не имеет решения?

Нет, если матрица коэффициентов необратима, то система может быть несовместной и не иметь решения, либо быть зависимой и иметь бесконечно много решений.

Пример 7

Решение системы 2 × 2 с помощью обратной матрицы

Решите заданную систему уравнений с помощью обратной матрицы.

3x+8y=54x+11y=73x+8y=54x+11y=7

Решение

Запишите систему с помощью матрицы коэффициентов, матрицы переменных и матрицы констант.

A=[38411],X=[xy],B=[57]A=[38411],X=[xy],B=[57]

Затем

[38411] [xy]=[57 ][38411] [xy]=[57]

Сначала нам нужно вычислить A−1.A−1. Используя формулу для вычисления обратной матрицы 2 на 2, мы имеем:

A−1=1ad−bc[d−b−ca] =13(11)−8(4)[11−8−43] =11[11−8−43]A−1=1ad−bc[d−b−ca] =13(11)−8(4)[11−8−43] =11[11−8−43]

Итак,

A−1=[11−8−43]A−1=[11−8−43]

Теперь мы готовы решать. Умножьте обе части уравнения на A−1.A−1.

(A−1)AX=(A−1)B[11−8−43] [38411] [xy]=[11−8−43] [57][1001] [xy]=[11(5 )+(−8)7−4(5)+3(7)][xy]=[−11](A−1)AX=(A−1)B[11−8−43] [38411] [ xy]=[11−8−43] [57][1001] [xy]=[11(5)+(−8)7−4(5)+3(7)][xy]=[−11]

Решение (−1,1). (−1,1).

вопросы и ответы

Можем ли мы найти XX, найдя произведение BA-1?BA-1?

Нет, напомним, что умножение матриц не является коммутативным, поэтому A−1B≠BA−1.A−1B≠BA−1. Рассмотрим наши действия по решению матричного уравнения.

(A-1)AX=(A-1)B[(A-1)A]X=(A-1)BIX=(A-1)BX=(A-1)B(A-1) )AX=(A−1)B[(A−1)A]X=(A−1)BIX=(A−1)BX=(A−1)B

Обратите внимание, что на первом шаге мы умножили оба сторон уравнения на A-1,A-1, но A-1A-1 был слева от AA с левой стороны и слева от BB с правой стороны. Поскольку умножение матриц не является коммутативным, порядок имеет значение.

Пример 8

Решение системы 3 × 3 с помощью обратной матрицы

Решите следующую систему с помощью обратной матрицы.

5x+15y+56z=35-4x-11y-41z=-26-x-3y-11z=-75x+15y+56z=35-4x-11y-41z=-26-x-3y-11z=- 7

Решение

Напишите уравнение AX=B. AX=B.

[51556-4-11-41-1-3-11] [xyz]=[35-26-7][51556-4-11-41-1-3-11] [xyz]=[35- 26−7]

Во-первых, мы найдем обратное к АА путем добавления к тождеству.

[51556-4-11-41-1-3-11|100010001][51556-4-11-41-1-3-11|100010001]

Умножить строку 1 на 15,15.

[13565-4-11-41-1-3-11|1500010001][13565-4-11-41-1-3-11|1500010001]

Умножить строку 1 на 4 и добавить ко второй строке. | 150045101501] [13565011950015 | 150045101501]

Умножение ряда 2 на −3 и добавить в строку 1.

[10-15011950015 | −115–3045101501] [10–15011950015 | −115 — 305101501] [10–15011950015 | −115 — 305101501]. 5.

[10−1501195001|−115−304510105][10−1501195001|−115−304510105]

Умножить строку 3 на 1515 и прибавить к строке 1.

[10001195001|-2-314510105][10001195001|-2-314510105]

Умножить строку 3 на -195-195 и добавить к строке 2.

[10001-00001|-2-191-31][-2-191-31 |−2−31−31−19105]

Итак,

A−1=[−2−31−31−19105]A−1=[−2−31−31−19105]

Умножить обе части уравнение на A−1. A−1. Нам нужно A-1AX=A-1B:A-1AX=A-1B:

[-2-31-31-19105] [51556-4-11-41-1-3-11] [xyz]=[ −2−31−31−19105] [35−26−7][−2−31−31−19105] [51556−4−11−41−1−3−11] [xyz]=[−2−31 −31−19105] [35−26−7]

Таким образом,

A−1B=[−70+78−7−105−26+13335+0−35]=[120]A−1B=[−70+78−7−105−26+13335+ 0−35]=[120]

Решение: (1,2,0).(1,2,0).

Попытайся #4

Решите систему, используя обратную матрицу коэффициентов.

2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2 2x−17y+11z=0 −x+11y−7z=8 3y-2z=-2

Как

Дана система уравнений. Решите ее с помощью обратной матрицы с помощью калькулятора.

Сохраните матрицу коэффициентов и матрицу констант как матричные переменные [A][A] и [B].[B].
Введите умножение в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
Если матрица коэффициентов обратима, калькулятор представит матрицу решения; если матрица коэффициентов необратима, калькулятор выдаст сообщение об ошибке.

Пример 9

Использование калькулятора для решения системы уравнений с обратными матрицами

Решите систему уравнений с обратными матрицами с помощью калькулятора 4y+z=−2

Решение

На странице матрицы калькулятора введите матрицу коэффициентов в качестве матричной переменной [A],[A] и введите матрицу констант в качестве матричной переменной [B].[B].

[A]=[231331241], [B]=[32−27−2][A]=[231331241], [B]=[32−27−2]

На главном экране калькулятора, введите умножение для решения X, X, вызывая каждую переменную матрицы по мере необходимости.

[A]-1×[B][A]-1×[B]

Вычислите выражение.

[−59−34252][−59−34252]

7.

7 Секционные упражнения

Устный

В предыдущем разделе мы показали, что умножение матриц некоммутативно, то есть в большинстве случаев AB≠BAAB≠BA. Можете ли вы объяснить, почему умножение матриц является коммутативным для обратных матриц, то есть A−1A=AA−1?A−1A=AA−1?

Любая ли матрица 2×22×2 имеет обратную? Объясните, почему да или почему нет. Объясните, какое условие необходимо для существования обратного.

Можете ли вы объяснить, может ли матрица 2×22×2 с целым рядом нулей иметь обратную?

Может ли матрица с целым столбцом нулей иметь обратную? Объясните, почему да или почему нет.

Может ли матрица с нулями по диагонали иметь обратную? Если да, то найдите пример. Если нет, то докажите, почему. Для простоты предположим матрицу 2×22×2.

Алгебраический

В следующих упражнениях покажите, что матрица AA является обратной матрицей B.B.

А=[10-11],В=[1011]А=[10-11],В=[1011]

А=[1234],В=[-2132-12]А=[1234],В=[-2132-12]

А=[4570],В=[01715-435]А=[4570],В=[01715-435]

А=[-2123-1],В=[-2-1-6-4]А=[-2123-1],В=[-2-1-6-4]

10.

A=[10101−1011],B=12[21−10110−11]A=[10101−1011],B=12[21−10110−11]

11.

А=[123402169],B=14[60-217-3-5-1224]A=[123402169],B=14[60-217-3-5-1224]

12.

A=[3821115612],B=136[−684−67−261−1−225]A=[3821115612],B=136[−684−67−261−1−225]

Для следующих упражнений найдите мультипликативную обратную каждую матрицу, если она существует.

13.

[3−219][3−219]

14.

[-2231][-2231]

15.

[-3792][-3792]

16.

[−4−3−58][−4−3−58]

17.

[1122][1122]

18.

[0110][0110]

19.

[0,51,51-0,5][0,51,51-0,5]

20.

[106-217302][106-217302]

21.

[01-3410105][01-3410105]

22.

[12-1-341-2-4-5][12-1-341-2-4-5]

23.

[19−32564−27][19]−32564−27]

24.

[1-23-48-12142][1-23-48-12142]

25.

[121212131415161718][121212131415161718]

26.

[123456789][123456789]

Для следующих упражнений решите систему, используя обратную матрицу 2×22×2.

27.

5x−6y=−614x+3y=−25x−6y=−614x+3y=−2

28.

8x+4y=-1003x-4y=18x+4y=-1003x-4y=1

29.

3x−2y=6−x+5y=−23x−2y=6−x+5y=−2

30.

5x−4y=−54x+y=2,35x−4y=−54x+y=2,3

31.

−3x−4y=912x+4y=−6−3x−4y=912x+4y=−6

32.

−2x+3y=310−x+5y=12−2x+3y=310−x+5y=12

33.

85x−45y=25−85x+15y=71085x−45y=25−85x+15y=710

34.

12x+15y=-1412x-35y=-9412x+15y=-1412x-35y=-94

Для следующих упражнений решите систему, используя обратную систему 3×33×3. матрица.

35.

3x-2y+5z=215x+4y=37x-2y-5z=53x-2y+5z=215x+4y=37x-2y-5z=5

36.

4x+4y+4z=402x-3y+4z=-12-x+3y+4z=94x+4y+4z=402x-3y+4z=-12-x+3y+4z=9

37.

6x-5y-z=31-x+2y+z=-63x+3y+2z=136x-5y-z=31-x+2y+z=-63x+3y+2z=13

38.

6x−5y+2z=−42x+5y−z=122x+5y+z=126x−5y+2z=−42x+5y−z=122x+5y+z=12

39.

4x-2y+3z=-122x+2y-9z=336y-4z=14x-2y+3z=-122x+2y-9z=336y-4z=1

40.

110x−15y+4z=−41215x−20y+25z=−101310x+4y−310z=23110x−15y+4z=−41215x−20y+25z=−101310x+4y−310z=23

41.

12x-15y+15z=31100-34x-14y+12z=740-45x-12y+32z=1412x-15y+15z=31100-34x-14y+12z=740-45x-12y+32z=14

42.

0,1x+0,2y+0,3z=-1,40,1x-0,2y+0,3z=0,60,4y+0,9z=-20,1x+0,2y+0,3z=-1,40,1x-0,2y+0,3z= 0,60,4г+0,9z=−2

Технология

В следующих упражнениях используйте калькулятор для решения системы уравнений с обратными матрицами.

43.

2x-y=-3-x+2y=2,32x-y=-3-x+2y=2,3

44.

−12x−32y=−432052x+115y=314−12x−32y=−432052x+115y=314

45.

12,3x-2y-2,5z=236,9x+7y-7,5z=-78y-5z=-1012,3x-2y-2,5z=236,9x+7y-7,5z=-78y-5z=-10

46.

0,5x-3y+6z=-0,80,7x-2y=-0,060,5x+4y+5z=00,5x-3y+6z=-0,80,7x-2y=-0,060,5x+4y+5z=0

Расширения

Для следующих упражнений найдите обратную заданную матрицу.

47.

[1010010101100011][1010010101100011]

48.

[−1025000202−101−301][−1025000202−101−301]

49.

[1-230010214-23-5011][1-230010214-23-5011]

50.

[1202302100003010200100120][1202302100003010200100120]

51.

[100000010000001000000100000010111111][100000010000001000000100000010111111]

Реальные приложения

Для следующих упражнений напишите систему уравнений, описывающую ситуацию. Затем решите систему, используя обратную матрицу.

52.

На баскетбольный матч продано 2400 билетов. Если цены на 1 и 2 этаж были разными, а общая сумма денег составила 64 000 долларов, сколько стоил каждый билет?

53.

Если в предыдущем упражнении вам сказали, что на второй этаж продано на 400 билетов больше, чем на первый, сколько стоил каждый билет?

54.

Продовольственная акция собрала два разных вида консервов, стручковую фасоль и фасоль. Общее количество собранных банок составило 350, а общий вес всей пожертвованной еды составил 348 фунтов 12 унций. Если банки с зеленой фасолью весят на 2 унции меньше, чем банки с фасолью, сколько из каждой банки было пожертвовано?

55.

Учеников попросили принести в класс свои любимые фрукты. 95% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были в два раза популярнее бананов, а яблоки на 5% менее популярны, чем бананы, каков процент каждого фрукта в отдельности?

56.

Женское общество устроило распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 1 доллар, а печенье с шоколадной крошкой — в 0,75 доллара. Они собрали 700 долларов и продали 850 предметов. Сколько пирожных и сколько печенья было продано?

57.

Магазину одежды необходимо заказать новый инвентарь. В продаже есть три разных типа шляп: соломенные шляпы, шапочки и ковбойские шляпы. Соломенная шляпа стоит 13,99 долларов, шапочка — 7,99 долларов, а ковбойская шляпа — 14,49 долларов. Если в прошлом квартале было продано 100 головных уборов, выручка от продаж составила 1119 долларов, а количество проданных шапок было на 10 больше, чем ковбойских шляп, сколько каждой из них должен заказать магазин одежды взамен уже проданных?

58.

Анна, Эшли и Андреа вместе весят 370 фунтов. Если Андреа весит на 20 фунтов больше, чем Эшли, а Анна весит в 1,5 раза больше, чем Эшли, сколько весит каждая девочка?

59.

Трое соседей по комнате разделили упаковку из 12 плиток мороженого, но никто не помнит, кто сколько съел. Если Том съел в два раза больше плитки мороженого, чем Джо, а Альберт съел на три плитки меньше, чем Том, сколько плиток мороженого съел каждый сосед по комнате?

60.

Фермер построил курятник из проволочной сетки, дерева и фанеры. Проволочная сетка стоила 2 доллара за квадратный фут, дерево — 10 долларов за квадратный фут, а фанера — 5 долларов за квадратный фут. Фермер потратил в общей сложности 51 доллар, а общее количество использованных материалов составило 14 футов 2,14 фута 2. Он использовал проволочную сетку на 3 фута 23 фута больше, чем фанеру. Сколько каждого материала использовал фермер?

61.

У Джея на заднем дворе растут лимонные, апельсиновые и гранатовые деревья. Апельсин весит 8 унций, лимон 5 унций, а гранат 11 унций. Джей собрал 142 фрукта общим весом 70 фунтов 10 унций. Он собрал в 15,5 раз больше апельсинов, чем гранатов. Сколько плодов каждого сорвал Джей?

Калькулятор обратной системы уравнений Образование

Тип фильтра:

Калькулятор обратной функции Mathway

Детали: Шаг 1: Введите ниже функцию, для которой вы хотите найти обратную. Калькулятор обратной функции находит обратную заданной функции. Если f (x) f ( x ) — заданная функция, то обратная функция вычисляется путем замены переменных местами и выражения x как функции y, т. Е. x = f (y) x = f ( y ).

› Проверено 2 дня назад

› Просмотр: Детали

› Получите больше: EducationView Education

Калькулятор обратной функции — найдите обратную функцию с помощью …

Подробности: WebHow для расчета обратной функции (пошагово): Вычислите обратную функцию (f-1) заданной функции, выполнив следующие шаги: Сначала возьмите функцию f (y), имеющую y в качестве переменной. …

› Проверено 8 дней назад

› Посмотреть: Подробности

› Получить больше: EducationView Education

Функции Обратный калькулятор — Symbolab

обратные функции шага -Бесплатные функции обратного шага0 Подробности: Web обратные функции find8 -шаг. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. Используя этот сайт, вы соглашаетесь с нашими …

› Проверено 9 дней назад

› Посмотреть: Детали

› Получить больше: EducationView Education

Калькулятор обратной функции — Бесплатный онлайн калькулятор — BYJUS

чрезвычайно простой в использовании онлайн-инструмент. Выполните следующие шаги, чтобы найти обратную функцию. Шаг 1: Введите любую функцию в поле ввода …

› Проверено 6 дней назад

› View: Details

› Подробнее: EducationView Education

Калькулятор линейных уравнений: Метод обратной матрицы — OnlineMSchool

Details: WebЕсли в вашем уравнении отсутствует какая-либо переменная, то в этом месте калькулятора, введите ноль. Если перед переменной в уравнении нет номера, то в соответствующее поле введите …

› Verified 6 days ago

› View: Details

› Get more: EducationView Education

Решатель систем уравнений: WolframAlpha

Детали: WebEigenvalue Calculator; Калькулятор обратной матрицы; Что такое системы уравнений? Система уравнений представляет собой набор из одного или нескольких уравнений, включающих ряд переменных. …

› Подтверждено 7 дней назад

› Посмотреть: Детали

› Получить больше: EducationView Education

Обратный калькулятор матрицы: WolframAlpha

Детали0048 WebБольше, чем просто онлайн-калькулятор обратной матрицы. WolframAlpha — идеальный сайт для вычисления обратной матрицы. Используйте WolframAlpha для просмотра пошаговых методов …

› Verified 6 days ago

› View: Details

› Get more: EducationView Education

Калькулятор метода обратной матрицы — Reshish

6 WebЧтобы решить систему линейных уравнений методом обратной матрицы, вам необходимо выполнить следующие шаги. Задайте основную матрицу и вычислите обратную ей (если она не вырожденная). …

›Проверено 3 дня назад

› Просмотр: Подробная информация

›Получить больше: EducationView Education

Система уравнений Калькулятор — Mathpapa

Детали: . уравнения шаг за шагом. Пример (Нажмите для просмотра) x+y=7; x+2y=11 Попробуйте прямо сейчас. Введите уравнения в поле …

› Проверено 7 дней назад

› Просмотр: Детали

› Подробнее: EducationView Education

Калькулятор системы уравнений — Symbolab

Подробности: Калькулятор системы уравнений WebFree — пошаговое решение системы уравнений Обновление до версии Pro Продолжить работу с сайтом Этот веб-сайт использует файлы cookie для обеспечения вы получите лучший опыт.

› Проверено 2 дня назад

› Посмотреть: Подробности

› Получить больше: EducationView Education

Обратный матричный метод — решение любых систем уравнения

Подробности: WebСпособ использования обратной матрицы для решения систем уравнений заключается в следующем: 1) сохранение системы уравнений в матричном виде, 2) вычисление обратной . 3) Умножьте…

›Проверено 6 дней назад

› Просмотр: Подробная информация

›Получить больше: Образование образования

Калькулятор. уравнения: линейные, квадратные, кубические, обратные, 4-й степени, тригонометрические и гиперболические. Применяется: группировки, замены, табличные формулы, нахождение рационального корня, …

›Проверено 3 дня назад

› Просмотр: Подробная информация

›Получить больше: EducationView Education

Система линейных уравнений с использованием обратной матрицы (4 переменная)

. легко для вас, чтобы определить обратную матрицу за доли секунды с шагами. LinearEquationsCalculator.com. Калькулятор дробей; Решение …

› Проверено 6 дней назад

› View: Details

› Get more: EducationView Education

Решить систему уравнений Калькулятор обратной матрицы

Подробности: WebSolving систем уравнений с использованием обратных матриц вы матричный калькулятор wolfram alpha 2 урок линейной по методу 6 1 алгебра 3 обратных решения решить заданное …

› Проверено 1 дня назад

› Просмотр: Детали

› Получить больше: EducationView Education

Калькулятор системы уравнений — Знакомство с электроникой

Детали: WebКалькулятор системы уравнений 2×2 вычисляет решение 2 линейных уравнений, содержащих 2 переменные.

Решение методом обратной матрицы. Решение систем линейных уравнений с помощью обратной матрицы. Решение матричных уравнений

Предупреждение

Матричный метод решения систем линейных уравнений

Примеры решения системы линейных уравнений матричным методом

Теорема условия существования обратной матрицы

Алгоритм нахождения обратной матрицы

Решение матричных уравнений

Матричный метод в экономическом анализе

Пример решения неоднородной СЛАУ.

решаем системы линейных алгебраических уравнений (слау)

Три случая при решении систем линейных уравнений

Примеры решения систем линейных уравнений методом Крамера

К началу страницы

Продолжаем решать системы методом Крамера вместе

Действия над матрицами

Обратная матрица. Решение систем линейных уравнений матричным способом

Решение систем линейных уравнений методом обыкновенных жордановых исключений

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

Решение систем дифференциальных уравнений матричным способом — справочник студента

Решить систему уравнений матричным методом самостоятельно, а затем посмотреть решение

Матричный метод онлайн

Глава 4. Матрицы и дифференциальные уравнения

Исследование методов решения системы дифференциальных уравнений с постоянной матрицей (стр. 1 из 3)

3. Нахождение собственных чисел и построение ФСР

8. Решение неоднородной системы

Заключение

4. Построение фундаментальной матрицы решений методом Эйлера

Решение алгебраических уравнений методом крамера.

Системы линейных алгебраических уравнений

Решение СЛАУ методом Крамера

Описание метода Крамера.

Примеры решения систем уравнений методом Крамера.

Метод Крамера.

5.Обратная матрица.Способы нахождения. Достаточное условие существования обратной матрицы.

3.4: Решающие системы с инверсиями

Матрица идентичности

Нахождение мультипликативного обратного путем увеличения тождества

Нахождение мультипликативной обратной матрицы \(2×2\) с использованием формулы

Нахождение обратной мультипликативной матрицы с помощью калькулятора

Решение системы линейных уравнений с использованием обратной матрицы

Ключевые уравнения

Авторы и авторство

Как решать системы с использованием обратных матриц — Криста Кинг Математика

Мы знаем, как решать системы уравнений, но теперь мы посмотрим, как это сделать, используя обратную матрицу

Как использовать обратные матрицы для решения систем уравнений

Пройти курс

Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂

Использование обратной матрицы для решения системы

Получите доступ к полному курсу линейной алгебры

Решение системы линейных уравнений с использованием обратной матрицы | Колледж Алгебра |

Общее примечание. Решение системы уравнений с использованием обратной матрицы

Вопросы и ответы

Если матрица коэффициентов не имеет обратной, означает ли это, что система не имеет решения?

Пример 7. Решение системы 2 × 2 с использованием обратной матрицы

Решение

Пример 8. Решение системы 3 × 3 с использованием обратной матрицы

Решение

Попробуйте 4

Как сделать: Имея систему уравнений, решите с помощью калькулятора обратные матрицы.

Пример 9. Использование калькулятора для решения системы уравнений с обратными матрицами

Решение

Лицензии и атрибуты

Лицензионный контент CC, Конкретное авторство

Курсы PDF, Упражнения, Документы pdf, ppt, бесплатно PDF

Титр

7.7 Решение систем с инверсиями — Алгебра колледжа

Цели обучения

Нахождение обратной матрицы

Матрица тождества и мультипликативная обратная

Пример 1

Показывая, что матрица идентичности действует как 1

Решение

Как

Пример 2

Демонстрация того, что матрица

Решение

Попытайся #1

Нахождение мультипликативного обратного с помощью умножения матриц

Пример 3