Числовые системы. Элементы теории множеств и алгебры. Натуральные числа. Целые числа. Рациональные числа. Действительные числа. Комплексные числа
- Акции
- Книги
- Художественная литература
- Художественная литература
- Детективы
- Поэзия
- Фантастика
- Подарочные и эксклюзивные издания
 Досуг
Досуг- Дом, быт
- Домашние животные, аквариум, пчеловодство
- Рукоделие
- Садоводство
- Спорт
- Кулинария
- Специализированная литература
- Военная техника и оружие, униформа, награды
- Эзотерика
- Философия
- Искусство, культура, кино и эстрада
- Архитектура
- Музыка
- История
- Краеведение
- Мать и дитя
- Медицина специальная
- Медицина и здоровье
- Наука и техника
- Автомобильная тематика
- Компьютер
- Психология
- Экономическая литература
- Юридическая литература
- Детская литература
- Детская школьная
- Детская дошкольная
- Раскраски
- Энциклопедии школьные, дошкольные
- Учебная и методическая литература.
 Словари
Словари- Учебная школьная литература
- Универсальные энциклопедии (справочники)
- Методика (школьная)
- Методика (дошкольная)
- Иностранные языки (школьные учебники)
- Литература на иностранных языках
- Иностранные языки (худож.
 )
)
- Иностранные языки (худож.
- Комиксы Показать все книги
- Художественная литература
- Подарки и сувениры
- Игры и игрушки
- Товары для творчества
- Календари
- Канцтовары
- Карты и путеводители
- Наука и техника
- Автор
Молдаванский Д.
 И.
И. - Год издания 2019
- Издательство URSS
В настоящей работе приводится аксиоматическое построение систем натуральных, целых, рациональных, действительных и комплексных чисел.
 Показано, как из предлагаемой системы аксиом выводятся утверждения, соответствующие интуитивным представлениям читателя о свойствах данной числовой системы. В частности, доказаны основные свойства отношения делимости целых чисел. В предположении непротиворечивости аксиоматики натуральных чисел доказывается непротиворечивость всех остальных систем аксиом, а именно: показано, как, располагая моделью для натуральных чисел, построить последовательно модели для целых, рациональных, действительных и комплексных чисел. В каждом случае установлена также единственность модели. При формулировке аксиом и доказательстве всех утверждений используются язык и методы современной алгебры; подробному изложению необходимых сведений из алгебры и теории множеств посвящен первый, вводный, параграф пособия. книга предназначена для преподавателей и студентов математических факультетов университетов.
Показано, как из предлагаемой системы аксиом выводятся утверждения, соответствующие интуитивным представлениям читателя о свойствах данной числовой системы. В частности, доказаны основные свойства отношения делимости целых чисел. В предположении непротиворечивости аксиоматики натуральных чисел доказывается непротиворечивость всех остальных систем аксиом, а именно: показано, как, располагая моделью для натуральных чисел, построить последовательно модели для целых, рациональных, действительных и комплексных чисел. В каждом случае установлена также единственность модели. При формулировке аксиом и доказательстве всех утверждений используются язык и методы современной алгебры; подробному изложению необходимых сведений из алгебры и теории множеств посвящен первый, вводный, параграф пособия. книга предназначена для преподавателей и студентов математических факультетов университетов.
Новости
Double, Float — не вещественные числа / Хабр
Во многих источниках тип double и float, числа с плавающей запятой/точкой зачем-то называют вещественными. Такое чувство что кто-то когда-то совершил ошибку или не внимательно написал эту глупость и все как один начали её повторять, совершенно не задумываясь о чём они говорят.
Такое чувство что кто-то когда-то совершил ошибку или не внимательно написал эту глупость и все как один начали её повторять, совершенно не задумываясь о чём они говорят.
Ладно это были бы просто троечники студенты и любители, так эту ошибку говорят и те, кто обучают специалистов. И эта проблема терминологии не одного ЯП, их правда много (Java, C++, C#, Python, JS и т.д.) везде, где бы я не искал, всегда находятся статьи, ответы, лекции, где дробные числа называют вещественными!
Вот ОЧЕНЬ МАЛЕНЬКАЯ выборка:
https://javarush.ru/quests/lectures/questsyntaxpro.level04.lecture06 — JavaRush
https://docs-python.ru/tutorial/osnovnye-vstroennye-tipy-python/tip-dannyh-float-veschestvennye-chisla/ — Docs Python3
http://cppstudio.com/post/310/ — CppStudio
https://ejudge.ru/study/3sem/sem07.pdf — Ejudge
https://ru.wikipedia.org/wiki/Система_типов_Си — даже всеми любимая Wikipedia!
Ещё раз повторюсь это очень маленькая выборка, можете набрать в гугл поиске, по ключевым словам, и удостовериться что их полно.

Начнём с простого, что такое вещественное число коим называют double и float. Будет немного формул, но не пугайтесь, прочитайте пожалуйста до конца, они очень простые, к каждой я даю интуитивное объяснение.
Вещественное число
Определение можете прочитать в Википедии или дочитать до конца мою статью, где я простым языком скажу или вы сами поймёте, но нужно проследить за мыслью, которую я хочу донести до вас. Я напишу формулой из теории множеств:
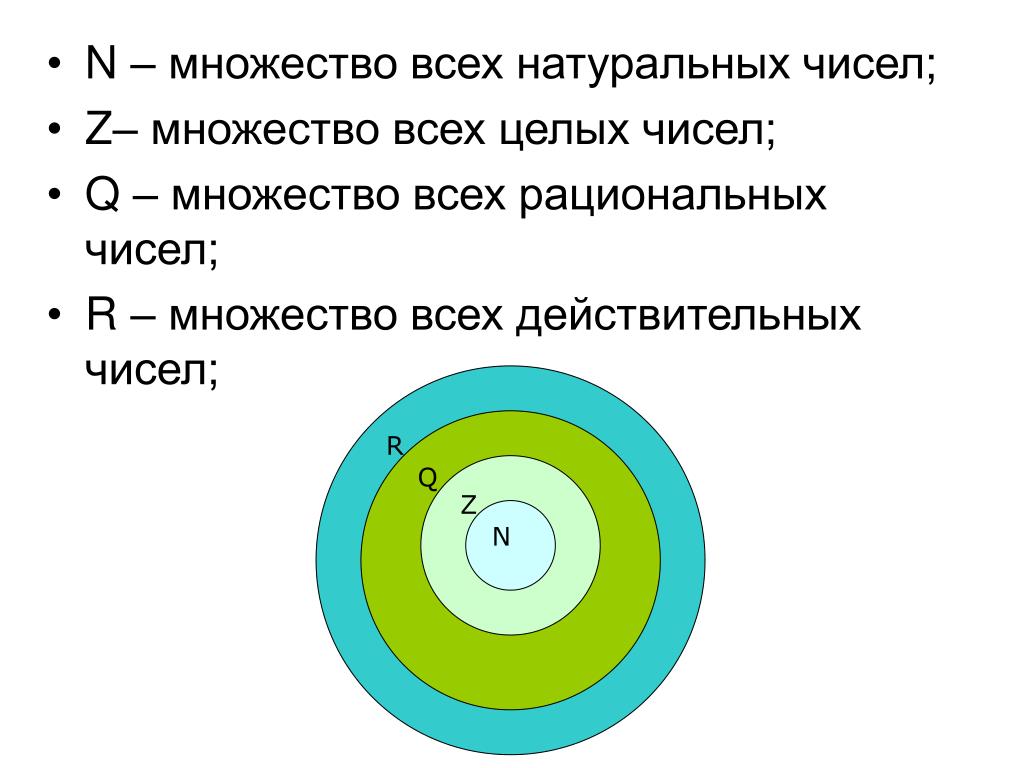
R = Q ∪ I
Где, R — множество вещественных чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел.
Так же Q ⊂ R и I ⊂ R.
Расшифровка тем, кто не очень с теорией множеств. Вещественные числа эта числа которые включают в себя Рациональные и Иррациональные числа (R = Q ∪ I), т.к. Вещественные числа включают их в себя, то Рациональные числа и Иррациональные числа являются подмножеством множества Вещественных (Q ⊂ R и I ⊂ R), причём строго, то есть Q != R и I != R, это очевидная мысль, но её требуется подчеркнуть.
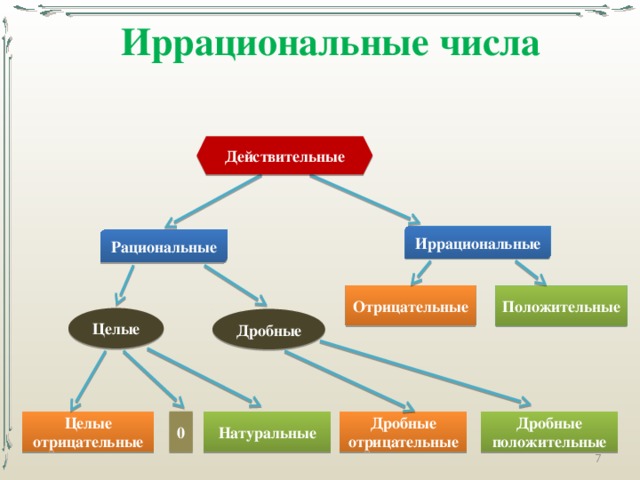
Теперь к самому интересному, какие числа называются Рациональными и Иррациональными (представляю себя преподавателем начальных курсов технических вузов).
Рациональные
Начнём с Рациональных, возьмём определение из википедии.
Рациональное число (от лат. ratio «отношение, деление, дробь») — число, которое можно представить в виде обыкновенной дроби m/n, где m — целое число, а n — натуральное.
Так же стоит отметить, что Рациональные включают в себя Целые и Натуральные числа (-1, 0, 1, 2 …) их можно выразить в виде дроби, 1 = 1/1, 2 = 2/1, -1 = -1/1, 0 = 0/1 и т.д.
Почему это важно? Потому что Иррациональные числа не включают в себя Целые и Натуральные числа, это отдельный класс чисел.
Иррациональные
Берём определение из Википедии.
Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби m/n, где m,n — целые числа, n != 0.
Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Так же приведу примеры иррациональных чисел, чтобы стало понятно: π (число пи), e (число Эйлера), √2.
Вы начали что-то подозревать? Если нет я помогу вам.
Первое предложение определения — это то, о чём я вам говорил, то, что Иррациональные числа — это отдельный класс чисел и он не включает в себя Целые и Натуральные.
Но самое важное здесь это второе предложение «Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.».
Что это значит? Заметили, что в примерах я дал вам буквенное обозначение? Это не просто так, это представление иррационального числа, ВАЖНО — сама запись π это не само иррациональное число, это всего лишь его представление, и оно является чем угодно, но не иррациональным числом. Само Иррациональное число оно бесконечно. Понимаете?
То есть его невозможно записать по определению. Никакой памяти в компьютере не хватит чтобы его записать. Это невозможно!
Никакой памяти в компьютере не хватит чтобы его записать. Это невозможно!
И мало того что в большинстве (я не проверял прям на всех, но очень сомневаюсь, что хотя бы в одном это есть) языков в которых используется термин Вещественный тип нельзя чисто синтаксически сделать запись по типу: «double a = π», попросту будет ошибка компиляции, так ещё если и возможно с помощью латинских букв подключая библиотеки, то в конечном-то итоге эта переменная будет ссылаться на конечное представление, а то есть рациональное этого иррационального числа!
Всё с чем мы можем работать это ТОЛЬКО РАЦИОНАЛЬНЫЕ ЧИСЛА, представления иррациональных чисел они ТОЖЕ рациональные и ТОЛЬКО рациональные. Они большие, они могут быть ооооочень большими, но они всё равно рациональные!
R = Q ∪ I, если мы исключаем I из-за невозможности работы с ними в прямом смысле без представлений получается R’ = R\I, R’ = Q, а Q у нас рациональные числа.
Так почему же так много людей и весьма неглупых всё ещё допускают эту простую ошибку? Эту ошибку можно было описать в пару предложений, но я хотел донести до вас последовательно как к этому прийти, используя общепринятую терминологию.
Спасибо.
P.S. Это моя оригинальная статья AfterWing, не является переводом, доработкой другой какой-либо статьи на русском/английском и др. языках.
21. Реальные числа — логика и доказательство 3.18.4 документация
21.1. Системы счисления
Мы уже познакомились с некоторыми фундаментальными системами счисления: натуральными числами \(\mathbb{N}\), целыми числами \(\mathbb{Z}\) и рациональными числами \( \mathbb{Q}\). В некотором смысле каждый последующий элемент списка был призван исправить недостатки предыдущей системы. Мы можем вычесть любое целое число из любого другого целого числа и получить другое целое число, и мы можем разделить любое рациональное число на ненулевое рациональное число и получить рациональное число.
Целые числа удовлетворяют всем следующим свойствам:
Сложение ассоциативно и коммутативно.
Существует аддитивная единица \(0\), и каждый элемент \(x\) имеет аддитивный обратный \(-x\).

Умножение ассоциативно и коммутативно.
Существует мультипликативная идентичность \(1\).
Умножение опережает сложение: для любых \(x\), \(y\) и \(z\) имеем \(x (y + z) = x y + x z\).
Заказ \(\leq\) является полным заказом.
Для любых элементов \(x\), \(y\) и \(z\), если \(x \leq y\), то \(x + z \leq y + z\).
Для любых элементов \(x\) и \(y\), если \(0 \leq x\) и \(0 \leq y\), то \(0 \leq x y\).
Первые пять предложений говорят, что с \(\times\), \(+\), \(0\) и \(1\) целые числа образуют коммутативное кольцо , а последние три говорят, что вместе с \(\leq\) структура представляет собой заказал кольцо . У натуральных чисел нет аддитивных инверсий, поэтому они удовлетворяют несколько более слабому набору аксиом, которые делают их упорядоченным полукольцом . С другой стороны, рациональные числа также образуют упорядоченное кольцо, удовлетворяющее следующему дополнительному свойству:
Это делает их экземпляром упорядоченного поля .
Стоит знать, что когда у нас есть натуральные числа, можно построить целые и рациональные числа, используя уже знакомые вам теоретико-множественные конструкции. Например, мы можем взять целое число как пару \((i, n)\) натуральных чисел, где \(i\) равно 0 или 1, с тем намерением, что \((0, n)\) представляет положительное целое число \(n\), а \((1, n)\) представляет отрицательное целое число \(-(n+1)\). (Мы используем \(-(n+1)\) вместо \(-n\), чтобы избежать двух представлений \(0\).) С этим определением целые числа просто \(\{0, 1\ } \times \mathbb{N}\). Затем мы можем перейти к определению операций сложения и умножения, обратной аддитивной функции и отношения порядка и доказать, что они обладают нужными свойствами.
Побочным эффектом этой конструкции является то, что сами натуральные числа не являются целыми; например, мы должны различать натуральное число \(2\) и целое число \(2\). Так обстоит дело в Лин. В обычной математике принято думать о натуральных числах как о подмножестве целых чисел.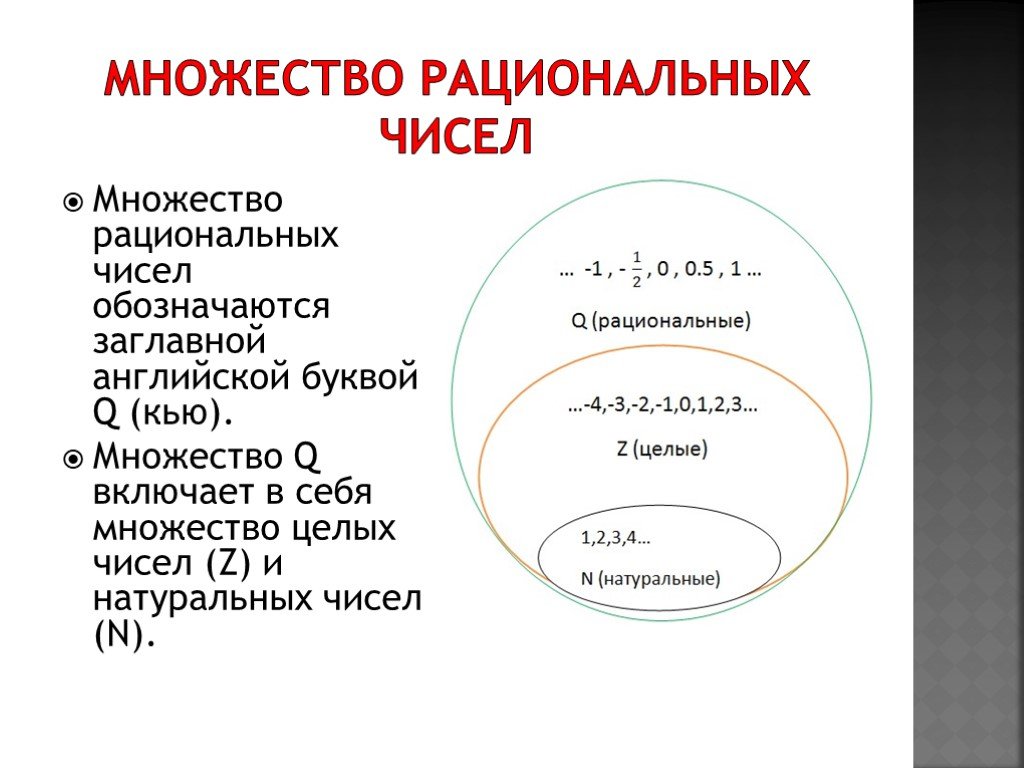 Однако, как только мы создадим целые числа, мы можем отбросить старую версию натуральных чисел и впоследствии идентифицировать натуральные числа как неотрицательные целые числа.
Однако, как только мы создадим целые числа, мы можем отбросить старую версию натуральных чисел и впоследствии идентифицировать натуральные числа как неотрицательные целые числа.
Мы можем сделать то же самое для рациональных чисел, определив их как множество пар \((a, b)\) в \(\mathbb{Z} \times \mathbb{N}\), где либо \( a = 0\) и \(b = 1\), или \(b > 0\) и \(a\) и \(b\) не имеют общего делителя (кроме \(1\) и \(- 1\)). Идея состоит в том, что \((a, b)\) представляет \(a/b\). При таком определении рациональные числа на самом деле являются подмножеством \(\mathbb{Z} \times \mathbb{N}\), и мы можем соответствующим образом определить все операции.
В следующем разделе мы определим более сложный подход, который будет масштабироваться до определения действительных чисел. А в следующей главе мы покажем, как построить натуральные числа из аксиом теории множеств. Это показывает, что мы можем построить все системы счисления снизу вверх.
Но сначала давайте остановимся на мгновение, чтобы подумать, зачем нужны реальные числа. 2 = 2 \). Но кажется интуитивно ясным, что должно быть что-то номер со следующим свойством: \(\sqrt{2}\) — длина диагонали квадрата со стороной \(1\). Точно так же \(\pi\), площадь круга с радиусом 1, отсутствует в рациональных числах. Именно такие дефекты и предназначены для устранения реальных чисел.
2 = 2 \). Но кажется интуитивно ясным, что должно быть что-то номер со следующим свойством: \(\sqrt{2}\) — длина диагонали квадрата со стороной \(1\). Точно так же \(\pi\), площадь круга с радиусом 1, отсутствует в рациональных числах. Именно такие дефекты и предназначены для устранения реальных чисел.
Возможно, вы привыкли думать о действительных числах как о (потенциально) бесконечных десятичных дробях: например, \(\sqrt{2} = 1,41421356\ldots\) и \(\pi = 3,14159265\ldots\). Главная цель этой главы — сделать «…» точным. Идея состоит в том, что мы можем взять бесконечное десятичное число для представления последовательности рациональных приближений. Например, мы можем аппроксимировать квадратный корень из 2 последовательностью \(1, 1,4, 1,41, 1,414, \ldots\). Мы хотели бы определить \(\sqrt{2}\) как «предел» этой последовательности, но мы видели, что последовательность не имеет предела в рациональных числах. Поэтому мы должны создавать новые объекты, реальные числа, чтобы служить этой цели.
Фактически, мы определим действительные числа более или менее, чтобы были такими последовательностями рациональных приближений. Но нам придется иметь дело с тем фактом, что, например, существует множества способов аппроксимации квадратного корня из двух. Например, мы можем с тем же успехом приближаться к нему сверху, \(2, 1,5, 1,42, \ldots\), или колеблясь сверху и снизу. В следующем разделе мы покажем, как «склеить» все эти последовательности вместе и рассматривать их как единый объект.
21.2. Факторные конструкции
Пусть \(A\) — любое множество, и пусть \(\equiv\) — любое отношение эквивалентности на \(A\). Напомним из раздела 13.3, что мы можем сопоставить каждому элементу \(a\) множества \(A\) класс эквивалентности \([a]\), где \(b \in [a]\) означает \(b \equiv а\). Это присваивание имеет то свойство, что для любых \(a\) и \(b\), \(a \equiv b\) тогда и только тогда, когда \([a] = [b]\).
Для любого множества \(A\) и отношения эквивалентности \(\equiv\) определим \(A / \mathord{\equiv}\) как множество \(\{ [ a ] \mid a \in A \}\) из класса эквивалентности класса \(A\) по модулю \(\equiv\).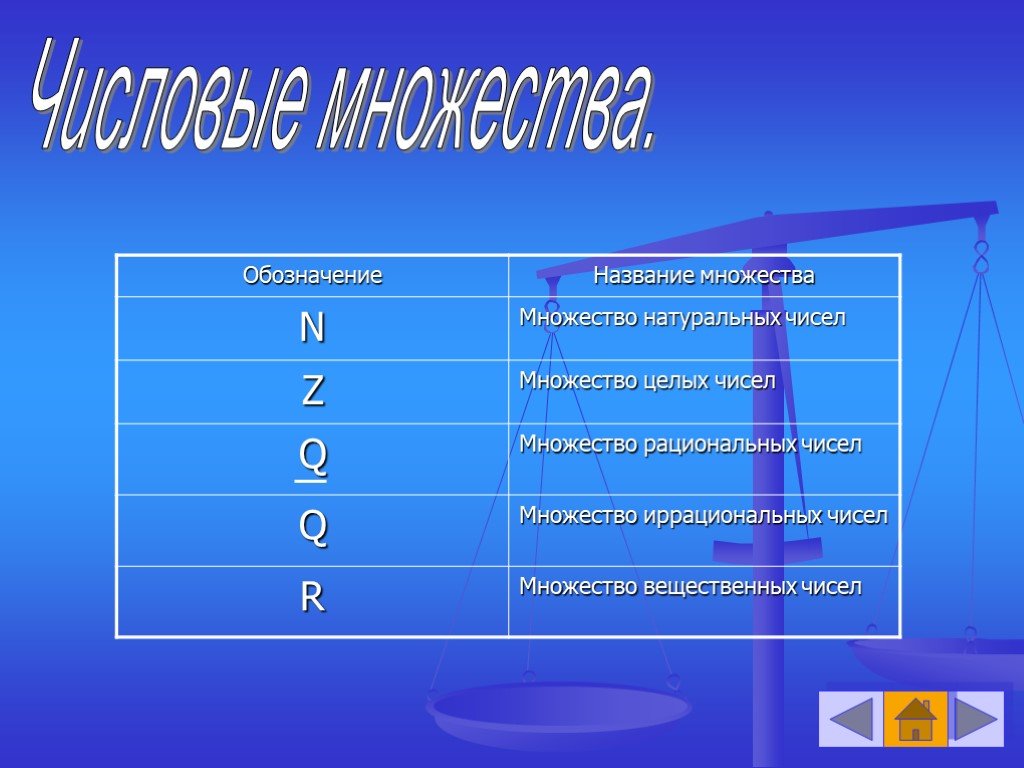 Этот набор называется «\(A\) по модулю \(\mathord{\equiv}\)» или частным от \(A\) на \(\equiv\). Вы можете думать об этом как о наборе \(A\), в котором эквивалентные элементы «склеены», чтобы создать более грубый набор.
Этот набор называется «\(A\) по модулю \(\mathord{\equiv}\)» или частным от \(A\) на \(\equiv\). Вы можете думать об этом как о наборе \(A\), в котором эквивалентные элементы «склеены», чтобы создать более грубый набор.
Например, если мы рассмотрим целые числа \(\mathbb{Z}\), где \(\equiv\) обозначает эквивалентность по модулю 5 (как в разделе 19.4), тогда \(\mathbb{Z} / \mathord{\ эквив}\) просто \(\{ [0], [1], [2], [3], [4] \}\). Мы можем определить сложение на \(\mathbb{Z} / \mathord{\equiv}\) как \([a] + [b] = [a + b]\). Чтобы это определение имело смысл, важно знать, что правая часть не зависит от того, какие представители \([a]\) и \([b]\) мы выбираем. Другими словами, нам нужно знать, что всякий раз, когда \([a] = [a’]\) и \([b] = [b’]\), то \([a + b] = [a’ + b ‘]\). Это, в свою очередь, равносильно тому, что если \(a \equiv a’\) и \(b \equiv b’\), то \(a + b \equiv a’ + b’\). Другими словами, мы требуем, чтобы операция сложения соблюдает отношение эквивалентности, и мы видели в разделе 19.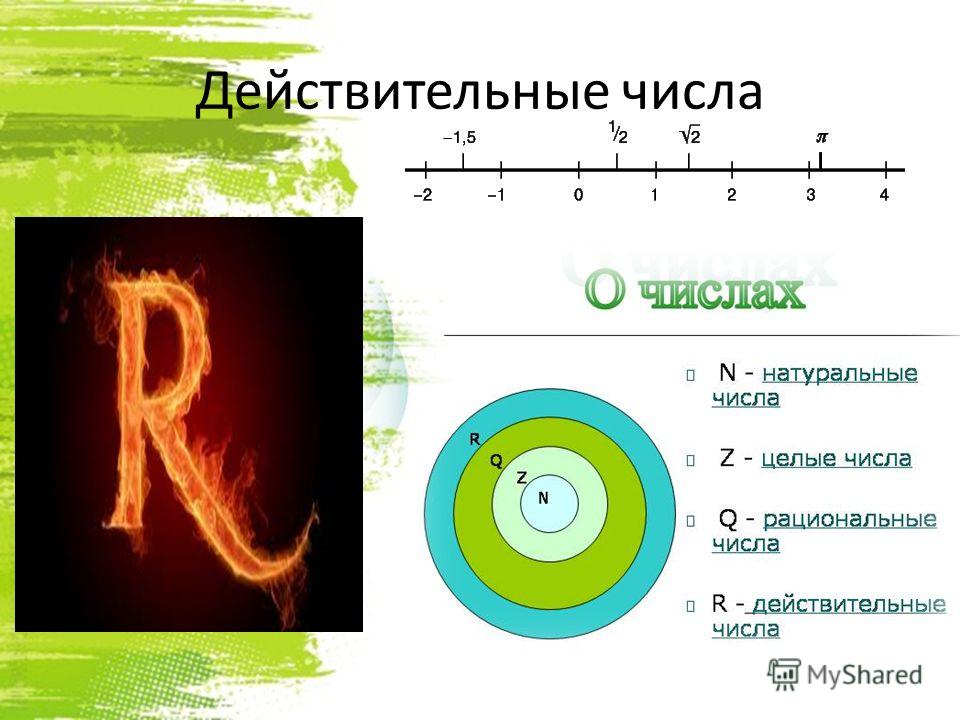 4, что это действительно так.
4, что это действительно так.
Эта общая стратегия перевода функции, определенной на множестве, в функцию, определенную на частном множестве, дается следующей теоремой.
Теорема. Пусть \(A\) и \(B\) — произвольные множества, \(\equiv\) — любое отношение эквивалентности, определенное на \(A\), и пусть \(f : A \to B\). Предположим, что \(f\) соблюдает отношение эквивалентности, то есть для каждого \(a\) и \(a’\) в \(A\), если \(a \equiv a’\), то \ (f(a) = f(a’)\). Тогда существует единственная функция \(\bar f : A / \mathord{\equiv} \to B\), определяемая равенством \(\bar f ([a]) = f(a)\) для каждого \(a \) в\).
Доказательство. Мы определили значение \(\bar f\) в классе эквивалентности \(x\), написав \(x = [a]\) и установив \(\bar f(x) = f(a) \). Другими словами, мы говорим, что \(\bar f(x) = y\) тогда и только тогда, когда существует \(a\) такое, что \(x = [a]\), и \(f(a) = у\). Что сомнительно в этом определении, так это то, что оно априори может зависеть от того, как мы выражаем \(х\) в этой форме; другими словами, нам нужно показать, что существует уникальных \(y\), удовлетворяющих этому описанию. В частности, нам нужно знать, что если \(x = [a] = [a’]\), то \(f(a) = f(a’)\). Но поскольку \([a] = [a’]\) эквивалентно \(a \equiv a’\), это означает, что \(f\) соблюдает отношение эквивалентности, что мы и предполагали.
В частности, нам нужно знать, что если \(x = [a] = [a’]\), то \(f(a) = f(a’)\). Но поскольку \([a] = [a’]\) эквивалентно \(a \equiv a’\), это означает, что \(f\) соблюдает отношение эквивалентности, что мы и предполагали.
Математики часто «определяют» \(\bar f\) уравнением \(\bar f ([a])= f(a)\), а затем выражают приведенное выше доказательство как доказательство того, что «\(\ бар f\) хорошо определен». Это смущает. На самом деле они имеют в виду то, что говорит теорема, а именно, что существует уникальная функция, удовлетворяющая этому описанию.
Чтобы построить целые числа, начните с \(\mathbb{N} \times \mathbb{N}\). Думайте о паре натуральных чисел \((m, n)\) как о представлении \(m — n\), где вычитание происходит в целых числах (которые мы еще не построили!). Например, как \((2, 5)\), так и \((6, 9)\) представляют целое число \(-3\). Интуитивно пары \((m, n)\) и \((m’, n’)\) будут представлять одно и то же целое число, когда \(m — n = m’ — n’\), но мы не можем сказать, что это тем не менее, потому что мы еще не определили подходящее понятие вычитания.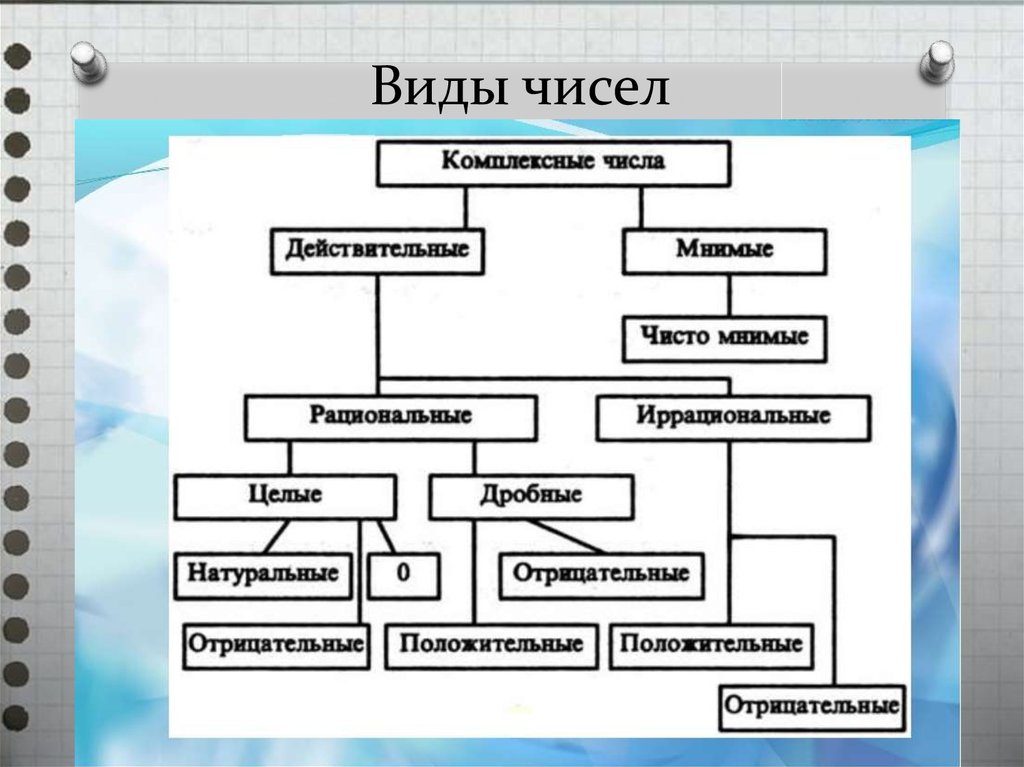 Но уравнение эквивалентно \(m + n’ = m’ + n\), и это имеет смысл с добавлением натуральных чисел.
Но уравнение эквивалентно \(m + n’ = m’ + n\), и это имеет смысл с добавлением натуральных чисел.
Определение. Определить отношение \(\equiv\) на \(\mathbb{N} \times \mathbb{N}\) посредством \((m, n) \equiv (m’, n’)\) тогда и только тогда, когда \(т + п’ = т’ + п\).
Предложение. \(\equiv\) является отношением эквивалентности.
Доказательство. Для рефлексивности ясно, что \((m, n) \equiv (m, n)\), так как \(m + n = m + n\).
Для симметрии предположим \((m, n) \equiv (m’, n’)\). Это означает \(m + n’ = m’ + n\). Но из симметрии равенства следует \((m’, n’) \equiv (m, n)\), что и требовалось.
Для транзитивности предположим \((m, n) \equiv (m’, n’)\) и \((m’, n’) = (m», n»)\). Тогда имеем \(m + n’ = m’ + n\) и \(m’ + n» = n’ + m»\). Складывая эти уравнения, получаем
\[m + n’ + m’ + n» = m’ + n + n’ + m».\]
Вычитая \(m’ + n’\) с обеих сторон, получаем \( m + n» = n + m»\), что эквивалентно \((m, n) = (m», n»)\), что и требовалось.
Теперь мы можем определить целые числа как \(\mathbb{N} \times \mathbb{N} / \mathord{\equiv}\). Как определить сложение? Если \([(m, n)]\) представляет \(m — n\), а \([(u, v)]\) представляет \(u — v\), то \([(m, n )] + [(u, v)]\) должно представлять \((m + u) — (n + v)\). Таким образом, имеет смысл определить \([(m, n)] + [(u, v)]\) как \([(m + u) — (n + v)]\). Чтобы это работало, нам нужно знать, что операция, которая переводит \((m, n)\) и \((u, v)\) в \((m + u, n + v)\), соблюдает эквивалентность связь.
Предложение. Если \((m, n) \equiv (m’, n’)\) и \((u, v) \equiv (u’, v’)\), то \((m + u, n + v) \экв (т’ + и’, п’ + v’)\).
Доказательство. Первая эквивалентность означает \(m + n’ = m’ + n\), а вторая означает \(u + v’ = u’ + v\). Складывая два уравнения, мы получаем \((m + u) + (n’ + v’) \equiv (m’ + u’) + (n + v)\), что в точности равносильно выражению \(( m + u, n + v) \equiv (m’ + u’, n’ + v’)\).
Каждое натуральное число \(n\) может быть представлено целым числом \([(n, 0)]\), и, в частности, \(0\) представлено как \([(0, 0) ]\). Более того, если \([(m, n)]\) — любое целое число, мы можем определить его отрицание как \([(n, m)]\), поскольку \([(m, n)] + [( n, m)] = [(m + n, n + m)] = [(0, 0)]\), так как \((m + n, n + m) \equiv (0, 0)\). Короче говоря, мы «изобрели» отрицательные числа! 9{>0}\) обозначает строго положительные целые числа. Идея, конечно, в том, что \((a, b)\) представляет \((a / b)\). Имея это в виду, имеет смысл определить \((a, b) \equiv (c, d)\), если \(a d = b c\). Мы могли бы также определить здесь сложение, умножение и порядок. Детали утомительны, однако, и не очень освещают. Поэтому мы обратимся вместо этого к построению действительных чисел.
Более того, если \([(m, n)]\) — любое целое число, мы можем определить его отрицание как \([(n, m)]\), поскольку \([(m, n)] + [( n, m)] = [(m + n, n + m)] = [(0, 0)]\), так как \((m + n, n + m) \equiv (0, 0)\). Короче говоря, мы «изобрели» отрицательные числа! 9{>0}\) обозначает строго положительные целые числа. Идея, конечно, в том, что \((a, b)\) представляет \((a / b)\). Имея это в виду, имеет смысл определить \((a, b) \equiv (c, d)\), если \(a d = b c\). Мы могли бы также определить здесь сложение, умножение и порядок. Детали утомительны, однако, и не очень освещают. Поэтому мы обратимся вместо этого к построению действительных чисел.
21.3. Построение действительных чисел
Проблема, с которой мы сталкиваемся, заключается в том, что последовательность рациональных чисел \(1, 1,4, 1,41, 1,414, 1,4142, \ldots\) приближается к значению, которое
.0043 было бы квадратным корнем из 2, но нет никакого рационального числа, которое могло бы играть эту роль. Следующее определение фиксирует понятие о том, что эта последовательность чисел «кажется приближающейся к значению», не ссылаясь на значение, к которому она приближается.
Определение. Последовательность рациональных чисел \((q_i)_{i \in \mathbb{N}}\) равна Коши , если для каждого рационального числа \(\varepsilon > 0\) существует некоторое натуральное число \(N \in \mathbb{N}\) такое, что для всех \(i, j \geq N\) мы имеем \(|q_i — q_j| < \varepsilon\).
Грубо говоря, последовательность Коши — это последовательность, в которой элементы становятся произвольно близкими не только к своим последователям, но и ко всем последующим элементам. В математике обычно используется \(\varepsilon\) для представления количества, которое предназначено для обозначения чего-то малого; фразу «для каждого \(\varepsilon > 0\)» следует читать как «независимо от того, насколько мал \(\varepsilon\)». Таким образом, последовательность называется Коши, если для любого \(\varepsilon > 0\), сколь бы малым он ни был, существует некоторая точка \(N\), за которой элементы остаются на расстоянии \(\varepsilon\) одного другой.
Последовательности Коши можно использовать для описания этих пробелов в рациональных числах, но, как отмечалось выше, для описания одного и того же пробела можно использовать множество последовательностей Коши. На данном этапе несколько неверно говорить, что они «приближаются к одной и той же точке», поскольку нет никакой рациональной точки, к которой они приближаются; более точное утверждение состоит в том, что последовательности в конечном итоге становятся сколь угодно близкими.
На данном этапе несколько неверно говорить, что они «приближаются к одной и той же точке», поскольку нет никакой рациональной точки, к которой они приближаются; более точное утверждение состоит в том, что последовательности в конечном итоге становятся сколь угодно близкими.
Определение. Две последовательности Коши \(p = (p_i)_{i \in \mathbb{N}}\) и \(q = (q_i)_{i \in \mathbb{N}}\) равны эквивалентно , если для каждого рационального числа \(\varepsilon > 0\) существует некоторое натуральное число \(N \in \mathbb{N}\) такое, что для всех \(i \geq N\) мы имеем, что \(|p_i — q_i| < \varepsilon\). Мы будем писать \(p \equiv q\), чтобы показать, что \(p\) эквивалентно \(q\).
Предложение. \(\equiv\) — отношение эквивалентности последовательностей Коши.
Доказательство. Рефлексивность и симметрия просты, поэтому докажем транзитивность. Предположим, \((p_i) \equiv (q_i)\) и \((q_i) \equiv (r_i)\).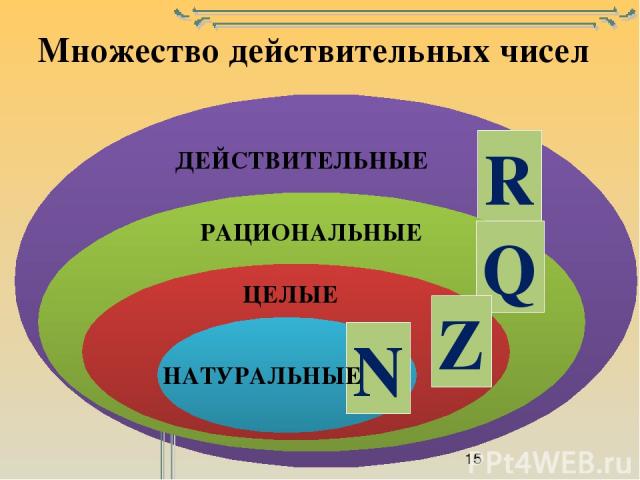 Мы хотим показать, что последовательность \((p_i)\) эквивалентна \((r_i)\). Итак, при любом \(\varepsilon > 0\) выберите \(N_0\) достаточно большим, чтобы для каждого \(i \ge N_0\) \(|p_i — q_i| < \varepsilon / 2\). Выберите другое число, \(N_1\), чтобы для каждого \(i \geq N_1\) \(|q_i - r_i| < \varepsilon / 2\). Пусть \(N = \max(N_0, N_1)\). Тогда для каждого \(i \geq N\) имеем
Мы хотим показать, что последовательность \((p_i)\) эквивалентна \((r_i)\). Итак, при любом \(\varepsilon > 0\) выберите \(N_0\) достаточно большим, чтобы для каждого \(i \ge N_0\) \(|p_i — q_i| < \varepsilon / 2\). Выберите другое число, \(N_1\), чтобы для каждого \(i \geq N_1\) \(|q_i - r_i| < \varepsilon / 2\). Пусть \(N = \max(N_0, N_1)\). Тогда для каждого \(i \geq N\) имеем
\[|p_i — r_i | = |(p_i — q_i) + (q_i — r_i)| \leq |p_i — q_i| + |q_i — r_i| < \varepsilon / 2 + \varepsilon / 2 = \varepsilon,\]
по мере необходимости.
Обратите внимание, что доказательство использует неравенство треугольника , которое утверждает для любых рациональных чисел \(a\) и \(b\), \(|a + b| \leq |a| + |b|\) . Если мы определим \(|a|\) как максимум \(a\) и \(-a\), то неравенство треугольника действительно выполняется для любого упорядоченного кольца:
Теорема. Пусть \(a\) и \(b\) — элементы любого упорядоченного кольца. Тогда \(|a + b| \leq |a| + |b|\).
Доказательство. По определению модуля достаточно показать, что \(a + b \leq |a| + |b|\) и \(-(a + b) \leq |a| + |b|\). Первое утверждение следует из того, что \(a \leq |a|\) и \(b \leq |b|\). Аналогично для второго утверждения имеем \(-a \leq |a|\) и \(-b \leq |b|\), так что \(-(a + b) = -a + — b \leq | а|+|б|\).
В приведенной выше теореме, если мы допустим \(a = x — y\) и \(b = y — z\), мы получим \(|x — z| \leq |x — y| + |y — з|\). Тот факт, что \(|x — y|\) представляет собой расстояние между \(x\) и \(y\) на числовой прямой, объясняет название: для любых трех «точек» \(x\), \(y \) и \(z\), расстояние от \(x\) до \(z\) не может быть больше, чем расстояние от \(x\) до \(y\) плюс расстояние от \ (у\) в \(г\).
Пусть теперь \(A\) будет множеством последовательностей Коши рациональных чисел, и определим действительные числа, \(\mathbb{R}\), как \(A / \mathord{\equiv}\). Другими словами, действительные числа — это множество последовательности рациональных чисел Коши по модулю отношения эквивалентности, которое мы только что определили.
Одного набора \(\mathbb{R}\) недостаточно: мы также хотели бы знать, как складывать, вычитать, умножать и делить действительные числа. Как и в случае с целыми числами, нам нужно определить операции над базовым набором, а затем показать, что они соблюдают отношение эквивалентности. Например, мы расскажем, как сложить последовательности Коши рациональных чисел, а затем покажем, что если \(p_1 \equiv p_2\) и \(q_1 \equiv q_2\), то \(p_1 + q_1 \equiv p_2 + q_2\) . Затем мы можем поднять это определение до \(\mathbb{R}\), определив \([p] + [q]\) как \([p + q]\).
К счастью, в последовательностях Коши легко определить сложение, вычитание и умножение. Если \(p = (p_i)_{i \in \mathbb{N}}\) и \(q = (q_i)_{i \in \mathbb{N}}\) — последовательности Коши, пусть \(p + q = (p_i + q_i)_{i \in \mathbb{N}}\), и аналогично для вычитания и умножения. Сложнее показать, что эти последовательности сами являются Коши, и показать, что операции обладают соответствующими алгебраическими свойствами. Мы просим вас доказать некоторые из этих свойств в упражнениях.
Мы просим вас доказать некоторые из этих свойств в упражнениях.
Каждое рациональное число \(q\) можно отождествить с постоянной последовательностью Коши \(q, q, q, \ldots\), поэтому действительные числа включают все рациональные числа. Следующий шаг состоит в том, чтобы абстрагироваться от деталей конкретной конструкции, которую мы выбрали, чтобы впредь мы могли работать с действительными числами абстрактно и больше не думать о них как о заданных классами эквивалентности последовательностей рациональных чисел Коши.
21.4. Полнота действительных чисел
Мы построили действительные числа, чтобы заполнить пробелы в рациональных числах. Откуда мы знаем, что у нас есть все? Возможно, нам нужно построить еще больше чисел, используя последовательности Коши действительных чисел? Следующая теорема говорит нам, что, напротив, нет необходимости расширять действительные числа таким образом.
Определение. Пусть \(r\) — действительное число.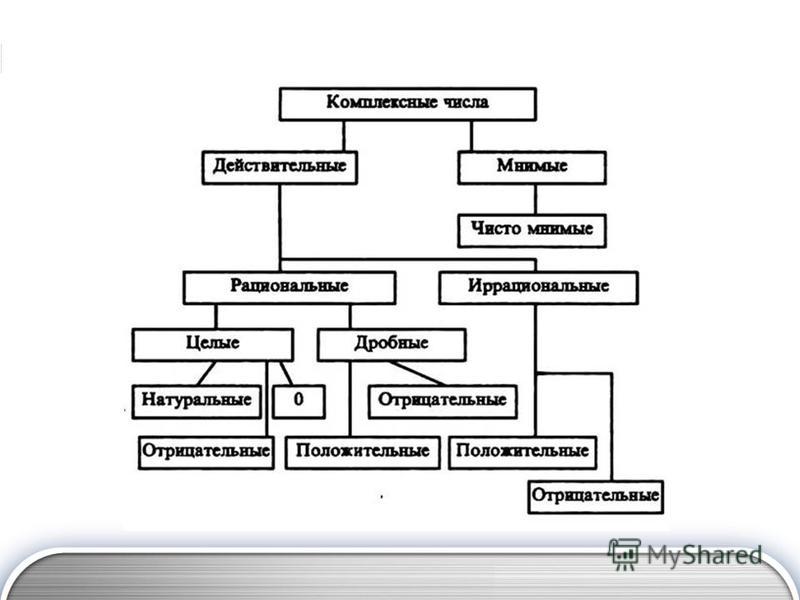 Последовательность \((r_i)_{i \in \mathbb{N}}\) действительных чисел сходится к \(r\), если для каждого \(\varepsilon > 0\) существует \( N\) такие, что для любого \(i \geq N\) \(|r_i — r| < \varepsilon\).
Последовательность \((r_i)_{i \in \mathbb{N}}\) действительных чисел сходится к \(r\), если для каждого \(\varepsilon > 0\) существует \( N\) такие, что для любого \(i \geq N\) \(|r_i — r| < \varepsilon\).
Определение. Последовательность \((r_i)_{i \in \mathbb{N}}\) сходится , если она сходится к некоторому \(r\).
Теорема. Любая последовательность Коши действительных чисел сходится.
Утверждение теоремы часто выражается в том, что действительные числа полны . Грубо говоря, это говорит о том, что везде, где вы ищете реальное число, вы обязательно его найдете. Здесь аналогичный принцип.
Определение. Элемент \(u \in \mathbb{R}\) называется верхней границей подмножества \(S \subseteq \mathbb{R}\), если все в \(S\) меньше или равно \(и\). \(S\) называется ограниченным , если существует верхняя граница для \(S\). Элемент \(u\) называется 92 < 2\}\), то рациональное число 2 является верхней границей для \(S\), но \(S\) не имеет наименьшей верхней границы в \(\mathbb{Q}\).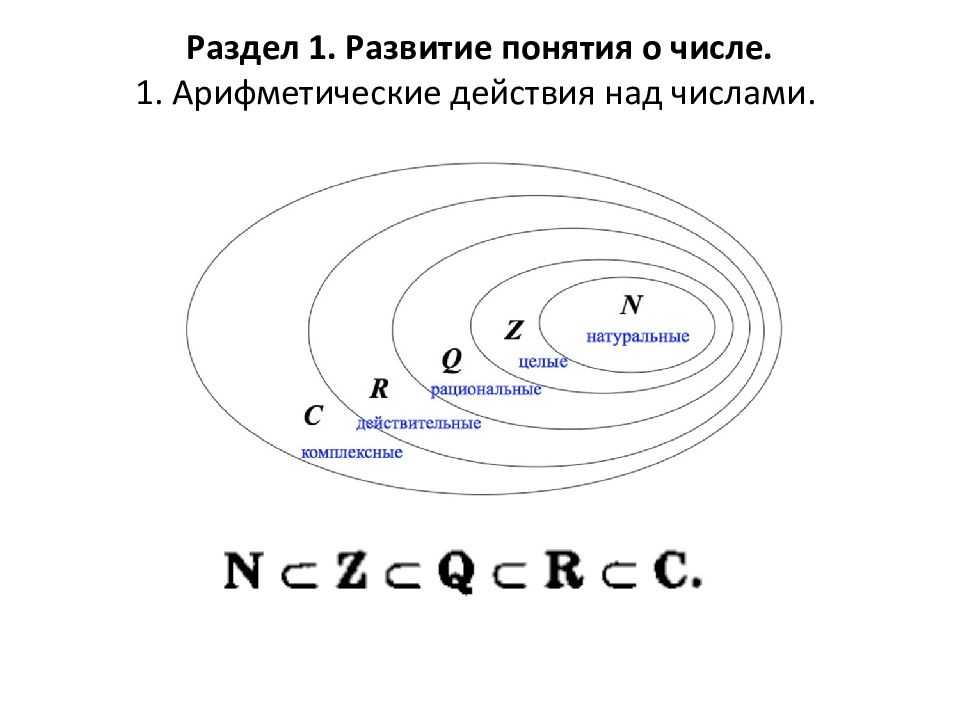
Фундаментальная теорема состоит в том, что действительные числа точно характеризуются тем свойством, что они представляют собой полное упорядоченное поле, так что каждое действительное число \(r\) меньше или равно некоторому натуральному числу \(N\). Любые две модели, отвечающие этим требованиям, должны вести себя совершенно одинаково, по крайней мере, в отношении констант \(0\) и \(1\), операций \(+\) и \(*\) и отношения \(\leq\) обеспокоены. Этот факт чрезвычайно важен, потому что он позволяет нам не думать о построении последовательности Коши в обычной математике. Как только мы показали, что наша конструкция удовлетворяет этим требованиям, мы можем считать \(\mathbb{R}\) уникальным полным полностью упорядоченным полем и игнорировать любые детали реализации. Мы также вольны реализовать \(\mathbb{R}\) любым способом, который мы выберем, и до тех пор, пока он соответствует этому интерфейсу, и пока они не ссылаются на базовые представления, любые теоремы, которые мы доказываем о действительных числах будет одинаково хорошо выполняться для всех конструкций.
21.5. Альтернативная конструкция
Многие источники используют альтернативную конструкцию реалов, считая их вместо сокращениями Дедекинда . Разрез Дедекинда — это упорядоченная пара \((A, B)\) множеств рациональных чисел со следующими свойствами:
Каждое рациональное число \(q\) принадлежит либо \(A\), либо \(B \).
Каждый \(a \in A\) меньше любого \(b \in B\).
В \(A\) нет наибольшего элемента.
\(A\) и \(B\) не пусты.
Первые два свойства показывают, почему мы называем эту пару «разрезом». Множество \(A\) содержит все рациональные числа слева от некоторой отметки на числовой прямой и \(B\) все точки справа. Третье свойство сообщает нам кое-что о том, что происходит именно на этой отметке. Но есть две возможности: либо \(B\) имеет наименьший элемент, либо его нет. Представьте себе ситуацию, когда \(A\) не имеет наибольшего элемента, а \(B\) не имеет наименьшего элемента, может быть сложно, но рассмотрим пример \(A = \{x \in \mathbb{Q} \mid x^2 < 2\}\) и \(B = \{x \in \mathbb{Q} \mid x^2 > 2\}\). 2 = 2\), но есть рациональные числа с любой стороны, которые произвольно близки; таким образом, ни \(A\), ни \(B\) не содержат конечной точки.
2 = 2\), но есть рациональные числа с любой стороны, которые произвольно близки; таким образом, ни \(A\), ни \(B\) не содержат конечной точки.
Мы можем определить \(\mathbb{R}\) как множество разрезов Дедекинда. Разрез Дедекинда \((A, B)\) соответствует рациональному числу \(q\), если \(q\) является наименьшим элементом \(B\), и иррациональному числу, если \(B\) не имеет наименьшего элемента. Определить сложение на \(\mathbb{R}\) просто:
\[(A_1, B_1) + (A_2, B_2) = ( \{a_1 + a_2 \mid a_1 \in A_1, a_2 \in A_2 \}, \{b_1 + b_2 \mid b_1 \in B_1, b_2 \in B_2 \}).\]
Некоторые авторы предпочитают эту конструкцию конструкции последовательности Коши, поскольку она позволяет избежать взятия частного множества и, таким образом, удаляет сложность демонстрации того, что арифметические операции соблюдают эквивалентность. Другие предпочитают последовательности Коши, поскольку они обеспечивают более четкое представление о приближении: если действительное число \(r\) задано последовательностью Коши \((q_i)_{i \in \mathbb{N}}\), то произвольно близкое рациональное приближение \(r\) дается \(q_N\) для достаточно большого \(N\).
Однако для большинства математиков в большинстве случаев разница несущественна. Обе конструкции создают полные линейные упорядоченные поля, и в определенном смысле они создают одно и то же полное линейное упорядоченное поле. Строго говоря, множество вещественных чисел Коши не равно множеству вещественных чисел Дедекинда, поскольку одно состоит из классов эквивалентности рациональных последовательностей Коши, а другое состоит из пар множеств рациональных чисел. Но между двумя множествами существует биекция, которая сохраняет свойства поля. То есть существует биекция \(f\) из веществ Коши в числа Дедекинда такая, что 9{-1}\)
\(f(x) \leq f(y) \iff x \leq y\)
Мы говорим, что эти две конструкции изоморфны и что функция \(f\) является изоморфизмом . Поскольку мы часто заботимся о действительных числах только в связи с их статусом полного упорядоченного поля, а две конструкции неразличимы как упорядоченные поля, не имеет значения, какая конструкция используется.
21.6. Упражнения
Покажите, что сложение целых чисел, как определено в разделе 21.2, является коммутативным и ассоциативным.
Покажите из построения целых чисел в разделе 21.2, что \(a + 0 = a\) для каждого целого числа \(a\).
Определить вычитание целых чисел с помощью \(a — b = a + (-b)\) и показать, что \(a — b + b = a\) для каждой пары целых чисел \(a\) и \( б\).
Определите умножение для целых чисел, сначала определив его в базовом представлении, а затем показав, что операция соблюдает отношение эквивалентности.
Покажите, что каждая последовательность Коши ограничена: то есть, если \((q_i)_{i \in \mathbb{N}}\) является Коши, то существует некоторое рациональное \(M\) такое, что \(|q_i |\leq M\) для всех \(i\). Подсказка: попробуйте указать \(\varepsilon = 1\).
Пусть \(p = (p_i)_{i \in \mathbb{N}}\) и \(q = (q_i)_{i \in \mathbb{N}}\) — последовательности Коши.
 Определите \(p + q = (p_i + q_i)_{i \in \mathbb{N}}\) и \(p q = (p_i q_i)_{i \in \mathbb{N}}\).
Определите \(p + q = (p_i + q_i)_{i \in \mathbb{N}}\) и \(p q = (p_i q_i)_{i \in \mathbb{N}}\).Покажите, что \(p + q\) является Коши. То есть для произвольного \(\varepsilon > 0\) покажите, что существует \(N\) такое, что для всех \(i, j \geq N\), \(|(p_i + q_i) — (p_j + q_j)|<\varepsilon\).
Покажите, что \(p q\) является Коши. В дополнение к неравенству треугольника вам будет полезно предыдущее упражнение.
Эти две части показывают, что сложение последовательностей Коши соблюдает эквивалентность.
Покажите, что если \(p, p’, q\) — последовательности Коши и \(p \equiv p’\), то \(p + q \equiv p’ + q\).
Используя первую часть этой задачи, покажите, что если \(p, p’, q, q’\) являются последовательностями Коши, \(p \equiv p’\) и \(q \equiv q’\) , то \(p + q \equiv p’ + q’\). Вы можете использовать тот факт, что сложение действительных чисел коммутативно.
Покажите, что если \((A_1, B_1)\) и \((A_2, B_2)\) являются разрезами Дедекинда, то \((A_1, B_1) + (A_2, B_2)\) также являются разрезами Дедекинда.

Различные типы чисел — что такое простое число, рациональное число и целое число
Числа всегда были важной частью человеческой жизни, поскольку числа полезны для них во многих отношениях, например, для подсчета, измерения или маркировки объектов.
И со временем люди открыли множество таких чисел, которые не только очень полезны для них, но и выглядят очень завораживающе.
Но эти разные типы чисел немного сложно запомнить, поэтому я решил написать эту статью. Итак, начнем.
Натуральные числа
Все числа больше 0 и начинаются с 1 называются Натуральными числами, например 1, 2, 3, 4…. до бесконечности. Натуральные числа имеют положительную природу. Набор натуральных чисел обозначается N . Например:
N = {1, 2, 3, 4, 5}
Целые числа
Целые числа начинаются с 0 и доходят до бесконечности, что делает их надмножеством натуральных чисел. Также, как следует из названия, «целое» означает «полное», поэтому числа, которые являются полными или не дробными, десятичными или отрицательными, называются целыми числами. Набор целых чисел обозначается W .
Набор целых чисел обозначается W .
N = {0, 1, 2, 3, 4, 5}
Множество целых чисел и натуральных чисел также включает следующие типы чисел:
Простые и составные числа
Простые числа: Простое число — это натуральное число, которое делится только само на себя и на 1. Например, 2, 3, 5, 7, 11. Здесь 4, 6, 9 не являются простыми числами, потому что 4 и 6 делятся на 2, а 6 и 9 делятся на 3. Составные числа: С другой стороны, составное число — это натуральное число, которое делится на любое другое число, кроме 1. Другими словами, все натуральные числа, кроме простых, являются составными числами.
Целые числа
Целые числа представляют собой набор целых чисел плюс они включают в себя противоположные натуральные числа отрицательные числа, например …-3, -2, -1, 0, 1, 2, 3… Набор целых чисел обозначаются Z
Рациональные числа
Все те числа, которые могут быть представлены в виде дроби, т. е. в форме p/q, где p и q — целые числа, а q ≠ 0, называются рациональными числами. Например 2/3, 8/11, -5/7. Набор рациональных чисел представлен Q . Все натуральные числа, целые числа и целые числа являются рациональными числами. Обратите внимание, что десятичное расширение всех рациональных чисел заканчивается или не заканчивается повторяющимся .
е. в форме p/q, где p и q — целые числа, а q ≠ 0, называются рациональными числами. Например 2/3, 8/11, -5/7. Набор рациональных чисел представлен Q . Все натуральные числа, целые числа и целые числа являются рациональными числами. Обратите внимание, что десятичное расширение всех рациональных чисел заканчивается или не заканчивается повторяющимся .
Иррациональное число
Числа, которые не могут быть представлены дробью или формой p/q, называются иррациональными числами. Их десятичное расширение равно без завершения и без повторения . Например 1.10100110001111…., Пи и √2.
Вещественные числа
Совокупность всех рациональных и иррациональных чисел называется Вещественными числами. Каждое действительное число может быть представлено на числовой прямой. Другими словами, каждая точка на числовой прямой соответствует действительному числу и наоборот. Вот почему они называются действительными числами. Он включает в себя все числа, описанные выше.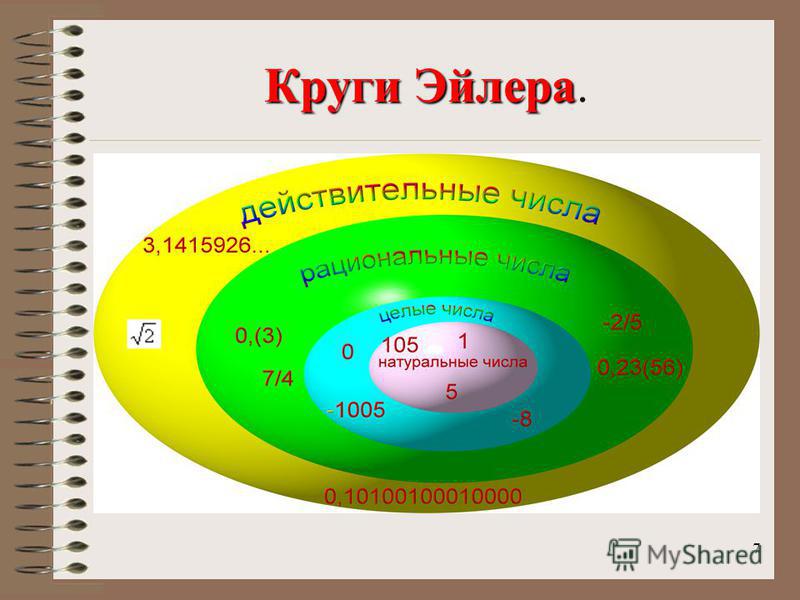

 Досуг
Досуг Словари
Словари )
) И.
И. Показано, как из предлагаемой системы аксиом выводятся утверждения, соответствующие интуитивным представлениям читателя о свойствах данной числовой системы. В частности, доказаны основные свойства отношения делимости целых чисел. В предположении непротиворечивости аксиоматики натуральных чисел доказывается непротиворечивость всех остальных систем аксиом, а именно: показано, как, располагая моделью для натуральных чисел, построить последовательно модели для целых, рациональных, действительных и комплексных чисел. В каждом случае установлена также единственность модели. При формулировке аксиом и доказательстве всех утверждений используются язык и методы современной алгебры; подробному изложению необходимых сведений из алгебры и теории множеств посвящен первый, вводный, параграф пособия. книга предназначена для преподавателей и студентов математических факультетов университетов.
Показано, как из предлагаемой системы аксиом выводятся утверждения, соответствующие интуитивным представлениям читателя о свойствах данной числовой системы. В частности, доказаны основные свойства отношения делимости целых чисел. В предположении непротиворечивости аксиоматики натуральных чисел доказывается непротиворечивость всех остальных систем аксиом, а именно: показано, как, располагая моделью для натуральных чисел, построить последовательно модели для целых, рациональных, действительных и комплексных чисел. В каждом случае установлена также единственность модели. При формулировке аксиом и доказательстве всех утверждений используются язык и методы современной алгебры; подробному изложению необходимых сведений из алгебры и теории множеств посвящен первый, вводный, параграф пособия. книга предназначена для преподавателей и студентов математических факультетов университетов.
 Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.
 Определите \(p + q = (p_i + q_i)_{i \in \mathbb{N}}\) и \(p q = (p_i q_i)_{i \in \mathbb{N}}\).
Определите \(p + q = (p_i + q_i)_{i \in \mathbb{N}}\) и \(p q = (p_i q_i)_{i \in \mathbb{N}}\).