Натуральный логарифм ln: Натуральный логарифм | это… Что такое Натуральный логарифм?

Zero To Hero

Содержание:

1.	Число e означает рост
2.	Натуральный логарифм означает время
3.	Этот нестандартный логарифмический счёт
4.	Логарифмическое умножение — просто умора
5.	Использование натурального логарифма при произвольном росте
6.	Отпадный пример: Правило 72
7.	Дополнение: Натуральный логарифм от e

Мы уже разобрались с экспоненциальной функцией в посвящённой ей статье, и нашей следующей целью становится натуральный логарифм.

В учебниках математики определение натурального логарифма такое, что ничего «натурального», естественного в нём нет: он определяется как действие, обратное функции e^x, странной уже самой по себе.

Так что вот вам новое, упрощённое объяснение: Натуральный логарифм — это время, необходимое, чтобы вырасти до определённого уровня.

Представьте, что вы сделали инвестицию мишками Гамми (а кто так не делает?) с непрерывной доходностью 100% годовых. Если вы преследуете цель достичь десятикратного роста вклада, при условии «сложных процентов», вам пришлось бы ждать всего-то ln(10) = 2.3 года. Не можете понять, почему необходимо только пару лет, чтобы достичь 10х роста? Не понимаете, почему последовательность не 1, 2, 4, 8? Почитайте про число e.

Число e и натуральный логарифм — братья-близнецы:

• e^x — уровень, достигнутый при непрерывном росте за определённый промежуток времени.
• натуральный логарифм (ln) — промежуток времени, необходимый для роста до определённого уровня.

Совсем неплохо, правда? Пока математики подбирают слова, чтобы дать вам длинное путанное определение, давайте поближе посмотрим на это простое и ясное.

Число e означает рост

Число e означает непрерывный рост. Как мы видели в прошлом примере, e^x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии «сложных процентов».

Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:

e^x = e^{процент * время} = e^{1.0 * время} = e^время

Очевидно, что e^x означает:

• насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).
• например, через 3 промежутка времени я получу в e³ = 20.08 раз больше «штуковин».

e^x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.

Натуральный логарифм означает время

Натуральный логарифм — это инверсия числа e, такой причудливый термин для обозначения противоположности. Кстати, о причудах; по латыни он называется logarithmus naturali, отсюда и появилась аббревиатура ln.

И что эта инверсия или противоположность означает?

• e^x позволяет нам подставить время и получить рост.
• ln(x) позволяет нам взять рост или доход и узнать время, необходимое для его получения.

Например:

• e³ равняется 20.08. Через три отрезка времени у нас будет в 20.08 раз больше того, с чего мы начали.
• ln(20.08) будет примерно 3. Если вас интересует рост в 20.08 раз, вам понадобится 3 промежутка времени (опять же, при условии стопроцентного непрерывного роста).

Всё ещё читаете? Натуральный логарифм показывает время, нужное, чтобы достичь желаемого уровня.

Этот нестандартный логарифмический счёт

Вы проходили логарифмы — это странные существа. Как им удалось превратить умножение в сложение? А деление в вычитание? Давайте посмотрим.

Чему равняется ln(1)? Интуитивно понятно, что вопрос стоит так: сколько нужно ждать, чтобы получить в 1 раз больше того, что у меня есть?

Ноль. Нуль. Нисколько. У вас уже это есть единожды. Не требуется нисколько времени, чтобы от уровня 1 дорости до уровня 1.

• ln(1) = 0

Хорошо, что насчёт дробного значения? Через сколько у нас останется 1/2 от имеющегося количества? Мы знаем, что при стопроцентном непрерывном росте ln(2) означает время, необходимое для удвоения. Если мы обратим время вспять (т.е. подождём отрицательное количество времени), то получим половину от того, что имеем.

• ln(1/2) = —ln(2) = —0.693

Логично, правда? Если мы вернёмся назад (время вспять) на 0.693 секунды, то обнаружим половину имеющегося количества. Вообще можно переворачивать дробь и брать отрицательное значение: ln(1/3) = —ln(3) = —1.09. Это означает, что, если мы вернёмся в прошлое на 1.09 отрезков времени, то обнаружим только треть от нынешнего числа.

Ладно, а как насчёт логарифма отрицательного числа? Сколько времени нужно, чтобы «вырастить» колонию бактерий от 1 до —3?

Это невозможно! Нельзя получить отрицательное число бактерий, не так ли? Вы можете получить максимум (эээ… минимум) нуль, но вам никак не получить отрицательное число этих маленьких тварей. В отрицательном числе бактерий просто нет смысла.

• ln(отрицательное число) = неопределено

«Неопределено» означает, что нет такого промежутка времени, который надо было бы прождать, чтобы получить отрицательное значение.

Логарифмическое умножение — просто умора

Сколько времени займёт четырёхкратный рост? Конечно, можно просто взять ln(4). Но это слишком просто, мы пойдём другим путём.

Можно представить четырёхкратный рост как удвоение (требующее ln(2) единиц времени) и затем снова удвоение (требующее ещё ln(2) единиц времени):

• Время на 4х рост = ln(4) = Время на удвоится и затем ещё раз удвоится = ln(2) + ln(2)

Интересно. Любой показатель роста, скажем, 20, можно рассматривать как удвоение сразу после 10-кратного увеличения. Или роста в 4 раза, и затем в 5 раз. Либо же утроение и затем увеличение в 6.666 раз. Видите закономерность?

• ln(a*b) = ln(a) + ln(b)

Логарифм от A, умноженного на B, есть log(A) + log(B). Это отношение сразу обретает смысл, если оперировать в терминах роста.

Если вас интересует 30-кратный рост, вы можете подождать ln(30) за один присест, либо же подождать ln(3) Для утроения, и затем ещё ln(10) для удесятирения.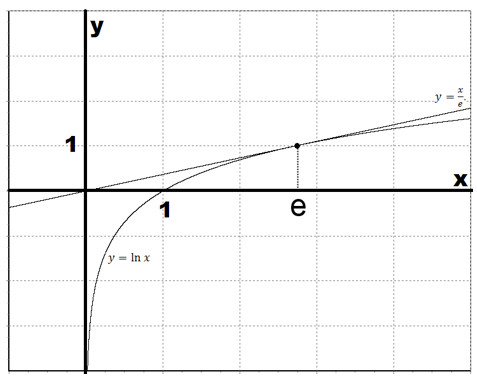 Конечный результат тот же самый, так что конечно время должно оставаться постоянным (и остаётся).

Что на счёт деления? В частности, ln(5/3) означает: сколько времени понадобится для того, чтобы вырасти в 5 раз, и затем получить 1/3 от этого?

Отлично, рост в 5 раз есть ln(5). Рост в 1/3 раза займёт -ln(3) единиц времени. Итак,

• ln(5/3) = ln(5) – ln(3)

Сие означает: дайте вырасти в 5 раз, и затем «вернитесь во времени» к той отметке, где останется всего треть от того количества, так что у вас получится 5/3 рост. В общем получается

• ln(a/b) = ln(a) – ln(b)

Я надеюсь, что странная арифметика логарифмов начинает обретать для вас смысл: умножение показателей роста становится сложением единиц времени роста, а деление превращается в вычитание единиц времени. Не надо запоминать правила, попробуйте осознать их.

Использование натурального логарифма при произвольном росте

— Ну конечно, — скажете вы, — это всё хорошо, если рост 100%-ный, а что в случае 5%, которые я получаю?»

Нет проблем.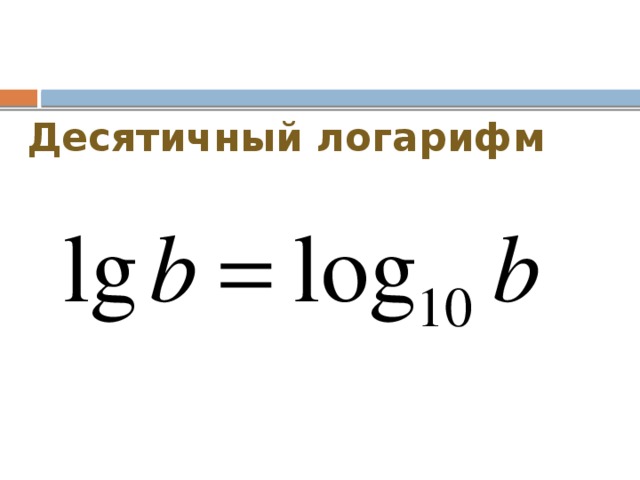 «Время», которое мы рассчитываем с помощью ln(), на самом деле является комбинацией процентной ставки и времени, тот самый Х из уравнения e^x. Мы всего лишь решили задать процент как 100% для простоты, но мы вольны использовать любые числа.

Допустим, мы хотим достичь 30-кратного роста: берём ln(30) и получаем 3.4 Это означает:

• e^x = рост
• e^3.4 = 30

Очевидно, это уравнение означает «100%-ная доходность на протяжении 3.4 лет даёт рост в 30 раз». Мы можем записать это уравнение в таком виде:

• e^x = e^{ставка*время}
• e^{100% * 3.4 года} = 30

Мы можем менять значения «ставки» и «времени», лишь бы ставка * время оставалось 3.4. Например, если нас интересует 30-кратный рост — сколько нам придётся ждать при процентной ставке 5%?

• ln(30) = 3.4
• ставка * время = 3.4
• 0.05 * время = 3.4
• время = 3.4 / 0.05 = 68 лет

Я рассуждаю так: «ln(30) = 3. 4, значит, при 100%-ном росте это займёт 3.4 года. Если я удвою скорость роста, необходимое время уменьшится вдвое».

• 100% за 3.4 года = 1.0 * 3.4 = 3.4
• 200% за 1.7 года = 2.0 * 1.7 = 3.4 [200%-ный рост означает уменьшение времени вдвое]
• 50% за 6.8 года = 0.5 * 6.8 = 3.4 [50%-ный рост означает, что понадобится в 2 раза больше времени]
• 5% за 68 года = .05 * 68 = 3.4 [5%-ный рост означает, что понадобится в 20 раз больше времени].

Здорово, правда? Натуральный логарифм может использоваться с любыми значениями процентной ставки и времени, поскольку их произведение остаётся постоянным. Можете перемещать значения переменных сколько душе угодно.

Отпадный пример: Правило семидесяти двух

Правило семидесяти двух — математический приём, позволяющий оценить, сколько времени понадобится, чтобы ваши деньги удвоились. Сейчас мы его выведем (да!), и более того, мы попробуем уяснить его суть.

Сколько времени понадобится, чтобы удвоить ваши деньги при 100% ставке, нарастающей ежегодно?

Оп-па. Мы использовали натуральный логарифм для случая с непрерывным ростом, а теперь ты ведёшь речь о ежегодном начислении? Не станет ли это формула непригодной для такого случая? Да, станет, однако для реальных процентных ставок вроде 5%, 6% или даже 15%, разница между ежегодным начислением процентов и непрерывным ростом будет невелика. Так что грубая оценка работает, мм, грубо, так что мы сделаем вид, что у нас полностью непрерывное начисление.

Теперь вопрос прост: Как быстро можно удвоиться при 100%-ном росте? ln(2) = 0.693. Нужно 0.693 единиц времени (лет — в нашем случае), чтобы удвоить нашу сумму с непрерывным ростом 100%.

Так, а что если процентная ставка — не 100%, а скажем, 5% или 10%?

Легко! Поскольку ставка * время = 0.693, мы удвоим сумму:

• ставка * время = 0.693
• время = 0.693 / ставка

Получается, если рост 10%-ный, это займёт 0.693 / 0.10 = 6.93 лет на удвоение.

Чтобы упростить вычисления, давайте домножим обе части на 100, тогда можно будет говорить «10», а не «0. 10″:

• время на удвоение = 69.3 / ставка, где ставка выражена в процентах.

Теперь черёд удваиваться при ставке 5%, 69.3 / 5 = 13.86 лет. Однако 69.3 — не самое удобное делимое. Давайте выберем близкое число, 72, которое удобно делить на 2, 3, 4, 6, 8 и другие числа.

• время на удвоение = 72 / ставка

что и является правилом семидесяти двух. Всё шито-крыто.

Если вам нужно найти время для утроения, можете использовать ln(3) ~ 109.8 и получить

• время на утроение = 110 / ставка

Что является ещё одним полезным правилом. «Правило 72» применимо росту по процентным ставкам, росту населения, культур бактерий, и всего, что растёт экспоненциально.

Что дальше?

Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.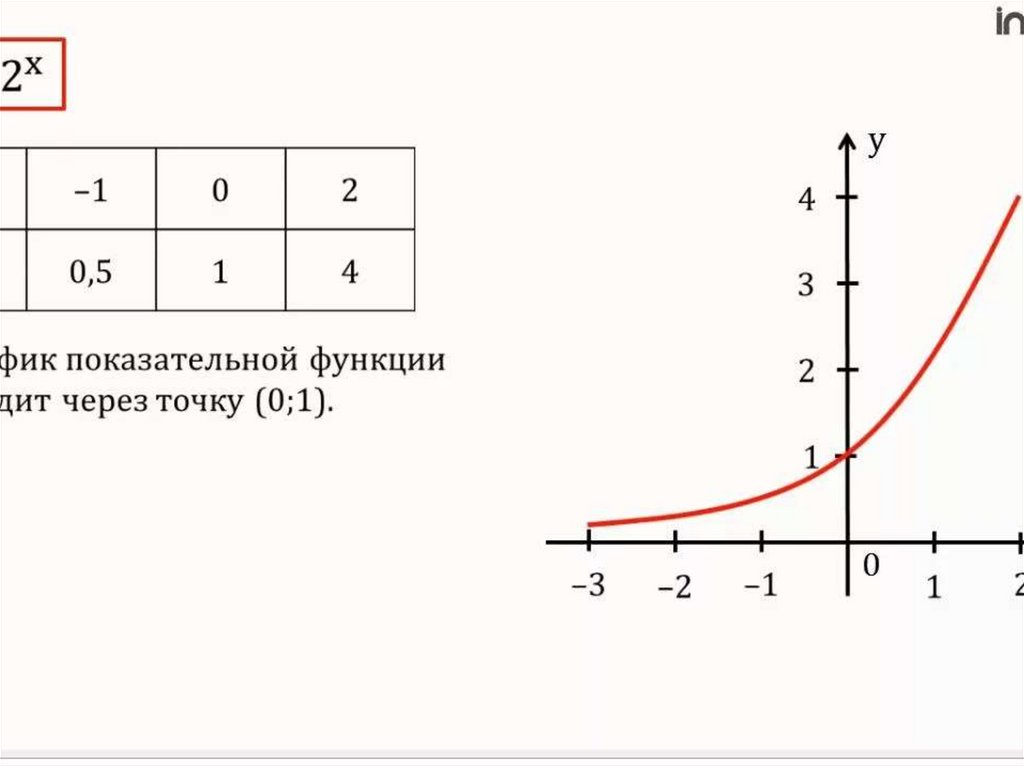

Каждый раз, когда вы видите ln(x), вспоминайте «время, нужное, чтобы вырасти в Х раз». В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.

Дополнение: Натуральный логарифм от e

Быстрая викторина: сколько будет ln(e)?

• математический робот скажет: поскольку они определены как инверсия одна другой, очевидно, что ln(e) = 1.
• понимающий человек: ln(e) это число времени, чтобы вырасти в «е» раз (около 2.718). Однако число e само по себе является мерой роста в 1 раз, так что ln(e) = 1.

Мыслите ясно.

Перевод статьи «Demystifying the Natural Logarithm (ln)»

Натуральный логарифм | это… Что такое Натуральный логарифм?

График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log_e(x) или иногда просто log(x), если основание e подразумевается.^[1]

Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e

2=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e¹ = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени.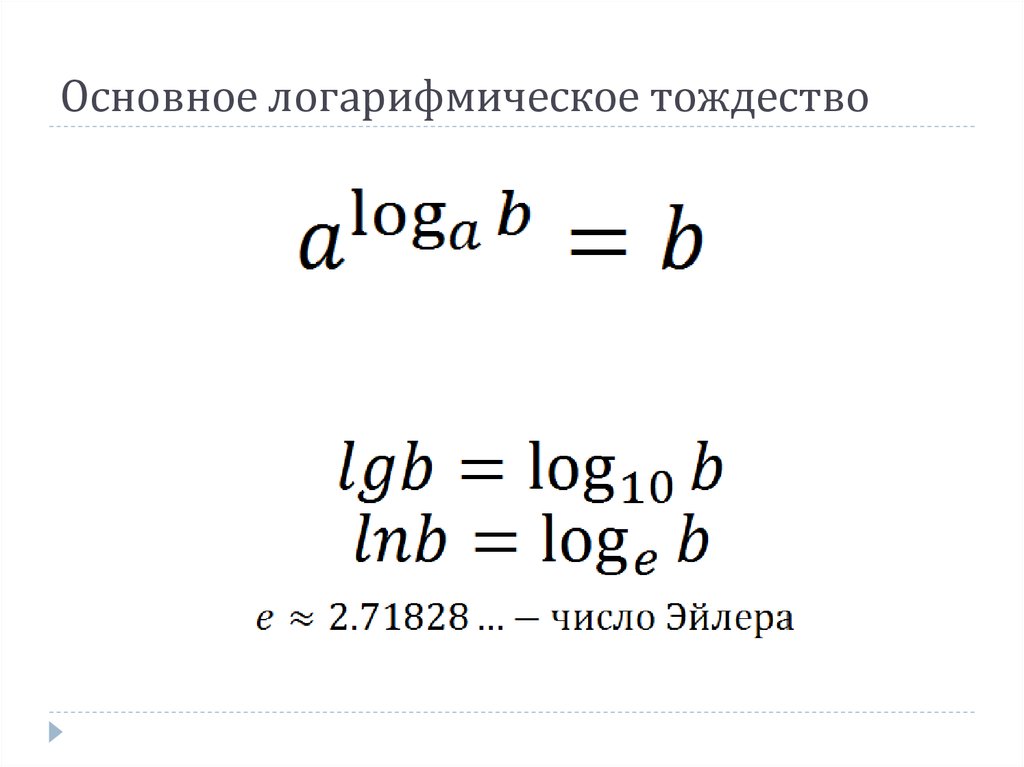 Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

Содержание 1 История 2 Конвенции об обозначениях 2.1 Русская (и советская в целом) система 2.2 Англо-американская система 2.3 Техника 3 Происхождение термина натуральный логарифм 4 Определение 5 Свойства 6 Производная, ряд Тейлора 7 Натуральный логарифм в интегрировании 8 Численное значение 8.1 Высокая точность 8.2 Вычислительная сложность 9 Непрерывные дроби 10 Комплексные логарифмы 11 См. также 12 Примечания 13 Ссылки

История

Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году^[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов. ^[3] Ранее его называли гиперболическим логарифмом,^[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.

Конвенции об обозначениях

Русская (и советская в целом) система

Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln² ln³ 4x⁵ = [ln([ln(4x⁵)]³)]².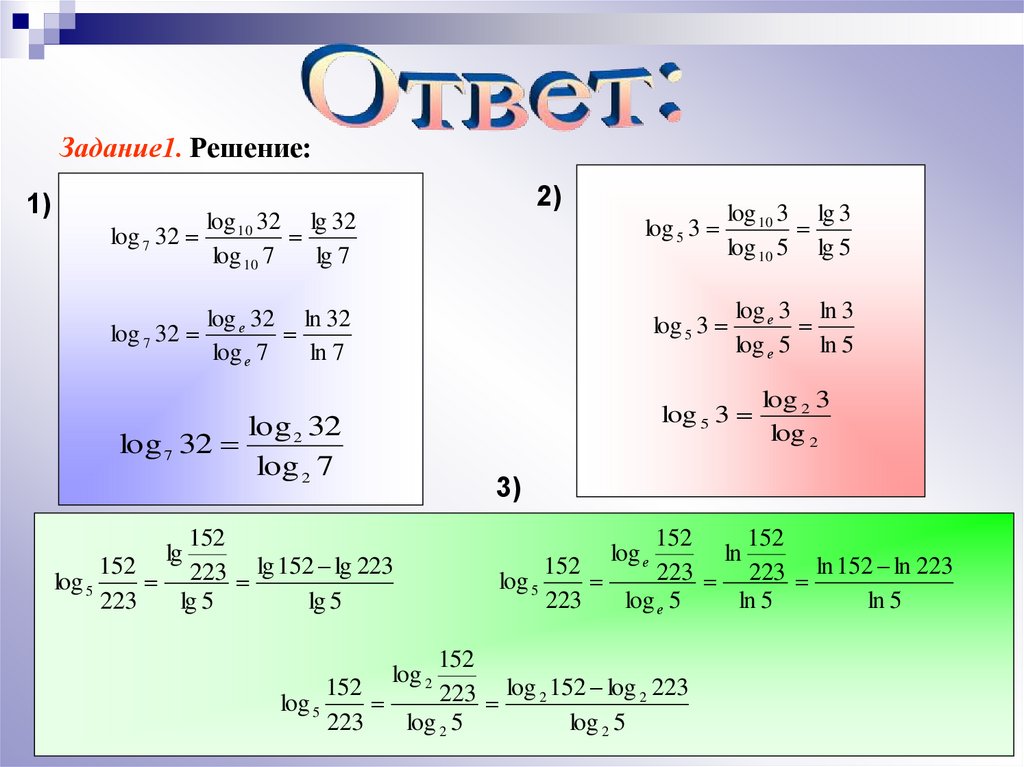

Англо-американская система

Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log₁₀(x)».

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «log_e(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log₁₀(x).

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log₂(x)» (хотя часто вместо этого пишется просто lg(x)).

Техника

В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.

В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.

Происхождение термина

натуральный логарифм

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.

[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.^[6][7][8]

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:^[9]

Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.^[10]

Определение

ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.

Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Число e может быть определено как единственное действительное число a такое, что ln(

a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Свойства

(комплексный логарифм)

Производная, ряд Тейлора

Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 < x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.

Производная натурального логарифма равна

На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:

Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.

Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:

^[11]

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:

Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.

Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа

y нужно просто для x присвоить значение .

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

В другом виде:

и

Ниже дан пример для g(x) = tan(x):

Пусть f(x) = cos(x) и f’(x)= — sin(x):

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Численное значение

Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула:^[12][13]

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Основная статья: Комплексный логарифм

Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида e^x для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого e^x = 0, и оказывается, что e^2πi = 1 = e⁰. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e^z = e^z+2nπi для всех комплексных z и целых n.

Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i⁴ = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.

См. также

• Джон Непер — изобретатель логарифмов
• Интегральный логарифм
• Число e
• Леонард Эйлер

Примечания

1. ↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
2. ↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.
3. ↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
4. ↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
5. ↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
6. ↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
7. ↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
8. ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
9. ↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007.  — P. 331. — ISBN 0-618-95825-8
10. ↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
11. ↑ «Logarithmic Expansions» at Math3.org
12. ↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
13. ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.

Ссылки

• Demystifying the Natural Logarithm (ln) | BetterExplained

x$, уже достаточно странный показатель.

Но есть свежее интуитивное объяснение: Естественный бревно дает вам время, необходимое для достижения определенного уровня роста .

Предположим, вы инвестируете в мармеладных мишек (у кого нет?) с процентной ставкой 100% в год, которая постоянно растет. Если вам нужен 10-кратный рост, при непрерывном начислении сложных процентов , вам придется подождать всего $\ln(10)$ или 2,302 года. Не понимаете, почему для десятикратного роста требуется всего несколько лет? Не видите, почему шаблон не 1, 2, 4, 8? Подробнее об эл. 93$ это 20.08. Через 3 единицы времени мы получаем в 20,08 раз больше, чем мы начали.

$\ln(20.08)$ равно примерно 3. Если нам нужен рост 20,08, мы подождем 3 единицы времени (опять же, предполагая 100% непрерывный темп роста).

Со мной? Естественный журнал дает нам время, необходимое для достижения желаемого роста.

Логарифмическая арифметика ненормальна

Вы уже изучали бревна раньше, и это были странные звери. Как они превратили умножение в сложение? Деление на вычитание? Давайте посмотрим.

Что такое $\ln(1)$? Интуитивно возникает вопрос: как долго мне ждать, чтобы получить 1x мою текущую сумму?

Ноль. Почтовый индекс Нада. Вы уже на в 1 раз больше вашей текущей суммы! Чтобы вырасти с 1 до 1, не требуется времени.

• $\ln(1) = 0$

Хорошо, а как насчет дробного значения? Как долго я получу 1/2 моей текущей суммы? Предполагая, что вы непрерывно растете на 100 %, мы знаем, что $\ln(2)$ — это время, за которое удвоится. Если мы реверсируем это (т. е. возьмем отрицательное время), мы получим половину нашего текущего значения.

• $\ln(.5) = – \ln(2) = -.693$

Логично, правда? Если мы вернемся назад на 0,693 единицы (скажем, минус секунды), у нас будет половина текущего количества. В общем, вы можете перевернуть дробь и взять отрицательное значение: $\ln(1/3) = – \ln(3) = -1,09$. Это означает, что если мы вернемся на 1,09 единицы времени назад, у нас будет треть того, что у нас есть сейчас.

Хорошо, а как насчет натурального логарифма отрицательного числа? Сколько времени требуется, чтобы «вырастить» вашу колонию бактерий с 1 до -3?

Это невозможно! У вас не может быть «отрицательного» количества бактерий, не так ли? В лучшем случае (э.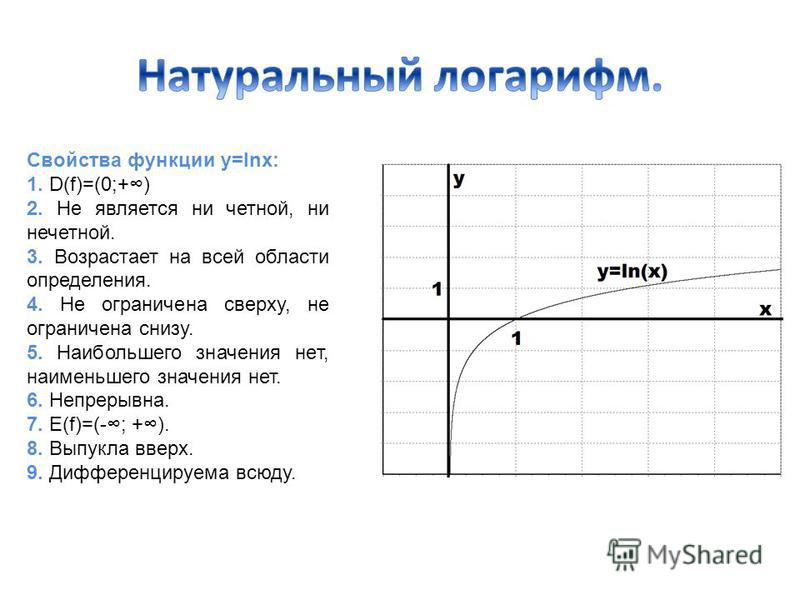 .. как минимум) у вас может быть ноль, но нет никакого способа получить отрицательное количество маленьких тварей. Отрицательные бактерии просто не имеют смысла.

• $\ln(\text{отрицательное число}) = \text{undefined}$

Undefined просто означает, что «у вас нет времени ждать», чтобы получить отрицательную сумму. (Что ж, если использовать воображаемые экспоненты, решение есть. Но сегодня давайте оставим его реальным.)

Логарифмическое умножение — это очень весело

Сколько времени нужно, чтобы увеличить текущее количество в 9 раз? Конечно, мы могли бы просто использовать ln(9). Но это слишком просто, давайте будем другими.

Мы можем рассматривать 9-кратный рост как утроение (затрачиваем $\ln(3)$ единиц времени), а затем снова утроение (затрачивая еще $\ln(3)$ единиц времени):

• Время роста 9x = $ \ln(9)$ = время утроиться и снова утроиться = $\ln(3) + \ln(3)$

Интересно. Любое число роста, например 20, можно рассматривать как 2-кратный рост, за которым следует 10-кратный рост. Или 4-кратный рост, за которым следует 5-кратный рост. Или 3-кратный рост, за которым следует 6,666-кратный рост. Видишь узор?

• $\ln(a*b) = \ln(a) + \ln(b)$

Логарифм a, умноженный на b = log(a) + log(b). Эта связь имеет смысл , если вы думаете о времени роста.

Если мы хотим вырасти в 30 раз, мы можем подождать $\ln(30)$ сразу или просто подождать, пока $\ln(3)$ утроится, а затем подождать, пока $\ln(10)$ вырастет в 10 раз. снова. Чистый эффект тот же, поэтому чистое время тоже должно быть таким же (и это так).

Как насчет деления? $\ln(5/3)$ означает: сколько времени потребуется, чтобы увеличиться в 5 раз, а затем взять 1/3 от этого?

Увеличение в 5 раз равно $\ln(5)$. Увеличение на 1/3 составляет $-\ln(3)$ единиц времени. Итак,

• $\ln(5/3) = \ln(5) – \ln(3)$

Что говорит: Увеличьте 5 раз и «вернитесь в прошлое», пока у вас не будет трети этого количества, поэтому у вас останется рост 5/3. В общем случае имеем

• $\ln(a/b) = \ln(a) – \ln(b)$

Я надеюсь, странная логарифмическая математика начинает обретать смысл: умножение роста становится сложением времени, деление роста становится вычитанием времени. Не запоминайте правила, 9{3,4} = 30 900 200 долл. США

И интуитивно это уравнение означает «100% доход за 3,4 года — это 30-кратный рост». Мы можем рассматривать уравнение как:

Мы можем изменить «скорость» и «время», если скорость * время = 3,4. Например, предположим, что мы хотим 30-кратного роста — как долго мы будем ждать, предполагая доходность 5%?

• $\ln(30) = 3,4$
• $\text{ставка} * \text{время} = 3,4$
• $.05 * \text{время} = 3,4$
• $\text{время} = 3,4 / 0,05 = 68 \text{лет}$

Интуитивно я думаю: «$\ln(30) = 3,4$, поэтому при 100% росте потребуется 3,4 года. Если я удвою скорость роста, я сократю вдвое необходимое время».

• 100% на 3,4 года = 1,0 * 3,4 = 3,4
• 200 % на 1,7 года = 2,0 * 1,7 = 3,4 [рост на 200 % означает половину времени]
• 50 % в течение 6,8 лет = 0,5 * 6,8 = 3,4 [рост 50 % означает удвоение времени]
• 5 % на 68 лет = 0,05 * 68 = 3,4 [рост 5 % означает увеличение времени в 20 раз]

Круто, да? Натуральное бревно можно использовать с любыми процентная ставка или время , пока их продукт одинаков. Вы можете менять переменные как хотите.

Удивительный пример: Правило 72

Правило 72 — это быстрый способ вычислить в уме время, необходимое для удвоения ваших денег. Мы собираемся вывести это (ура!) И, что еще лучше, мы будем понимать это интуитивно.

Сколько времени нужно, чтобы удвоить ваши деньги при 100% годовых, начисляемых каждый год?

Ой . Мы использовали натуральный бревно для непрерывные ставки , но теперь вы просите годовых процентов? Не испортит ли это нашу формулу? Да, будет, но при разумных процентных ставках , таких как 5%, 6% или даже 15%, нет большой разницы между ежегодно начисляемыми процентами и полностью непрерывными процентами. Таким образом, грубая формула работает, ну, грубо, и мы притворимся, что получаем полностью непрерывный процент.

Теперь вопрос прост: как долго можно удвоить при 100% процентной ставки? ln(2) = 0,693. Требуется 0,693 единицы времени (в данном случае лет), чтобы удвоить ваши деньги с непрерывным начислением сложных процентов со ставкой 100%.

Хорошо, а что, если наша заинтересованность не равна 100 %? Что, если она составляет 5 % или 10 %?

Простой. Пока ставка * время = 0,693, мы удвоим наши деньги:

• ставка * время = 0,693
.
• время = 0,693/скорость

Итак, если бы у нас был только 10-процентный рост, удвоение заняло бы 0,693 / 0,10 или 6,93 года.

Для упрощения давайте умножим на 100, чтобы мы могли говорить о 10, а не о 0,10:

• время удвоения = 69,3/скорость, где скорость предполагается в процентах.

Теперь время удвоения при 5% росте составляет 69,3/5 или 13,86 лет. Однако 69,3 — не самое делимое число. Давайте выберем ближайшего соседа, 72, который можно разделить на 2, 3, 4, 6, 8 и многие другие числа.

• время удвоения = 72/скорость

это правило 72! Легко свежий.

Если вы хотите найти время утроения, вы должны использовать ln(3) ~ 109,8 и получить

• время утроения = 110 / скорость

Еще одно полезное практическое правило. Правило 72 полезно для процентных ставок, роста населения, бактериальных культур и всего, что растет в геометрической прогрессии.

Куда отсюда?

Я надеюсь, что естественный журнал имеет больше смысла — он говорит вам раз , необходимых для любого количества экспоненциального роста. Я считаю это «естественным», потому что e — это универсальная скорость роста, поэтому ln можно считать «универсальным» способом выяснить, сколько времени требуется для роста.

Когда вы видите $\ln(x)$, просто подумайте «количество времени, необходимое для роста до x». В следующей статье мы объединим e и ln, и воздух наполнится сладким ароматом математики.

Приложение: Естественный журнал E

Быстрый тест: что такое $\ln(e)$?

• Математический робот говорит: Поскольку они определены как обратные функции, ясно, что $\ln(e) = 1$
• Интуитивный человек: ln(e) — это время, необходимое для получения «e» единиц роста (около 2,718). Но e равно количеству роста после 1 единица времени , поэтому $\ln(e) = 1$.

Думай интуитивно.

Другие сообщения из этой серии

90 = 1?)
1. Использование логарифмов в реальном мире
2. Как думать с помощью экспонент и логарифмов
3. Сравнение дискретного и непрерывного роста
4. Что на самом деле означает показатель степени?
5. В: Почему e особенный? (2,718…, а не 2, 3,7 или другое число?)

Натуральный логарифм (ln) | Определение, правила и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• В этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Самые популярные вопросы
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.

  No related posts.