Как Найти Число От Натурального Логарифма :: orwarabmu1981
11.03.2016 07:06
Таблица десятичных логарифмов целых чисел от 0 до 99. Натуральный логарифм.
называемого основным логарифмическим тождеством. Как же быть в том случае, если, например, надо выразить число 8299 как число 10 в какой-то степени? Как найти это число с определённой степенью точности, которое в данном случае равно 3,919…? Выход – это логарифм и логарифмические таблицы. Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел..
- Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается.
- Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.
Простота. - Раздел: Математика. Для начала рассмотрим несколько задач. Задача 1. Найти положительный корень уравнения х4 = 81. Логарифм числа по основанию е, где е – иррациональное число, приближенно равное 2,7, называют натуральным логарифмом числа.
Простота.Логарифм числа есть само число i Уведомление: Проверка на прочность: провалена. Теория Шеннона — Колмогорова.
Количество информации — один бит — 1 0 1. Вопросы: 1. Какой достоверности информация в двух битах информации — 1. Какова избыточность информации в битах информации — 1. Итог — одна большая ЛАЖА. Теория ignatt Количество информации есть количество разнообразия. Избыточность информации от нуля до бесконечности. Натуральный ряд чисел имеет точку сходимости.
Десятичные (lg) и натуральные логарифмы (ln). Основное логарифмическое тождество. сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа z. Натуральные логарифмы принято обозначать так: lnN. Соответсвенно знак ln есть сокращение слов logarithm natural — натуральный логарифм.
Вычислить, найти натуральный логарифм. N (число). В логарифмической функции имеет запись. Логарифм числа 54 по основанию 2 = нулю. Избыточность информации от точки сходимости натурального ряда чисел (от нуля), через избыточность информации равной единице (множество 1 2 3 4 5 6 7) до бесконечной.
Число e. Натуральные логарифмы. Число e принято за основание натуральных логарифмов: логарифм по основанию e называется натуральным логарифмом и обозначается ln x, т. е. ln x = loge x. Определение 2.12 Найдем связь между натуральным и.
Т. е. Имеется число, мощности множества, превосходящее мощность множества натурального ряда чисел. Это число два в 5. В логарифмической функции имеет запись. Логарифм числа 5. Множество 5. 4 имеет один член множества. Никакого разнообразия нет, следовательно, равно нулю информации. Аксиома — количество информации есть количество разнообразия).
Логарифм числа 7 по основанию 2 = 1. Это следует из того, что первое множество, мощности, превосходящей мощность множества натурального ряда чисел есть множество 1 2 3 4 5 6 7.
Множество 7 является обращенным множеством множества 1 2 3 4 5 6. Следовательно, вместо множества 1 2 3 4 5 6 можно записать его обращенное множество равное 7. Наибольшее количество информации содержится в натуральном ряде чисел как содержащем наибольшее разнообразие. Натуральный ряд чисел бесконечен, следовательно, количество информации бесконечно (Аксиома — количество информации есть количество разноообразия). Избыточность информации от точки сходимости натурального ряда чисел (от нуля), через избыточность информации равной единице (множество 1 2 3 4 5 6 7) до бесконечной избыточности (множество натурального ряда чисел).
Исходя из вышеизложенного и свойств чисел информационного поля следует — Логарифм любого числа натурального ряда чисел равен самому числу. Каждое число натурального ряда чисел в информационном поле имеет свою индивидуальную мантиссу, показывающую связь числа натурального ряда чисел со всем множеством натурального ряда. N = N f (N) f (1) где N f(N) — число натурального ряда чисел со своей индивидуальной мантиссой.
Показывает связь всех чисел натурального ряда чисел, но не принадлежит ни одному числу натурального ряда. При такой ситуации нет необходимости в расчетах логарифмов чисел.
Таблицы Брадиса не нужны) Подтверждаются принятые аксиомы как обоснованные. Сообщение отредактировал Owen — 2.
Теги:
Как Найти Число От Натурального Логарифма
Что такое натуральный логарифм. Натуральный логарифм
1.1. Определение степени для целого показателя степени
X 1 = XX 2 = X * X
X 3 = X * X * X
…
X N = X * X * … * X — N раз
1.2. Нулевая степень.
По определению принято считать, что нулевая степень любого числа равна 1:1.3. Отрицательная степень.
X -N = 1/X N1.4. Дробная степень, корень.
X 1/N = корень степени N из Х.Например: X 1/2 = √X.
1.5. Формула сложения степеней.
X (N+M) = X N *X M1.6.Формула вычитания степеней.
X (N-M) = X N /X M1.7. Формула умножения степеней.
X N*M = (X N) M1.
8. Формула возведения дроби в степень. (X/Y) N = X N /Y N2. Число e.
Значение числа e равно следующему пределу:E = lim(1+1/N), при N → ∞.
С точностью 17 знаков число e равно 2.71828182845904512.
3. Равенство Эйлера.
Это равенство связывает пять чисел, играющих особую роль в математике: 0, 1, число e, число пи, мнимую единицу.E (i*пи) + 1 = 0
4. Экспоненциальная функция exp (x)
exp(x) = e x5. Производная экспоненциальной функции
Экспоненциальная функция обладает замечательным свойством: производная функции равна самой экспоненциальной функции:(exp(x))» = exp(x)
6. Логарифм.
6.1. Определение функции логарифм
Если x = b y , то логарифмом называется функцияЛогарифм показывает в какую степень надо возвести число — основание логарифма (b), чтобы получить заданное число (X). Функция логарифм определена для X больше нуля.
Например: Log 10 (100) = 2.
6.2. Десятичный логарифм
Это логарифм по основанию 10:Y = Log 10 (x) .
Обозначается Log(x): Log(x) = Log 10 (x).
Пример использования десятичного логарифма — децибел .
6.3. Децибел
Пункт выделен в отдельную страницу Децибел6.4. Двоичный логарифм
Это логарифм по основанию 2:Y = Log 2 (x).
Обозначается Lg(x): Lg(x) = Log 2 (X)
6.5. Натуральный логарифм
Это логарифм по основанию e:Y = Log e (x) .
Обозначается Ln(x): Ln(x) = Log e (X)
Натуральный логарифм — обратная функция к экспоненциальной функции exp (X).
6.6. Характерные точки
Log a (1) = 0Log a (a) = 1
6.7. Формула логарифма произведения
Log a (x*y) = Log a (x)+Log a (y)6.8. Формула логарифма частного
Log a (x/y) = Log a (x)-Log a (y)6.9. Формула логарифма степени
Log a (x y) = y*Log a (x)6.10. Формула преобразования к логарифму с другим основанием
Log b (x) = (Log a (x))/Log a (b)Пример:
Log 2 (8) = Log 10 (8)/Log 10 (2) =0.903089986991943552 / 0.301029995663981184 = 3
7.
Формулы полезные в жизниЧасто возникают задачи пересчета объема в площадь или в длину и обратная задача — пересчет площади в объем. Например, доски продаются кубами (кубометрами), а нам требуется рассчитать какую площадь стены можно обшить досками содержащимися в определенном объеме, см. расчет досок, сколько досок в кубе . Или, известны размеры стены, надо рассчитать число кирпичей, см. расчет кирпича .
Разрешается использовать материалы сайта при условии установки активной ссылки на источник.
Урок и презентация на темы: «Натуральные логарифмы. Основание натурального логарифма. Логарифм натурального числа»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 10–11 классов «Логарифмы»
Что такое натуральный логарифм
Ребята, на прошлом уроке мы с вами узнали новое, особенное число – е.
x$ в точке (0;1) равен 45°. Тогда угол наклона касательной к графику натурального логарифма в точке (1;0) также будет равен 45°. Обе эти касательные будут параллельны прямой $y=x$. Давайте схематично изобразим касательные: Свойства функции $y=\ln{x}$
1. $D(f)=(0;+∞)$.2. Не является ни четной, ни нечетной.
3. Возрастает на всей области определения.
4. Не ограничена сверху, не ограничена снизу.
5. Наибольшего значения нет, наименьшего значения нет.
6. Непрерывна.
7. $E(f)=(-∞; +∞)$.
8. Выпукла вверх.
9. Дифференцируема всюду.
В курсе высшей математики доказано, что производная обратной функции есть величина, обратная производной данной функции
.Углубляться в доказательство не имеет большого смысла, давайте просто запишем формулу: $y»=(\ln{x})»=\frac{1}{x}$.
Пример.
Вычислить значение производной функции: $y=\ln(2x-7)$ в точке $х=4$.
Решение.
В общем виде наша функция представляют функцию $y=f(kx+m)$, производные таких функций мы умеем вычислять.
6=1$.
$x=±1$.
Точка $х=-1$ не принадлежит области определения. Тогда имеем одну стационарную точку $х=1$. Найдем промежутки возрастания и убывания:
Точка $х=1$ – точка минимума, тогда $y_min=1-6*\ln{1}=1$.
Ответ: Функция убывает на отрезке (0;1], функция возрастает на луче $
2 .
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x )», либо «ln(x )» , а для обозначения логарифма по основанию 10 — «log 10 (x )».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(
log e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:
Если основание b равно e , то производная равна просто 1/x , а при x = 1 эта производная равна 1.
Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора , чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.
Определение
Формально ln(a ) может быть определён как площадь под кривой графика 1/x от 1 до a , т. е. как интеграл :
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
при условии, что y = (x −1)/(x +1) и x > 0.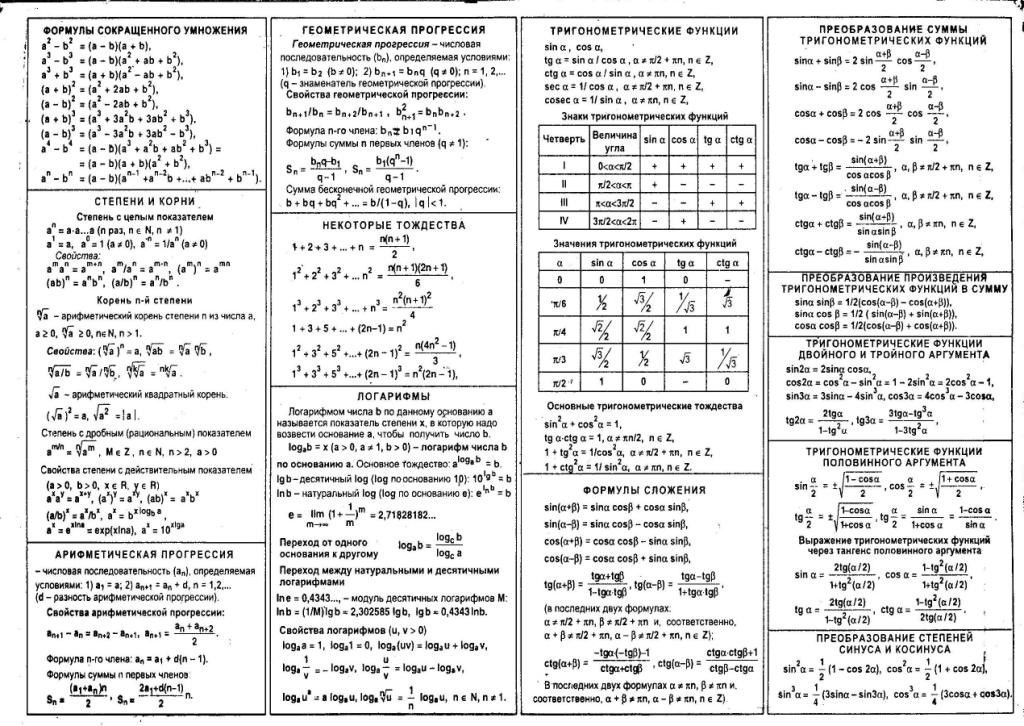
Для ln(x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона , чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции.
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M (n ) ln n ). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M (n ) — вычислительная сложность умножения двух n -значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби , но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида
Есть, однако, две трудности: не существует x , для которого e x = 0, и оказывается, что e 2πi = 1 = e 0 . Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то e z = e z +2nπi для всех комплексных z и целых n .Логарифм не может быть определён на всей комплексной плоскости , и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2 πi . Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi , и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi , или 10πi или −6 πi , и так далее.
См. также
- Джон Непер — изобретатель логарифмов
Примечания
- Mathematics for physical chemistry . — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5
, Extract of page 9
- J J O»Connor and E F Robertson The number e . The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано
- Cajori Florian A History of Mathematics, 5th ed . — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- Flashman, Martin Estimating Integrals using Polynomials . Архивировано из первоисточника 12 февраля 2012.
— 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5
, Extract of page 9Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.
Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.
Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.
Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.
Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно.
Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .
Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».
Вам понадобится
- Доступ в интернет, Microsoft Office Excel или калькулятор.
Инструкция
Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами.
Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.
Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню.
Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.
Видео по теме
Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.
Если , то .
Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.
Вконтакте
Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:
Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.
Приведем некоторые тождества:
Приведем основные алгебраические выражения:
;
.
Внимание! может существовать только при x>0, x≠1, y>0.
Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.
Обозначения:
- lg x — десятичный;
- ln x — натуральный.
Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.
График натурального логарифмаПостроим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.
Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:
Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:
Для удобства мы можем взять пять опорных точек:
;
;
.
;
.
Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.
Построив по точкам график, получаем приблизительный график:
Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.
Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .
Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .
Изучая график, возникает вопрос — как ведет себя функция при y
Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х
Предел натурального log можно записать таким образом:
Формула замены основания логарифмаИметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.
Начнем с логарифмического тождества:
Тогда любое число, либо переменную у можно представить в виде:
где х — любое число (положительное согласно свойствам логарифма).
Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:
Воспользуемся свойством (только вместо «с» у нас выражение):
Отсюда получаем универсальную формулу:
.
В частности, если z=e, то тогда:
.
Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.
Решаем задачиДля того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.
Задача 1 . Необходимо решить уравнение ln x = 3.
Решение: Используя определение логарифма: если , то , получаем:
Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.
Решение: Используя определение логарифма: если , то , получаем:
.
Еще раз применим определение логарифма:
.
Таким образом:
.
Можно приближенно вычислить ответ, а можно оставить его и в таком виде.
Задача 3. Решите уравнение .
Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:
.
Перед нами квадратное уравнение. Найдем его дискриминант:
Первый корень уравнения:
.
Второй корень уравнения:
.
Вспоминая о том, что мы производили подстановку t = ln x, получаем:
В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.
В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.
В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.
В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.
В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.
Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.
Натуральный логарифм Функция y=ln x ее свойства
Доказательство основного свойства натурального логарифма
Что такое число 0?
Вещественная функция натурального логарифма ln(x) определена только для x>0. Таким образом, натуральный логарифм нуля равен undefined .
Что такое журнал 0?
log 0 равно undefined . Это не настоящее число, потому что вы никогда не сможете получить ноль, возведя что-либо в степень чего-либо еще. Вы никогда не сможете достичь нуля, вы можете только приблизиться к нему, используя бесконечно большую и отрицательную силу.
Почему ln не определен в 0?
9х=0. Вот почему ln 0 не определен.Есть ли у LOGX 0 ответ?
Есть ли у logx 0 ответ? № ; ничто в любой степени равно 0, кроме 0, и 0 не может быть основанием журнала.
Может ли логарифмическая шкала начинаться с 0?
Логарифм нуля не определен — математически невозможно нанести ноль на логарифмическую шкалу .
Вместо нуля вы можете ввести меньшее значение (скажем, -10 по логарифмической шкале), а затем использовать специальные метки, чтобы правильно пометить график (чтобы он был помечен «0», а не «-10»).0005
Является ли 1 0 бесконечностью или неопределенностью?
Таким образом, 1/0 не является бесконечностью и 0/0 не является неопределенным, поскольку деление на ноль не определено. Когда что-то не определено, не следует спрашивать, какова его ценность.
Бесконечность бесконечность?
Ответ: ∞ . Естественная логарифмическая функция строго возрастает, поэтому она всегда растет, хотя и медленно. Производная y’=1x, поэтому она никогда не равна 0 и всегда положительна.
Почему ln of undefined?
Функция натурального логарифма ln(x) определена только для x>0. Нет значения y, которое вы можете заменить, чтобы сделать x = 0. Таким образом, натуральный логарифм нуля не определен .
Что такое журнал бесконечности?
Loge ∞ = ∞ , или ln (∞) = ∞ Мы можем заключить, что как натуральный логарифм, так и десятичный логарифм для обращения бесконечности имеют одно и то же значение, т.
е. бесконечность.
Что такое E в математике?
Число e, также известное как число Эйлера, равно математическая константа, приблизительно равная 2,71828 , которую можно охарактеризовать разными способами. Это основание натуральных логарифмов. Это предел (1 + 1/n) n , когда n приближается к бесконечности, выражение, которое возникает при изучении сложных процентов.
Какой LOGX 1?
Ответ: ответ ⅒ .
Как выглядит график LN?
youtube.com/watch?v=Zrfl6MkTWTY»
Как нанести ноль на график?
youtube.com/watch?v=AvY1UqB1fio”
Как нанести нули на график?
youtube.com/watch?v=uFsiWLd5m3U”
Что такое 0, разделенное на что-либо?
Решения НЕТ, поэтому любое ненулевое число, деленное на 0 , равно undefined .
Является ли 0 действительным числом?
На самом деле действительные числа — это практически любые числа, которые только можно придумать.
… Действительные числа могут быть положительными или отрицательными, и включают число ноль . Их называют действительными числами, потому что они не мнимые, а это другая система чисел.
Каков ответ 0 0?
Объяснение: 00 не определено . Выражение само по себе вступает в противоречие с двумя фактами арифметики: любое число, деленное само на себя, равно единице, а ноль, деленный на любое число, равен нулю. Когда у нас есть оба этих случая вместе, как в случае 00, мы говорим, что это не определено.
Является ли число равным 0 бесконечности?
Чему равен натуральный логарифм нуля? … Вещественная функция натурального логарифма ln(x) определена только для x>0. Итак, натуральный логарифм нуля не определено .
Что такое Арктан бесконечность?
арктан(∞) = ? Арктангенс — это функция арктангенса. Предел арктангенса х, когда х стремится к бесконечности, равен пи/2 радиана или 90 градусов: Предел арктангенса х, когда х приближается к минус бесконечности, равен -пи/2 радиан или -90 градусов: арктангенс ►
Что такое грех бесконечности?
Функция синуса — это функция от действительных чисел до диапазона [-1, 1].
Бесконечность не является реальным числом, поэтому грех(бесконечность) бессмысленно . 97 просмотров Ответ запрошен.
Каково значение e повышения до 0?
Чему равно значение e в степени 0? Значение e 0 равно 1 .
Каковы правила для ln?
| Правило или Специальный случай | Формула |
|---|---|
| Продукт | LN (XY) = LN (x)+LN (Y) |
| 77777 = ln | |
| 777777 = LN | |
| 777777 = LN (y) | |
| 7 70137 70137 70137 70137 70137777. )−ln(y) | |
| Логарифм мощности | ln(xy)=yln(x) |
| Логарифм e | ln(e)=1 |
3 Что такое основание ln?
Кроме того, ln3 означает логарифм 3 с e в качестве основания и e=2,71828 и, следовательно, ln3= 1,0986 (используя научный калькулятор) и, следовательно, ln3≠1 .
Что такое log2 бесконечность?
Поскольку возведение 2 в бесконечность приведет к бесконечности, мы говорим, что логарифмическая база 2 бесконечности сама является бесконечностью .
Есть ли у ln предел?
Поскольку сами числа неограниченно возрастают, мы показали, что, сделав x достаточно большим, мы можем сделать f(x)=lnx сколь угодно большим. Таким образом, предел бесконечен, когда x достигает ∞ .
Что такое ln отрицательной бесконечности?
Ответ не определен. Домен lnx равен x≥0, поэтому −∞ не находится в домене .
Что такое буква Σ?
Сигма /ˈsɪɡmə/ (прописная Σ, строчная σ, строчная в конце слова ς; греческий: σίγμα) равна восемнадцатая буква греческого алфавита . В системе греческих цифр имеет значение 200. В общей математике прописная буква Σ используется как оператор суммирования.
Действительно ли число ea?
да e действительное и иррациональное число . … число Эйлера. e — важная математическая константа, основанная на натуральном логарифме. Оно приблизительно равно 2,71828 и является пределом (1+1/n) n при приближении n к бесконечности и сумме бесконечного ряда e=1 + 1/1 + 1/1,2 + 1/1,2.
Что такое цифра?
Цифра представляет собой одиночный символ, используемый для составления цифр . 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 — это десять цифр, которые мы используем в повседневных числительных. Пример: число 153 состоит из 3 цифр («1», «5» и «3»).
Что такое LOGX 3?
Объяснение: Вспомните определение логарифма, т.е. Если logb(a)=c истинно, то a=bc , и если основание не указано явно, мы всегда предполагаем, что это основание 10 (если оно не написано как lnx, и в этом случае основанием является иррациональное число e ) logx=3→ х=103→х 92 — это журнал (лог х).
Является ли EE журналом?
| Связанные ссылки | ||||
|---|---|---|---|---|
| Натуральный калькулятор журнала | BOG BASE 2 | |||
| Разница между LOG и LN | Formula | . Натуральная логарифмическая функция Логарифм с основанием e называется натуральным логарифмом. Обозначается lnx. Как рассчитать ln?Общая формула для вычисления Ln(x) с функцией Log: Ln(x) = Log(x)/Log(e) или эквивалентно Ln(x) = Log(x)/0,4342944819. Может ли ln быть отрицательным? Функция натурального логарифма ln(x) определена только для x>0. Таким образом, натуральный логарифм отрицательного числа равен undefined . Где 0 на графике?Горизонтальная ось в координатной плоскости называется осью x. Вертикальная ось называется осью Y. Точка, в которой пересекаются две оси, называется началом координат. Начало координат находится в 0 по оси x и 0 по оси y . Как выглядит график 0 0? Точка (0,0) называется началом координат. Это точка пересечения осей x и y. Ось x и ось y делят прямоугольную систему координат на четыре области, называемые квадрантами. Как выглядит 0 1 на графике? Точка (0,1) находится на положительной части оси y под углом θ=π2 к оси x. Как найти ноль?youtube.com/watch?v=3XJWVLx1snU” Каков наклон 0?Наклон линии можно рассматривать как «подъем над линией». «Когда «подъем» равен нулю, тогда линия горизонтальна или плоская, а наклон линии равен нулю. Проще говоря, нулевой наклон идеально плоский в горизонтальном направлении . Что делать, если точка пересечения с осью y равна 0?Поскольку уравнение y = 0 имеет точку пересечения y, равную 0, ваш график по существу представляет собой ось x . Натуральный логарифм — Academic KidsFrom Academic Kids Натуральный логарифм является логарифмом по основанию e , где e приблизительно равно 2,71828… (точная дробь не может быть указана, т.к. e — иррациональное число, как и пи). Натуральный логарифм определен для всех положительных действительных чисел x , а также может быть определен для ненулевых комплексных чисел, как будет объяснено ниже. ln(x)
Нотационные соглашения Математики обычно понимают либо « LN ( x ) » или «log x )», чтобы среднее log E ( x ), i.e. x и напишите «log 10 ( x )», если предполагается десятичный логарифм x . Инженеры, биологи и некоторые другие пишут только «ln( x )» или (иногда) «log e ( x )», когда они означают натуральный логарифм x , и принимают «log( x )» как log 10 ( x ) или, в контексте вычислений, log 2 ( x ). Большая часть причин думать о десятичных логарифмах устарела вскоре после 1970 года, когда широкое распространение получили портативные калькуляторы (подробнее об этом см. десятичный логарифм). Тем не менее, поскольку калькуляторы производятся и часто используются инженерами, соглашения, к которым привыкли инженеры, продолжали использоваться в калькуляторах, поэтому теперь большинство нематематиков принимают «log( x )» для обозначения десятичного логарифма числа . x и используйте только «ln( x )» для обозначения натурального логарифма x . Совсем недавно, в 1984 году, Пол Халмос в своей автобиографии выразил презрение к тому, что он считал детским обозначением «ln», которое, по его словам, никогда не использовал ни один математик. на самом деле запись была изобретена в 1893 году Ирвингом Стрингемом, профессором математики в Беркли. Чтобы избежать путаницы, Википедия использует запись ln( x ) для натурального логарифма x и log 10 ( x ) для десятичного логарифма x . Ln — обратная натуральная экспоненциальная функцияЭта функция — обратная экспоненциальная функция, таким образом, он держит
Другими словами, логарифмическая функция — это биекция множества положительных действительных чисел на множество всех действительных чисел. Точнее, это изоморфизм группы положительных действительных чисел при умножении на группу действительных чисел при сложении. Логарифмы могут быть определены с любым положительным основанием, кроме 1, а не только с e , и они всегда полезны для решения уравнений, в которых неизвестное выступает как показатель степени какой-либо другой величины. Что в них такого «естественного»?Первоначально кажется, что в мире, использующем базу 10 почти для всех расчетов, эта база будет более «естественной», чем база e . Причина, по которой мы называем ln( x ) «естественным», двояка: во-первых, натуральный логарифм можно довольно легко определить с помощью простого интеграла или ряда Тейлора, как будет объяснено ниже; это неверно для других логарифмов. Во-вторых, выражения, в которых неизвестная переменная стоит как показатель степени e встречаются гораздо чаще, чем показатели степени 10 (из-за «естественных» свойств экспоненциальной функции, которые позволяют ей описывать рост и затухание), поэтому натуральный логарифм более полезен на практике. Конкретнее, рассмотрим задачу дифференцирования логарифмической функции: Когда x равно 1, а основание (b) равно e , то наклон графика будет равен 1. Предпочтительный способ работы с такими многозначными функциями в комплексном анализе — через римановы поверхности: тогда функция ln определяется не на комплексной плоскости, а вместо этого на подходящей римановой поверхности, имеющей счетное число «листьев» и значений функции отличаются на 2π i от листа к листу. Числовое значениеЧтобы вычислить числовое значение натурального логарифма числа, разложение в ряд Тейлора можно переписать как: 9{2} \, ( \frac{1}{9} + \ldots ) ) ) ) ) | ||
Натуральная логарифмическая функция y=lnx является обратной экспоненциальной функции с естественным основанием y=ex.
Таким образом, он находится между Q1 и Q2.
Хотя эта функция не была введена Нейпиром, ее иногда называют 9-й.0003 Логарифм Непера .
люди, которые используют log( x ) со строчными буквами l для обозначения log e ( х ).
) С 2005 года некоторые математики приняли запись «ln», но большинство используют «log». В теоретической информатике логарифм по основанию 2 записывается как LG( х ), чтобы избежать путаницы. Это использование было предложено Эдвардом Рейнгольдом и популяризировано Дональдом Кнутом.
{i \phi}