Нахождение длины отрезка по координатам – .

примеры, решения, как найти середину отрезка по координатам

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Yandex.RTB R-A-339285-1 Определение 1

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок AB.

Если отрезок AB продолжить в обе стороны от точек A и B, мы получим прямую AB. Тогда отрезок AB – часть полученной прямой, ограниченный точками A и B. Отрезок AB объединяет точки A и B, являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K, лежащую между точками A и B, можно сказать, что точка K лежит на отрезке AB.

Определение 2

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка AB обозначим следующим образом: AB.

Определение 3

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка AB обозначить точкой C, то верным будет равенство: AC=CB

И далее мы рассмотрим, как же определять координаты середины отрезка (точки C) при заданных координатах концов отрезка (A и B), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Исходные данные: координатная прямая Ox и несовпадающие точки на ней: A и B. Этим точкам соответствуют действительные числа xA и xB. Точка C – середина отрезка AB: необходимо определить координату xC.

Поскольку точка C является серединой отрезка АВ, верным будет являться равенство: |АС| = 

zaochnik.com

Как найти длину отрезка 🚩 Длина отрезка через координаты 🚩 Математика

13 апреля 2011

Автор КакПросто!

Пусть отрезок задан двумя точками в плоскости координат, тогда можно найти его длину с помощью теоремы Пифагора.

Статьи по теме:

Инструкция

Пусть заданы координаты концов отрезка (x1; y1) и (x2; y2). Начертите отрезок в системе координат.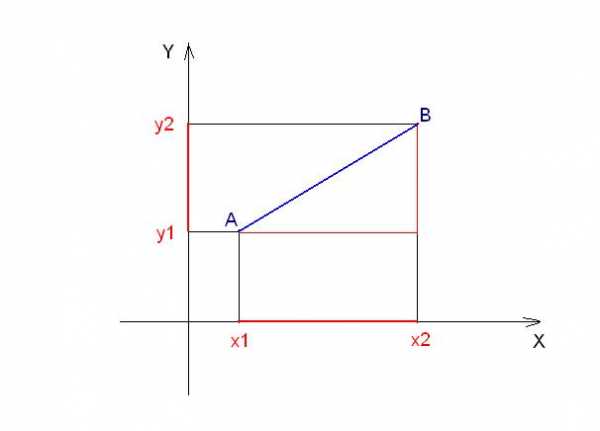 Опустите перпендикуляры из концов отрезка на оси X и Y. Отрезки, отмеченные на рисунке красным, являются проекциями исходного отрезка на оси координат. Если выполнить параллельный перенос, отрезков-проекций к концам отрезков, то получится прямоугольный треугольник. Катетами этого треугольника будут являться перенесенные проекции, а гипотенузой — сам отрезок AB.

Длины проекций легко вычисляются. Длина проекции на ось Y будет равна y2-y1, а длина проекции на ось X — x2-x1. Тогда по теореме Пифагора |AB|² = (y2 — y1)² + (x2 — x1)², где |AB| — длина отрезка.

Представив эту схему нахождения длины отрезка в общем случае, легко вычислять длину отрезка, не строя отрезок. Посчитаем длину отрезка, координаты концов которого (1;3) и (2;5). Тогда |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5, таким образом длина искомого отрезка равна 5^1/2.

Видео по теме

Источники:

• Длина отрезка
• что такое длина отрезка

Совет полезен?

Распечатать

Как найти длину отрезка

Статьи по теме:

Не получили ответ на свой вопрос?
Спросите нашего эксперта:

www.kakprosto.ru

Как найти длину отрезка на координатной прямой?

#1

Отрезок — геометрическое место точек, находящихся на одной прямой и заключенных в пределах его концов. Концами отрезка являются точки. Отрезок является замкнутым множеством, следовательно, можно определить его размер. Мерой размера для отрезка является его длина. Вычислить длину отрезка можно точно и приблизительно. Для приблизительного вычисления необходимо использовать подручные средства. Как найти длину отрезка используя линейку? Достаточно приложить начало линейки к началу отрезка и посмотреть на какой цифре кончается отрезок. Это и будет его длина. Но следует учесть некоторые нюансы: . Длину отрезка невозможно абсолютно точно вычислить. . Масштабы и единицы измерения могут не совпадать

#2

Но как найти длину отрезка с высокой или абсолютной точностью? Для пространства каждой размерности существуют свои формулы. Рассмотрим простейший, одномерный случай. Декартовой системой для одномерного случая является обыкновенная координатная прямая. В реальной жизни мы сталкиваемся с сотнями примеров различных координатных прямых. Это и линейки, и строительные рулетки, и лента портного и даже трасса, где каждый километр отмечен порядковым номером. Нет ничего проще, чем измерить отрезок в одномерном пространстве. Особо легко, если начало отрезка совпадает с началом отсчёта (нулём) координатной прямой. В таком случае его длина будет совпадать с модулем координаты его конца. К примеру: если отрезок выходит из нуля, а конец его имеет координату 5, то длина отрезка будет равна пяти.

#3

Также нет задачи легче, чем как сравнить два отрезка, исходящих из нуля. Больше будет тот отрезок, модуль чьей координаты будет большим. Например: из нуля на координатной плоскости в разные стороны выходят два отрезка. Координата отрезка, выходящего влево равна -7, а выходящего вправо — 4. Модуль первого отрезка равен 7 со знаком «+» , а модуль второго — 4 с тем же знаком. Следовательно первый отрезок длиннее второго. Если отрезок начинается не в нуле, тогда следует пользоваться универсальной формулой вычисления длины для одномерного пространства. Звучит она следующим образом: «Для того чтобы найти длину отрезка в одномерном пространстве необходимо из значения координаты правого конца вычесть значение координаты левого конца».

#4

Задача схожа с тем, как найти координаты середины отрезка, только в нашем случае координаты вычитаются, а не складываются и делятся пополам. Рассмотрим пример. Пусть отрезок имеет начало в точке 2, а конец в точке 11. Найти длину отрезка. Для этого вычтем из правой координаты значение левой: 11-2 = 9. Ответ: 9. Следует отметить, что можно наоборот, вычитать координату правого конца из левого, но тогда придётся брать результат по его абсолютному значению (модулю) . 2-11 = -9. Модуль -9 равен 9. Результат не изменился. Такой приём может помочь в решении специальных задач. Также следует рассмотреть примеры для двумерного пространства.

#5

Для двумерного пространства существуют специальные формулы, которые являются обобщением одномерного случая. Сразу рассмотрим конкретный пример, по пути решения объясняя формулы. Для её решения необходимо знать как называется отрезок, соединяющий 2 точки окружности. Такой отрезок называется хордой. Дана хорда с концами А (1;1) и B (4;5) . Найти длину отрезка AB. Длина отрезка АВ будет равна арифметическому квадратному корню из суммы квадратов разностей соответствующих координат точек. Эта форму выводится из теоремы Пифагора. Теперь по порядку. Чтобы найти разность соответствующих координат необходимо из x-координаты точки В вычесть x-координату точки А. Получим 4-1 = 3. Проводим такую же операцию и для y-координаты. Получим 5-1 = 4. Теперь каждую полученную разность возводим в квадрат: 3*3=9,4*4=16. Полученные результаты складываем: 9+16=25. Далее извлекаем квадратный корень. Корень из 25 = 5. Ответ: длина АВ = 5.

uznay-kak.ru

No related posts.