В системе координат построим полуокружность радиуса \(1\) с центром в начале координат.
Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике \(AOX\):
sinα=AXAO;cosα=OXAO.
Так как радиус полуокружности \(R = AO = 1\), то sinα=AX;cosα=OX.
Длина отрезка \(AX\) равна величине координаты \(y\) точки \(A\), а длина отрезка \(OX\) равна величине координаты \(x\) точки \(A\):
Acosα;sinα.
Следовательно, для углов 0°≤α≤180° видно, что −1≤cosα≤1;0≤sinα≤1.
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
tgα=AXOX=sinαcosα.
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для 0°;90°;180°.
sin0°=0;cos0°=1;tg0°=0;sin90°=1;cos90°=0;tg90° не существует;sin180°=0;cos180°=−1;tg180°=0.
Рассмотрим оба острых угла в треугольнике \(AOX\). Если вместе они образуют 90°, то оба выразим через α.
Если sinα=AXAO;cosα=OXAO, то sin90°−α=OXAO;cos90°−α=AXAO.
Видим, что справедливы равенства:
cos90°−α=sinα;sin90°−α=cosα.
Рассмотрим тупой угол, который также выразим через α.
Справедливы следующие равенства:
sin180°−α=sinα;cos180°−α=−cosα.
Эти формулы называются формулами приведения:
cos90°−α=sinα;sin90°−α=cosα.
sin180°−α=sinα;cos180°−α=−cosα.
Если в треугольнике \(AOX\) применить теорему Пифагора, получаем AX2+OX2=1. Заменив отрезки соответственно синусом и косинусом, мы напишем
Главное тригонометрическое тождество
sin2α+cos2α=1.
Это тождество позволяет вычислить величину синуса угла, если дан косинус
(как уже отмечено, синус для углов 0°≤α≤180° только 0 или положительный):
sin2α+cos2α=1;sin2α=1−cos2α;sinα=1−cos2α
— или величину косинуса угла, если дан синус:
sin2α+cos2α=1;cos2α=1−sin2α;cosα=±1−sin2α.
Для острых углов косинус положительный, а для тупых углов берём отрицательное значение.
Определения синуса, косинуса, тангенса и котангенса
Синус угла
(обозначается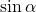 
) – ордината точки 
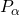, полученной поворотом точки 
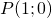вокруг начала координат на угол .Косинус угла (обозначается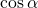 
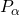, полученной поворотом точки 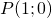вокруг начала координат на угол .Тангенс угла (обозначается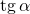 
) – отношение синуса угла к его косинусу, т.е.
![\[\operatorname{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f3cba66971d7fd1d95998220eb211676_l3.png)
Котангенс угла (обозначается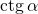 
) – отношение косинуса угла к его синусу, т.е.
![\[\operatorname{ctg}\alpha = \frac{\cos\alpha}{\sin\alpha}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-f6efc9004c51766c5c3efc271d310896_l3.png)
Таблица значений синуса, косинуса, тангенса и котангенса
Калькулятор синусов, косинусов, тангенсов и котангенсов
Данный калькулятор поможет легко вычислить значения этих тригонометрических функций от углов, заданных в градусах, радианах или градах.
Онлайн калькулятор: Тригонометрические функции
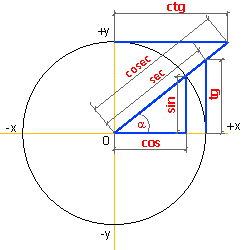Простейшие тригонометрические функцииТригонометрические функции — вид элементарных функций, к которым относятся следующие функции:
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
versin — версинус (синус-верзус)
vercos — коверсинус (косинус-верзус)
haversin — гаверсинус (половина от синус-верзус)
exsec — экссеканс
excsc — экскосеканс
Для того чтобы вычислить все эти тригонометрические функции сразу для заданного угла, введите значение угла в поле Угол и получите результат в виде таблицы значений всех функций для этого угла. Угол можно задать в градусах, радианах, градах, минутах и секундах, для выбора единицы измерения — просто щелкните на ее название.
Тригонометрические функции
Единицы измерения Точность вычисленияЗнаков после запятой: 10
save Сохранить extension Виджет
Как известно из школы, синус угла (sin) — это отношение длины противоположного этому углу катета к гипотенузе, а косинус (cos) — это отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
Тангенс: (отношение длины противоположного углу катета к прилежащему катету)
Котангенс: (отношение длины прилежащего к углу катета к противоположному катету)
Секанс: (отношение длины гипотенузы к прилежащему к углу катету)
Редко используемые тригонометрические функции:
Версинус:
Коверсинус:
Гаверсинус:
Экссеканс:
Экскосеканс:
Синус, косинус, тангенс, котангенс угла
Рассмотрим прямоугольный треугольник ABC.
Синус острого угла прямоугольного треугольника
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности, которой соответствует угол \alpha называют синусом произвольного угла поворота \alpha.
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha называют косинусом произвольного угла поворота \alpha.
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha.
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha.
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM, где M — точка единичной окружности, то
\sin \alpha=y_{M}, \cos \alpha=x_{M}, tg \alpha=\frac{y_{M}}{x_{M}}, ctg \alpha=\frac{x_{M}}{y_{M}}.
Например, если \angle AOM = -\frac{\pi}{4}, то: ордината точки M равна -\frac{\sqrt{2}}{2}, абсцисса равна \frac{\sqrt{2}}{2} и потому
\sin \left (-\frac{\pi}{4} \right )=-\frac{\sqrt{2}}{2};
\cos \left (\frac{\pi}{4} \right )=\frac{\sqrt{2}}{2};
tg \left (-\frac{\pi}{4} \right )=-1;
ctg \left (-\frac{\pi}{4} \right )=-1.
Таблица значений синусов косинусов тангенсов котангенсов
Значения основных часто встречающихся углов приведены в таблице:
| 0^{\circ} (0) | 30^{\circ}\left(\frac{\pi}{6}\right) | 45^{\circ}\left(\frac{\pi}{4}\right) | 60^{\circ}\left(\frac{\pi}{3}\right) | 90^{\circ}\left(\frac{\pi}{2}\right) | 180^{\circ}\left(\pi\right) | 270^{\circ}\left(\frac{3\pi}{2}\right) | 360^{\circ}\left(2\pi\right) | |
| \sin\alpha | 0 | \frac12 | \frac{\sqrt 2}{2} | \frac{\sqrt 3}{2} | 1 | 0 | −1 | 0 |
| \cos\alpha | 1 | \frac{\sqrt 3}{2} | \frac{\sqrt 2}{2} | \frac12 | 0 | −1 | 0 | 1 |
| tg \alpha | 0 | \frac{\sqrt 3}{3} | 1 | \sqrt3 | — | 0 | — | 0 |
| ctg \alpha | — | \sqrt3 | 1 | \frac{\sqrt 3}{3} | 0 | — | 0 | — |
Калькулятор онлайн вычисляет тригонометрические функции для любого значения угла α заданного в градусах: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec), версинус (синус-верзус) (versin), коверсинус (косинус-верзус) (vercos), гаверсинус (половина от синус-верзус) (haversin), экссеканс (exsec), экскосеканс (excsc).
Вычислить значения синуса и косинуса для стандартных значений углов можно с помощью тригонометрической окружности (тригонометрического круга). Например по тригонометрическому кругу можно найти значение синуса 45 градусов, косинуса 60 градусов или косинуса 90 градусов.
Вычислить значения для тангенсов и котангенсов можно с помощью
| Тригонометрические функций на единичной окружности | Тригонометрический круг (тригонометрическая окружность) |
Тригонометрическая таблица основных значений синусов, косинусов, тангенсов и котангенсов.
| α | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin(α) | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
| cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
| tg(α) | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 | √3/3 | 1 | √3 | — | -√3 | -1 | -√3/3 | 0 |
| ctg(α) | — | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | — | √3 | 1 | √3/3 | 0 | -√3/3 | -1 | -√3 | — |
| α | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/4 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
I. Для справки:
- тригонометрические функции
- — элементарные функции, которые возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Основные тригонометрические функции:
- синус угла α
- обозначается sin(α) — отношение длины противоположного этому углу катета к гипотенузе;
- косинус угла α
- обозначается cos(α) — отношение прилежащего этому углу катета к гипотенузе.
Остальные тригонометрические функции можно выразить через синус и косинус:
- тангенс
- обозначается tg(α) — отношение длины противоположного углу катета к прилежащему катету;
- котангенс
- обозначается ctg(α) — отношение длины прилежащего к углу катета к противоположному катету;
- секанс
- обозначается sec(α) — отношение длины гипотенузы к прилежащему к углу катету;
- косеканс
- обозначается cosec(α) — отношение длины гипотенузы к противоположному катету.
Редко используемые тригонометрические функции:
- версинус
- обозначается versin(α) — единица минус косинус угла α;
- коверсинус
- обозначается vercos(α) — единица минус синус угла α;
- гаверсинус
- обозначается haversin(α) — половина версинуса угла α;
- экссеканс
- обозначается exsec(α) — секанс угла α минус единица;
- экскосеканс
- обозначается excsc(α) — косеканс угла α минус единица.
II. Примечание:
- Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до сотых).
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла
Синус, косинус произвольного угла
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.
Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
90000 Sine, Cosine, Tangent, explained and with Examples and practice identifying opposite, adjacent sides and hypotenuse 90001 90002 This page explains the sine, cosine, tangent ratio, gives on an overview of their range of values and provides practice problems on identifying the sides that are opposite and adjacent to a given angle. 90003 90002 The Sine, Cosine and Tangent functions express the ratios of sides of a right triangle. 90003 90006 To which triangle (s) below does SOHCAHTOA apply? 90007 90002 Show Answer 90003 90002 90011 90012 90003 90002 90015 Interactive Angles 90016 SOHCAHTOA 90017 90018 90003 90002 Try activating either $$ \ angle A $$ or $$ \ angle B $$ to explore the way that the adjacent and the opposite sides change based on the angle.90003 90016 Status: 90017 Angle activated: $$ \ red {none} \ text {, waiting for you to choose an angle.} $$ 90002 90016 Answer: 90017 90016 sine 90017 of an angle is always the ratio of the $$ \ frac {opposite side} {hypotenuse} $$. 90003 90002 $ sine (angle) = \ frac {\ text {opposite side}} {\ text {hypotenuse}} $ 90003 90006 Example 1 90007 90002 $$ sin (\ angle \ red L) = \ frac {opposite} {hypotenuse} \\ sin (\ angle \ red L) = \ frac {9} {15} $$ 90003 90006 Example 2 90007 90002 $$ sin (\ angle \ red K) = \ frac {opposite} {hypotenuse} \\ sin (\ angle \ red K) = \ frac {12} {15} $$ 90003 90002 90016 Remember: 90017 When we use the words ‘opposite’ and ‘adjacent,’ we always have to have a specific angle in mind.90003 90006 Range of Values of Sine 90007 90002 For those comfortable in «Math Speak», the domain and range of Sine is as follows. 90003 90048 90049 90016 Domain of Sine 90017 = all real numbers 90052 90049 90016 Range of Sine 90017 = {-1 ≤ y ≤ 1} 90052 90057 90002 The sine of an angle has a range of values from -1 to 1 inclusive. Below is a table of values illustrating some key sine values that span the entire range of values. 90003 90060 90061 90062 90016 Angle 90017 90065 90066 90016 Sine of the Angle 90017 90065 90070 90061 90072 270 ° 90065 90072 sin (270 °) = -1 (smallest value that sine can have) 90065 90070 90061 90072 330 ° 90065 90072 sin (330 °) = -½ 90065 90070 90061 90072 0 ° 90065 90072 sin (0 °) = 0 90065 90070 90061 90072 30 ° 90065 90072 sin (30 °) = ½ 90065 90070 90061 90072 90 ° 90065 90072 sin (90 °) = 1 (greatest value that sine can have) 90065 90070 90101 90002 The 90016 cosine 90017 of an angle is always the ratio of the (adjacent side / hypotenuse).90003 90002 $ cosine (angle) = \ frac {\ text {adjacent side}} {\ text {hypotenuse}} $ 90003 90006 Example 1 90007 90002 $$ cos (\ angle \ red L) = \ frac {adjacent} {hypotenuse} \\ cos (\ angle \ red L) = \ frac {12} {15} $$ 90003 90006 Example 2 90007 90002 $$ cos (\ angle \ red K) = \ frac {adjacent} {hypotenuse} \\ cos (\ angle \ red K) = \ frac {9} {15} $$ 90003 90006 Range of Values of Cosine 90007 90002 For those comfortable in «Math Speak», the domain and range of cosine is as follows.90003 90048 90049 90016 Domain of Cosine 90017 = all real numbers 90052 90049 90016 Range of Cosine 90017 = {-1 ≤ y ≤ 1} 90052 90057 90002 The cosine of an angle has a range of values from -1 to 1 inclusive. Below is a table of values illustrating some key cosine values that span the entire range of values. 90003 90060 90061 90072 90016 Angle 90017 90065 90072 90016 Cosine of the Angle 90017 90065 90070 90061 90072 0 ° 90065 90072 cos (0 °) = 1 (greatest value that cosine can ever have) 90065 90070 90061 90072 60 ° 90065 90072 cos (60 °) = ½ 90065 90070 90061 90072 90 ° 90065 90072 cos (90 °) = 0 90065 90070 90061 90072 120 ° 90065 90072 cos (120 °) = -½ 90065 90070 90061 90072 180 ° 90065 90072 cos (180 °) = -1 (smallest value that cosine can ever have) 90065 90070 90101 90002 The 90016 tangent 90017 of an angle is always the ratio of the (opposite side / adjacent side).90003 90002 $ tangent (angle) = \ frac {\ text {opposite side}} {\ text {adjacent side}} $ 90003 90006 Example 1 90007 90002 $$ tan (\ angle \ red L) = \ frac {opposite} {adjacent} \\ tan (\ angle \ red L) = \ frac {9} {12} $$ 90003 90006 Example 2 90007 90002 $$ tan (\ angle \ red K) = \ frac {opposite} {adjacent} \\ tan (\ angle \ red K) = \ frac {12} {9} $$ 90003 .90000 Finding an Angle in a Right Angled Triangle 90001 90002 Angle from Any Two Sides 90003 90004 We can find an 90005 unknown angle 90006 in a right-angled triangle, as long as we know the lengths of 90005 two of its sides 90006. 90009 90004 90009 90012 Example 90013 90004 The ladder leans against a wall as shown. 90009 90004 What is the 90005 angle 90006 between the ladder and the wall? 90009 90004 90009 90022 The answer is to use Sine, Cosine or Tangent! 90009 90004 But which one to use? We have a special phrase «SOHCAHTOA» to help us, and we use it like this: 90009 90004 90005 Step 1 90006: find the 90005 names 90006 of the two sides we know 90009 90004 90009 90034 90035 90005 Adjacent 90006 is adjacent to the angle, 90038 90039 90035 90005 Opposite 90006 is opposite the angle, 90038 90039 90035 and the longest side is the 90005 Hypotenuse 90006.90039 90049 90012 Example: in our ladder example we know the length of: 90013 90034 90035 the side 90005 Opposite 90006 the angle «x», which is 90005 2.5 90006 90039 90035 the longest side, called the 90005 Hypotenuse 90006, which is 90005 5 90006 90039 90049 90004 90005 Step 2 90006: now use the first letters of those two sides (90005 O 90006 pposite and 90005 H 90006 ypotenuse) and the phrase «SOHCAHTOA» to find which one of Sine, Cosine 90005 or 90006 Tangent to use: 90009 90076 90077 90078 90004 90005 90081 SOH… 90082 90006 90009 90085 90078 90004 90005 S 90006 ine: sin (θ) = 90005 O 90006 pposite / 90005 H 90006 ypotenuse 90009 90085 90096 90077 90078 90004 90005 90081 … CAH … 90082 90006 90009 90085 90078 90004 90005 C 90006 osine: cos (θ) = 90005 A 90006 djacent / 90005 H 90006 ypotenuse 90009 90085 90096 90077 90078 90004 90005 90081 … TOA 90082 90006 90009 90085 90078 90004 90005 T 90006 angent: tan (θ) = 90005 O 90006 pposite / 90005 A 90006 djacent 90009 90085 90096 90137 90004 In our example that is 90005 O 90006 pposite and 90005 H 90006 ypotenuse, and that gives us «90005 SOH 90006 cahtoa», which tells us we need to use 90005 Sine 90006.90009 90004 90005 Step 3 90006: Put our values into the Sine equation: 90009 90022 90005 S 90006 in (x) = 90005 O 90006 pposite / 90005 H 90006 ypotenuse = 2.5 / 5 = 90005 0.5 90006 90009 90004 90005 Step 4 90006: Now solve that equation! 90009 90022 sin (x) = 0.5 90009 90004 Next (trust me for the moment) we can re-arrange that into this: 90009 90022 x = sin 90171 -1 90172 (0.5) 90009 90004 And then get our calculator, key in 0.5 and use the sin 90171 -1 90172 button to get the answer: 90009 90022 x = 90005 30 ° 90006 90009 And we have our answer! 90012 But what is the meaning of 90005 sin 90171 -1 90172 90006 …? 90013 90022 Well, the Sine function 90081 90005 «sin» 90006 90082 takes an angle and gives us the 90005 ratio 90006 «opposite / hypotenuse», 90009 90004 90009 90004 But 90081 90005 sin 90171 -1 90172 90006 90082 (called «inverse sine») goes the other way… 90038 … it takes the 90005 ratio 90006 «opposite / hypotenuse» and gives us an angle. 90009 90012 Example: 90013 90034 90035 Sine Function: sin (90005 30 ° 90006) = 90005 0.5 90006 90039 90035 Inverse Sine Function: sin 90171 -1 90172 (90005 0.5 90006) = 90005 30 ° 90006 90039 90049 90004 90009 90076 90077 90078 90085 90078 On the calculator press one of the following (depending 90038 on your brand of calculator): either ‘2ndF sin’ or ‘shift sin’.90085 90096 90137 90022 On your calculator, try using 90005 sin 90006 and 90005 sin 90171 -1 90172 90006 to see what results you get! 90009 90022 Also try 90005 cos 90006 and 90005 cos 90171 -1 90172 90006. And 90005 tan 90006 and 90005 tan 90171 -1 90172 90006. 90038 Go on, have a try now. 90009 90002 Step By Step 90003 90004 These are the four steps we need to follow: 90009 90034 90035 90005 Step 1 90006 Find which two sides we know — out of Opposite, Adjacent and Hypotenuse.90039 90035 90005 Step 2 90006 Use SOHCAHTOA to decide which one of Sine, Cosine 90005 or 90006 Tangent to use in this question. 90039 90035 90005 Step 3 90006 For Sine calculate Opposite / Hypotenuse, for Cosine calculate Adjacent / Hypotenuse 90005 or 90006 for Tangent calculate Opposite / Adjacent. 90039 90035 90005 Step 4 90006 Find the angle from your calculator, using one of sin 90171 -1 90172, cos 90171 -1 90172 90005 or 90006 tan 90171 -1 90172 90039 90049 90002 Examples 90003 90004 Let’s look at a couple more examples: 90009 90004 90009 90012 Example 90013 90004 Find the angle of elevation of the plane from point A on the ground.90009 90038 90034 90035 90005 Step 1 90006 The two sides we know are 90005 O 90006 pposite (300) and 90005 A 90006 djacent (400). 90039 90035 90005 Step 2 90006 SOHCAH 90005 TOA 90006 tells us we must use 90005 T 90006 angent. 90039 90035 90005 Step 3 90006 Calculate 90005 Opposite / Adjacent 90006 = 300/400 = 90005 0.75 90006 90039 90035 90005 Step 4 90006 Find the angle from your calculator using 90005 tan 90171 -1 90172 90006 90039 90049 90004 Tan x ° = opposite / adjacent = 300/400 = 0.75 90009 90004 90005 tan 90171 -1 90172 90006 of 0.75 = 90005 36.9 ° 90006 (correct to 1 decimal place) 90009 90004 Unless you’re told otherwise, angles are usually rounded to one place of decimals. 90009 90004 90009 90012 Example 90013 90004 Find the size of angle a ° 90009 90038 90034 90035 90005 Step 1 90006 The two sides we know are 90005 A 90006 djacent (6,750) and 90005 H 90006 ypotenuse (8,100). 90039 90035 90005 Step 2 90006 SOH 90005 CAH 90006 TOA tells us we must use 90005 C 90006 osine.90039 90035 90005 Step 3 90006 Calculate Adjacent / Hypotenuse = 6,750 / 8,100 = 0.8333 90039 90035 90005 Step 4 90006 Find the angle from your calculator using 90005 cos 90171 -1 90172 90006 of 0.8333: 90039 90049 90004 cos a ° = 6,750 / 8,100 = 0.8333 90009 90004 90005 cos 90171 -1 90172 90006 of 0.8333 = 90005 33.6 ° 90006 (to 1 decimal place) 90009 90004 90009 90004 90009 .90000 Graphs of Sine, Cosine and Tangent 90001 90002 90003 A sine wave made by a circle: 90004 90005 90002 90003 A sine wave produced naturally by a bouncing spring: 90004 90005 90010 Plot of Sine 90011 90012 90005 90012 The Sine Function has this beautiful up-down curve (which repeats every 2π radians, or 360 °). 90005 90012 It starts at 90017 0 90018, heads up to 90017 1 90018 by π / 2 radians (90 °) and then heads down to 90017 -1 90018. 90005 90010 Plot of Cosine 90011 90012 90005 90012 Cosine is just like Sine, but it starts at 1 and heads down until π radians (180 °) and then heads up again.90005 90010 Plot of Sine and Cosine 90011 90012 90005 90012 In fact Sine and Cosine are like 90017 good friends 90018: they follow each other, exactly π / 2 radians (90 °) apart. 90005 90010 Plot of the Tangent Function 90011 90012 90005 90012 The Tangent function has a completely different shape … it goes between negative and positive Infinity, crossing through 0, and at every π radians (180 °), as shown on this plot. 90005 90012 At π / 2 radians (90 °), and at -π / 2 (-90 °), 3π / 2 (270 °), etc, the function is officially 90017 undefined 90018, because it could be 90017 positive Infinity 90018 or 90017 negative Infinity 90018.90005 90010 Inverse Sine, Cosine and Tangent 90011 90012 The Inverse Sine, Cosine and Tangent graphs are: 90005 90012 90057 Inverse Sine 90005 90012 90057 Inverse Cosine 90005 90012 90057 Inverse Tangent 90005 90065 Mirror Images 90066 90012 Here is 90017 Cosine 90018 and 90017 Inverse Cosine 90018 plotted on the same graph: 90005 90002 90057 Cosine and Inverse Cosine 90005 90012 They are mirror images (about the diagonal)! 90005 90012 The same is true for 90017 Sine 90018 and 90017 Inverse Sine 90018 and for 90017 Tangent 90018 and 90017 Inverse Tangent 90018.Can you see this in the graphs above? 90005 90012 90005 .90000 Inverse Sine, Cosine, Tangent 90001 90002 90003 90004 Quick Answer: 90005 90002 For a right-angled triangle: 90003 90002 90003 90002 90003 90002 The 90013 sine 90014 function sin takes angle θ and gives the ratio 90015 opposite 90016 90017 hypotenuse 90018 90003 90002 The 90013 inverse sine 90014 function sin 90023 -1 90024 takes the ratio 90015 opposite 90016 90017 hypotenuse 90018 and gives angle θ 90003 90002 And cosine and tangent follow a similar idea.90003 90004 Example (lengths are only to one decimal place): 90005 90002 90003 90002 90013 sin (35 °) 90014 = Opposite / Hypotenuse 90003 90002 = 2.8 / 4.9 90003 90002 = 0.57 … 90003 90002 90013 sin 90023 -1 90024 (Opposite / Hypotenuse) 90014 = sin 90023 -1 90024 (0.57 …) 90003 90002 = 35 ° 90003 90004 And now for the details: 90005 90002 Sine, Cosine and Tangent are all based on a Right-Angled Triangle 90003 90002 They are very similar functions… so we will look at the 90013 Sine Function 90014 and then 90013 Inverse Sine 90014 to learn what it is all about. 90003 90064 Sine Function 90065 90002 90003 90002 The Sine of angle 90013 90070 θ 90071 90014 is: 90003 90074 90075 the 90013 length of the side Opposite 90014 angle 90013 90070 θ 90071 90014 90082 90075 divided by the 90013 length of the Hypotenuse 90014 90082 90087 90088 Or more simply: 90003 90090 sin (90070 θ 90071) = Opposite / Hypotenuse 90003 90004 Example: What is the sine of 35 °? 90005 90096 90097 90098 90099 90098 90002 Using this triangle (lengths are only to one decimal place): 90003 90002 sin (35 °) = Opposite / Hypotenuse 90104 = 2.8 / 4.9 90104 = 90013 0.57 … 90014 90003 90099 90110 90111 90002 The Sine Function can help us solve things like this: 90003 90002 90003 90004 Example: Use the 90013 sine function 90014 to find 90013 «d» 90014 90005 90002 We know 90003 90074 90075 The angle the cable makes with the seabed is 39 ° 90082 90075 The cable’s length is 30 m. 90082 90087 90002 And we want to know «d» (the distance down). 90003 90002 Start with: sin 39 ° = opposite / hypotenuse 90003 90002 sin 39 ° = d / 30 90003 90002 Swap Sides: d / 30 = sin 39 ° 90003 90002 Use a calculator to find sin 39 °: d / 30 = 0.6293 … 90003 90002 Multiply both sides by 30: d = 0.6293 … x 30 90003 90002 d = 90013 18.88 90014 to 2 decimal places 90003 90090 The depth «d» is 90013 18.88 m 90014 90003 90064 Inverse Sine Function 90065 90002 But sometimes it is the 90013 angle 90014 we need to find. 90003 90002 This is where «Inverse Sine» comes in. 90003 90090 It answers the question «what 90013 angle 90014 has sine equal to opposite / hypotenuse?» 90003 90088 The symbol for inverse sine is 90013 sin 90023 -1 90024 90014, or sometimes 90013 arcsin 90014.90003 90002 90003 90004 Example: Find the angle 90013 «a» 90014 90005 90002 We know 90003 90074 90075 The distance down is 18.88 m. 90082 90075 The cable’s length is 30 m. 90082 90087 90002 And we want to know the angle «a» 90003 90002 90003 90002 Start with: sin a ° = opposite / hypotenuse 90003 90002 sin a ° = 18.88 / 30 90003 90002 Calculate 18.88 / 30: sin a ° = 0.6293 … 90003 90002 What 90013 angle 90014 has sine equal to 0.6293 …? 90104 The 90013 Inverse Sine 90014 will tell us. 90003 90002 Inverse Sine: a ° = 90013 sin 90023 -1 90024 90014 (0.6293 …) 90003 90002 Use a calculator to find 90013 sin 90023 -1 90024 90014 (0.6293 …): a ° = 90013 39.0 ° 90014 (to 1 decimal place) 90003 90090 The angle «a» is 90013 39.0 ° 90014 90003 90064 They Are Like Forward and Backwards! 90065 90074 90075 sin takes an 90013 angle 90014 and gives us the 90013 ratio 90014 «opposite / hypotenuse» 90082 90075 sin 90023 -1 90024 takes the 90013 ratio 90014 «opposite / hypotenuse» and gives us the 90013 angle.90014 90082 90087 90004 Example: 90005 90002 Sine Function: sin (90013 30 ° 90014) = 90013 0.5 90014 90003 90002 Inverse Sine: sin 90023 -1 90024 (90013 0.5 90014) = 90013 30 ° 90014 90003 90253 Calculator 90065 90255 90097 90098 90099 90098 On the calculator you press one of the following (depending on your brand of calculator): either ‘2ndF sin’ or ‘shift sin’. 90099 90110 90111 90090 On your calculator, try using sin and then sin 90023 -1 90024 to see what happens 90003 90253 More Than One Angle! 90065 90088 Inverse Sine 90013 only shows you one angle 90014… but there are more angles that could work. 90003 90273 Example: Here are two angles where opposite / hypotenuse = 0.5 90005 90090 90104 90003 90088 In fact there are 90013 infinitely many angles 90014, because you can keep adding (or subtracting) 360 °: 90003 90090 90003 90088 Remember this, because there are times when you actually need one of the other angles! 90003 90253 Summary 90065 90002 90003 90002 The Sine of angle 90013 90070 θ 90071 90014 is: 90003 90090 sin (90070 θ 90071) = Opposite / Hypotenuse 90003 90002 And Inverse Sine is: 90003 90090 sin 90023 -1 90024 (Opposite / Hypotenuse) = 90070 θ 90071 90003 90002 90003 90064 What About «cos» and «tan»…? 90065 90002 Exactly the same idea, but different side ratios. 90003 90314 Cosine 90315 90002 90003 90002 The Cosine of angle 90013 90070 θ 90071 90014 is: 90003 90090 cos (90070 θ 90071) = Adjacent / Hypotenuse 90003 90002 And Inverse Cosine is: 90003 90090 cos 90023 -1 90024 (Adjacent / Hypotenuse) = 90070 θ 90071 90003 90002 90003 90004 Example: Find the size of angle a ° 90005 90002 cos a ° = Adjacent / Hypotenuse 90003 90002 cos a ° = 6,750 / 8,100 = 0.8333 … 90003 90002 a ° = 90013 cos 90023 -1 90024 90014 (0.8333 …) = 90013 33.6 ° 90014 (to 1 decimal place) 90003 90314 Tangent 90315 90002 90003 90002 The Tangent of angle 90013 90070 θ 90071 90014 is: 90003 90090 tan (90070 θ 90071) = Opposite / Adjacent 90003 90002 So Inverse Tangent is: 90003 90090 tan 90023 -1 90024 (Opposite / Adjacent) = 90070 θ 90071 90003 90002 90003 90004 Example: Find the size of angle x ° 90005 90002 tan x ° = Opposite / Adjacent 90003 90002 tan x ° = 300/400 = 0.75 90003 90002 x ° = 90013 tan 90023 -1 90024 90014 (0.75) = 90013 36.9 ° 90014 (correct to 1 decimal place) 90003 90002 90003 90064 Other Names 90065 90002 Sometimes sin 90023 -1 90024 is called 90013 asin 90014 or 90013 arcsin 90014 90104 Likewise cos 90023 -1 90024 is called 90013 acos 90014 or 90013 arccos 90014 90104 And tan 90023 -1 90024 is called 90013 atan 90014 or 90013 arctan 90014 90003 90004 Examples: 90005 90074 90075 90013 arcsin (y) 90014 is the same as 90013 sin 90023 -1 90024 (y) 90014 90104 90082 90075 90013 atan (θ) 90014 is the same as 90013 tan 90023 -1 90024 (θ) 90014 90104 90082 90075 etc.90082 90087 90064 The Graphs 90065 90002 And lastly, here are the graphs of Sine, Inverse Sine, Cosine and Inverse Cosine: 90003 90104 Sine 90104 Inverse Sine 90104 Cosine 90104 Inverse Cosine 90002 Did you notice anything about the graphs? 90003 90074 90075 They look similar somehow, right? 90082 90075 But the Inverse Sine and Inverse Cosine do not «go on forever» like Sine and Cosine do … 90082 90087 90002 Let us look at the example of Cosine.90003 90002 Here is 90013 Cosine 90014 and 90013 Inverse Cosine 90014 plotted on the same graph: 90003 90090 90104 Cosine and Inverse Cosine 90003 90002 They are mirror images (about the diagonal) 90003 90002 But why does Inverse Cosine get chopped off at top and bottom (the dots are not really part of the function) …? 90003 90002 Because to be a function it can only give 90013 one answer 90014 90104 when we ask 90070 «what is cos 90023 -1 90024 (x)?» 90071 90003 90004 One Answer or Infinitely Many Answers 90005 90002 But we saw earlier that there are 90013 infinitely many answers 90014, and the dotted line on the graph shows this.90003 90002 So yes there 90013 are 90014 infinitely many answers … 90003 90002 … but imagine you type 0.5 into your calculator, press cos 90023 -1 90024 and it gives you a never ending list of possible answers … 90003 90090 So we have this rule that 90013 a function can only give one answer 90014. 90003 90002 So, by chopping it off like that we get just one answer, but 90013 we should remember that there could be other answers 90014. 90003 90064 Tangent and Inverse Tangent 90065 90002 And here is the tangent function and inverse tangent.Can you see how they are mirror images (about the diagonal) …? 90003 90104 Tangent 90104 Inverse Tangent 90002 90003 90002 90003 .