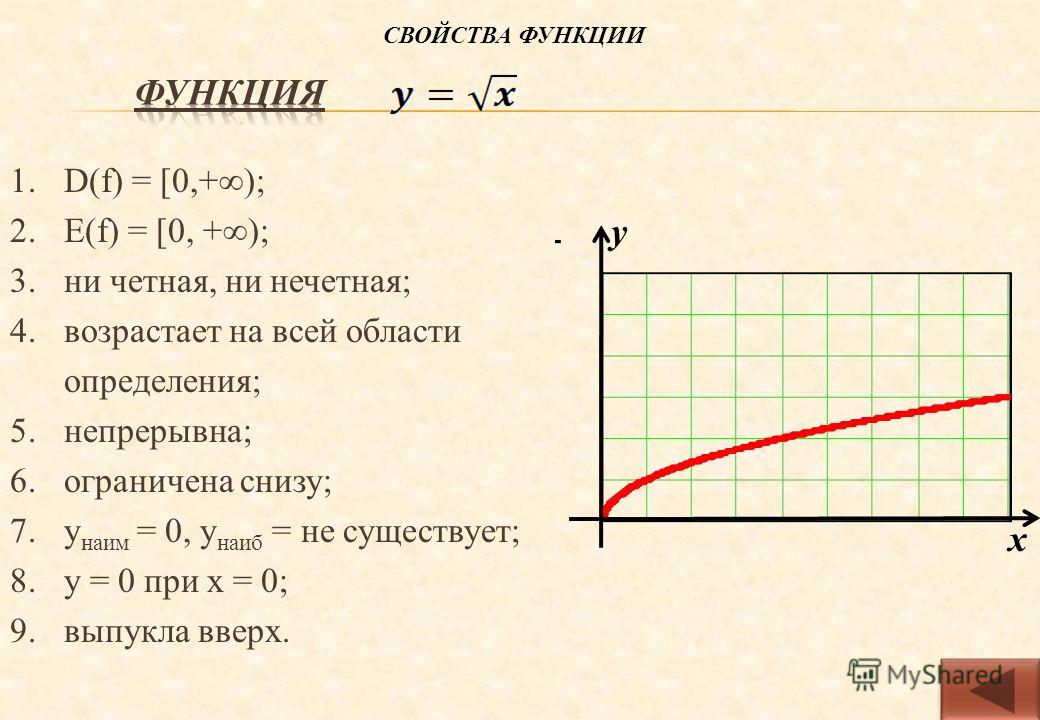
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни
чётная ни нечётная функция (функция
общего вида) —
функция, не обладающая симметрией.
Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная степень где — произвольное целое число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение точки пересечения графика с осью Oy . Для этого нужно вычислить значение f (0). Найти также точки пересечения графика с осью Ox , для чего найти корни уравнения f (x
) = 0 (или убедиться в отсутствии корней).
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то
точка называется точкой
устранимого разрыва функции (в комплексном
анализе -устранимая
особая точка).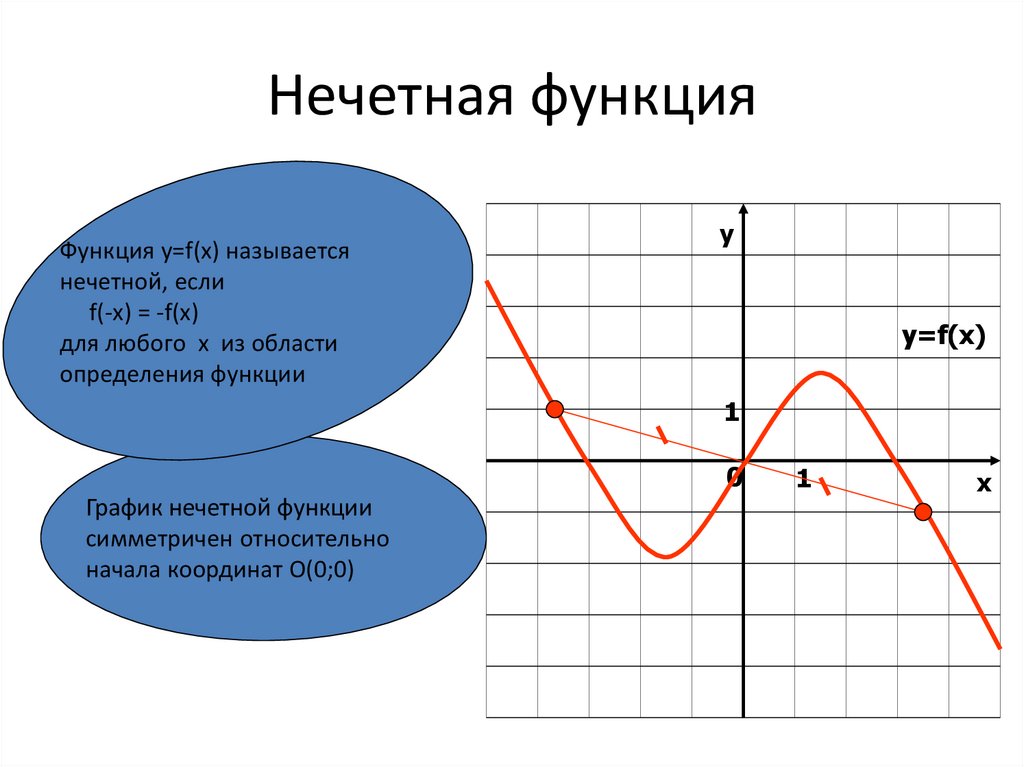
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода .
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная
асимптота — прямая вида при
условии существования
.
Наклонная
Наклонная асимптота — прямая вида при условии существования пределов
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в
п. 2.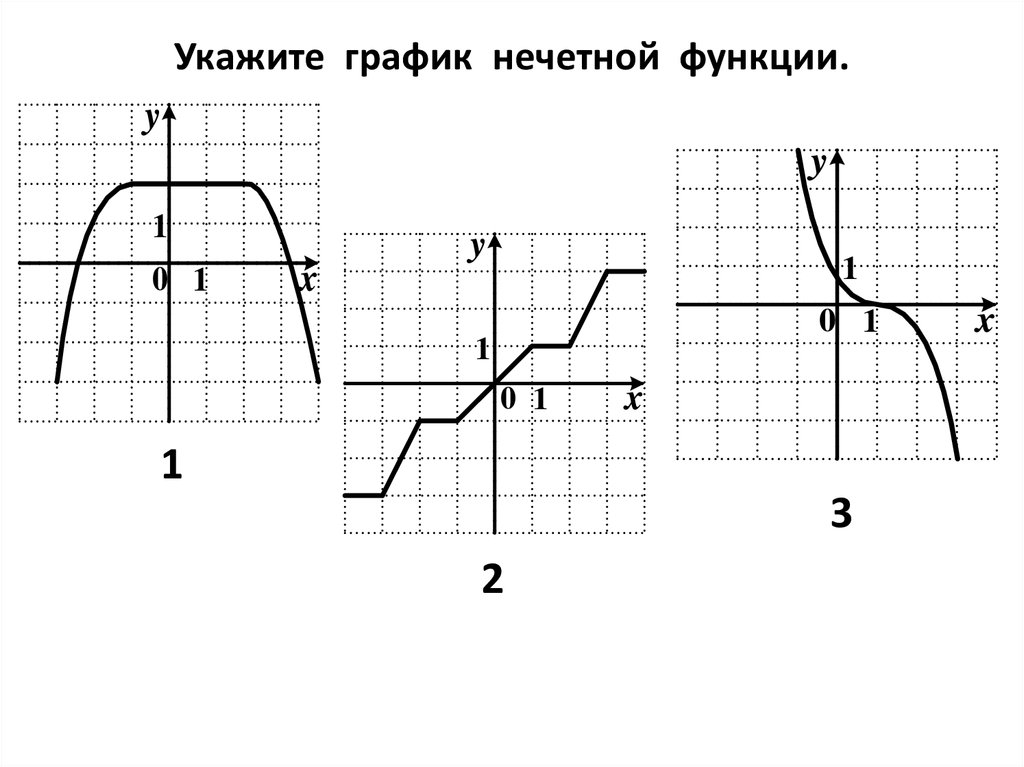 ), то ,
и предел находится
по формуле горизонтальной асимптоты, .
), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x
)возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках.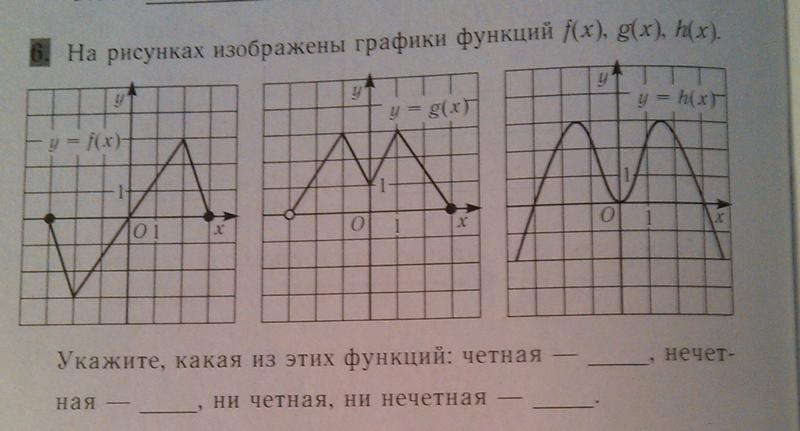 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x}
и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y}
. Найденные координаты точек нанесите на координатную плоскость, а затем соедините эти точки, чтобы построить график функции.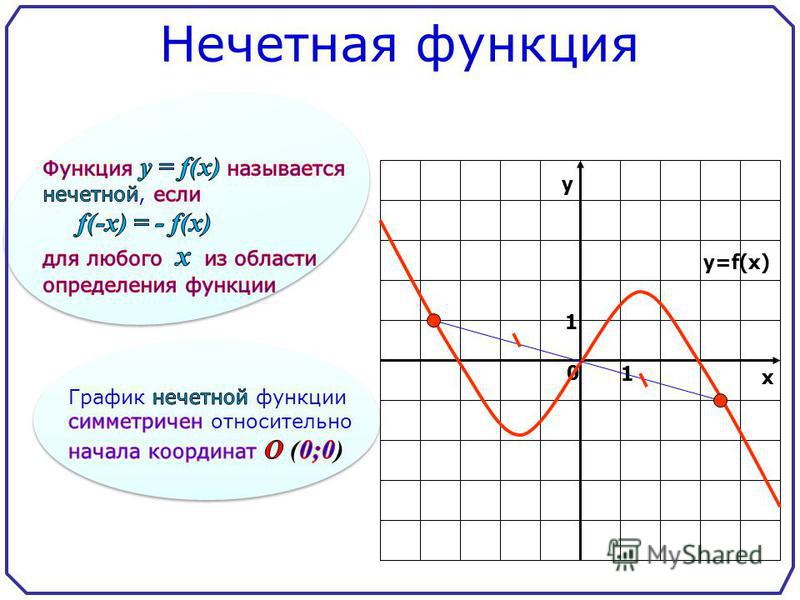
- (1,3) и (-1,3)
- (2,9) и (-2,9)
Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.
- Если в функцию подставить несколько положительных и соответствующих отрицательных значений x {\displaystyle x}
, значения y {\displaystyle y}
будут различаться по знаку.
 {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т. е. функция является четной.
е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
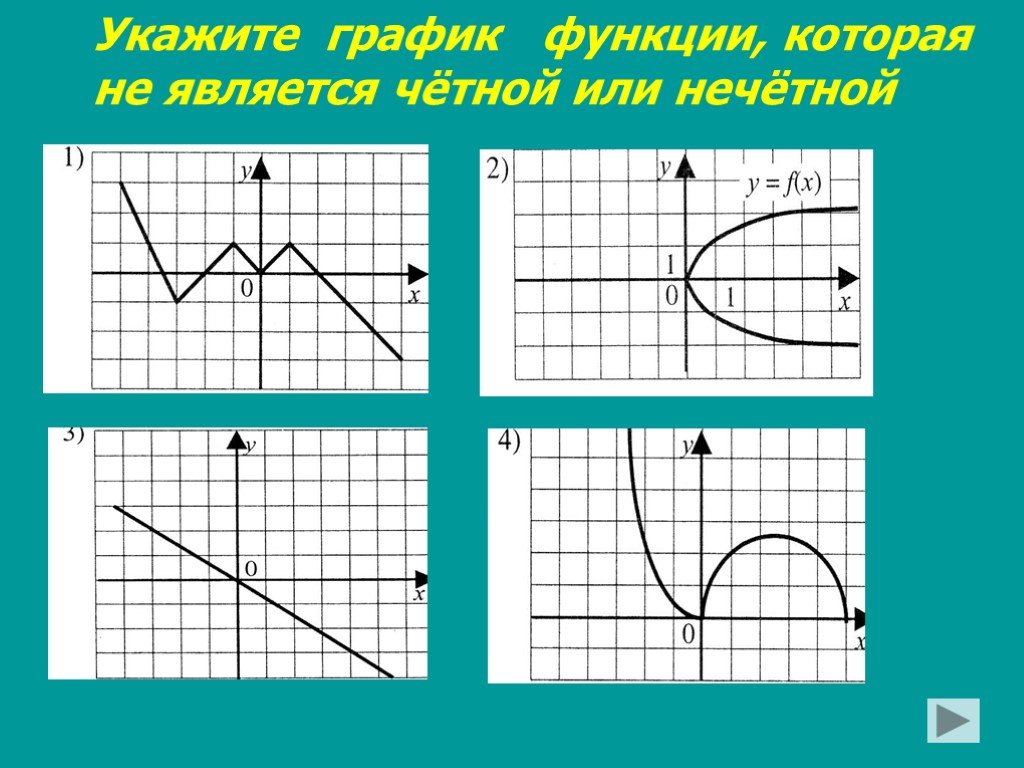
Существуют и функции, не являющиеся ни четными, ни нечетными.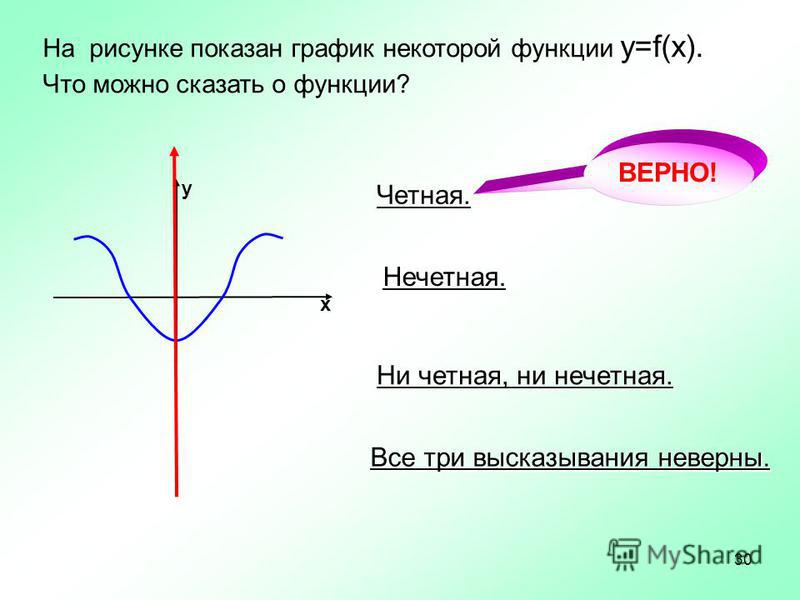 Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }
Нечётные и чётные функции | это… Что такое Нечётные и чётные функции?
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.
Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.
— пример нечётной функции.
— пример чётной функции.
нечётная
ни чётная, ни нечётная.
Другие определения:
- Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
- Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
- Индифферентная функция[источник не указан 240 дней] — функция, не обладающая симметрией.
 В эту категорию относят функции не подпадающие под предыдущие 2 категории.
В эту категорию относят функции не подпадающие под предыдущие 2 категории.
Содержание
|
Определения
Определения вводятся для любой симметричной относительно нуля области определения , например, отрезка или интервала.
- Функция называется чётной, если справедливо равенство
- Функция называется нечётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется индифферентной[источник не указан 240 дней]
(или функцией общего вида).
Свойства
- График нечётной функции симметричен относительно начала координат .
- График чётной функции симметричен относительно оси ординат .

- Произвольная функция может быть единственным образом представлена в виде суммы нечётной и чётной функций:
где
- Функция — единственная функция, одновременно являющаяся нечётной и чётной.
- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Произведение двух функций одной чётности чётно.
- Произведение двух функций разной чётности нечётно.
- Композиция двух нечётных функций нечётна.
- Композиция чётной функции с чётной/нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот!).
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка имеет ту же чётность, что и первоначальная функция.
Примеры
Нечётные функции
- Нечётная степень где — произвольное целое число.

- Синус .
- Тангенс .
Чётные функции
- Чётная степень где — произвольное целое число.
- Косинус .
- Абсолютная величина (модуль) .
Вариации и обобщения
- Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.
Четные и нечетные функции
Четные и нечетные — термины, используемые для описания симметрии функции. Четная функция симметрична относительно оси Y координатной плоскости, а нечетная функция симметрична относительно начала координат. Большинство функций не являются ни четными, ни нечетными. Единственная функция, которая является и четной, и нечетной, это f(x) = 0.
Как определить, является ли функция четной или нечетной
Мы можем проверить симметрию функции либо алгебраически, либо изучив график, как подробно описано ниже. .
Четные и нечетные функции: алгебраическая проверка
Чтобы функция была четной, должно выполняться следующее:
f(x) = f(-x)
Это означает, что каждое значение x и значение -x имеют то же значение у. Таким образом, чтобы увидеть, является ли функция четной, подставьте -x в x и упростите. Если результирующая функция совпадает с исходной, то функция четная.
Таким образом, чтобы увидеть, является ли функция четной, подставьте -x в x и упростите. Если результирующая функция совпадает с исходной, то функция четная.
Пример
Определите, является ли f(x) = 5x 4 + 4x 2 + 2 четной функцией.
Чтобы f(x) была четной функцией, f(x) должно быть равно f(-x). Подстановка -x в f(x) дает:
Поскольку f(x) = f(-x), 5x 4 + 4x 2 + 2 является четной функцией.
Чтобы функция была нечетной, должно выполняться следующее:
f(-x) = -f(x)
Это означает, что каждое значение x имеет значение y, противоположное значению y соответствующих им -х значение. Чтобы узнать, является ли функция нечетной, подставьте -x к x и упростите. Если результирующая функция является исходной функцией, умноженной на -1, то функция нечетная.
Пример
Определите, является ли f(x) = 5x 5 — 4x 3 + 2x нечетной функцией.
Чтобы f(x) была нечетной функцией, f(-x) должно быть равно -f(x). Подстановка -x в f(x) дает:
Подстановка -x в f(x) дает:
Поскольку f(-x) = -f(x), 5x 5 — 4x 3 + 2x является нечетной функцией.
Если функция не подчиняется правилу f(x) = f(-x) или f(-x) = -f(x), функция не является ни четной, ни нечетной. Большинство функций не являются ни четными, ни нечетными, и единственная функция, которая одновременно является и четной, и нечетной, равна f(x) = 0,9.0003
Обратите внимание, что даже полиномиальные функции имеют только четные степени. Нечетные функции, являющиеся полиномами, имеют только нечетные показатели. Однако это верно только для многочленов, и существует много других типов функций, таких как рациональные и тригонометрические функции, которые являются четными или нечетными без соблюдения этого правила.
Четные и нечетные функции: графическая проверка
Имея график функции, чтобы проверить, является ли он четным или нечетным, рассмотрите симметрию графика. Напомним, что четная функция симметрична относительно оси y, а нечетная функция симметрична относительно начала координат.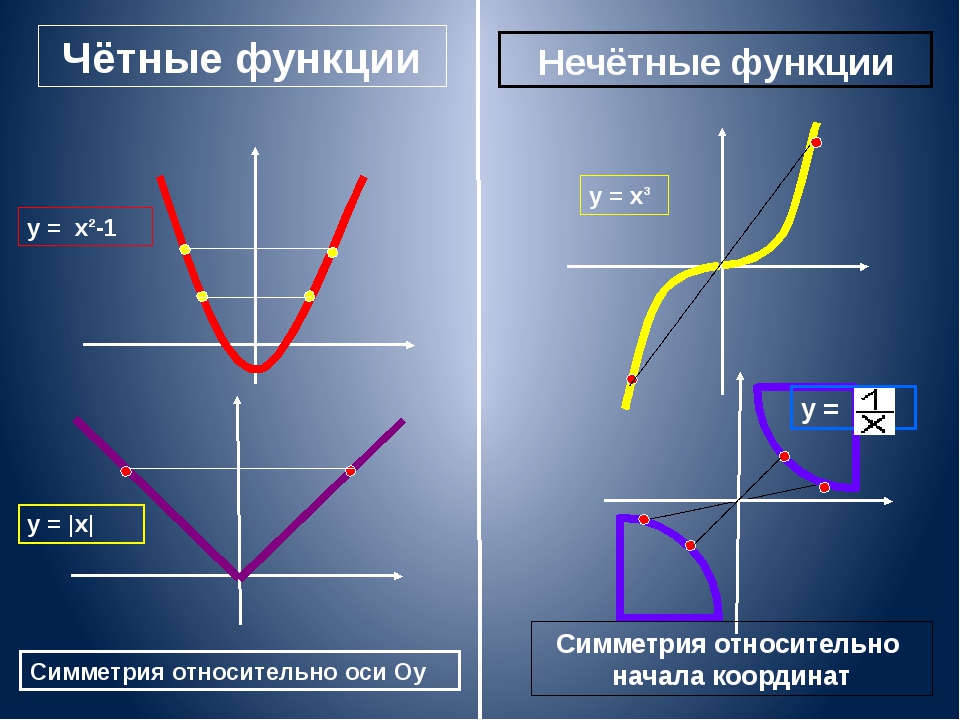
Чтобы наглядно представить, что это означает для четной функции, представьте, что график складывается по оси Y. Если сгибание графика по оси Y приводит к сворачиванию графика поверх самого себя, функция является четной. График параболы с центром относительно оси Y, показанный на рисунке ниже, является четной функцией:
четный
Для нечетной функции симметричность относительно начала координат означает, что если мы повернем график функции на 180° вокруг начало координат, мы получим тот же график. Другой способ представить это — сначала сложить график по оси Y, а затем по оси X. Опять же, если мы получим тот же график, функция будет нечетной. Следующий график представляет собой нечетную функцию:
нечетный
Один из способов запомнить разницу между четными и нечетными функциями состоит в том, чтобы помнить, что и «нечетные», и «происхождение» начинаются с буквы «о». Тогда вам просто нужно помнить, что функции другого типа, даже функции, симметричны относительно оси Y.
В вашем распоряжении не всегда будет график функции, поэтому иногда вам нужно доказать, что функция четная или нечетная (или ни одна из них), используя алгебру.
Свойства четных и нечетных функций
Ниже приведены некоторые свойства четных и нечетных функций.
Свойства сложения и вычитания
Свойства сложения и вычитания нечетных и четных функций следующие:
- четный + четный = четный
- нечетное + нечетное = нечетное
- нечетный — нечетный = нечетный
- четный — четный = четный
- четный + нечетный = ни четный, ни нечетный, если только одна из функций не равна f(x) = 0.
Свойства умножения и деления
- четный × четный = четный
- нечетное × нечетное = четное
- четное × нечетное = нечетное
- четный &дел; четный = четный
- нечетное &дел; нечетное = четное
- четный &дел; нечетный = нечетный
Четные и нечетные функции — определение, свойства, графики, примеры
В математике мы изучаем различные типы функций. Мы можем определить, является ли функция четной или нечетной, алгебраически или графически. Четные и нечетные функции можно проверить, подставив отрицательные входные данные (-x) вместо x в функцию f(x) и рассмотрев соответствующее выходное значение. Четные и нечетные функции классифицируются на основе их отношений симметрии. Четные и нечетные функции названы на основании того, что степенная функция f(x) = x n — четная функция, если n четное, а f(x) — нечетная функция, если n нечетное.
Мы можем определить, является ли функция четной или нечетной, алгебраически или графически. Четные и нечетные функции можно проверить, подставив отрицательные входные данные (-x) вместо x в функцию f(x) и рассмотрев соответствующее выходное значение. Четные и нечетные функции классифицируются на основе их отношений симметрии. Четные и нечетные функции названы на основании того, что степенная функция f(x) = x n — четная функция, если n четное, а f(x) — нечетная функция, если n нечетное.
Давайте изучим другие четные и нечетные функции и поймем их свойства, графики и использование четных и нечетных функций в интегрировании. Функция может быть четной или нечетной, или одновременно четной и нечетной, или ни четной, ни нечетной. Давайте рассмотрим различные примеры, чтобы понять концепцию.
| 1. | Что такое четные и нечетные функции? |
| 2. | Четные и нечетные функции в тригонометрии |
3. | Интегральные свойства четных и нечетных функций |
| 4. | График четных и нечетных функций |
| 5. | Свойства четных и нечетных функций |
| 6. | Часто задаваемые вопросы о четных и нечетных функциях |
Что такое четные и нечетные функции?
Обычно мы считаем вещественную функцию четной или нечетной. Чтобы определить, является ли функция четной или нечетной, мы подставляем -x вместо x в функцию f(x), то есть мы проверяем выходное значение f(-x), чтобы определить тип функции. Четные и нечетные функции симметричны. Давайте сначала разберемся с их определениями.
Четные и нечетные функции Определение
- Четная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с f(x), для всех значений x в области f функция называется четной функцией. Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f.
 Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
f(-x) = (-x) 2 = x 2 для всех значений x, поскольку квадрат отрицательного числа равен квадрату положительного значения числа. Отсюда следует f(-x) = f(x) для всех x. Следовательно, f(x) = x 2 — четная функция. Точно так же такие функции, как x 4 , x 6 , x 8 и т. д., являются четными функциями. - Нечетная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с отрицательным значением f(x), для всех значений x в области определения f, функция называется нечетной. Нечетная функция должна содержать следующее уравнение: f(-x) = -f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x.
 Рассмотрим пример, f(x) = x 3 .
Рассмотрим пример, f(x) = x 3 .
f(-x) = (-x) 3 = -(x 3 ) для всех значений x, поскольку куб отрицательного числа совпадает с отрицательным значением куба положительного значения числа . Отсюда следует f(-x) = -f(x) для всех x. Следовательно, f(x) = x 3 — нечетная функция. Точно так же такие функции, как x 5 , x 7 , x 9 и т. д., являются нечетными функциями. - И четные, и нечетные функции — Действительнозначная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет условию f(-x) = f(x) и f(-x) = -f (x) для всех значений x в области определения функции f(x). Существует только одна функция, которая одновременно является четной и нечетной, и это нулевая функция, f(x) = 0 для всех x. Мы знаем, что для нулевой функции f(-x) = -f(x) = f(x) = 0 для всех значений x. Следовательно, f(x) = 0 — четная и нечетная функция.

- Ни четная, ни нечетная функция — Говорят, что функция f(x) с действительным знаком не является ни четной, ни нечетной, если она не удовлетворяет условию f(-x) = f(x) и f(-x) = -f (x) хотя бы для одного значения x в области определения функции f(x). Давайте рассмотрим пример, чтобы лучше понять определение. Рассмотрим f(x) = 2x 5 + 3x 2 + 1, f(-x) = 2(-x) 5 + 3(-x) 2 + 1 = -2x 5 + 3x 2 + 1, что не равно ни f(x), ни -f(x). Следовательно, f(x) = 2x 5 + 3x 2 + 1 не является ни четной, ни нечетной функцией.
Четные и нечетные функции в тригонометрии
В этом разделе мы разделим тригонометрические функции на четные и нечетные. У нас есть шесть тригонометрических отношений (синус, косинус, тангенс, котангенс, косеканс и секанс). Эти тригонометрические отношения дают положительные значения в разных квадрантах для различных мер углов.
В первом квадранте (где все координаты x и y положительны) все шесть тригонометрических отношений имеют положительные значения. Во втором квадранте положительны только синус и косеканс. В третьем квадранте положительны только тангенс и котангенс. В четвертом квадранте положительны только косинус и секанс. На основании этих признаков мы разделим их на четные и нечетные функции.
Если тригонометрическое соотношение четное или нечетное, можно проверить через единичный круг. Угол, измеренный в направлении против часовой стрелки, является положительным углом, тогда как угол, измеренный в направлении по часовой стрелке, является отрицательным углом.
- sinθ = y, sin(-θ) = -y; Следовательно, sin(-θ) = -sinθ. Следовательно, sinθ — нечетная функция.
- cosθ = y, cos(-θ) = y; Следовательно, cos(-θ) = cosθ. Следовательно, cosθ — четная функция.
- тангенс θ = у, тангенс (-θ) = -у; Следовательно, tan(-θ) = -tanθ. Следовательно, tanθ — нечетная функция.

- cosecθ = y, cosec(-θ) = -y; Следовательно, cosec(-θ) = -cosecθ. Следовательно, cosecθ — нечетная функция.
- секθ = у, сек(-θ) = у; Следовательно, sec(-θ) = secθ. Следовательно, secθ — четная функция.
- кроватка θ = у, кроватка (-θ) = -у; Следовательно, cot(-θ) = -cotθ. Следовательно, cotθ — нечетная функция.
Интегральные свойства четных и нечетных функций
Интеграл функции дает площадь под кривой. Мы используем свойства четных и нечетных функций при решении определенных интегралов. Для этого нам нужно знать пределы интеграла и характер функции. Если функция четная или нечетная, а интервал равен [-a, a], мы можем применить следующие два правила: 9{а}\) f(x) dx = 0
График четных и нечетных функций
Теперь посмотрим, как графически ведут себя четные и нечетные функции. График четной функции симметричен относительно оси Y . Другими словами, график четной функции остается прежним после отражения относительно оси у.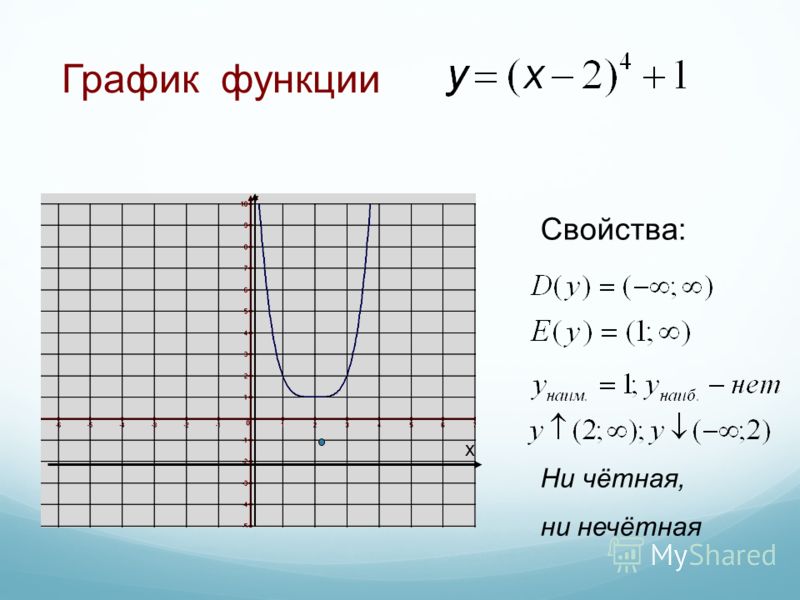 Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Принимая во внимание, что график нечетной функции симметричен относительно начала координат . Другими словами, график нечетной функции находится на одном и том же расстоянии от начала координат, но в противоположных направлениях. Для любых двух противоположных входных значений x функция имеет противоположные значения y. Вот несколько примеров четных и нечетных функций.
Свойства четных и нечетных функций
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разница между двумя четными функциями четна, а разница между двумя нечетными функциями нечетна.
- Сумма четной и нечетной функций не является ни четной, ни нечетной, если только одна из них не является нулевой функцией.
- Произведение двух четных функций является четным, и произведение двух нечетных функций также является четной функцией.

- Произведение четной и нечетной функций нечетно.
- Частное двух четных функций четно, и частное двух нечетных функций также является четной функцией.
- Частное четной и нечетной функций нечетно.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.
- Композиция четной и нечетной функций четна.
Важные замечания о четных и нечетных функциях
- Функция f(x) четна, если f(-x) = f(x), для всех значений x в D(f), и нечетна, если f (-x) = -f(x) для всех значений x.
- В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции.
- График четной функции симметричен относительно оси Y, а график нечетной функции симметричен относительно начала координат.
- f(x) = 0 — единственная функция, которая является четной и нечетной.
Темы, связанные с четными и нечетными функциями
- Функция четности
- Нечетная функция
- Типы функций
Часто задаваемые вопросы о четных и нечетных функциях
Что такое четные и нечетные функции в математике?
Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f(-x) = -f(x), для все значения х.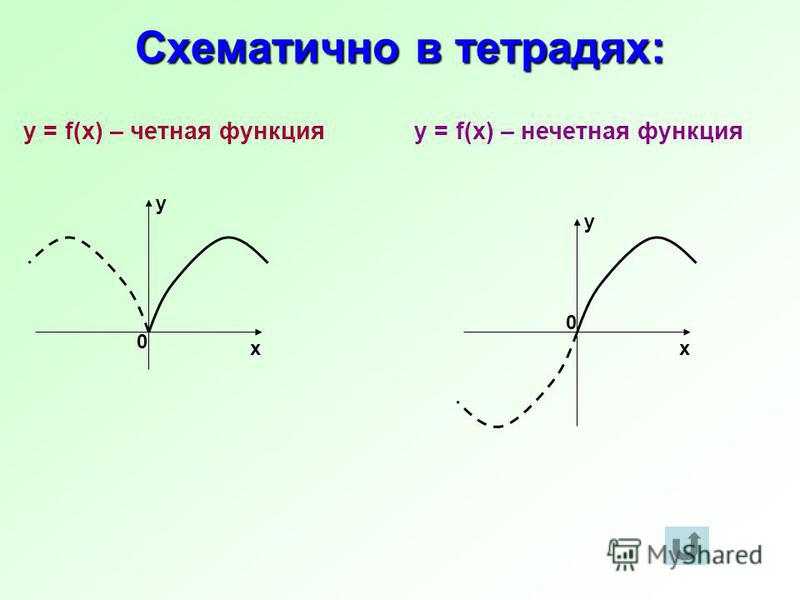 График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
Как определить четные и нечетные функции алгебраически?
Чтобы проверить, является ли функция четной или нечетной алгебраически, мы проверяем, является ли f(-x) = f(x) или f(-x) = -f(x) для всех значений x соответственно. Если мы заменяем x на -x в функции и значение функции становится отрицательным, то функция называется нечетной функцией. Если мы заменим x на -x в функции и значение функции не изменится, то функция будет известна даже как функция.
Если функция f четная, то какой тип симметрии имеет график f?
Четные и нечетные функции показывают разные типы симметрии. Даже функции имеют линейную симметрию. Линия симметрии является осью Y. Даже функции — это функции, в которых, когда мы заменяем x на -x, значение функции для этого конкретного x не меняется. График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
Какие тригонометрические функции являются четными и нечетными функциями?
В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. Различные тригонометрические отношения имеют положительные и отрицательные значения в разных квадрантах. Следовательно, используя единичный круг, мы можем видеть, что cosθ и secθ — четные функции, а остальные четыре тригонометрических отношения — нечетные.
Как определить графически четные и нечетные функции?
График четной функции симметричен относительно оси y. График нечетной функции симметричен относительно начала координат. График четной функции остается прежним после отражения относительно оси у. График нечетной функции находится на одинаковом расстоянии от начала координат, но в противоположных направлениях. Используя те же критерии, мы можем идентифицировать четные и нечетные функции графически.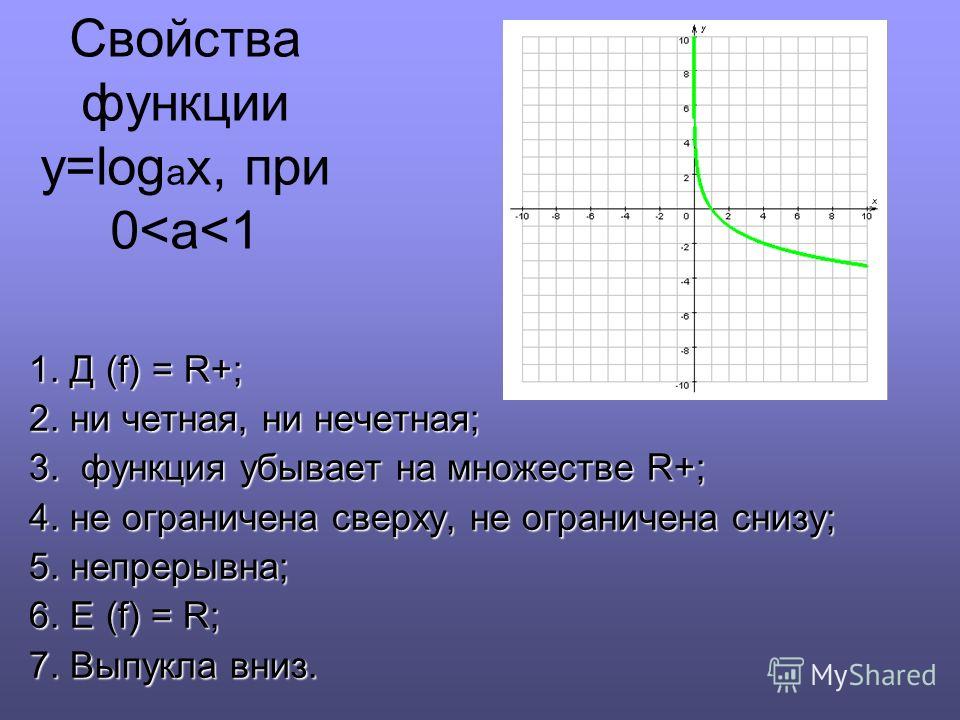

 {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.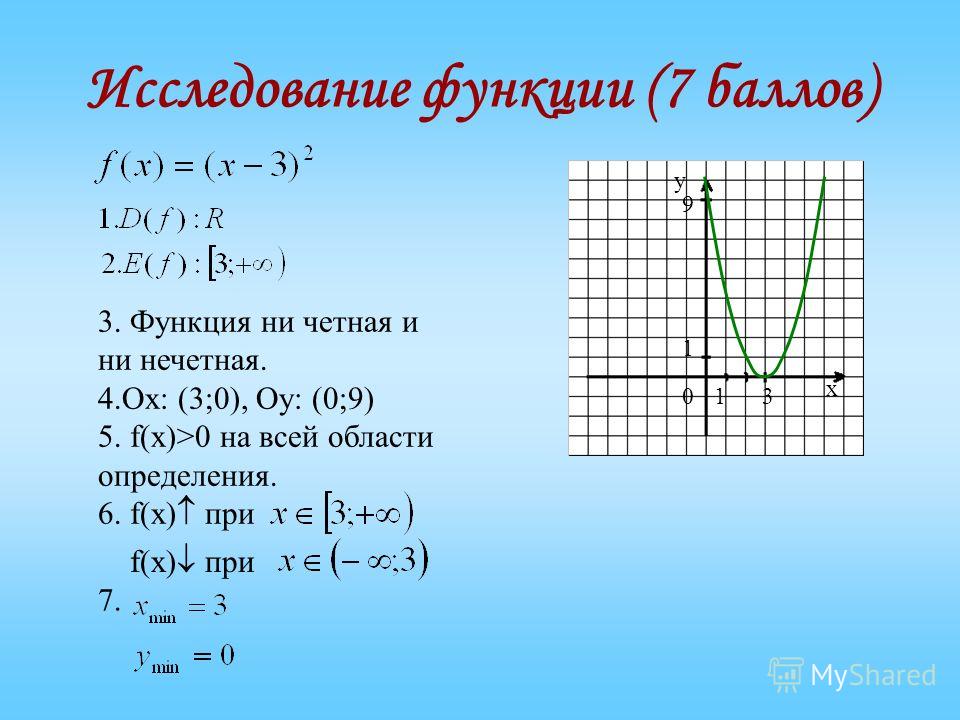 В эту категорию относят функции не подпадающие под предыдущие 2 категории.
В эту категорию относят функции не подпадающие под предыдущие 2 категории.
 Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .  Рассмотрим пример, f(x) = x 3 .
Рассмотрим пример, f(x) = x 3 .