Не основные тригонометрические функции: Недопустимое название | Математика | Fandom

Урок 7. Введение в тригонометрию. Теория 11 класс онлайн-подготовка на Ростелеком Лицей

 

 

Подготовка к ЕГЭ по математике

 

Эксперимент

Урок 7.Введение в тригонометрию.

Теория

 

Конспект урока

Сегодня мы с вами начинаем раздел, который имеет пугающее для многих название «Тригонометрия». Давайте сразу выясним, что это не отдельный предмет, похожий по названию на геометрию, как некоторые думают. Хотя в переводе с греческого слово «тригонометрия» означает «измерение треугольников» и имеет прямое отношение к геометрии. Кроме этого тригонометрические вычисления широко применяются в физике и технике. Но начнем мы с вами именно с рассмотрения того, как основные тригонометрические функции вводятся в геометрии с помощью прямоугольного треугольника.

Только что мы использовали термин «тригонометрическая функция» ‑ это означает, что мы введем целый класс определенных законов соответствия одной переменной величины от другой.

 

Тригонометрические функции в прямоугольном треугольнике и тригонометрическая окружность

 

 

Для этого рассмотрим прямоугольный треугольник, в котором для удобства используются стандартные обозначения сторон и углов, которые вы можете видеть на рисунке:

 

 

Рассмотрим, например, угол  и введем для него следующие действия:

— отношение противолежащего катета к гипотенузе назовем синусом, т.е. 

— отношение прилежащего катета к гипотенузе назовем косинусом, т.е. ;

— отношение противолежащего катета к прилежащему назовем тангенсом, т.е. ;

— отношение прилежащего катета к противолежащему назовем котангенсом, т.е. .

 

Все эти действия с углом называют тригонометрическими функциями. Сам угол, при этом, принято называть аргументом тригонометрической функции и его можно обозначать, например, иксом, как это обыкновенно принято в алгебре.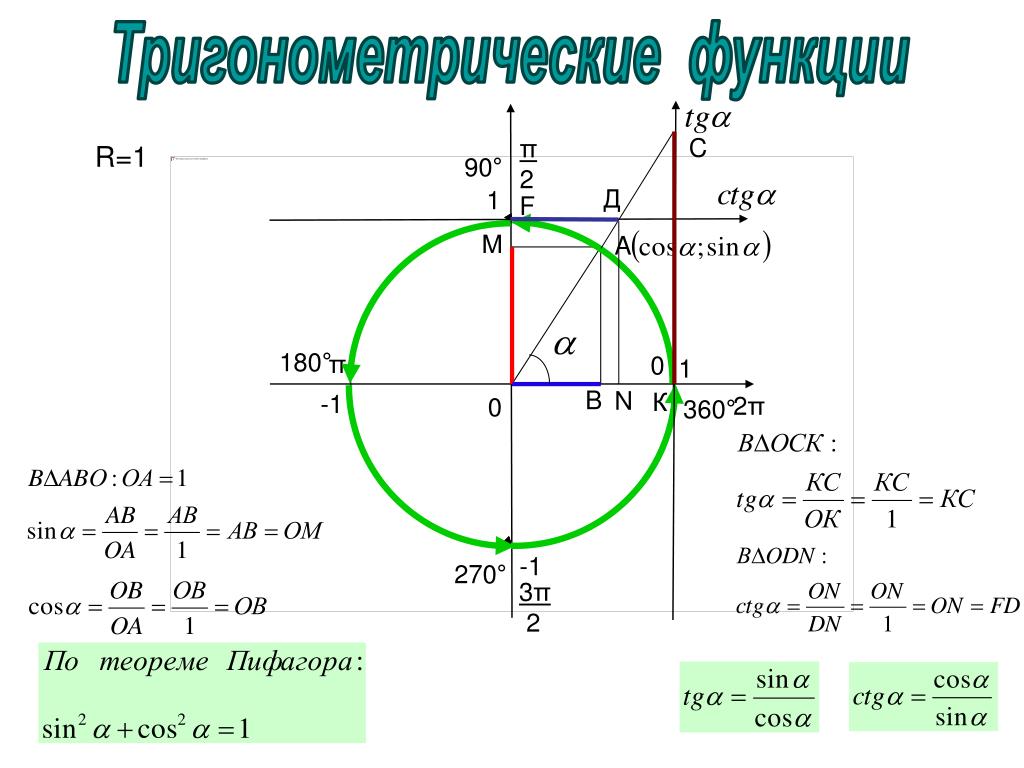

Важно сразу понять, что тригонометрические функции зависят именно от угла в прямоугольном треугольнике, а не от его сторон. Это легко доказать, если рассмотреть треугольник, подобный данному, в нем длины сторон будут другими, а все углы и отношения сторон не изменятся, т.е. останутся неизменными и тригонометрические функции углов.

После такого определения тригонометрических функций может возникнуть вопрос: «А существует ли например ? Ведь угла  в прямоугольном треугольнике быть не может». Как ни странно, но ответ на этот вопрос утвердительный, причем, значение этого выражения равно , а это еще больше удивляет, поскольку все тригонометрические функции являются отношением сторон прямоугольного треугольника, а длины сторон являются положительными числами.

Но никакого парадокса в этом нет. Дело в том, что, например, в физике при описании некоторых процессов необходимо использовать тригонометрические функции углов не только больших , но и больших  и даже .

Для этого необходимо ввести более обобщенное правило вычисления тригонометрических функций с помощью так называемой «единичной тригонометрической окружности».

Она представляет собой окружность с единичным радиусом, изображенную так, что ее центр находится в начале координат декартовой плоскости.

 

Для изображения углов в этой окружности необходимо договориться, откуда их откладывать. Принято за луч отсчета углов принимать положительное направление оси абсцисс, т.е. оси иксов. Направлением отложения углов принято считать направление против часовой стрелки. Исходя из этих договоренностей, отложим сначала острый угол . Именно для таких острых углов мы уже умеем вычислять значения тригонометрических функций в прямоугольном треугольнике. Оказывается, что с помощью изображенной окружности также можно вычислять тригонометрические функции, только более удобно.

Значения синуса и косинуса острого угла  являются координатами точки  пересечения стороны этого угла с единичной окружностью:

Это можно записывать в таком виде:

:

Исходя из того факта, что координаты по оси абсцисс показывают значение косинуса, а координаты по оси ординат значения синуса угла, названия осей в системе координат с единичной окружностью удобно переименовать так, как вы видите на рисунке:

 Ось абсцисс переименовывается в ось косинусов, а ось ординат в ось синусов.

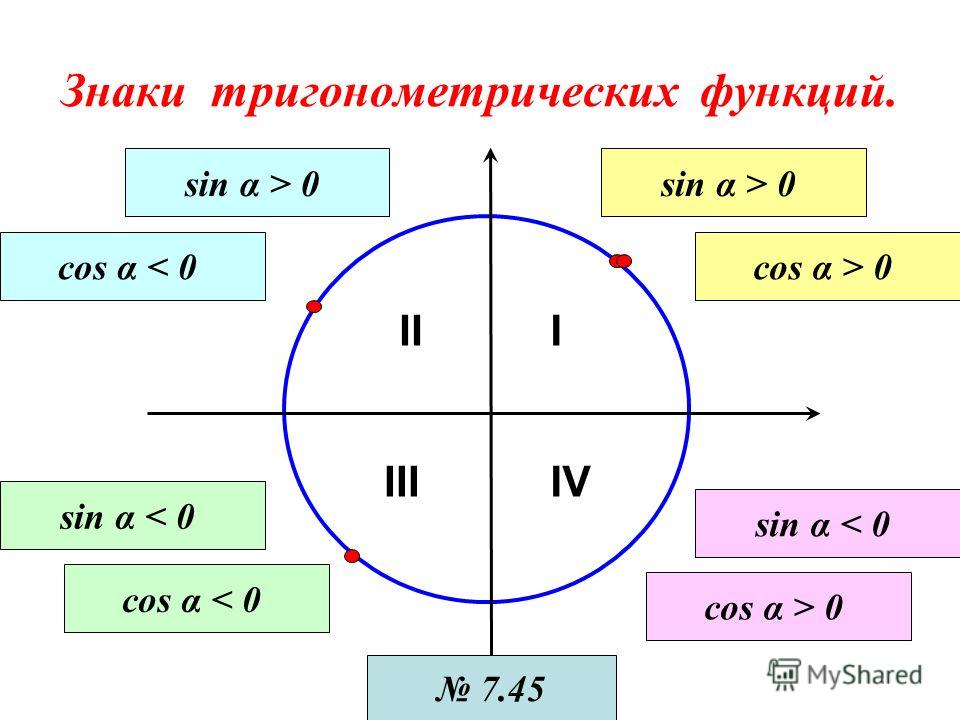
Указанное правило определения синуса и косинуса обобщается и на тупые углы, и на углы, лежащие в диапазоне от  до . В таком случае синусы и косинусы могут принимать, как положительные, так и отрицательные значения. Различные 

знаки значений этих тригонометрических функций в зависимости от того, в какую четверть попадает рассматриваемый угол, принято изображать следующим образом:

Как видите, знаки тригонометрических функций определяются положительными и отрицательными направлениями соответствующих им осей.

Кроме того, стоит обратить внимание на то, что поскольку наибольшая координата точки на единичной окружности и по оси абсцисс и по оси ординат равна единице, а наименьшая минус единице, то и значения синуса и косинуса ограничены этими числами:

Эти записи еще принято записывать в таком виде:

Для того чтобы ввести функции тангенса и котангенса на тригонометрической окружности, необходимо изобразить дополнительные элементы: касательную к окружности в точке A – по ней определяется значение тангенса угла , и касательную к в точке B – по ней определяется значение котангенса угла .

 

Однако мы не будем углубляться в определение тангенсов и котангенсов по тригонометрической окружности, т. к. их легко можно вычислить, зная значения синуса и косинуса данного угла, что мы уже умеем делать. Если вам интересно ознакомиться с  вычислением тангенса и котангенса по тригонометрической окружности, повторите программу курса алгебры 10 класса.

Укажем только изображение на окружности знаков тангенсов и котангенсов в зависимости от угла:

Отметим, что аналогично диапазонам значений синуса и косинуса можно указать диапазоны значений тангенса и котангенса. Исходя из их определения на тригонометрической окружности, значения этих функций не ограничены:

Что можно записать еще так:

Кроме углов в диапазоне от  до  тригонометрическая окружность позволяет работать и с углами, которые больше  и даже с отрицательными углами. Такие значения углов хоть и кажутся бессмысленными для геометрии, но используются для описания некоторых физических процессов. Например, что вы ответите на вопрос: «На какой угол повернется стрелка часов за сутки?» За такое время она выполнит два полных оборота, а за один оборот пройдет , т.

е. за сутки повернется на . Как видите, такие значения имеют вполне практический смысл. Знаки углов используются для обозначения направления вращения – одно из направлений договариваются измерять положительными углами, а другое отрицательными. Как же это учитывать в тригонометрической окружности?

 

На окружности с такими углами работают следующим образом:

1) Углы, которые больше , откладываются против часовой стрелки с прохождением начала отсчета столько раз, сколько это нужно. Например, для построения угла  необходимо пройти два полных оборота и еще . Для окончательного положения и вычисляются все тригонометрические функции. Несложно увидеть, что значение всех тригонометрических функций для  и для  будут одинаковыми.

2) Отрицательные углы откладываются точно по тому же принципу, что и положительные, только по часовой стрелке.

Уже по способу построения больших углов можно сделать вывод, что значения синусов и косинусов углов, которые отличаются на , одинаковы.

Если проанализировать значения тангенсов и котангенсов, то они будут одинаковы для углов, отличающихся на .

 

Такие минимальные ненулевые числа, при добавлении которых к аргументу, не меняется значение функции, называют периодом этой функции.

Таким образом, период синуса и косинуса равен , а тангенса и котангенса . А это означает, что сколько не добавляй или отнимай эти периоды от рассматриваемых углов, значения тригонометрических функций не изменятся.

Например, , а  и т.д.

Позже мы еще вернемся к более подробному объяснению и применению этого свойства тригонометрических функций.

 

Основные тригонометрические тождества

 

 

Между тригонометрическими функциями одного и того же аргумента существуют определенные соотношения, которые очень часто используются и называются основные тригонометрические тождества.

 

Они выглядят следующим образом:

1), так называемая «тригонометрическая единица»

2)

3)

4)

5)

Заметим, что, например, обозначение  обозначает, что вся тригонометрическая функция возводится в квадрат.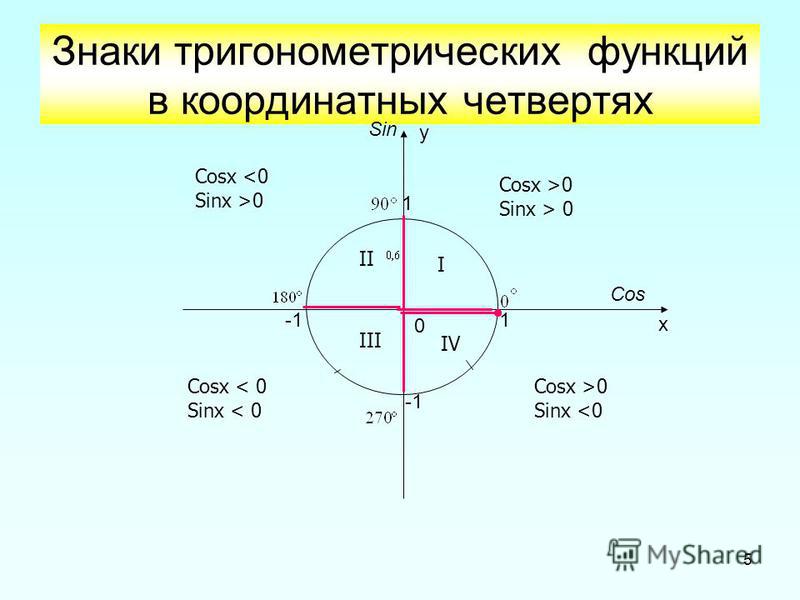 Т.е. это можно представить в такой форме: . Важно понимать, что это не равно такой записи как , в этом случае возводится в квадрат только аргумент, а не вся функция, к тому же выражения такого вида встречаются крайне редко.

Из первого тождества есть два очень полезных следствия, которые могут пригодиться при решении многих типов заданий. После несложных преобразований можно выразить синус через косинус того же угла и наоборот:

Два возможных знака выражений появляются, т.к. извлечение арифметического квадратного корня дает только неотрицательные значения, а синус и косинус, как мы уже видели, могут иметь и отрицательные значения. Причем знаки этих функций удобнее всего определять именно с помощью тригонометрической окружности в зависимости от того, какие углы в них присутствуют.

 

Градусы и радианы. Таблица значений тригонометрических функций

 

 

Теперь давайте вспомним о том, что измерение углов можно осуществлять двумя способами: в градусах и в радианах. Укажем определения одного градуса и одного радиана.

 

Один градус – это угол, образованный двумя радиусами, которые стягивают дугу равную  окружности.

Один радиан – это угол, образованный двумя радиусами, которые стягивает дуга равная по длине радиусам.

Т.е. это просто два различных способа измерять углы, которые абсолютно равноправны. В описании физических процессов, которые характеризуются тригонометрическими функциями, принято использовать радианную меру углов, поэтому нам тоже придется к ней привыкать.

Измерять углы в радианах принято долями числа «пи», например,  или . При этом значение числа «пи», которое равно 3,14, можно подставлять, но это делается редко.

Для перевода градусной меры углов в радианную пользуются тем фактом, что угол , из чего легко получить общую формулу перевода:

Например, переведем  в радианы: .

Существует и обратная формула перевода из радиан в градусы:

Например, переведем  в градусы: .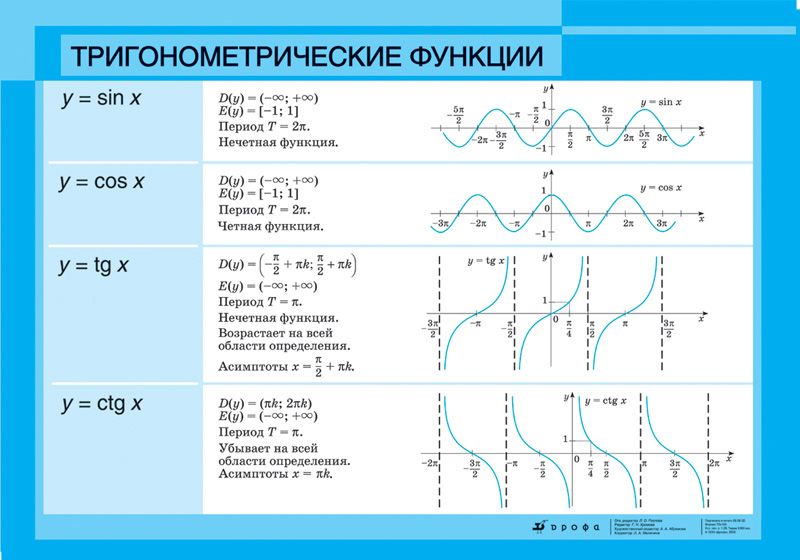

Использовать радианную меру угла в этой теме мы будем достаточно часто.

Теперь самое время вспомнить, какие конкретно значения могут давать тригонометрические функции различных углов. Для некоторых углов, кратных , существует таблица значений тригонометрических функций. В ней для удобства приведены углы в градусной и радианной мерах.

Эти углы часто встречаются во многих задачах и в указанной таблице желательно уметь уверенно ориентироваться. Значения тангенса и котангенса некоторых углов не имеют смысла, что указано в таблице в виде прочерков. Подумайте сами почему так или ознакомьтесь с этим более подробно во вставке к уроку.

 

Формулы приведения

 

 

Последнее, с чем нам надо ознакомиться в нашем первом уроке по тригонометрии, это преобразование тригонометрических функций по так называемым формулам приведения.

 

 

Оказывается, что есть определенный вид выражений для тригонометрических функций, который достаточно часто встречается и удобно упрощается.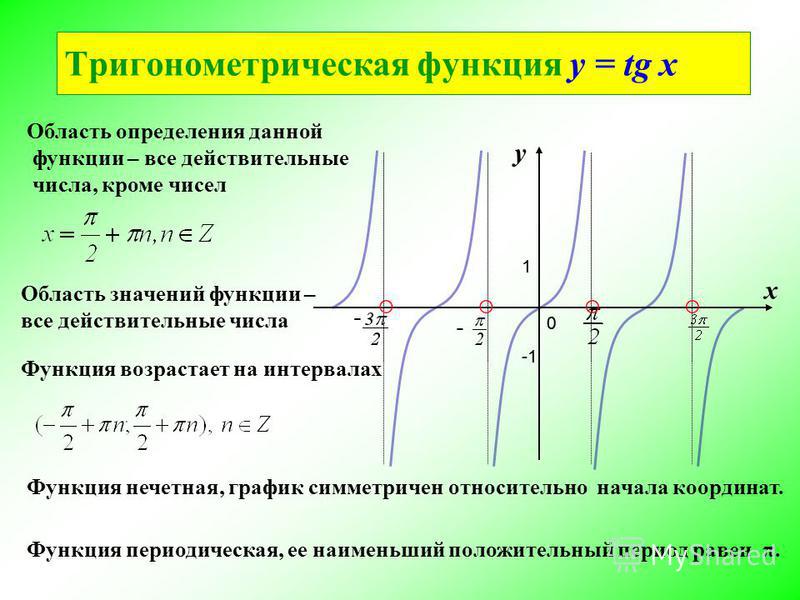 Например, это такие выражения:  и т.п.

Т.е. речь пойдет о функциях, у которых в качестве аргумента выступает произвольный угол, измененный на целую или половинную часть . Такие функции упрощаются до аргумента, который равен произвольному углу добавления или вычитания частей . Например,  , а . Как видим результатом может стать противоположная функция, и функция может поменять знак. 

Поэтому правила преобразования таких функций можно разбить на два этапа. Во-первых, необходимо определить какая функция получится после преобразования: 

1) Если произвольный аргумент изменен на целое число , то функция не изменяется. Это верно для функций типа , где  любое целое число;

2) Если произвольный аргумент изменен на половинное число частей , то функция меняется на противоположную (кофункцию). Это верно для функций типа , где  любое целое нечетное число.

Во-вторых, необходимо определить знак результирующей функции. Это действие выполняется с помощью тригонометрической окружности. При этом для удобства предполагаем, что произвольный угол острый. Понять это удобнее на примере.

Рассмотрим функцию . Т.к. в ней произвольный аргумент изменен на половинное число частей , то она преобразуется в кофункцию, т.е. в синус. Осталось определить ее знак. Выполним это с помощью единичной окружности:

Отложим на ней указанное в функции смещение аргумента на , что равно  и добавим острый угол . В результате иксовая координата точки пересечения луча, которым ограничен наш угол, с окружностью оказалась положительной. Нас интересует именно координата по оси абсцисс, т.к. именно по ней определяется значение косинуса, который мы преобразуем. Таким образом, имеем, что результирующая функция будет с положительным знаком.

Т.е. .

После рассмотренного примера можно понять, почему такие формулы называют формулами приведения. Как видим, они позволяют привести функцию к более простому виду.

Иногда основные формулы приведения предлагают в виде таблицы, однако она достаточно большая и сложная для запоминания, поэтому удобнее запомнить более короткие правила преобразований.

Более подробно разобраться со смыслом формул приведения вы сможете, повторив тему «Тригонометрия» из курса 10 класса.

Используя тригонометрическую окружность можно ввести понятие четности тригонометрических функций, т.е. указать, что будет при подстановке в функцию аргумента с противоположным знаком. Вот эти результаты:

1) — нечетная функция

2) — четная функция

3) — нечетная функция

4) — нечетная функция

Попробуйте сами проверить правильность этих формул. А более подробно мы поговорим о них на следующих уроках.

 

Заключение

 

 

На этом уроке мы ввели основные понятия, связанные с тригонометрическими функциями и их простейшими преобразованиями.

 

В практической части урока мы познакомимся с основными задачами на вычисление и преобразование тригонометрических выражений.   

Полезные ссылки:

1)    Алгебра 9 класс: «Числовая окружность» 

2)    Алгебра 9 класс: «Числовая окружность на координатной плоскости. Синус и косинус» 

3)    Алгебра 9 класс: «Синус и косинус. Их свойства и уравнения» 

4)    Алгебра 9 класс: «Тригонометрические функции числового аргумента» 

5)    Алгебра 9 класс: «Тригонометрические функции углового аргумента» 

6)    Алгебра 10 класс: «Введение (длина дуги окружности)» 

7)    Алгебра 10 класс: «Числовая окружность» 

8)    Алгебра 10 класс: «Числовая окружность на координатной плоскости» 

9)    Алгебра 10 класс: «Синус и косинус» 

10)  Алгебра 10 класс: «Тангенс и котангенс» 

11)  Алгебра 10 класс: «Тригонометрические функции числового аргумента» 

12)  Алгебра 10 класс: «Тригонометрические функции числового аргумента (типовые задачи)» 

13)  Алгебра 10 класс: «Тригонометрические функции углового аргумента» 

14)  Алгебра 10 класс: «Тригонометрические функции углового аргумента и типовые задачи» 

15)  Алгебра 10 класс: «Формулы приведения» 

16)  Алгебра 10 класс: «Формулы приведения и решение типовых задач» 

 

 

Урок алгебры 9 класс.

«Основные тригонометрические тождества. Решение задач». | План-конспект урока по алгебре (9 класс) на тему:

Урок №65  алгебра 9 класс                           дата: 15.02.2017 г.

Тема урока: «Основные тригонометрические тождества.  Решение задач».

Цель урока: знать основные тригонометрические тождества, уметь применять их при решении задач.

Задачи:

Образовательные: повторить и  обобщить теоретический материал по теме: «Основные тригонометрические тождества», формировать умения применять основные тригонометрические  тождества для преобразования тригонометрических выражений.

Развивающие: развивать внимание, память, логическое мышление, навыки самостоятельной работы,  познавательный интерес к предмету, учить учащихся совместной деятельности, формировать дисциплинированность, ответственность за дело коллектива, усилить практическую направленность данной темы для качественной подготовки к ВОУД.

Воспитательные: воспитать положительные мотивы к учению, ответственности, активности, взаимовыручки, умение работать в команде, в паре.

Тип урока: урок закрепления и обобщения.

Оборудование: презентация PowerPoint, рабочая тетрадь, раздаточный материал, лист самооценки, стикеры двух цветов,  лист настроения, ноутбуки.

План урока:

Этап урока	Деятельность учащихся
Организационный момент.	Подготовка к уроку.
Мотивационный этап урока.	Знакомство с учителем, настрой на работу.
Озвучивание темы урока, постановка его цели.	Узнают тему урока, участвуют в постановке цели урока, эмоционально настраиваются на урок.
Актуализация опорных знаний: опрос теоретической части.	Отвечают на поставленные вопросы по теоретической части раздела «Тригонометрия»
Работа в группах.	Составляют постер к ключевому слову, зашифрованному в ребусе.
Работа с таблицей значений тригонометрических функций.	Повторяют знания значений тригонометрических функций.
Работа с формулами.	Выполнение задания на знание основных тригонометрических функций.
Познавательный элемент урока.	Знакомятся со способами быстрого запоминания основного тригонометрического тождества.
Работа в парах.	Преобразовывают выражения с помощью основных тригонометрических тождеств, ответы сопоставляют с буквами и получают имя математика ПИТИСКУС.
Историческая справка.	Слушают материал из истории тригонометрии.
Релаксация.	Расслабляются, настраиваются на дальнейшую работу.
Работа в парах.	По известному значению одной тригонометрической функции нахождение другой.
Тестирование .	Решение заданий из базы ВОУД.
Тригонометрия в жизни человека.	Узнают интересные сведения  о роле тригонометрии в жизни человека.
Постановка домашнего задания.	Знакомятся с  домашним  заданием, записывают его в дневник.
Итог урока.	Оценивают свою деятельность на уроке.
Рефлексия.	Высказывают свое мнение о уроке.

Ход урока:

1. Орг.момент.  Встали все, приготовились, садитесь.
2. Мотивационный этап урока.

Пускай кому- то мил английский,
Кому – то химия важна,
Без математики же всем нам
Но ни туда и ни сюда
Нам уравнения, как поэмы
А синусы поддерживают дух
Нам косинусы, будто песни,
А формулы тригонометрии
Ласкают слух!

Всем здравствуйте,  я рада приветствовать вас на уроке алгебры. Алгебры, которую любят многие, урока, которого ждут с нетерпением.

3. Озвучивание темы урока, постановка цели.

    -Ребята, вспомните,  какой раздел алгебры  мы сейчас изучаем?  (Тригонометрия).

Тригонометрия – один из интереснейших разделов математики, но почему-то большинство учащихся считают его самым трудным. Объяснить это можно тем, что в этом разделе много формул. И самая первая группа формул – основные тригонометрические тождества. Без знаний этих формул ни одно тригонометрическое выражение не преобразуешь.

    Тема сегодняшнего урока: «Основные тригонометрические тождества. Решение задач».

    Давайте, совместно определим цели нашей работы на уроке. Для этого я вам предлагаю дополнить предложения:

Знать:

Уметь:

   Цель нашего урока  повторить материал по теме: «Тригонометрия. Основные тригонометрические тождества» и применить его при решении заданий.

   Ребята, обратите внимание на лист самооценивания, который лежит на вашей парте. (Приложение 1).  На каждом этапе урока вы должны себя оценить и поставить балл в данный лист. Оценивание производить по пятибалльной системе.

Перед  тем как приступить к заданиям, давайте настроимся на нашу совместную работу. Хором все вместе:  «Я  знаю!  Я  умею!  Я  решу!»

4. Актуализация опорных знаний .

1. Опрос теоретической части.

  Для достижения цели урока нам необходимо вспомнить материал прошлых занятий. Отвечаем на вопросы:

-Что называется единичной окружностью?

-Какие направления поворота единичного радиуса известны?

-В каких единицах измеряется угол поворота единичного радиуса?

-Что такое угол в один радиан? Сколько приблизительно градусов содержит угол в 1 радиан ?

-Сформулируйте правила перевода из градусной меры угла в радианную меру и наоборот. —Переведите в радианы: 300     ,  900.

-Переведите в градусную меру следующие углы:     ,  

-Какие тригонометрические функции вы знаете?.

-От чего зависит значение тригонометрических функций.

-Определите, углом, какой четверти является угол , если:

 1)  =2)  =,

3)  =4)  =5)  = (3),  

 6)  =

Хорошо, с теоретической частью нашего урока вы справились. Оцените вашу работу на данном этапе по пятибалльной шкале .

2. Работа в группах.

    Продолжим работу по повторению теории. Работаем в группах, у каждого на листе самоцениванияприкрепленстикер,  ребята у кого стикер зеленого цвета, образуют 1 группу, с розовым – вторую.

 Вспоминаем, правила работы в группе:

1. Группа совместно обсуждает и решает, выдвигает идеи или опровергает их.

2. Каждый член группы должен работать в полную меру своих сил.

3. Во время работы с уважением относитесь к товарищам: принимая или отвергая идею, делайте это вежливо. Помните, что каждый имеет право на ошибку.

4.  Помните, что успех группы зависит от того, насколько каждый проявит свои достоинства.

  А также каждой группе нужно выбрать спикера, для презентации своей работы.

Задание: разгадайте  ребус.

1 группа: здесь зашифровано слово, которое переводиться с латинского языка как «изгиб, дуга». (Приложение 2).

2 группа: здесь зашифровано слово, которое означает «синус дополнения». (Приложение 3).

Затем, разгадав ребус, расширьте его значение,  т.е. запишите все, что вы знаете о нем, другими словами создайте постер.

На данное задание вам дается 3 минуты. (После создания постера  спикеры групп его презентуют).

Молодцы, ребята, оцените вашу работу на данном этапе по пятибалльной шкале .

3. Работа с таблицей

   -Изучая раздел “Тригонометрия” мы часто пользуемся табличными значениями тригонометрических функций .Давайте их вспомним. ( На слайде изображена таблица значений тригонометрических функций, которая заполняется  после правильного ответа учащегося). (Приложение 4).

— Оцените вашу работу на данном этапе по пятибалльной шкале.

4. Задание на знание основных тригонометрических тождеств.

-А теперь проверим ваши знания основных тригонометрических тождеств, открываем тетради ,  находим  №1 ваша задача установить соответствие между левой и правой частью  тождества. Работаем самостоятельно. (Приложение 5).

Ответы:

1	2	3	4	5	6	7	8	9	10
M	L	N	E	B	C	A	K	H	D

Оцените вашу работу на данном этапе по пятибалльной шкале , используя критерии:

10 заданий –«5».

8-9 заданий –«4».

5-7 заданий –«3».

1-4 заданий –«2».

5. Как запомнить формулу основное тригонометрическое  тождество.

-Основное тригонометрическое тождество     это одна из основных формул тригонометрии, в математике оно называется «тригонометрическая единица»,  ее хорошо запомнить можно с помощью стихотворения:

Косинус квадрат

Очень рад.

К нему едет брат

Синус квадрат!

Когда они встретятся

Окружность удивиться:

Выйдет целая семья,

То есть единица!

6. Решить данные примеры и результаты заменить соответствующими буквами.

-Работаем  дальше! А теперь работа в группах. Посмотрите на стикеры, у кого на стикере изображен треугольник,  вы образуете 1 группу, у кого окружность- вторую.

Ваша задача, решив задания заменить ответы буквами.   Кто,  верно,  решит все примеры, получит имя математика, в книге которого впервые встречается термин – тригонометрия.

(Приложение 6

Правильный ответ:

1	2	3	4	5	6	7	8
П	и	т	и	с	к	у	с

-Кто не справился  или допустил ошибки, обратитесь за помощью к тем, кто справился или подойдите ко мне после урока.

-Какие знания мы применяли для решения данных выражений?(Выполняя упрощение выражений  использовали тригонометрические тождества.формулы сокращенного умножения, значения тригонометрических функций).

-Для успешного выполнения преобразований тригонометрических выражений необходимо свободно  владеть тригонометрическими тождествами и формулами сокращенного умножения.

-Оцените вашу работу на данном этапе по пятибалльной шкале.

7. Историческая справка.

Питискус — это имя немецкого математика в названии книги,  которого впервые встречается термин  “Тригонометрия”  в 1505 году.

“Тригонометрия” – слово греческое и в переводе означает измерение треугольников.

Своим становлением тригонометрия обязана арабским ученым Аль-Батуни, Аль- Хорезми, индийскому ученому Бхаскара и азербайджанскому астроному и математику НасиреддинТуси.

И только в XVIII веке знаменитый математик  Леонард Эйлер первым ввел известные всем определения тригонометрических функций. Так возникли тригонометрические формулы. И математика продвинулась на большой шаг вперед.

8. Релаксация. (Звучит спокойная расслабляющая музыка.)

Давайте немного отдохнем. Сядьте поудобнее на стуле, запрокиньте ногу на колено, придержите ее руками, закройте глаза. Это поза бесконечности. Сосредоточьтесь над знаком бесконечность – вытянутая горизонтальная восьмерка. Она находиться над вами, плавно колеблется над вашей головой. Вы это ярко представили. Постарайтесь удержать это изображение в вашем мысленном образе в течении нескольких секунд. (Пауза – молчание в течении 5 секунд). Откройте глаза, ребята.  Знак бесконечности в философии  связан со здоровьем и когда человек сталкивается с бесконечностью, он невольно задумывается о своем здоровье.  

-Отдохнули? Работаем дальше!

9. Работа в парах.

В тетради под №2 вам дано задание, по известному значению одной тригонометрической функции найти значение  другой. Обратите внимание в какой четверти находится угол α. Работаем в парах. (Приложение 7).

-Оцените вашу работу на данном этапе по пятибалльной шкале.

10. Самостоятельная работа.

Мы ребята повторили основные понятия, тригонометрические тождества. Эти знания вам нужны при сдаче ВОУД, ЕНТ, государственного экзамена  по алгебре , сейчас мы проведем самостоятельную работу, которая состоит из 4 тестовых заданий из базы ВОУД. (Приложение 8 – электронный тест).

Ответы:

1	2	3	4
3	1	4	1

После завершения времени учащиеся делают проверку и оценивают свою работу.

Критерии оценивания:

За правильно выполненные 4 заданий – оценка «5».

За правильно выполненные 3 задания – оценка «4».

За правильно выполненные 2 задания – оценка «3».

За правильно выполненные 1заданий – оценка «2».

   -Коррекционную работу сделать дома, если возникли затруднения , прошу подойти ко мне после урока.

11. Применение тригонометрии в жизни человека.

-Ребята, а вы знаете, в какой области нам нужны знания по теме «Тригонометрия»?

-Одна из областей, где тригонометрия играет важную роль — медицина. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически- тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров.

12. Домашнее задание:  а вот в каких, еще областях нужны знания тригонометрии вы узнаете при подготовке  сообщения на тему: «Тригонометрия  в жизни человека»,    №304  с.111.
13. Итог урока.

Подведем итог, мы сегодня повторили материал по тригонометрии, решали задания на применение основных тригонометрических тождеств. Вы все молодцы.

В течении урока вы оценивали себя, подсчитайте количество баллов, и по критериям, которые даны в конце таблице поставьте оценку вашей работе на уроке. (Приложение 1) .

Кто получил «5», «4», «3», «2»? я рада, что больше положительных оценок.

14.  Рефлексия.

-Ребята вам понравился урок?

 -Что понравилось больше всего?

-Что не понравилось?

-Спасибо.

   -А теперь, ребята, посмотрите на экран здесь изображен график тригонометрической функции у= sinх, он имеет название — синусоида, с ним и его свойствами вы познакомитесь в 10 классе. Посмотрите на плавную кривую этого графика, она образует гребни  которые отображают позитив, хорошее настроение и впадины, которые отображают унылое настроение. Точно такой же график изображен на у вас на листе самооценивания.(Приложение 1)Поставьте смайлик в том месте графика, которое отражает ваши ощущения на уроке: чувствовали ли вы себя на гребне волны или же, наоборот, в самой нижней точке.

  -Поделитесь со мной своим настроением, сдайте свои листы с эмоциями мне.

А свой смайлик я ставлю на самый верх гребня, так как мне очень понравилось с вами работать.  Спасибо за урок!

Приложение 1.

Лист самооценки урока алгебры та тему:

«Основные тригонометрические тождества.  Решение  задач».

Имя ученика (-цы)         ____________________________________

№	Этап урока	Балл	Максимальный балл
1	Теоретический опрос.		5
2	Работа в группе.		5
3	Работа с таблицей тригонометрических значений.		5
4	Работа с формулами		5
5	Работа в группе.		5
6	Работа в парах. По известному значению одной тригонометрической функции найти значение  другой		5
7	Тестирование		5
Набранный балл			35
Итоговая оценка

Критерии оценивания:

33-35 баллов – оценка «5»,

26-32 баллов – оценка «4»,

18-25 баллов – оценка «3»,

0-17 баллов – оценка «2».

Приложение 2.

Приложение 3.

Приложение 4.

sin
cos
tg
ctg

Приложение 5.

1		A
2		B
3		C
4		D
5		E	sin2α
6		H
7	через	K
8		L	1-sin2α
9	через  и	M	1
10	через  и	N	-cos2α

Приложение 6.

1. 3 sin2 α+ 3 cos2 α
2. (1 – cosα)(1 + cosα) при α =90°
3. 1- sin2 400
4. 2-2cos(-600)
5. tgαctgα
6. (ctg2α+ 1)(1 – sin2α)
7. tgαctgα-1
8. cos2 α+ ctg2α+sin2α

и	с	т	П	к	у
1		cos2 40°	3	ctg2α	0

Приложение 7.

Четверть	Дано:	Найти:	Решение:
I	sinα=0,6
II	cosα=	sinα
III	tgα=	ctgα
IV	cosα=	tgα

1.

3: Основные тригонометрические функции — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

61220

Цели обучения

• Найти шесть значений тригонометрической функции угла в прямоугольном треугольнике.

Синус, косинус, тангенс и другие отношения сторон прямоугольного треугольника.

Синус, косинус и тангенс

Тригонометрия — это изучение отношений между сторонами и углами прямоугольных треугольников. Ноги называются смежными или напротив в зависимости от того, какой острый угол используется.

Рисунок \(\PageIndex{1}\)

\(\begin{aligned} a \text{ прилегает к } \angle B \qquad a \text{ находится напротив } \angle A \\ b \text{ примыкает к } \угол A \qquad b \text{ противоположен } \угол B\\ c \text{ является гипотенузой }\end{aligned}\)

Три основных тригонометрических соотношения называются синус, косинус и тангенс. Для прямоугольного треугольника △ABC имеем:

\(\begin{aligned}
&\text { sine Ratio: } \dfrac{\text {противоположный катет}}{\text {гипотенуза}} \qquad \sin A= \dfrac{a}{c} \text { or } \sin B=\dfrac{b}{c}\\
&\text { Отношение косинуса: } \dfrac{\text {смежный отрезок}}{\text { гипотенуза}} \qquad \cos A=\dfrac{b}{c} \text { or } \cos B=\dfrac{a}{c}\\
&\text {Коэффициент касательной: } \dfrac{\text {противоположный отрезок}}{\text {соседний отрезок}} \qquad \tan A=\dfrac{a}{b} \text { or } \tan B=\dfrac{b}{a}
\end{aligned}\)

Простой способ запомнить соотношения — использовать SOH-CAH-TOA.

Рисунок \(\PageIndex{2}\)

Несколько важных моментов:

• Всегда уменьшайте коэффициенты (дроби), когда можете.
• Используйте Теорему Пифагора , чтобы найти недостающую сторону (если она есть).
• Если в знаменателе есть радикал , рационализировать знаменатель.

Что, если бы вам дали прямоугольный треугольник и сказали, что его стороны равны 3, 4 и 5 дюймам? Как найти синус, косинус и тангенс одного из непрямых углов треугольника? 9{2} \\
13 &=c \\
\sin A &=\frac{l e g \text {противоположная} \angle A}{\text {гипотенуза}}=\frac{12}{13} & \cos A = \ frac {\ text {отвод, примыкающий к } \ угол A} {\ text {гипотенуза}} = \ frac {5} {13}, \\
\ tan A & = \ frac {\ text {противоположный отвод} \angle A}{\text {ножка, смежная с } \angle A}=\frac{12}{5}
\end{aligned}\)

Пример \(\PageIndex{2}\)

Найти синус , косинус и тангенс \(\угол B\).

Рисунок \(\PageIndex{4}\)

Найдите длину недостающей стороны. 9{\ circ} = \ dfrac {6} {6 \ sqrt {3}} = \ dfrac {1} {\ sqrt {3}} \ cdot \ dfrac {\ sqrt {3}} {\ sqrt {3}} = \dfrac{\sqrt{3}}{3}\)

Пример \(\PageIndex{4}\)

Ответьте на вопросы по следующему изображению. Сократите все дроби.

Рисунок \(\PageIndex{6}\)

Что такое sin A, cos A и tan A?

Решение

\(\begin{array}{l}
\sin A=\frac{16}{20}=\frac{4}{5} \\
\cos A=\frac{12 }{20}=\frac{3}{5} \\
\tan A=\frac{16}{12}=\frac{4}{3}
\end{массив}\)

Ресурсы

Словарь

Срок	Определение
Острый угол	Острый угол – это угол, величина которого меньше 90 градусов.
Смежные углы	Два угла смежны, если они имеют общую сторону и вершину. Слово «прилегающий» означает «рядом с» или «рядом с».
Гипотенуза	Гипотенуза прямоугольного треугольника — это наибольшая сторона прямоугольного треугольника. Это напротив правого угла.
Стороны прямоугольного треугольника	Катетами прямоугольного треугольника являются две более короткие стороны прямоугольного треугольника. Ноги примыкают к прямому углу.
напротив	Число, противоположное числу \(x\), равно \(−x\). Число и его противоположность всегда в сумме дают ноль. 92\), где а и b — катеты треугольника, а с — гипотенуза треугольника.
Радикальный	Знак \(\sqrt{}\), или квадратный корень.
синус	Синус угла в прямоугольном треугольнике — это величина, которая находится путем деления длины стороны, противолежащей данному углу, на длину гипотенузы.
Тригонометрические соотношения	Соотношения, которые помогают нам понять отношения между сторонами и углами прямоугольных треугольников.

Дополнительные ресурсы

Интерактивный элемент

Видео: Введение в тригонометрические функции с использованием треугольных Реальный мир: синус косинус тангенс

---

Эта страница под названием 1.3: Основные тригонометрические функции распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

   Показать страницу TOC

   нет

2. Теги

   1. источник[1]-k12-4213
   2. источник[2]-k12-4213

Триггерные функции — обзор

Разделы функций триггера обзор функции единиц измерения — градус, радиан, град сторона маркировки — противолежащая, прилежащая, гипотенуза

Триггерные функции: обзор Согласно простейшему определению, тригонометрическая (буквально «измеряющая треугольник») функция, является одной из многих функций, связанных один непрямой угол прямоугольного треугольника к отношению длин любых двух сторон треугольника (или наоборот). Таким образом, любая тригонометрическая функция (f) всегда удовлетворяет условию любой из следующие уравнения: f(q) = a / b ИЛИ f(a/b) = q, где q — мера некоторого угла в треугольнике, а и b длины двух конкретных сторон. Это означает, что Если выполняется первое уравнение, мы можем выберите любой прямоугольный треугольник, затем измерьте один непрямых углов, и когда мы оцениваем тригонометрическая функция на этом угле , результат будет быть отношением длин двух сторон треугольника . Однако, если выполняется последнее уравнение, мы можем выбрать любое правое треугольника, затем вычислить отношение длин двух конкретных сторон, и когда мы вычисляем тригонометрическую функцию при любом отношении к результат будет мерой одного из треугольники непрямые. (Они называются обратными триггерами ). функции , так как они делают обратное или наоборот предыдущие триггерные функции. ) Это соотношение между углом и стороной соотношения в прямоугольном треугольнике — одна из самых важных идей в тригонометрия. Кроме того, тригонометрические функции работают на любой прямоугольный треугольник. Отсюда — для прямоугольного треугольника — если мы возьмем измерения одного из непрямых углов треугольника, мы можем математически вывести отношение длин любых двух стороны треугольника триггерными функциями. И если мы измерим любое отношение сторон, мы можем математически вывести меру одного из непрямых углов треугольника обратным триггерные функции. Что еще более важно, если мы знаем измерение одного из углов треугольника, и затем мы используем тригонометрический Функция для определения отношения длин двух сторон треугольника. стороны, и мы случайно знаем длины одного из этих стороны в отношении, мы можем тогда алгебраически определить длина другой из этих двух сторон. (т.е. если мы определим что a / b = 2, и мы знаем, что a = 6, то мы делаем вывод, что b = 3. ) Так как в прямом треугольнике три стороны и два непрямых угла треугольник, тригонометрическим функциям потребуется способ указать, какие стороны связаны на какой угол. (Бесполезно знать, что соотношение длина двух сторон равна 2, если мы не знаем, какая из сторон три стороны, о которых мы говорим. Аналогично, если мы определим что один из углов равен 40°, было бы неплохо знать под каким углом это утверждение верно. По определенному соглашению мы обозначаем стороны как напротив , рядом с и гипотенуза относительно к нашему углу интерес к. полное объяснение Как упоминалось ранее, первый тип тригонометрической функции, которая связывает угол с отношением сторон, всегда удовлетворяет следующее уравнение: f(q) = a / b. Поскольку для любого угла q существует три способов выбора числителя (а) и трех способов выбора знаменатель (b), мы можем создать следующие девять тригонометрических функций: f(q) = опп/опп f(q) = опп/прил f(q) = оппс/гип f(q) = прил/опп f(q) = прил/прил f(q) = прил/гип f(q) = гип/опп f(q) = гип/прил f(q) = гип/гип Три диагональные функции, показанные красным цветом, всегда равны единице. Они вырождены и поэтому бесполезны для нас. Поэтому мы удалить эти вырожденные функции и присвоить метки остальные шесть, обычно записываются в следующем порядке: 66 синус(q) = opp/hyp косеканс(q) = hyp/opp косинус(q) = adj/hyp секанс(q) = hyp(yp/adj 96 96 q) = opp/adj котангенс(q) = adj/opp Кроме того, функции обычно сокращаются: синус (sin), косинус (cos), тангенс (tan) косеканс (csc), секанс (sec) и котангенс (cot). Не перегружайтесь. Безусловно, два самых важных триггера Функции, которые нужно запомнить, это синус и косинус. Все остальные триггеры функции первого рода могут быть получены из этих двух функций. Например, функции справа — это просто мультипликативные обратная соответствующей функции слева (что делает они гораздо менее полезны). Более того, sin(x)/cos(x) = (opp/hyp) / (adj/hyp) = opp / adj = tan(x). Следовательно, касательная функция такая же, как частное функций синуса и косинуса (функция касательной все еще довольно удобна). sin(q) = opp/hyp csc(q) = 1/sin(q) cos(q) = adj/hyp sec(q) = 1/cos(q) tan(q) = sin(q)/cos(q) cot(q) = 1/tan(q) Рассмотрим эти функции подробнее. Вы заметите, что есть функции синуса, секанса и тангенса, и есть являются соответствующими «ко»-функциями. Они получают свои странные имена из различных подобных идей в геометрии. Вы можете предположить, что кофункции следует переименовать в мультипликативное обратные соответствующие синус, секанс и тангенс функции. Однако у этого безумия есть метод. Кофункция данной триггерной функции (f) по определению есть берется функция, полученная после дополнения ее параметра. Поскольку дополнение любого угла q равно 90° — q, факт можно показать, что выполняются следующие соотношения синус(90° — q) = косинус(q) секанс(90° — q) = косеканс(q) тангенс(90° — q) = котангенс(q) оправдывает соглашение об именах. Триггерные функции оцениваются по-разному в зависимости от единиц измерения. на q, например градус, радиан или град. Например, sin(90°) = 1, а sin(90)=0,89399…. объяснение Точно так же, как мы можем определить тригонометрические функции вида f(q) = а/б которые принимают непрямой угол в качестве параметра и возвращают соотношение длин двух сторон треугольника, мы можем сделать реверс: определить триггер функции формы f(a / b) = q которые принимают отношение длин двух сторон в качестве параметра и возвращает измерение одного из непрямых углов. обратные функции арксинус (opp/hyp) = q арккосеканс(hyp/opp) = q арккосинус(adj/hyp) = q арктангенс(hyp/adj) = q арктангенс(opp/adj) = q арккотангенс (прил/опп) = q Как и прежде, функции обычно обозначаются аббревиатурой: арксинус (arcsin), арккосинус (arccos), арктангенс (arctan) арккосеканс (arccsc), арксеканс (arcsec) и арккотангенс (arccot). No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт