Примеры решенных задач по физике на тему «Свободное движение тела, брошенного под углом к горизонту»
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Принцип решения этих задач заключается в разложении скорости свободно падающего тела на две составляющие — горизонтальную и вертикальную. Горизонтальная составляющая скорости постоянна, вертикальное движение происходит с ускорением свободного падения g=9.8 м/с2. Также может применяться закон сохранения механической энергии, согласно которому сумма потенциальной и кинетической энерги тела в данном случае постоянна.
Материальная точка брошена под углом к горизонту с начальной скоростью 15 м/с. Начальная кинетическая энергия в 3 раза больше кинетической энергии точки в верхней точке траектории. На какую высоту поднималась точка?
На какую высоту поднималась точка?
Тело брошено под углом 40 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние, которое пролетит тело до падения, высоту подъема в верхней точке траектории и время в полете.
Тело брошено с башни высотой H вниз, под углом α к горизонту, с начальной скоростью v. Найти расстояние от башни до места падения тела.
Тело массой 0,5 кг брошено с поверхност Земли под углом 30 градусов к горизонту, с начальной скоростью 10 м/с. Найти потенциальную и кинетическую энергии тела через 0,4 с.
Материальная точка брошена вверх с поверхности Земли под углом к горизонту с начальной скоростью 10 м/с. Определить скорость точки на высоте 3 м.
Тело брошено вверх с поверхности Земли под углом 60 градусов с начальной скоростью 10 м/с. Найти расстояние до точки падения, скорость тела в точке падения и время в полете.
Тело брошено вверх под углом к горизонту с начальной скоростю 20 м/с. Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Расстояние до точки падения в 4 раза больше максимальной высоты подъема. Найти угол, под которым брошено тело.
Тело брошено с высоты 5 м под углом 30 градусов к горизонту с начальной скоростью 22 м/с. Найти дальность полета тела и время полета тела.
Тело брошено с поверхности Земли под углом к горизонту с начальной скоростью 30 м/с. Найти тангенциальное и нормальное ускорения тела через 1с после броска.
Тело брошено с поверхности Зесли под углом 30 градусов к горизонту с начальной скоростью 14,7 м/с. Найти тангенциальное и нормальное ускорения тела через 1,25с после броска.
Тело брошено под углом 60 градусов к горизонту с начальной скоростью 20 м/с. Через какое время угол между скоростью и горизонтом станет равным 45 градусов?
Мяч, брошенный в спортзале под углом к горизонту, с начальной скоростью 20 м/с, в верхней точке траектории коснулся потолка на высоте 8м и упал на некотором расстоянии от места броска. Найти это расстояние и угол, под которым брошено тело.
Тело, брошеное с поверхности Земли под углом к горизонту, упало через 2,2с. Найти максимальную высоту подъема тела.
Камень брошен под углом 30 градусов к горизонту. На некоторой высоте камень побывал дважды — через время 1с и 3 с после броска. Найти эту высоту и начальную скорость камня.
Камень брошен под углом 30 градусов к горизонту с начальной скоростью 10 м/с. Найти расстояние от точки бросания до камня через 4 с.
Снаряд выпущен в момент, когда самолет пролетает над орудием, под углом к горизонту с начальной скоростью 500 м/с. Снаряд поразил самолет на высоте 3,5 км через 10с после выстрела. Какова скорость самолета?
Ядро массой 5 кг брошено с поверхности Земли под углом 60 градусов к горизонту. На разгон гири потрачена энергия 500Дж. Определить дальность полета и время в полете.
Тело брошено с высоты 100м вниз под углом 30 градусов к горизонту с начальной скоростью 5 м/с. Найти дальность полета тела.
Тело массой 200г, брошеное с поверхности Земли под углом к горизонту, упало на расстоянии 5м через время 1,2с. Найти работу по броску тела.
Ниже предлагаем вам посмотреть видеоуроки по данной теме:
Движение тела, брошенного под углом к горизонту
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля.
 Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα. - Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним.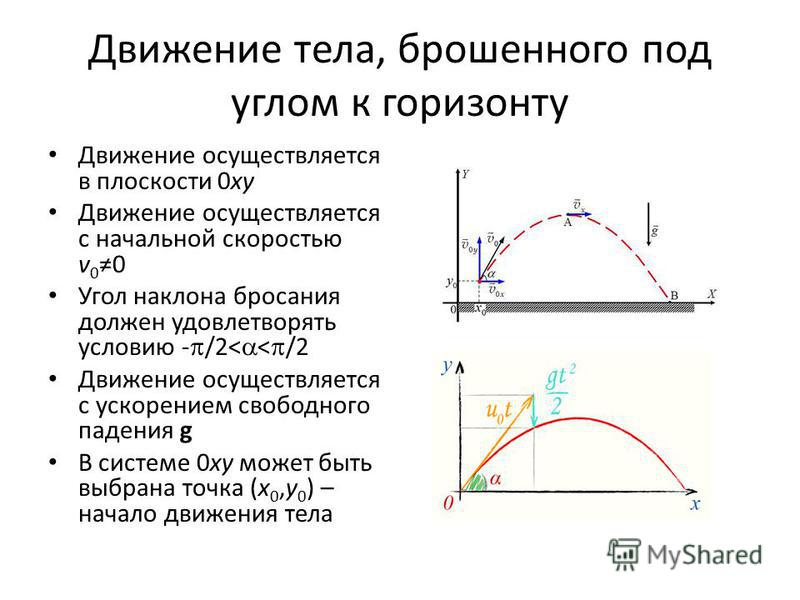 Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562 С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22..
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22..
Отсюда высота H равна:
H=mgl1mg..+mv22mg..=l1+v22g..
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2.β2g..=v2sin2.(90−2α)o2g..
Отсюда:
l1=h−v2sin2.(90−2α)o2g..
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g..=h−(gt)2sin2.(90−2α)o2g..+(gt)22g..
H=h−gt2sin2.(90−2α)2..+gt22..=h−gt22..(sin2.(90−2α)o−1)
H=1,4−10·0,422..(sin2.(90−60)o−1)
H=1,4−5·0,16(sin2.
H=1,4−0,8((12..)2−1)=1,4−0,8(14..−1)
H=1,4+0,6=2 (м)
.
.
.
.
Ответ: 20pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17980В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.

- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18741Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 40k
(а) перемещение тела как функция времени r(t), (б) вектор средней скорости ltlt v gtgt, усредненный за первые t секунд и за все время движения.
И.Е. ИРОДОВ, ЛА СЕНА И С.С. КРОТОВ-ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ-Релятивистская механика
21 видеоРЕКЛАМА
Аб Падхай каро бина адс ке
Khareedo DN Pro и dekhorukisi sari видео бина!
Обновлено: 27-06-2022
लिखित उत्तर
Ответ
Правильный ответ: (a) r=v0t+gt2/2; (б) ⟨v⟩t=v0+gt/2, ⟨v⟩=v0−g(v0g)/g2.
Решение
Так как тело находится под действием силы тяжести с постоянным ускорением →g, его вектор скорости и вектор смещения: →r=0 при t=0) (2)
Итак, <→v> за первые t секунд
<→v>=Δ→rΔt=→rt=→v0+→gt2 (3)
Отсюда из уравнения (3), <→v> за первые t секунд
<→v>=→v0+→g2τ (4)
Для вычисления t возьмите
→v⋅→v=(→v0+→gt)⋅(→v0+→gt)=v20+2(→v0⋅→g)t+g2t2
или, v2=v20+(→v0⋅ →g)t+g2t2
Но мы имеем v=v0 при t=0 и
Также при t=τ (рисунок). (также из сохранения энергии)
(также из сохранения энергии)
Следовательно, используя это свойство в уравнении. (5)
v20−v20+2(→v0⋅→g)τ+g2τ2
Поскольку τ≠0, значит, τ=−2(→vo⋅→g)g2
Подставляя это значение τ в уравнение (4), средняя скорость за время полета
<→v≥→v0−→g(→v0⋅→g)g2
Экзамены.
संबंधित वीडियो
Тело брошено со скоростью v_0 под углом theta_0 к горизонту. Найдите (а) мгновенную мощность, развиваемую силой тяжести через время t, отсчитываемую от момента проецирования, и (б) среднюю мощность, развиваемую силой тяжести за время t.
11297581
Если на предыдущей иллюстрации, заряженная частица проецируется под углом альфа с осью x с величиной скорости. Найди. вектор скорости как функция времени vec v (t). б. вектор положения в функции времени vec r (t).
11313782
Показан график времени положения, который представляет собой полукруг в форме от t = 2 до t = 8 сек. Найдите время t, при котором мгновенная скорость равна средней скорости за первую t секунды. @ к горизонту. Начальная скорость каждого тела равна v_0=25м//с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с. 92j , где a и b — положительные константы, а I и j — орты осей x и y. Найти: а) уравнение траектории точки y(x) , построить эту функцию, б) зависимость от времени векторов скорости v и ускорения w, а также модулей этих величин, в) время зависимость угла α между векторами w и v, (г) вектор средней скорости, усредненной за первые t секунд движения, и модуль этого вектора.
@ к горизонту. Начальная скорость каждого тела равна v_0=25м//с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через t=1,70 с. 92j , где a и b — положительные константы, а I и j — орты осей x и y. Найти: а) уравнение траектории точки y(x) , построить эту функцию, б) зависимость от времени векторов скорости v и ускорения w, а также модулей этих величин, в) время зависимость угла α между векторами w и v, (г) вектор средней скорости, усредненной за первые t секунд движения, и модуль этого вектора.
12305802
Тело массой m брошено под углом к горизонту с начальной скоростью v0. Пренебрегая сопротивлением воздуха, найти: 93 , где k — константа, а v — скорость тела.
12305896
Текст Решение
Тело массы m брошено под углом альфа к горизонту с начальной скоростью v_0 . Найти среднюю мощность, развиваемую силой тяжести за все время движения тела, и мгновенную мощность силы тяжести в зависимости от времени.
12305921
Для тела, движущегося с равноускорением a , начальная и конечная скорости в интервале времени t равны u и v соответственно. Тогда его средняя скорость в интервале времени t равна
Тогда его средняя скорость в интервале времени t равна
13399090
Тело брошено под углом α к горизонту с начальной скоростью v_0. Пренебрегая сопротивлением воздуха, найти (i) время движения, (ii) максимальную высоту подъема и горизонтальную дальность, ( iii) угол проекции, при котором они равны, (iv) угол проекции, при котором дальность по горизонтали максимальна, и угол, при котором дальность по вертикали максимальна.
17089286
Тело массой m=1кг брошено под углом θ=45∘ к горизонту с начальной скоростью u=10м/с. Найти среднюю мощность, сообщаемую силой тяжести за все время движения тела.
32506531
एक एकविमीय एकविमीय के कण की स्थिति x (मीटर में) से t = 4 सेकण्ड में पिंड का विस्थापन, (ii) समय अंत अंत000 t = 2 सेकण्ड से t = 4 सेकण्ड के लिये पिंड क औसत वेग वेग |
332112842
Движущаяся частица проходит половину кругового пути радиуса r за время t . Найдите среднюю скорость и среднюю скорость тела.
376757351
Калькулятор горизонтального движения снаряда
Этот калькулятор горизонтального движения снаряда является инструментом для решения частного случая движения снаряда, когда объект запускается горизонтально с приподнятой плоскости . Введите любые два значения, а остальные будут рассчитаны в мгновение ока! Кроме того, траектория будет отображаться под результатами.
Введите любые два значения, а остальные будут рассчитаны в мгновение ока! Кроме того, траектория будет отображаться под результатами.
Продолжайте прокручивать, чтобы узнать уравнения горизонтального движения снаряда и простой пример расчета — у вас не должно возникнуть проблем с упражнениями после прочтения нашего объяснения!
Уравнения горизонтального движения снаряда
Как мы уже говорили, уравнения горизонтального движения снаряда являются частным случаем общих формул. Нам не нужно указывать угол запуска, так как он параллелен земле (поэтому угол равен 0°). В результате имеем только одну составляющую начальной скорости – Vx=VV_x = VVx=V, тогда как Vy=0V_y = 0Vy=0.
Мы возьмем начальную точку в начале координат. Тогда уравнения движения можно записать так:
Расстояние 92y=–21gt2, где ggg — ускорение свободного падения, а hhh — высота над уровнем моря. Скорость Ускорение Уравнения горизонтального движения снаряда 92 = h31gt2=h. Из этого уравнения можно найти, что время полета равно: t=2hgt = \sqrt{\frac{2h}{g}}t=g2h дальность полета снаряда — полное горизонтальное расстояние, пройденное за время полета. Тогда мы можем записать уравнение как: r=Vt=v2hgr = Vt = v\sqrt{\frac{2h}{g}}r=Vt=vg2h Опять же, эта формула будет сложнее, если угол не был установлен на 0 °. Если вам интересно это увидеть, проверьте калькулятор дальности полета снаряда. Мы не будем вычислять здесь максимальную высоту (вместо этого см. калькулятор максимальной высоты), так как у нас нет начальной составляющей вертикальной скорости, а это значит, что максимальная высота та, с которой мы начинаем. Во всех расчетах мы пренебрегали сопротивлением воздуха, действующим на снаряд. Таким образом, сохраняется сумма кинетической и потенциальной энергий. Подробнее о последнем вы можете прочитать в нашем калькуляторе потенциальной энергии. Предположим, мы хотим рассчитать время полета и расстояние, пройденное мячом, брошенным с Эйфелевой башни только с горизонтальной скоростью, например, 7 м/с. Введите скорость . В нашем случае это 7 м/с. При необходимости измените единицы измерения. Введите начальную высоту, с которой начинается движение . Эйфелева башня имеет высоту 324 метра (1063 фута), но верхняя платформа находится на высоте 276 м (906 футов) над землей. Итак, вводим 276 м в нужное поле. Наш калькулятор горизонтального движения снаряда показывает время полета, расстояние и траекторию! Мы выяснили, что мяч достигает земли за 7,5 секунды, а его горизонтальное перемещение составляет ~52,52 м. Помните, что наши инструменты очень гибкие: просто введите любые два значения, и калькулятор горизонтального движения снаряда сделает свою работу. Вы можете, например, проверить, какая скорость необходима, чтобы бросить мяч на расстояние 100 м от основания башни. Чтобы рассчитать горизонтальное расстояние при движении снаряда, выполните указанные шаги: Умножить вертикальную высоту Возьмите квадратный корень из результата шага 1 и умножьте на начальную скорость проекции Вы также можете умножить на начальную скорость Для расчета времени полета снаряда при горизонтальном движении выполните следующие действия: Узнать высоту по вертикали 902:37 ч откуда брошен снаряд. Умножьте Возьмите квадратный корень из результата шага 2 , и вы получите время полета при горизонтальном движении снаряда. № , горизонтального ускорения при движении снаряда нет. Скорость снаряда постоянна в горизонтальном направлении . Следовательно, ускорение также равно нулю в горизонтальном направлении. 9,8 м/с² .

Пример расчета горизонтального движения снаряда
 Потрясающий!
Потрясающий! Часто задаваемые вопросы
Как рассчитать горизонтальное расстояние при движении снаряда?
h на 2 и разделить на ускорение свободного падения g . u , чтобы получить горизонтальное расстояние. u на время, необходимое снаряду, чтобы достичь земли t , чтобы получить расстояние по горизонтали.
Как рассчитать время полета снаряда при горизонтальном движении?
ч на 2 и разделите на g , ускорение свободного падения. Есть ли горизонтальное ускорение при движении снаряда?
Каково вертикальное ускорение снаряда, когда он летит горизонтально?
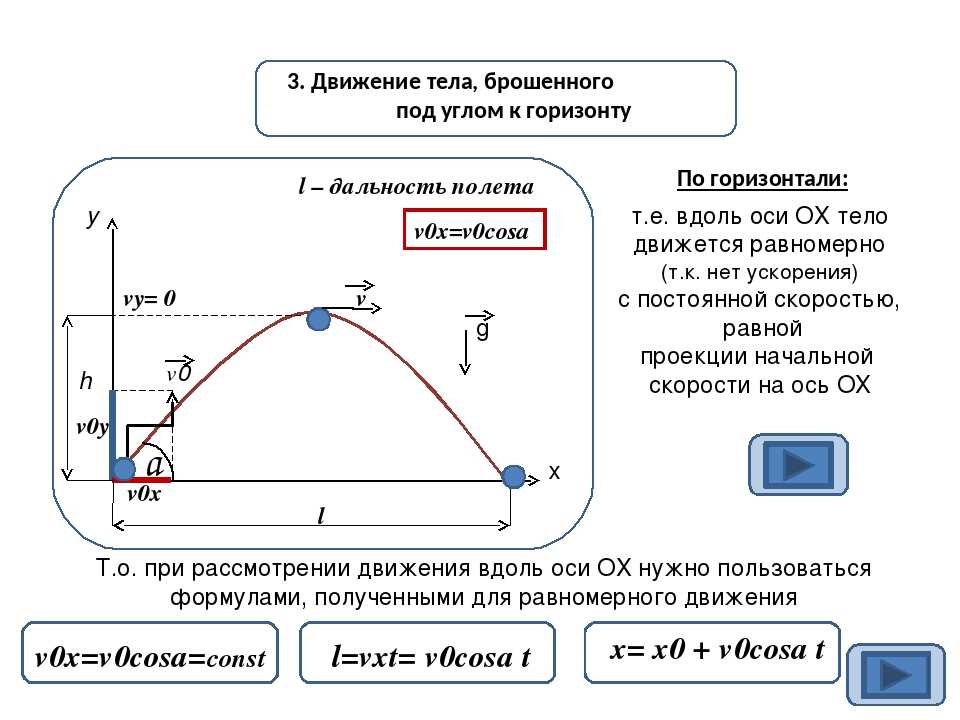

 Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.