Развернутый угол это в геометрии: Что такое развёрнутый угол? Ответ на webmath.ru

Определение угла. Развёрнутый угол. Сравнение углов наложением. | Методическая разработка по геометрии (7 класс) по теме:

План-конспект урока

по теме

«Определение угла. Развернутый угол. Сравнение углов наложением».

Цели урока:

1.Образовательные:

• повторить правила построения углов и научить разным способам обозначения  угла;
• ввести понятие развернутого угла;
• сформировать умение сравнивать углы наложением.

2.Развивающие:

• развитие способности конкретизировать теоретические знания при решении задач;
• развитие умения анализировать предложенный материал;
• развитие умения работы с  текстовыми источниками информации;
• способствовать развитию монологической речи и диалога как формы обобщения и закрепления знаний

3. Воспитательные:

• воспитание культуры математической речи;
• воспитание культуры математической  записи при решении задач;
• воспитание  культуры делового общения, сотрудничества.

Ход урока:

1.Организационный момент.

   Учитель начинает урок с того, что проверяет готовность  класс к уроку.

Просит  открыть тетрадь и записать: число, классная работа,  и оставить две строчки  для записи темы урока, которую мы запишем  в конце урока.

Ставит задачу перед учащимися: проанализировать то, чем мы сегодня  будем заниматься на уроке и постараться сформулировать тему сегодняшнего   урока.

2.Актуализация знаний учащихся.

Учитель. Сейчас мы с вами отправимся в путешествие.

(Демонстрация слайдов №1, №2)

Учитель. Чтобы наше путешествие прошло успешно, проведем устную работу.

Устная работа.

Демонстрация плаката на интерактивной доске.

1. Какие фигуры изображены на плакате.

•                          •

2)  

3)

4) Какие точки принадлежат прямой m , а какие не принадлежат.

3.Изучение нового материала.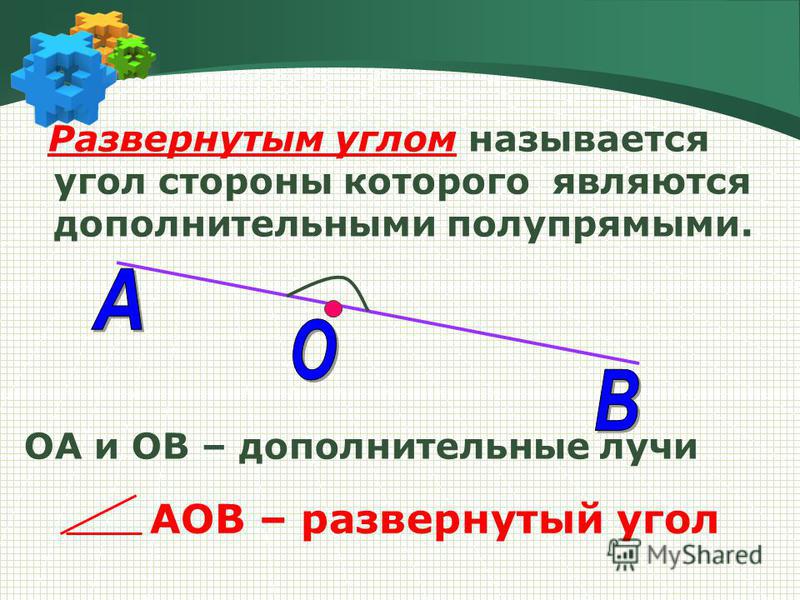

(Демонстрация слайдов № 3, №4)

3.1.Определение угла. Символическая запись угла. Обозначение угла. Стороны угла, вершина угла.  

(Демонстрация слайдов № 5,№6)

                             

3.2.Проверка усвоения. (Демонстрация слайдов №7)

3.3. Принадлежность точек данному углу.( Демонстрация слайдов № 8, №9)

3.4.Понятие развёрнутого  угла.( Демонстрация слайда № 10.)

3.5. Работа с текстом учебника стр.136. Определение развёрнутого угла. 

3.6.Работа в рабочей тетради. Выполняют № 27.2.

Демонстрация слайда №11. Найдите на рисунке развернутые углы и обведите их. Запишите названия развернутых углов.

Проверка . Демонстрация слайда № 12

3.7. Физкультминутка. Демонстрация  слайда №13.

Быстро встали, улыбнулись.

Выше – выше потянулись.

Ну-ка, плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали. Сели, встали.

И на месте побежали.

3.8. Сравнение углов наложением. Демонстрация слайда № 14.

3.9. Работа в группах с моделями  углов (прямого, острого, тупого). Путем наложения  сравниваются  углы. Учащиеся делают выводы.

3.9. Учитель объясняет,  как можно сравнить углы с помощью прозрачной плёнки.

 

3.10.Работа с учебником. Выполняют № 516.

Демонстрация слайдов № 15, № 16.

11. Сравнение острого, прямого и тупого углов.

Демонстрация слайдов № 17, №18

3.12.Подводится анализ изучаемого материала. Совместно с учащимися формулируется тема урока. Демонстрация слайдов № 19, № 20.

4. Рефлексия. Учащимся предлагается продолжить предложения.

                   Демонстрация слайдов № 21, №22.

•Сегодня я узнал…

•Я выполнял задания …

•Я понял, что…

•Теперь я могу…

•Я научился…

•Я приобрел…

•У меня получилось…

5. Задание на дом с пояснением. Демонстрация слайда  № 23

•§§ 27, 28      № 506, №507, №517

Развернутый угол в геометрии :: SYL.ru

Притягивают толпы незнакомцев: признаки духовно одаренных людей

Несколько причин попробовать маски для лица с серой (хотя они и плохо пахнут)

Скатерть, красные салфетки и пять свечей: как провести праздники по фэн-шуй

С индейкой и беконом: праздничная кассероль из семи слоев (рецепт)

Уход и отдых: как подготовить кожу к выходу в свет или важному событию

В Новый год с новым образом — но без стрижки: как выбрать длинную прическу

Делаем крафтовый подсвечник из фисташек (инструкция и фото)

Тенденции причесок с косами на 2023 год, основные тренды и главные особенности

Можно и так готовить: уловки с замороженной курицей, о которых мало кто знает

Румяные и нежные. Готовим выпечку как в школьной столовой

Автор YuliiaT May 3, 2016

В этой статье будет рассматриваться одна из основных геометрических фигур – угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол – важное понятие геометрии, которое и будет основной темой этой статьи.

Введение в понятие геометрического угла

В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.

Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии – это точка, прямая на плоскости и собственно сама плоскость.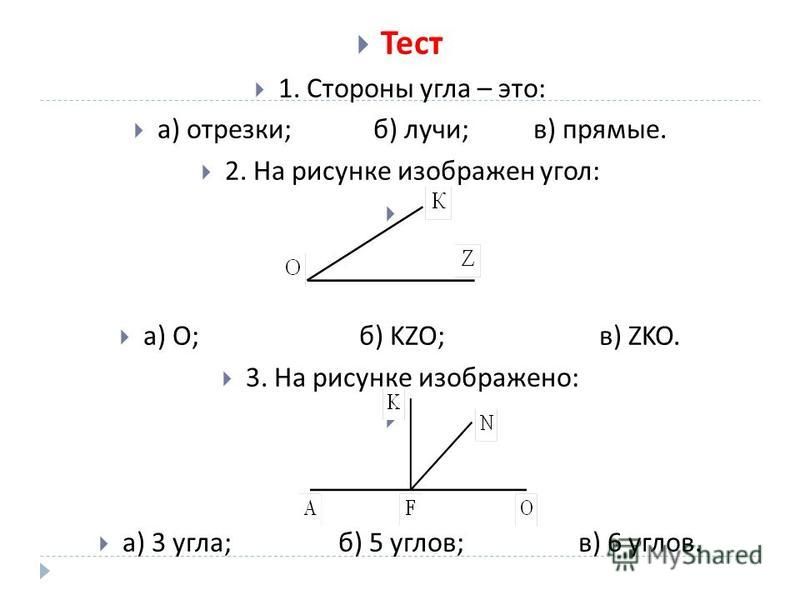 Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью – поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии – это часть прямой, у которой есть начало, но нет конца.

Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон – это его вершина.

Виды углов и геометрии

Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:

1. Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
2. Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
3. Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
4. Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.

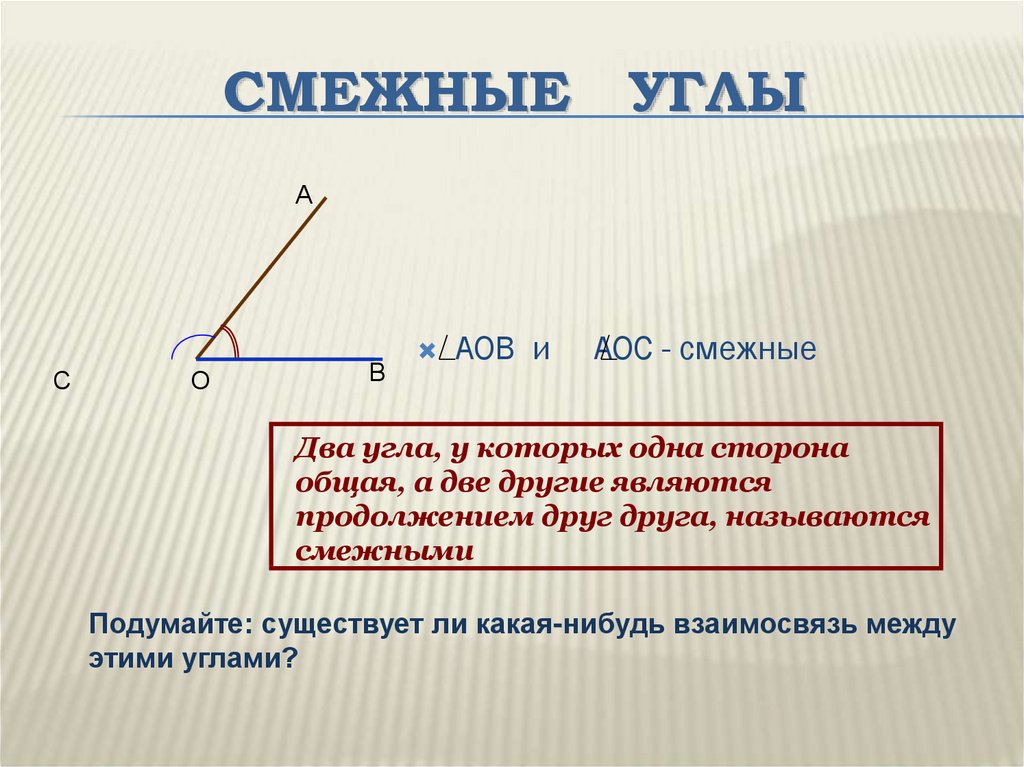
Понятие развернутого угла

Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.

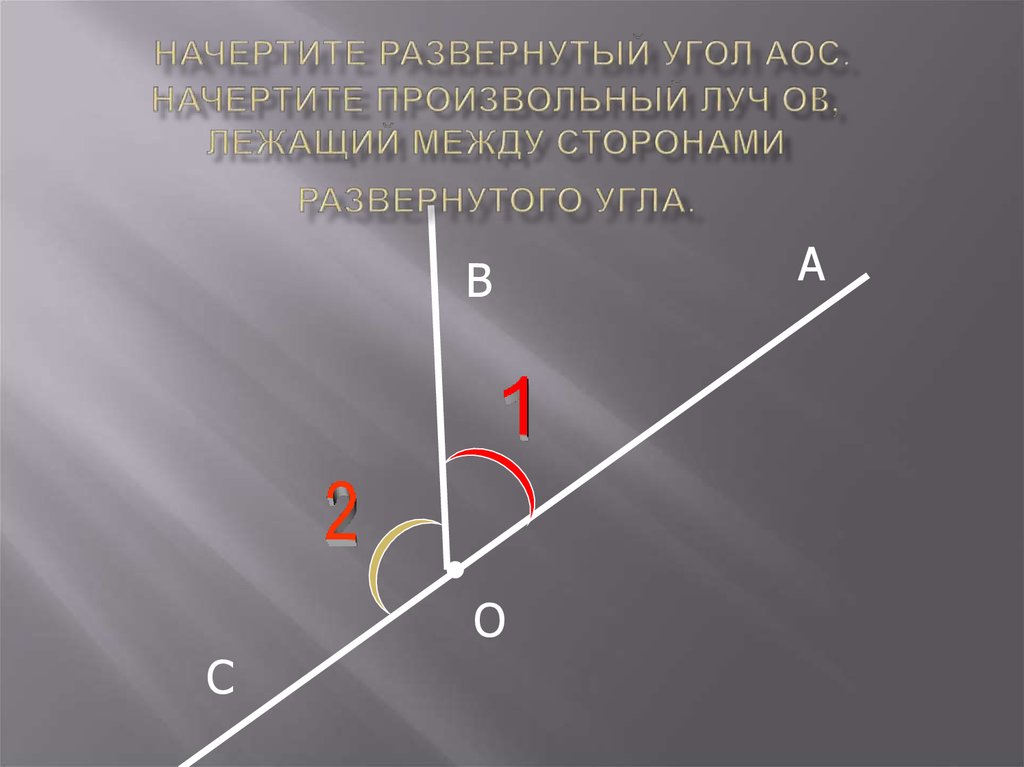
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.

Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов.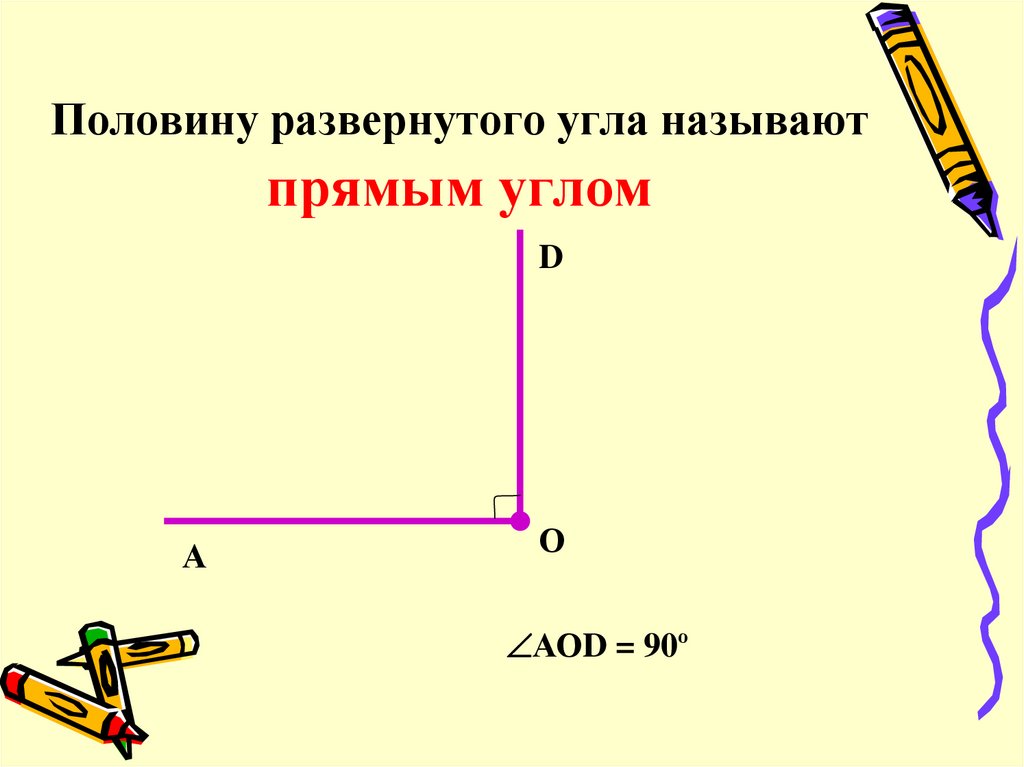 Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.

Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой – тупым.

Свойства развернутых углов

Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:

1. Стороны развернутого угла антипараллельны и составляют прямую.
2. Величина развернутого угла всегда составляет 180˚.
3. Два смежных угла вместе всегда составляют развернутый угол.
4. Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
5. Половина развернутого угла – это прямой угол.

Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.

Задачи с развернутыми углами

Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.

1. Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
2. Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
3. Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
4. Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.

Решения и ответы:

1. Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
2. Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
3. Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
4. Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х . Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.

Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.

Похожие статьи

• Тригонометрия с нуля: основные понятия, история
• Египетский треугольник — загадка древности
• Чем отличаются мыши от крыс? Описание и сравнение крыс и мышей
• Цилиндр. Виды, объём цилиндра, площадь поверхности
• Развал-схождение колес своими руками: пошаговая инструкция
• История оригами. История возникновения оригами
• Герб Армении: история, описание, значение символики

Также читайте

Что такое прямой угол? Определение, свойства, примеры, факты

Что такое угол?

Когда две прямые линии или лучи встречаются в общей конечной точке, образуется угол. Общая точка касания двух лучей называется вершиной угла. Мы используем символ ∠ для обозначения угла. Мы используем градусы (°) для измерения угла с помощью транспортира. Например, 45 градусов представляются как 45°.

Существуют различные типы уголков:

• Острый угол
• Тупой угол
• Прямой угол
• Прямой угол
• Рефлекторный угол

Что такое прямой угол?

Прямой угол в геометрии определяется как угол, равный 180 градусам. Причина, по которой угол называется прямым, заключается в том, что он выглядит как прямая линия.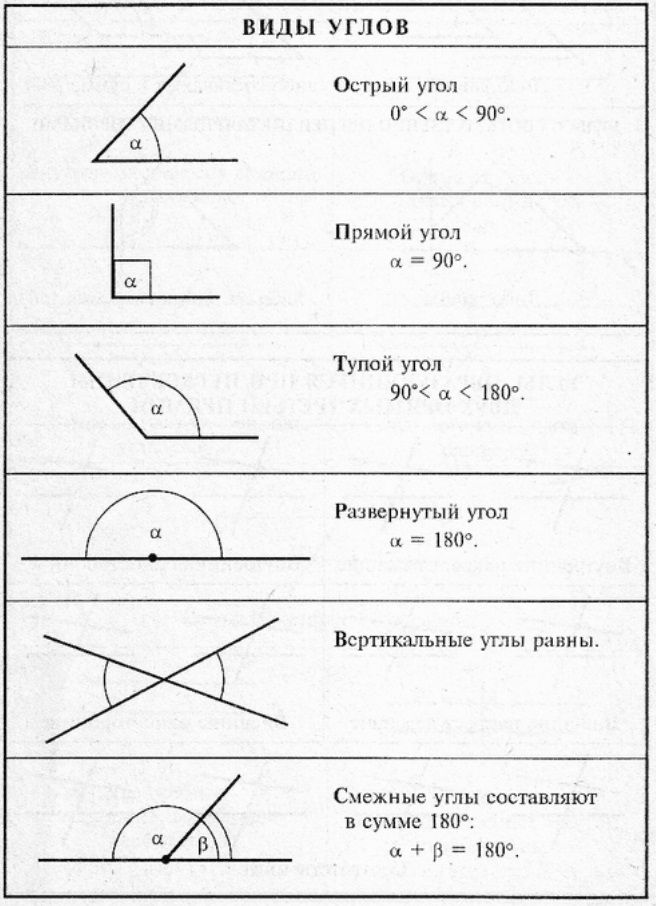 Другими словами, это угол, стороны которого лежат в противоположных направлениях от вершины на одной прямой.

Примеры прямого угла

Некоторые из его примеров в нашей повседневной жизни:

• Плоская поверхность имеет угол 180 градусов.
• Плоская наклонная лестница.
• Угол между минутной и часовой стрелками в 6:00.
• Линейка, которую мы используем.

Свойства прямого угла

Его свойства следующие:

• Он образован поворотом одного луча на 180° по отношению к другому лучу.
• Меняет направление точки.
• Это ровно половина оборота, т. е. половина полного угла.
• Его также можно получить, соединив два прямых угла, т. е. 90° + 90° = 180°.
• Мы обозначили прямой угол как π .
• Также известен как плоский уголок.

Пара прямых углов

Пара прямых углов — это пара углов, образующих прямую линию. Сумма двух и более углов, входящих в эту пару, всегда равна 180°. Мы также называем их линейными парами углов .

На приведенном выше изображении показаны два угла ∠ a = 125° и ∠ b = 55° , которые вместе составляют 180°. Прямой угол имеет общую сторону и общую вершину. На приведенном выше рисунке OS — это общее плечо, а O — общая вершина.

Иногда на прямой есть 3 угла. Например, на приведенном ниже рисунке ∠ AOB + ∠ BOC + ∠ COD = 180°

Пример 1: Найдите значение ∠ COD на следующей диаграмме.

Решение : ∠ AOD — прямой угол.

▲ AOB + ♂ BOC + T COD = 180 °

60 ° + 90 ° + ↑COD = 180 °

T COD = 30 °

Пример. 30° под прямым углом.

Решение : Прямой угол = 180°

180°30°=6.

Пример 3: Найдите все комбинации, образующие прямые углы на следующем рисунке.

Solution : Straight angles are:

∠ VXY , ∠ YXZ and ∠ ZXU

∠ VXY , and ∠ YXU

∠ VXZ , and ∠ ZXU

∠ VXW и ∠ WXU

∠ WXV , ∠ VXY and ∠ YXZ

∠ WXV , and ∠ VXZ

∠ WXY , and ∠ YXZ ∠ WXU and ∠ UXZ

Practice Problems

1

Что из нижеперечисленного является мерой двух прямых углов?

90 °

180 °

270 °

360 °

Правильный ответ: 180 °
Два правых углы = 2 ✕ 90 ° = 180 °

2

Найдите значение x + 2

2

, x и x + 10 образуют линейную пару.

$x = 156°$

$x = 66°$

$x = 56°$

$x = 76°$

Правильный ответ: $x = 56°$
$x + 2 + x + x + 10 = 180°$
$3x + 12 = 180°$
$3x = 168°$
$x = 56°$

3

Что неверно в отношении прямого угла?

Состоит из двух прямых углов.

Также известен как плоский угол.

В радианах это называется π.

Два прямых угла образуют рефлекторный угол.

Правильный ответ: два прямых угла образуют рефлекторный угол.
Рефлекторный угол – это угол, лежащий между прямым углом и полным углом.

4

Какая часть полного угла является прямым углом?

Половина

Один — Четвертый

Один — Восемь

Один — Пятый

Правильный ответ: Половина
Прямой угол = 180° }$=$\frac{1}{2}$

Часто задаваемые вопросы

В чем разница между прямым углом и прямой линией?

Прямой угол равен 180 градусам, а прямая линия является соединением двух точек.

В чем разница между парой дополнительных углов и парой прямых углов?

Пара дополнительных углов — это пара углов, сумма которых равна 180°, но углы могут быть или не быть смежными. С другой стороны, пара прямых углов — это пара углов, которые всегда примыкают друг к другу и имеют сумму 180°.

Чему равна сумма внутреннего угла и внешнего угла?

Сумма внутреннего и внешнего углов равна 180°, так как они лежат на одной прямой.

Прямой угол – значение, свойства, примеры

Прямой угол имеет размер 180° и выглядит как прямая линия, поэтому это математический способ выражения прямой линии. Это угол, стороны которого лежат в противоположных направлениях от вершины и соединяются вместе, образуя 180°. Давайте узнаем больше о прямом угле в этой статье.

1.	Определение прямого угла
2.	Свойства прямого угла
3.	Прямой угол Градус
4.	Рисование прямого угла с помощью транспортира
5.	Часто задаваемые вопросы о прямых углах

Определение прямого угла

Всякий раз, когда два луча соединяются вместе, они образуют угол, а угол, образуемый двумя лучами в противоположных направлениях, называется прямым углом. В геометрии прямым углом называют угол, точка вершины которого имеет значение 180 градусов.

Другими словами, когда стороны угла направлены в противоположные стороны, они образуют прямой угол. Руки образуют прямую линию через вершину.

Свойства прямого угла

Важными свойствами прямых углов являются следующие.

• Прямой угол образован поворотом одного луча на 180° по отношению к другому лучу.
• Прямой угол меняет направление точки на противоположное.
• Прямой угол равен половине оборота.
• Прямой угол можно также получить, соединив два прямых угла.

Прямоугольный Градус

Градус или мера прямого угла всегда составляет 180º. В традиционной системе измерения углов мы считаем, что прямой угол равен 9.0°, а угол вокруг точки равен 360°. Прямой угол состоит из двух прямых углов. Обратите внимание на рисунок, приведенный ниже, чтобы понять этот факт.

Рисование прямого угла с помощью транспортира

Прямой угол можно легко построить с помощью транспортира. Следуйте инструкциям ниже, чтобы нарисовать прямой угол с помощью транспортира:

• Шаг 1: Нарисуйте прямую линию и назовите ее AB и отметьте стрелку на B.
• Шаг 2: Поместите транспортир на линию AB так, чтобы базовая линия транспортира находилась над линией AB. Убедитесь, что B указывает на 0°.
• Шаг 3: Начиная с 0° на внутренней шкале и удерживая транспортир на месте, медленно перемещайте карандаш, пока не достигнете 180°. Отметьте эту точку как C, а также отметьте здесь стрелку.
• Шаг 4: Соедините точку C с линией AB. Таким образом, образуется прямой угол CAB, равный 180º.

На следующем рисунке показано, как с помощью этих шагов строится прямой угол.

Пара прямых углов

Пара углов, образующих прямую линию, называется парой прямых углов. Сумма двух углов, входящих в пару прямых углов, всегда равна 180°. Они также известны как линейные пары углов. На изображении ниже показаны два угла a = 135° и b = 45° , которые вместе составляют 180°. Пары прямых углов имеют следующие общие свойства. У них есть общее плечо и общая вершина. На следующем рисунке QS — это общее плечо, а Q — общая вершина.

Прямые углы в реальной жизни

В повседневной жизни мы часто сталкиваемся с прямыми углами. Некоторые примеры прямого угла приведены ниже.

• Часы, показывающие 6 часов, образуют прямой угол.
• Прямоугольная столешница представляет собой прямой угол.
• Ваша линия взгляда — прекрасный пример прямого угла.

Все указанные ниже углы прямые. Отличаются они только ориентацией. Следуя им, мы можем найти множество прямых углов вокруг себя.

Темы, относящиеся к прямым углам

• Острый угол
• Центральный угол
• Прямая линия
• Уголки

Важные примечания:

• Прямой угол образуется при повороте одного луча на 180° по отношению к другому лучу.
• Прямой угол равен половине оборота.
• В радианах прямой угол обозначается π.
• Прямой угол меняет направление точки на противоположное.
• Прямой угол также называют «плоским углом».
• Пара прямых углов представляет собой набор двух смежных углов на прямой линии, сумма которых составляет 180°
• Если ∠A + ∠B = 180°, то ∠A и ∠B образуют пару прямых углов (линейную пару).

 

Примеры прямого угла

1. Пример 1. Определите пары прямых уголков на следующем рисунке.

   Решение:

   Здесь ∠AOC,∠BOD прямые углы. ∠AOD и ∠COD имеют общее плечо OD и общую вершину O. Они находятся на одной прямой AC. Итак, ∠AOD и ∠COD образуют пару прямых углов. Видно, что:

   ∠1 + ∠2 = 180°
   ∠2 + ∠3 = 180°
   ∠3 + ∠4 = 180°
   ∠4 + ∠1 = 180°
   Итак, всего 4 пары прямых углов.

2. Пример 2: Если часовая стрелка часов находится в положении 6, а минутная стрелка в положении 12, какой угол образуется при этом? Он образует прямой угол или прямой угол?

   Решение:

   Если часовая стрелка часов на 6, а минутная на 12, время 6 часов и стрелки образуют прямую линию. Поскольку угол между стрелками в положении «6 часов» составляет 180º, часы показывают прямой угол.

3. Пример 3: Тиа утверждает, что «Если два конгруэнтных угла образуют пару прямых или прямых углов, то эти углы прямые». Проверьте, правильная она или нет.
   Решение:

   Если два угла образуют пару прямых углов (линейную пару), то они оба в сумме дают 180º, что означает ∠A + ∠B = 180º

   Здесь углы равны,

   ∠A = ∠B
   ∠А + ∠В = 180°
   2∠А = 180
   ∠А = 90°
   ∠А = ∠В = 90°
   Значит, Тия права.

перейти к слайдуперейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?

Мастерство в математике приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Забронировать бесплатный пробный урок

Практические вопросы по прямому углу

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о прямых углах

Что такое прямой угол в математике?

Когда два луча или стороны угла направлены в противоположные стороны, они образуют прямую линию. Угол, образованный этими двумя лучами, равен 180°.