Нечетная функция | это… Что такое Нечетная функция?
ТолкованиеПеревод
- Нечетная функция
f(x) = x — пример нечётной функции.
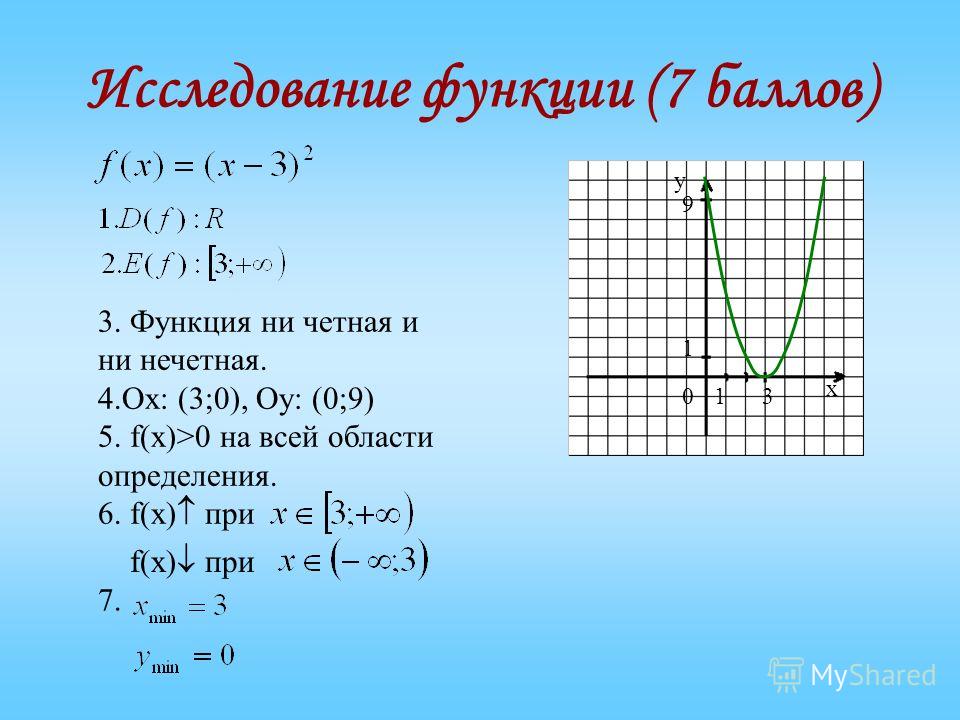
f(x) = x2 — пример чётной функции.
f(x) = x3, нечётная
f(x) = x3 + 1 ни чётная, ни нечётная
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.
Или по-другому
Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.
Содержание
- 1 Определения
- 2 Свойства
- 3 Примеры
 1 Нечётные функции
1 Нечётные функции- 3.2 Чётные функции
- 4 Вариации и обобщения
Определения
- Функция называется нечётной, если справедливо равенство
- Функция f называется чётной, если справедливо равенство
- Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Свойства
- График нечётной функции симметричен относительно начала координат O.
- График чётной функции симметричен относительно оси ординат Oy.
- Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:
- f(x) = g(x) + h(x),
где
- Функция — единственная функция, одновременно являющаяся нечётной и чётной.
- Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.

- Произведение или дробь двух нечётных функций чётно.
- Произведение или дробь двух чётных функций чётно.
- Произведение или дробь нечётной и чётной функций нечётно.
- Композиция двух нечётных функция нечётна.
- Композиция двух чётных функций чётна.
- Композиция чётной функции с нечётной чётна.
- Композиция любой функции с чётной чётна (но не наоборот).
- Функция, обратная чётной, чётна, а нечётной — нечётна.
- Производная чётной функции нечётна, а нечётной — чётна.
- То же верно про производную третьего, пятого и вообще любого нечётного порядка.
- Производная чётного порядка сохраняет чётность.
Примеры
Нечётные функции
- Нечётная степень где — произвольное целое число.
- Синус .
- Тангенс .
Чётные функции
- Косинус .
Вариации и обобщения
- Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

Wikimedia Foundation. 2010.
Игры ⚽ Нужен реферат?
- Нечеткие множества
- Нечетное число
Полезное
Является ли четной или нечетной функция а. Четные и нечетные функции. Периодические функции. Наибольшее и наименьшее значение функции на промежутке
— (матем.) Функция у = f (x) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f (x) = f (x). Если же f (x) = f (x), то функция f (x) называется нечётной. Например, у = cosx, у = x2… …
F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Функция, удовлетворяющая равенству f (x) = f (x). См. Чётные и нечётные функции … Большая советская энциклопедия
F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
f(x) = x3 … Википедия
F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия
Специальные функции, введённые французским математиком Э. Матье (E. Mathieu) в 1868 при решении задач о колебании эллиптической мембраны. М. ф. применяются также при изучении распространения электромагнитных волн в эллиптическом цилиндре … Большая советская энциклопедия
Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция
определена на всей числовой оси. Найдем
производную
.
Найдем
производную
.
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т.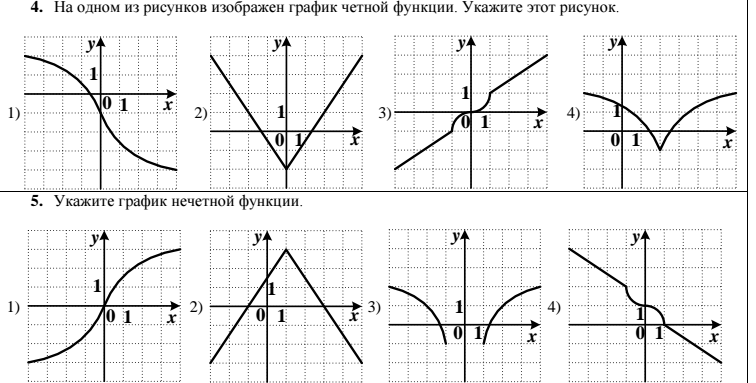
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. Для обозначения используют запись y=f(x). У каждой функции существует ряд основных свойств, таких как монотонность, четность, периодичность и другие.
Рассмотри подробнее свойство четности.
Функция y=f(x) называется четной, если она удовлетворяет следующим двум условиям:
2. Значение функции в точке х, принадлежащей области определения функции должно равняться значению функции в точке -х. То есть для любой точки х, из области определения функции должно выполняться следующее равенство f(x) = f(-x).
Определение 1. Функцияназываетсячетной (нечетной ),
если вместе с каждым значением переменной
значение –х также принадлежит
и выполняется равенство
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –х одновременно принадлежат
).
Например, функция
не является четной и нечетной, так как
ее область определения
не симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотя
и симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу , так как если
точка
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как если
График нечетной
функции симметричен относительно начала
координат, так как если
принадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или нечетности функции бывают полезны следующие утверждения.
Теорема 1. а) Сумма двух четных (нечетных) функций есть функция четная (нечетная).
б) Произведение двух четных (нечетных) функций есть функция четная.
в) Произведение четной и нечетной функций есть функция нечетная.
г) Если f – четная
функция на множествеХ , а функцияg определена на
множестве
,
то функция
–
четная.
д) Если f – нечетная
функция на множествеХ , а функцияg определена на
множестве
и четная (нечетная), то функция
–
четная (нечетная).
Доказательство . Докажем, например, б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функций
и
.
г) Пусть f – четная
функция. Тогда.
Тогда.
Остальные утверждения теоремы доказываются аналогично. Теорема доказана.
Теорема 2. Любую функцию
,
заданную на множествеХ , симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство . Функцию
можно записать в виде
.
Функция
– четная, так как
,
а функция
– нечетная, поскольку.
Таким образом,
,
где
–
четная, а
–
нечетная функции. Теорема доказана.
Определение 2. Функция
называетсяпериодической , если
существует число
,
такое, что при любом
числа
и
также
принадлежат области определения
и выполняются равенства
Такое число T называетсяпериодом функции
.
Из определения 1 следует, что если Т – период функции
,
то и число –Т тоже является
периодом функции
(так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
С помощью метода
математической индукции можно показать,
что еслиТ – период функцииf ,
то и
,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из положительных периодов функции называется ееосновным периодом.
Теорема 3. ЕслиТ – основной период функцииf , то остальные периоды кратны ему.
Доказательство . Предположим
противное, то есть что существует периодфункцииf (>0),
не кратныйТ . Тогда, разделивнаТ с остатком, получим
,
где
.
Поэтому
то есть
– период функцииf ,
причем
,
а это противоречит тому, чтоТ –
основной период функцииf .
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
Найдем период функции
.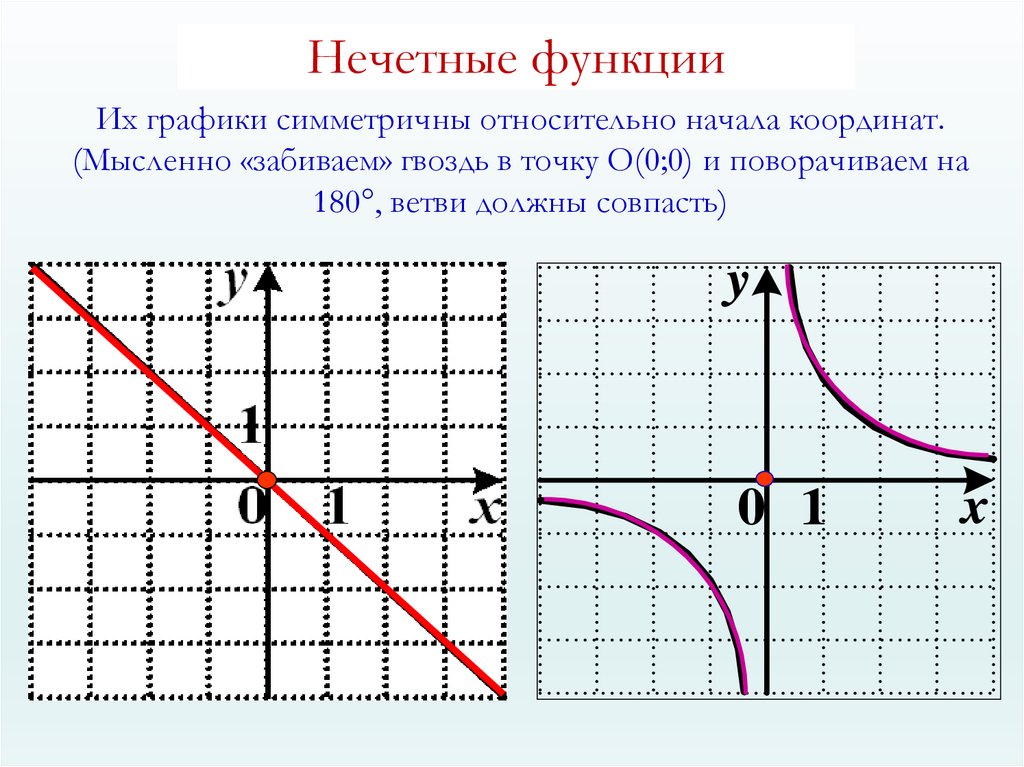 Пусть
Пусть
— период этой функции. Тогда
(так как
.
илиилиили
.
Значение T , определяемое
из первого равенства, не может быть
периодом, так как зависит отх , т.е.
является функцией отх , а не постоянным
числом. Период определяется из второго
равенства:
.
Периодов бесконечно много, при
наименьший
положительный период получается при
:
.
Это – основной период функции
.
Примером более сложной периодической функции является функция Дирихле
Заметим, что если T –
рациональное число, то
и
являются рациональными числами при
рациональномх и иррациональными
при иррациональномх . Поэтому
при любом рациональном числе T .
Следовательно, любое рациональное числоT является периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомn сколь угодно близким к нулю).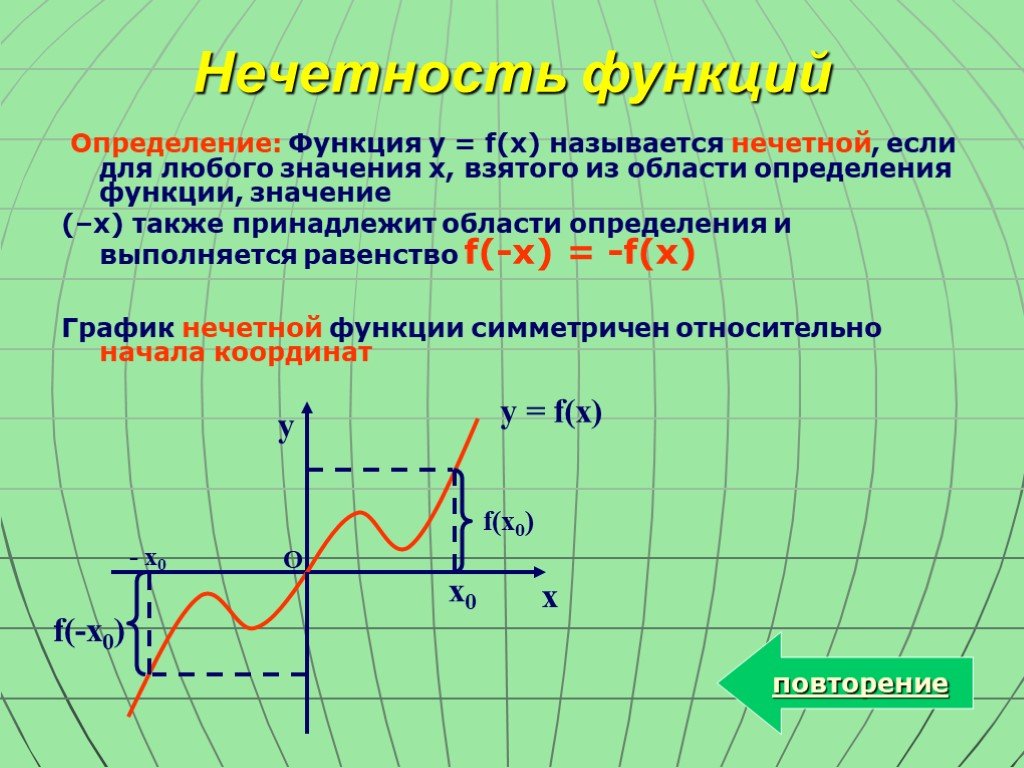 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
.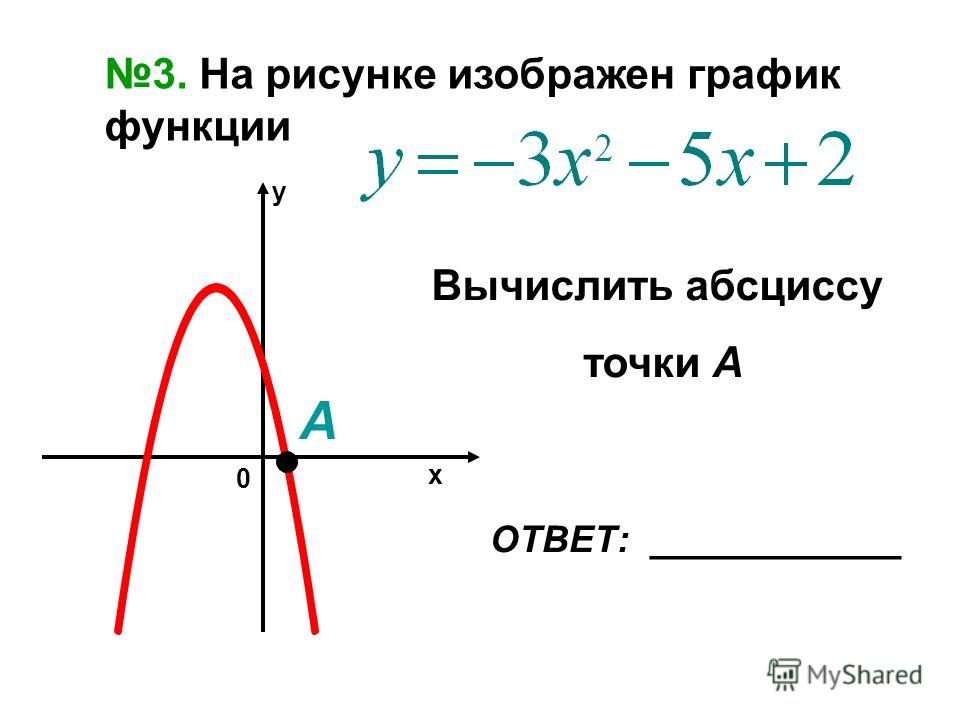 {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
— Нечетные и четные функции.
Задавать вопрос
спросил
Изменено 8 лет, 7 месяцев назад
Просмотрено 663 раза
$\begingroup$
У меня есть книга, в которой написано:
Если функция $f$ удовлетворяет условию $f(-x)=f(x)$ для всех $x$ в своей области определения, то $f$ называется четной функцией.
Однако, если $f(-x)=-f(x)$ для каждого $x$ в области определения $f$, то $f$ называется нечетной функцией.
А вот это непонятно. Потому что в нем не упоминается, что происходит, когда для конкретной функции $a$ находится в своей области, а $-a$ — нет. Неоднозначность возникает в такой функции, как $f:\{-5,-1,0,1,6\} \to \{-6,0,1,5\}$, заданной $f(-5)=5 , f(-1)=f(1)=1, f(0)=0$ и $f(6)=-6.$ Мы не можем решить, к какой из следующих категорий относится функция $f$:
1. И нечетные, и четные,
2. Нечетные,
3. Четные и
4. Ни нечетные, ни четные.
[Это потому, что я предположил, что никому не нужна пятая категория вроде «не могу решить».]
Может ли кто-нибудь для этого сформулировать формальные недвусмысленные определения нечетных и четных функций? А также, что касается такой проблемы, может ли кто-нибудь сказать мне, существует ли какая-либо международная организация по математике (например, ИЮПАК существует для химии), которая решает, какие определения и соглашения принять, и если она существует, как я могу найти эти правила? ?
Я знаю, что такой вопрос может показаться глупым, но у меня есть набор вопросов для собеседований, в котором есть следующий вопрос:
«Приведите пример функции, которая одновременно является и нечетной, и четной. Ваш выбор уникален?» — Ответ на вторую часть вопроса зависит от точного определения нечетных и четных функций.
Ваш выбор уникален?» — Ответ на вторую часть вопроса зависит от точного определения нечетных и четных функций.
- функции
- ссылка-запрос
- определение
$\endgroup$
$\begingroup$
Определение функции нечетных и четных требует, чтобы область определения $D_f$ функции $f$ была такой, что $\forall x\in D_f\left(-x\in D_f\right)$. Когда $D_f$ удовлетворяет этому свойству, то $f$ называется нечетным , если $\forall x\in D_f(f(-x)=-f(x))$, и четным, если $ \forall x\in D_f(f(-x)=f(x))$.
А также, что касается такой проблемы, может ли кто-нибудь сказать мне, существует ли какая-либо международная организация по математике (например, ИЮПАК существует для химии), которая решает, какие определения и соглашения принять, и если она существует, как я могу найти эти правила?
Я не думаю, что такое существует, но есть какие-то универсальные неписаные условности.
Связанные: 1, 2.
$\endgroup$
17
$\begingroup$
Определение совершенно ясное. Если -x не находится в домене, то очевидно, что f(x) = f(-x) неверно.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Четные и нечетные функции — A Plus Topper
by Prasanna
(1) Четная функция: Если поставить (–x) вместо x в заданной функции и если f(–x) = f(x), ∀ x ∈ domain, то функция f(x) называется четной функцией. например f(x) = e x + e -x , f(x) = x 2 , f(x) = x sin x, f(x) = cos x, f(x) = x 2 cos x все четные функции.
Примеры:
- f(x) = x 2 + 1
- f(x) = cos x
(2) Нечетная функция: Если поставить (–x) вместо x в заданной функции и если f(–x) = –f(x), ∀ x ∈ domain, то f(x) называется странная функция. например f(x) = e x – e -x , f(x) = x 3 , f(x) = sin x, f(x) = x cos x, f(x) = x 2 sin x все нечетные функции.
например f(x) = e x – e -x , f(x) = x 3 , f(x) = sin x, f(x) = x cos x, f(x) = x 2 sin x все нечетные функции.
Примеры:
- f(x) = x 3 – x
- f(x) = sin x
Свойства четной и нечетной функции
- График четной функции всегда симметричен относительно оси Y. График нечетной функции всегда симметричен относительно начала координат.
- Произведение двух четных функций является четной функцией.
- Сумма и разность двух четных функций является четной функцией.
- Сумма и разность двух нечетных функций является нечетной функцией.
- Произведение двух нечетных функций является четной функцией.
- Произведение четной и нечетной функций является нечетной функцией. Не обязательно, чтобы каждая функция была четной или нечетной. Некоторые функции могут быть ни четными, ни нечетными. например f (х) = х 2 + x 3 , f(x) = log e x, f(x) = e x .

- Сумма четной и нечетной функций не является ни четной, ни нечетной функцией.
- Нулевая функция f(x) = 0 — единственная функция, которая одновременно является четной и нечетной.
Периодическая функция
Функция называется периодической, если каждое ее значение повторяется через определенный интервал. Таким образом, функция f(x) будет периодической, если существует положительное действительное число T такое, что f(x + T) = f(x), ∀ x ∈ domain. Здесь наименьшее положительное значение T называется периодом функции.
Ясно, что f(x) = f(x + T) = f(x + 2T) = f(x + 3T) = …… e . г ., sin x, cos x, tan x — периодические функции с периодом 2π, 2π и π соответственно.
Некоторые стандартные результаты о периодических функциях
Составная функция
Если f : A ⟶ B и g : B ⟶ C – две функции, то составная функция f и g, gof A ⟶ C, будет определена как gof(x) = g[f(x)], ∀ x ∈ A.
Свойства композиции функции:
- f четный, g четный ⇒ функция тумана четный.
- f нечетно, g нечетно ⇒ туман – нечетная функция.
- f – четное, g – нечетное ⇒ туман – четная функция.
- f — нечетное, g — четное ⇒ туман — четная функция.
- Композиция функций не является коммутативной, т. е. туман ≠ gof.
- Композиция функций ассоциативна, т. е. (туман) oh = fo (goh)
- Если f : A ⟶ B — биекция, а g : B ⟶ A — обратная f. Тогда туман = I B и gof = I A , где I A и I B — тождественные функции на множествах A и B соответственно.
- Если f : A ⟶ B и g : B ⟶ C две биекции, то gof A ⟶ C биекция и (gof) -1 = (f -1 og -1 ).
- туман ≠ гоф, но если туман = гоф, то либо f -1 = g, либо g -1 = f также, (туман)(x) = (gof)(x) = (x).
- gof(x) — это просто g-образ f(x), где f(x) — f-образ элементов x ∈ A.


 1 Нечётные функции
1 Нечётные функции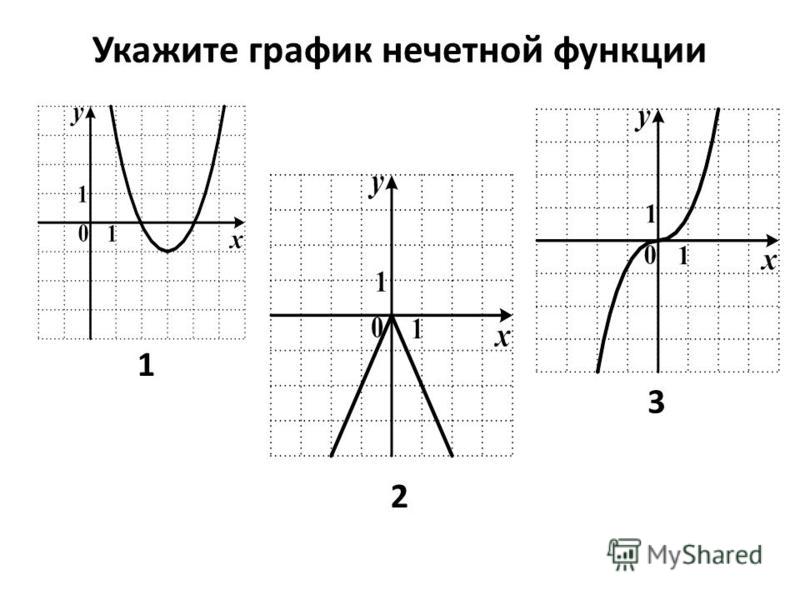
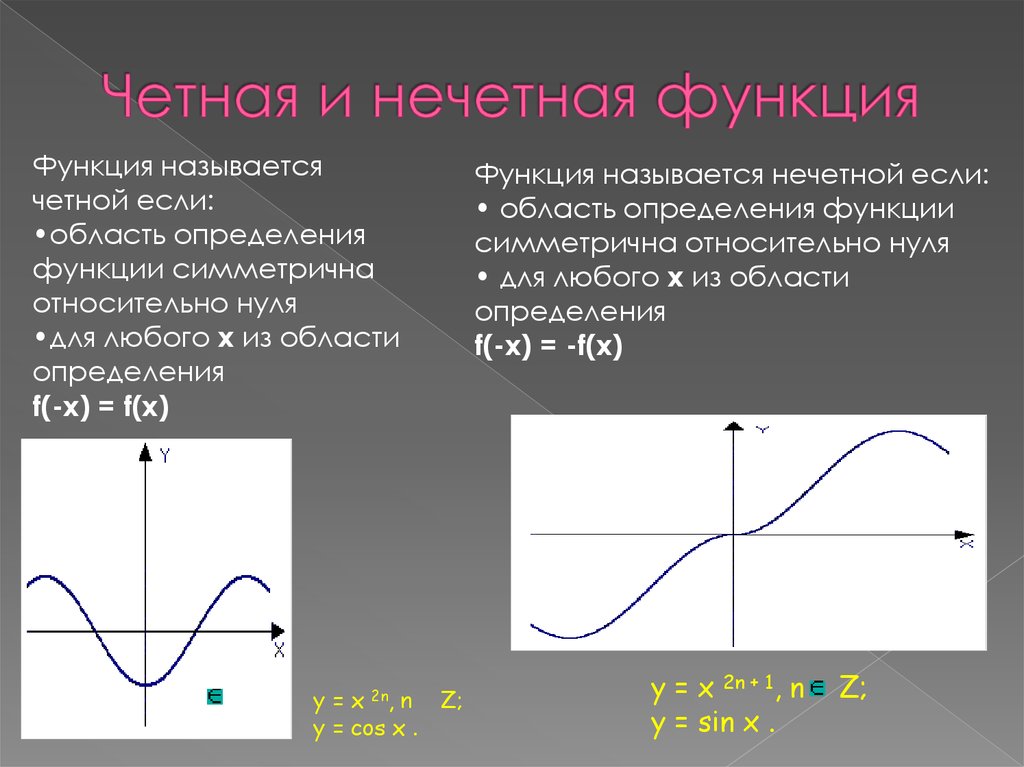 Однако, если $f(-x)=-f(x)$ для каждого $x$ в области определения $f$, то $f$ называется нечетной функцией.
Однако, если $f(-x)=-f(x)$ для каждого $x$ в области определения $f$, то $f$ называется нечетной функцией. 
