Cложение ⭐ и умножение числовых неравенств: правила, свойства, примеры
Что означает сложение и умножение числовых неравенств
Определение 1Числовым неравенством в математике называют выражение, которое содержит пару сторон, разделенных каким-то из знаков неравенства: ≠,< , ≤, ≥, >.
Заметим, что в числовом неравенстве каждая его часть представляет собой число или числовое выражение.
Пример 1Примеры записи числовых неравенств:
1 <5,3;
21,5>(10-4,9);
3≠81,5;
17-32>1.
Определение 2Неравенство с одной переменной в математике представляет собой такое выражение, в состав которого включены две части, разделенные знаком неравенства, к примеру, ≠,<,≤,≥,>.
Слева или справа в неравенстве с одной переменной находится алгебраическое выражение, содержащее одну переменную.
Пример 2Примеры записи неравенств с одной переменной:
x2+4≤x-1;
5x+2>0;
1×2+1≤1+x.
Такие понятия, как «больше», «меньше» в случае пары неких выражений а и b связаны с отношением разности данных выражений и нуля:
a>b⇔a-b>0
a <b⇔a-b<0
a=b⇔a-b=0
Определение 3Неравенствами одного знака, или неравенствами одного смысла, являются такие выражения в математике, которые соединены идентичными знаками неравенства.
Приведем пример неравенств одного знака:
x + 5 > y
25 > y — 2
Определение 4Неравенствами противоположных знаков, или неравенствами противоположных смыслов, являются такие выражения в математике, которые соединены неодинаковыми знаками неравенств.
Пример 4Пример неравенств противоположных знаков:
x + 5 < y
25 > y — 2
Запишем несколько ключевых свойство неравенств:
- Антирефлексивность для строгого неравенства, рефлексивность для нестрогого неравенства выражаются в следующем виде: a>a, a< a в случае ложных неравенств; a≥a, a≤a в случае истинных неравенств.
- Антисимметричность можно записать таким образом: a>b⇔b<a;a≥b⇔b≤a .
- Транзитивность: a>bb>c⇒a>c,a<bb<c⇒a<;a≥bb≥c⇒a≥c,a≤bb≤c⇒a≤c.
Рассматривая неравенства с точки зрения ключевых действий в математике, можно записать следующие свойства, которыми они обладают:
- При выполнении сложения знак не меняется: a<⇒a+c<+c.
 Аналогичным образом для: ≤,≥,>.
Аналогичным образом для: ≤,≥,>. - При выполнении вычитания знак не меняется: a<⇒a-c<-c. Аналогичным образом для: ≤,≥,>.
- При выполнении умножения на число со знаком плюс знак неравенства не меняется: a<bk>0⇒ka<b. Аналогичным образом для: ≤,≥,>.
- При выполнении умножения на число, меньше нуля, знак неравенства меняется: a<bk<0⇒ka>kb. Аналогичным образом для: ≤,≥,>.
- При выполнении деления на число со знаком плюс знак неравенства не меняется: a<bk<0⇒ak<bk. Аналогичным образом для: ≤,≥,>.
- При выполнении умножения на число, меньше нуля, знак неравенства меняется: a<bk<0⇒ak>bk. Аналогичным образом для: ≤,≥,>.
- Знак меняется в случае чисел, которые являются обратными для заданных положительных чисел: a<ba>0,b>0⇒1a>1b. Аналогичным образом для: ≤,≥,>.
Существует несколько полезных правил, которые целесообразно использовать, чтобы значительно упростить решение заданий на уроках и самостоятельных работ по алгебре в восьмом классе на сложение и умножение неравенств:
- Складывать какое-либо конечное количество неравенств, обладающих одинаковым знаком, нужно с сохранением данного знака: a<bc<d⋯k<m⇒a+c+⋯+k<b+d+⋯+m.
 Аналогичным образом для: ≤,≥,>.
Аналогичным образом для: ≤,≥,>. - Умножать какое-либо конечное количество неравенств, которые имеют одинаковый знак и состоят из положительных чисел, следует с сохранением данного знака: a<bc<d⋯k<ma,b,…,m>0⇒a·c·…·k<b·d·…·m. Аналогичным образом для:≤,≥,>.
- Возвести в натуральную степень обе части неравенства, которые являются положительными, можно с сохранением данного знака: a<ba,b>d⇒an<n,n∈ℕ. Аналогичным образом для: ≤,≥,>.
Правило и свойство сложения числовых неравенств
Теорема 1В том случае, когда а < b и с < d, получим, что а + с < b + d.
Рассмотрим некое числовое неравенство в виде:
а < b
Попробуем сложить записанное неравенство с каким-то числом с. Для этого прибавим это число к левой и правой частям неравенства. Получим:
а + с < b + с
Запишем следующее неравенство:
с < d
Суммируем обе его части с неким числом b. В результате получим:
b + с < b + d
Проанализируем полученные неравенства со слагаемым:
а + с < b + с
b + с < b + d
Заметим, что из этого следует:
а + с < b + d
Таким образом, можно сформулировать объяснение свойства сложения неравенств: результатом почленного сложения верных неравенств, которые имеют знаки в одну сторону, является верное неравенство.
Неравенства с одинаковым знаком допустимо складывать почленно, чтобы получить в итоге неравенство с аналогичным знаком.
Источник: izamorfix.ru
Пример 5В качестве примера попробуем выполнить почленное сложение двух верных неравенств:
7 < 10
1 < 2
Перепишем выражения в столбик и запишем ответ, согласно правилу сложения неравенств, которые имеют одинаковые знаки:
Источник: izamorfix.ru
Правила и свойства умножения числовых неравенств
Теорема 2В том случае, когда а < b и с < d, при этом а, b, с и d являются положительными числами, получим, что ас < bd.
Пусть дано некое неравенство:
а < b
Умножим записанное выражение на положительное число с. Получим в результате:
ас < bс
Представим, что имеется второе неравенство:
с < d
Выполним умножение данного неравенства на положительное число b. В таком случае, получим:
bс < bd
Запишем полученные в результате вычислений неравенства:
ас < bс
bс < bd
Заметим, что:
ас < bd.
Результатом почленного умножения неравенств, которые имеют одинаковый знак и положительные члены, является неравенство с аналогичным знаком.
Источник: izamorfix.ru
Рассмотрим в качестве примера пару неравенств:
4 > 2
5 > 3
Воспользуемся правилом и выполним их умножение:
4>2× 5>3 20>6
Свойство и правило почленного умножения применимы для любого количества неравенств данного типа.
Рассмотрим следующие неравенства:
ас < bс
bс < bd
В том случае, когда какое-либо число из перечисленных в этих неравенствах меньше нуля, следующее неравенство может быть неверным:
ас < bd
СледствиеВ том случае, когда числа а и b являются положительными, а также а < b, получим, что аn<bn при n из множества натуральных чисел.
В действительности, если выполнить полученное умножение n неравенств а < b, которые являются верными, при а и b в виде положительных чисел, то в результате получится верное неравенство, записанное в виде:
аn<bn
Примеры решения заданий с пояснениями
Задача 1Даны следующие числа:
-114;
-1,3; 0,(9);
115;
0,9.
Эти числа нужно записать по возрастанию.
Решение:
Заметим, что данные числовые выражения и числа можно сравнить между собой. Тогда получим верное числовое неравенство:
-1,3<-114<0,9<0,(9)<t115
Ответ: -1,3<-114<0,9<0,(9)<115
Задача 2Даны следующие числа:
0,5;
-23;
-12;
113;
1,33.
Требуется сравнить эти числа между собой.
Решение:
Заметим, что данные числовые выражения и числа можно сравнить между собой. Тогда получим верное числовое неравенство:
-23<-12<0,5<1,33<113
Ответ: -23<-12<0,5<1,33<113
Задача 3Дано некое число а. Нужно определить, является число а положительным или отрицательным при условии, что:
a+2<b+2b<-1
Решение:
Рассмотрим выражение:
a+2<b+2b<-1
Заметим, что при вычитании 2 из обеих частей неравенства, выполняется свойство, при котором в результате получится верное неравенство. Выполним преобразования:
a+2<b+2⇒a<b
Воспользуемся свойством транзитивности:
a<b<-1⇒a<-1
Заметим, что к полученному неравенству повторно можно применить свойство транзитивности:
a<b<-1⇒a<-1
Можно сделать вывод о том, что число а является отрицательным.
Ответ: а является отрицательным числом.
Задача 4Дано некое число а. Нужно определить, является число а положительным или отрицательным при условии, что:
5a>5bb>13
Решение:
Заметим, что при делении на 5 обеих частей неравенства, выполняется свойство, при котором в результате получится верное неравенство. Выполним преобразования:
5a>5b⇒a>b
Воспользуемся свойством транзитивности:
a>b>13⇒a>13
Заметим, что к полученному неравенству повторно можно применить свойство транзитивности:
a>13>0⇒a>0
Можно сделать вывод о том, что число а является положительным.
Ответ: а является положительным числом.
Задача 5Необходимо определить значение выражения 2x, если известно, что:
1<x<2.
Решение:
Воспользуемся свойством неравенств и выполним умножение обеих частей начального неравенства на 2:
2<2x<4
Ответ: 2<2x<4.
Задача 6Необходимо определить значение выражения 5-3x, если известно, что:
1<x<2.
Решение:
Воспользуемся свойством неравенств и выполним умножение обеих частей начального неравенства на -3.
-3>-3x>-6
Применим свойство неравенств второй раз и выполним сложение обеих частей полученного неравенства с числом 5.
5-3>5-3x>5-6
Произведем простые вычисления и развернем неравенство, получим:
2>5-3x>-1
-1<5-3x<2
Ответ: -1<5-3x<2.
Задача 7Требуется вычислить значение выражения1x, если известно, что:
2<x<3.
Решение:
Воспользуемся свойством неравенств и выполним преобразования:
12>1x>13
13<1x<12
Ответ: 13<1x<12
Задача 8Требуется вычислить значение выражения 1x, если известно, что:
14<x<0,5.
Решение
Воспользуемся свойством неравенств и выполним преобразования:
11/4>1x>10,5
2<1x<4
Ответ: 2<1x<4
Задача 9Имеется некий квадрат с периметром, значение которого соответствует следующему интервалу:
7,6см≤P≤8,4см
Необходимо оценить, какова площадь заданного квадрата.
Решение:
Выразим периметр квадрата через его сторону:
P = 4a
В результате модно оценить сторону этой геометрической фигуры:
7,6см≤4a≤8,4см|:4
1,9см≤a≤2,1см
Исходя из свойства неравенств, возведем во вторую степень обе его стороны. Так как части неравенства являются положительными, знак сохраняется без изменений. Выполним преобразования:
1,92см2≤a2≤2,12см2⇒3,61см2≤S≤4,41см2
Ответ: 3,61см2≤S≤4,41см2.
§1. Понятие равносильности уравнений и неравенств — ЗФТШ, МФТИ
Пусть на некоторых числовых множествах Х1, Х2Х_1,\;Х_2 заданы соответственно функции f(x), g(x)f(x),\;g(x) .
Решить неравенство (уравнение) – это значит найти все числа aa, после подстановки которых, вместо xx получается верное числовое неравенство (равенство), или доказать, что неравенство (уравнение) не имеет решений. Ясно, что число aa является решением только тогда, когдa aa принадлежит ОДЗ.
При решении неравенств и уравнений фундаментальное значение имеет понятие равносильности, и в нашем задании это будет играть большую роль.
Отсюда следует, что вместо того, чтобы решать данное неравенство (уравнение), можно решать любое другое, равносильное данному. Замену одного неравенства (уравнения) другим, равносильным данному на XX, называют равносильным переходом на XX. Равносильный переход обозначают двойной стрелкой ⇔\Leftrightarrow.
Важно понимать, что для доказательства неравносильности двух неравенств (уравнений) нет необходимости решать каждое из неравенств (уравнений), а затем убеждаться в том, что множества их решений не совпадают – достаточно указать одно решение одного из неравенств (уравнений), которое не является решением другого неравенства (уравнения).
Приведём несколько примеров операций, приводящих к равносильным уравнениям или неравенствам.
1. Если функции f(x),g(x),h(x)f(x),g(x),h(x) определены на множестве XX, то на XX
а) f(x)≤g(x)⇔f(x)+h(x)≤g(x)+h(x)f(x)\leq g(x)\Leftrightarrow f(x)+h(x)\leq g(x)+h(x).
б) f(x)=g(x)⇔f(x)+h(x)=g(x)+h(x)f(x)=g(x)\Leftrightarrow f(x)+h(x)=g(x)+h(x). {2n+1}(x).
{2n+1}(x).
Неравенства абсолютного значения
Выражения абсолютного значения не обязательно должны быть абсолютно равными; у них тоже могут быть неравенства. Эээ, неравенства. Однако все становится немного странно, когда у нас есть абсолютные значения и неравенства в одной комнате вместе.
Пример задачи
Решить | х | < 1.
Если бы это было уравнение, у нас было бы в сумке следующее: x = 1 или x = -1. Но подумайте о том, что на самом деле означает абсолютное значение. Это расстояние от 0 до числа. Если у нас есть | х | < 1, нам нужны все числа, расстояние которых от 0 меньше 1.
Да, это они. На числовой прямой мы видим, что x = -1 и x = 1 являются границами этого составного неравенства, -1 < x < 1. Иными словами, это x > -1 и . x < 1. Или, в-третьих, решения нашего неравенства находятся между ±1. Нужно ли нам выражаться четвертым способом? Надеюсь, что нет, потому что мы отключились.
Это шаблон, который повторяется для многих абсолютных значений неравенства. Если у нас есть |(некоторые вещи)| < какое-то число n , тогда наш ответ — n < (кое-что) < n . Затем мы находим нашу переменную. Не н , другой, внутри материала. Мы не показывали это здесь, но вы знаете, что это там.
Пример задачи
Решить |2 x + 3| ≤ 5.
Частичное равенство знаков ничего не меняет. Очень похоже на тот дешевый мотель, в котором мы останавливались во время нашего путешествия прошлым летом. Мы получаем нервы, просто вспоминая простыни в этом месте.
У нас есть какой-то знак «меньше», поэтому любые решения, которые мы можем найти, будут между -5 и 5.
-5 ≤ 2 x + 3 ≤ 5
Да, вот так. Теперь мы можем найти нашу переменную. Начнем с вычитания 3 из каждой секции.
-8 ≤ 2 x ≤ 2
Пришло время разделить коэффициент от переменной. Наши ладони начали потеть; Как насчет твоего? Они должны, так как мы делим знаки неравенства вокруг. Однако 2 положительный, так что у нас все хорошо. Вытирая руки полотенцем и делясь, мы получаем наши решения:
Однако 2 положительный, так что у нас все хорошо. Вытирая руки полотенцем и делясь, мы получаем наши решения:
-4 ≤ x ≤ 1
Все это хорошо, но что делать, когда абсолютное значение «больше» числа? Ответ не будет выглядеть так же, как в случае «меньше». Это не может быть просто, не так ли?
Пример задачи
Решить | х | ≥ 6.
Давайте снова подумаем об этом с точки зрения расстояния: мы хотим, чтобы все числа, которые имеют расстояние больше или равное 6 единицам от 0. Как только у нас будут все эти числа, мы поместим их в платья и устроить чаепитие.
Похоже, что наши решения могут быть меньше или равны -6 или больше или равны 6. Это еще одно сложное неравенство, но на этот раз оно соединено с помощью «или»:
x ≤ — 6 или x ≥ 6
Может показаться странным, что числа меньше -6 могут быть решением задачи, которая начинается со знака «больше чем», но подставьте число и проверьте его: |-7| ≥ 6? Ага, |-7| равно 7. И 7 определенно больше и страшнее, чем 6, потому что 7 8 9.
И 7 определенно больше и страшнее, чем 6, потому что 7 8 9.
Пример задачи
Решить |-2 x – 1| > 7.
Первым делом встаем и растягиваемся. Мы долго работали над этим неравенством, и это убивает нас. Сделав это, мы проверяем знак неравенства. Это знак «больше чем», поэтому мы знаем, что у нас будет составное неравенство «или». Одно из неравенств будет нашим исходным выражением, только без полос абсолютного значения.
-2 x – 1 > 7
-2 x > 8
x < -4
Вы это видели? Отрицательное деление — мы должны изменить все знаки. Все они, включая знак неравенства.
Другая половина раствора будет противоположна тому, что находится внутри стержней.
-(-2 x – 1) > 7
-2 x – 1 < -7
У нас есть еще отрицательное умножение. Переверни это неравенство, переверни его хорошенько.
-2 x < -6
x > 3
И тогда мы должны изменить его снова. Шиш, решайся уже. Вы хотите указать влево или вправо?
Шиш, решайся уже. Вы хотите указать влево или вправо?
Наше полное решение: x < -4 или x > 3. Мы немного нервничаем из-за нашего ответа; там было много вывесок, и мы слышали какие-то тревожные звуки, пока он был в другой комнате. Итак, давайте перепроверим.
Подстановка -5, что меньше -4:
|-2(-5) – 1| > 7
|10 – 1| > 7
|9| > 7
Подставляем 4, что больше 3:
|-2(4) – 1| > 7
|-8 – 1| > 7
|-9| > 7
Ладно, все круто. И оказывается, что эти звуки были просто его расстроенной скрипкой. Мы думали, что он пытается вызвать группу пауков. Мы были этот близки к вызову истребителя.
Резюме
Столкнулись с абсолютным неравенством и не знаете, что делать?
- Если неравенство имеет знак «меньше» (<) с выражением абсолютного значения слева, то решение представляет собой составное неравенство «и» между константой ±.
- — n < (что-то) < n
- Если неравенство имеет знак «больше» (>) с выражением абсолютного значения слева, то решение представляет собой составное неравенство «или» .

- Первая половина представляет собой исходное выражение с удаленными знаками абсолютного значения.
- (что-то) > n
- Вторая половина переворачивает знак неравенства и меняет все, что находится за пределами полос абсолютного значения, на противоположный знак.
- (что-то) < - n
- Первая половина представляет собой исходное выражение с удаленными знаками абсолютного значения.
- Если вы не можете вспомнить эти правила или просто не знаете, что делать, нарисуйте небольшую числовую линию. Глядя на это, вы не запутаетесь.
Быстрый вопрос: что произойдет, если мы попытаемся найти | х | < -1? Или | х | > -1? Происходит следующее: «Это ловушка!» Абсолютное значение всегда будет положительным, поэтому решения нет. Любое значение x будет больше любого отрицательного числа и никогда не может быть меньше отрицательного числа. Не поддавайтесь на это, или кальмары в скафандрах будут продолжать кричать на вас.
Алгебра: колебания настроения неравенства
Чтобы решить неравенство, содержащее только одну переменную, выполните те же действия, что и при решении уравнений.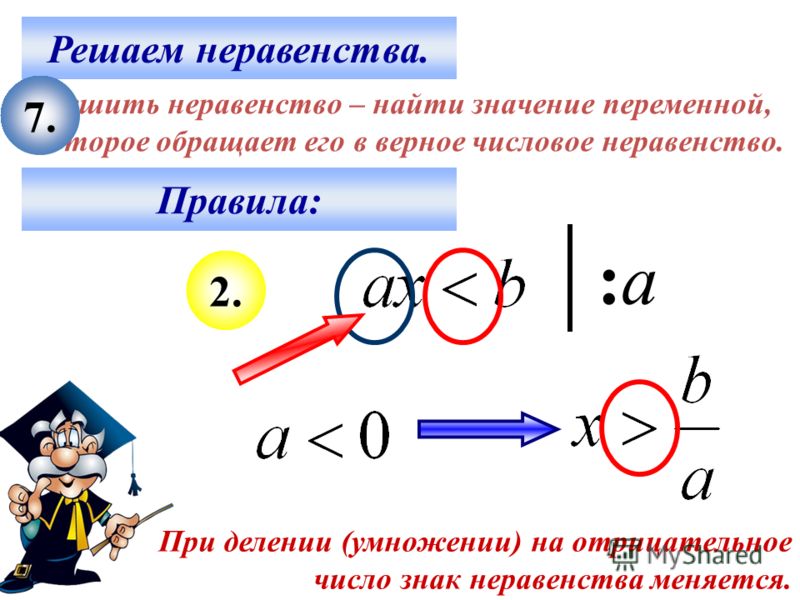 Другими словами, упростите обе части неравенства, изолируйте переменную, а затем исключите коэффициент переменной. Однако есть одно существенное различие между уравнениями и неравенствами: при решении неравенства, если вы когда-либо умножаете или делите обе части на отрицательное число, вы должны поменять знак неравенства.
Другими словами, упростите обе части неравенства, изолируйте переменную, а затем исключите коэффициент переменной. Однако есть одно существенное различие между уравнениями и неравенствами: при решении неравенства, если вы когда-либо умножаете или делите обе части на отрицательное число, вы должны поменять знак неравенства.
Что я имею в виду под «обратным» знаком неравенства? Замените знаки меньше на знаки больше и наоборот. (Меньше или равно знакам становится больше или равно знакам, и наоборот.) Я называю это перепадом настроения неравенства. Помните, это происходит только тогда, когда вы умножаете или делите на отрицательное число, и это происходит только тогда, когда вы пытаетесь исключить коэффициент. Итак, просто не забудьте проверить отрицательный коэффициент, когда вы его устраняете, и при необходимости измените знак неравенства.
Критическая точка
Когда вы решали уравнения, вам советовали делать то же самое с обеими сторонами знака равенства. Теперь выполните те же действия, но вместо этого сделайте все по обе стороны от знака неравенства.
Теперь выполните те же действия, но вместо этого сделайте все по обе стороны от знака неравенства.
Пример 2 : Решите неравенство -5 x + 3 > -32.
Решение : поскольку обе стороны уже упрощены (ни одна из сторон не содержит одинаковых терминов), изолируйте переменную, вычитая 3 с обеих сторон знака «больше». Обратите внимание, что знак неравенства еще не изменился, потому что вам еще не 9.0225 умножение или деление на отрицательное число.
- -5 x > -35
Пора убрать коэффициент. Сделайте это, разделив обе части на -5. Не забудьте поменять знак неравенства, так как вы делите на отрицательное число.
- х
У вас проблемы
Задача 2. Решите неравенство 2( w — 6) ¤ 18.
Итак, любое число меньше 7 при подключении на x , должно сделать это утверждение о неравенстве верным.

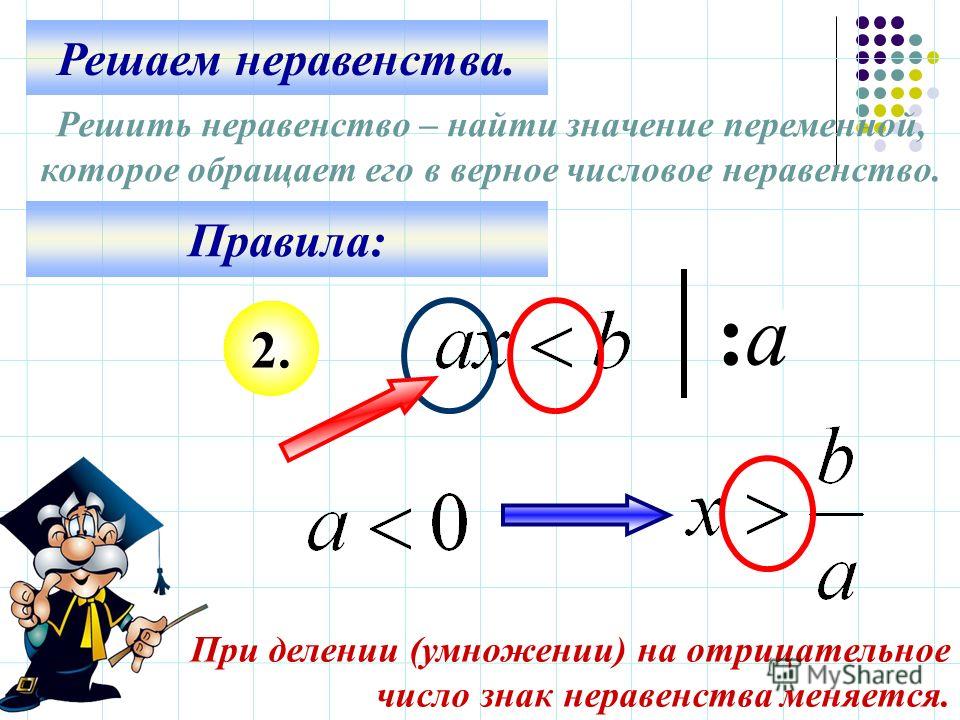 Аналогичным образом для: ≤,≥,>.
Аналогичным образом для: ≤,≥,>.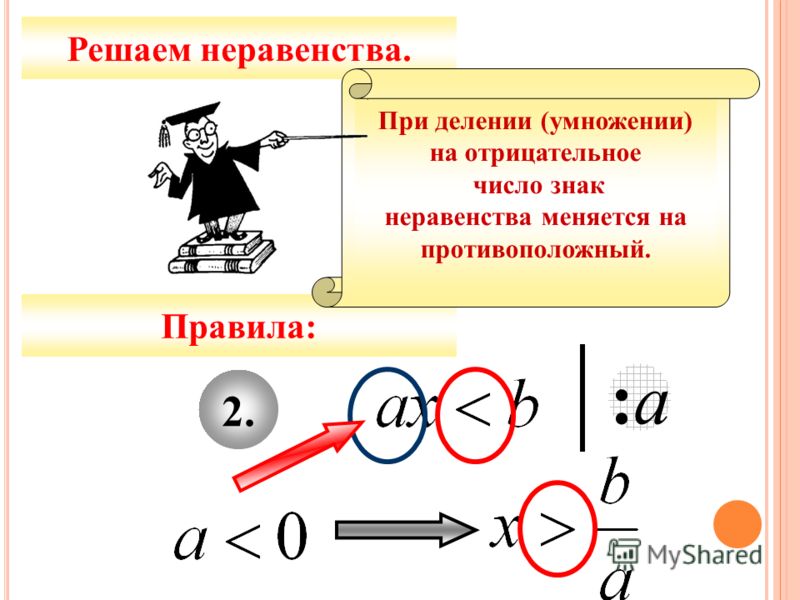 Аналогичным образом для: ≤,≥,>.
Аналогичным образом для: ≤,≥,>.