Нечетные числа от 1 до 15: Таблица нечётных чисел от 0 до 100

Цикл for

Назад в начало

Простой перебор

Цикл в любом языке программирования — это многократное выполнение одного и то же действия. Цикл for проходится по данной последо­ватель­ности элементов. Он состоит из двух компонент: переменной (переменных) цикла и итерируемой (перебираемой) последовательности. Приведу пример:

for i in ‘one’, ‘two’, ‘three’:
    print(i)
# one
# two
# three

Приведу еще несколько примеров:

for i in ‘1’, ‘hello’, 2, 1990, True, False:
    print(i)
for j in ‘orange’, ‘red’, ‘purple’:
    print(j)
for k in ‘first’, ‘last’:
    print(k)

Функция range()

Теперь пришло время познакомиться с встроенной в Python функцией range(). «range» переводится как «диапазон». Она может принимать один, два или три аргумента. Если задан только один, то генерируются числа от 0 до указанного числа, не включая его. Если заданы два, то числа генерируются от первого до второго, не включая его. Если заданы три, то третье число – это шаг. Рассмотрим случай с одним аргументом:

for number in range(5):
    print(number)
for number in 0, 1, 2, 3, 4:
    print(number)

Напечатаются числа от 0 до 4. Это связано с тем, что функция range с одним аргументом генерирует диапазон от 0 до n-1, где n — это переданный аргумент.

Передадим в функцию два аргумента: 5 и 10. В этом случае range cгенерирует последовательность чисел от 5 до 9.

for el in range(5,10,2):
    print(el)

Если передать в range три аргумента: 5, 10, 2, то мы получим последовательность от 5 до 10 с шагом в 2

for el in range(5,10):
    print(el)

Перебор строк и функция len()

С помошью цикла for мы можем перебрать любую последовательность, например, строку:

for letter in ‘hello’:
    print(letter)
for l in ‘python’:
    print(l)

Любая последовательность имеет длину, это означает, что мы можем ее посчитать

Примеры решения задач

1. Посчитать сумму чисел от 0 до number

number = int(input())
summa = 0
for i in range(number+1):
    # summa = summa + i
    summa += i
print(summa)

2. Посчитать сумму четных чисел от 0 до number

number = int(input())
summa = 0
for i in range(number+1):
    if i % 2 == 0:
        # summa = summa + i
        summa += i
print(summa)

3. Посчитать произведение чисел от 1 до number

number = int(input())
multi = 1
for i in range(1, number+1):
    multi *= i
print(multi)

Решение задач

1. Вывести числа от 0 до 10.

2. Вывести числа от 0 до n, где n — это случайное число или число, введенное с клавиатуры

3. Вывести нечетные числа в диапазона от 0 до n (диапазон — это последовательность чисел от 0 до n)

4. Вывести четные числа из диапазона от 0 до n.

5. Вывести числа, делящиеся на три без остатка, в диапазоне от 0 до n.

6. Вывести числа, делящиеся на три или на семь без остатка, в диапазоне от 0 до n.

7. Найти сумму всех чисел от 1 до n.

7. Найти сумму четных чисел от 1 до n.

8. Даны два целых числа a и b a

9. Найти сумму чисел от 1 до n, делящихся на 3 .

10. Дано целое число n. Найти сумму 1 + 1/2 + 1/3 + … + 1/n

11. Дано целое число n. Найти сумму 1 + 2 + 4 + 8 + 16 + … + 2**n
где 2**n — это 2*2*2*…*2 раз. Таким образом, 2**4 = 2*2*2*2. Операция ** называется операцией возведения в степень.

12. Дано целое число n. Найти сумму: 1.1 + 1.2 + 1.3 + … + (1 + 0.1*n)

13. Дано целое число n. Найти значение выражения 1.1 − 1.2 + 1.3 − … (N слагаемых, знаки чередуются).

14. Дано целое число n. Найти квадрат данного числа, используя для его вычисления следующую формулу: n**2 = 1 + 3 + 5 + … + (2*N − 1) После добавления к сумме каждого слагаемого выводить текущее значение суммы

15. Дано вещественное число A и целое число N (> 0). Найти A в степени N: A**N = A * A * … * A (числа A перемножаются N раз). Операцию ** не использовать.

16. По данному натуральному n ≤ 30 выведите лесенку из n ступенек, i-я ступенька состоит из чисел от 1 до i без пробелов. Посмотрите статью про ввод и вывод данных.

17. Дано целое число n. Найти сумму 1**1 + 2**2 + … + n**n.

18. Даны целые положительные числа A и B (A

Четные и нечетные числа | План-конспект урока по математике (2 класс) по теме:

План урока математики

во 2 «А» классе МОУ «СОШ № 51»

г. Саратова

учитель Кузьмина М.В.

Четные и нечетные числа

(Урок введения нового знания)

Основные цели:

1. Познакомиться с понятиями четности-нечетности

(учить видеть, что:

1. сумма двух четных чисел – четное число;
2. сумма двух нечетных чисел – четное число;
3. сумма четного и нечетного чисел – нечетное число).

2. Продолжить работу с простыми задачами на умножение, основываясь на знании смысла действия умножения и таблицы умножения числа 2.
3. Решать простые задачи на деление, основываясь на знании взаимосвязи умножения и деления.
4. Продолжать учить таблицу умножения числа 2 и соответствующих ей случаев деления.
5. Развивать умение решать комбинаторные задачи на перестановку.
6. Развивать интеллектуальные и коммуникативные общеучебные умения.
7. Развивать организационные общеучебные умения, в том числе самостоятельно  оценивать  результаты  своих  действий, самого себя, находить и исправлять собственные ошибки.

Ход урока

I. Актуализация знаний

1. Организационный момент

Повторение таблицы умножения числа 2 и соответствующих ей случаев деления.

2. Индивидуальная работа (4 ученика получают карточки с заданиями)

1 карточка

Какое число пропущено?

7 + 8 = 15

6 + 8 = 14

9 + 4 = 13

2 + 10 = 12

Найди и исправь ошибки

18 – 9 = 7 (9)

9 + 6 = 15

13 – 6 = 8 (7)

7 + 6 = 13

15 – 8 = 9 (7)

16 – 9 = 7

5 + 7 = 12

11 – 2 = 8 (9)

3 карточка

Между некоторыми числами поставь знаки действий: «+» «-» или «*», чтобы выполнялись равенства:

2   4   6   8 = 4

2   4   6   8 = 6

2   4   6   8 = 8

2   4   6   8 = 10

4 карточка

Составь выражение и посчитай:

1. сколько лапок у 3 гусят? 2*3 = 6
2. сколько лапок у 2 котят? 4*2 = 8
3. сколько крыльев у 4 кутят? 2*4 = 8

3. Фронтальная работа

а) соревнования по группам

«Кто первый решит?»

18 : 9 = 2                 4 – 2 = 8                     5 – 2 = 10

8 : 2 = 4                       12 : 2 = 6                    10 : 5 = 2

2 – 3 = 6               2 – 2 = 4                      6 – 2 = 12

16 : 2 = 8              14 : 7 = 2                     16 : 8 = 2

6 : 2 = 3                       18 : 2 = 9                     2 – 8 = 16

10 : 2 = 5              14 : 2 = 7                     9 – 2 = 18

Что можно сказать об ответах, которые получились в 1, 2, 3 столбиках? Что это за числа?

б) составьте слова, найдите лишнее:

ПОКТА                 ЧАТРЕПКА

СОКОН                     ПКАША

РЕЖВАКА             ФРША

Какие из этих предметов используются только по два? Верно ли выполнено задание? Какой вопрос был самым трудным? Самым легким? Какую оценку заслужили?

II. «Открытие» нового знания

Работа с учебником

1. Задание 1 (стр. 66)

Как разложить варежки по 2 (парами)?

Проанализировать вместе с детьми задание и рисунок. Сделать вывод, как должны производить деление: варежки разложить парами в соответствии с их цветами, при этом варежка останется без пары.

Варежки разложить в классе не можем, заменим их кругами.

Практическая работа

Возьми 7 кружков и разложи их по 2.

Дети раскладывают на партах 7 кружков по 2. Делают вывод: 7 по 2 не делится, один кружок остается.

2. Задание 2 (стр. 66)

а) по два 6 красных кружков, 9 синих кружков, 10 зеленых кружков;

б) на две равные части 3 красных кружка, 4 синих кружка, 5 зеленых кружков.

Практическая работа

Дети самостоятельно на партах раскладывают кружки, а два человека работают у доски. После того, как задание выполнено, они объясняют, как делили кружки «по 2» и «на 2 равные части». Делают вывод. Остальные ребята оценивают выполненное задание, выставляют оценку.

а) дети раскладывают красные, синие, зеленые кружки по 2;

б) дети раскладывают красные, синие, зеленые кружки на 2 равные части.

3. Работа с текстом учебника со знаком вопроса:

1. какие кружки удалось разложить парами?
2. какие не удалось?
3. почему?

Дети отвечают на вопросы, делают вывод, записывают на доске числа, которые можно (нельзя) разделить по два

6, 4, 10                 9, 3, 5, 7

Как называются эти числа? (ответы детей)

4. Работа с текстом учебника с восклицательным знаком:

Вывод:         Числа 4, 6, 10 делятся на 2. Они называются четными.

Числа 3, 5, 7, 9 не делятся на 2. Они называются нечетными.

5. Задание 3 (стр. 66).

Прочитайте сначала четные, потом нечетные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.

(дети читают по очереди).

6. Работа с текстом учебника со знаком вопроса:

Что ты заметил?

7. Работа с текстом учебника с восклицательным знаком:

Вывод: Четные и нечетные числа в числовом ряду чередуются.

8. Выполнение задания 4.

Выполни действия:

а) умножь на 2 все четные числа в числовом ряду от 1 до 10. Расскажи, какие получились числа – четные или нечетные?

б) умножь на 2 все нечетные числа в этом же ряду. Расскажи, какие получились числа – четные или нечетные?

Дети записывают в тетрадь

а)         2         4         6         8         10

4         8         12         16         20

б)         1         3         5         7         9

2         6         10         14         18

Делают вывод: записанные числа четные и нечетные.

9. Работа с текстом учебника с восклицательным знаком:

Какое число, четное или нечетное получается при умножении любого числа на 2?

Вывод: При умножении любого числа на 2 получается четное число.

III. Формулирование темы и целей урока

Как вы думаете, для чего нам может пригодиться то, что мы сейчас узнали? Чем мы сегодня будем заниматься?

(ответы детей)

Сейчас узнаем тему:

«Четные и нечетные числа» (запись на доске)

Физминутка

Мы устали, засиделись

Мы устали, засиделись,

Нам размяться захотелось.

Отложили мы тетрадки,

Приступили мы к зарядке

(Одна рука вверх, другая вниз, рывками менять руки.)

То на стену посмотрели,

То в окошко поглядели.

Вправо, влево поворот.

(Повороты корпусом.)

А потом наоборот.

Приседанья начинаем,

Ноги до конца сгибаем.

Вверх и вниз, вверх и вниз,

Приседать не торопись!

(Приседанья.)

И в последний раз присели,

А теперь за парты сели.

(Дети садятся за парты.)

IV. Первичное закрепление

(использование нового знания при решении задач)

Задание 5 (а) стр. 67.

Сделайте рисунок и решите задачу.

Восемь  ребят  разделились  в  группы  по  2  человека.  Сколько  групп получилось.

Практическая работа

Просчитайте и объясните задание. Как будем его выполнять?

 (ответы детей, составление плана действий, выполнение задания в тетрадях, на доске)

Какую оценку заслужили?

V. Самостоятельная работа в парах

Задание 5 (б) стр. 67

Восемь ребят разделились на 2 группы поровну. Сколько человек в одной группе?

Можно ли по нашему плану выполнить это задание? Почему? В чем отличие?

(дети самостоятельно работают по плану:

1. разъясняют друг другу задание;
2. записывают решение;
3. взаимопроверка;
4. презентация результата одним учеником из пары)

Верно выполнено задание? Чем отличаются решения этих задач? Сравни их решения.

Какую оценку заслужили?(пара получает оценку  за правильность  работы, за точность формулировок).

Придумайте и решите похожие задачи.

(заслушивается несколько вариантов подобных задач).

VI. Систематизация и повторение

1. Работа в парах (по вариантам)

1 в – № 6 (1, 2 столбик)

2 в – № 6 (3, 4 столбик)

Вставь вместо «*» знаки «·» или «:».

8 * 2 = 4           2 * 5 = 10

6 * 2 = 12          4 * 2 = 2

7 * 2 = 14         18 * 9 = 2

16 * 8 = 2         3 * 2 = 6

Выполняется самостоятельно с последующей взаимопроверкой и обсуждением. Правильность полученных результатов обсуждается классом.

Физминутка

Рисуй треугольник

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

Ты по периметру веди.

Рисуй восьмерку.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы наконец.

Зарядка окончилась.

Ты молодец!

(Дети представляют внешний вид геометрических фигур)

2. Фронтальная работа, на перестановку четырех элементов.

№ 9 (стр. 67)

Сколько различных четных и двузначных чисел можно написать с помощью цифр 1, 3, 2, 0, если:

а) цифры в числе могут повторяться;

б) цифры в числе не повторяются.

Последовательность работы:

а) на доске записаны цифры 1, 3, 2, 0

Детям предлагается назвать все возможные способы получения двухзначных чисел, когда цифры в числе повторяются, отобрать из них только четные. Получается, что возможен только один вариант – 22.

б) устанавливается закономерность, по которой записываются двузначные числа, когда цифры в числе не повторяются (фиксируется первая цифра, а вторые меняются), при этом двузначные числа должны быть четными. Из всех возможных вариантов выбираются следующие числа: 10, 12, 20, 30, 32.

VII. Итоги урока

Чем занимались на уроке?

Какое задание понравилось больше всего?

Какое задание захотелось выполнить еще раз?

Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»

1. какое число получится, если

а)         сложить два четных числа;

три четных числа;

два нечетных числа;

три нечетных числа.

б)         из четного вычесть четное;

из нечетного вычесть четное;

из нечетного вычесть нечетное.

Обоснуйте свои ответы

(после каждого ответа на доске выставляются карточки с буквами Ч – четное, Н – нечетное)

ч        ч        ч        н        ч        н        ч

А теперь получите оценку за урок.

(карточки переворачиваются, там слово МОЛОДЦЫ)

VIII. Предполагаемая домашняя работа

(включая вариант и инвариант)

Задание 7, 8.

Нечетные числа — Math28

Содержание

Что такое нечетные числа?

Нечетные числа – это те числа, которые не кратны 2, следовательно, нечетное число не делится на 2. Нечетное число не может иметь десятичных знаков.

Другой вариант проверки нечетности числа — это когда последняя цифра заканчивается на 1, 3, 5, 7 или 9.

Математически можно получить нечетное число, используя следующее уравнение:

Нечетное число = 2n + 1

Где n — любое целое число.

Нечетные числа образуют арифметическую прогрессию с разницей в 2, это означает, что добавление или вычитание 2 из нечетного числа дает еще одно нечетное число.

Примечание : Отрицательные числа также могут быть нечетными.

---

Операции с нечетными числами

Сложение и вычитание для получения нечетного числа

При сложении или вычитании четного числа с нечетным числом в результате получается нечетное число.

четное число + нечетное число = нечетное число
нечетное число + четное число = нечетное число

Узнайте больше о: « Сумма ». →

Узнайте больше о: « Вычитание ». →

Умножение для получения нечетного числа

При умножении нечетного числа на нечетное число получается нечетное число.

нечетное число х нечетное число = нечетное число

Узнайте больше о: « Умножение ». →

---

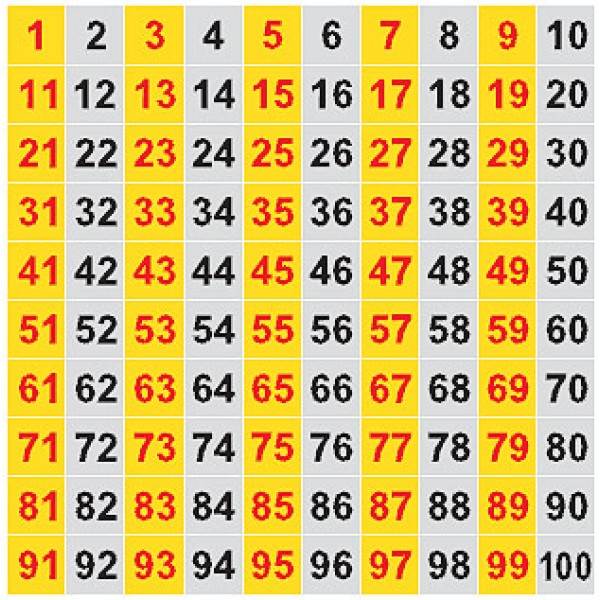
Нечетные числа от 1 до 100

В таблице синим фоном показаны нечетные числа.

1	2	3	4	5	6	7	8	9	10
11	12	13	14	15	16	17	18	19	20
21	22	23	24	25	26	27	28	29	30
31	32	33	34	35	36	37	38	39	40
41	42	43	44	45	46	47	48	49	50
51	52	53	54	55	56	57	58	59	60
61	62	63	64	65	66	67	68	69	70
71	72	73	74	75	76	77	78	79	80
81	82	83	84	85	86	87	88	89	90
91	92	93	94	95	96	97	98	99	100

Нечетные числа от 1 до 100: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41. , 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91 , 93, 95, 97 и 99.

Из таблицы видно, что у каждого нечетного числа последней цифрой является число 1, 3, 5, 7 или 9, а каждое число с белым фоном соответствует четным числам.

Узнайте больше о: « Четные числа ». →

Нечетные номера Список от 1 до 100

Содержание

Нечетные номера

Номера, которые не могут быть соединены вместе, называются нечетными. Другими словами, все числа нечетны, за исключением кратных двум. В этом эссе давайте больше узнаем о нечетных числах.

Что такое нечетные числа?

Нечетное число — это число, которое нельзя разделить на две равные части. Или, другими словами, нечетные числа — это положительные целые числа, которые нельзя разделить на наборы по два. Примеры включают 1, 3, 5, 7 и т. д. Давайте используем обувь и вишни в качестве примера, чтобы помочь нам визуализировать это. Предположим, что у нас есть туфли со следующими числами: 1, 3, 5 и 7. Наоборот, у нас есть вишни, которые идут парами по 2, 4, 6 и 8. Пары этих чисел можно понять, взглянув на рисунок. показано ниже.

Как проверить, нечетное ли число?

Чтобы проверить, является ли заданное число четным или нечетным, необходимо проверить число, данное на своем (или юнитовом) месте. Это конкретное число на своем месте скажет вам, является ли число нечетным или четным.

• Четные числа заканчиваются на 0, 2, 4, 6, 8
• Нечетные числа заканчиваются на 1, 3, 5, 7, 9

Это простые приемы, позволяющие определить четные числа или нет.

Подумайте о числах 42, 248 и 356, которые заканчиваются четным числом, т.е. 2, 8 и 6. Следовательно, данные числа 42, 248 и 356  являются четными числами. Таким образом, числа не являются нечетными числами. Точно так же 75 и 327 являются нечетными числами, поскольку они заканчиваются на 5 и 7.

Свойства нечетных чисел

Существуют три свойства четных чисел, которые обсуждаются в таблице ниже. ЭКСПЛУАТАЦИЯ ПРИМЕР Дополнительное имущество нечетное + нечетное = четное 5 + 5 = 10 Свойство вычитания нечетный – нечетный = четный 9 – 7 = 2 Свойство умножения нечетное x нечетное = нечетное

7 х 5 = 35

Свойство сложения

• Сложение обоих четных чисел даст результат четных чисел.
• При сложении четного и нечетного результат будет нечетным.
• Сложение обоих нечетных чисел даст результат четных чисел.

Свойство вычитания

• Вычитание четных чисел из четных чисел даст результат четных чисел.
• При вычитании нечетного из четного или четного из нечетного в результате будет нечетное.
• Вычитание нечетных чисел из нечетных даст результат нечетных чисел.

Свойство умножения

• Умножение четных и четных чисел даст результат четных чисел.
• При умножении нечетных и четных чисел результат будет четным.
• Умножение нечетных и нечетных чисел даст результат нечетных чисел.

Нечетные числа от 1 до 100

Ниже приведены нечетные числа от 1 до 100. 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99.

Таблица нечетных чисел от 1 до 100

Также предоставляется таблица нечетных чисел от 1 до 100, которую можно сохранить для дальнейшего использования

Типы нечетные числа

В основном существует два типа нечетных чисел

• Последовательные нечетные числа
• Составные нечетные числа

Давайте подробно обсудим вышеупомянутые типы нечетных чисел

Последовательные нечетные числа

Ниже приведены примеры последовательных нечетных чисел: 3, 5, 7, 9, 11 и т. д. Последовательные числа — это те, которые последовательно следуют друг за другом по порядку, от наименьшего к наибольшему. Например, все натуральные числа 1, 2, 3, 4 и так далее идут последовательно. Следовательно, мы можем перечислить все нечетные числа в порядке от наименьшего числа к наибольшему всякий раз, когда нам нужно перечислить последовательные нечетные числа. Например, нечетные числа 3, 5, 7, 9, 11 и так далее — все последовательные нечетные числа.

Составные нечетные числа

Составное нечетное число — это положительное нечетное целое число, которое можно умножить на одно или два меньших положительных числа. 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95 и 99 являются составными нечетными числами до 100.

Факты о нечетных числах

Эти факты о нечетных числах оживят ваши уроки математики:

• В числовой строке 1 — первое положительное нечетное число.
• Любое целое число, которое нельзя разделить на два, считается нечетным.
• Результат деления нечетного целого числа на два всегда равен единице.
• Четным числам соответствуют цифры 0, 2, 4, 6 или 8, а нечетным — цифры 1, 3, 5, 7 или 9.

Список нечетных чисел

От 1 до 50 25 нечетных чисел, а от 1 до 100 50. В диапазоне от 1 до 1000 500 нечетных чисел и 500 четных чисел.

Диапазон номеров	Количество нечетных номеров
от 1 до 50	25
от 1 до 100	50
от 1 до 200	100
от 1 до 300	150
от 1 до 500	250
от 1 до 1000	500
от 1 до 10000	5000

Статьи по теме:

Имя всех форм, 2D, 3D по математике, английский и хинди для детей

Составной номер — определение, пример, список от 1 до 100

Названия номеров от 1 до 100 на английском и хинди

Простые числа от 1 до 100 — Trick, Chart, List

Решенные примеры нечетных чисел

Que: Найдите сумму наименьшего и наибольшего трехзначного нечетного числа, а также докажите, что оно делится на 2.

Решение : Наименьшее трехзначное нечетное число = 101

Наибольшее трехзначное нечетное число = 999

Сумма обоих чисел = 101 + 999 = 1100

Число 1100 делится на 2 (по правилу делимости на 2) из 2).

Это доказывает, что число четное.

Que : Следующие числа нечетные или четные?

1. 23
2. 13 + 17
3. 39 – 37

Раствор :

1. 23 не делится на 2, поэтому число нечетное.
2. 13 + 17 = 30, делится на 2, нечетное число
3. 39 – 37 = 2, четное число

Нашли эту статью полезной?

Свяжитесь с нами через чат или позвоните нашему старшему эксперту-консультанту по телефону +91-9625869989 t , чтобы узнать больше о различных потоках и доступных вариантах. Мы были бы рады, если бы мы могли добавить некоторые из ваших идей. Если у вас есть определенная цель получить самые высокие оценки, вы можете разрешить свои сомнения с помощью нашего приложения (https://play.