Непрерывные случайные величины. Пример решения задачи на Викиматик
В теории вероятностей приходится иметь дело со случайными величинами, все значения которых нельзя перебрать. Например, нельзя взять и «перебрать» все значения случайной величины $X$ — время службы часов, поскольку время может измеряться в часах, минутах, секундах, миллисекундах, и т.д. Можно лишь указать некоторый интервал, в пределах которого находятся значения случайной величины.
Непрерывная случайная величина — это случайная величина, значения которой целиком заполняют некоторый интервал.
Функция распределения непрерывной случайной величины
Поскольку перебрать все значения непрерывной случайной величины не представляется возможным, то задать ее можно с помощью функции распределения.
Функцией распределения случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X < x\right)$.
Свойства функции распределения:
1. $0\le F\left(x\right)\le 1$.
2. Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha < X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$.
3. $F\left(x\right)$ — неубывающая.
4. ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.
Пример 1. Непрерывная случайная величина $X$ задана следующей функцией распределения $F(x)=\left\{\begin{matrix}
0,\ x\le 0\\
x,\ 0 < x\le 1\\
1,\ x>1
\end{matrix}\right.$. Вероятность попадания случайной величины $X$ в интервал $\left(0,3;0,7\right)$ можем найти как разность значений функции распределения $F\left(x\right)$ на концах этого интервала, то есть:
$$P\left(0,3 < X < 0,7\right)=F\left(0,7\right)-F\left(0,3\right)=0,7-0,3=0,4.$$
Плотность распределения вероятностей
Функция $f\left(x\right)={F}'(x)$ называется плотностью распределения вероятностей, то есть это производная первого порядка, взятая от самой функции распределения $F\left(x\right)$.
Свойства функции $f\left(x\right)$.
1. $f\left(x\right)\ge 0$.
2. $\int^x_{-\infty }{f\left(t\right)dt}=F\left(x\right)$.
3. Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$ — это $P\left(\alpha < X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Геометрически это означает, что вероятность попадания случайной величины $X$ в интервал $\left(\alpha ;\ \beta \right)$ равна площади криволинейной трапеции, которая будет ограничена графиком функции $f\left(x\right)$, прямыми $x=\alpha ,\ x=\beta $ и осью $Ox$.
4. $\int^{+\infty }_{-\infty }{f\left(x\right)}=1$.
Пример 2. Непрерывная случайная величина $X$ задана следующей функцией распределения $F(x)=\left\{\begin{matrix}
0,\ x\le 0\\
x,\ 0 < x\le 1\\
1,\ x>1
\end{matrix}\right.$. Тогда функция плотности $f\left(x\right)={F}'(x)=\left\{\begin{matrix}
0,\ x\le 0 \\
1,\ 0 < x\le 1\\
0,\ x>1
\end{matrix}\right.$
Математическое ожидание непрерывной случайной величины
Математическое ожидание непрерывной случайной величины $X$ вычисляется по формуле
$$M\left(X\right)=\int^{+\infty }_{-\infty }{xf\left(x\right)dx}.$$
Пример 3. Найдем $M\left(X\right)$ для случайной величины $X$ из примера $2$.
$$M\left(X\right)=\int^{+\infty }_{-\infty }{xf\left(x\right)\ dx}=\int^1_0{x\ dx}={{x^2}\over {2}}\bigg|_0^1={{1}\over {2}}.$$
Дисперсия непрерывной случайной величины
Дисперсия непрерывной случайной величины $X$ вычисляется по формуле
$$D\left(X\right)=\int^{+\infty }_{-\infty }{x^2f\left(x\right)\ dx}-{\left[M\left(X\right)\right]}^2.$$
Пример 4. Найдем $D\left(X\right)$для случайной величины $X$ из примера $2$.
$$D\left(X\right)=\int^{+\infty }_{-\infty }{x^2f\left(x\right)\ dx}-{\left[M\left(X\right)\right]}^2=\int^1_0{x^2\ dx}-{\left({{1}\over {2}}\right)}^2={{x^3}\over {3}}\bigg|_0^1-{{1}\over {4}}={{1}\over {3}}-{{1}\over {4}}={{1}\over{12}}.$$
Данная статья полезна?
Да НетЧисловые характеристики непрерывной случайной величины — Студопедия
Понятия математического ожидания М(Х) и дисперсии D(X), введенные ранее для дискретной случайной величины, можно распространить на непрерывные случайные величины.
· Математическое ожидание М(Х) непрерывной случайной величины Х определяется равенством:

при условии, что этот интеграл сходится.
· Дисперсия D(X) непрерывной случайной величины Х определяется равенством:


· Среднее квадратическое отклонение σ(Х)непрерывной случайной величины определяется равенством:
 .
.
Все свойства математического ожидания и дисперсии, рассмотренные ранее для дискретных случайных величин, справедливы и для непрерывных.
Задача 5.3.Случайная величина Х задана дифференциальной функцией f(x):

Найти M(X), D(X), σ(Х), а также P(1 < х < 5).
Решение:
M(X)=  =
= 
 +
+ 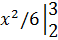 =8/9
=8/9  0+9/6
0+9/6  4/6=31/18,
4/6=31/18,
D(X)= 
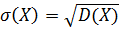 =
=  =
=  /
/ 
P 
 =
= 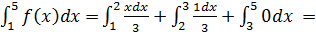

Задачи
5.1.Непрерывная случайная величина Х задана функцией распределения:

Найти дифференциальную функцию распределения f (x), а также
Р(‒1/2 < Х < 1/2).
5.2.Непрерывная случайная величина Х задана функцией распределения:

Найти дифференциальную функцию распределения f (x) , а также
Р(2π /9 < Х < π /2).
5.3. Непрерывная случайная величина Х задана плотностью распределения:

Найти: а) число с; б) М(Х), D(X).
5.4. Непрерывная случайная величина Х задана плотностью распределения:

Найти: а) число с; б) М(Х), D(X).
5.5. Задана плотность распределения вероятностей непрерывной случайной величины Х:

Найти: а) F(х) и построить ее график; б) M(X), D(X), σ(Х); в) вероятность того, что в четырех независимых испытаниях величина
5.6. Задана плотность распределения вероятностей непрерывной случайной величины Х:

Найти: а) F(х) и построить ее график; б) M(X), D(X), σ(Х); в) вероятность того, что в трех независимых испытаниях величина Х примет ровно 2 раза значение, принадлежащее отрезку [1; 2,5].
5.7. Функция f(х) задана в виде:

Найти: а) значение постоянной с, при которой функция будет плотностью вероятности некоторой случайной величины Х; б) функцию распределения F(x).
5.8.
Функция f(x) задана в виде:
Найти: а) значение постоянной с, при которой функция будет плотностью вероятности некоторой случайной величины Х; б) функцию распределения F(x).
5.9. Случайная величина Х, сосредоточенная на интервале (3;7), задана функцией распределения F(х)=  . Найти вероятность того, что случайная величина Х примет значение: а) меньше 5, б) не меньше 7.
. Найти вероятность того, что случайная величина Х примет значение: а) меньше 5, б) не меньше 7.
5.10. Случайная величина Х, сосредоточенная на интервале (-1;4), задана функцией распределения F(х)=  . Найти вероятность того, что случайная величина Х примет значение: а) меньше 2, б) меньше 4.
. Найти вероятность того, что случайная величина Х примет значение: а) меньше 2, б) меньше 4.
5.11. Случайная величина задана дифференциальной функцией распределения:

Найти: а) число с; б) М(Х); в) вероятность Р(Х > М(Х)).
5.12. Случайная величина задана дифференциальной функцией распределения:

Найти: а) М(Х); б) вероятность Р(Х ≤ М(Х)).
5.13. Распределение Ремя задается плотностью вероятности:

Доказать, что f(x) действительно является плотностью распределения вероятностей.
5.14. Задана плотность распределения вероятностей непрерывной случайной величины Х:

Найти число с.
5.15.Случайная величина Х распределена по закону Симпсона (равнобедренного треугольника) на отрезке [-2;2] (рис. 5.4). Найти аналитическое выражение для плотности вероятности f(x) на всей числовой оси.


Рис. 5.4 Рис. 5.5
5.16. Случайная величина Х распределена по закону «прямоугольного треугольника» в интервале (0;4) (рис. 5.5). Найти аналитическое выражение для плотности вероятности f(x) на всей числовой оси.
Ответы
5.1. 
P (-1/2<X<1/2)=2/3.
5.2. 
P (2π /9<Х< π /2)=1/2.
5.3. а) с =1/6, б) М(Х)=3  , в) D(X)=26/81.
, в) D(X)=26/81.
 5.4. а) с=3/2, б) М(Х)=3/5, в) D(X)=12/175.
5.4. а) с=3/2, б) М(Х)=3/5, в) D(X)=12/175.
5.5. 
б) M(X)=3  , D(X)=2/9, σ(Х)=
, D(X)=2/9, σ(Х)= 
в) 3/8.
 5.6.
5.6. 
б) M(X)=2  , D(X)=3
, D(X)=3  , σ(Х)=
, σ(Х)= 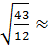 1,893.
1,893.
в) 9/64.
5.7. а) с =  ; б)
; б) 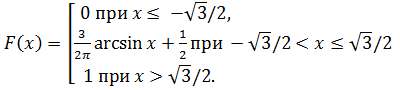
5.8.а) с =1/2; б) 
5.9.а)1/4; б) 0.
5.10. а)3/5; б) 1.
5.11.а) с = 2; б) М(Х)= 2; в) 1-ln2 2 ≈ 0,5185.
5.12. а) М(Х)= π /2 ; б) 1/2
5.14. с = 1.
5.15. 
5.16. 
Непрерывная случайная величина, функция распределения и плотность
Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала. Для непрерывной случайной величины невозможно указать все возможные значения, поэтому обозначают интервалы этих значений, которые связаны с определёнными вероятностями.
Примерами непрерывных случайных величин могут служить: диаметр детали, обтачиваемой до заданного размера, рост человека, дальность полёта снаряда и др.
Так как для непрерывных случайных величин функция F(x), в отличие от дискретных случайных величин, нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю.
Это значит, что для непрерывной случайной величины бессмысленно говорить о распределении вероятностей между её значениями: каждое из них имеет нулевую вероятность. Однако в некотором смысле среди значений непрерывной случайной величины есть «более и менее вероятные». Например, вряд ли у кого-либо возникнет сомнение, что значение случайной величины — роста наугад встреченного человека — 170 см — более вероятно, чем 220 см, хотя и одно, и другое значение могут встретиться на практике.
В качестве закона распределения, имеющего смысл только для непрерывных случайных величин, вводится понятие плотности распределения или плотности вероятности. Подойдём к нему путём сравнения смысла функции распределения для непрерывной случайной величины и для дискретной случайной величины.
Итак, функцией распределения случайной величины (как
дискретной, так и непрерывной) или интегральной функцией называется функция  ,
которая определяет вероятность, что значение случайной величины X меньше или
равно граничному значению х.
,
которая определяет вероятность, что значение случайной величины X меньше или
равно граничному значению х.
Для дискретной случайной величины в точках её значений x1, x2, …, xi,… сосредоточены массы вероятностей p1, p2, …, pi,…, причём сумма всех масс равна 1. Перенесём эту интерпретацию на случай непрерывной случайной величины. Представим себе, что масса, равная 1, не сосредоточена в отдельных точках, а непрерывно «размазана» по оси абсцисс Оx с какой-то неравномерной плотностью. Вероятность попадания случайной величины на любой участок Δx будет интерпретироваться как масса, приходящаяся на этот участок, а средняя плотность на этом участке — как отношение массы к длине. Только что мы ввели важное понятие теории вероятностей: плотность распределения.
Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:
 .
.
Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:

вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:

или
 .
.
При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x):
 .
.
График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).

Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.
Свойства функции плотности вероятности непрерывной случайной величины
1. Вероятность того, что случайная величина примет какое-либо значение из интервала
 (и площадь фигуры,
которую ограничивают график функции f(x) и ось
Ох) равна единице:
(и площадь фигуры,
которую ограничивают график функции f(x) и ось
Ох) равна единице:

2. Функция плотности вероятности не может принимать отрицательные значения:
 ,
,
а за пределами существования распределения её значение равно нулю
Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.
Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.
Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.
Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.
Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:

Найти функцию f(x) плотности
вероятности непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 4 до 8:
 .
.
Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:

График функции F(x) — парабола:

График функции f(x) — прямая:

Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:
 .
.
Пример 2. Функция плотности вероятности непрерывной случайной величины дана в виде:
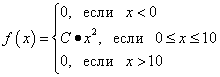
Вычислить коэффициент C. Найти функцию F(x)
распределения вероятностей непрерывной случайной величины. Построить графики обеих функций. Найти вероятность того, что
непрерывная случайная величина примет какое-либо значение в интервале от 0 до 5:
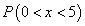 .
.
Решение. Коэффициент C найдём, пользуясь свойством 1 функции плотности вероятности:

Таким образом, функция плотности вероятности непрерывной случайной величины:

Интегрируя, найдём функцию F(x) распределения вероятностей. Если x < 0, то F(x) = 0. Если 0 < x < 10, то
 .
.
x > 10, то F(x) = 1.
Таким образом, полная запись функции распределения вероятностей:

График функции f(x):
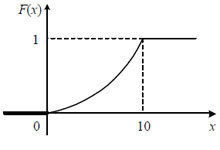
График функции F(x):
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 0 до 5:
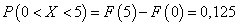 .
.
Пример 3. Плотность вероятности непрерывной
случайной величины X задана равенством
 ,
при этом
,
при этом  .
Найти коэффициент А, вероятность того, что непрерывная случайная величина
X примет какое-либо значение из интервала ]0, 5[, функцию распределения
непрерывной случайной величины X.
.
Найти коэффициент А, вероятность того, что непрерывная случайная величина
X примет какое-либо значение из интервала ]0, 5[, функцию распределения
непрерывной случайной величины X.
Решение. По условию  приходим к равенству
приходим к равенству
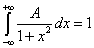 .
.
Но

Следовательно,  ,
откуда
,
откуда  . Итак,
. Итак,
 .
.
Теперь находим вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала ]0, 5[:

Теперь получим функцию распределения данной случайной величины:

Пример 5. Плотность распределения непрерывной случайной величины задана формулой:
 (при x > 0)
(при x > 0)
(a — положительный коэффициент).
1) найти функцию распределения непрерывной случайной величины;
2) найти вероятность того, что непрерывная случайная величина примет значение, лежащее между 1 и 2.
Решение.
1) При x < 0 f(x) = 0,
значит  . При
x > 0
. При
x > 0  .
Первый интеграл равен нулю. Второй
.
Первый интеграл равен нулю. Второй  .
Итак, функция распределения данной непрерывной случайной величины имеет вид:
.
Итак, функция распределения данной непрерывной случайной величины имеет вид:

2) вероятность попадания непрерывной случайной величины на участок между 1 и 2 вычислим как приращение функции распределения на этом участке:

Пример 6. Непрерывная случайная величина имеет плотность
 при
при 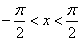 .
.
1) найти вероятность попадания непрерывной случайной величины на участок от 0 до π/4;
2) функцию распределения непрерывной случайной величины.
Решение.
1) находим вероятность:
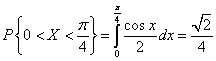 .
.
2) находим функцию распределения непрерывной случайной величины:

Пример 7. Плотность распределения непрерывной случайной величины задана формулой
 .
.
Найти вероятность попадания непрерывной случайной величины на участок (-1; +1)
Решение.
 .
.

Начало темы «Теория вероятностей»
Непрерывные случайные величины. Функция распределения. Плотность вероятности.
Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
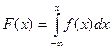
Свойства плотности распределения.
1) Плотность распределения – неотрицательная функция.

2) Несобственный интеграл от плотности распределения в пределах от — ¥ до ¥ равен единице.

Пример.
Случайная величина подчинена закону распределения с плотностью:

Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до  .
.
Решение.
Построим график плотности распределения:


Для нахождения коэффициента а воспользуемся свойством  .
.
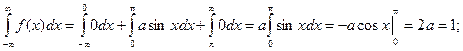

Находим вероятность попадания случайной величины в заданный интервал.
Пример.
Задана непрерывная случайная величина х своей функцией распределения f(x).

Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал  .
.
Решение.
Найдем коэффициент А.

Найдем функцию распределения:
1) На участке  :
: 
2) На участке 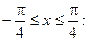

3) На участке 

Итого: 

Построим график плотности распределения:
f(x)



Построим график функции распределения:
F(x)


Найдем вероятность попадания случайной величины в интервал  .
.

Ту же самую вероятность можно искать и другим способом:

Функция распределения дискретной и непрерывной случайной величины
Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение меньшее x, то есть
F(x) = р(Х<х)
Также функцию F(x) называют интегральной функцией распределения.
Плотность распределения вероятности (также называют дифференциальной функцией) функции распределения определяет непрерывную случайную величину.
Случайная величина X называется непрерывной, если её функция распределения непрерывна на всей числовой оси.
Обозначение: F(x)
1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей:
0≤F(x)≤1
2. Функция монотонно возрастающая, т. е. если xj > xi , то F(xj) > F(xi)
3.
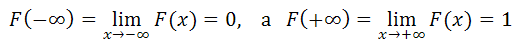
4. P(a≤X<b) = F(b) — F(a)
Пример 1 (Функция распределения дискретной случайной величины)
По заданному закону распределения случайной величины X, вычислить функцию распределения дискретной случайной величины.
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение
Если x≤0, то F(x)=Р(Х<0)=0, следовательно событие при Р(Х<0) невозможно.
Если 0<x≤1, то F(x)=Р(Х<1)=Р(Х=0)=0.2
Если 1<x≤2, то F(x)=Р(Х<2)=Р(Х=0)+Р(Х=1)=0.2+0.1=0.3
Если 2<x≤3, то F(x)=Р(Х<3)=Р(Х=0)+Р(Х=1)+Р(Х=2)=0.2+0.1+0.25=0.55
Если 3<x≤4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=3)=
=0.2+0.1+0.25+0.15=0.7
Если x>4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=)+Р(Х=4)=
=0.2+0.1+0.25+0.15+0.3=1
Получаем функцию распределения дискретной СВ в аналитическом виде:
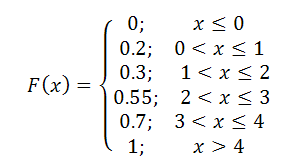
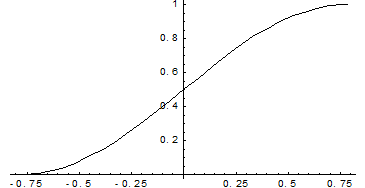
График функции распределения дискретной случайной величины имеет вид:

Пример 2 (Функция распределения непрерывной случайной величины)
Пример для непрерывной случайной величины X можно посмотреть здесь.Функция распределения. Функция плотности распределения непрерывной случайной величины
Функцией распределения называют функцию  определяющую вероятность того, что случайная величина
определяющую вероятность того, что случайная величина  в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее  , т. е.
, т. е. 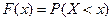 .
.
Пример 38. Дан ряд распределения случайной величины  :
:
 | –2 | |||
 | 0,4 | 0,1 | 0,2 | 0,3 |
Составить функцию распределения  и построить ее график.
и построить ее график.
Решение:
при 
при 
при 
при 
при 
 |
Рис. 1. График функции распределения
Вероятность того, что случайная величина примет значение, заключенное в интервале  , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 
Для непрерывной случайной величины:
 (3.9)
(3.9)
Пример 39. Случайная величина  задана функцией распределения
задана функцией распределения

Найдите вероятность того, что в результате испытания  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 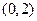 .
.
Решение.  Так как на интервале
Так как на интервале 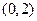
 , то
, то  Следовательно,
Следовательно, 
Плотностью распределения вероятностей непрерывной случайной величины  называют функцию
называют функцию  – первую производную от функции распределения
– первую производную от функции распределения 
Пример 40. Дана функция распределения случайной величины  :
:

Найдите плотность распределения  .
.
Решение. Плотность распределения равна первой производной от функции распределения:

Вероятность того, что непрерывная случайная величина  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  равна определенному интегралу от плотности распределения, взятому в пределах от
равна определенному интегралу от плотности распределения, взятому в пределах от  до
до  :
:  .
.
Пример 41. Задана плотность вероятности случайной величины 

Найдите вероятность того, что в результате испытания X примет значение, принадлежащее интервалу  .
.
Решение. Искомая вероятность равна:

Зная плотность  распределения можно найти функцию распределения по формуле
распределения можно найти функцию распределения по формуле  .
.
Пример 42. Найдите функцию распределения  по данной плотности распределения:
по данной плотности распределения:
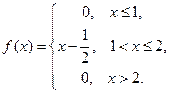
Решение. Используем формулу  .
.
Если  , то
, то  . Следовательно,
. Следовательно,  .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
Итак, искомая функция распределения имеет вид:

Несобственный интеграл от плотности распределения в пределах
от  до
до  равен единице:
равен единице:  (основное условие нормировки).
(основное условие нормировки).
Пример 43. Случайная величина задана плотностью распределения

Найдите коэффициент  .
.
Решение. Воспользуемся формулой  .
.
 .
.
Следовательно, 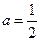 .
.
Непрерывные случайные величины. 1. Интегральная функция распределения
1. Интегральная функция распределения. Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом, который мы сейчас рассмотрим. Пусть X — непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х — действительное число. Под выражением Х<х понимается событие «случайная величина Л’ приняла значение, меньшее х». Вероятность этого события Р(Х< х) есть некоторая функция переменной х
Р(х) = Р(Х < х).
Определение. Интегральной функцией распределения (или кратко функцией распределения) непрерывной случайной величины X называется функция F(х), равная вероятности того, что X приняла значение, меньшее х:
F(х) = Р(Х < х). (9.4)
Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.
Укажем свойства, которыми обладает функция F(х).
1. 0 £ F(х) £ 1.
Это свойство следует из того, что F(х) есть вероятность.
2. F(х) — неубывающая функция, т.е. если х1< х2, то F(х}) £F(х2).
Доказательство. Предположим, что х1 <х2. Событие «X примет значение, меньшее х2» можно представить в виде суммы двух несовместимых событий: «X примет значение, меньшее х1 и «X примет значение, удовлетворяющее неравенствам х1£ Х< х2». Обозначим вероятности последних двух событий соответственно через Р(Х< х1) и Р(х1£Х<х2). По теореме о вероятности суммы двух несовместимых событий
Р(Х < х2) = Р(Х< х1) +Р(х1£Х<х2).
откуда с учетом (9.4)
Р(х1£Х<х2)= F(х2)- F(х1). (9.5)
Так как вероятность любого события есть число неотрицательное, то Р(х1£Х<х2)³0 и, значит, F(х2)³F(х1).
Формула (9.5) утверждает свойство 3.
5. Вероятность попадания случайной величины Х в полуинтервал [а; b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):
Р(а£Х<b) = F(b)-F(а). (9.6)
Пример 9.9. Случайная величина X задана функцией распределения

Найдем вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0; 2).
х
Решение. Так как на полуинтервале [0; 2) F(х) =  то
то
Р(0£Х<2) = F(2)-F(0)= 
В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F(х) с непрерывной или кусочно-непрерывной производной.
4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
Р(Х = х1) = 0. (9.7)
Доказательство. Положив в (9.5) х2 = х1+ Dх, будем иметь
Р(х1 £ X < х1+ Dх) = F(х1+ Dх) — F(х1). (9.8)
Так как F(х) — непрерывная функция, то, перейдя в (9.8) к пределу при Dх®0, получим искомое равенство (9.7). Из свойства 4 следует свойство 5.
5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы
Р(a<X <b) = Р(a£ X £ b) = Р(a£ X <b) = Р(a<X £ b) . (9.9)
6. Если возможные значения случайной величины X принадлежат интервалу (а; b), то 1) F(х) = 0 при х £а; 2) F(х) = 1 при х³b.
Доказательство. 1) Пусть х1 £а. Тогда событие Х< х1 невозможно, и, следовательно, вероятность его равна нулю.
2) Пусть х2 ³ b. Тогда событие X < х2 достоверно, и, следовательно, вероятность его равна 1.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
F(-¥) =  =0; F(¥) =
=0; F(¥) =  == 1.
== 1.
2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины ДГ(или ее плотностью вероятности) называется функция f(х) равная производной интегральной функции: f(х) =F’(х)
Так как F(х) — неубывающая функция, то f(х) ³ 0 (см. подразд. 3.7, п. 1).
Теорема 9.3. Вероятность попадания непрерывной случайной величины X в интервал (а; b) равна определенному интегралу от дифференциальной функции распределения величины X, взятому в пределах от а до b:
Р(а<Х<b)=  . (9.10)
. (9.10)
Доказательство. Так как F(х)является первообразной для f(х), то на основании формулы Ньютона— Лейбница (см. подразд. 4.4, п. 2)
 =F(b)-F(а). (9.11)
=F(b)-F(а). (9.11)
Теперь с учетом соотношений (9.6), (9.9), (9.11) получим искомое равенство.
Из (9.10) следует, что геометрически (см. подразд. 4.3, п. 2) вероятность Р(а<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности у =f(х) и отрезками прямых у = 0, х = а и х = b.
Следствие.В частности, если f(х)) — четная функция и концы интервала симметричны относительно начала координат, то
Р(-а<Х<a)= Р(½Х½<a)= 2  (9.12)
(9.12)
Заменяя в формуле (9.11) а на -¥ и b на х, получаем
F(x)-F(-¥)=  .
.
откуда, в силу найденного выше следствия (см. п. 1),
F(x)=  . (9.13)
. (9.13)
Формула (9.13) дает возможность отыскать интегральную функцию распределения F(x) по ее плотности вероятности.
Отметим, что из формулы (9.13) и из только что отмеченного следствия вытекает, что
 =1 (9.14)
=1 (9.14)
Пример 9.10. Задана плотность вероятности случайной величины X
f(x)=  (—¥< x < +¥)
(—¥< x < +¥)
Требуется найти коэффициент А, функцию распределения F(х) и вероятность попадания случайной величины Х винтервал (0; 1).
Решение. Коэффициент А найдем, воспользовавшись соотношением (9.14). Так как
 =
=  =
=  +
+  =A arctg x
=A arctg x  + A arctg x
+ A arctg x  =
=
= A arctg (+¥)-A arctg (-¥)=Аp,
то Аp = 1, откуда А =1/p.
Применяя формулу (9.13), получаем функцию распределения F(х):
F(х)=  =
=  A arctg x
A arctg x  =
=  [ arctg x- arctg (-¥)]=
[ arctg x- arctg (-¥)]=
==  +
+  arctg x.
arctg x.
Наконец, формулы (9.6) и (9.9) с учетом найденной функции F(х) дают
P(0< x < 1)= F(1)— F(0)=  .
.
Непрерывные случайные переменные — математика A-Level, версия
Непрерывная случайная величина — это случайная величина, данные которой могут принимать бесконечно много значений. Например, случайная величина, измеряющая время, необходимое для того, чтобы что-то сделать, является непрерывной, поскольку существует бесконечное количество возможных вариантов выполнения.
Для любой непрерывной случайной величины с функцией плотности вероятности f (x) имеем:

Это полезный факт.
Пример
X — непрерывная случайная величина с функцией плотности вероятности, заданной следующим образом: f (x) = cx для 0 ≤ x ≤ 1, где c — постоянная. Найдите c.
Если мы проинтегрируем f (x) между 0 и 1, мы получим c / 2. Следовательно, c / 2 = 1 (из полезного факта выше!), Что дает c = 2.
Кумулятивная функция распределения (c.d.f.)
Если X — непрерывная случайная величина с p.d.f. f (x) определена на a ≤ x ≤ b, то кумулятивная функция распределения (c.d.f.), написанное F (t), определяется как:
Итак, c.d.f. находится путем интегрирования p.d.f. между минимальным значением X и t.
Точно так же функция плотности вероятности непрерывной случайной величины может быть получена путем дифференцирования кумулятивного распределения.
КДФ. может использоваться для определения вероятности того, что случайная величина находится между двумя значениями:
P (s ≤ X ≤ t) = вероятность того, что X находится между s и t. Но это равно вероятности того, что X ≤ t минус вероятность того, что X ≤ s.
[Нам нужна вероятность того, что X находится в красной области:]

Отсюда:
Ожидания и отклонения
При использовании дискретных случайных величин ожидалось S x P (X = x), где P (X = x) было pdf. Неудивительно, что для нахождения математического ожидания непрерывной случайной величины мы интегрировать, а не суммировать, например:
Как и в случае дискретных случайных величин, Var (X) = E (X 2 ) — [E (X)] 2
.2 & \ quad | x | \ leq 1 \\ 0 & \ quad \ text {иначе} \ end {array} \ right. \ end {уравнение}- Найдите постоянную $ c $.
- Найдите $ EX $ и Var $ (X) $.
- Найдите $ P (X \ geq \ frac {1} {2}) $.
- Решение
- Чтобы найти $ c $, мы можем использовать $ \ int _ {- \ infty} ^ {\ infty} f_X (u) du = 1 $:
$ 1 $$ = \ int _ {- \ infty} ^ {\ infty} f_X (u) du $ $ = \ int _ {- 1} ^ {1} cu ^ 2du $ $ = \ frac {2} {3} c.3 du $ $ = 0. $
Фактически, мы могли бы предположить, что $ EX = 0 $, потому что PDF симметричен относительно $ x = 0 $. Чтобы найти Var $ (X) $, мы имеем$ \ textrm {Var} (X) $$ = EX ^ 2- (EX) ^ 2 = EX ^ 2 $ $ = \ int _ {- 1} ^ {1} u ^ 2 f_X (u) du $ $ = \ frac {3} {2} \ int _ {- 1} ^ {1} u ^ 4 du $ $ = \ frac {3} {5}.2 $, найдите CDF $ Y $. - Решение
Прежде всего отметим, что $ R_Y = [0, \ infty) $. Для $ y \ in [0, \ infty) $ имеем
$ F_Y (г) $ $ = P (Y \ leq y) $$ = P (X ^ 2 \ leq y) $$ = P (- \ sqrt {y} \ leq X \ leq \ sqrt {y}) $ $ = \ int _ {- \ sqrt {y}} ^ {\ sqrt {y}} \ frac {1} {2} e ^ {- | x |} dx $ $ = \ int_ {0} ^ {\ sqrt {y}} e ^ {- x} dx $ $ = 1-е ^ {- \ sqrt {y}}.3 & \ quad 0 \ frac {1} {3}) $. - Решение
У нас есть
$ P (X \ leq \ frac {2} {3} | X> \ frac {1} {3}) $$ = \ frac {P (\ frac {1} {3} \ frac {1} {3})} долл. США$ = \ frac {\ int _ {\ frac {1} {3}} ^ {\ frac {2} {3}} 4x ^ 3 dx} {\ int _ {\ frac {1} {3}} ^ {1 } 4x ^ 3 dx} долл. США$ = \ frac {3} {16}.{\ infty} f_X (t) dtdx = EX. $$ Левая часть представляет собой двойной интеграл. В частности, это интеграл от $ f_X (t) $ по заштрихованная область на рисунке 4.4.  Рис.4.4 — Заштрихованная область показывает область двойного интеграла задачи 5.
Мы можем взять интеграл по $ x $ или $ t $. Таким образом, мы можем написать
Рис.4.4 — Заштрихованная область показывает область двойного интеграла задачи 5.
Мы можем взять интеграл по $ x $ или $ t $. Таким образом, мы можем написать$ \ int_ {0} ^ {\ infty} \ int_ {x} ^ {\ infty} f_X (t) dtdx $ $ = \ int_ {0} ^ {\ infty} \ int_ {0} ^ {t} f_X (t) dx dt $ $ = \ int_ {0} ^ {\ infty} f_X (t) \ left (\ int_ {0} ^ {t} 1 dx \ right) dt $ $ = \ int_ {0} ^ {\ infty} tf_X (t) dt = EX \ hspace {20pt} \ textrm {поскольку $ X $ — положительная случайная величина}.$
Задача. Пусть $ X \ sim Uniform (- \ frac {\ pi} {2}, \ pi) $ и $ Y = \ sin (X) $. Найдите $ f_Y (y) $.
- Решение
Здесь $ Y = g (X) $, где $ g $ — дифференцируемая функция. Хотя $ g $ не монотонный, он может делится на конечное число областей, в которых он монотонен.Таким образом, мы можем использовать Уравнение 4.6. Отметим, что поскольку $ R_X = [- \ frac {\ pi} {2}, \ pi] $, $ R_Y = [- 1,1] $. Глядя на график $ g (x) = \ sin (x) $ над $ [- \ frac {\ pi} {2}, \ pi] $, мы замечаем, что для $ y \ in (0,1) $ есть два решения для $ y = g (x) $, а для $ y \ in (-1,0) $ есть только одно решение. В частности, если $ y \ in (0,1) $, у нас есть два решения: $ x_1 = \ arcsin (y) $ и $ x_2 = \ pi- \ arcsin (y) $. Если $ y \ in (-1,0) $, у нас есть одно решение, $ x_1 = \ arcsin (y) $. Таким образом, для $ y \ in (-1,0) $ имеем
$ f_Y (y) $ $ = \ frac {f_X (x_1)} {| g ‘(x_1) |} $$ = \ frac {f_X (\ arcsin (y))} {| \ cos (\ arcsin (y)) |} долларов$ = \ frac {\ frac {2} {3 \ pi}} {\ sqrt {1-y ^ 2}}.$
Для $ y \ in (0,1) $ имеем$ f_Y (y) $ $ = \ frac {f_X (x_1)} {| g ‘(x_1) |} + \ frac {f_X (x_2)} {| g’ (x_2) |} долларов$ = \ frac {f_X (\ arcsin (y))} {| \ cos (\ arcsin (y)) |} + \ frac {f_X (\ pi- \ arcsin (y))} {| \ cos (\ pi- \ arcsin (y)) |} долларов$ = \ frac {\ frac {2} {3 \ pi}} {\ sqrt {1-y ^ 2}} + \ frac {\ frac {2} {3 \ pi}} {\ sqrt {1-y ^ 2}} долл. США$ = \ frac {4} {3 \ pi \ sqrt {1-y ^ 2}}.2}} & \ quad -1
.Учебники и примечания по непрерывным случайным переменным| Машинное обучение
В предыдущем уроке мы рассмотрели дискретные случайные величины. В этом разделе мы рассмотрим случайные величины, которые могут решить проблемы, связанные с непрерывным выходом.
Непрерывные случайные переменные
По умолчанию:
Непрерывная случайная величина — это функция, которая отображает пространство выборки случайного эксперимента на интервал в пространстве реальных значений.{2,5} = 0,1875 $$.
Полный CDF выглядит следующим образом:$$ a $$ $$ Cdf (a) $$ $$ <2 $$ $$ 0 $$ $$ \ le 2.5 $$ $$ 0,1875 $$ $$ \ le 3 $$ $$ 0,4167 $$ $$ \ le 3.5 $$ $$ 0,6875 $$ $$ \ le 4 $$ $$ 1 $$ Примечание:
В отличие от f (x), cdf (x) действительно является подсчетом вероятностей и, следовательно, следует ограничению $$ 0 \ le cdf (c) \ le 1 $$.{‘} (x) = f (x) $$
Значение cdf (x) принимает значение 0, как $$ x \ to — \ infty $$, и 1, как $$ x \ to \ infty $$.
Обычно непрерывная случайная величина обозначается с помощью ее функции cdf. Например: X — случайная величина с распределением cdf (x).Некоторые специфические дистрибутивы
Равномерное распределение
Опять же, начиная с простейшего из всех распределений, X = Uniform (N) используется для моделирования сценариев, в которых все результаты одинаково возможны.{- \ lambda x}, x \ ge 0 $$.
Важным моментом в экспоненциальном распределении является то, что оно используется для моделирования времени ожидания наступления события. Популярным примером этого является время ожидания ядерного распада радиоактивного изотопа, распределенное экспоненциально, а $$ \ lambda $$ известен как период полураспада изотопа.
Еще одним важным аспектом этого дистрибутива является нехватка памяти. Когда время ожидания действия моделируется с использованием экспоненциального распределения, вероятность того, что оно произойдет в следующие N минут, остается неизменной независимо от прошедшего времени.{2} $$ — дисперсия данного распределения. Стандартное нормальное распределение , обозначенное Z, является нормальным распределением со средним значением $$ = 0 $$ и отклонением $$ = 1 $$.Нормальное распределение используется для моделирования статистики больших наборов данных, измерения ошибок в собранных данных и т. Д. Интересным моментом стандартного нормального распределения является то, что оно симметрично относительно оси y и следует колоколообразной кривой .
$$ Uni (c, d) $$ $$ Exp (\ lambda), x \ ge 0 $$ $$ N (\ mu, \ sigma ^ {2}), x \ in {\ rm I! R} $$ $$ \ frac {1} {d-c} $$ $$ \ lambda e ^ {- \ lambda x} $$ $$ \ frac {1} {\ sqrt {2 \ sigma ^ {2} \ pi}} e ^ {\ frac {- (x- \ mu) ^ {2}} {2 \ sigma ^ {2}} } $$ $$ \ frac {x-c} {d-c} $$ $$ 1-e ^ {- \ lambda x} $$ $$ \ frac {1} {2} [1 + erf (\ frac {x- \ mu} {\ sigma \ sqrt {2}})] $$ Ожидаемое значение
Резюме:
Ожидаемое значение для случайной переменной дает среднее или среднее значение, вычисленное по всем возможным результатам переменной.{d} x * f (x) dx \ end {уравнение} Ожидаемое значение часто обозначается $$ \ mu $$. $$ f (x) dx $$ обозначает значение вероятности, с которой X может принять бесконечно малый диапазон $$ dx $$.Следующие свойства ожидаемого значения все еще сохраняются (аналогично дискретным случайным величинам):
$$ E (X + Y) = E (X) + E (Y) $$
$$ E (cX + d) = c * E (X) + d $$Еще одно дополнительное свойство: когда $$ Y = h (X) $$, где $$ X $$ — случайная величина с $$ f (x) $$ в формате pdf, $$ E (Y) = E (h ( x)) = \ int _ {- \ infty} ^ {\ infty} h (x) f (x) dx $$
Дисперсия и стандартное отклонение
\ begin {Equation} Вар (Х) = Е ((Х- \ му) ^ 2) \ end {уравнение} \ begin {уравнение} \ sigma = \ sqrt {Var (X)} \ end {уравнение} Резюме:Где $$ \ sigma $$ — так называемое стандартное отклонение.{th} $$ квантиль.
Предоставил: Шубхакар Редди Типиредди
.дискретных и непрерывных случайных величин
Дискретные и непрерывные случайные переменныеДискретный и непрерывный Случайные переменные:
Переменная — это количество, значение которого изменяется.
A дискретная переменная — переменная, значение которой получается путем подсчета.
Примеры : количество присутствующих студентов
количество красных шариков в банке
количество голов при подбрасывании трех монет
ученики класса
A непрерывная переменная — это переменная, значение которой получается путем измерения.
Примеры : рост учеников в классе
вес учеников в классе
время, необходимое, чтобы добраться до школы
расстояние между классами
A случайная величина переменная, значение которой является числовым результатом случайного явления.
▪ Случайная величина обозначается заглавная буква
▪ Распределение вероятностей случайная величина X сообщает, каковы возможные значения X и как вероятности присваиваются этим значениям
▪ Случайная величина может быть дискретной или непрерывный
A дискретный случайный переменная X имеет счетное количество возможных значений.
Пример : Пусть X представляет собой сумму двух игральных костей.
Тогда вероятность распределение X выглядит следующим образом:
х
2
3
4
5
6
7
8
9
10
11
12
П ( X )
Построение графика вероятности распределения дискретной случайной величины, построить гистограмму вероятностей .
A непрерывный случайный переменная X принимает все значения в заданном интервале чисел.
▪ Распределение вероятностей Непрерывная случайная величина показана кривой плотности .
▪ Вероятность того, что X находится между интервал чисел — это площадь под кривой плотности между интервалом конечные точки
▪ Вероятность того, что непрерывная случайная величина X точно равна числу ноль
Средства и варианты Случайные переменные:
Среднее значение дискретной случайная величина X — ее средневзвешенная величина.Каждое значение X взвешивается его вероятность.
Чтобы найти среднее значение X, умножьте каждое значение X на его вероятность, затем сложите все продукты.
Среднее значение случайного переменная X называется ожидаемым значением X.
Закон больших чисел:
Как количество наблюдения увеличивается, среднее из наблюдаемых значений, , приближается к среднему значению по совокупности, .
Чем больше вариаций в результатов, тем больше испытаний необходимо, чтобы убедиться, что близко к.
Правила для средств:
Если X — случайная величина и a и b — фиксированные числа, тогда
Если X и Y случайны переменные, то
Пример:
Предположим, что уравнение Y = 20 + 100X преобразует оценку X по математике PSAT в SAT оценка по математике, Y.Предположим, средний балл по математике в PSAT равен 48. Что такое средний балл? Результаты SAT по математике?
Пример :
Пусть представляют средний SAT оценка по математике.
Пусть представляют средний SAT словесная оценка.
представляет собой средний комбинированный балл по SAT.затем средний совокупный общий балл за SAT.
Разница Дискретная случайная переменная:
Если X — дискретный случайный переменная со средним значением, тогда дисперсия X равна
Стандартное отклонение — квадратный корень из дисперсии.
Правила отклонений:
Если X — случайная величина и a и b — фиксированные числа, тогда
Если X и Y независимы случайные величины, то
Пример :
Предположим, что уравнение Y = 20 + 100X преобразует оценку X по математике PSAT в SAT оценка по математике, Y.Предположим, стандартное отклонение для оценки по математике PSAT составляет 1,5. точки. Какое стандартное отклонение для СУББОТА оценка по математике?
Допустим, стандартный отклонение для оценки SAT по математике составляет 150 баллов, а стандартное отклонение для устная оценка SAT — 165 баллов. Какое стандартное отклонение для комбинированный результат SAT?
*** Потому что SAT оценка по математике и вербальная оценка SAT не являются независимо, правило добавления отклонений не применяется!
.
- Решение
- Решение
- Решение
- Чтобы найти $ c $, мы можем использовать $ \ int _ {- \ infty} ^ {\ infty} f_X (u) du = 1 $:

 Рис.4.4 — Заштрихованная область показывает область двойного интеграла задачи 5.
Мы можем взять интеграл по $ x $ или $ t $. Таким образом, мы можем написать
Рис.4.4 — Заштрихованная область показывает область двойного интеграла задачи 5.
Мы можем взять интеграл по $ x $ или $ t $. Таким образом, мы можем написать