Определение непрерывности функции в точке
Непрерывность в точке
Определение непрерывности
- Непрерывность функции в точке
- Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, включая саму точку, и если предел при x стремящемся к x0 существует и равен значению функции в x0:
.
Здесь подразумевается, что x0 – это конечная точка. Значение функции в ней может быть только конечным числом.
Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.
Если в определении предела функции в точке , сама точка исключалась из рассмотрения, и мы применяли только проколотые окрестности этой точки, то при определении непрерывности, функция должна быть определена в этой точке и иметь значение, равное предельному.
Поэтому при определении непрерывности, можно заменить проколотые окрестности точки простыми окрестностями. Обычно так и делают, хотя никакого противоречия не возникнет, если и при определении непрерывности использовать проколотые окрестности.
- Непрерывность функции в точке по Гейне
- Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, и если для любой последовательности {xn}, сходящейся к x0: , элементы которой принадлежат окрестности U(x0), последовательность {f(xn) } сходится к f(x0):
. - Непрерывность функции в точке по Коши
- Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности U(x0) этой точки, и если, для любого сколь угодно малого положительного числа ε > 0, существует такое число δε > 0, зависящее от ε, что для всех x, принадлежащих δε — окрестности точки x0: , значения функции принадлежат ε — окрестности точки f(x0):
.
Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.
Легко видеть, что определение непрерывности отличается от определения предела только тем, что вместо проколотой окрестности точки используется просто окрестность точки, которая содержит . При этом значение предела может быть равным только значению функции в этой точке: .
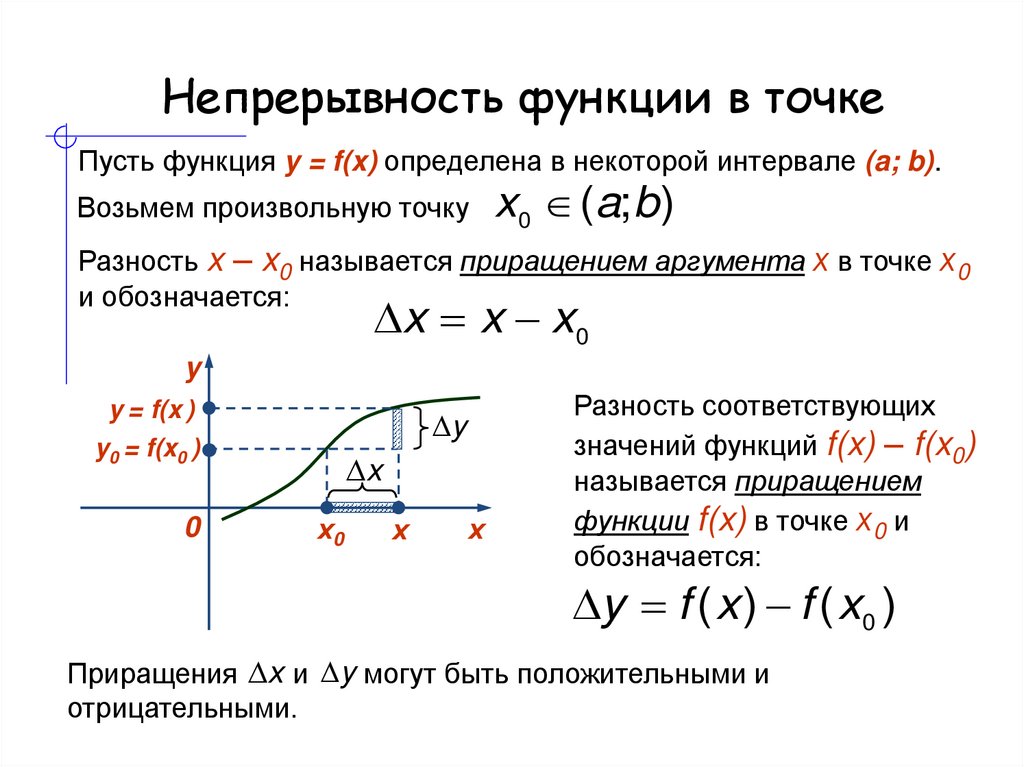
Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Далее мы рассматриваем новую функцию:
.
Ее называют приращением функции в точке . Считаем, что она зависит от переменной : . Тогда можно дать еще одно определение.
- Непрерывность функции в точке в терминах приращений
- Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности этой точки, и если предел приращения этой функции в точке , при , равен нулю:
.
Определение отсутствия непрерывности
Теперь приведем определение того, что функция не является непрерывной в точке .
Определение отсутствия непрерывности функции в точке
Функция , определенная на некоторой окрестности точки не является непрерывной в этой точке,
если предела функции при не существует,
или он не равен значению функции в точке :
.
По Гейне это означает, что существует такая последовательность , для которой предел либо не существует, либо он не равен :
.
По Коши это означает, что существует такое , так что для любого существует , для которого :
.
Непрерывность на концах отрезка
В рассмотренных выше определениях считается, что функция определена на некоторой окрестности слева и справа от точки . Если функция определена на некотором отрезке , то мы можем применять эти определения для внутренних точек отрезка, для которых . Для концов отрезка a и b нужно дать определение односторонней непрерывности, аналогичное определению односторонних пределов.
- Непрерывность функции справа (слева)
- Функция f(x) называется непрерывной справа (слева) в точке x0, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x0 равен значению функции в x0:
.
Примеры
Все примеры Доказать, что следующие функции непрерывны на своих областях определения:
1) , используя определения непрерывности по Гейне и Коши ⇓;
2) , используя определение непрерывности по Коши ⇓.
Пример 1
Все примеры ⇑ Используя определения по Гейне и Коши доказать, что функция непрерывна для всех x.
Решение
Пусть есть произвольное число. Докажем, что заданная функция непрерывна в точке . Функция определена для всех x. Поэтому она определена в точке и в любой ее окрестности.
Используем определение по Гейне
Используем определение непрерывности по Гейне ⇑. Пусть есть произвольная последовательность, сходящаяся к : .
Применяя свойство предела произведения последовательностей имеем:
.
Поскольку есть произвольная последовательность, сходящаяся к , то
.
Непрерывность доказана.
Используем определение по Коши
Используем определение непрерывности по Коши ⇑.
Рассмотрим случай . Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П1.1) .
Применим формулу:
.
Учитывая (П1.1), сделаем оценку:
;
(П1.2) .
Применяя (П1.2), оценим абсолютную величину разности:
;
(П1.3) .
Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П1.3), если и если , то .
Это означает, что для любого положительного всегда найдется . Тогда для всех x, удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .
Теперь рассмотрим точку . В этом случае
.
Вводим положительные числа и :
.
Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что функция непрерывна в точке .
Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна на всей действительной оси.
Пример 2
Все примеры ⇑ Используя определение непрерывности по Коши ⇑ доказать, что функция непрерывна для всех .
Решение
Заданная функция определена при . Докажем, что она непрерывна в точке .
Рассмотрим случай .
Мы вправе рассматривать функцию на любой окрестности точки . Поэтому будем считать, что
(П2.1) .
Применим формулу:
(П2.2) .
Положим . Тогда
.
Учитывая (П2.1), сделаем оценку:
.
Итак,
.
Применяя это неравенство, и используя (П2.2), оценим разность:
.
Итак,
(П2.3) .
Вводим положительные числа и , связав их соотношениями:
.
Согласно свойствам неравенств, если выполняется (П2.3), если и если , то .
Это означает, что для любого положительного всегда найдется . Тогда для всех x, удовлетворяющих неравенству , автоматически выполняется неравенство:
.
Это означает, что функция непрерывна в точке .
Теперь рассмотрим точку . Нам нужно показать, что заданная функция непрерывна в этой точке справа. В этом случае
.
Вводим положительные числа и :
.
Отсюда видно, что для любого положительного всегда найдется . Тогда для всех x, таких что , выполняется неравенство:
.
Это означает, что . То есть функция непрерывна справа в точке .
Аналогичным способом можно доказать, что функция , где n – натуральное число, непрерывна при .
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1.
Москва, 1983.
Knowen — 4.8. Непрерывность функции
Определение 4.20 (по Коши). Функция $f\colon E\to \mathbb {R}$ непрерывна в точке $a\in E$, если
$$\forall \varepsilon >0\ \exists \delta >0\ \forall x \in B_\delta (a)\cap E\colon f(x)\in B_\varepsilon (f(a)).$$
Замечание. Если точка $a$ не является предельной точкой множества $E$, то условие непрерывности в этой точке всегда выполняется. Действительно, $\exists \delta >0\ B_\delta (a)\cap E = \{ a\} \Rightarrow$
$f(B_\delta (a) \cap E) = \{ f(a)\} \subset B_\varepsilon (f(a))$.
Если точка $a$ предельная точка $E$, то утверждение, что $f$ непрерывна в точке $a$, эквивалентно утверждению $\lim \limits _{E\ni x\to a} f(x) = f(a)$.
Определение 4.21 (по Гейне). Функция $f\colon E\to \mathbb {R}$ непрерывна в точке $a\in E$, если
$$\forall \{ x_ n\} , x_ n \in E\ (\lim \limits _{n\to \infty }x_ n = a \Rightarrow \lim \limits _{n\to \infty }f(x_ n) = f(a)).
$$
Теорема 4.11. Определения непрерывности функции по Коши и по Гейне эквивалентны.
$\blacktriangle $ $(\Rightarrow )$ Покажем, что если выполняется определение непрерывности по Коши, то выполняется и определение по Гейне.
Пусть $f\colon E\to \mathbb {R}$ и $\forall \varepsilon >0\ \exists \delta >0\ \forall x\in B_\delta (a) \cap E\colon f(x) \in B_\varepsilon (f(a))\ (*)$
Пусть $x_ n\in E\ x_ n\to a$, тогда $\exists N\ \forall n>N\colon x_ n\in B_\delta (a)\cap E \stackrel{(*)}{\Rightarrow } \forall n > N\colon f(x_ n) \in B_\varepsilon (f(a))$.
Получим $\forall \varepsilon >0\ \exists N\ \forall n > N\colon f(x_ n) \in B_\varepsilon (f(a))$, т.е. $f(x_ n) \to f(a)$. Определение по Гейне выполняется.
$(\Leftarrow )$ Покажем, что если выполняется определение по Гейне, то выполняется и определение по Коши.
Если точка $a\in E$ не является предельной точкой, то оба определения выполняются.
Если $a\in E$ — предельная точка, то по определению предела функции по Гейне $\lim \limits _{E\ni x\to a} f(x) = f(a)$, а значит, $f$ непрерывна в точке $a$ в смысле определения Коши.
$\blacksquare $
Определение 4.22. Пусть $f\colon E\to \mathbb {R}, a$ — предельная точка $E$. Функция $f$ разрывна (имеет разрыв) в точке $a$, если функция $f$ не является непрерывной в этой точке. При этом говорят, что точка $a$ является точкой разрыва функции $f$.
Пример: Пусть $D\colon \mathbb {R}\to \mathbb {R}$, где $D(x) = \begin{cases} 1, x\in \mathbb {Q}\\0, x\in \mathbb {R}\backslash \mathbb {Q}\end{cases}$ — функция Дирихле. Покажем, что функция Дирихле разрывна в каждой точке. Пусть $a\in \mathbb {R}$. Тогда
$\left. \begin{array}{l} \lim \limits _{x\to a} (D|_\mathbb {Q})(x) = 1,\\\lim \limits _{x\to a} (D|_{\mathbb {R}\backslash \mathbb {Q}})(x) = 0 \end{array}\right\} \Rightarrow \nexists \lim \limits _{x\to a} D(x) \Rightarrow f$ разрывна в точке $a$.
Преемственность | математика | Britannica
- Ключевые люди:
- Рене-Луи Бэр
- Похожие темы:
- функция
Просмотреть весь связанный контент →
непрерывность , в математике, строгая формулировка интуитивного понятия функции, которая изменяется без резких разрывов или скачков.
Функция — это отношение, в котором каждое значение независимой переменной, скажем, x — связано со значением зависимой переменной — скажем, y . Непрерывность функции иногда выражается в том, что если значения x близки друг к другу, то значения y функции также будут близки. Но если на вопрос «Насколько близко?» спрашивается, возникают трудности.
Для близких значений x расстояние между значениями y может быть большим, даже если функция не имеет внезапных скачков. Например, если y = 1,000 x
Напротив, функция, равная 0 для x меньше или равно 1 и равно 2 для x больше 1 не является непрерывным в точке x = 1, потому что разница между значением функции в 1 и в любой точке очень мала больше 1 никогда не меньше 2.Функция называется непрерывной тогда и только тогда, когда она непрерывна в каждой точке своей области определения. Говорят, что функция непрерывна на интервале или подмножестве его области определения тогда и только тогда, когда она непрерывна в каждой точке интервала. Сумма, разность и произведение непрерывных функций с той же областью определения также непрерывны, как и частное, за исключением точек, в которых знаменатель равен нулю. Непрерывность также можно определить в терминах пределов, сказав, что f ( x ) является непрерывным в x 0 своей области определения тогда и только тогда, когда для значений x в своей области
Более абстрактное определение непрерывности может быть дано в терминах множеств , как это делается в топологии, говоря, что для любого открытого набора значений y соответствующий набор значений x также открыт.
(Множество называется «открытым», если каждый из его элементов имеет «окрестность» или охватывающую его область, полностью лежащую внутри множества.) Непрерывные функции — это самый основной и широко изучаемый класс функций в математическом анализе, а также наиболее часто встречающиеся в физических ситуациях.
Эта статья была недавно отредактирована и обновлена Уильямом Л. Хошем.
Непрерывная функция — исчисление
На этой странице перечислены основные термины исчисления. Этот термин широко используется, и полное понимание его определения имеет решающее значение.
См. полный список основных терминов
Содержание
- 1 Определение функций одной переменной
- 1.1 В точке
- 1.2 Определение односторонней сплошности
- 1.3 На интервале
Определение для функций одной переменной
В точке
Рассмотрим функцию и действительное число, которое определено в открытом интервале, содержащем , т.
е. определено в и непосредственно слева и справа от . Мы говорим, что он непрерывен в , если он удовлетворяет следующим эквивалентным определениям:| № | Стенография | Что говорит определение |
|---|---|---|
| 1 | с точки зрения лимитов | . Другими словами, предел существования и равен значению функции при . |
| 2 | с точки зрения односторонних ограничений | . Другими словами, левый предел at , правый предел at и значение at равны. |
| 3 | с точки зрения непрерывности слева и справа | непрерывен как влево, так и вправо в . |
| 4 | Для каждого существует такое, что для всех удовлетворяющих (т. е. ), мы имеем (т. е. ). | |
| 4′ | (вариант) | Для каждого существует такое, что для всех удовлетворяющих (т. е. ), мы имеем (т. е. ). |
| 5 | в пересчете на центрированные открытые шары (то же, что и без символов) | Для каждого открытого шара (т. е. открытого интервала) с центром в , существует открытый шар (т. е. открытый интервал) с центром в так, что образ открытого шара с центром в лежит внутри открытого шара с центром в . [ПОКАЗАТЬ БОЛЬШЕ] |
| 6 | с точки зрения не обязательно центрированных открытых шаров | Для каждого открытого шара (т. е. открытого интервала), содержащего , существует открытый шар, содержащий такой, что образ открытого шара, содержащего , лежит внутри открытого шара, содержащего . |
Определение односторонней непрерывности
Левая непрерывность : Рассмотрим функцию и действительное число, такое, что определено в и непосредственно слева от . Мы говорим, что непрерывна слева at, если левый предел at существует и равен , т. е. .
Правая непрерывность : Рассмотрим функцию и действительное число, которые определены в и непосредственно справа от . Мы говорим, что оно непрерывно справа, если правый предел at существует и равен , т.