Непрерывность функции и точки разрыва функции: Непрерывность функции в точке и на промежутке. С примерами

Непрерывность функции в точке и на промежутке. С примерами

• Примеры и условия непрерывности функции. Непрерывность в точке и на промежутке
• Установить непрерывность функции в точке самостоятельно, а затем посмотреть решение
• Что такое непрерывное изменение функции
• Основные свойства непрерывных функций

На этом уроке будем учиться устанавливать непрерывность функции. Будем делать это с помощью пределов, причем односторонних — правого и левого, которые совсем не страшны, несмотря на то что записываются как и .

Но что такое вообще непрерывность функции? Пока мы не дошли до строгого определения, проще всего представить себе линию, которую можно начертить, не отрывая карандаш от бумаги. Если такая линия начерчена, то она непрерывна. Эта линия и является графиком непрерывной функции. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Графически функция непрерывна в точке , если её график не «разрывается» в этой точке.

График такой непрерывной функции — показан на рисунке ниже.

Определение непрерывности функции через предел. Функция является непрерывной в точке при соблюдении трёх условий:

1. Функция определена в точке .

2. Существует предел функции в точке , при этом правый и левый пределы равны: . Правый и левый пределы вычисляются как предел вообще: в выражение функции вместо икса подставляется то, к чему стремится икс, причём вместе с плюс нулём при правом пределе и с минус нулём при левом пределе.

3. Предел функции в точке равен значению функции в этой точке:

А могут ли правый и левый пределы хоть когда-нибудь быть не равны, если к значению, к которому стремится икс, прибавляется или вычитается всего лишь нуль? Могут. Когда и почему — это объяснено на уроке о точках разрыва функции и их видах

.

Если хотя бы одно из перечисленных условий не соблюдено, функция не является непрерывной в точке. При этом говорят, что функция терпит разрыв, а точки на графике, в которых график прерывается, называются точками разрыва функции. График такой функции , терпящей разрыв в точке x=2 — на рисунке ниже.

Пример 1. Функция f(x) определена следующим образом:

Будет ли эта функция непрерывной в каждой из граничных точек её ветвей, то есть в точках x = 0, x = 1, x = 3?

Решение. Проверяем все три условия непрерывности функции в каждой граничной точке. Первое условие соблюдается, так как то, что функция определена в каждой из граничных точек, следует из определения функции. Осталось проверить остальные два условия.

Точка x = 0. Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

.

Предел функции и значение функции в точке x = 0 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Как видим, предел функции и значение функции в точке x = 0 равны. Следовательно, функция является непрерывной в точке x = 0.

Точка x = 1. Найдём левосторонний предел в этой точке:

.

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 1 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 1 равны. Следовательно, функция является непрерывной в точке x = 1.

Точка x = 3. Найдём левосторонний предел в этой точке:

Найдём правосторонний предел:

Предел функции и значение функции в точке x = 3 должны быть найдены при той ветви функции, которая включает в себя эту точку, то есть второй ветви. Находим их:

.

Предел функции и значение функции в точке x = 3 равны. Следовательно, функция является непрерывной в точке x = 3.

Основной вывод: данная функция является непрерывной в каждой граничной точке.

Пример 2. Установить, непрерывна ли функция в точке x = 2.

Правильное решение и ответ.

Пример 3. Установить, непрерывна ли функция в точке x = 8.

Правильное решение и ответ.

Непрерывное изменение функции можно определить как изменение постепенное, без скачков, при котором малое изменение аргумента влечёт малое изменение функции .

Проиллюстрируем это непрерывное изменение функции на примере.

Пусть над столом висит на нитке груз. Под действием этого груза нитка растягивается, поэтому расстояние l груза от точки подвеса нити является функцией массы груза m, то есть l = f(m), m≥0.

Если немного изменить массу груза, то расстояние l изменится мало: малым изменениям m соответствуют малые изменения l. Однако если масса груза близка к пределу прочности нити, то небольшое увеличение массы груза может вызвать разрыв нити: расстояние l скачкообразно увеличится и станет равным расстоянию от точки подвеса до поверхности стола. График функции l = f(m) изображён на рисунке. На участке этот график является непрерывной (сплошной) линией, а в точке он прерывается. В результате получается график, состоящий из двух ветвей. Во всех точках, кроме , функция l = f(m) непрерывна, а в точке она имеет разрыв.

Исследование функции на непрерывность может быть как самостоятельной задачей, так и одним из этапов полного исследования функции и построения её графика.

Непрерывность функции на промежутке

Пусть функция y = f(x) определена в интервале ]a, b[ и непрерывна в каждой точке этого интервала.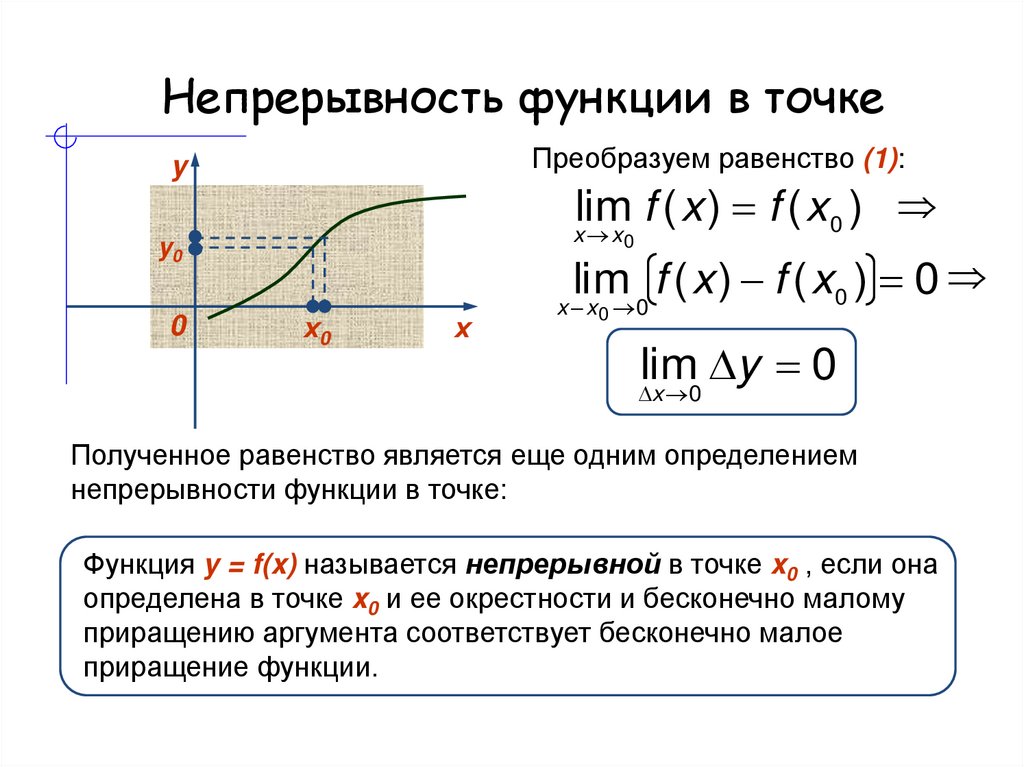 Тогда она называется непрерывной в интервале ]a, b[. Аналогично определяется понятие непрерывности функции на промежутках вида ]- ∞, b[, ]a, + ∞[, ]- ∞, + ∞[. Пусть теперь функция y = f(x) определена на отрезке [a, b]. Разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок. Здесь следует упомянуть о так называемой односторонней непрерывности: в точке a, оставаясь на отрезке [a, b], мы можем приближаться только справа, а к точке b — только слева. Функция называется непрерывной на отрезке [a, b

], если она непрерывна во всех внутренних точках этого отрезка, непрерывна справа в точке a и непрерывна слева в точке b.

Примером непрерывной функции может служить любая из элементарных функций. Каждая элементарная функция непрерывна на любом отрезке, на котором она определена.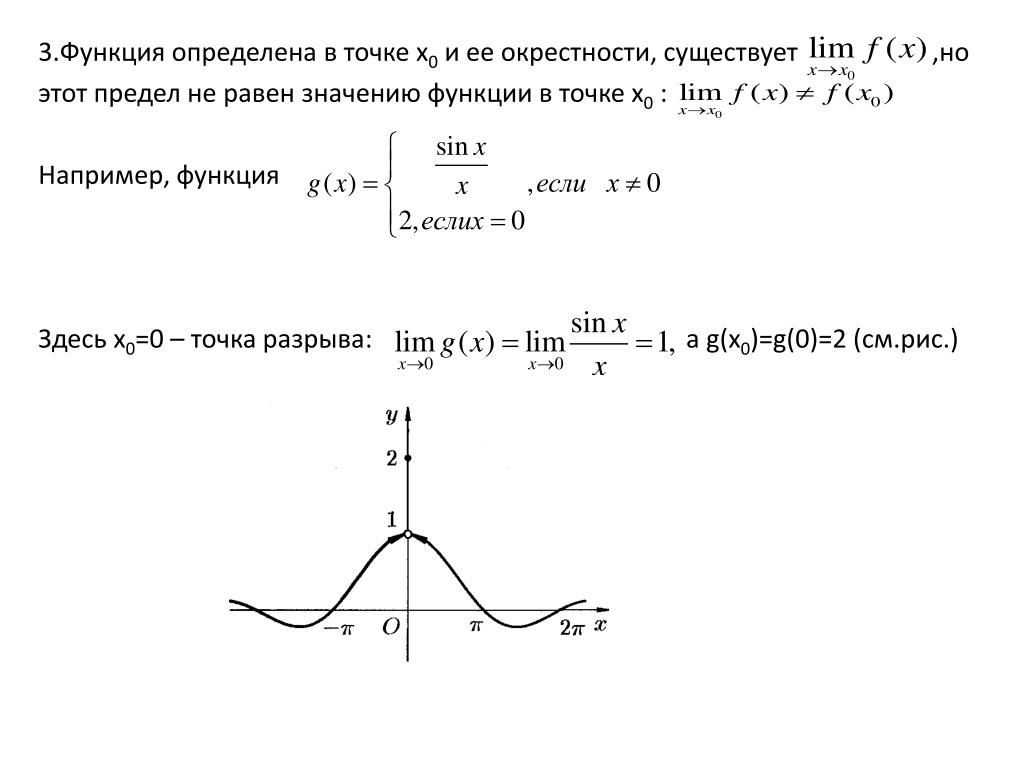 Например, функции и непрерывны на любом отрезке [a, b], функция непрерывна на отрезке [0, b], функция непрерывна на любом отрезке, не содержащем точку a = 2.

---

Пример 4. Исследовать функцию на непрерывность.

Решение. Проверяем первое условие. Функция не определена в точках — 3 и 3. По меньшей мере одно из условий непрерывности функции на всей числовой прямой не выполняется. Поэтому данная функция является непрерывной на интервалах

.

---

Пример 5. Определить, при каком значении параметра a непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

.

Найдём правосторонний предел при :

.

Очевидно, что значение в точке x = 2 должно быть равно ax:

Ответ: функция непрерывна на всей области определения при a = 1,5.

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Производная, дифференциал и их применение

Пройти тест по теме Предел

---

Пример 6. Определить, при каких значениях параметров a и b

непрерывна на всей области определения функция

Решение.
Найдём левосторонний предел функции в точке :

.

Следовательно, значение в точке должно быть равно 1:

.

Найдём левосторонний функции в точке :

.

Очевидно, что значение функции в точке должно быть равно :

Ответ: функция непрерывна на всей области определения при a = 1; b = -3.

К понятию непрерывной функции математика пришла, изучая в первую очередь различные законы движения. Пространство и время бесконечны, и зависимость, например, пути s от времени t, выраженная законом s = f(t), даёт пример непрерывной функции f(t).

Непрерывно изменяется и температура нагреваемой воды, она также является непрерывной функцией от времени: T = f(t).

В математическом анализе доказаны некоторые свойства, которыми обладают непрерывные функции. Приведём важнейшие из этих свойств.

1. Если непрерывная на интервале функция принимает на концах интервала значения разных знаков, то в некоторой точке этого отрезка она принимает значение, равное нулю. В более формальном изложении это свойство дано в теореме, известной как первая теорема Больцано-Коши.

2. Функция f(x), непрерывная на интервале [a, b], принимает все промежуточные значения между значениями в концевых точках, то есть, между f(a) и f(b). В более формальном изложении это свойство дано в теореме, известной как вторая теорема Больцано-Коши.

3. Если функция непрерывна на интервале, то на этом интервале она достигает своего наибольшего и своего наименьшего значения: если m — наименьшее, а M — наибольшее значение функции на интервале [a, b], то найдутся на этом отрезке такие точки и , что и . Теорема, в которой изложено это свойство, называется второй теоремой Вейерштрасса.

Пример 7. Используя первое из приведённых выше свойств непрерывных функций, доказать, что уравнение имеет по меньшей мере один вещественный корень в интервале [1; 2].

Решение.

Пусть .

Вычислим значения функции при x = 1 и x = 2.

.

.

Получили, что функция на концах интервала принимает значения разных знаков:
и , т. е.

Следовательно, в интервале [1; 2] существует такое число a, при котором f(a) = 0. То есть, уравнение имеет по меньшей мере один вещественный корень в данном интервале.

Установление непрерывности функции может быть как самостоятельной задачей, так и частью Полного исследования функции и построения графика.

Пример 8. Есть ли у уравнения хотя бы один вещественный корень?

Решение.
Функция определена на интервале .

Вычислим значения функции при x = 0 и .

.

.

Получили
и .

Следовательно, существует такое число a, при котором f(a) = 0. Ответ на вопрос задачи: уравнение имеет по меньшей мере один вещественный корень.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Предел

Весь раздел «Исследование функций»

• Непрерывность функции
• Точки разрыва функции и их виды
• Экстремумы функции
• Наименьшее и наибольшее значения функции
• Асимптоты
• Возрастание, убывание и монотонность функции
• Выпуклость и вогнутость графика функции, точки перегиба
• Полное исследование функций и построение графиков
• Функции двух и трёх переменных
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

4.

Непрерывность функций. Точки разрыва и их классификация

4.1. Основные теоретические сведения

Определение. Функция у = f(x) называется непрерывной в точке х₀, если эта функция определена в какой-нибудь окрестности точки х₀ и если

то есть бесконечно малому приращению аргумента в окрестности точки х₀ соответствует бесконечно малое приращение функции.

Определение. Функция у=f(x) непрерывна в точке х₀, если она определена в некоторой окрестности этой точки и если предел функции при стремлении независимой переменной х к х₀ существует и равен значению функции при х=х₀, то есть

Определение. Пусть х → х₀, оставаясь все время слева от х₀. Если при этом условии f(x) стремится к пределу, то он называется левым пределом функции f(x) в точке х₀, то есть

Аналогично определяется и правый предел

Определение. Функция непрерывна в точке х₀ если:

• функция определена в точке х₀;

• существуют левый и правый пределы функции f(x) при х → х₀;

• все три числа (х₀), f(x₀ –0), f(x₀ +0) совпадают, то есть

Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой его точке.

Теорема. Если две функции f(x) и g(x) определены в одном и том же

интервале и обе непрерывны в точке х₀, то в той же точке будут непрерывны и функции

Теорема. Сложная функция, состоящая из конечного числа непрерывных функций, является непрерывной.

Все основные элементарные функции непрерывны в своей области определения.

Определение. Если в какой-либо точке х₀ функция не является непрерывной, то точка х₀ называется точкой разрыва функции, а сама функция – разрывной в этой точке.

Определение. Если в точке х₀ существует конечный lim f(x) = А

(левосторонний и правосторонний пределы существуют, конечны и равны между собой), но он не совпадает со значением функции в точке, или же функция в точке не определена, то точка х₀ называется точкой устранимого разрыва.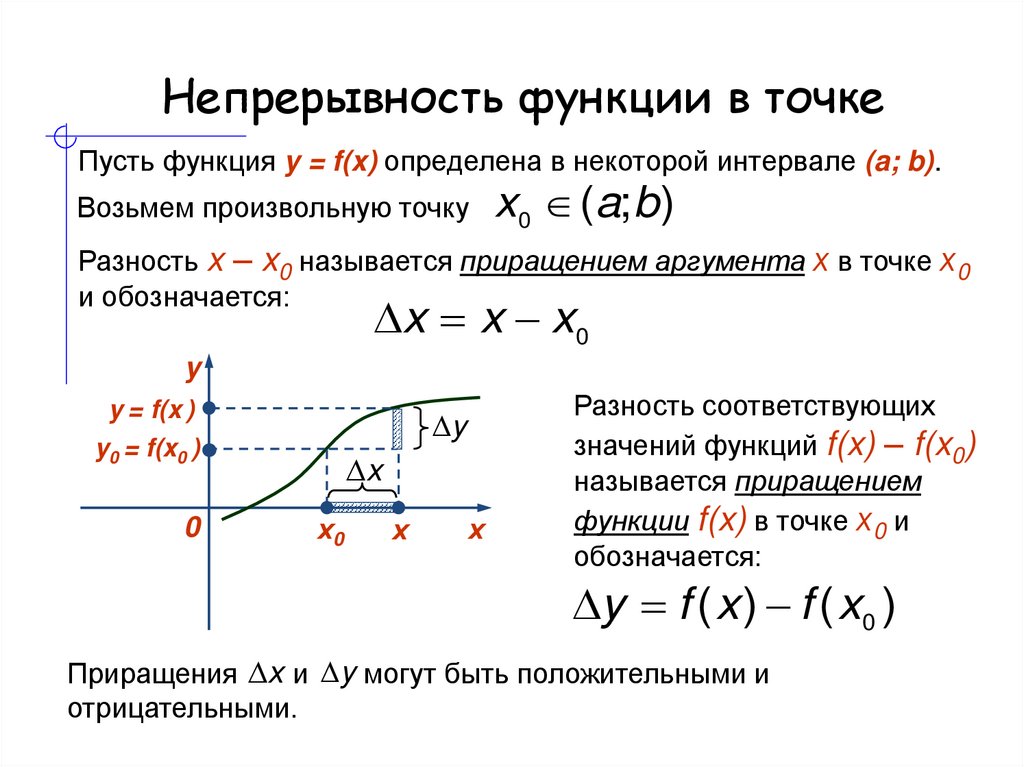 Принятое изображение точки устранимого разрыва представлено на рис. 1.

Рис. 1

Определение. Точкой разрыва первого рода или точкой конечного разрыва называется такая точка х₀, в которой функция имеет левый и правый конечные пределы, но они не равны между собой.

На рис. 2 приведено графическое представление разрыва функции первого рода в точке х₀

Рис.2

Определение. Если хотя бы один из пределов f(x₀ – 0) или f(x₀ + 0) не существует или бесконечен, то точка х₀ называется точкой разрыва, второго рода.

Графические представления разрывов функций второго рода в точке х₀ приведены на рис. 3 (а, б, в).

Приведенные выше определения непрерывности функции f(x) в точке х₀

представлены на рис. 4, где отмечено, что основной посылкой при определении непрерывности функции (необходимым условием) в точке х₀ является то, что f(x) определена в точке и ее окрестности.

Рис.3

Пример Исследовать на непрерывность, определить характер точек разрыва,

изобразить в окрестности точек разрыва функцию

Решение.

Это рациональная функция Она определена и непрерывна при всех значениях х, кроме х = 1, так как при х = 1 знаменатель обращается, в нуль. В точке х = 1 функция терпит разрыв. Вычислим предел этой функции при

х → 1, имеем

Конечный предел функции при х→ 1 существует, а функция в точке

х = 1 не определена; значит точка х = 1 является точкой устранимого разрыва.

Если доопределить функцию, то есть положить f (1) = 5, то функция

будет непрерывной.

Рис. 4

Поведение функции в окрестности точки х = 1 изображено на рис. 4.

Замечание. Данная функция

неопределенная при х = 1, совпадает с непрерывной функцией

во всех точках кроме х =1

Пример.

Исследовать на непрерывность функцию и определить характер ее точек разрыва

Решение.

Область определения функции – вся числовая ось. На интервалах(–, 0), (0,+) функция непрерывна. Разрыв возможен только в точке х = 0, в которой изменяется аналитическое задание функции.

Найдем односторонние пределы функции:

Левый и правый пределы хотя и конечны, но не равны между собой. Поэтому в точке х = 0 функция имеет разрыв первого рода. Скачок функции в точке разрыва равен

Поведение функции в окрестности точки х = 0 изображено на рис. 5.

Рис. 5

Пример Исследовать функцию f(x) на непрерывность, определить характер ее точек разрыва, изобразить ее поведение в окрестности точек разрыва.

Решение.

Функция определена и непрерывна на всей числовой оси, кроме точек х, = –2 и х₂ = 2, причем

не существует.

Вычисляем односторонние пределы в точке х, = –2.

Итак, в точке х = –2 функция терпит разрыв второго рода. Исследуем характер разрыва функции в точке х₂ =2. Имеем

В точке х₂ =2 функция также терпит разрыв второго рода.

Поведение функции в окрестности точек х_х= –2 и х₂ = 2 изображено на рис. 6.

Рис.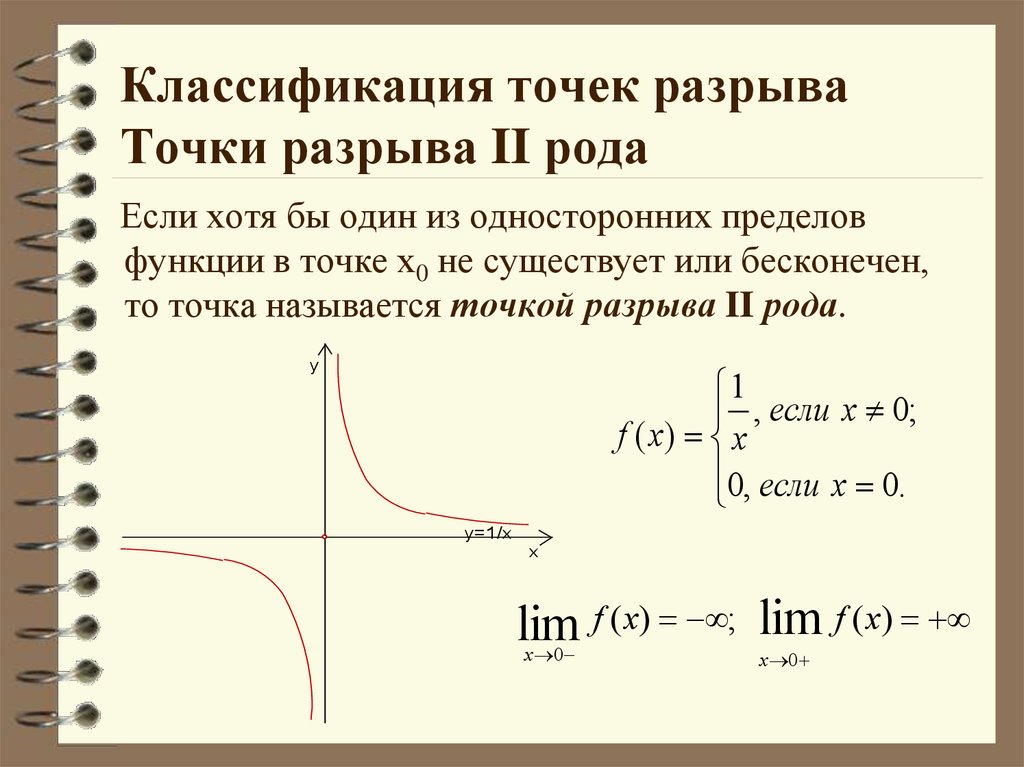 6

Пример.

Исследовать функцию f(x) = e^x+i на непрерывность, определить характер точек разрыва, изобразить поведение функции в окрестности точек разрыва.

Решение.

Функция неопределена прих = –3, поэтому функция непрерывна при всехкромех = –3. Определим характер разрыва функции. Имеем

то есть один из пределов равен бесконечности, а значит функция терпит разрыв

второго рода.

Поведение функции f(x) = e^x+3 в окрестности точки разрыва х = –3 изображено на рис. 7

Рис. 7

4.2. Упражнения для самостоятельной работы студентов

1. Исследовать функции на непрерывность, определить характер их точек разрыва, изобразить графически поведение функций в окрестности

2. 2 = 2x$, который отлично оценивается при $x=0$. Итак, я заключаю, что функция дифференцируема при $x=0$.

Вопрос

Верно ли это? Или я, возможно, что-то упускаю из виду?

• реальный анализ
• производные
• непрерывность

$\endgroup$

2

$\begingroup$

РЕДАКТИРОВАТЬ: Неправильный ответ

Функция. $f$ дифференцируема при $x=0$, если

$$ \lim_{h \rightarrow 0} \dfrac{f(0+h) — f(0)}{h} $$ 92}= \lim_{h \rightarrow 0} \dfrac{1-cos(h)}{h}\lim_{h \rightarrow 0}\frac{1}{h}=\lim_{h \rightarrow 0}\ гидроразрыв{1}{ч}$$ Этот предел не существует, поэтому $f'(0)$ не существует.

$\endgroup$

2

$\begingroup$

Возможно, вы слишком много думаете об этом.

Функция А. $f$ дифференцируема при $x=0$, если

$$ \lim_{h \rightarrow 0} \dfrac{f(0+h) — f(0)}{h} $$

существует. Возможно, рассмотрим пределы левой и правой руки. Они равны? Что можно сделать, если их нет?

$\endgroup$

$\begingroup$

Как я упоминал в своем комментарии, покажите, что обе односторонние производные существуют и равны друг другу при $x = 0$.

1. Предел существует тогда и только тогда, когда существуют оба односторонних предела.
2. Производная — это предел.
3. Следовательно, производная существует тогда и только тогда, когда существуют обе односторонние производные. 92$ при $x = 0$ равно $0$.
4. Вычислите производную от $\dfrac{1-\cos x}x$ при $x = 0$. Назовем ее $L$ (если она вообще существует, а если нет, то $f(x)$ не дифференцируема при $x = 0$).
5. Примените факт из шага 3, чтобы (немедленно) получить, что правая производная $\dfrac{1-\cos x}x$ равна $L$.
6. Наконец, $f(x)$ дифференцируема при $x = 0$ тогда и только тогда, когда $L = 0$.

$\endgroup$

Непрерывность

Непрерывность

Во многих случаях вы можете вычислить, подставив x вместо x:

Например,

Эта ситуация возникает достаточно часто, чтобы иметь название.

Определение. Функция А является 90 105 непрерывным 90 106 в a, если

Это определение действительно включает в себя три вещи, каждая из которых вам нужна. проверить, чтобы показать, что f непрерывна в a:

1. определяется.

2. определяется.

3. Оба равны: .

Что это означает геометрически? Вот три критерия выше изобразительным языком:

1. «определено» означает, что на графике есть точка в а.

2. «определяется» означает график приближается к одному числовому значению, когда вы приближаетесь к a.

3. » » означает что значение, к которому вы приближаетесь, — это значение, которое фактически принимает f на — «без сюрпризов».

Первый критерий означает, что в график. Это также исключает вертикальные асимптоты. Вот некоторые фотографии этих видов разрывы :

Второй критерий означает, что граф не может «прыгать» на а. Это разрыв прыжка :

Разрыв скачка возникает, когда левый и правый пределы не равны.

Третий критерий означает, что граф «заполнен» на как и следовало ожидать. Вы не приближаетесь к ожидая одно значение, а затем обнаруживая, что это что-то отличается, как вы делаете ниже:

Это называется съемным разрывом . потому что вы можете сделать функцию непрерывной, заполнив дыра. С точки зрения ограничений, это означает, что существует, но .

Вот некоторые классы непрерывных функций:

(a) Многочлен непрерывен для всех x.

(b) непрерывна для всех x.

(c) Тригонометрические функции непрерывны везде, где они определены.

(d) непрерывна при всех x и непрерывна при .

(e) непрерывен для всех x, для которых определенный.

Утверждение о многочленах, например, следует из свойства пределов. Если многочлен, я показал, что

Именно это и означает быть непрерывным в в.

Например, непрерывно для всех x, так как это многочлен.

Утверждение for является довольно простым предельным доказательством, но я не буду его приводить. это. И операторы для триггерных функций, , и зависят от тщательного определения этих функций; Я обсужу кое-что из этого позже. В качестве примера высказывания о триггерных функций, непрерывен для всех x, кроме нечетных кратно . (не определено нечетным кратно .)

Предельное доказательство для не слишком сложно, но как только вы результаты на и , вы можете использовать тот факт, что

Вы должны убедиться, что корень, который вы берете, определен в точка.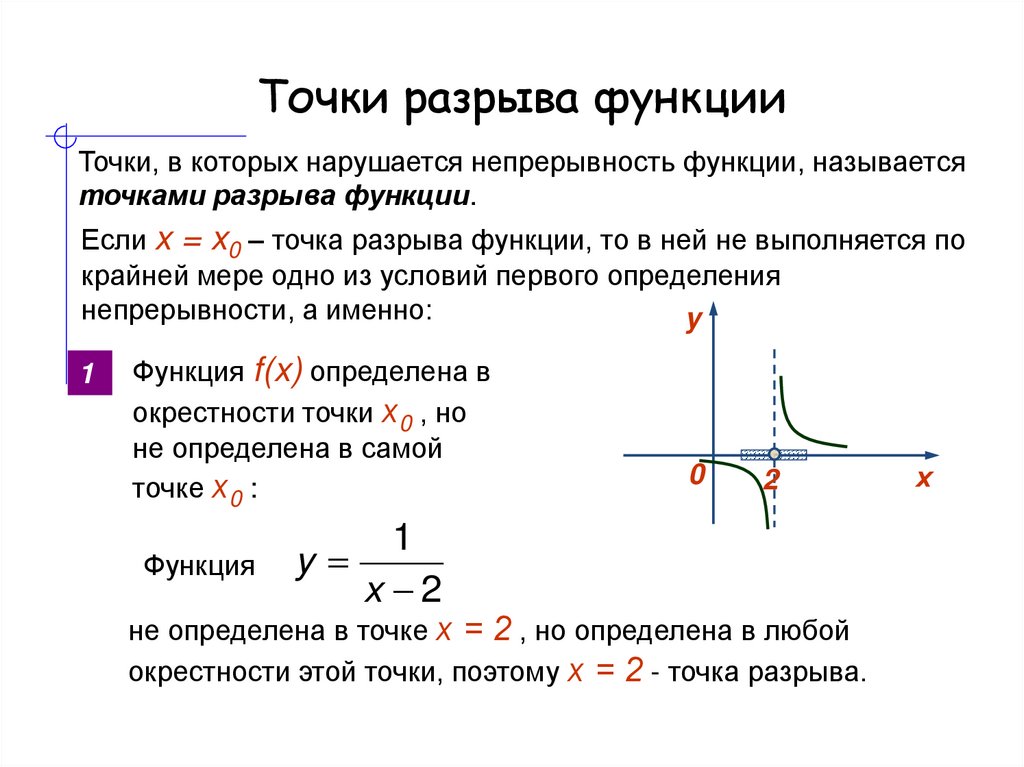 Например, является непрерывным для . Помните, что это не определено для .

---

Пример. Какой разрыв имеет ?

Обратите внимание, что

Однако не определено. Поэтому есть съемный разрыв в . Я мог бы сделать функцию непрерывной в определяя .

---

Пример. Пусть

Какой разрыв имеет при ?

Обратите внимание, что

Таким образом, левый и правый пределы не равны. Следовательно, там является разрывом скачка при .

---

Вы также можете получить непрерывные функции, комбинируя непрерывные функционирует различными способами.

Теорема. (a) Если f и g непрерывны в точке , то и их сумма .

(b) Если f и g непрерывны в точке , то и их разность .

(c) Если f и g непрерывны в точке , то их произведение .

(d) Если f и g непрерывны в точке , и если , то частное непрерывно в .

(e) Если f непрерывна в точке и если g непрерывна в точке , то композиция непрерывна в точке .

Доказательство. Доказательства довольно легкие следствия наших теорем о пределах. Я докажу (с) на примере.

Предположим, что f и g непрерывны в точке . Это значит, что

Умножая левую и правую части, я получаю

По правилу предела произведения

Поэтому,

Вот что значит быть непрерывным при .

---

Вот несколько иллюстраций к этим правилам.

Так как и непрерывны для всех x, их сумма и их произведение непрерывны для все х.

Фактор непрерывен для всех x, кроме (где частное не определено).

Композиция — важный метод построения непрерывного функции. Например, непрерывно для всех x. многочлен также непрерывен при всех x. Композит

Он непрерывен для всех x.

---

Пример. Пусть

При каких значениях x функция f непрерывна?

Функция непрерывна, за исключением, возможно, «разрыва». точки» между тремя частями. Я должен проверить точки и по отдельности.

В ,

Поскольку левые и правые пределы не совпадают,

Следовательно, f не является непрерывным в точке .

В ,

Левый и правый пределы совпадают, поэтому

Теперь, так

Следовательно, f непрерывна в точке .

Вывод: f непрерывно для всех x, кроме .

---

Пример. Пусть

При каких значениях x функция f непрерывна?

f является частным двух полиномов, а полиномы непрерывны для всех х. Следовательно, непрерывна во всех точках, кроме тех, которые делают дно равным 0.

Напишите ф как

Следовательно, f непрерывна для всех x, кроме и . (Обратите внимание, что вы не можете отменить -terms, пока не увидите, где f не определено.)

Однако разрыв at является устранимым разрывом:

не определено, но если бы я определил , то новое значение f было бы непрерывным в точке .

С другой стороны, разрыв at является вертикальным асимптота; независимо от того, как я определяю, функция будет по-прежнему быть прерывистым в .

---

Непрерывные функции имеют промежуточное значение свойство . Грубо говоря, это говорит о том, что если непрерывная функция переходит от одного значения к другому, он не пропускает значения в между. Это соответствует геометрической интуиции, согласно которой граф непрерывной функции не имеет пробелов, скачков или дыр. Здесь это точное утверждение.

Теорема. ( Промежуточное значение Теорема ) Пусть — непрерывная функция на отрезке . Если m — число между и , то в интервал такой, что

Теорема проиллюстрирована на картинке ниже:

Попробуйте сами: выберите любую высоту m между и . Двигайтесь горизонтально от вашего выбранной высоты к графику, затем вниз от графика, пока не нажмете ось х. Место, где вы попали на ось X, находится в точке c. Ты всегда будешь сделать это, если f непрерывна. Интуитивная идея состоит в том, что, будучи непрерывный, f не может пропустить ни одно значение при переходе от к .

Доказательство теоремы о промежуточном значении использует некоторые глубокие свойства реальных чисел, поэтому я не буду приводить его здесь. По крайней мере, вы можете видеть из рисунка, что результат геометрически обоснован.

Теорема иллюстрирует важный момент: Вы можете знать что-то существует без возможности найти это.

Если я возьму ключи от твоей машины и брошу их в соседнее кукурузное поле, ты знаю что твои ключи в поле — но найти их — это отдельная история!

Теорема о промежуточном значении говорит, что существует число с таким что . Это не говорит вам, как найти это, хотя обычно вы можете аппроксимировать с настолько близко, насколько вам нужно.

И кстати — может быть более чем один номер c который работает. Несмотря на то, что формулировка теоремы гласит: «Там есть» (единственное число), математики используют эти слова для обозначения «есть по крайней мере

---

Пример. Предположим, что f — непрерывная функция, , и . Докажите, что для некоторого числа x между 4 и 7, .

Поскольку и непрерывны, непрерывно. Подключите 4 и 7:

42 находится между 27 и 51, поэтому я могу применить промежуточное значение Теорема к . Он говорит, что между 4 и 7 такие, что .

---

Пример. Приблизительное решение задачи уравнение

Вот график:

Похоже, что есть корень между -0,5 и 0.

Умный человек мог бы сказать в этот момент: «Почему бы просто не посмотреть вверх? общая формула решения уравнения 5-й степени?» все, есть общая квадратичная формула для квадратичных.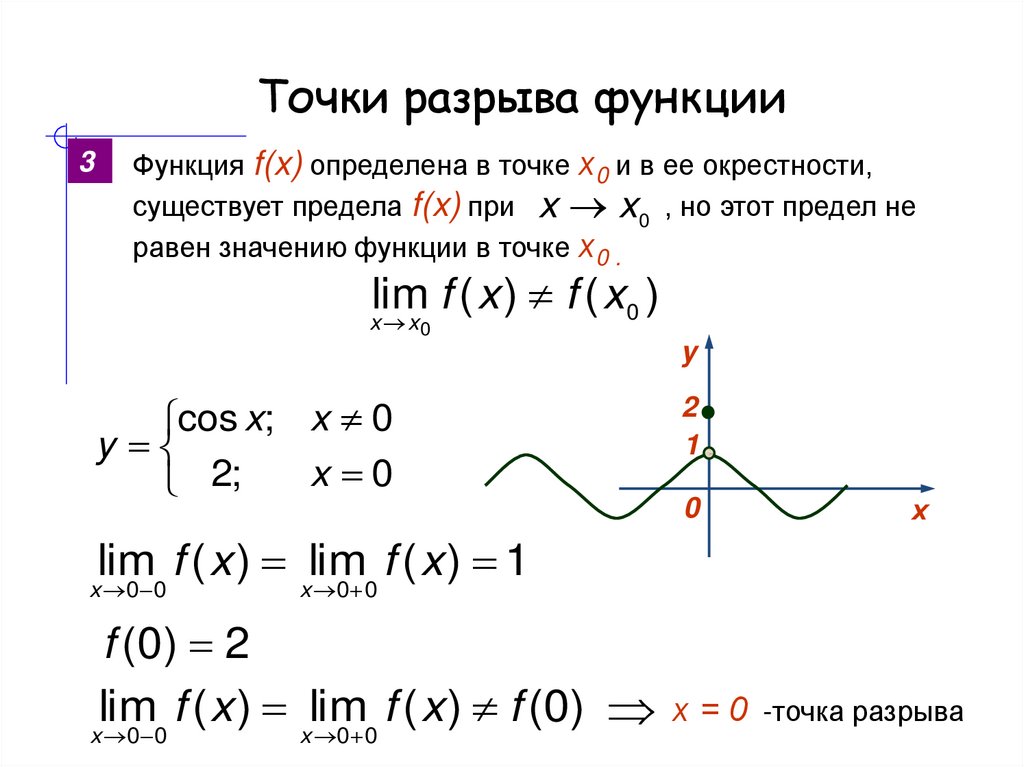 .. и есть общая кубическая формула и общая формула четвертой степени, хотя вам, вероятно, придется искать их в книге таблиц.

К сожалению, вы никогда не найдете общей формулы пятой степени ни в одном книга столов. Нильс Хенрик Абель и Паоло Руффини показали почти 150 лет назад не было общего квинтика, а Эварист Галуа чуть позже показал, что с высшим образованием не повезет уравнения же.

Можно еще аппроксимировать корень, а промежуточный Теорема о ценности гарантирует , что она существует.

f (будучи многочленом) заведомо непрерывен. В этой ситуации IVT говорит, что f не может перейти от отрицательного к положительному без прохождения через 0 где-то посередине.

Заметить, что

Таким образом, я знаю, что есть корень между -0,5 и 0.

Я аппроксимирую корень на пополам . В каждый шаг, я буду знать, что корень пойман между двумя числами. Больной подключите середину к f.