Неравенств знаки: Знаки неравенств — урок. Алгебра, 8 класс.

01Математика — 9 класс. Алгебра — Точки и знаки в методе интервалов

Skip to main content

2. Классы
3. 9 класс. Алгебра
4. 07. Метод интервалов и рациональные неравенства
5. Теория: 02. Точки и знаки в методе интервалов

• 1Точки и знаки в нестрогом неравенстве
• 2знакопостоянство в неравенстве
• 3Точки и неравенства
• 4знаки и неравенства

Задание

Решение

Найдем корни числителя \(\displaystyle x-1 \) и знаменателя \(\displaystyle x-3{\small : } \)

\(\displaystyle x-1=0 \) или \(\displaystyle x-3=0{ \small ,} \)

\(\displaystyle x=1 \) или \(\displaystyle x=3{\small .} \)

Поскольку знак неравенства нестрогий, то 

• все нули числителя, которые не обращают в ноль знаменатель, обозначаются закрашенными;
• все нули знаменателя всегда обозначаются выколотыми.

Так как \(\displaystyle x=1\) обращает в ноль числитель и не обращает в ноль знаменатель, то она обозначается закрашенной. Поскольку \(\displaystyle x=3 \) обращает в ноль знаменатель, то она обозначается выколотой:

 

Получили три интервала:

\(\displaystyle (-\infty;1){ \small ,} \, (1;3)\) и \(\displaystyle (3;+\infty){\small .}\)

Определим знак функции \(\displaystyle f(x)=\frac{x-1}{x-3}\) на каждом из интервалов. Для этого вычислим значение функции \(\displaystyle f(x)=\frac{x-1}{x-3}\) в произвольно выбранной точке интервала.

На интервале \(\displaystyle (-\infty;1) \) функция \(\displaystyle f(x) \) положительна

Для интервала \(\displaystyle (-\infty;1)\) выберем \(\displaystyle x=0 \in (-\infty;1){\small .}\) Определим знак значения функции в точке \(\displaystyle x=0{ \small :}\)

\(\displaystyle f(0)=\frac{0-1}{0-3}>0{\small .}\)

Пишем знак плюс в интервале \(\displaystyle (-\infty;1){\small :}\)

На интервале \(\displaystyle (1;3) \) функция \(\displaystyle f(x) \) отрицательна

Для интервала \(\displaystyle (1;3)\) выберем \(\displaystyle x=2 \in (1;3){\small . }\) Определим знак значения функции в точке \(\displaystyle x=2 { \small :}\)

\(\displaystyle f(2)=\frac{2-1}{2-3}<0{\small .}\)

Пишем знак минус в интервале \(\displaystyle (1;3){\small :}\)

На интервале \(\displaystyle (3;+\infty) \) функция \(\displaystyle f(x) \) положительна

Для интервала \(\displaystyle (3;+\infty)\) выберем \(\displaystyle x=4 \in (3;+\infty){\small .}\) Определим знак значения функции в точке \(\displaystyle x=4 { \small :}\)

\(\displaystyle f(4)=\frac{4-1}{4-3}>0{\small .}\)

Пишем знак плюс

в интервале \(\displaystyle (3;+\infty){\small :}\)

Таким образом, получили следующие знаки на интервалах \(\displaystyle (-\infty;1){ \small ,} \, (1;3)\) и \(\displaystyle (3;+\infty){\small :}\)

Вход

Войти через

Регистрация

080. Решение рациональных неравенств методом . интервалов

Рациональным неравенством называется неравенство, в которое входят только рациональные функции (выражения).

Неравенства вида (или (или ) обычно решают Методом интервалов. Здесь , , – это рациональные функции (многочлены степеней и , т. е. ;

).

Метод интервалов основывается на важном свойстве рациональной функции: в интервале между двумя соседними критическими точками рациональная функция принимает либо только положительные, либо только отрицательные значения, т. е. сохраняет знак.

Если мы рассматриваем двучлен тогда точка делит числовую ось на две части: справа от точки двучлен принимает положительные значения, а слева от точки двучлен принимает отрицательные значения (рис. 6.1).

При использовании метода интервалов нужно придерживаться приведенной ниже последовательности действий.

1. Рациональное неравенство приводим к стандартному виду: или (в случае строгого неравенства), или (в случае нестрогого неравенства).

2. Числитель и знаменатель левой части неравенства раскладываем на множители.

3. Находим все критические точки рациональной функции.

4. Разбиваем числовую ось критическими точками на конечное число интервалов.

5. Определяем знак левой части неравенства на каждом интервале, то есть на интервале справа от наибольшего значения критической точки ставим знак «+», на следующем за ним интервале (справа налево) ставим знак «–», потом – знак «+», потом – знак «–» и так далее. Важно помнить, что все вышесказанное имеет место только для многочленов

Стандартного вида: когда перед переменной такого многочлена стоит знак «+», то есть, например, а не .

Если многочлен имеет нестандартный вид , тогда справа от наибольшей критической точки (числа) не обязательно будет стоять знак «+». Потому, неравенства нестандартного вида можно решать таким образом: найти знак левой части неравенства на любом интервале (не обязательно на последнем интервале справа), а дальше на соседних интервалах будут противоположные знаки.

6. Записываем решение неравенства в виде интервалов. Тогда множеством всех решений неравенств вида или будет объединение всех интервалов, где стоит знак «+». А множест-вом всех решений неравенств вида или будет объединение всех интервалов, где стоит знак «–».

При этом, если неравенство нестрогое, то точки, которые соответствуют множителям числителя, отмечаем на числовой оси полными кружками. А точки, которые соответствуют множителям знаменателя, – отмечаем пустыми кружками. Если неравенство строгое, тогда отмечаем все точки пустыми кружками.

При решении неравенств нужно найти ОДЗ неравенства и с его помощью проверить полученные результаты.

ОДЗ неравенства – это множество всех значений переменных, при которых обе части неравенства имеют смысл.

Рассмотрим более подробно использование метода интервалов для решения целых рациональных и дробно-рациональных неравенств с одним неизвестным.

Любое рациональное неравенство ‑ой степени с одним неизвестным можно привести к стандартному (или каноническому) виду:

;

;

Или ;

.

Рассмотрим Общую схему решения таких неравенств методом интервалов на примере неравенства вида:

.

1. Разложим левую часть неравенства на множители:

.

2. Запишем множители левой части неравенства с нечетными показателями как множители первой степени. Множители с четными показателями можно опустить (не писать), т. к. они не изменяют знак неравенства. При этом обязательно выпишем те значения , при которых множители с четными показателями обращаются в нуль. Тогда неравенство примет вид:

;

При оно равносильно неравенству , при оно равносильно неравенству .

3. Отметим на числовой оси числа (– наибольшее число) (рис. 6.2).

4. Справа от ставим знак «+» и проводим «кривую знаков» через каждое число (рис. 6.3).

5. Выбираем нужный нам знак (в нашем случае это знак «+») и записываем ответ в виде интервалов (рис. 6.4). При этом исключаем из найденных решений те значения переменных, при которых множители левой части неравенства с четными показателями обращаются в ноль.

Записываем ответ в виде: .

Пример 6. Решите неравенство .

Решение. ОДЗ: Найдем нули выражения , это будут значения или . Отметим найденные значения на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале. Знак исходного неравенства «+», потому решением неравенства будет объединение двух интервалов (рис. 6.5).

Ответ. .

Пример 7. Решите неравенство .

Решение. Изменяем знак перед переменной в первой скобке и получаем неравенство равносильное данному. Разбиваем область допустимых значений на три интервала (в соответствии со значениями в критических точках): . Находим знак на каждом интервале. Знак исходного неравенства «–», поэтому решением неравенства будет объединение двух интервалов (рис. 6.6).

Ответ. .

Пример 8. Решите неравенство .

Решение. Множитель не изменит знак неравенства при . Тогда исходное неравенство можно записать в виде . Разбиваем область допустимых значений на два интервала (в соответствии со значениями в критических точках) , и находим знак на каждом интервале. Знак исходного неравенства «+», поэтому решением неравенства будет объединение двух интервалов (рис. 6.7)

Ответ. .

Пример 9. Решите неравенство .

Решение. 1. Дискриминант квадратного трехчлена равен: первый коэффициент значит, выражение при и не изменяет знак неравенства.

2. Выражение при . Следовательно, это выражение также не изменяет знак неравенства.

3. Изменим знак перед переменной в первой скобке. Для этого умножим обе части неравенства на и запишем все множители неравенства как множители в первой степени. Выражение не изменяет знак неравенства, потому его можно не записывать, однако нужно проверить, является ли точка решением исходного неравенства. Получим: (рис. 6.8).

Точка Не принадлежит области решений исходного неравенства, поэтому эта точка не будет решением неравенства.

Ответ. .

При решении дробно-рациональных неравенств используют следующие утверждения:

1. Неравенства и равносильны неравенствам и соответственно.

2. Неравенства и равносильны системам неравенств и соответственно.

Таким образом, решение дробно-рациональных неравенств, как правило, сводится к решению целых рациональных неравенств.

Пример 10. Решите неравенство .

Решение. ОДЗ неравенства: Запишем исходное неравенство в виде . Нули этого неравенства: Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.9).

Ответ. .

Пример 11. Решите неравенство .

Решение. ОДЗ неравенства: Выполним тождественные преобразования выражения:

.

Запишем исходное неравенство в виде:

Нули этого неравенства: Обозначим эти точки на числовой прямой (с учетом ОДЗ) и найдем знак выражения на каждом интервале (рис. 6.10).

Ответ. .

Метод интервалов удобно использовать и для решения неравенств вида: а также .

Пример 12. Решите неравенство .

Решение. В выражениях и показатели степени – это четные числа, поэтому ; при . Следовательно, эти выражения не изменяют знак неравенства (рис. 6.11). Запишем исходное неравенство в виде равносильного неравенства: .

Значения и Не могут быть решением неравенства, поэтому их нужно исключить из интервала решений.

Ответ. .

< Предыдущая		Следующая >

, ≤, ≥ – легко

В вашем браузере отключен JavaScript.

Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.

Попробуйте 30 дней бесплатно

Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!

• org/ListItem»> Математика
• Средняя школа
• Решение уравнений
• Символы неравенства: <, >, ≤, ≥

Рейтинг

Ø 5,0 / 1 оценка

Вы должны войти в систему, чтобы иметь возможность дать оценку.

Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!

Перейти в Google

Авторы

Юджин Ли

Основы по теме

Символы неравенства: <, >, ≤, ≥

Символы неравенства — это сокращенное обозначение, используемое для сравнения различных величин. Существует четыре символа неравенства: «больше», «меньше», «больше или равно» и «меньше или равно».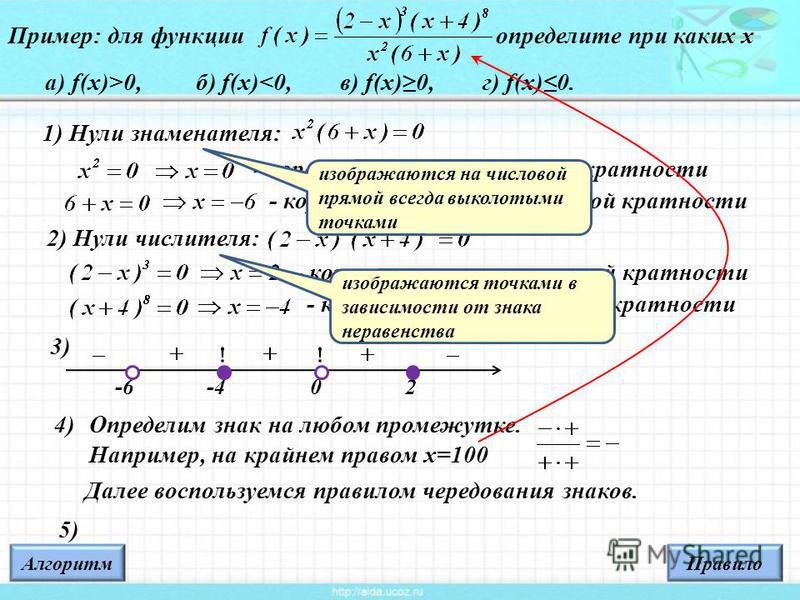 Так, например, предложение «5 больше 2» можно записать как 5>2. Хороший способ запомнить, какое число больше, — думать о каждом символе как о рту; рот всегда будет есть большее из двух сравниваемых чисел. Узнайте о символах неравенства, помогая вампиру Кристоферу упаковать максимальное количество припасов, необходимых для поездки в Калифорнию. Общий основной справочник: CCSS.MATH.CONTENT.6.EE.B.8

Стенограмма

Символы неравенства: <, >, ≤, ≥

Вампир Кристофер — гурман, и ему нужна свежая, новая история для своего блога: Вампир-вегетарианец. Он работает над новым произведением, поэтому хочет отправиться туда, где растет его любимый фрукт: красный апельсин. Он прочитал на Вампедии, что в Калифорнии растут красные апельсины, и это прекрасно, потому что он всегда хотел посетить там подземные сады. Чтобы помочь ему упаковать вещи, он использует свои знания о символы неравенства . И все его припасы разложены в его постели? Капы, проверьте.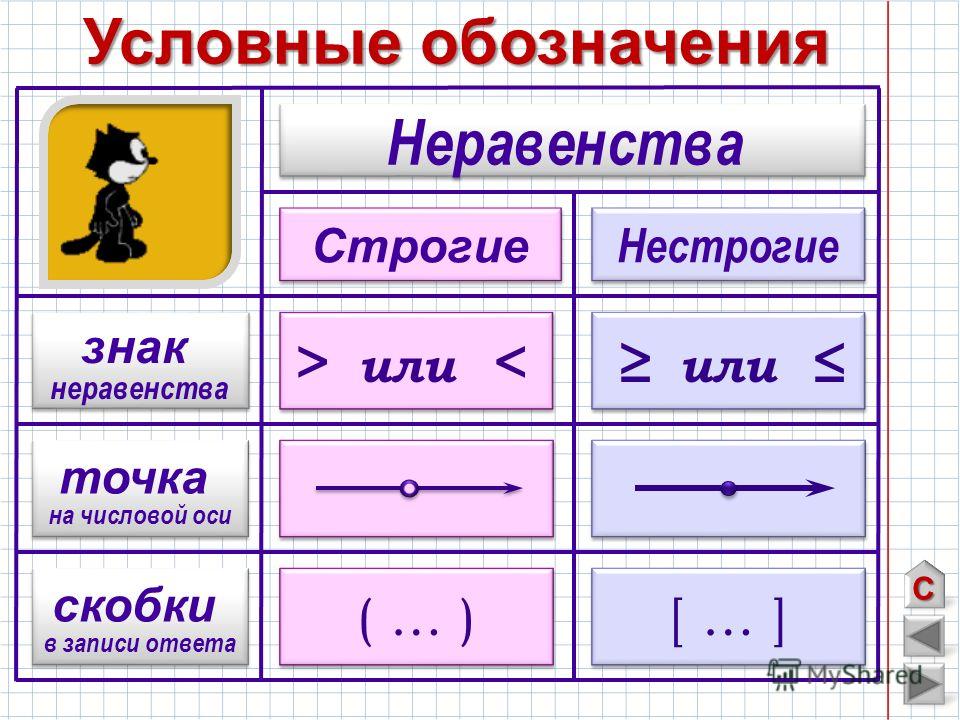 Гель для волос, проверьте. Сок красного апельсина, проверьте. Но сколько из этих вещей ему разрешено брать с собой в самолет? Давайте посмотрим на числовую прямую.

Использование неравенств

Путешествие вампира Кристофера продлится меньше, чем 15 дней. Для неравенств с «меньше» мы используем этот знак <. Кроме того, для этой поездки Крис не может взять больше, чем 1000 мл красного апельсинового сока в самолете. Для таких неравенств, как « меньше или равно », мы используем этот символ: ≤. Нашему гурману-вампиру также нужно упаковать более 1 флакона геля для волос, так как он закончился во время своего последнего отпуска. Нарисуем это на числовой прямой. Для неравенств с «более чем» мы используем символ « больше, чем ». Ему также нужно упаковать не менее 16 плащей, по одной на каждый день и две на всякий случай. Для неравенств с ‘ не менее », мы используем символ « больше или равно ».

Краткий обзор неравенств. Представьте себе рот

Давайте еще раз посмотрим на различные символов неравенства . Хороший способ запомнить, какое число больше, — думать о каждом знаке как о рту . Рот всегда будет съедать большее из двух сравниваемых чисел. Например, давайте сравним 2 и 4. Поскольку 2 меньше 4, рот съест 4. Если рот открывается вправо, читается: «а» равно 9.0077 меньше ‘б’. Однако, если рот открывается влево, это читается: «а» на больше, чем «б». Как мы видели ранее, символы «больше» и «меньше» также можно комбинировать со знаком равенства . Когда мы говорим « столько же» или «не более », мы имеем в виду «меньше или равно», что означает, что а может быть меньше b или равно b. Но когда мы говорим « по крайней мере », мы имеем в виду «больше или равно». Здесь a может быть больше b или равно b. Давайте посмотрим, как вампир Кристофер наслаждается отдыхом. О НЕТ! Никаких больше кровавых апельсинов?!? Это может немного усложнить его отпуск…

Символы неравенства:

<, >, ≤, ≥ упражнение

Хотите применить полученные знания? Вы можете просмотреть и попрактиковаться с заданиями к видео Символы неравенства: <, >, ≤, ≥ .

• Объясните символы неравенства.

  Подсказки

  Здесь вы видите числовую строку для $>65$.

  $\ge~$ то же самое, что $~>~$, включая отношение $~=~$.

  Здесь вы видите числовую строку для $\le 55$.

  Обратите внимание на круг.

  Решение

  Чтобы различать символы неравенства:

  • $<~$ для отношения меньше . Вы видите рядом числовую строку относительно. Тот факт, что Кристофер проводит в путешествии на меньше 15 дней, представлен пустым кружком.
  • $\le$ для отношения меньше или равно . Отличием этого символа от символа $<$ является знак $=$. Это видно по закрашенному кругу.
  • $>$ для отношения больше . Подобно отношению $<$, соответствующий круг пуст.
  • $\ge$ для отношения больше или равно . Он также включает знак $=$, который может быть показан закрашенным кружком.

• Определите символ, который правильно описывает связь.

  Подсказки

  Взгляните на этот пример:

  4$ больше, чем 2$.

  Можно написать как $4>2$.

  Или вы можете записать это как $2<4$.

  По крайней мере указывает больше или равно.

  Запомните знаки отношения:

  • $<$ меньше
  • $\le$ меньше или равно
  • $>$ больше
  • $\ge$ больше или равно

  Решение

  Кристофер уже знает, что его поездка займет менее 15 дней. Менее указывает на символ $<$ или меньше: $<15$. Для представления на числовой прямой вы используете пустой круг, окружающий 15.

  Количество красного апельсина, которое он может взять с собой, ограничено $1000~ml$, включая эту сумму. Это указывает на символ $\le$- или меньше или равно: $\le 1000$. Здесь вы используете заполненный круг.

  Кристофер знает, сколько геля для волос ему нужно. Таким образом, он приходит к выводу, что упаковал более одной бутылки геля для волос. Это указывает на $>$- или больше, чем символ: $>1$. Снова вы используете пустой круг.

  И последнее, но не менее важное: он упаковывает несколько плащей: по крайней мере один на каждый день и один запасной, всего 16. По крайней мере, указывает на $\ge$- или больше или равно-символ: $\ge 16$. Здесь вы используете закрашенный кружок на числовой прямой.

  Но что это? Придя в сад кровавых апельсинов, Кристофер обнаруживает табличку: «Извините! Никаких кровавых апельсинов.

• Найдите соответствующее математическое неравенство, соответствующее числовой прямой.

  

  Подсказки

  Эта числовая линия представляет собой неравенство $x\le 7$.

  • Стрелка влево указывает на $<$ или $\le$.
  • Закрашенный кружок означает меньше или равно.

  Эта числовая строка означает $x>-20$.

  Символ $\ge$ можно исключить из-за пустого круга.

  Решение

  Сначала рассмотрим числовые ряды в целом.

  • Стрелка влево указывает на отношение $<$ или $\le$.
  • Стрелка вправо указывает на отношение $>$ или $\ge$.

  Вы можете решить, должны ли вы использовать $<$ или $\le$ соответственно $>$ или $\ge$ в зависимости от круга.

  • Пустой кружок означает $<$ или $>$ в зависимости от направления стрелки.
  • Закрашенный кружок означает $\le$ или $\ge$.

  Таким образом, мы можем определить соответствующее неравенство слева направо:

  • $x\le 8$
  • $x<8$
  • $x>4$
  • $x\ge 4$

• Изучите неравенство по разным текстовым задачам.

  

  Подсказки

  По крайней мере указывает больше или равно.

  Больше указывает на символ $>$.

  Различают меньше ($<$) и меньше или равно ($\le$).

  Решение

  Вы можете запомнить различные ключевые слова, которые указывают на символ неравенства:

  • Больше означает больше, чем $>$.
  • Не менее означает, что значение больше или равно $\ge$.

  Ограничение скорости Конечно, ограничение скорости не означает, что вы должны ехать быстрее этого ограничения. Получаем неравенство $x\le 45$.

  День рождения Вы хотели бы пригласить менее 10 друзей. Получаем $x<10$.

  Наушники Больше указывает на символ $>$. Это дает нам $x>25$.

• Решите, какой символ неравенства использовать.

  Подсказки

  Обратите внимание

  • $5<7$ но
  • $-5>-7$

  Если вы измените знак чисел, вы также должны изменить символ неравенства.

  Позаботьтесь об использовании $>$ или $\ge$:

  • $7\ge 7$, но $7\не > 7$
  • $7>4$, а также $7\ge 4$

  Решение

  Вы можете представить символ больше чем рот.

  Большее число съедает большее.

  • Например, $4>2$. Вы также можете использовать знак $\ge$.
  • Аналогично $2<4$ и $2\le 4$. Порядок изменен.

  Обратите внимание на знак чисел:

  • $-2>-4$, а также $-2\ge -4$.
  • Наоборот, мы можем заключить $-4<-2$ или $-4\le -2$.

• Определите соответствующее неравенство.

  Подсказки

  Обратите внимание на кружок:

  • Пустые кружки означают $>$ или $<$.
  • Закрашенные кружки обозначают $\ge$ или $\le$.

  Кружком обозначено число, которое вы должны использовать в неравенстве.

  Кружок указывает с одной стороны на число $65$, а с другой на то, что $65$ принадлежит неравенству.

  Стрелка вправо указывает на $>$ или $\ge$.

  Вместе мы можем заключить следующее неравенство для этой числовой прямой:

  $x\ge 65$.

  Решение

  Вы используете числовые линии для представления неравенств.

  Сначала вы рисуете круг точно на месте соответствующего числа.

  В зависимости от символа неравенства кружок заполнен или пуст:

  • Пусто: $>$ или $<$
  • Заполнено: $\ge$ или $\le$

  Вы можете выбрать $<$ или $\le$ соответственно $>$ или $\ge$ в зависимости от направления стрелки.

  Здесь вы видите четыре различных числовых ряда сверху вниз:

  • $x>-6$
  • $x\le -2$
  • $x<4$
  • $x\ge 2$

Еще видео по теме Решение уравнений

Символы неравенства: <, >, ≤, ≥

Что делает числовое предложение истинным или ложным?

Умные расчеты с деньгами

Одношаговые уравнения с умножением и делением

Компания

• Наша команда
• Цены
• Вакансии

Платформа

Как это работает

• Обучающие видео
• Упражнения
• Диван-герой
• Рабочие листы
• Чат

Справка

• Часто задаваемые вопросы
• Дайте нам отзыв

Юридический

• Условия
• Право на отзыв
• Политика конфиденциальности
• Свяжитесь с нами
• Не продавать мою личную информацию

Есть вопросы? Свяжитесь с нами!

help@sofatutor.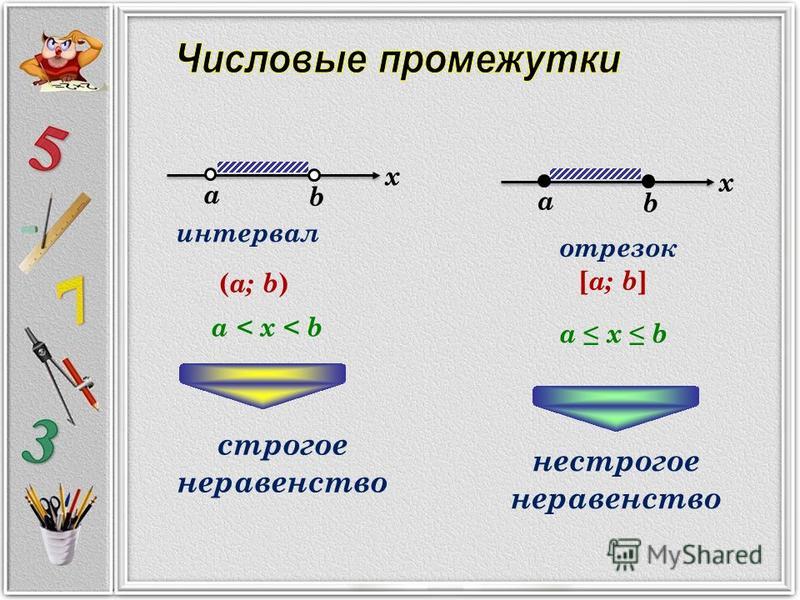 com

• дивантутор.com
• диван-репетитор.ch
• диван-репетитор.ат
• дивантутор.com
• ru.sofatutor.co.uk

Есть вопросы? Свяжитесь с нами!

[email protected]

Введение в неравенства

Неравенство говорит нам об относительном размере значений.

Математика не всегда говорит о «равно», иногда мы знаем только, что что-то больше или меньше.

Пример: Алекс и Билли участвуют в гонке, и Билли побеждает!

Что мы знаем?

Мы не знаем как быстро они бежали, но мы знаем, что Билли был быстрее Алекса:

Билли был быстрее Алекса

Мы можем записать это так:

b > a

( Где «b» означает, насколько быстрым был Билли, «>» означает «больше чем», а «a» означает, насколько быстрым был Алекс)

Мы называем такие вещи неравенствами (потому что они не «равны»)

Больше или меньше

Два наиболее распространенных неравенства:

Символ	Слова	Пример использования
>	больше	5 > 2
<	меньше	7 < 9

Их легко запомнить: «маленький» конец всегда указывает на меньшее число, например:

Символ «больше чем»: БОЛЬШОЙ > маленький

 

Пример: Алекс играет в футбол до 15 лет.

Сколько лет Алексею?

Мы не знаем точно сколько лет Алексу, потому что не сказано «равно»

Но мы знаем «меньше 15», поэтому мы можем написать:

Возраст < 15

Маленький конец указывает на «Возраст», потому что возраст меньше 15 лет.

… или равно!

Мы также можем иметь неравенства, включающие «равно», например:

Символ	Слова	Пример использования
≥	больше или равно	х ≥ 1
≤	меньше или равно	г ≤ 3

Пример: для просмотра фильма вам должно быть не менее 13 лет.