\(\displaystyle (x-2)(x+4)>0{\small .}\)
Запишем неравенство \(\displaystyle (x-2)(x+4)>0 \) в виде систем эквивалентных линейных неравенств.
Все решения неравенства \(\displaystyle (x-2)(x+4)>0\) получаются, когда
- либо \(\displaystyle x-2>0{ \small ,}\, x+4>0\) – оба множителя больше нуля;
- либо \(\displaystyle x-2<0{ \small ,}\, x+4<0\) – оба множителя меньше нуля.
Если это переписать в виде систем, то получаем:
\(\displaystyle \left\{\begin{aligned}x-2&>0{ \small ,}\\x+4&> 0\end{aligned}\right.\) или \(\displaystyle \left\{\begin{aligned}x-2&< 0{ \small ,}\\x+4& < 0{\small .}\end{aligned}\right.\)
Перенося все числа вправо, получаем:
\(\displaystyle \left\{\begin{aligned}x&>2{ \small ,}\\x&> -4\end{aligned}\right.\) или \(\displaystyle \left\{\begin{aligned}x&< 2{ \small ,}\\x& < -4{\small .
Решим получившиеся системы.
\(\displaystyle \left\{ \begin{aligned} x&>2{ \small ,}\\ x &>-4{\small .} \end{aligned} \right.\) Неравенство \(\displaystyle x>2\) соответствует множеству точек на прямой:
Значит, решения – \(\displaystyle x\in (2;+\infty){\small .} \)
| или | \(\displaystyle \left\{ \begin{aligned} x&<2{ \small ,}\\ x &<-4{\small .} \end{aligned} \right.\) Неравенство \(\displaystyle x< 2\) соответствует множеству точек на прямой:
Значит, решения – \(\displaystyle x\in (-\infty;-4){\small .} \)
|
Объединяя полученные решения, получаем ответ:
\(\displaystyle x\in (2;+\infty)\qquad\) или \(\displaystyle \qquad x\in (-\infty;-4) \)
Ответ: \(\displaystyle x\in (-\infty;-4)\cup (2;+\infty){\small .} \)
Вход
Войти через
Регистрация
Следствие неравенства. Алгебра 10-11 класс Мордкович. – Рамблер/класс
Следствие неравенства. Алгебра 10-11 класс Мордкович. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Какое неравенство (2) называют следствием неравенства (1)?
ответы
Если решение неравенства
f(x) > g(x) (1)
содержится в решении неравенства
то неравенство (2) называют следствием неравенства (1),
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Юмор
Олимпиады
ЕГЭ
9 класс
похожие вопросы 5
ГДЗ по геометрии 8 класс Атанасян.
Гл.V №441. Докажите, что прямые,….
Не понимаю, как решить задачу Гл.V №441.
Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
(Подробнее…)
11 класс8 классГеометрияАтанасян Л.С.
№ 59.8 ГДЗ Алгебра 10-11 класс Мордкович. Сколько решений имеет система уравнений?
Применяя графический метод, определите, сколько решений имеет система уравнений: (Подробнее…)
ГДЗАлгебра10 класс11 классМордкович А.Г.
Решите систему уравнений. Поможете? № 59.21 ГДЗ Алгебра 10-11 класс Мордкович.
Решите систему уравнений: (Подробнее…)
ГДЗАлгебра10 класс11 классМордкович А.Г.
№ 11.15 ГДЗ Алгебра 10-11 класс Мордкович. Сколько решений имеет система уравнений?
Помогите определить!
Сколько решений имеет система уравнений: (Подробнее…)
ГДЗАлгебра10 класс11 классМордкович А.Г.
Хелп № 1117 ГДЗ Геометрия 9 класс Атанасян Л.
С.
Найдите площадь круга, вписанного: а) в равносторонний треугольник со стороной а; б) в прямоугольный треугольник с катетом а и (Подробнее…)
ГДЗГеометрия9 классАтанасян Л.С.
Неравенство Чебышева | Brilliant Math & Science Wiki
Содержание
- Определение
- Доказательство
- Стратегии и приложения
- Непрерывная версия
- Смотрите также
Неравенство Чебышева утверждает, что
a1b1+a2b2+⋯+anbnn≥a1+a2+⋯+ann×b1+b2+⋯+bnn≥a1bn+a2bn−1+⋯+anb1n,\begin{выровнено} \dfrac{a_1b_1+a_2b_2+\cdots+a_nb_n}{n} &\ge &\dfrac{a_1+a_2+\cdots+a_n}{n} \times \dfrac{b_1+b_2+\cdots+b_n}{n} \\ &\ge &\dfrac{a_1b_n+a_2b_{n-1}+\cdots+a_nb_1}{n}, \end{выровнено}na1b1+a2b2+⋯+anbn≥≥na1+a2+⋯+an×nb1+b2+⋯+bnna1 bn+a2bn−1+⋯+anb1,
или аналогичный,
9{ n }{ { a }_{ i }{ b }_{ n+1-i } } }{ n } }.
n∑i=1naibi≥n∑i=1nai ×n∑i=1nbi≥n∑i=1naibn+1−i.Интуиция о том, что сумма попарных произведений максимизируется жадным алгоритмом, обеспечивается неравенством перегруппировки, которое гарантирует, что bn — максимально возможный результат сложения попарных произведений. Неравенство Чебышева дает полезную нижнюю границу того, каким может быть точное значение a1b1+⋯+anbna_1b_1+\cdots+a_nb_na1b1+⋯+anbn.
Доказательство неравенства Чебышева очень похоже на доказательство неравенства перестановки:
Так как a1≥a2≥⋯≥ana_1\ge a_2\ge \cdots\ge a_na1≥a2≥⋯≥an и b1≥b2≥⋯≥bn,b_1\ge b_2\ge \cdots \ge b_n,b1 ≥b2≥⋯≥bn, для любых iii и jjj верно следующее:
(ai−aj)(bi−bj)≥0⇒aibi+ajbj≥aibj+ajbi.\left( { a }_{ i }-{ a }_{ j } \right) \left( { b }_ { i }-{ b }_{ j } \right) \ge 0 \Rightarrow { a }_{ i }{ b }_{ i }+{ a }_{ j }{ b }_{ j }\ge { a }_{ i }{ b }_{ j }+{ a }_{ j }{ b }_{ i }.(ai−aj)(bi−bj)≥0⇒aibi +ajbj≥aibj+ajbi.
n a_ib_i &\geq a_1b_n+a_2b_1+\cdots+a_nb_{n-1}, \end{align}i=1∑naibii=1∑naibii=1∑naibii=1∑naibi≥a1b1 +a2b2+⋯+anbn≥a1b2+a2b3+⋯+anb1≥a1b3+a2b4+⋯+anb2⋮≥a1 bn+a2b1+⋯+anbn−1,и сложение этих nnn неравенств дает результат. □_\квадрат□
Поскольку неравенство Чебышева требует знания порядка следования переменных, во многих случаях его нельзя использовать напрямую. Например, взгляните на следующую задачу:
Пусть a,b,c,x,y,za,b,c,x,y,za,b,c,x,y,z — положительные действительные числа такие, что a+b+c=7a+b+c=7a +b+c=7 и x+y+z=15x+y+z=15x+y+z=15. Каково наименьшее возможное значение ax+by+cz?ax+by+cz?ax+by+cz?
Ложное решение: По неравенству Чебышева имеем
ax+by+cz3≥a+b+c3⋅x+y+z3=353,\frac{ax+by+cz}{3} \geq \frac{a+b+c}{3} \cdot \ frac{x+y+z}{3} = \frac{35}{3},3ax+by+cz≥3a+b+c⋅3x+y+z=335,
, поэтому минимальное возможное значение ax+by+czax+by+czax+by+cz равно 35.
В приведенном выше решении работает , а не , потому что оно неявно предполагает, что a,b,ca,b,ca,b,c и x,y,zx,y,zx,y,z имеют одинаковый порядок, что не является обязательно так. Действительно, взяв a=4,b=2,c=1,x=4,y=5,z=6a=4, b=2, c=1, x=4, y=5, z=6a=4 ,b=2,c=1,x=4,y=5,z=6 дает ax+by+cz=32ax+by+cz=32ax+by+cz=32, что значительно меньше предполагаемого минимума 35.
В результате Чебышева можно использовать только тогда, когда задан или определен порядок переменных. Это означает, что его часто применяют, предполагая определенный порядок без потери общности (((например, a≥b≥c),a \geq b \geq c),a≥b≥c), и это применимо к цепочке неравенств. Два общих примера, которые следует иметь в виду, включают следующее:
- a≥b≥c ⟹ a+b≥a+c≥b+ca \geq b \geq c \ подразумевает a+b \geq a+c \geq b +ca≥b≥c⟹a+b≥a+c≥b+c
- a≥b≥c ⟹ 1a≤1b≤1c.a \geq b \geq c \ подразумевает \frac{1}{a} \leq \frac{1}{b} \leq \frac{1}{c} .a≥b≥c⟹a1≤b1≤c1.
Можно комбинировать:
Пусть a,b,ca,b,ca,b,c — положительные действительные числа.
Покажите, что
aba+b+bcb+c+cac+a≤3(ab+bc+ca)2(a+b+c).\frac{ab}{a+b}+\frac{bc}{b+c }+\frac{ca}{c+a} \leq \frac{3(ab+bc+ca)}{2(a+b+c)}.a+bab+b+cbc+c+aca ≤2(a+b+c)3(ab+bc+ca).
Предположим без ограничения общности, что a≥b≥ca \geq b \geq ca≥b≥c. Отсюда следует, что 1a≤1b≤1c\frac{1}{a} \leq \frac{1}{b} \leq \frac{1}{c}a1≤b1≤c1, и поэтому 1a+1b ≤1a+1c≤1b+1c\frac{1}{a}+\frac{1}{b} \leq \frac{1}{a}+\frac{1}{c} \leq \frac{1 {b}+\frac{1}{c}a1+b1≤a1+c1≤b1+c1. Снова взяв обратное значение, получаем 9.0017
11a+1b≥11a+1c≥11b+1c ⟹ aba+b≥aca+c≥bcb+c\frac{1}{\frac{1}{a}+\frac{1}{b}} \geq \frac{1}{\frac{1}{a}+\frac{1}{c}} \geq \frac{1}{\frac{1}{b}+\frac{1}{c}} \подразумевает \frac{ab}{a+b} \geq \frac{ac}{a+c} \geq \frac{bc}{b+c}a1+b11≥a1+c11 ≥b1+c11⟹a+bab≥a+cac≥b+cbc Верно и то, что
a+b≥a+c≥b+c.a+b \geq a+c \geq b+c.a+b≥a+c≥b+c.
Применение неравенства Чебышева к этим двум последовательностям дает
(a+b)(aba+b)+(a+c)(aca+c)+(b+c)(bcb+c)≥13((a+b)+(b+c)+(c +a))(aba+b+aca+c+bcb+c),(a+b)\left(\frac{ab}{a+b}\right)+(a+c)\left(\frac {ac}{a+c}\right)+(b+c)\left(\frac{bc}{b+c}\right) \geq \frac{1}{3}\big((a+b )+(b+c)+(c+a)\big)\left(\frac{ab}{a+b}+\frac{ac}{a+c}+\frac{bc}{b+c }\right),(a+b)(a+bab)+(a+c)(a+cac)+(b+c)(b+cbc)≥31((a+b)+ (b+c)+(c+a))(a+bab+a+cac+b+cbc), 9n}{a+b} \geq Cb+can+c+abn+a+bcn≥C
Учитывая, что a,ba,ba,b и ccc — положительные действительные числа, удовлетворяющие условиям a+b+c=3a +b+c=3a+b+c=3, nnn — целое положительное число.
Существует также непрерывная версия неравенства Чебышева: если fff и ggg обе невозрастающие функции или обе неубывающие функции на [0,1][0,1][0,1] и обе интегрируемы по этот интервал, то 91 g(x)\, dx.∫01f(x)g(x)dx≥∫01f(x)dx∫01g(x)dx.
- Неравенство перегруппировки
Цитировать как: Неравенство Чебышева. Brilliant.org . Извлекаются из https://brilliant.org/wiki/chebyshev-inequality/
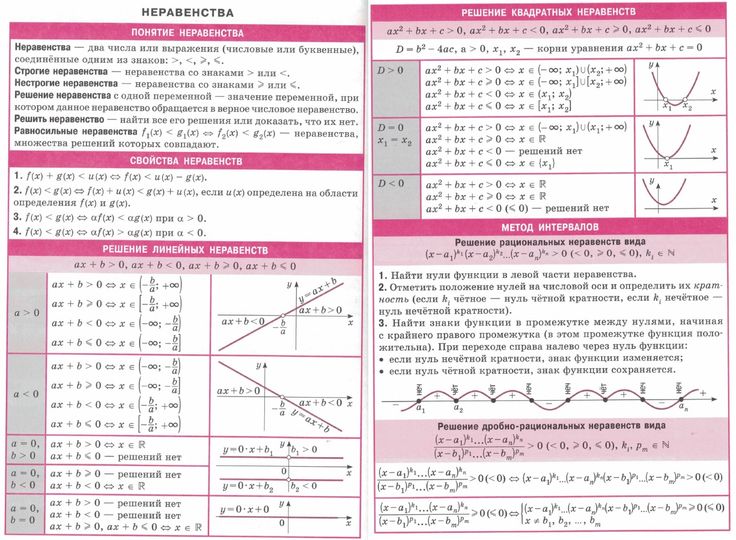
Алгебра: решение квадратных неравенств с одной переменной
До сих пор этот раздел был переполнен процедурами, требующими точных пошаговых инструкций, и окончательная тема раздела не будет отличаться. На самом деле, в последних нескольких темах было сделано так много шагов, что вы, вероятно, почувствуете, что собираете мебель из Икеи, но потерпите еще немного, и вы узнаете все, что вам нужно знать о квадратичных уравнениях.
Помните, в разделе «Линейные неравенства» вы узнали, что решение неравенства часто выражается в виде графика, потому что почти всегда существует бесконечное число возможных решений? Это по-прежнему верно, если неравенство содержит квадратный многочлен, например 2 x 2 + x — 2
Позвольте мне еще раз освежить вашу память. Что вы используете для построения графика неравенства, содержащего только одну переменную, числовую прямую или координатную плоскость? Если вы ответили на «координатную плоскость», оооо, извините, вы ошиблись, но, по крайней мере, вы уйдете с приятными подарками на прощание и домашней версией нашей игры. Правильный ответ — числовая линия; количество осей в графической системе должно соответствовать количеству уникальных букв в уравнении или неравенстве. Например, с 2 x 2 + x — 2 x (не x и y оба), вы должны использовать числовую линию для построения графика.
Пока хватит разговоров; позвольте мне объяснить шаги, которые вы будете выполнять, чтобы решить квадратное неравенство:
w3.org/1999/xhtml»> Talk the Talk
критических чисел — это значения x , для которых неравенство равно 0 или не определено. Они разбивают числовую прямую на отрезки, называемые интервалами .
- Представьте, что символ неравенства является знаком равенства, и решите соответствующее квадратное уравнение . Эти решения называются критическими числами неравенства. Вы не меняете этот знак неравенства на знак равенства навсегда, как только вы найдете критические числа, вы можете изменить его обратно.
- Нанесите решения на числовую прямую . Просто отметьте критические числа на числовой прямой либо открытыми, либо закрытыми точками, в зависимости от того, допускает ли символ возможность равенства (точно так же, как вы делали это на графиках линейных неравенств с числовыми линиями).
- Используйте тестовые значения, чтобы найти интервал решения (с ). Критические числа разобьют числовую прямую на сегменты, называемые интервалами .
Несмотря на то, что диаграмма, которую вы создаете во время этого процесса, говорит вам, что решение есть, большинство учителей не хотят, чтобы вы просто давали диаграмму в качестве ответа. Обычно они хотят, чтобы вы выражали этот интервал как оператор неравенства.
Пример 5 : Решите неравенство и нарисуйте решение.
- 2 x 2 + x — 2
Решение : претендент на мгновение, что это фактически уравнение 2 x 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 — — .
Мальчик, эти критические числа, безусловно, уродливы. Это хорошая идея ввести их в калькулятор, чтобы выяснить, какой десятичной дроби они приблизительно равны, чтобы вы могли нанести их на числовую прямую, как я сделал на рис. 13.2. (Поскольку символ неравенства
Рисунок 13.2 Критические числа разбивают числовую прямую на три отмеченных интервала. Обратите внимание, что когда обе конечные точки интервала являются критическими числами, полезно записать этот интервал в виде составного неравенства.
Теперь выберите одно значение для представления каждого интервала (я выбрал самые простые из возможных: x = -2, x = 0 и x = 1) и подставьте их в исходное неравенство, чтобы увидеть какие значения приводят к истинным утверждениям.
Тест x = -2 Тест x = 0 Тест x = 1 93 23 23 23 23 23 23 23 23 23 23 23 23 233 23 23 23 23 233 23 23 23 23 233 23 23 233 23 23 233 23 23 233 23 233 23 233 23 233 23 233 23 23 2 (2229 8 x . 2(1) 2 + (1)-2 2(4)-2-2 2(0)-2 2(1)+1-2 8-4 2-1 9 9 Интервал, содержащий 00125 x = 0 (средний интервал на рис. 13.2) — единственное, которое делает неравенство верным, поэтому это правильное решение: -1,28 x точно верно, вам придется использовать фактические, уродливые критические числа, и а не их десятичные эквиваленты: 4 -2 1 Чтобы построить график решения, просто нарисуйте числовую линию с рис. 13.2 и затемните интервал решения, чтобы в итоге получилось что-то вроде рис. 13.3.
Рисунок 13.3 График решения неравенства 2 x 2 + x — 2
You’ve Got Problems
Problem 5: Solve the inequality and graph the solution 2 x 2 + 5 x — 3 ¥ 0.
Покажите, что
Для всех вариантов a,b,ca,b,ca,b,c и nnn, какова наибольшая константа CCC, удовлетворяющая приведенному выше неравенству?
Выберите тестовое значение из каждого интервала и подставьте его в исходное неравенство для x . Если проверочное значение делает неравенство верным, то и все остальные значения в том же интервале будут верны, поэтому оно является частью решения.
К сожалению, этот квадрат нельзя разложить на множители, поэтому вам придется использовать либо формулу квадрата, либо завершить квадрат, чтобы получить решения, которые будут
2(0) 2 + (0) — 2