Линейные неравенства. — tutomath.ru репетитор по математике
Home » 9 класс » Линейные неравенства.
Posted on Author admin 0
Линейные неравенства называются так, потому что в основе лежит линейная функция или формула прямой (y=ax+b). Линейная функция характерна тем, что переменная x находится в числители и в первой степени.
Видео урок по теме «Линейные неравенства».
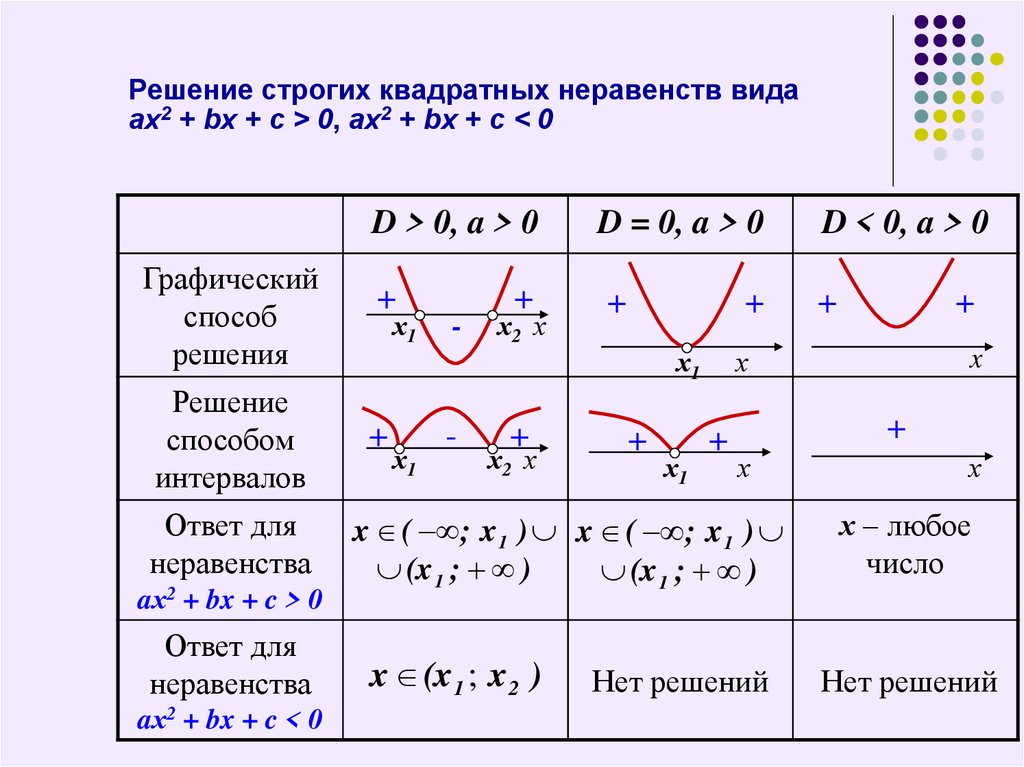
Вид линейного неравенства.
Классические линейные неравенства имеют вид:
ax+b>0
ax+b<0
ax+b≤0
ax+b≥0
Но линейные неравенства не всегда имеют такой вид, сначала очень часто неравенство необходимо упростить и только после этого мы можем оценить вид неравенства.
Чтобы решить неравенство его необходимо упростить.
По каким правилам упрощают неравенства?
ПРАВИЛО 1:
В неравенствах, как и в уравнениях мы имеем право переносить любую часть неравенства из одной стороны в другую при этом необходимо изменить знак на противоположный (плюс меняем на минус, минус меняем на плюс).
Например:
2x+5<3
По правилу, мы переносим неизвестные в одну сторону, а известные в другую. Неизвестное в нашем неравенстве это 2x, а известное число 5 и 3. Неизвестное мы оставим в левой части неравенства, а все известные перенесем в правую часть.
ЛЕВАЯ ЧАСТЬ<ПРАВАЯ ЧАСТЬ
Число +5 находится в левой части, при переносе через знак неравенства « < » плюс меняется на минус.
2x+5<3
2x<3-5
Чтобы решать дальше неравенство, необходимо применить следующее правило.
ПРАВИЛО 2:
Можно умножать и делить всё неравенство на положительное число, знак неравенства при этом не измениться.
Продолжим решение неравенства:
2x<3-5
2x<-2 |:2
Таким знаком «|» мы обозначаем, что всё неравенство и левая часть и правая часть будет поделена на число 2.
Почему мы делим именно на 2? На число 2 мы делим все неравенство, потому что нам необходимо получить в левой части x.
2x<-2 |:2
2x:2<-2:2
1x<-1
x<-1
Знак неравенства мы не изменили до деления на число 2 стоял знак меньше « < » и после деления на число 2 всего уравнения остался этот же знак неравенства « < ».
Не всегда коэффициент при переменной x положительное число, часто бывает также перед переменной x стоит отрицательное число. В таком случае надо применить следующее правило.
ПРАВИЛО 3:
Можно умножать и делить всё неравенство на отрицательное число, знак неравенства при этом измениться было < на > или ≤ на ≥ и на оборот.
Рассмотрим пример:
-2x<-2
Мы видим, что перед переменной x стоим коэффициент -2, нам необходимо получить в результате x, поэтому делим все неравенство на -2.
-2x<-2 |: (-2) -2x: (-2)>-2: (-2)
x>1
Как вы видите знак неравенства мы поменяли с < на >, потому что поделили всё неравенство на отрицательное число (-2).
Рассмотрим подробно примеры:
3x-1>8
Перенесем -1 с левой стороны в правую сторону неравенства, знак поменяем с минуса на плюс.
3x>8+1
3x>9
Поделим все неравенство на 3
3x>9 |: 3
3x:3>9:3
x>3
У неравенства в ответ записываю промежутки, в нашем случае переменная x больше 3.
По другому можно сказать от 3 до плюс бесконечности.
Ответ: x∈(3; +∞)
Правило оформления неравенств.
Сразу необходимо вспомнить и повторить правила оформления неравенств.
Если такие знаки у неравенства < или > то неравенство называется строгим. Скобки круглые и точка пустая.
<> ○ ()
Если такие знаки у неравенства ≤ или ≥ то неравенство называется нестрогим. Скобки квадратные и точка закрашенная.
≤ ≥ • []
Следующий пример:
5-4x≤17
Перед числом 5 не стоит никакого знака, когда нет знака, считаться что знак “+”.
5-4x≤17
-4x≤17-5
-4x≤12
Перед переменной x стоит число -4, поэтому делим все уравнение на -4.
-4x≤12 |: (-4)
-4x: (-4)≤12: (-4)
После деления на отрицательное число знак неравенства поменялся с ≤ на ≥
x≥-3
Переменная x больше либо равна -3. В ответ запишем x∈[-3; +∞). У бесконечности скобки всегда круглые.
Ответ: x∈[-3; +∞)
Примеры (решение разобрано в видео уроке):
1) 10x≤0
2) -10x≤0
3) 3x +8≥-2x-12
4) 0,2x<3
5) 1/2 x<2/3 x+6 6) 6,5+12x>0,5
7) 3(x+1)-5<5(x-2)
8) 4x-2(2x-2) ≥x+2
9) 2⋅10x-5⋅3+ 1/4 ⋅12- 1/4 ⋅4x≥7
10) 1/3(3x-6)+(6x-12)≤1
Линейные неравенства
Урок 26. Подготовка к ОГЭ по математике 9 класс
Цели нашего урока: вспомнить, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными; вспомнить, как решаются такие неравенства.
Конспект урока «Линейные неравенства»
Вопросы занятия:
· вспомнить, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными;
· повторить способы решения линейных неравенств.
Материал урока
Но прежде, давайте вспомним, что такое числовое неравенство.
Определение.
Числовым неравенством называется символическая запись, в которой два числа или числовых выражения связаны одним из знаков сравнения.
Напомним, что:
Определение.
Решением неравенства с одной переменной
Определение.
Решить
неравенство – значит найти все его решения или
доказать, что решений нет.
Определение.
Равносильными называются неравенства, множества решений которых совпадают.
Равносильными неравенства получаются, если:
Теперь давайте повторим основные свойства числовых неравенств.
Неравенство с переменными может при одних значениях переменных быть верным, при других – нет.
Определение.
Доказать неравенство – значит, доказать, что оно имеет место при всех допустимых значениях переменных.
Как правило, для доказательства неравенств используют метод составления разности между левой и правой частями и оценки её знака.
Рассмотрим пример.
Пример.
Определение.
Линейные неравенства – это неравенства вида:
Особенностью
линейных неравенств является то, что в таких неравенствах х присутствует
только в первой степени, нет деления на х и х не стоит под знаком
корня.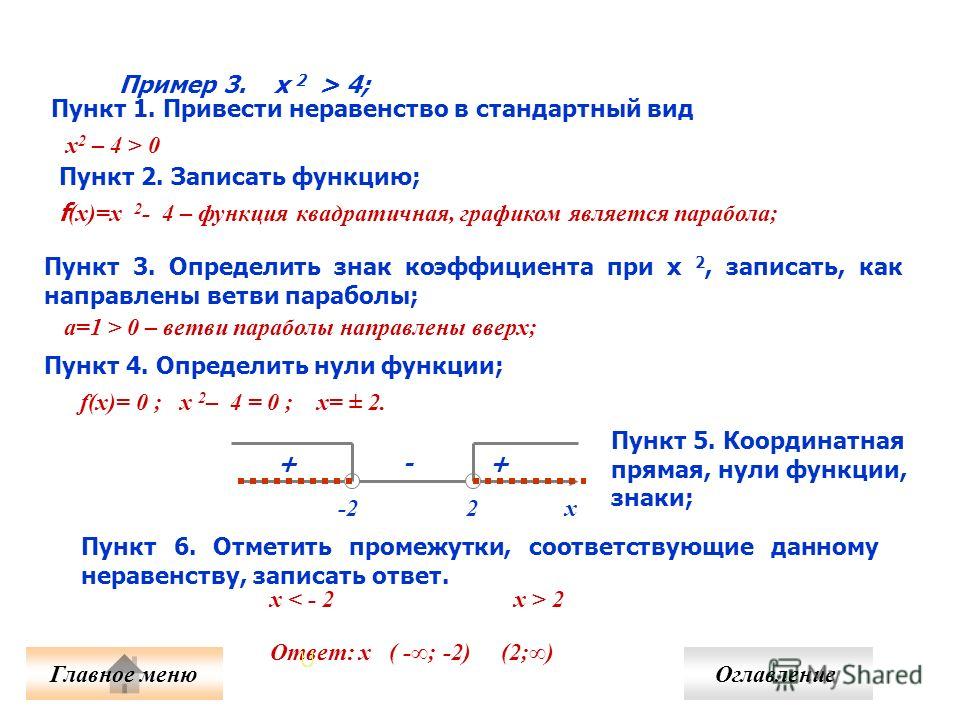
Как правило, решениями линейных неравенств являются числовые промежутки. Давайте немного вспомним, как связаны числовые неравенства с числовыми промежутками.
Если неравенство строгое, то концы промежутка на числовой прямой будут «выколотыми» и при записи в виде интервала, скобки будут круглыми. Если же неравенства нестрогие, то на числовой прямой концы интервала будут закрашены, а интервал берётся в квадратные скобки.
Рассмотрим пример.
В зависимости от знака коэффициентов решениями линейных неравенств будут разные промежутки.
Рассмотрим несколько примеров.
Пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Пример.
Пример.
Пример.
Часто приходится решать линейные неравенства с двумя переменными.
Определение.
Линейные неравенства с двумя переменными – это неравенства вида
Заметим,
что обе переменные должны быть в первой степени.
Определение.
Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.
Так как неравенство с двумя переменными имеет множество решений, то их сложно перечислить. Увидеть множество решений неравенства с двумя переменными позволяет график.
Итоги урока
Сегодня мы вспомнили, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными. Вспомнили, как решаются такие неравенства.
Предыдущий урок 25 Системы уравнений второй степени с двумя переменными
Следующий урок 27 Системы линейных неравенств с одной переменной
Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ОГЭ по математике 9 класс
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Линейные неравенства: определение, правила, формулы, методы
- Автор Рачана
- Последнее изменение 20-10-2022
Линейные неравенства: В математике неравенство возникает при неравном сравнении двух математических выражений или двух чисел.
В общем случае неравенства могут быть как числовыми, так и алгебраическими. Числовое неравенство возникает при сравнении двух чисел на числовой прямой в зависимости от их значения. Алгебраическое неравенство возникает, когда одно выражение больше или меньше другого выражения. Существует несколько способов представления различных видов неравенств.
Между любыми двумя величинами (скажем, \(x\) и \(y\)) во Вселенной выполняются только три условия: \(‘ < ',\,' > ‘\) и \(‘ = ‘, \) т. е. \(x < y, \, x > y\) и \(x = y.\) Символы \(‘ > ‘,\,’ < ',\,'\, \le ',\, ' \ge '\) называются знаком неравенства или неравенства. В этой статье мы узнаем все о линейных равенствах.
Определение линейных неравенств
Линейные неравенства определяются как выражения, в которых два значения сравниваются с использованием символов неравенства. Неравенство называется линейным, если показатель степени каждой входящей в него переменной имеет только первую степень и в нем нет члена, включающего произведение переменных.
Мы можем определить неравенство как утверждение, включающее переменную(ые) и знак неравенства \( > ,\, < ,\,\, \le ,\, \ge \) или два действительных числа или два алгебраических выражения, связанных соотношением символы \( > ,\, < ,\,\, \le ,\, \ge \) образуют неравенство.
Если \(х\) и \(у\) две величины, то обе эти величины будут удовлетворять любому из следующих четырех условий (соотношений): т. е. либо \(х < у, \, х > у ,\,x \le y\) или \(x \ge y.\) Каждое из четырех приведенных выше условий является неравенством.
Изучение концепций 11-го экзамена CBSE
Линейное неравенство с одной переменной
Если \(a, b\) и \(c\) являются действительными числами, то каждое из следующих уравнений называется линейным неравенством с одной переменной:
1. \(ax + b > c.\) Читается как: \(ax + b\) больше, чем \(c.\)
2. \(ax + b < c.\) Читается как: \ (ax + b\) меньше \(c.\)
3. \(ax + b \ge c.\) Читается как: \(ax + b\) больше или равно \(c.
\ )
4. \(ax + b \le c.\) Читается как: \(ax + b\) меньше или равно \(c.\)
В неравенстве знаки \(‘ > ‘,\,’ < ‘,\,’ \ge ‘\) и \(‘ \le ‘\) называются знаками неравенства.
Изучение концепций экзамена на Embibe
Пример линейных неравенств
Линейное неравенство только с одной переменной называется линейным неравенством с одной переменной и может быть записано как \(ax + b < 0\) или \(ax + b > 0\) или \(ax + b \ge 0\) или \(ax + b \le 0\), где \(a,b\) — вещественные числа и \(a \ne 0.\)
\( ax \le 0,\,ax + by + c > 0,\,ax \ge 5\) by \(x \le 10,\) и т. д. — несколько примеров линейных неравенств.
Правила линейных неравенств
Алгебраическое решение линейного неравенства : Решить заданное линейное неравенство означает найти значение или значения используемой в нем переменной. Таким образом, решить неравенство \(3x + 5 > 8\) — значит найти переменную \(x\), а решить неравенство \(8 — 5y < 3\) - найти переменную \(y\) и скоро.
Для решения данного линейного неравенства необходимо принять следующие рабочие правила:
Правило 1 : При переносе положительного члена из одной части неравенства в другую его часть знак члена становится отрицательным.
Правило 2 : При переносе отрицательного члена из одной части неравенства в другую его часть знак члена становится положительным.
Практические вопросы 11-го экзамена CBSE
Правило 3 : Если каждый член неравенства умножается или делится на одно и то же положительное число, знак неравенства остается прежним.
То есть, если \(p\) положительно и \(p = 0.\)
1. \(x < y \Rightarrow px
3. \(x \le y \Rightarrow px \le py\) и \(\left( {\frac{x}{p}} \right) \le \left( {\frac{y} {p}} \right)\)
4.
\(x \ge y \Rightarrow px \ge py\) и \(\left( {\frac{x}{p}} \right) \ge \left( {\frac{y}{p}} \right)\)
Правило 4: Если каждый член неравенства умножается или делится на одно и то же отрицательное число, знак неравенства меняется на противоположный. Это если \(p\) отрицательно.
1. \(x < y \Rightarrow px > py\) и \(\left({\frac{x}{p}}\right) > \left({\frac{y}{p}} \ справа)\)
2. \(x \ge y \Rightarrow px \le py\) и \(\left( {\frac{x}{p}} \right) \le \left( {\frac{y }{p}} \right)\)
Правило 5: Если знак каждого члена в обеих частях неравенства меняется, знак неравенства меняется на противоположный.
Правило 6: Если обе части неравенства положительны или обе отрицательны, то при взятии их обратных величин знак неравенства меняется на противоположный.
То есть, если \(x\) и \(y\) либо положительны, либо оба отрицательны, то:
1. \(x > y \Leftrightarrow \frac{1}{x} < \frac{ 1}{y}\)
2.
\(x \le y \Leftrightarrow \frac{1}{x} \ge \frac{1}{y}\)
3. \(x \ge y \Leftrightarrow \ frac{1}{x} \le \frac{1}{y}\) и так далее.
Замещающий набор и набор решений
Замещающий набор: Набор, из которого выбираются значения переменной, участвующей в неравенстве, называется замещающим набором. Обычно мы используем \(N\) (набор натуральных чисел; \(1,2,3,4,….\)) или \(W\) (набор целых чисел; \(0,1,2 ,3,….\)) или \(I\) (набор целых чисел; \(… – 3, – 2, – 1,0,1,2,3,….\)) или \(R\) (действительное число) в качестве замещающего набора.
Набор решений: Решением неравенства является число, подстановка которого вместо переменной делает неравенство верным. Множество всех решений данного неравенства называется множеством решений неравенства. Набор решений является подмножеством замещающего набора.
Метод решения линейного неравенства с одной переменной
Для решения линейного неравенства с одной переменной используются следующие шаги.
1. Удалите дроби (или десятичные дроби), умножив обе части на соответствующий коэффициент.
2. Поместите все переменные члены в одну сторону, а все константы в другую.
3. Сделать коэффициент при переменной \(1.\)
4. Выбрать набор решений из набора замещения.
Практические экзаменационные вопросы
Представление набора решений линейного неравенства с одной переменной на числовой прямой
Используйте следующие правила для представления решения линейного неравенства с одной переменной на числовой прямой
1. Если неравенство включает в себя \( \le \) или \(\ge \) рисование закрашенного круга или темного круга \(\left( . \right)\) на числовой прямой, затем включается число, соответствующее закрашенному кругу или темному кругу в наборе решений.
Например: Если также включено \(2\), т. е. \(x \le 2,\), то кружок будет затемнен, а график будет таким, как показано ниже:
2. Если неравенство включает \( > \) или \( < ,\), затем нарисуйте незаполненный круг или пустой круг \(\left( o \right)\) на числе, линия показывает, что число, соответствующее незаполненному кругу или пустому кругу исключается из набора решений.
Например, \(x < 2\) и \(x \in R\)
Попытка 11-го экзамена CBSE Пробные тесты
Решенные примеры – линейные неравенства (практические задачи)
Q.5. Если замещающий набор представляет собой набор целых чисел, (\(I\) или \(Z\)), между \(- 6\) и \(8,\) , найдите набор решений числа \(15 – 3x > x – 3.\)
Ответ: Данное неравенство имеет вид \(15 – 3x > x – 3.\)
\( \Стрелка вправо \, – 3x – x > – 3 – 15\)
\(\Стрелка вправо\, – 4x > – 18\)
\( \Стрелка вправо \frac{{ – 4x}}{{ – 4}} < \frac{{ – 18}}{{ – 4}}\) (Деление на отрицательное число меняет знак неравенства).
\( \Rightarrow x < 4.5\)
Поскольку набор замещения представляет собой набор целых чисел между \( – 6\) и \(8.\)
Следовательно, набор решений \( = \left\{{ – 5, – 4, – 3, – 2, – 1,0,1,2,3,4} \право\}.\)
Q.1.
Если замещающий набор представляет собой набор натуральных чисел \(\left( N \right),\) , найдите набор решений \(3x + 4 < 16.\)
Ответ: Данное неравенство: \(3x + 4 < 16\)
\( \Стрелка вправо 3x < 16 – 4\)
\( \Стрелка вправо 3x < 12\)
\( \Стрелка вправо \frac{{ 3x}}{3} < \frac{{12}}{3}\)
т. е. \(x < 4\)
Так как замещающий набор \( = N\) (множество натуральных чисел)
Следовательно, набор решений \( = \left\{{1,2,3} \right\}.\)
Q.2. \(\frac{x}{2} – 5 \le \frac{x}{3} – 4,\) , где \(x\) — положительное нечетное целое число.
Ответ: Данное неравенство: \(\frac{x}{2} – 5 \le \frac{x}{3} – 4,\)
\( \Rightarrow \frac{x}{2} – \frac{x}{3} \le – 4 + 5\)
\( \Стрелка вправо \frac{{3x – 2x}}{6} \le 1\)
\( \Стрелка вправо x \le 6\)
Поскольку \(x\) является положительным нечетным целым числом
Следовательно, набор решений \( = \left\{{1,3,5} \right\}.
\)
Q.3. Учитывая, что \(x \in R,\) решить следующее неравенство и построить график решения на числовой прямой: \( – 1 \le 3 + 4x < 23.\)
Ответ: Дано: \( – 1 \le 3 + 4x < 23;\,x \in R\)
\( \Rightarrow \, – 1 \le 3 + 4x\) и \(3 + 4x < 23\)
\( \Стрелка вправо\, – 4 \le 4x\) и \(4x < 20\)
\( \Стрелка вправо\, – 1 \le x\) и \(x < 5\)
\ ( \Rightarrow \, – 1 \le x < 5;\,x \in R\)
Следовательно, решение \(\left\{ { – 1 \le x < 5;\,x \in R} \right\ }\)
Решение на числовой прямой:
Q.4. Перечислите множество решений \(50 – 3\left({2x – 5} \right) < 25,\) при условии, что \(x \in W.\) Также представим полученное множество решений на числовой прямой.
Ответ: Дано: \(50 – 3\влево({2x – 5} \вправо) < 25\)
\(\Стрелка вправо 50 – 6x + 15 < 25\)
\( \Стрелка вправо 65 – 6x < 25\)
\( \Стрелка вправо \, – 6x < 25 – 65\)
\( \Стрелка вправо \, – 6x < – 40\)
\( \Стрелка вправо \frac{{ – 6x}}{ { – 6}} > \frac{{ – 40}}{{ – 6}}\)(Деление на отрицательное число меняет знак неравенства).
\( \Rightarrow x > 6\frac{2}{3}\)
Требуемый набор решений \( = \left\{{7,8,9……} \right\}\)
Искомое число строка
Попытка пробных тестов
РезюмеВ этой статье мы узнали об определении линейных неравенств, примере линейных неравенств, правилах линейных неравенств, наборе замен и наборе решений, методе решения линейного неравенства. с одной переменной, представление множества решений линейного неравенства с одной переменной на числовой прямой и т.д. Также были решенные примеры линейных неравенств и часто задаваемые вопросы по ним.
Результат обучения этой статьи заключается в том, что система линейных неравенств используется для определения наилучшего решения проблемы.
Решения NCERT для линейных неравенств класса 11 Глава
Часто задаваемые вопросы (FAQ) — линейные неравенства Q.1. Объясните линейные неравенства на примере?
Ответ: Неравенство называется линейным тогда и только тогда, когда показатель степени каждой входящей в него переменной имеет только первую степень.
Нет члена, включающего произведение переменных.
Если \(a,b\) и \(c\) — действительные числа, то каждое из следующих называется линейным неравенством с одной переменной.
Пример: \(2x + 1 \le 2,\,2x + 3y + 5 > 7x + 2,\,5x \ge 5,\,y \le 10.\)
Q.2. Как решить задачу о неравенстве?
Ответ: Для решения линейного неравенства с одной переменной используются следующие шаги.
1. Удалите дроби (или десятичные дроби), умножив обе части на соответствующий коэффициент.
2. Поместите все переменные члены в одну сторону, а все константы в другую.
3. Сделать коэффициент при переменной \(1.\)
4. Выбрать набор решений из набора замещения.
Q.3. Как представить множество решений линейного неравенства на числовой прямой?
Ответ: Используйте следующие правила для представления решения линейного неравенства с одной переменной на числовой прямой
1.
Если неравенство включает \( \le \) или \( \ge \) рисование закрашенный кружок или темный кружок \(\left( . \right)\) на числовой прямой, число, соответствующее закрашенному кружку или темному кружку, включается в набор решений.
2. Если неравенство включает \( > \) или \( < ,\), то нарисуйте незакрашенный кружок или пустой кружок \(\left( o \right)\) на числе, линию, показывающую, что число, соответствующее незаполненный кружок или пустой кружок исключается из набора решений.
Q.4. Что такое сменный комплект?
Ответ: Замещающий набор: Набор, из которого выбираются значения переменной, участвующей в неравенстве, называется замещающим набором. Как правило, мы используем либо \(N\) (множество натуральных чисел; \(1,2,3,4,…..\)) или \(W\) (множество целых чисел; \(0,1, 2,3,….\)) или \(I\) (набор целых чисел;\(….. – 3,\, – 2,\, – 1,\,0,\,1,\,2, \,3,\,….\)) или \(R\) (действительное число) в качестве замещающего набора.
Q.5. Как решать линейные неравенства?
Ans Для решения данного линейного неравенства необходимо принять следующие рабочие правила:
Правило 1: При переносе положительного члена из одной части неравенства в другую его часть знак члена становится отрицательным.
Правило 2: При переносе отрицательного члена из одной части неравенства в другую его часть знак члена становится положительным.
Правило 3: Если каждый член неравенства умножить или разделить на одно и то же положительное число, знак неравенства останется прежним.
Правило 4: Если каждый член неравенства умножить или разделить на одно и то же отрицательное число, знак неравенства меняется на противоположный.
Правило 5: Если изменить знак каждого члена в обеих частях неравенства, знак неравенства изменится на противоположный.
Правило 6: Если обе части неравенства положительны или обе отрицательны, то при взятии их обратных величин знак неравенства меняется на противоположный.
Мы надеемся, что эта подробная статья о линейных неравенствах окажется вам полезной. Если у вас есть какие-либо вопросы по этой статье, отправьте нам сообщение через поле для комментариев ниже, и мы свяжемся с вами как можно скорее.
Линейные неравенства (одна переменная)
Это «Линейные неравенства (одна переменная)», раздел 2.8 из книги «Начальная алгебра» (v. 1.0). Для получения подробной информации об этом (включая лицензирование) нажмите здесь.
Для получения дополнительной информации об источнике этой книги или о том, почему она доступна бесплатно, посетите домашнюю страницу проекта. Там вы можете просматривать или скачивать дополнительные книги. Чтобы загрузить ZIP-файл с этой книгой для использования в автономном режиме, просто нажмите здесь.
Помогла ли вам эта книга? Рассмотрите возможность передачи:
Помощь Creative Commons
Creative Commons поддерживает свободную культуру от музыки до образования.
Их лицензии помогли сделать эту книгу доступной для вас.
Помогите государственной школе
DonorsChoose.org помогает таким людям, как вы, помогать учителям финансировать их классные проекты, от художественных принадлежностей до книг и калькуляторов.
2.8 Линейные неравенства (одна переменная)
Цели обучения
- Определите линейные неравенства и проверьте решения.
- Решайте линейные неравенства и выражайте решения графически на числовой прямой и в интервальной записи.
- Решайте сложные линейные неравенства и выражайте решения графически на числовой прямой и в виде интервалов.
- Решите приложения, включающие линейные неравенства, и интерпретируйте результаты.
Определение линейного неравенства
Линейное неравенство Математическое утверждение, относящее линейное выражение к меньшему или большему, чем другое. это математическое утверждение, которое связывает линейное выражение как меньшее или большее, чем другое.
Ниже приведены некоторые примеры линейных неравенств, все из которых решаются в этом разделе:
Решение линейного неравенстваВещественное число, которое дает истинное утверждение, когда его значение заменяет переменную. это действительное число, которое даст истинное утверждение при замене переменной. Линейные неравенства либо имеют бесконечно много решений, либо не имеют решений. Если существует бесконечно много решений, изобразите набор решений на числовой прямой и/или выразите решение, используя интервальную запись.
Пример 1: Являются ли x=−2 и x=4 решениями уравнения 3x+7<16?
Решение: Подставим значения x , упростим и проверим, получим ли мы верное утверждение.
Ответ: x=−2 является решением, а x=4 — нет.
Алгебра линейных неравенств
Все методы решения линейных уравнений, кроме одного, применимы и к решению линейных неравенств. Вы можете прибавлять или вычитать любое действительное число к обеим частям неравенства, а также умножать или делить обе части на любые 9.
0143 положительное действительное число для создания эквивалентных неравенств. Например,
Вычитание 7 с каждой стороны и деление каждой стороны на +5 приводит к эквивалентному неравенству, которое верно.
Пример 2: Решите и нарисуйте набор решений: 3x+7<16.
Решение:
Полезно потратить минуту и выбрать несколько значений из набора решений, подставить их в исходное неравенство, а затем проверить результаты. Как указано, вы должны ожидать, что x=0 решит исходное неравенство, а x=5 — нет.
Такая проверка показывает, что неравенство решено правильно. Это можно сделать мысленно.
Ответ: Обозначение интервала: (−∞, 3)
При работе с линейными неравенствами при умножении или делении на отрицательное число применяется другое правило. Чтобы проиллюстрировать проблему, рассмотрим истинное утверждение 10>−5 и разделим обе части на −5.
Деление на -5 приводит к ложному утверждению.
Чтобы сохранить истинное утверждение, неравенство должно быть обращено.
Та же проблема возникает при умножении на отрицательное число. Это приводит к следующему новому правилу: при умножении или делении на отрицательное число инвертировать неравенство . Это легко забыть сделать, поэтому будьте особенно внимательны и следите за отрицательными коэффициентами.
В общем случае, учитывая алгебраические выражения A и B , где c — положительное ненулевое действительное число, мы имеем следующие свойства неравенств Свойства, используемые для получения эквивалентных неравенств и используемые в качестве средства для их решения.:
Мы используем эти свойства для получения эквивалентных неравенств, которые имеют один и тот же набор решений. Один с тем же набором решений, где переменная изолирована. Процесс аналогичен решению линейных уравнений.
Пример 3: Решите: −2x+1≥21.
Решение:
Ответ: Обозначение интервала: (−∞, −10]
Пример 4: Решить: −7(2x+1)<1,
8
80011 Ответ: Обозначение интервала: (−47, ∞)
Пример 5: Решите: 5x−3(2x−1)≥2(x−3).
Решение:
Ответ: Обозначение интервала: (−∞, 3]
Попробуйте! Решите: 3−5(x−1)≤28. )
Решение для видео
(нажмите, чтобы посмотреть видео) Составные неравенства
Ниже приведены некоторые примеры составных линейных неравенств:
Эти составные неравенстваДва или более неравенства в одном утверждении, соединенные словом «и» или словом «или». на самом деле два неравенства в одном утверждении, соединенные словом «и» или словом «или». Например,
является составным неравенством, поскольку его можно разложить следующим образом:
Решите каждое неравенство по отдельности, и пересечение двух наборов решений решит исходное составное неравенство. Хотя этот метод работает, есть еще один метод, который обычно требует меньшего количества шагов. Примените свойства этого раздела ко всем трем частям составного неравенства с целью выделение переменной в середине оператора для определения границ набора решений.
Пример 6: Решите: −3<2x+5<17.
Решение:
Ответ: Обозначение интервала: (−4, 6)
Пример 7: Решите: −1≤12x−3<1.
Решение:
Ответ: Обозначение интервала: [4, 8)
Важно отметить, что при умножении или делении всех трех частей сложного неравенства на отрицательное число необходимо обратить все неравенства в утверждении. Например,
Приведенный выше ответ можно записать в эквивалентной форме, где меньшие числа лежат слева, а большие числа — справа, как они появляются на числовой прямой.
Используя обозначение интервала, напишите (−10, 5).
Попробуйте! Решите: −8≤2(−3x+5)<34.
Ответ: (−4, 3]
Решение для видео
(нажмите, чтобы посмотреть видео) Для составных неравенств со словом «или» вы должны решить оба неравенства по отдельности, а затем рассмотреть объединение наборов решений.
Значения в этом союзе решают любое неравенство.
Пример 8: Решите: 3x+1<10 или 2x−1≥11
Решение: Решите каждое неравенство и сформируйте объединение, объединив наборы решений.
Ответ: Интервальное обозначение: (−∞, 3)∪[6, ∞)
Попробуйте! Решите: 4x−1<−5 или 4x−1>5.
Ответ: (−∞,−1)∪(32, ∞)
Решение для видео
(нажмите, чтобы посмотреть видео) Применение линейных неравенств
Некоторые ключевые слова и фразы, обозначающие неравенства, приведены ниже:
Ключевые фразы Перевод Число не менее 5. х ≥5 Число 5 или более включительно . Число не более 3. х≤3 Число 3 или менее включительно . Число строго меньше 4. х<4 Число на меньше 4, не включительно . Число на больше, чем 7. х>7 Число более 7, не включительно . Число между 2 и 10. 2<х<10 Число не меньше 5 и не больше 15. 5≤x≤15 Число может находиться в диапазоне от 5 до 15.
Как и во всех приложениях, несколько раз внимательно прочитайте задачу и найдите ключевые слова и фразы. Определите неизвестные и назначьте переменные. Далее переведем формулировку в математическое неравенство. Наконец, используйте изученные свойства, чтобы решить неравенство и выразить решение графически или в интервальной записи.
Пример 9: Переведите: Пять меньше, чем удвоенное число, не более чем 25.
Решение: Сначала выберите переменную для неизвестного числа и определите ключевые слова и фразы.
Ответ: 2n−5≤25. Ключевая фраза «максимум» указывает, что количество имеет максимальное значение 25 или меньше.
Пример 10: Температура в пустыне может колебаться от 10°C до 45°C в сутки. Найдите эквивалентный диапазон в градусах Фаренгейта, F , учитывая, что C=59(F-32).
Решение: Составьте сложное неравенство, в котором температура в градусах Цельсия находится в диапазоне от 10°C до 45°C включительно. Затем подставьте в неравенство выражение, эквивалентное температуре по Цельсию, и найдите F .
Ответ: Эквивалентный диапазон Фаренгейта составляет от 50°F до 113°F.
Пример 11: В первых четырех видах соревнований гимнастка набирает 7,5, 8,2, 8,5 и 9,0 баллов. Что она должна набрать в пятом упражнении, чтобы средний балл был не менее 8,5?
Решение: Среднее значение должно быть не менее 8,5; это означает, что среднее значение должно быть больше или равно 8,5.
Ответ: Она должна набрать не менее 9,3 в пятом упражнении.
Ключевые выводы
- Неравенства обычно имеют бесконечно много решений. Решения представлены графически на числовой прямой или с использованием интервальной записи, или и того, и другого.
- Все правила решения линейных неравенств, кроме одного, такие же, как и для решения линейных уравнений. Если вы разделите или умножите неравенство на отрицательное число, переверните неравенство, чтобы получить эквивалентное неравенство.
- Составные неравенства со словом «или» требуют, чтобы мы решили каждое неравенство и образовали объединение каждого набора решений. Это значения, которые решают хотя бы одно из заданных неравенств.
- Составные неравенства со словом «и» требуют пересечения множеств решений для каждого неравенства. Это значения, которые решают оба или все заданные неравенства.
- Общие рекомендации по решению текстовых задач применимы к приложениям, связанным с неравенствами. Помните о новом списке ключевых слов и фраз, которые указывают на математическую установку, включающую неравенства.
Упражнения по теме
Часть A: Проверка решений
Определите, является ли заданное число решением данного неравенства.
1. 2x−3<6; x=−1
2. −3x+1≤0; х=-2
3,5х-20>0; х=3
4. 12х+1>-34; х=-14
5. -5<7х+1<9; х=0
6. −20≤−3x−5≤−10; x=5
7. x<−3 или x>3; x=−10
8. x<0 или x≥1; х=12
9. 2x+1<−3 или 2x+1≥5; x=2
10. 4x−1<−17 или 3x+2≥6; x=1
Часть B: Решение линейных неравенств
Решите и нарисуйте набор решений. Кроме того, представьте набор решений в интервальной записи.
11. x+5>1
12. x−3<−4
13. 6x≤24
14. 4x>−8
15. −7x≤14 –
x 16,008x 5>9
17. 7x−3≤25
18. 12x+7>−53
19. −2x+5<−7
20. −2x+4≤4
21. −15x+10>20
22. −8x+1≤29
23. 17x−3<1
24. 12x−13>23
25. 53x+1208
25. 53x+12089
600812
. −34x−12≥52
27. −15x+34<−15
28. −23x+1<−3
29. 2(−3x+1)<14
30. −7(x −2)+1<15
31. 9x−3(3x+4)>−12
32. 12x−4(3x+5)≤−2
33. 5−3(2x−6)≥ −1
34. 9x−(10x−12)<22
35. 2(x−7)−3(x+3)≤−3
36. 5x−3>3x+7
37. 4(3x−2)≤−2(x+3)+12
38. 5(x−3)≥15x−(10x+4)
39. 12x+1>2(6x−3)−5
40. 3(x−2)+5>2(3x +5)+2
41. −4(3x−1)+2x≤2(4x−1)−3
42. −2(x−2)+14x<7(2x+1)
Составьте алгебраическое неравенство и решите его.
43. Сумма трехкратного числа и числа, умноженного на 4, больше отрицательного числа 8.
44. Сумма числа, умноженного на 7 и трехкратного числа, меньше или равно 1.
45. При вычитании числа из 10, результат не более 12.
46. Если из 6 вычесть число 5 раз, получится не менее 26.
47. Если к числу, умноженному на три, прибавить пять, то результат будет меньше двадцати.
48. Если из числа, умноженного на два, вычесть три, то результат будет больше или равен девяти.
49. Билл зарабатывает 12 долларов в день плюс 0,25 доллара за каждого человека, которого он регистрирует для голосования. Сколько человек он должен зарегистрировать, чтобы зарабатывать не менее 50 долларов в день?
50. Членство в гольф-клубе стоит 100 долларов в месяц, а каждый раунд игры в гольф стоит всего 25 долларов. Сколько раундов в гольф может сыграть участник, если он хочет, чтобы его расходы не превышали 250 долларов в месяц?
51. Джо получил 72, 85 и 75 баллов за первые три экзамена по алгебре. Что он должен набрать на четвертом экзамене, чтобы средний балл был не менее 80?
52. Морис заработал 4, 7 и 9 баллов из 10 в первых трех тестах. Что он должен набрать в четвертом тесте, чтобы получить в среднем не менее 7 баллов?
53. Компьютер настроен на отключение при температуре выше 40°C. Приведите эквивалентное утверждение, используя градусы Фаренгейта. (Подсказка: C=59(F−32).)
54. Определенная марка косметики гарантированно не работает, если температура ниже 35°C. Приведите эквивалентное утверждение, используя градусы Фаренгейта.
Часть C: Составные неравенства
Решите и нарисуйте набор решений. Кроме того, представьте набор решений в интервальной записи.
55. −1 56. −10≤5x<20
57. −2≤4x+6<10
58. −10≤3x−1≤−4
59. −15<3x−6≤6
60. −22<5x+3≤3
61. −1≤12x−5≤1
62. 1<8x+5<5
63. − 15≤23x−15<45
64. −12<34x−23≤12
65. −3≤3(x−1)≤3
66. −12<6(x−3)≤0
67. 4<−2(x+3)<6
68. −5≤5(−x+1)<15
69. −32≤14(12x−1)+34<32
70. −4≤−13(3x+12)<4
71. −2≤12−2(x−3)≤20
72. −5<2(x−1)−3(x+2)<5
73. 3x≤−15 или 2x>6
74. 4x−1<−17 или 3x+2≥8
75. −2x+1<−1 или –2x+1>1
76. 7x+4≤4 или 6x−5≥1
77. 3x−7<14 или 2x+3>7
78. −3x +1<−5 или −4x−3>−23
79. 12x−2<−1 или 12x−2>1
80. 13x+3≥−2 или 13x+3≤2
81. 3x+7≤7 или -5x+6>6
82. −10x−3≤17 или 20x−6>−26
83. 2x−10<−2 или −3x+4>−5
85. 3x<18 и 5x>−20
86. x+7≤5 и x−3≥−10
87. 2x−1<5 и 3x−1<10
88. 5x+2<− 13 и 3x+4>13
Составьте составное неравенство для следующего и затем решите.
89. Пять больше двух, умноженное на какое-то число, находится в диапазоне от 15 до 25.
90. Четыре вычитается из трех, умноженное на какое-то число, равное от -4 до 14.
91. Клинт хочет получить четверку, которая составляет минимум 80, но меньше 90. Какой диапазон он должен набрать на четвертом экзамене, если первые три были 65, 75 и 90?
92. Некоторые антифризы эффективны в диапазоне температур от −35°C до 120°C. Найдите эквивалентный диапазон в градусах Фаренгейта.
93. Средняя температура в Лондоне колеблется от 23°C летом до 14°C зимой. Найдите эквивалентный диапазон в градусах Фаренгейта.
94. Если основание треугольника равно 5 дюймам, то в каком диапазоне должна быть высота, чтобы площадь была от 10 квадратных дюймов до 20 квадратных дюймов?
95. Прямоугольник имеет длину 7 дюймов. Найдите все возможные ширины, если площадь должна быть не менее 14 квадратных дюймов и не более 28 квадратных дюймов.
96. Прямоугольник имеет ширину 3 сантиметра. Найдите все возможные длины, если периметр должен быть не меньше 12 сантиметров и не больше 26 сантиметров.
97. Периметр квадрата должен быть от 40 футов до 200 футов. Найдите длины всех возможных сторон, удовлетворяющих этому условию.
98. Если два раза угол находится между 180 и 270 градусами, то каковы границы исходного угла?
99. Если три раза угол будет между 270 градусами и 360 градусами, то каковы границы первоначального угла?
Часть D: Темы на доске обсуждений
100. Исследуйте и обсудите использование нотации построителя множеств с пересечениями и объединениями.
101. Можем ли мы объединить логическое «или» в одно утверждение, как мы делаем для логического «и»?
Ответы
1: Да
3: Нет
5: Да
7: Да
9: Да
11: x>−4; (−4, ∞)
13: x≤4; (−∞, 4]
15: x≥−2; [−2, ∞)
17: x≤4; (−∞, 4]
19: x>6; (6, ∞)
21: x<−23; (−∞, −23)
23: x<28; (−∞, 28)
25: x≤−110;(−∞, −110]
27: x>194; (194, ∞)
29: x>−2;(−2, ∞)
31: ∅
8 33: x≤4;(−∞, 4]
Затем подставьте в неравенство выражение, эквивалентное температуре по Цельсию, и найдите F .
x<−3 или x>3; x=−10
12x+1>2(6x−3)−5
Сколько раундов в гольф может сыграть участник, если он хочет, чтобы его расходы не превышали 250 долларов в месяц?56. −10≤5x<20
57. −2≤4x+6<10
58.
−10≤3x−1≤−4
59. −15<3x−6≤6
60. −22<5x+3≤3
61. −1≤12x−5≤1
62. 1<8x+5<5
63. − 15≤23x−15<45
64. −12<34x−23≤12
65. −3≤3(x−1)≤3
66. −12<6(x−3)≤0
67. 4<−2(x+3)<6
68. −5≤5(−x+1)<15
69. −32≤14(12x−1)+34<32
70. −4≤−13(3x+12)<4
71. −2≤12−2(x−3)≤20
72. −5<2(x−1)−3(x+2)<5
73. 3x≤−15 или 2x>6
74. 4x−1<−17 или 3x+2≥8
75. −2x+1<−1 или –2x+1>1
76. 7x+4≤4 или 6x−5≥1
77. 3x−7<14 или 2x+3>7
78. −3x +1<−5 или −4x−3>−23
79. 12x−2<−1 или 12x−2>1
80. 13x+3≥−2 или 13x+3≤2
81. 3x+7≤7 или -5x+6>6
82. −10x−3≤17 или 20x−6>−26
83. 2x−10<−2 или −3x+4>−5
85. 3x<18 и 5x>−20
86. x+7≤5 и x−3≥−10
87. 2x−1<5 и 3x−1<10
88. 5x+2<− 13 и 3x+4>13
Составьте составное неравенство для следующего и затем решите.
89. Пять больше двух, умноженное на какое-то число, находится в диапазоне от 15 до 25.
90. Четыре вычитается из трех, умноженное на какое-то число, равное от -4 до 14.
91. Клинт хочет получить четверку, которая составляет минимум 80, но меньше 90. Какой диапазон он должен набрать на четвертом экзамене, если первые три были 65, 75 и 90?
92. Некоторые антифризы эффективны в диапазоне температур от −35°C до 120°C. Найдите эквивалентный диапазон в градусах Фаренгейта.
93. Средняя температура в Лондоне колеблется от 23°C летом до 14°C зимой. Найдите эквивалентный диапазон в градусах Фаренгейта.
94. Если основание треугольника равно 5 дюймам, то в каком диапазоне должна быть высота, чтобы площадь была от 10 квадратных дюймов до 20 квадратных дюймов?
95. Прямоугольник имеет длину 7 дюймов. Найдите все возможные ширины, если площадь должна быть не менее 14 квадратных дюймов и не более 28 квадратных дюймов.
96. Прямоугольник имеет ширину 3 сантиметра.
Найдите все возможные длины, если периметр должен быть не меньше 12 сантиметров и не больше 26 сантиметров.
97. Периметр квадрата должен быть от 40 футов до 200 футов. Найдите длины всех возможных сторон, удовлетворяющих этому условию.
98. Если два раза угол находится между 180 и 270 градусами, то каковы границы исходного угла?
99. Если три раза угол будет между 270 градусами и 360 градусами, то каковы границы первоначального угла?
Часть D: Темы на доске обсуждений
100. Исследуйте и обсудите использование нотации построителя множеств с пересечениями и объединениями.
101. Можем ли мы объединить логическое «или» в одно утверждение, как мы делаем для логического «и»?
Ответы
1: Да
3: Нет
5: Да
7: Да
9: Да
11: x>−4; (−4, ∞)
13: x≤4; (−∞, 4]
15: x≥−2; [−2, ∞)
17: x≤4; (−∞, 4]
19: x>6; (6, ∞)
21: x<−23; (−∞, −23)
23: x<28; (−∞, 28)
25: x≤−110;(−∞, −110]
27: x>194; (194, ∞)
29: x>−2;(−2, ∞)
31: ∅
35: х≥-20; [−20, ∞)
37: x≤1; (−∞, 1]
39: R
41: х≥12; [12, ∞)
43: n>−4
45: n≥−2
47: n<5
49: Билл должен зарегистрировать не менее 152 человек.