определение, способы решения с примерами
В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.
- Определение предела функции
- Решение пределов
- С заданным числом
- С бесконечностью
- С неопределенностью (икс стремится к бесконечности)
- С неопределенностью (икс стремится к конкретному числу)
Определение предела функции
Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.
Запись предела:
- предел обозначается значком lim;
- под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x, но не обязательно, например: “x→1″;
- затем справа дописывается сама функция, например:
Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):
Читается как “предел функции при икс, стремящемся к единице”.
x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).
Решение пределов
С заданным числом
Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1):
Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).
С бесконечностью
В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:
Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:
- 3 – 1 = 2
- 3 – 10 = -7
- 3 – 100 = -97
- 3 – 1000 – 997 и т.д.
Другой более сложный пример
Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.
- При x = 1, y = 12 + 3 · 1 – 6 = -2
- При x = 10, y = 102 + 3 · 10 – 6 = 124
- При x = 100, y = 1002 + 3 · 100 – 6 = 10294
Таким образом при “икс”, стремящемся к бесконечности, функция x2 + 3x – 6 неограниченно растет.
С неопределенностью (икс стремится к бесконечности)
В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.
Пример: давайте вычислим предел ниже.
Решение
Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:
Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:
1. Находим x в старшей степени для числителя (в нашем случае – это два).
2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).
Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).
3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.
4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.
С неопределенностью (икс стремится к конкретному числу)
И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.
В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.
Пример: Найдем предел функции ниже.
Решение
1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.
2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
В нашем случаем корнями выражения в числителе (2x2 – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5).
Знаменатель (x – 1) изначально является простым.
3. Получаем вот такой видоизмененный предел:
4. Дробь можно сократить на (x – 1):
5. Остается только подставить число 1 в выражение, получившееся под пределом:
Глава 43. Предел функции в точке и на бесконечности
Рассмотрим функцию , определенную на некотором множестве и точку , быть может, и не принадлежащую множеству , но обладающую тем свойством, что в любой –окрестности точки имеются точки множества значений аргумента , отличные от . Рассмотрим вопрос о сходимости соответствующей последовательности значений функции .
Существуют два определения Предела функции в точке.
Определение
Число называется Предельным значением функции в точке (или Пределом функции при X® A), если для любой сходящейся к А Последовательности значений аргумента , элементы которой отличны от , соответствующая последовательность значений функции сходится к .
Для обозначения предельного значения функции используется следующая символика: .
Отметим, что функция может иметь в точке только
Рассмотрим несколько Примеров.
1. Функция Имеет в точке предел, равный –2. Действительно, пусть – любая последовательность значений аргумента, сходящаяся к нулю, т. е. , тогда при в силу теорем о свойствах сходящихся последовательностей:
.
2. Функция определена для всех . В точке эта функция не имеет предела. Для доказательства возьмем две последовательности значений аргумента, сходящиеся к нулю:
и .
Соответствующие последовательности значений функций для них:
.
Таким образом, Определение 1 не удовлетворяется, так как для двух разных последовательностей значений аргумента, сходящихся к нулю, соответствующие последовательности значений функции имеют разные пределы.
Дадим другое определение пределу функции в точке . Пусть функция определена на некотором интервале , кроме быть может точки .
Определение
Число называется Пределом функции в точке , если для любого числа существует такое число , что для всех , Удовлетворяющих условиям при , выполняется неравенство .
Второе определение предела функции означает, что функция имеет предел в точке , если для любой E–окрестности точки можно найти такую d–окрестность точки , что, как только значение аргумента попадет в эту d–окрестность, соответствующее значение функции будет находиться в E–окрестности точки (см. рис. 4.3.1).
Рис. 4.3. 1
1
Первое определение предела функции основано на понятии предела числовой последовательности, и его называют определением, «на языке последовательностей» (предел функции по Гейне). Второе определение носит название «на языке d–e» (предел функции по Коши).
Теорема
Первое и второе определения предела функций Эквивалентны.
Введем понятия Односторонних пределов функции. Дадим определение односторонних пределов функции «на языке d–e».
Пусть функция определена на полуинтервале (соответственно на полуинтервале , кроме, быть может, точки .
Определение
Число B называется Правым (левым) пределом функции в точке А, если для любого существует такое , что для всех X из правой (левой) D –Окрестности точки А, Т. е. , выполняется неравенство .
Для правого (левого) предела функции используется символическая запись:
или
( или ).
Приведем в качестве Примера функцию
В точке эта функция имеет левый и правый пределы: , .
Пример
Найти правый и левый пределы функции .
Решение
– правый предел.
– левый предел.
Таким образом видим, что левый и правый пределы Не равны!
Теорема
Функция имеет в точке А Предел тогда и только тогда, когда в этой точке Существуют пределы как Справа, так и Слева, и они Равны. В этом случае их общее значение и является двусторонним пределом функции в точке .
| < Предыдущая | Следующая > |
|---|
— Является ли предел функцией?
Это прямо в переулке функционального анализа. Мы можем рассматривать предельную операцию как своего рода функционал (функционал — это функция, определенная в векторном пространстве со значениями в ее базовом поле).
Теперь мы можем рассмотреть $C[0, 1]$ пространство непрерывных функций, определенных на $[0, 1]$ (со значениями в $\mathbb{R}$), и определить для каждого $z \in [0 ,1]$ $$ T_z : C[0, 1] \to \mathbb{R} \\ T_z(f) = \lim_{x \to z} \, f(x) $$ Здесь следует отметить пару вещей:
- На самом деле это оценочная карта, поскольку каждая $f$ непрерывна, мы просто имеем $$ T_z(f) = f(z) $$
- Опять же можно показать, что это непрерывный функционал
- Мы можем рассматривать это как $$ T : [0,1] \times C[0,1] \to \mathbb{R} \\ T(z, f) = \lim_{x \to z} \, f(x) $$
Возвращаясь к первому пункту выше, я не думаю, что это именно тот тип карты, который вы искали. Проблема в том, что этот оператор не может быть определен правильно, если мы не считаем, что он определен в пространстве непрерывных функций (т.е. что произойдет, если у нас есть разрыв скачка? Какое значение мы должны принять тогда?). Я вижу, вы комментируете это в своем посте («удобно удалить этот набор $N$»), но каким будет наш удобный набор? Как бы вы тогда определили домен? Конечно, мы можем ослабить наши ограничения на домен и придумать других операторов, но я думаю, что пока достаточно функционального анализа 😉
Проблема в том, что этот оператор не может быть определен правильно, если мы не считаем, что он определен в пространстве непрерывных функций (т.е. что произойдет, если у нас есть разрыв скачка? Какое значение мы должны принять тогда?). Я вижу, вы комментируете это в своем посте («удобно удалить этот набор $N$»), но каким будет наш удобный набор? Как бы вы тогда определили домен? Конечно, мы можем ослабить наши ограничения на домен и придумать других операторов, но я думаю, что пока достаточно функционального анализа 😉
Я видел приведенное выше редактирование об изменении вашего домена в зависимости от функции, и у меня есть следующие комментарии по этому поводу:
- Если мы изменим домен для каждой функции, то у вас действительно не будет единой «функции ограничения». ‘, у вас есть функция, которая принимает на вход функцию, создает из нее функцию, а затем эта последняя функция — это то место, где фактически находится операция ограничения. Хотя это кажется хорошим для функционального программирования, с математической точки зрения это не кажется элегантным.
 В самом деле, какая польза от этого для нас? Это определенно не было бы линейно (мне очень нравится линейность)! Также я не уверен, как бы вы говорили здесь о преемственности; я хочу сказать, что ты можешь делать то, что вы сказали делать, но это не очень полезно.
В самом деле, какая польза от этого для нас? Это определенно не было бы линейно (мне очень нравится линейность)! Также я не уверен, как бы вы говорили здесь о преемственности; я хочу сказать, что ты можешь делать то, что вы сказали делать, но это не очень полезно. - Я бы предпочел изменить пробел следующим образом: $$ E = \{ f : \mathbb{R} \to \mathbb{R} \mid f \text{ непрерывен, за исключением конечного числа точек} \} $$ Если бы мы рассматривали только эти функции, то это пространство действительно было бы больше, чем $C(\mathbb{R})$, но оно все еще кажется достаточно элегантным, чтобы с ним можно было выполнять некоторые математические операции. Обратите внимание, что мы не можем рассматривать $f$, которые непрерывны, кроме как на счетном множестве (почему?). Если хотите, я могу более подробно рассказать, почему это пространство довольно красивое (однако для этого потребуется немного теории меры!).
Во всяком случае, я надеюсь, что это то, что вы искали!
исчисление— Как мы можем определить предел постоянной функции?
Во-первых, давайте признаем тот факт, что в зависимости от пространства, в котором вы работаете, может быть более одного определения предела. Например, предел функции для данного элемента домена, где и домен, и кодовый домен имеют некоторую меру, вы, вероятно, пойдете с определением $\epsilon — \delta$, а если вы говорите об ограничении бесконечной последовательности, вы необходимо иметь определение последовательности. Они связаны, но не совсем одно и то же.
Например, предел функции для данного элемента домена, где и домен, и кодовый домен имеют некоторую меру, вы, вероятно, пойдете с определением $\epsilon — \delta$, а если вы говорите об ограничении бесконечной последовательности, вы необходимо иметь определение последовательности. Они связаны, но не совсем одно и то же.
Цитата, которую вы цитируете из этой статьи в Википедии, на которую вы ссылаетесь, использует некоторое текстовое объяснение, чтобы облегчить понимание идеи предела, но это не точно в математические термины. Это должно только облегчить понимание идеи.
Теперь, если вы хотите как-то определить значение «подхода», вам придется взглянуть на определение лаймов. Независимо от выбранного вами определения (перефразированного на более распространенный английский):
$c$ — это $\lim$ $f$ в (что-то — либо элемент в вашем домене, либо что-то, что равно рядом с вашим доменом), если независимо от того, насколько близко вы хотите быть к $c$ (выбрав $\epsilon > 0$, вы можете определить некоторые условия, ограничивающие, какой элемент $x$ вы можете выбрать из своего домена — закройте туда, где вы хотите находиться в своем домене, чтобы для любого $x$ из вашего домена, выбранного таким образом, было верно, что вы находитесь настолько близко к $c$, насколько хотели, т.
е.
$|f(x) — c| < \эпсилон$
Это не настоящая цитата, это обобщение-перефразировка.
Таким образом, по-прежнему используя обычное английское объяснение, если вы приблизитесь в своем домене к некоторому $x_0$, вы будете близки к некоторому $c$ в вашем кодовом домене. Если вы уже в $c$, вы также очень, очень близко.
Здесь нет ничего о приближении, но в большинстве случаев большинство ваших значений даже около ваш $x_0$ дает значение, отличное от $c$, поэтому использование термина подход облегчает читателю понять. Но если тебе уже в $c$ технически вы не приближаетесь к , но это не делает определение недействительным. Поэтому, если вы не хотите правильно определить подход, вам придется сказать, что вы либо очень близки к сути, либо уже там.
Обратите внимание, что ваша функция может иногда переходить к $c$, а затем выходить из него.

 В самом деле, какая польза от этого для нас? Это определенно не было бы линейно (мне очень нравится линейность)! Также я не уверен, как бы вы говорили здесь о преемственности; я хочу сказать, что ты можешь делать то, что вы сказали делать, но это не очень полезно.
В самом деле, какая польза от этого для нас? Это определенно не было бы линейно (мне очень нравится линейность)! Также я не уверен, как бы вы говорили здесь о преемственности; я хочу сказать, что ты можешь делать то, что вы сказали делать, но это не очень полезно.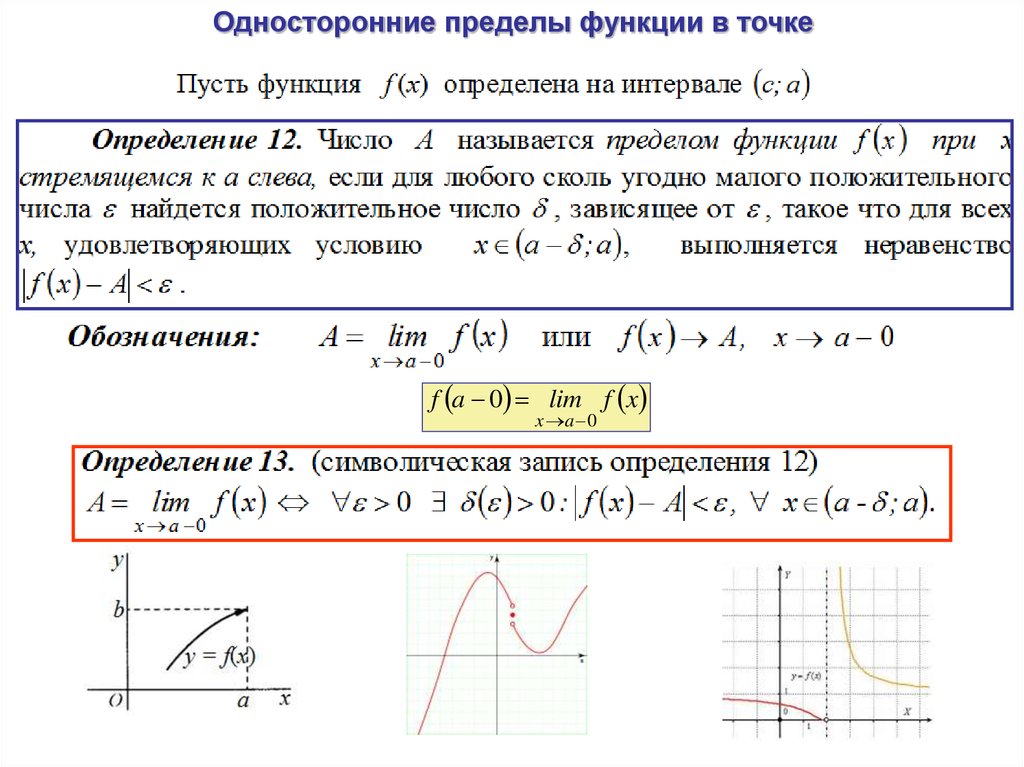 е.
е.