Неравенства с дробями и корнями. Упр. 695, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/класс
Неравенства с дробями и корнями. Упр. 695, Алгебра, 8 класс, Алимов Ш.А. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Корни..
. дроби… неравенства…. офигеть((
Лучший ответ
А я наоборот — дроби обожаю))
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые).
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Методика ознакомления с дробями
План:
1. Общие вопросы методики ознакомления младших школьников с дробями.
2. Методика ознакомления с долями величины
3. Сравнение дробей
4. Решение задач на нахождение доли числа и числа по его доле
Ознакомить учащихся с понятием доли, значит сформировать у них конкретное представление о долях, т. е. научить детей образовать доли практически.
Для формирования правильных представлений о долях надо использовать достаточное количество разнообразных наглядных пособий. Нам более удобными пособиями являются геометрические фигуры, из бумаги, в форме прямоугольника, круга, треугольника, отрезка и т.д.
Правильное
представление о долях, а позднее о дробях
будут сформированы тогда, когда ученики
своими руками получать, например,
половину квадрата, круга, четверть
отрезка и т.
д.
Доли записываются с помощью двух чисел. Одна вторая доля квадрата обозначается 1/2. Число 2 показывает, что квадрат разделен на 2 равные части, а число 1 показывает, что взяли одну такую часть.
Аналогично получает ¼, 1/6, 1/12. Решение задач на нахождение доли числа и числа по его доле также способствует формированию представлений о долях величины. Потому решение задач на нахождение доли числа и числа по его доле выполняется на наглядной основе.
Образование дробей, как и образование долей рассматривается с помощью наглядных пособий. Для сравнения дробей обычно используются иллюстрации е разными прямоугольниками.
Предлагаются специальные упражнения на сравнение дробей:
1. Вставьте пропущенный знак
2.
Конкретный смысл дроби ярко раскрывается
при решении задач на нахождение дроби
числа. Решение этих задач, как и задач
на нахождение доли числа, выполняется
с помощью соответствующих наглядных
пособий.
Например, у закройщика было 12 метров ткани. 3:2 всей ткани израсходовал. Сколько метров ткани израсходовал закройщик?
Различные упражнения с дробями следует чаще включать для устных и письменных работ на протяжении всего учебного года.
План:
1. Методика рассмотрения элементов алгебры.
2. Числовые равенства и неравенства.
3. Подготовка к ознакомлению с переменной. Элементы буквенной символики.
4. Неравенства с переменной.
5. Уравнение
Введение
элементов алгебры в начальный курс
математики позволяет с самого начала
обучения вести планомерную работу
отправленную на формирование у детей
таких важнейших математических понятий
как: выражение, равенство, неравенство,
уравнение. Ознакомление с использованием
буквы как символа обозначающего любое
число из известной детям области чисел,
создает условия для обобщения многих
на начальном курсе вопросов арифметической
теории, является хорошей подготовкой
к ознакомлению детей в дальнейшем с
понятиями в переменной функций.
Программой начальных классов предусматривается знакомство учащихся с использования буквенной символики, решений элементарных уравнений первой степени с одним неизвестным и применений их к задачам в одно действие. Эти вопросы изучаются в тесной связи с арифметическим материалом, что способствует формированию числа и арифметических действий.
С первых дней обучения начинается работа по формированию у учащихся понятий равенства. Первоначально дети учатся сравнивать множество предметов уравнивать неравные группы, преобразовывать равные группы в неравные. Уже при изучении десятка чисел вводятся упражнения сравнения. Сначала они выполняются с опоры на предметы.
При
изучении арифметических действий
включаются упражнения на сравнения
выражений, их делят на 3 группы.
1. Упражнение, направленное на уточнение знаний учащихся об арифметических действиях и на их применение. При ознакомлении учащихся с арифметическими действиями сравниваются выражение вида 5+3 и 5-3; 8*2 и 8/2. Сначала выражения сравниваются путем нахождения значений каждого и сравнения полученных чисел. В дальнейшем задание выполняется ни основе того, что сумма двух чисел больше их разности, а произведение — больше их частного; вычисление используется только для проверки результата. Сравнение выражений вида 7+7+7 и 7*3 проводится для закрепления знаний учащихся о связи сложения и умножения.
В процессе сравнения учащиеся знакомятся с порядком выполнения арифметических действий. Сначала рассматриваются выражения, содержание скобки, вида 16 — (1+6).
2.
После этого рассматривается порядок
действий в выражениях без скобок
содержащих действия одной и двух
степеней. Эти значения учащиеся усваивают
в процессе выполнения примеров.
3. Упражнения, при выполнении которые учащиеся усваивают и закрепляют знания по соотношению между компонентами и результатами арифметических действий. Они включаются уже при изучении чисел десятка.
В
этой группе упражнений учащиеся
знакомятся со случаями изменения
результатов действий в зависимости от
изменения одного из компонентов.
Сравниваются выражения, в которых
изменяется одно из слагаемых (6+3 и 6+4)
или уменьшаемое 8-2 и 9-2 и т.д. Подобные
задания включаются также при изучении
табличного умножения и деления и
выполняются с помощью вычислений ( 5*3 и
6*3, 16:2 и 18:2 ) и т.д. В дальнейшем можно
сравнивать эти выражения без опоры на
вычисления.
Рассмотренные упражнения тесно связаны с программным материалом и способствует его усвоению. Наряду с этим в процессе сравнения чисел и выражений учащиеся получают первые представления о равенстве и неравенстве.
Так,
в 1 классе, где ещё термины «равенство»
и «неравенство» не используются, учитель
может при проверке правильности
выполненных детьми вычислений задавать
вопросы в такой форме: «Коля прибавил
к шести восемь и получил 15. Верное это
решение или неверное?», или предлагать
детям упражнения в которых требуется
проверить решение данных примеров,
найти верные записи и т.д. Аналогично
при рассмотрении числовых неравенств
вида 5<6,8>4 и более сложных учитель
может задавать вопрос в такой форме:
«Верны ли эти записи?», а после введения
неравенства – «Верны ли эти неравенства?».
Начиная с 1 класса дети знакомятся и с преобразованиями числовых выражений, выполняемое на основе применения изученных элементов арифметической теории( нумерации, смысла действий и другое). Например, на основе знания нумерации, разрядного состава чисел учащиеся могут представить любое число в виде суммы его разрядных слагаемых. Это умение используется при рассмотрении преобразования выражений в связи с выражением многих вычислительных приемов.
В связи с подобными преобразованиями уже в I классе дети встречаются с «цепочкой» равенств.
Как решать неравенства с дробями?
Последняя обновленная дата: 01 -й март 2023
•
Общее представление: 228K
•
Просмотр сегодня: 3,12K
Ответ
Проверенные
228K+ виды
HINT: ЗДЕСЬ. ЗДЕСЬ. Мы спросили. неравенства с дробями. Во-первых, мы должны знать, какие основные математические операции необходимо применить для его упрощения.
Здесь мы используем математические операции, такие как сложение, вычитание, умножение, чтобы решить данное неравенство. Сначала попробуем удалить дроби. Затем мы пытаемся объединить похожие термины, чтобы упростить процесс. Затем мы оставляем неизвестные члены в одной части неравенства, а постоянный член — в другой. После этого мы решаем его, чтобы получить желаемый результат.
Полное пошаговое решение:
Необходимо упомянуть процедуру решения неравенств с дробями. Попытаемся объяснить это следующими шагами. Несмотря на то, что неравенства с дробями кажутся сложными, если мы выполним следующие шаги, их можно легко решить.
Шаги следующие:
(1) Перед тем, как начать использовать какие-либо процессы, чтобы попытаться решить неравенство, сначала начните с того, что просто возьмите неравенство перед собой. Запишите все негативы, которые вам нужно будет помнить при решении проблемы.
(2) Здесь обратите внимание на все математические операции в неравенстве, такие как умножение, вычитание, возведение в степень, скобки и тому подобное.
(3) Используйте обратный порядок действий, чтобы начать решение проблемы. На самом деле нам нужно начать со скобок, показателей степени, умножения или деления, сложения или вычитания. Но когда мы ищем переменную, мы будем использовать обратный порядок операций.
(4) Запишите неравенство в правильной форме. Одна сторона должна быть равна нулю, а другая сторона должна содержать только дроби. Если дробей больше одной, то упростите ее, умножив все члены на наименьший общий знаменатель всех дробей.
(5) Упростите, объединив одинаковые термины в левой части.
(6) Затем сложите или вычтите величины, чтобы получить неизвестные с одной стороны и постоянные члены с другой, а затем упростите неравенство.
(7) Помните, что если в задаче нужно умножить или разделить на отрицательное число, то нужно поменять знак неравенства.
Примечание:
Чтобы правильно понять эти шаги, рассмотрим один пример.
Пусть $4 < \left( {\dfrac{x}{8}} \right) + 5$.
Теперь вычитаем 5 с обеих сторон, получаем
$ \Rightarrow 4 — 5 < \left( {\dfrac{x}{8}} \right) + 5 - 5$
$ \Rightarrow — 1 < \left ( {\dfrac{x}{8}} \right) + 0$
$ \Rightarrow — 1 < \left( {\dfrac{x}{8}} \right)$
Теперь умножаем обе части на 8, получаем получить,
$ \Rightarrow — 1 \times 8 < 8 \times \left( {\dfrac{x}{8}} \right)$
$ \Rightarrow — 8 < x$
Следовательно, решение для $4 < \left ( {\dfrac{x}{8}} \right) + 5$ равно $x > — 8.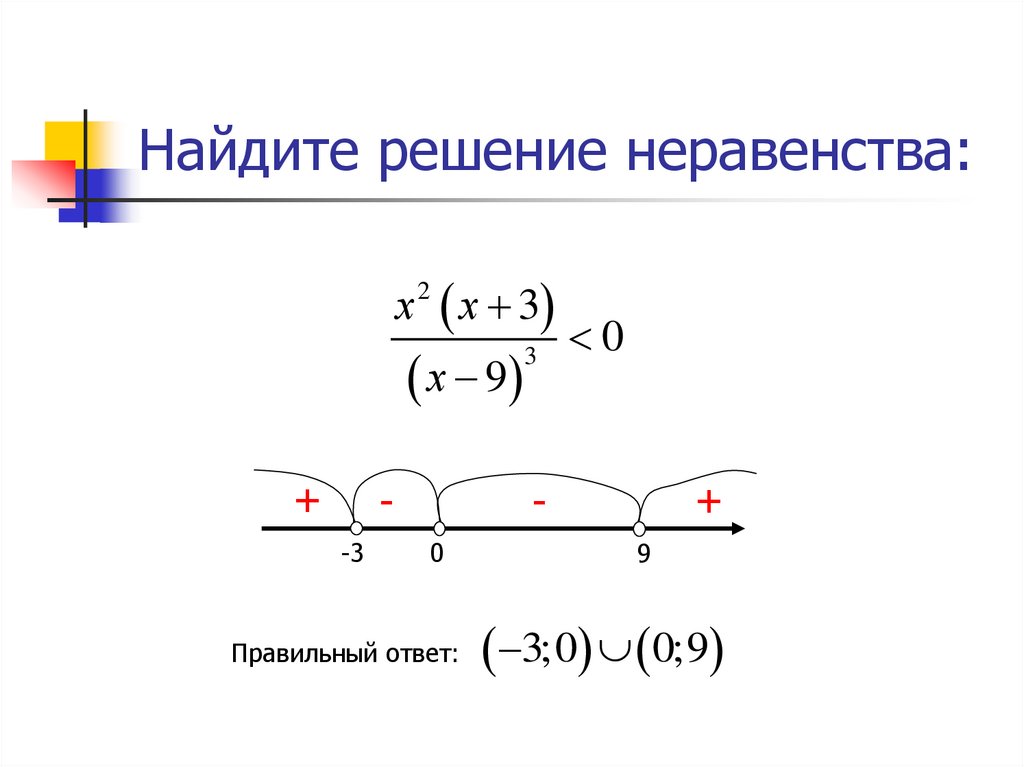
$
Неравенства дробей – Mathigon
План урока и цель
Учащиеся будут сравнивать дроби с разными знаменателями.
Стержни фракций представляют собой отличный инструмент для работы с эквивалентными фракциями. Это задание побуждает учащихся переходить от конкретного к абстрактному, создавая уравнения и неравенства с дробями, а затем численно объясняя, что происходит. Polypad предоставляет учащимся безопасное место для изучения и создания собственных примеров на удобном для них уровне, прежде чем постепенно подтолкнуть себя к созданию более сложных примеров по мере того, как они станут более уверенными в себе.
Разминка
Покажите учащимся эту стену дробей, построенную в Polypad:
https://mathigon.org/polypad/5f7dd84624271100125d72c1 Предложите им написать столько наборов эквивалентных дробей, сколько они смогут увидеть на картинке. Например. они могли написать 4/6=2/34/6=2/34/6=2/3, потому что линия для четырех групп 1/61/61/6 совпадает с линией для двух групп 1/ 31/31/3.
Учащиеся, которые быстро выполнят это задание, могут также записать другие отношения эквивалентных дробей, которые не отображаются на стене, используя знаменатели больше 10 или дроби больше 1. Предложите отстающим учащимся использовать столбцы для составления эквивалентных дробей.
После того, как учащиеся создадут свои наборы эквивалентных дробей, найдите время, чтобы поговорить о том, как они могут проверить свои ответы численно. Если вашим ученикам будет полезен более конкретный обзор этой идеи, вы можете создать с ними что-то вроде этого Polypad.
Основное задание
Покажите учащимся картинку ниже и задайте вопрос: Что больше: 2/32/32/3 или 5/75/75/7? Насколько?
Студенты, скорее всего, согласятся с картинкой, что ясно, что 5/7>2/35/7>2/35/7>2/3, но стоит отметить, что это не всегда может быть так очевидно, и что студенты не всегда смогут использовать Polypad, чтобы помочь им! Предложите студентам предложить способы определения того, что больше и на сколько.
С помощью инструмента «Перо» продемонстрируйте, как разделить каждую треть на семь частей, а каждую седьмую — на три части:
Спросите учащихся, могут ли они теперь лучше оценить, насколько 5/75/75/7 больше, чем 2/32/32/3. Может быть несколько ясно, что столбцы отличаются на 1/21. Подтвердите это, показав следующее: 5/7=15/215/7=15/215/7=15/21 и 2/3=14/212/3=14/212/3=14/21, так что не только можем ли мы вычислить, что 5/7>2/35/7>2/35/7>2/3, мы также можем вычислить, что 5/7−2/3=1/215/7-2/3=1 /215/7−2/3=1/21. Когда вы это сделаете, вы можете пометить Polypad, как показано на рисунке:
Поделитесь со студентами тем, что визуальное представление 5/75/75/7 и 2/32/32/3 ясно показывает, какая дробь больше и что нарисовано в таблице. линии для представления эквивалентных дробей также помогли показать разницу 1/211/211/21.
Затем предложите учащимся составить собственное неравенство дробей. Рассмотрите любой из следующих вариантов:
- Некоторые учащиеся могут просто захотеть изучить комбинации дробей без конкретной цели или задачи.
Предложите им пометить свою диаграмму, как показано выше, и поделиться с вами ссылкой на Polypad, когда закончите. Возможно, теперь они будут готовы перейти к некоторым из перечисленных ниже задач. - Предложите учащимся составить примеры, в которых дроби отличаются на определенную величину. Напишите на доске список единиц измерения (1/2, 1/3, 1/41/2, 1/3, 1/41/2, 1/3, 1/4 и т. д.) и попросите класс найти столько, сколько они могут. Отмечайте их по мере того, как учащиеся находят решения. Студенты могут показать свою работу на Polypad, как показано выше, и поделиться с вами ссылкой.
- Предложите учащимся придумать примеры эквивалентных дробей, в каждой строке которых используется более 1 типа единичных дробей (верхний и нижний столбцы дробей должны быть как минимум двух разных цветов).
- Предложите учащимся создать примеры, в которых два представления дробей максимально близки друг к другу, но не эквивалентны. Поделитесь с классом тем, что, основываясь на приведенном выше примере с 3-м и 7-м, наименьшая разница, обнаруженная классом, составляет 1/211/211/21. Бросьте им вызов, чтобы победить это.
Предложите им пометить свою диаграмму, как показано выше, и поделиться с вами ссылкой на Polypad, когда закончите. Возможно, теперь они будут готовы перейти к некоторым из перечисленных ниже задач.
Бросьте им вызов, чтобы победить это.Ниже приведены несколько примеров меньшего размера. У 1-го разница 1/1801/1801/180. У 2-го разница 1/1681/1681/168. У третьего разница 1/8401/8401/840. Используйте их, чтобы давать подсказки учащимся по мере необходимости.
Поддержка и расширение
Чтобы учащиеся привыкли к идее построения неравенств с дробями, предложите им построить собственную дробную стену и записать все различные неравенства, которые они могут с ее помощью составить. Поощряйте рассуждения, которые помогут им развить чувство числа и навыки оценки, например, при сравнении 3/73/73/7 с 5/9.5/95/9, предложите учащимся подумать, как каждая дробь соотносится с 21/1/21/2. Студентам также может быть полезно подумать о том, что происходит, когда мы сравниваем дроби с одним и тем же числителем, но разными знаменателями.
Создайте бесплатную учетную запись!
Бесплатные учетные записи Mathigon позволяют вам сохранять свою работу, настраивать классы и давать задания ученикам.