НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ ЗНАК МОДУЛЯ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Дерябина А.А. 1
1Муниципальное бюджетное общеобразовательное учреждение»Женская гуманитарная гимназия»
Гущина Г.И. 1
1МБОУ «Женская гуманитарная гимназия»
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение:
Цель работы – изучить способы решения неравенств с двумя переменными, содержащих знак модуля.
Поставленная цель обусловила решение ряда задач:
1. изучить теоретический материал о неравенствах и модуле числа, на котором будет основываться исследование;
изучить теоретический материал о неравенствах и модуле числа, на котором будет основываться исследование;
2. проанализировать практическое применение данного материала посредством решения типовых заданий;
3. рассмотреть различные способы решения неравенств с двумя переменными, содержащих знак модуля;
4. провести анализ сходств и различий данных способов;
5. систематизировать материал и вывести алгоритм решения данных неравенств различными способами;
6. рассмотреть практическое применение данных способов при решении неравенств с двумя переменными, содержащих знак модуля.
Актуальность данной темы обусловлена тем, что задания на неравенства с двумя переменными, содержащими знак модуля, встречаются в заданиях С части ЕГЭ, но не изучаются глубоко в школьном курсе математики (без углублённого изучения).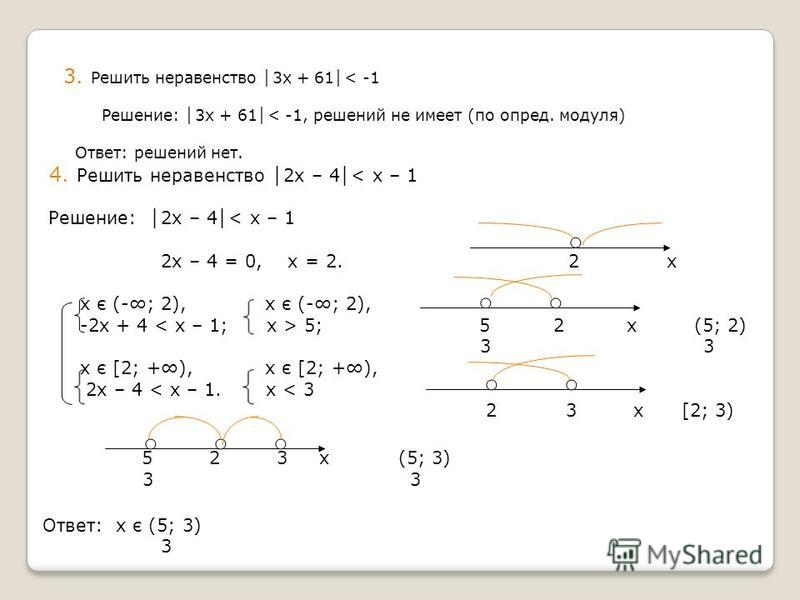
Объектом исследования являются неравенства с двумя переменными, содержащих знак модуля.
Предметом исследования являются способы решения данных неравенств.
Гипотеза: не все способы решения являются универсальными, поэтому в зависимости от общего вида неравенства и места расположения модуля будем выбирать тот или иной способ решения данных неравенств.
Типовые тестовые задания, содержащие переменную под знаком модуля
Задание №1: Найти площадь фигуры, заданной неравенством
Решение: Множество точек – ромб, полученный из ромба путем параллельного переноса точки пересечения диагоналей (0;0) в точку (3;2).
Диагонали ромба: d1 = 6, d2 = 4 S = 0,5d1d2 = 0,5 × 4 × 6 = 12
Ответ: S = 12
Задание №2: Изобразите на координатной плоскости фигуру, заданную неравенством и вычислить ее площадь.
Решение:
Это два симметричных относительно оси OY круга с центрами в точках (-2;0) и (2;0) и радиусом r =2.
Ответ:
Задание №3: Изобразите фигуру, заданную неравенством и найдите площадь данной фигуры. Решение: Данная фигура состоит из двух равных треугольников OCB и OAB, вершины которых имеют координаты
A = (1;2), B = (0;1), C = (-1;2)
Рассмотрим треугольник OAB: основание OB равно 1; высота, опущенная из вершины А к основанию равно 1. SOAB= 0,5·h·OB = 0,5·1·1 = 0,5 Так как треугольника равные, то S = 2SOAB= 1 Ответ: S = 1
Задание №4: Найдите S фигуры, заданной неравенством
Решение: Фигура, заданная неравенством – прямоугольник ABCD с вершинами
Для нахождения площади необходимы значения сторон AB и AD:
Ответ: S=1,5
Задание №5:
Изобразите фигуру, заданную системой неравенств .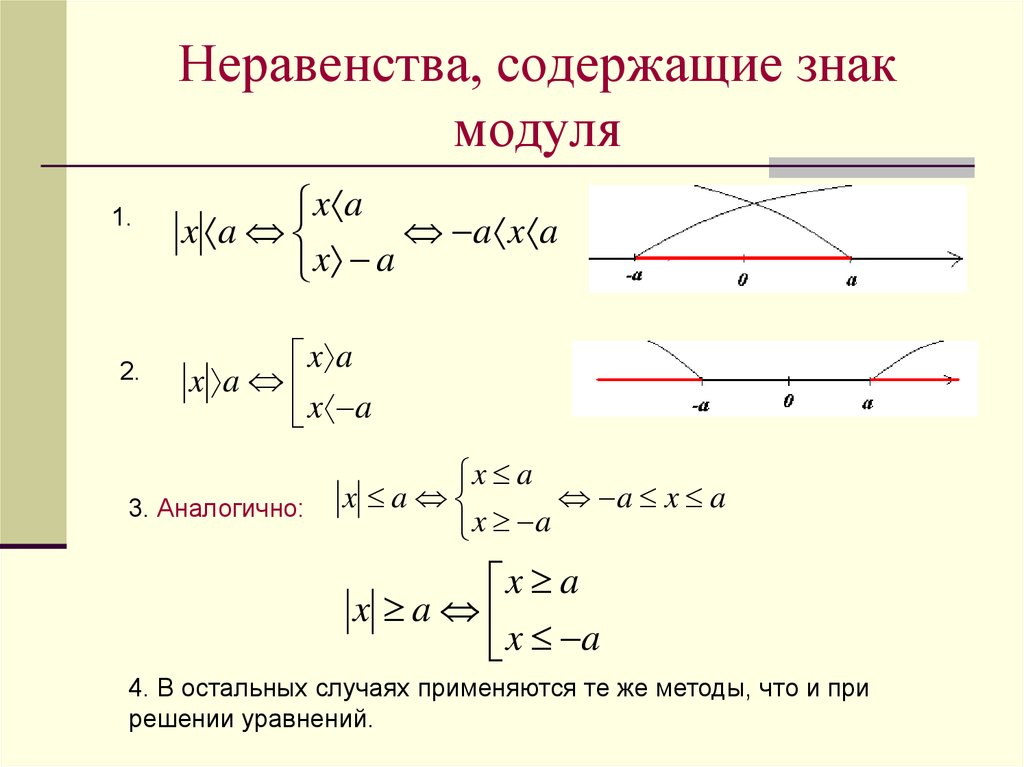
Решение: Первое неравенство системы задает круг с радиусом 2 и центром в начале координат. Второе неравенство задает прямые x = -2 и x = 2, множество точек располагается между этими прямыми. Третьим неравенством задаются прямые y = -2 и y = x, множество точек располагается выше прямой y = -2 и ниже прямой y = x
Фигура является общей частью внутренности прямоугольного треугольника ABC и внешности круга радиусом 2 с центром в начале координат.
Вершины треугольник АBC имеют координаты
А(-2;-2), В(2;2), С(2;-2)
Найдем площадь прямоугольного треугольника:
Для того, чтобы вычислить площадь фигуры нужно из площади треугольника ABC вычесть площадь полукруга с радиусом 2:
Ответ:
Задание №6: Найдите площадь фигуры, заданной неравенством .
Решение: Фигура состоит их двух равных треугольников OCB и OAB, вершины которых имеют координаты A = (1;2), B= (0;3), C = (-1;2)
Основание треугольника OAB равно 3, а высота, опущенная к основанию из вершины А равна 1.
SOAB= 0,5·h·OB = 0,5·3·1 = 1,5
Треугольники равны, поэтому S =2 SOAB= 3.
Ответ: S= 3
Задание №7: Решите систему неравенств:
Решение:
Предположим, что данная система неравенств имеет решение x, y, z, t.
Тогда, в частности, , т.е.
Аналогично получаем:
Перемножим все полученные неравенства: с одной стороны произведение четырех положительных чисел положительно, с другой стороны это произведение равно:
Приходим к противоречию.
Ответ: Система не имеет решений.
Задание №8: Существуют ли действительные числа a, b и с такие, что при всех действительных x и y выполняется неравенство:
Решение: Предположим, такие числа a, b, с существуют. Выберем x > 0 и y> 0 такие, что
Тогда разность между левой и правой частями равна a + b + с.
Если взять x< 0 и y< 0 такие, что
тогда разность будет равна –a – b – с.
Таким образом, с одной стороны a+ b + с > 0, с другой стороны a+ b + с < 0, что является противоречием.
Ответ: Нет, такие числа не существуют.
Задание №9: Сколько различных целочисленных решений имеет неравенство ?
При натуральных n уравнение имеет ровно 4n целочисленных решений, а при n = 0 решение единственно.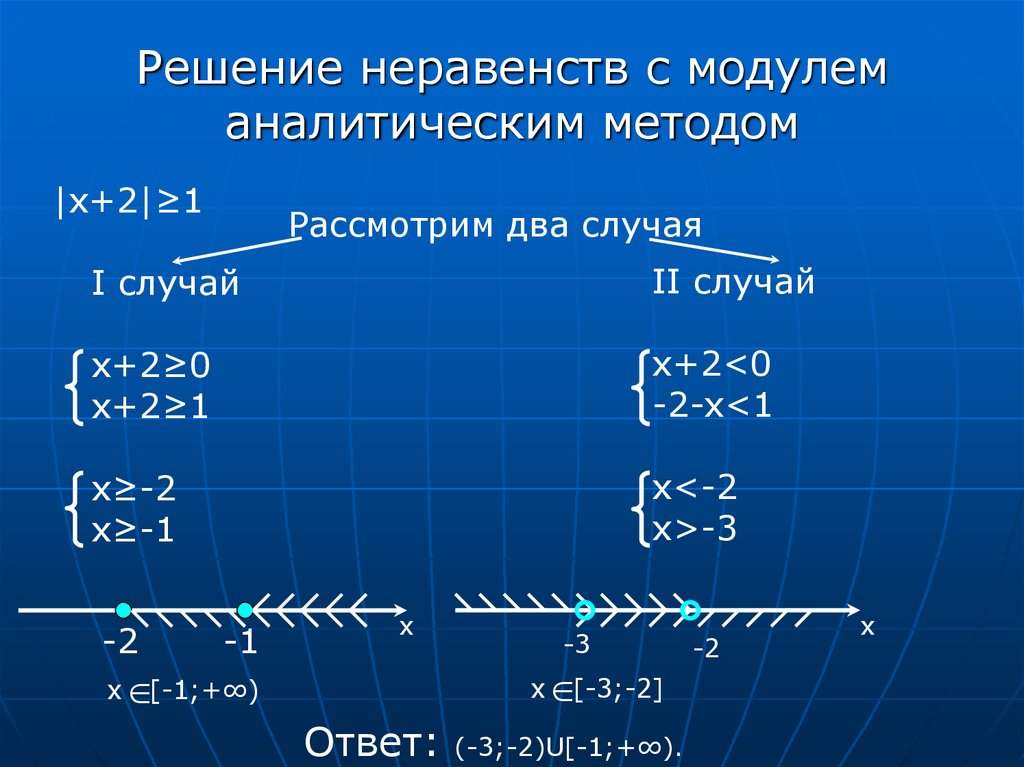
Ответ: 19801.
Способы решение неравенств с двумя переменными, содержащих знак модуля
Рассмотрим решение неравенств с двумя переменными, содержащие знак модуля, тремя способами: 1.Использование свойств неравенств, путем равносильных преобразований, и правил решения дробных неравенств.
2.Умножение обеих частей неравенства на неотрицательное число и дальнейшее решение полученного неравенства.
3.Возведение обеих частей в квадрат и решение полученного дробно-рационального неравенства.
Для того, чтобы рассмотреть все три способа, берем одно и тоже неравенство:
Способ №1. Использование свойств неравенств, путем равносильных преобразований
Использование свойств неравенств, путем равносильных преобразований
Равносильные переходы при решении неравенств:
Если , то при а > 0 — множество решений совпадает с областью определения функции f(x), а при равносильно
При решении воспользуемся теоремой:
Таким образом данное неравенство равносильно совокупности неравенств:
(1)
Имеем:
Воспользуемся тем, что
-
произведение двух множителей < 0, если каждый множитель > 0 (или каждый < 0)
-
произведение двух множителей < 0, если один из множителей < 0, а другой > 0
и запишем данную совокупность в виде совокупности систем, применив данное чередование к каждому из неравенств. Решим данные совокупности систем неравенств:
Решим данные совокупности систем неравенств:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1 , исключая точки расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Способ №1 является наиболее универсальным при решении неравенств. Если неравенство удовлетворяет одному из равносильных переходов, то оно может быть решено данным способом.
Способ №2. Умножение обеих частей на неотрицательное число
Т.к. модуль частного равен частному модулей, то:
есть число неотрицательное и от умножения на него данного неравенства равносильность не нарушается, если , поэтому:
Далее для решения будем использовать метод равносильных преобразований.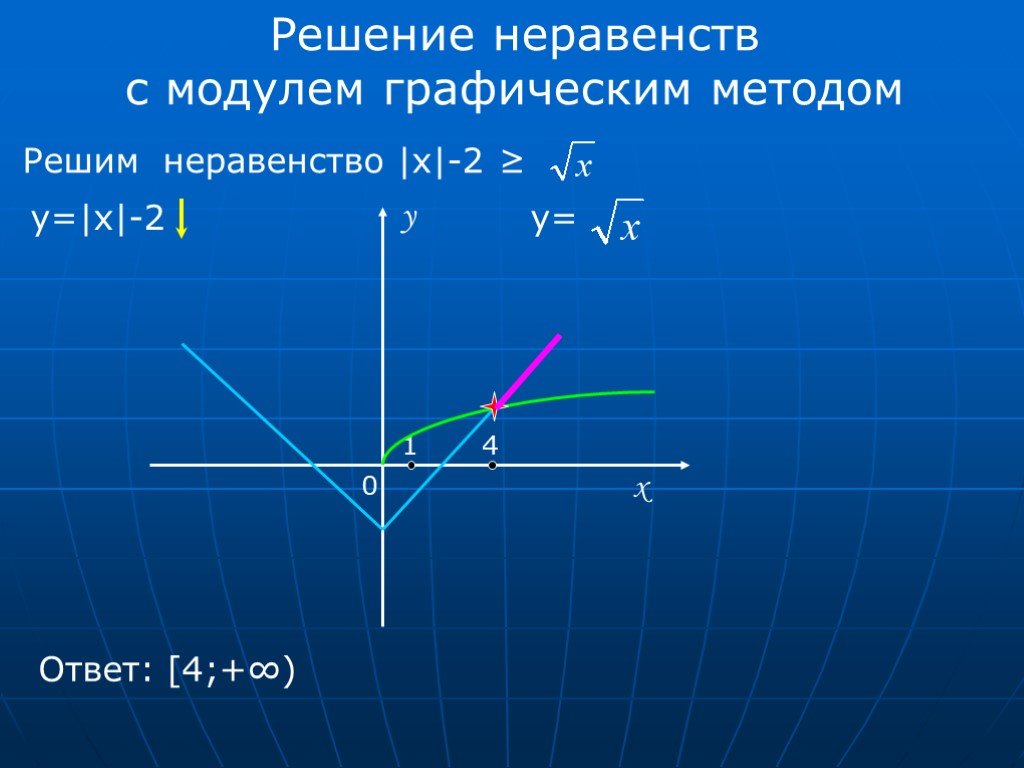
Воспользуемся методом одновременного раскрытия модуля и его определением:
Решим данные неравенства:
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1 , исключая точки расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ наиболее удобен при решении дробно-рациональных неравенств.
Способ №3. Возведение обеих частей в квадрат
Т. к. модуль частного равен частному модулей, то:
Т.к. обе части неравенства – числа неотрицательные, то равносильность не нарушается при возведении в квадрат обеих частей неравенства.
Перенесем 4 в левую сторону и приведем к общему знаменателю.
Таким образом данное неравенство равносильно системе:
Неравенство разложим на множители способом группировки.
Переходим к совокупности систем и решаем с учетом чередования знаков, как при способе равносильных преобразований.
Геометрическим решением данного неравенства являются все точки, лежащие в углах АОВ и А1ОВ1 , исключая точки расположенные на лучах ОА, ОD, ОВ и ОА1, ОС, ОВ1.
Данный способ можно использовать, если обе части неравенства есть числа неотрицательные, а возведение в квадрат не ведет к усложнению решения.
Алгоритм решения неравенств с двумя переменными, содержащих знак модуля
Вывод:
Научная новизна исследования:
— рассмотрено три способа решения одного неравенства с двумя переменными, содержащими знак модуля
— выведен алгоритм для каждого из трёх способов решения неравенств.
— даны рекомендации по выбору способа решения.
— представлено приложение с решениеми неравенств различными способами
Нужно заметить, что каждый из способов имеет свои преимущества, поэтому для успешного решения данных неравенств необходимо знать все способы. А какой из них наиболее удобный, зависит от вашего решения.
Практическая значимость исследования:
— может быть использован учителями математики при подготовке к урокам, при изучении тем: «Координаты и графики» и «Решение неравенств», и факультативным занятиям.
— может быть использован при проведении факультативных занятий и элективных курсов.
— для самостоятельной подготовки учащимися к ЕГЭ и вступительным экзаменам.
Приложение
1. Решить неравенство .
Воспользуемся тем, что если , а > 0, , запишем двойное неравенство в виде двух неравенств.
Геометрическим решением данного неравенства является множество точек плоскости, находящиеся между прямыми и , исключая точки, расположенные на прямых.
2. Решить неравенство .
При решении неравенства воспользуемся тем, что если
Геометрическим решением данного неравенства является множество точек плоскости, лежащих вне угла, образованного лучами AB и BC, исключая точки, расположенные на лучах.
3. Задача: Изобразить на координатной плоскости XOY фигуру M, состоящую из точек, координаты которых удовлетворяют неравенству .
Решение:
Построим график функций .
Получим, что данное неравенство задает множество точек, лежащих ниже прямой (для решения см. «Геометрическая интерпретация решений неравенств»), исключая точки на этой прямой.
4. Задача: Изобразите фигуру M, если она задана на координатной плоскости неравенствами:
.
Решение: Построим прямую и прямую .
Получим, что данные неравенства задают множество точек, лежащих в треугольниках OCB и BAO, включая точки на сторонах этих треугольников.
5. Задача: Изобразите фигуру M, если она задана на координатной плоскости неравенствами .
Решение: Изобразим прямую и прямую . Получим, что данные неравенства задают множество точек, лежащих в треугольниках ABC и CAO, включая точки на сторонах этих треугольников.
Получим, что данные неравенства задают множество точек, лежащих в треугольниках ABC и CAO, включая точки на сторонах этих треугольников.
6. Решить неравенство .
Геометрическим решением данного неравенства является множество точек в квадрате ABCD и на сторонах данного квадрата.
7. Решить неравенство .
Строим график функций . Искомая область находится «над» графиком функций, исключая точки, лежание на нем.
8. Решить неравенство .
Строим график функций и отражаем относительно оси X. Искомая область находится вне графика данной функции, исключая точки на данном графике функции.
9. Решить неравенство .
Данное неравенство равносильно совокупности систем неравенств:
Решения первой системы образуют
(исключая сторону ВС)
второй – (исключая стороны АВ и ОВ)
третий – (исключая стороны DC и ОC)
четвертой – (исключая стороны АD, OD, AO)
10. Решить неравенство .
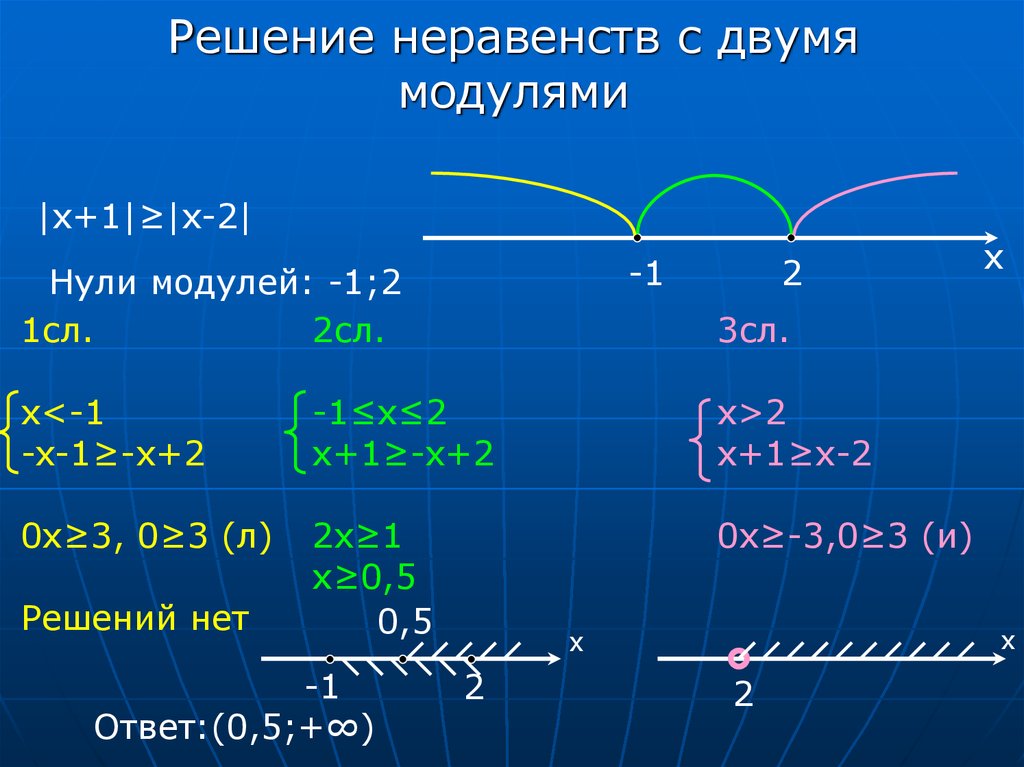
Решить неравенство .
Данное неравенство равносильно совокупности систем неравенств:
-
-
Решить систему неравенств
-
Данная система равносильна совокупности систем неравенств:
12. Решить совокупность неравенств
Данная совокупность равносильна совокупности систем неравенств:
Геометрическое решение системы:
Геометрическое решение совокупности:
Список используемой литературы
-
А.Ш.Блох, Т.Л.Трухан «Неравенства»
-
А.
 Х.Шахмейстер «Дробно-рациональные неравенства»
Х.Шахмейстер «Дробно-рациональные неравенства»
-
А.Ж. Жафяров «Математика. ЕГЭ. Решение задач уровня С1»
-
М.А.Иванов «Математика без репетитора»
-
Е.В. Ермолин, М.А. Лукина, Н.А. Цыпленкова «Уравнения и неравенства, содержащие модуль»
-
С.С. Самарова «Фигуры на координатной плоскости, заданные неравенствами». Учебно-методическое пособия для подготовки к ЕГЭ по математике.
-
http://compendium.su/
-
http://diffur.kemsu.ru/
-
http://diffur.kemsu.ru/
-
http://ppt4web.
 ru/
ru/
Просмотров работы: 1718
Функция y = (x) — презентация онлайн
Похожие презентации:
Тригонометрические функции y = sin x и y = cos x . Их свойства и графики
Свойства и график функции y=tg x, y=ctg x
Функции и их свойства. Предел последовательности и функции. Производная функции и дифференциал
Показательная функция, ее свойства и график
Методы решения тригонометрических уравнений
Функция y=sinx
Логарифмическая функция, ее свойства и график
Уравнения и неравенства. 11 класс
Построение графиков функции y = sinx и y = cosx
Показательная функция
1. Функция
y | x |Подготовил Кожемяко Никита,
9 класс
2008г.
Актуальность – собрать сведения по теме в связи с
подготовкой к экзамену
Проблема – в школьном курсе алгебры недостаточно
задач с модулем
Объект исследования – функция
Предмет исследования – функция у=|x|
Цель – рассмотреть решение распространённых
задач с модулем
Гипотеза – я предполагал, что задачи с модулем
решаются только графически
Задачи –
1.
 Вспомнить известную мне информацию о задачах
Вспомнить известную мне информацию о задачахс модулем
2.Придумать новые задачи
3.Проконсультироваться с учителем
4.Создать презентацию
5.Защитить работу
3. Определение модуля
В математике через |x| обозначается абсолютнаявеличина, или модуль числа х.
Абсолютная величина числа х равна этому числу, если
х>0, равна противоположному числу –х, если x<0, и
равна нулю, если х=0.
Таким образом, функция |x| определена для всех
х (-∞;+∞).
Множество её значений совпадает с множеством
неотрицательных чисел.
|x|=
х, если х≥0,
-х, если х<0.
График функции
у
0
Свойства функции
y | x |
х
1.D(f)=(-∞;+∞)
2.E(f)=[0;+∞)
3.Ограничена снизу
4.Возрастает
на[0;+∞)
убывает на(-∞;0]
5.Чётная функция
6. У наиб нет У наим. 0
7.Непрерывна
Решение уравнений
с модулем графическим методом
|x-3|-1=x3
y=|x-3|-1
0
Ответ: x=1
у
y=x3
1
4
x
Решение неравенств
с модулем графическим методом
Решим неравенство |x|-2 ≥
y=|x|-2
0
Ответ: [4;+∞)
y=
y
1
x
x
4
x
Решение уравнения с параметром и
модулем графическим способом
Сколько решений имеет уравнение
у
|x+2|+1 =c
y=|x+2|+1
y=c
Рассмотрим 3 случая
1
Iсл.
 c>1, 2 решения
c>1, 2 решенияIIсл. c<1, нет решений
IIIсл. c=1, 1 решение
0
x
8. Аналитический метод решения уравнения с модулем
Решим уравнение|x-3|=5I способ
Рассмотрим два случая
1 случай
2 случай
x-3≥0
x-3=5
x-3<0
3-x=5
x=5+3
-x=5-3
x=8, 8-3≥0 (и) x=-2, -2-3<0 (и)
Ответ:-2, 8
II способ
x-3=5 или x-3=-5
x=8
x=-2
9. Показательные уравнения с модулем
2|x+2| = 162|x+2| = 24
|x+2| = 4
I случай
x+2=4
x=2
Ответ: 2;-6
II случай
x+2=-4
x=-6
10. Логарифмическое уравнение с модулем
log2(|x-2| — 1) = 1ОДЗ: (|x-2| — 1) > 0:
|x-2| — 1 = 2
|x-2| = 3
I случай
II случай
x-2 = 3
x-2 = -3
x=5
x = -1
Ответ: 5;-1
11. Алгоритм решения уравнений с модулем
1. Найти нули модулей.2. Отметить нули на координатной
прямой.
3. Решить уравнение на каждом из
промежутков с помощью системы.
4.
 Написать ответ.
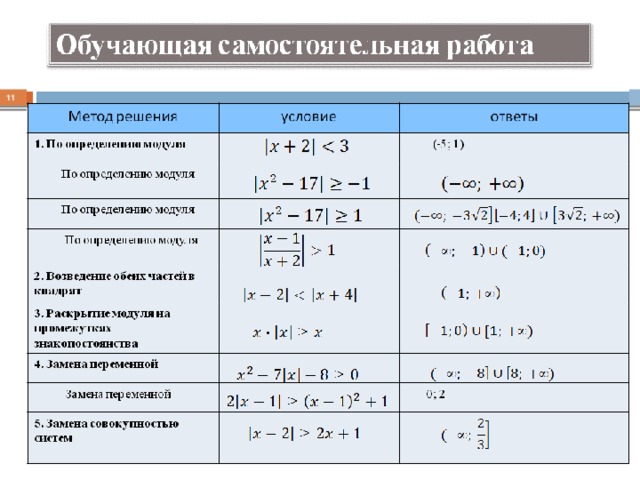
Написать ответ.12. Решение уравнений с двумя модулями
|x|=|x-3|+4-x|x|=0,|x-3|=0
Нули модулей: 0;3
0
3
1сл.
2сл.
3сл.
x<0
-x=3-x+4-x
0≤x≤3
x=-x+3+4-x
x>3
x=x-3+4-x
x=7, 7<0 (л)
x=7/3 ,0≤7/3≤3 (и)
x=1 ,1>3 (л)
Решений нет
Ответ: 7/3.
7/3 — корень
Решений нет
х
13. Решение неравенств с модулем аналитическим методом
|x+2|≥1Рассмотрим два случая
I случай
II случай
x+2≥0
x+2≥1
x+2<0
-2-x<1
x≥-2
x≥-1
x<-2
x>-3
-2
x
-1
x
[-1;+∞)
-3
x
Ответ:
[-3;-2]
(-3;-2)U[-1;+∞).
-2
x
Решение неравенств с модулем
различными методами
Третий способ. Имеем: |x-2.5|>2.
Геометрически выражение |x-2.5| означает расстояние р(x-2.5)
на координатной прямой между точками х и 2.5. Значит, нам
нужно
Найти все такие точки х, которые удалены от точки 2.5 более, чем
на 2это точки из промежутков (-∞;0.
 5) и (4.5;+∞)
5) и (4.5;+∞)Итак, получили следующее решения неравенства: х<0.5;x>4.5.
Четвёртый способ.
Поскольку обе части заданного неравенства неотрицательны,
то возведение их в квадрат есть равносильное преобразование
неравенства. Получим |2x-5|2>42
Воспользовавшись тем что |x|2=x2, получим
(2x-5-4)(2x-5+4)>0
Применив метод интервалов получим тот же ответ.
15. Алгоритм решения неравенств с модулем
1. Найти нули модулей.2. Отметить нули на координатной
прямой.
3. Решить неравенство на каждом из
промежутков с помощью системы.
4. Написать ответ.
16. Решение неравенств с двумя модулями
|x+1|≥|x-2|-1
Нули модулей: -1;2
1сл.
2сл.
2
3сл.
x<-1
-x-1≥-х+2
-1≤x≤2
х+1≥-x+2
x>2
х+1≥х-2
0x≥3, 0≥3 (л)
2х≥1
х≥0,5
0,5
0x≥-3,0≥3 (и)
Решений нет
-1
Ответ:(0,5;+∞)
х
х
х
2
2
Тригонометрические уравнения с
модулем
|sin(x+
)|=1
I случай
sin(x+ )=1
-sinx=1
sinx=-1
x=3 /2+2 n
/2+ n
Ответ:
II случай
sin(x+ )=-1
-sinx=-1
sinx=1
x= /2+2 n
Тригонометрические уравнения с
модулем
)
|cosx|=cos(x+
I cлучай
cosx<0
-cosx=cos(x+ )
cos( +x)=cos(x+ )
x+ =x+ +2
или -x- =x+
x=x+
-2x=2
0x=
x=
решений нет
2
Ответ:
+2
Тригонометрические уравнения с
модулем
)
|cosx|=cos(x+
II cлучай
cosx≥0
cosx=cos(x+ )
cos(x)=cos(x+ )
x =x+ +2
или -x=x+ +2
x=x+
-2x= +2
0x=
x=
—
решений нет
Ответ:
2
График функции у=|x+1|-|x-2|
Нули модулей: -1;2
1сл.

2сл.
x<-1
у=-x-1+х-2
-1≤x≤2
x>2
у=х+1+x-2 у=х+1-х+2
x<-1
у=-3
-1≤x≤2
у=2х-1
у=
-3, x<-1
2х-1, -1≤x≤2
3, x>2
3сл.
2
-1
х
у
x>2
у=3
0
х
Считают, что термин предложил использовать Котс, ученик
Ньютона. Знак модуля введен в XIX веке Вейерштрассом.
Роджер Котс (Roger Cotes;
10 июля 1682 — 5 июня
1716) — английский
математик и философ.
В двадцать четыре года был
назначен профессором
астрономии и
экспериментальной
философии в Кембриджском
университете. В 1713 он
подготовил второе издание
«Principia» Ньютона. Котс
оставил серию подробных
исследований по оптике.
Карл Те́одор Ви́льгельм
Ве́йерштрасс (нем. Karl
Theodor Wilhelm Weierstraß;
31 октября 1815 — 19
февраля 1897) —
выдающийся немецкий
математик, «отец
современного анализа».
22. Выводы
В ходе работы над проектом моя гипотеза неподтвердилась.

Я не только вспомнил графический способ, но и
научился решать уравнения и неравенства
аналитическим методом и строить графики с
несколькими модулями.
В дальнейшем можно рассмотреть аналитический
метод решения неравенств и уравнений с
модулем и параметром.
23. Список литературы
Алгебра:Для 8 кл.:учеб. пособие для учащихсяшк. и классов с углуб.изуч математики/
Н.Я.Виленкин, Г.С.Сурвило и др., под ред.
Н.Я.Виленкина – М.: Просвещение.
Мордкович А.Г. И др. Алгебра.9кл.: В двух
частях. Ч.2: Задачник для общеообразоват.
учреждений/М.:Мнемозина, 2004 г.
Мордкович А.Г. И др. Алгебра.9кл.: В двух
частях. Ч.2: Учебник для общеообразоват.
учреждений/М.:Мнемозина, 2004 г.
Мордкович А.Г. И др.Алгебра и начала анализа
10-11кл.: В двух частях. Ч.1: Задачник для
общеообразоват. учреждений/М.:Мнемозина,
2004 г.
Математика: Учеб. Для 6 кл. сред. шк./Н.Я.
Виленкин и др. М.: Просвещение, 1993.
English Русский Правила
Неравенство Коши-Шварца в $\mathbb{Z}$-модулях спросил
Изменено 10 лет, 8 месяцев назад
Просмотрено 329 раз
$\begingroup$
Неравенство Коши-Шварца для скалярных произведений 92\le f(v,v)(f(v,v)/4+f(w,w))$, но мы не можем добиться большего успеха с этой идеей, так как $\mathbb{Z}$ сам по себе не поле.
- неравенство
- модули
- внутренние продукты
$\endgroup$
4
$\begingroup$
То же доказательство дает $4 \times$ (неравенство Коши-Шварца). Поскольку значения $f$, рассматриваемые в неравенстве, являются действительными числами, а не элементами $Z$-модуля, деление на $4$ возможно и множитель $4$ можно убрать.
$\endgroup$
4
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Простое построение графиков линейных неравенств с двумя переменными
Purplemath
Во-первых, позвольте мне сказать, что рисовать графики линейных неравенств намного проще, чем кажется в вашей книге.
Вспомните, как вы решали линейные неравенства на числовой прямой. Предположим, вас попросили нарисовать что-то вроде x > 2. Как вы это сделали?
Содержание продолжается ниже
MathHelp.com
Графики линейных неравенств
Вы нашли свое решение, нарисовав числовую прямую и найдя часть «равно» (в этом примере x = 2). Затем вы отметили эту точку соответствующими обозначениями; а именно, открытая точка или скобка, указывающая, что точка x = 2 не была включена в решение. Тогда вы бы заштриховали все справа, потому что «больше чем» означает «все справа».
Шаги построения графика линейных неравенств с двумя переменными почти такие же, как и для построения графика случая с одной переменной.
Каковы этапы построения графика линейных неравенств?
- Решите неравенство, чтобы получить и только с одной стороны.
- Замените символ неравенства знаком «равно», создав уравнение прямой.
- Нарисуйте уравнение.
- Если исходное неравенство было «или равно», то нарисуйте сплошную линию для графика.
- Если, с другой стороны, исходное неравенство было «строгим» неравенством, то начертите график пунктирной линией.
- Заштрихуйте одну сторону прямой линии.
- Если решенное неравенство было » y больше чем», то заштрихуйте над линией.
- Если решенное неравенство было » y меньше», то заштриховать под чертой.
- Постройте график решения задачи y ≤ 2 x + 3,
Так же, как и в случае неравенства числовых прямых, мой первый шаг — найти часть «равно». Для линейных неравенств с двумя переменными часть «равно» представляет собой график прямой линии; в данном случае это означает, что часть «равно» — это строка y = 2 x + 3:
Для линейных неравенств с двумя переменными часть «равно» представляет собой график прямой линии; в данном случае это означает, что часть «равно» — это строка y = 2 x + 3:
Хорошо; линия дала мне границу между «областью» решения и областью не-решения.
Теперь я нахожусь в том месте, где учебник имеет тенденцию усложняться, с разговорами о «контрольных точках» и тому подобном. Но когда я делал неравенства с одной переменной (например, x < 3), я не стал заморачиваться с «тестовыми точками»; Я просто заштриховал одну или другую сторону. Я могу сделать то же самое здесь. Я проигнорирую «контрольную точку» и взгляну на исходное неравенство, y ≤ 2 x + 3.
Я уже нарисовал часть «или равно» — это просто линия. Теперь я готов сделать часть « и меньше». Другими словами, здесь мне нужно заштриховать одну сторону линии или другую. Теперь подумайте об этом: если мне нужно и МЕНЬШЕ линии, я хочу НАД линией или НИЖЕ?
Естественно, хочу ниже черты.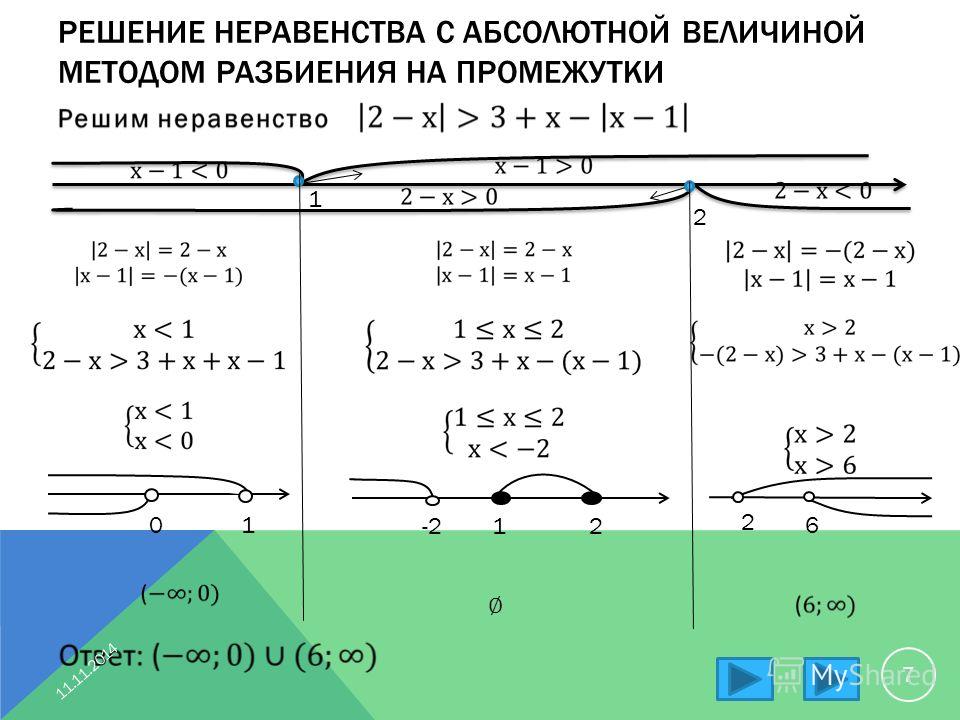 Поэтому я заштриховываю его:
Поэтому я заштриховываю его:
И это все, что нужно: заштрихованная сторона — это «область решения», которую они хотят.
Этот метод (рассмотрение исходного неравенства, чтобы увидеть, какую сторону закрасить) работал, потому что у нас было только y на одной стороне неравенства. Как и в случае, когда вы рисовали старые простые прямые линии, вы всегда хотите решить, что и должны быть одиночными с одной стороны. Это делает все остальное проще и для подобных неравенств избавляет от необходимости делать контрольные точки.
- Нарисуйте решение задачи 2 x − 3 y < 6.
Сначала я решу неравенство, чтобы получить y только с одной стороны:
2 x − 3 y < 6
−3 y < −2 x + 6
y > ( 2 / 3 ) x − 2
[Обратите внимание, как я перевернул знак неравенства в последней строке.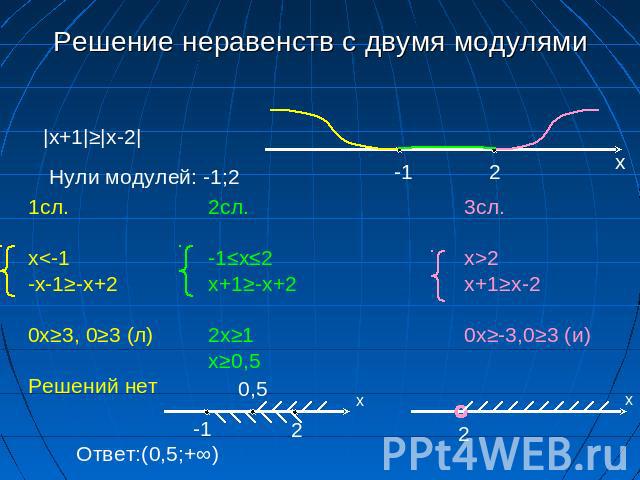 Я не должен забывать переворачивать неравенство, если я умножаю или делю на минус!]
Я не должен забывать переворачивать неравенство, если я умножаю или делю на минус!]
Теперь мне нужно найти часть «равно», которая представляет собой строку y = ( 2 / 3 ) x − 2. Это выглядит так:
Хорошо; часть «равно» дала мне линию, которая является границей между областью решения и областью не-решения.
Но это упражнение и есть то, что называется «строгим» неравенством. То есть это не неравенство «или равное»; это всего лишь « и больше». Так что это влияет на строку «равно».
Когда у меня были строгие неравенства на числовой прямой (например, x < 3), я обозначал это скобками (вместо квадратных скобок) или открытой [незаполненной] точкой (вместо закрытой [заполненной] точки ).
В случае этих линейных неравенств строгое неравенство обозначается штриховой линией. Таким образом, граница моей области решения на самом деле выглядит так:
Используя пунктирную линию, я все еще знаю, где находится граница, но я также знаю, что граница не включена в решение.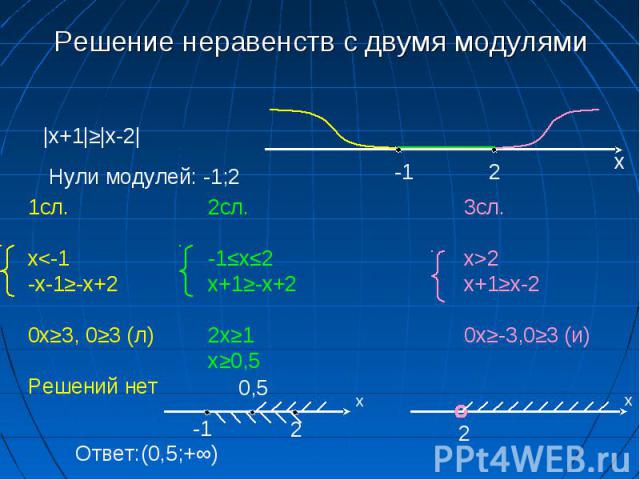

 Х.Шахмейстер «Дробно-рациональные неравенства»
Х.Шахмейстер «Дробно-рациональные неравенства»
 ru/
ru/