Теория множеств формулы: «Элементы теории множеств»

Помогите решить / разобраться (М)

ktyz1992	Двоеточие в формуле на языке теории множеств 25.01.2019, 18:04
25/01/19 2	Здравствуйте. Начал читать книгу по теории математической логике и теории множеств и наткнулся на обозначение ранее по тексту не введённое (а именно, двоеточие в формуле на стр. 12): . Читаю так: «Множеством называется множество элементов x, таких, что существуют элементы i принадлежащие множеству I» …непонятное двоеточие… «элементов x принадлежащих множеству «. Подскажите пожалуйста, как понимать это двоеточие.

mihaild	Re: Двоеточие в формуле на языке теории множеств 25.01.2019, 18:07
Заслуженный участник 16/07/14 6442 Москва	Как скобки, в которые заключен кусок формулы дальше (какой именно кусок — должно быть понятно из контекста; как правило — кусок до первой связки).

Xaositect	Re: Двоеточие в формуле на языке теории множеств 25.01.2019, 18:08
Заслуженный участник 06/10/08 6422	«такой, что» — это множество всех , для которых существует индекс такой, что . Иными словами, это множество всех элементов, принадлежащих хотя бы одному из множеств .

ktyz1992	Re: Двоеточие в формуле на языке теории множеств 25.01.2019, 18:16
25/01/19 2	Спасибо за разъяснение.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 4 ]

Модераторы: Модераторы Математики, Супермодераторы

Некоторые сведения из теории множеств

Похожие презентации:

Элементы теории множеств. Понятие множества

Элементы теории множеств

Теория Множеств

Элементы теории множеств.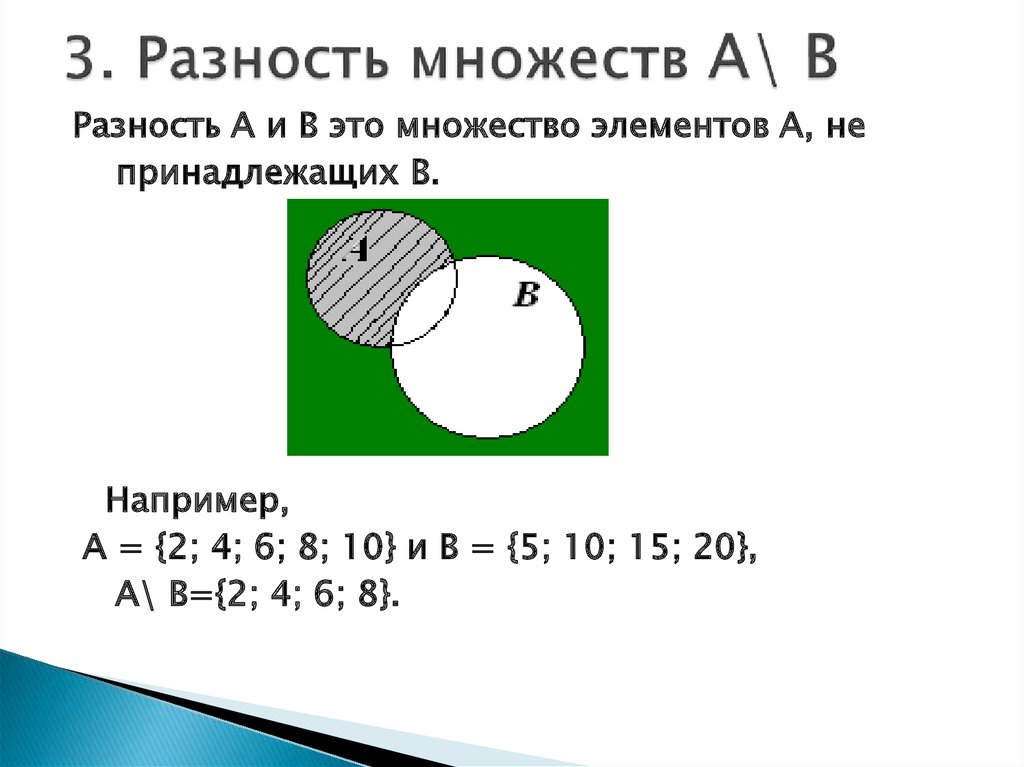 Математические основы информатики

Дискретная математика. Теория множеств

Теория множеств

Дискретная математика. Теория множеств

Понятие множества. Операции над множествами

Основные понятия теории множеств. Алгебра множеств

Элементы теории множеств

1. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ

МК
НЕКОТОРЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ МНОЖЕСТВ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
И АЛГЕБРЫ ЛОГИКИ

2. Ключевые слова

МК
Ключевые слова
множество
пустое множество
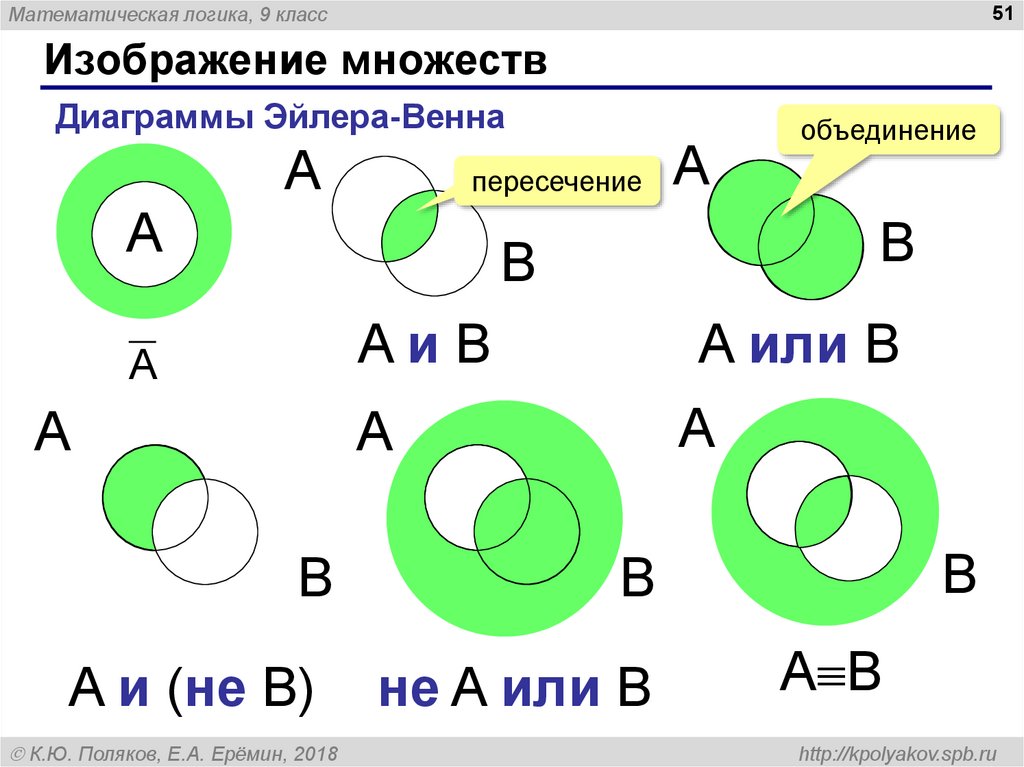
пересечение двух множеств
объединение двух множеств
дополнение множества
мощность множества
формула включений-исключений

3. Понятие множества

МК
Понятие множества
!
Множество — совокупность объектов произвольной
природы, которая рассматривается как единое целое.

4. Способы задания множества

МК
Способы задания множества
Перечисление всех
элементов множества
Словесное описание
множества
M = {1, 3, 5, 7, 9}
множество однозначных
нечетных чисел
A = {x | 10 ≤ x < 100}
множество целых
двузначных чисел
B = {0, 1}
цифры двоичного
алфавита
C = {А, Е, Ё, И, О, У, Ы, Э, Ю, Я}
гласные буквы русского
алфавита
?
Какие множества можно задавать перечислением
всех элементов?

5.

Стандартные обозначенияМК
Стандартные обозначения
Множества принято обозначать прописными буквами
латинского алфавита (A, B, C, …). Объекты, входящие в
состав множества, называются его элементами и
обозначаются строчными латинскими буквами.
Описание
Обозначение
x — элемент множества M
(x принадлежит множеству M)
x∈M
x не является элементом
множества М (x не принадлежит M)
x∉M
мощность (количество элементов)
множества М
|M|
пустое множество – множество, в
котором нет ни одного элемента
∅

6. Круги Эйлера

МК
Круги Эйлера
Для наглядного изображения множеств используются круги
Эйлера.
Точки внутри круга считаются элементами множества.
М
М
х
x∈M
х
x∉M

7. Подмножество

МК
Подмножество
Если каждый элемент множества P принадлежит множеству М, то говорят, что P есть подмножество М, и записывают:
P⊂М
Само множество М является
своим подмножеством:
М⊂М
М
Р
P⊂М
Пустое множество является
подмножеством М:
∅⊂М
Универсальное множество
содержит все возможные
подмножества одной природы. Обозначается буквой U.

8. Пересечение множеств

МК
Пересечение множеств
!
Пересечением двух множеств X и Y называется
множество их общих элементов. Обозначается X ∩ Y.
X
Y
X∩Y
Множества M и X не имеют
общих элементов:
M∩X=∅
P подмножество множества М:
М ∩P=P
X∩Y
Пересечение множеств М и М:
М ∩М=М

9. Объединение множеств

МК
Объединение множеств
!
Объединением двух множеств X и Y называется множество, состоящее из всех элементов этих множеств и
не содержащее никаких других элементов (X ∪ Y).
X
Y
M∪∅=М
X∪Y
P подмножество множества М:
М∪P=М
X∪Y
Объединение множеств М и М:
М∪М=М

10. Примеры пересечения и объединения множеств

МК
Примеры пересечения и объединения
множеств
X
?
Y
X
Возможно ли равенство: A ∪ В = A ∩ В ?
Y

11. Дополнение множества

МК
Дополнение множества
!
Пусть множество P является подмножеством
множества М. Дополнением P до М называется
множество, состоящее из тех элементов М, которые
не вошли в P. Обозначается P или P ’.
Дополнение М до М:
М’=∅
М
Р
P∪
=M
Дополнение пустого
множества до М:
∅’=М
Дополнение множества М
до универсального:
M∪M’=U

12. Мощность множества

МК
Мощность множества
!
Мощностью конечного множества называется число
его элементов.
Мощность множества X обозначается |X|.
Множество
Мощность
пустое множество
|∅|=0
A — множество букв русского алфавита
| А | = 33
В = {зима, весна, лето, осень}
|В|=4
Мощность любого конечного множества равно количеству
элементов данного множества.
Два множества являются равномощными, если между
ними можно установить взаимно-однозначное соответствие.

13. Формула включений-исключений

МК
Формула включений-исключений
!
Принципом включений-исключений называется
формула,
позволяющая
вычислить
мощность
объединения (пересечения) множеств, если известны
их мощности и мощности всех их пересечений
(объединений).
X
Y
X
|X∪Y| = |X| + |Y|
Y X
Y
Z
|X∪Y| = |X| + |Y| — |X∩Y|
|X∪Y∪Z| = |X| + |Y| + |Z| — |X∩Y| — |X∩Z| — |Y∩Z| + |X∩Y∩Z|

14. Формула включений-исключений

МК
Формула включений-исключений
!
Принципом включений-исключений называется
формула,
позволяющая
вычислить
мощность
объединения (пересечения) множеств, если известны
их мощности и мощности всех их пересечений
(объединений).
X
Y
X
|X∩Y| = 0
Y X
Y
Z
|X∩Y| = |X| + |Y| — |X∪Y|
|X∩Y∩Z| = |X| + |Y| + |Z| — |X∪Y| — |X∪Z| — |Y∪Z| + |X∪Y∪Z|

15. Вопросы и задания

МК
?
Вопросы и задания
В зимний лагерь отправляется 100 старшеклассников. Почти
все они увлекаются сноубордом, коньками или лыжами. При
этом многие из них занимаются несколькими видами спорта.
Всего кататься на сноуборде умеют 30 ребят, на лыжах —
28, на коньках — 42. Умением кататься на лыжах и сноуборде могут похвастаться 8 ребят, на лыжах и коньках — 10, на
сноуборде и коньках — 5, но только трое из них владеют
всеми тремя видами спорта. Сколько ребят не умеет
кататься ни на сноуборде, ни на лыжах, ни на коньках?
Решение:
Обозначим через S, L и K множество сноубордистов, лыжников и любителей коньков соответственно. Тогда:
|S∪L∪K| = |S| + |L| + |K| — |S∩L| — |S∩K| — |L∩K| + |S∩L∩K|=
= 30 + 28+ 42 — 8 — 5 — 10 + 3 =80
Ответ: 20 старшеклассников
=> 100 — 80 = 20

16. Самое главное

МК
Самое главное
Множество — это совокупность объектов произвольной
природы, которая рассматривается как единое целое.
Пересечением двух множеств X и Y называется
множество их общих элементов.
Объединением двух множеств X и Y называется
множество, состоящее из всех элементов этих множеств и
не содержащее никаких других элементов.
Пусть множество P является подмножеством множества М. Дополнением P до М называется множество,
состоящее из тех элементов М, которые не вошли в P.
Мощностью конечного множества называется число его
элементов.

17. Вопросы и задания

МК
Вопросы и задания
?
1. Сколько натуральных чисел от 1 до 1000 включительно
делятся на 3 или на 5, или на 7?
Решение:
1) [1000:3] = 333 чисел делятся на 3
2) [1000:5] = 200 чисел делятся на 5
3) [1000:7] = 142 числа делятся на 7
4) [1000:(3·5)] = 66 чисел делятся на 3 и 5
5) [1000:(3·7)] = 47 чисел делятся на 3 и 7
6) [1000:(5·7)] = 28 чисел делятся на 5 и 7
7) [1000:(3·5·7)] = 9 чисел делятся на 3, 5 и 7
8) По формуле включений-исключений
|X∪Y∪Z| = |X| + |Y| + |Z| — |X∩Y| — |X∩Z| — |Y∩Z| + |X∩Y∩Z|
получаем: 333 + 200 +142 – 66 – 47 – 28 + 9 = 543
Ответ: 543 числа

18. Вопросы и задания

МК
?
Вопросы и задания
2. Пусть A, B и C — некоторые
множества, обозначенные кругами, U — универсальное множество. С помощью операций
объединения, пересечения и
дополнения до универсального
множества выразите через A,
B и C следующие множества:
А
В
2
5
1
4
3
6
7
8
С
U
1) 1 ∪ 2 ∪ 3 ∪ 4 ∪ 5 ∪ 6
Ответ: А ∪ В
4) 2 ∪ 4 ∪ 5 ∪ 6
Ответ: (А ∩ В) ∪ (А ∩ С) ∪ (В ∩ С)
2) 2 ∪ 5
Ответ: А ∩ В
5) 1 ∪ 2 ∪ 3
Ответ: (А ∪ В) ∩ С
3) 5
Ответ: А ∩ В ∩ С
6) 8
Ответ: А ∪ В ∪ С

19.

Вопросы и заданияМК
Вопросы и задания
?
3. Из 100 человек 85 знают английский язык, 80 — испанский,
75 — немецкий. Каждый владеет хотя бы одним языком.
Сколько человек знают все три языка? Укажите множество
решений.
Решение (один из способов):
Анг. Исп.
1. 100 — 85 = 15 (чел.) –
не знают английского
?
2. 100 — 80 = 20 (чел.) –
не знают испанского
3. 100 — 75 = 25 (чел.) –
Нем.
не знают немецкого
4. 15 + 20 +25 = 60 (чел.) – 4. (15 + 20 +25) : 2 = 30 (чел.) –
могут знать два языка
могут знать только один язык
5. 100 — 60 = 40 (чел.) –
5. 100 — 30 = 70 (чел.) –
знают три языка
знают три языка
Ответ: от 40 до 70 человек включительно

20. Информационные источники

МК
Информационные источники
http://www.unikru.ru/userfiles/zoo-animal-friends-angela-waye.jpg
http://download.4-designer.com/files/20140221/Childlike-cartoon-alphabet-vector-material-62504.jpg
http://s4.pic4you. ru/y2014/07-04/12216/4477117.png
http://azbukadekor.ru/upload/iblock/475/475cddb0ce49566682e02adfdffd946e.jpg
http://st.gdefon.com/wallpapers_original/s/580857_babochki_raznotsvetnyie_radujnyie_5500x3765.jpg
https://pixabay.com/static/uploads/photo/2013/07/12/13/16/pencil-146715__180.png

English     Русский Правила

Теория множеств, формулы, вопросы и справочники

Математика известна как Королева наук с древних времен, и ее ландшафт значительно изменился, и все больше и больше студентов выбирают ее в качестве своей карьеры. Это доказанный факт, что мир Математика внес большой вклад в создание блестящих умов и может предложить прибыльную карьеру. Основными концентрациями субъекта являются структура, количество, пространство, а также изменение. Помимо предоставления больших академических возможностей, он также является неотъемлемой частью конкурсные экзамены . Популярной темой предмета является Теория множеств, , которая является частью программы 11 класса по математике . В этом блоге вы узнаете, что представляют собой формулы теории множеств и какие сформулированные вопросы связаны с ними.

Что такое теория множеств?

Теория множеств — это процесс сбора объектов, множеств, известных как элементы или числа. Считается, что каждый объект в Математика рассматривается как множество, а любая теорема рассматривается как исчисление предикатов. Это было принято аксиомами теории множеств. Давайте разберемся, какие формулы теории множеств важны для понимания.

Набор, который включает в себя все части данной коллекции, известен как универсальный набор, который распознается символом «µ». Произносится как мю.

Давайте разберемся с наборами A и B, двумя наборами.

• Количество элементов, преобладающих в наборе A или B, представлено как n(AᴜB)
• n(A∩B) количество элементов, присутствующих в наборах A и наборе Б
  .

n(AᴜB) = n(A) + (n(B) – n(A∩B)

n(AᴜBᴜC) = n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C)

Формулы теории множеств

Ниже приведены важные формулы теории множеств-

Формулы теории множеств для свойств

• Коммутативность:
  • А⋂В = В⋂А
  • А∪В = В∪А
• Ассоциативность:
  • А⋂ (В⋂С) = (А⋂В)⋂С
  • А∪ (В∪С) = (А∪В)∪С
• Распределяемость: A ⋂(B∪C) = (A ⋂B) ∪ (A⋂C)
• Закон идемпотента:
  • А ⋂ А = А
  • А ∪ А = А
• Закон Ø и ∪:
  • А ⋂ Ø = Ø
  • U ⋂ А = А
  • А ∪ Ø = А
  • U ∪ А = U

Теория множеств Формулы разности множеств

• А – А = Ø
• Б – А = В⋂ А’
• Б – А = В – (А⋂В)
• n(AUB) = n(A – B) + n(B – A) + n(A⋂B)
• n(A – B) = n(A∪B) – n(B)
• n(A – B) = n(A) – n(A⋂B)
• (A – B) = A, если A⋂B = Ø
• (А – В) ⋂ С = (А⋂ С) – (В⋂С)
• А ΔВ = (А-В) U (В-А)
• n(A ^‘ ) = n(∪) – n(A)

Теория множеств Формулы дополнительных множеств

• Закон двойного дополнения: (A’)’ = A
• Законы Пустого множества и Универсального множества: Ø’ = ∪ и ∪’ = Ø
• Закон дополнения: A∪A’ = U, A⋂A’ = Ø и A’ = U –  A
• Законы Де Моргана: (A ∪B)’ = A’ ⋂B’ и (A⋂B)’ = A’ ∪ B’

Формула теории множеств PDF

Вот PDF-файл для загрузки вышеупомянутых формул-

Формулы теории множеств Скачать

Нотация множеств как мы можем обозначить множество.

Обычный способ обозначения набора — перечисление его в фигурных скобках. Например: A= {желтый, зеленый, розовый, синий, красный} – набор цветов, W= {0,1, 2,3,4… 15} – набор целых чисел до 15. 

Определение набора 

При написании набора обязательно нужно определить или объяснить, из чего состоит актив. Упоминание правильного описания множества дает ясное представление о его членах. Например: 

• B= {a, e, i, o, u} – это набор, содержащий 5 элементов, которые являются гласными буквами английского алфавита 
• H= {-10…-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5…} — набор целых чисел

Равные множества  

Два заданных множества X и y I будут равны, только если оба имеют точное и одинаковое количество элементов. Например: Х= {8, 7, 9, 10} и Y = {7, 9, 8, 10}

Таким образом, X = Y

Нулевой набор

Пустое множество для нулевого множества является жизненно важным понятием теории множеств. Если существует множество без каких-либо элементов в нем, мы можем назвать его нулевым множеством. Пустое множество обозначается через A {} или A Φ.

Объединение множеств 

Объединение двух множеств может быть определено как A или B, что означает, что существует новое множество, содержащее элементы, встречающиеся как в множестве A, так и в множестве B. Например: 

C= { 6,7,8,5,9} 

D= {5, 6,4, 3,1,2} 

C ∪ D= {1,2,3,4,5,6,7,8,9}

Пересечение множеств

Вы будете столкнетесь с множеством вопросов, основанных на пересечении множеств, которые вы сможете решить, используя формулы теории множеств. Пересечение двух заданных множеств — это количество элементов, общих для обоих множеств. Например: 

E= {6,7,4,5,3,1}

F= {1,2,3,4,5}

E∩ F ={1,3,4,5}

Решенные примеры формул теории множеств

Чтобы прояснить свои формулы, относящиеся к теориям множеств, вам нужно понять очень важные вопросы, которые могут дать вам полное понимание предмета. Полный список вопросов с ответами выглядит следующим образом:

Q1. Всего в группе было 115 человек, у них были проверены удостоверения личности. Некоторые из них обрабатывали удостоверения избирателя, у некоторых были паспорта, а у некоторых были и те, и другие. Вопрос: если у 65 человек были паспорта, а у 30 человек были и те, и другие, сколько человек имели только удостоверение личности избирателя и были без паспорта?

Решение:
Используя формулу теории множеств: n(PᴜV) = n(P) + n(V) – n(P∩V)
115 = 65+n(V) – 30
n(V) ) = 80
Люди только с идентификатором избирателя = 80-30 = 50
Ответ: 50

Q2. Вопрос о цветах, давайте поймем, что 30% людей любят синий цвет, 40% людей проявляют интерес к красному цвету, 5% людей любят и красный, и синий цвета, 7% людей любят и красный, и зеленый, 10% людей любят зеленый и синий. Теперь вопрос в том, если 86% из них любили только один цвет, то какому проценту людей в возрасте нравились все три цвета?

Решение :
Используя формулу теории множеств:
n(RᴜBᴜG) = n(R) + n(B) + n(G) – n(R∩B) – n(B∩G) – n( R∩G) + n(R∩G∩B)

86 = 40+30+30-5-10-7+ n(R∩G∩B)
После решения ответ равен 8

Q3. На школьном конкурсе медали разыгрывались в различных номинациях. 36 медалей получили исполнители танцев, 18 медалей – музыкальные исполнители, 12 – драматические исполнители. Скажем, эти медали были розданы 45 людям, из которых 4 человека получили медали только во всех трех категориях, так сколько медалей было получено ровно в двух из этих категорий?

Решение:
Пусть
A = Награждены медалями в танцевальном исполнении
B = Награждены медалями в драматическом искусстве
C = Награждены в музыкальных жанрах

Что дано,

n(A) = 36
n(B) = 12
n(C) = 18
n(A ∪ B ∪C) = 45
n(A ∩ B ∩ C) = 4

Используя формулу теории множеств: n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3n(A ∩ B ∩ C)
= n(A ∩ B) + n(B ∩ C) + n(A ∩ C) – 3 × 4 ……..(i)
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n( А ∩ C) + n(A ∩ B ∩ C)
Следовательно, n(A ∩ B) + n(B ∩ C) + n(A ∩ C) = n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n( A ∪ B ∪ C)

Из (i) искомого числа

= n(A) + n(B) + n(C) + n(A ∩ B ∩ C) – n(A ∪ B ∪ C) – 12
= 36 + 12 + 18 + 4 – 45 – 12
= 70 – 67 = 3
Ответ: 3

Q4. Из группы из 100 человек 72 человека имеют право говорить по-английски, 43 человека могут говорить по-французски. Сколько людей могут говорить только на английском языке, и сколько людей могут говорить только на французском языке, и сколько людей говорят на обоих языках?

Решение:
Давайте сохраним A как группу людей, говорящих на английском языке.
Давайте сохраним B как группу людей, говорящих на французском языке
Давайте сохраним группу A и B людей, говорящих на английском языке, но не говорящих по-французски
Давайте сохраним B и A группу людей, которые могут говорить по-французски, а не по-английски.

A ∩ B — множество людей, говорящих на французском и английском языках.

Дано:

n(A) = 72
n(B) = 43
n(A ∪ B) = 100

Используя формулу теории множеств: n (A ∩ B) = n(A) + n(B) – n(A ∪ B)
= 72 + 43 – 100
= 115 – 100
= 15

Следовательно, количество людей, говорящих на французском и английском языках = 15

n(A) = n(A – B) + n(A ∩ B) ⇒ n(A – B) = n (A) – n(A ∩ B)
= 72 – 15
= 57

и n(B – A) = n(B) – n(A ∩ B)
= 43 – 15
= 28

Следовательно, количество людей, говорящих только по-английски = 57, а количество людей, говорящих по-французски, равно 28

Q5. Пусть A и B — два конечных множества, где n(A) = 20, n(B) = 28 и n(A ∪ B) = 36, поэтому найдем n(A ∩ B).

Решение:
Используя формулу теории множеств: n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Где n(A ∩B) = n(A) + n(B) – n(A ∪B)
= 20 + 28 – 36
= 48 – 36
= 12

и было обнаружено, что 45 из них любят математику, тогда как только 35 любят естествознание. 10 учащимся нравятся оба предмета. Используя формулу теории множеств, узнайте, скольким из них не нравится ни один из предметов?

Решение:
Всего детей – 100
n(A)No. студентов, которым нравится наука – 35
n(B)No. студентов, которым нравится математика – 45
n(A∩B) Число студентов, которые любят и математику, и естественные науки – 10

Таким образом, используя, n(AᴜB) = n(A) + (n(B) – n(A ∩B) получаем
35 + 45 – 10
= 70

Таким образом, количество учеников, которым не нравится ни один из предметов, равно
100 – 70 = 30
Ответ: 30

90 Алгебра Формулы

Вопросы по теории с диаграммами Венна

В1: В ходе опроса, проведенного школьной администрацией в классе X A из 30 учащихся, было обнаружено, что 8 учащимся нравятся как французский, так и английский языки. Принимая во внимание, что только 18 владеют английским языком. Согласно школьным правилам, учащиеся должны были владеть хотя бы одним из языков. Используя формулу теории множеств, узнайте, скольким студентам понравился французский язык.

Решение: 

Каждый учащийся обязан изучать один язык, поэтому мы можем сделать вывод, что: 
n(AᴜB) = n(µ) = 30

Двигаясь вперед с вопросом по теории множеств, мы знаем, что 18 студентов любят английский язык, а 8 студентов любят и английский, и французский языки. Следовательно, количество студентов, которым нравится только английский язык, равно 18-10 = 10.

Отсюда n(µ) = 30
n(E) = 10
n(F) = 30 – 10
= 20
Ответ is 20

Формулы и задачи теории множеств

Теперь, чтобы проверить ваши умственные способности, у нас есть список нерешенных вопросов, которые вам нужно решить, чтобы проверить свои знания. Ниже приведен список вопросов по теории множеств, составленный Кредитное плечо Edu :

Q1. Допустим, 70% людей любят кофе, 80% людей любят чай. Тогда, по крайней мере, какой процент людей любит и кофе, и чай?

Q2. Допустим, 70% людей любят пить кофе, 80% людей любят чай, 85% людей любят пить молоко. Найдите процент людей, которым нравятся все три?

Q3. Найдите эквивалентные множества в следующих вариантах?

(а) A = (1, 2, 3)       B = (4, 5)
(б) P = (q, s, m)       Q = (6, 9, 12)
(в) X = (x : x — простое число меньше 10) Y = (x : x ∈ N, x ≤ 4)
(d) R = (x : x = 2n + 3, n < 4, n ∈ N} S = {x : x = n/(n + 1), n ​​∈ R, n ≤ 4)
(e) Набор гласных в английском алфавите
(f) Набор согласных в английском алфавите

Q4. Пусть A = (a, b, c, d, e, f). Давайте вставим соответствующий символ ∈ или ∉ в пустое место.

(а) д __ А
(б) у __ А
(в) м __ А
(г) а __ А
(д) д __ А
(е) х __ А

Q5. В художественном классе 35 учеников, а в танцевальном классе 57 учеников. Давайте найдем количество учеников, которые занимаются либо искусством, либо танцами.

Q6. В группе из 40 человек каждый ученик играет в 1 игру в помещении: шахматы, скрэббл и шахматы. И 18 человек играют в шахматы, в то время как 20 человек играют в скрэббл и 27 играют в карром. 7 человек играют в шахматы и скрэббл, 12 человек играют в скрэббл и карром, 4 человека играют в шахматы, карром и скрэббл. Вы должны найти количество учеников, которые играют

A. Шахматы и карром
B. Шахматы, карром, но не скрэббл.

Q7. Пусть S останется как {1,2,3}. Запишите все возможные разделы S.

Q8. Найдите полный диапазон функции
f: R→где R определяется как f(x)=sin(x).

Q9. Найдите мощность множества A и B, которая объясняется в разделе:
A = (a, b, c, d) и B = (1, 4, 7, 9, 10, 12, 23)

Q10. Что из следующего списка не является собственностью группы?

А. Коммутативность
B. Ассоциативность
C. Существование инверсии для каждого элемента
D. Существование тождества

Читайте также: Решение вопросов о расположении мест по кругу

Это все о формулах теории множеств и вопросах, которые следует держать в голове. разум при пересмотре этой темы математики. Если вы хотите сделать карьеру в области прикладной математики и вычислений , тогда пусть Leverage Edu станет вашей рукой помощи. От выбора подходящего университета до создания портфолио кандидаты получат все преимущества, связанные с поступлением, благодаря нашим экспертам.

Формулы набора — изучите формулу для набора в математике

Формулы набора — это формулы, связанные с теорией множеств в математике. Набор — это набор четко определенных объектов, состоящий из отдельных элементов. Знание множеств помогает нам применять формулы множеств в областях, связанных со статистикой, вероятностью, геометрией и последовательностями.

Формулы множеств включают объединение, пересечение, дополнение и разность множеств. Диаграммы Венна обычно используются для визуализации формул множества, чтобы получить их доказательство. Давайте узнаем о формулах множества на нескольких решенных примерах.

Что такое формулы наборов?

Формулы множеств были получены из теории множеств, и их можно использовать в качестве справочника. Напомним обозначения множеств, символы, определения и свойства множеств перед формулой.

• Если n(A) и n(B) обозначают количество элементов в двух конечных множествах A и B соответственно, то для любых двух перекрывающихся множеств A и B n(A∪B) = n(A) + n (Б) — п(А⋂В)
• Если множества A и B не пересекаются, n(A∪B) = n(A) + n(B)
• Если A, B и C — 3 конечных множества в U, то n(A∪B∪C) = n(A) +n(B) + n(C) — n(B⋂C) — n (A⋂ B)- n (A⋂C) + n(A⋂B⋂C)

Множества Формулы свойств множеств

Множественные формулы имеют почти такие же свойства, как действительные числа или натуральные числа. Множества также следуют коммутативному свойству, ассоциативному свойству, дистрибутивному свойству. Формула множества, основанная на свойствах множеств, выглядит следующим образом.

Коммутативность:

• A⋂B = B⋂A 
• А∪В = В∪А

Ассоциативность:

• A⋂ (B⋂C) = (A⋂B)⋂C
• А∪ (В∪С) = (А∪В)∪С

Распределяемость: A ⋂(B∪C) = (A ⋂B) ∪ (A⋂C)

Закон идемпотента:

• A ⋂ A = A
• А ∪ А = А

Закон Ø и ∪:

•  A⋂ Ø = Ø
• U ⋂ А = А
• А ∪ Ø = А
• U ∪ А = U

Наборы Формулы комплементов Наборы

Формулы множества для дополнения множества включают основной закон дополнения, законы Де Моргана, двойное дополнение, а также закон пустого множества и универсального множества.

• Закон дополнения: A∪A’ = U, A⋂A’ = Ø и A’ = U — A
• Законы Де Моргана: (A ∪B)’ = A’ ⋂B’ и (A⋂B)’ = A’ ∪ B’
• Закон двойного дополнения: (A’)’ = A
• Законы Пустого множества и Универсального множества: Ø’ = ∪ и ∪’ = Ø

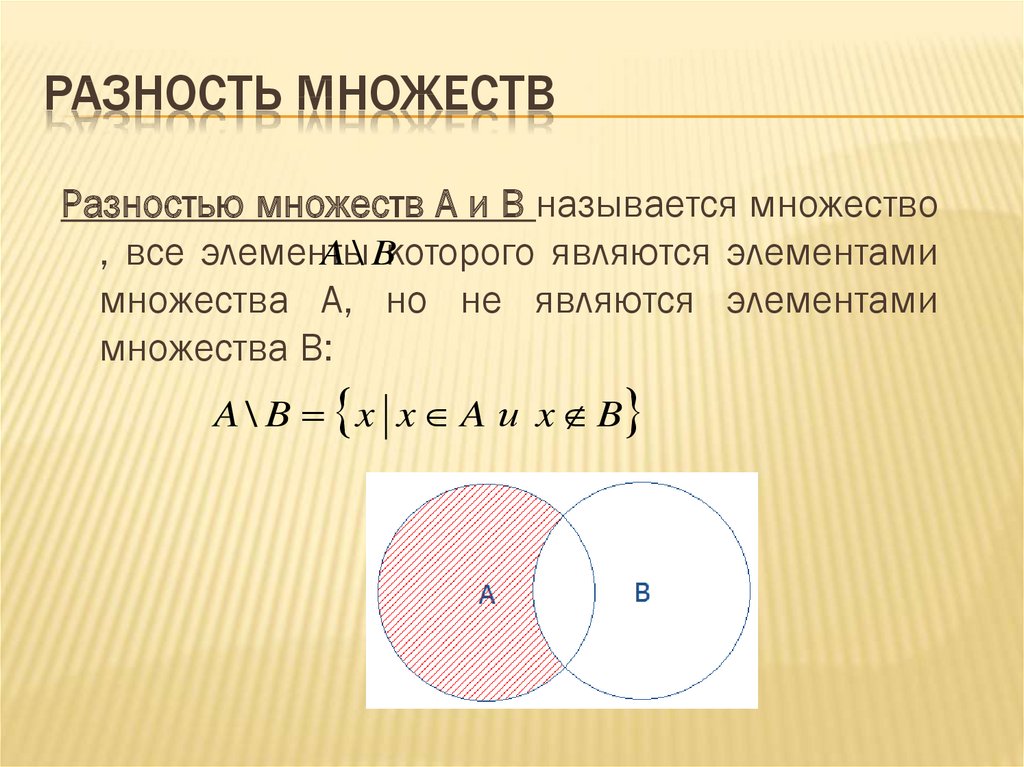
Наборы Формулы разности наборов

Формулы множества или разность множеств для двух множеств, для нулевого множества и для дополнения множества следующие.

• А — А = Ø
• Б — А = Б⋂ А’
• Б — А = В — (А⋂В)
• (A — B) = A, если A⋂B = Ø
• (А — В) ⋂ С = (А ⋂ С) — (В ⋂ С)
• А ΔВ = (А-В) U (В-А) 
• n(AUB) = n(A — B) + n(B — A) + n(A⋂B)
• n(A — B) = n(A∪B) — n(B)
• n(A — B) = n(A) — n(A⋂B)
• n(A ^‘ ) = n(∪) — n(A)

Другие важные формулы множеств

• n(U) = n(A) + n(B) + — n(A⋂B) + n((A∪B) ^‘ )
• n((A∪B) ^‘ ) = n(U) + n(A⋂B) — n(A) — n(B)

Давайте рассмотрим несколько решенных примеров, чтобы лучше понять формулы множеств.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Забронировать бесплатный пробный урок

Решенные примеры с использованием формул наборов

Пример 1:  В клубе каждый человек играет в шахматы, карром или и то, и другое. Количество людей, играющих в шахматы, карром или и то, и другое, составляет 11, 12 и 3 соответственно. Представив эту информацию в виде множеств и используя формулы множеств, найдите людей, которые играют либо в шахматы, либо в карром?

Решение:

Пусть n(шахматы)= n(P) и n(шахматы) = n(Q)

Тогда имеем n(шахматы или карром) = n(P∪Q) и n(шахматы и карром) = n(P ∩ Q)

При n(P) = 12 , n(Q) = 12 и (P ∩ Q) = 3

Применяя формулу множества, n(P ∪ Q) = n(P) + n(Q) — n( P∩Q) = 11 + 12 — 3 = 20

Ответ: количество людей, играющих и в шахматы, и в карром = 20

Пример 2:  В классе из 70 учеников 45 учеников любят играть в футбол , 52 учащихся любят играть в бейсбол. Все ученики любят играть хотя бы в одну из двух игр. Используя формулу множеств, найдите, сколько студентов любят играть в футбол или бейсбол ? Сколько студентов любят играть только в футбол?

Решение:

Дано: n(A U B ) = 70, n(A) = 45, n(B) = 52

Требуется найти n (A ⋂ B)

Используя формулу множеств, n (A ⋂ B)= n(A) + n(B) — n(A ∪ B)

n(A ⋂ B)= 45 + 52 — 70 = 27

Студенты, которые любят играть только в футбол = 45 — 27 =18

Ответ: 18 учащихся любят играть только в футбол.

Пример 3: Есть 100 студентов, 35 любят рисовать и 45 любят танцы, а 10 любят и то, и другое. Скольким ученикам нравится любой из них или ни один из них?

Решение:

Общее количество учеников = 100

Количество учеников, которые любят рисовать, n(P) = 35

Количество учеников, которые любят танцы, n(D) = 45 как и в обоих случаях, n(P∩D) = 10

Требуется найти n(A ∪ B), т. е. число студентов, которым нравится любой из них, и

Используя формулу множеств, n(P∪D) = n( P) + n(D) – n(P∩D)

⇒ 45 + 35 – 10 = 70

Количество учащихся, которым не нравится ни то, ни другое = Общее количество учащихся – n(P∪D) = 100 – 70 = 30  

Ответ: Следовательно 70 учащимся нравится любой из них, а 30 учащимся не нравится ни один из них.

Часто задаваемые вопросы о формулах наборов

Что такое формула наборов?

Формула множества задается в общем случае как n(A∪B) = n(A) + n(B) — n(A⋂B), где A и B — два множества, а n(A∪B) показывает количество элементов, присутствующих либо в A, либо в B, а n(A⋂B) показывает количество элементов, присутствующих как в A, так и в B.

Что такое формула пересечения множеств?

Формула множества для пересечения множеств A и B обозначается ⋂. n(A⋂B) означает элементы, общие для обоих множеств A и B. n(A⋂B) = n(A) + n(B) — n(A∪B)

Каковы применения формул для множеств ?

Формулы набора имеют широкий спектр применения во многих абстрактных концепциях.

No related posts.