Неравенства с модулем решать: Решение неравенств с модулем. Модуль раскрытие. Неравенства содержащие модуль. Неравенства с модулем примеры решения.

Как решить неравенство с модулем (одним, двумя): примеры

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Решение неравенств с модулем

В данной публикации мы рассмотрим, что из себя представляют неравенства с модулем (одним или двумя), а также на практических примерах покажем, как их решать.

Примечание: что такое модуль числа, мы рассмотрели в отдельной публикации.

• Внешний вид неравенств
• Решение неравенств

Внешний вид неравенств

Неравенства с одним модулем выглядят следующим образом:

• |x| > 5
  (модуль икс больше 5)
• |x – 7| < 4
  (модуль икс минус 7 меньше 4)
• |x + 2| ≥ 11
  (модуль икс плюс 2 больше или равен 11)

В модуле указывается неизвестная переменная x или выражение с ней.

Решение неравенств

Разберем по порядку решение представленных выше примеров.

|x| > 5

Это следует понимать таким образом: на числовой оси существуют такие точки, расстояние от которых до нуля больше пяти. Т.е. это точки больше 5 или меньше -5, следовательно, у данного неравенства два решения: x₁ ∈ (-∞; -5) и x₂ ∈ (5; ∞).

|x – 7| < 4

Т.е. на числовой линейке существует такое множество точек x, расстояние от которых до точки 7 меньше 4. Следовательно, неравенство имеет следующее решение:
7 – 4 < x < 7 + 4 или x ∈ (3; 11).

|x + 2| ≥ 11

Данное неравенство можно представить в таком виде: |x – (-2)| ≥ 11.

Таким образом, на числовой оси точки x находятся на расстоянии не менее 11 от точки -2. Значит:

• x₁  ≥ 9 (-2 + 11) или x₁ ∈ [9; ∞)
• x₂ ≤ -13 (-2 – 11) или x₂ ∈ (-∞; -13]

Примечание:

Некоторые неравенства могут содержать два модуля: например: |x| > |y|.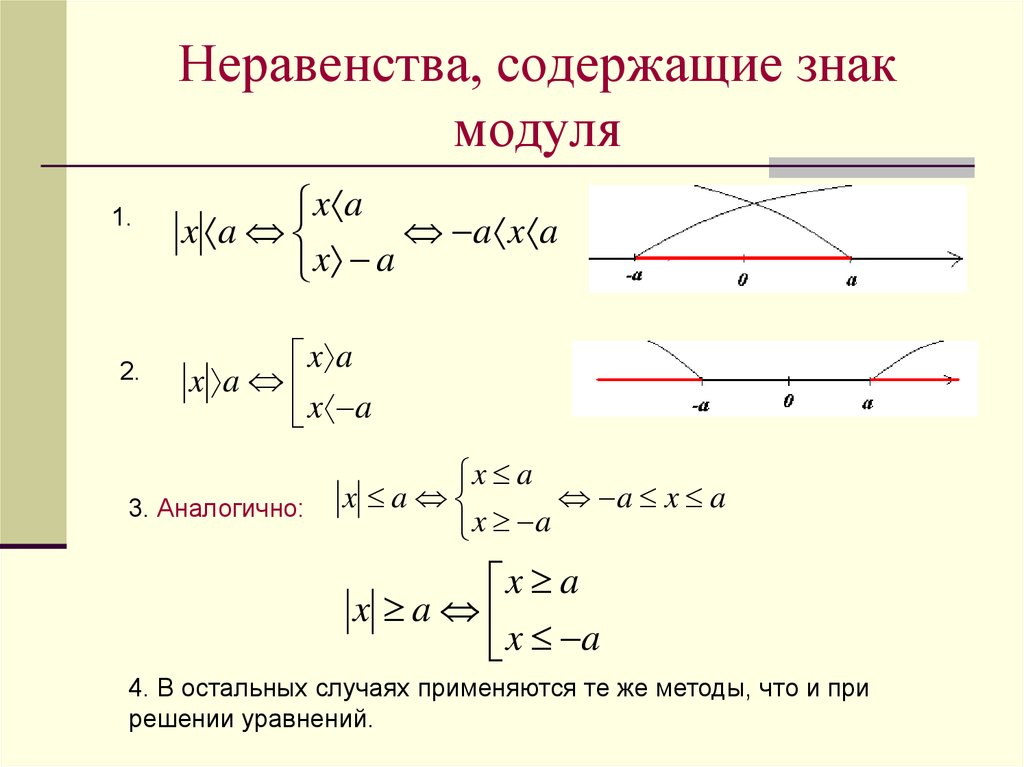
Для него, также, есть два решения: x₁ ∈ (-∞; -y) и x₂ ∈ (y; ∞).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Неравенства с модулем.

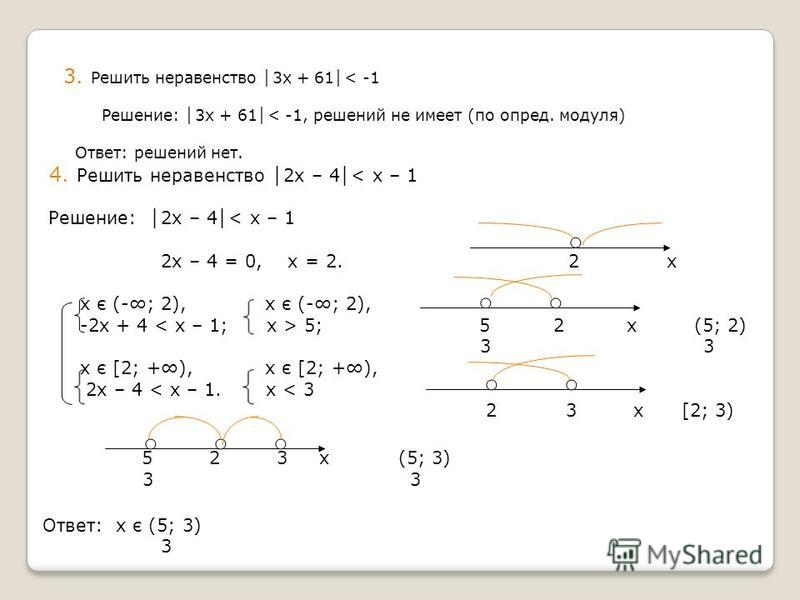Способы решения неравенств с модулями

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Неравенства с модулем

2. Способы решения неравенств с модулями:

2
1. По определению модуля
2. Возведение обоих частей неравенства
в квадрат
3. Замена переменной
4. Раскрытие модуля на промежутке
знакопостоянства
5. Равносильность неравенств системам
6. Важный частный случай

3. 1.По определению модуля

3
| f (x) | < а
-a
|3x-1|<7
-7< 3x-1 <7
-6< 3x <8
8
-2< x <
3
8
Ответ: 2;
3
| f (x) |> а
a
5x 2 4
-a
a
5 x 2 4
5 x 2 4
5 x 6
5 x 2
2 6
Ответ : ; ;
5 5

4.

2.Возведение обеих частей в квадрат4
|x2-1| > |x2-x|
(x2-1)2 > (x2-x)2 — равносильность не нарушена
(x2-1+ x2-x)(x2-1-x2+x) > 0 – разность квадратов
(2×2-x-1)(x-1) > 0
—
+
1
2
+
1

5. 3.Замена переменной

5
+
-2
0
—
+
3
t

6. 4. Раскрытие модуля на промежутках знакопостоянства

6
|x-1| + |2-x| > 3
x-1
—
2-x
+
1
+
Нули подмодульных выражений: x =1 и x =2
2
+
+
—
а)
б)
в)
x 1
( x 1) 2 x 3
x 1
x 0
1 x 2
x 1 x 3
x 2
x 3 x 3
x 2
x 3
0
1
х ;0
1 x 2
1 3 неверное
Ответ : ;0 3;
2
3
х 3;

7. 5. Равносильность неравенств системам или их совокупности

7
См. решение по определению
Равносильно неравенству:
Можно записать в виде
системы
Неравенство равносильно двум
неравенствам:
Можно записать в виде совокупности

8.

5. Равносильность неравенств системам (примеры)8
№1
3x | 2 x | 5
№2
5 x 7 | x 2 |
| 2 x | 5 3x
| x 2 | 5 x 7
2 x 5 3 x
2 x 3 x 5
1
x 1 2
x 1 3
4
x 2 5x 7
x 2 7 5x
1
x 2 4
x 5
6
1
Ответ : ( ;1 ]
2
1
Ответ : ( ;2 )
4

9. 6. Один частный случай

9
x 1
1
x 2
x 1
x 2
ОДЗ : x 2
1
умножим на |x+2|>0 в ОДЗ
| x 1 | | x 2 |
возведем в квадрат, обе части
( x 1 x 2)( x 1 x 2) 0
(2 x 1)( 3) 0
2x 1 0
x 12
для преобразования используем
разность квадратов
Учитывая ОДЗ, получим:
1
Ответ : ( ; 2) ( 2; )
2
Обучающая самостоятельная работа
10
Метод решения
1. По определению модуля
условие
ответы
(-5; 1)
По определению модуля
По определению модуля
По определению модуля
(-∞; −2) ∪ (−2; −0,5)
2. Возведение обеих частей в
квадрат
3. Раскрытие модуля на
промежутках
знакопостоянства
4. Замена переменной
Замена переменной
5. Замена совокупностью
систем
0; 2
11

English     Русский Правила

Как решать неравенства по модулю

Как решать неравенства по модулю :

В этом разделе мы узнаем, как решить неравенство по модулю.

Решение неравенств по модулю — концепция

Если задан вопрос в любой из следующих форм, мы должны следовать данным методам для решения x.

Вопросы в форме	Первый шаг, который нужно сделать	Решение
|х — а| <  r	-г < х - а < г	(-р + а, г + а)
|х — а| ≤ г	-r ≤  x — a ≤  r	[а- г, а + г]
|х — а| > р	x — a < -r  и  x — a > r	(∞,a-r)U(a+r,∞)
|х — а| ≥  р	х — а ≤ -r и х — а ≥ r	(∞,а-р]U[а+r,∞)

Решение неравенств по модулю – Примеры

Пример 1 :

Решите абсолютное неравенство, приведенное ниже

|x — 9| < 2

и выразить решение в виде интервалов.

Решение:

-2 < x - 9 < 2

Прибавьте 9 к уравнению

-2 + 9 < x - 9 + 9 < 2 + 9

7 < x < 11

5 90 множество решений вышеуказанного абсолютного неравенства есть (7, 11).

Пример 2 :

Решите абсолютное неравенство, приведенное ниже

|2/ (x — 4)| > 1 , x ≠ 4

и выразить решение в виде интервалов.

Решение:

Из данного неравенства имеем, что 2 > (x — 4)

-2 < x - 4 < 2

Прибавляем 4 по всему неравенству

-2 + 4 < x - 4 + 4 < 2 + 4

2 < x < 6

Мы не можем выразить решение в виде (2, 6). Потому что в середине 2 и 6 у нас есть значение 4.

Итак, мы должны разбить его на два интервала.

(2, 4) U (4, 6)

Пример 3:

Решите неравенство абсолютного значения, приведенное ниже

|3 — (3x/4)| ≤  1/4

и выразить решение в виде интервалов.

Решение:

(-1/4) ≤ 3 – (3x/4)  ≤ (1/4)

(-1/4) ≤ (12 – 3x)/4  ≤ (1/4)

Умножить на 4 во всем уравнении

-1 ≤ (12 — 3x) ≤ 1

Вычесть 12 во всем уравнении

-1 — 12 ≤ 12 — 3x — 12 ≤ 1 -12

-13 ≤ — ≤ -11

Делится на (-3) во всем уравнении

-13/(-3) ≤ — 3x ≤ -11

13/3 ≤ x ≤ 11/3

11/3 ≤ x ≤ 13/3

Следовательно, набор решений приведенного выше абсолютного неравенства равен [11/3, 13/3].

Пример 4 :

Решите абсолютное неравенство, приведенное ниже

|6x + 10| ≥  3

и выразить решение в виде интервалов.

Решение:

6x + 10 ≤ -3 и 6x + 10 ≥ 3

6x + 10 ≤ -3 Вычесть 10 с обеих сторон 6x + 10 — 10 ≤ -3 — 10 6x ≤ -13 Разделить на 6 с обеих сторон  x ≤ -13/6

6x + 10 ≥ 3 Вычитание 10 с обеих сторон 6x + 10 — 10 ≥ 3 — 10 6x ≥ -7 Разделите на 6 с обеих сторон x ≥ -7/6

Следовательно, набор решений приведенного выше абсолютного неравенства равен (-∞, -13/6] U [-7/6, ∞).

Мы надеемся, что после изучения вышеизложенного учащиеся поняли, как решать неравенства с модулями.

Помимо материала, указанного в этом разделе, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

неравенство — Решение системы неравенств по модулю N

спросил 7 лет, 1 месяц назад

Изменено 2 года, 1 месяц назад

Просмотрено 2к раз

$\begingroup$

У меня проблема, которая сводится к двум неизвестным, $X_1$ и $X_2$, где:

$X_1 \cdot M + A\bmod N = X_2$

And:

$X_1 \lt L_1\ bmod N$

$X_2 \lt L_2\bmod N$

Я могу перепробовать все возможные $X_1 \lt L_1$, пока не найду ту, которая дает $X_2 \lt L_2\bmod N$, и решить одну такую ​​задачу за меньшее чем за минуту. Тем не менее, мне нужно решить тысячи таких задач, поэтому любое повышение эффективности очень поможет.

Два вопроса, которые я нашел, указывают на то, что неравенство бессмысленно по модулю / сравнениям. Однако в данном случае неравенство имеет вполне конкретный смысл — ограничить диапазон допустимых значений для $X_1$ и $X_2$. Вот эти вопросы:

решение-неравенства по модулю-1

существование-неравенств-со-сравнениями

• неравенство
• модульная арифметика
• диофантовые уравнения

3

3
• $\endgroup$

  $\begingroup$

  Я остановился на следующем решении:

  Попробуйте $X_1 = 0$.

  Если в результате получится $X_2 \ge L_2$, вычислите $D = \lceil (N — X_2) / M \rceil$.

  Попробуйте $X_1 + D\bmod M$.

  Повторить при необходимости. Это позволяет мне пропустить большинство значений $X_1$, которые не дадут $X_2$ в требуемом диапазоне.

  $\endgroup$

  1

  $\begingroup$

  Почему бы вам не попробовать использовать расширенный алгоритм Евклида для решения $1.

  No related posts.