Четность нечетность функции калькулятор онлайн: Четность и нечетность функции | Онлайн калькулятор

Четность нечетность функции онлайн калькулятор с решением. Четность функции

Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.

Определение 1.

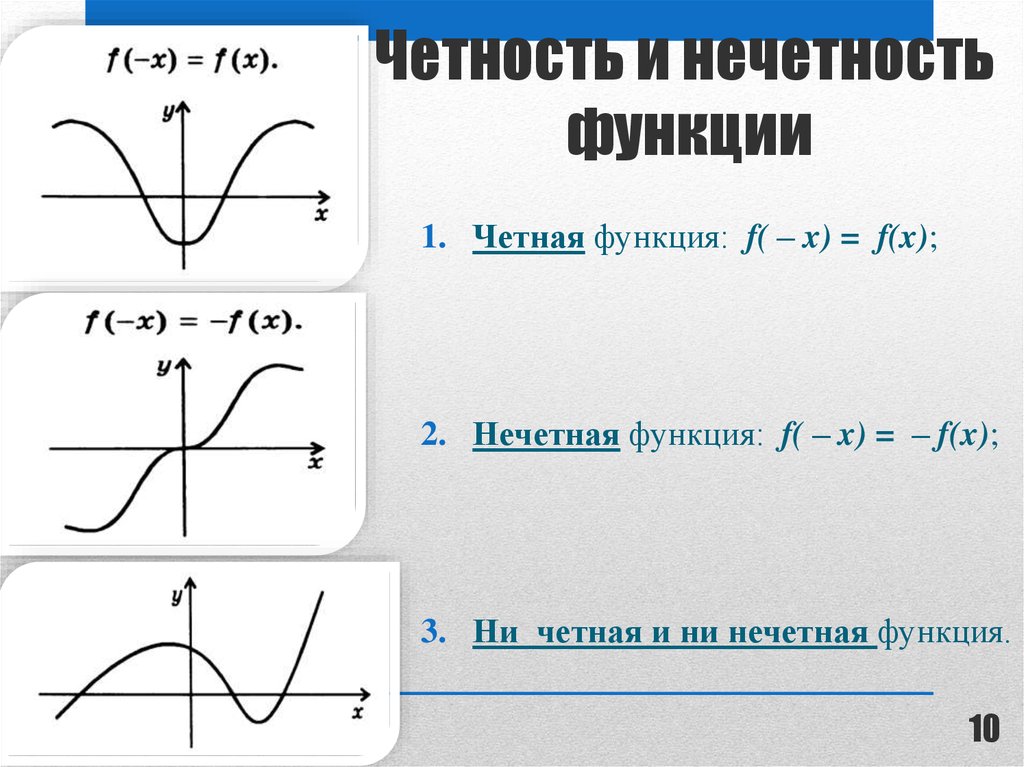
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).

Определение 2.

Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).

Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.

Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.

Доказать, что у = х 3 ~ нечетная функция.

Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.

Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.

Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).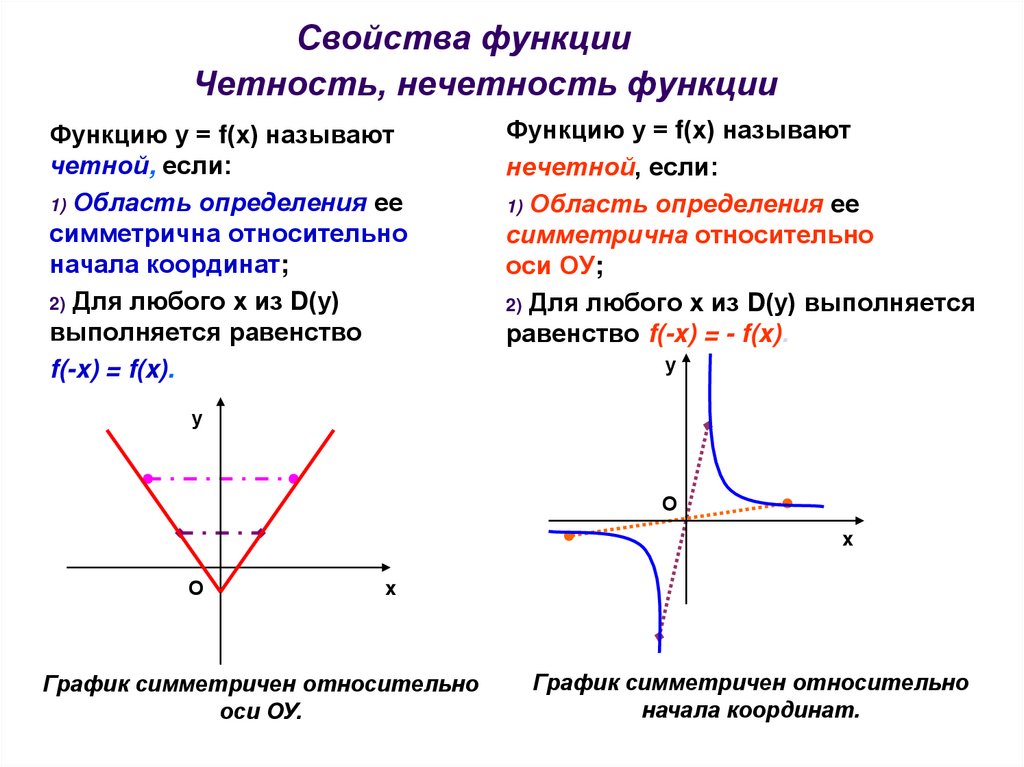

{2}} \neq 1 для любого x \in [-1;1] .

Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .

Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).

а) Если при x > 0 четная функция возрастает, то убывает она при x

б) Когда при x > 0 четная функция убывает, то возрастает она при x

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x

г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.

Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)

Необходимое условие

Согласно теореме Ферма: f»(x)=0 тогда, когда у функции f(x) , что дифференцируема в точке x_{0} , появится экстремум в этой точке.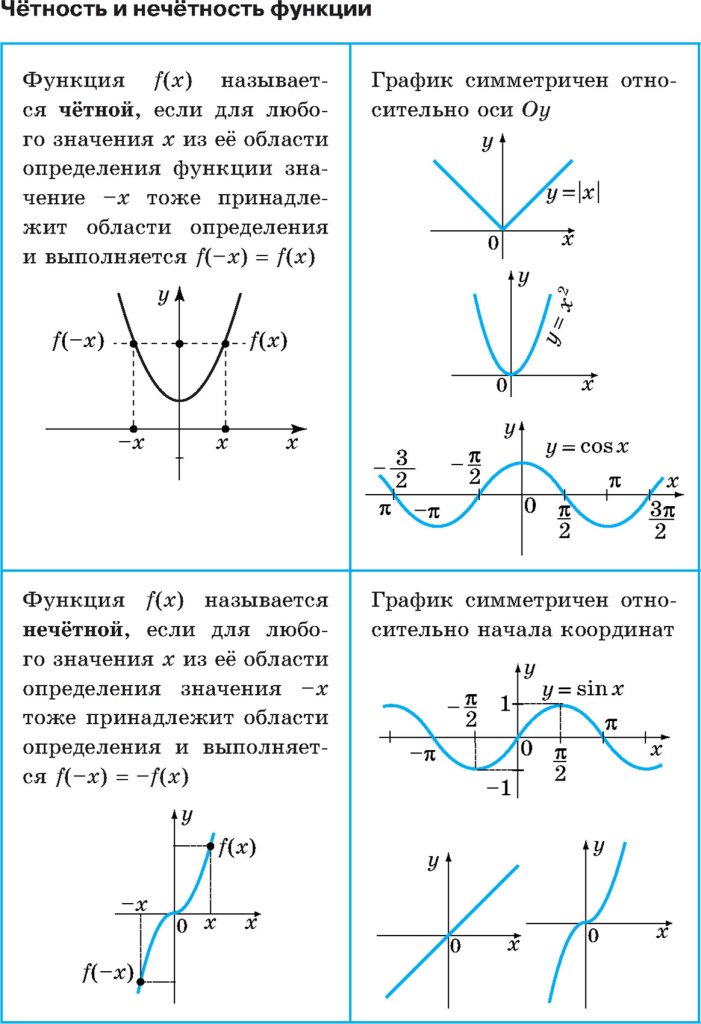

Достаточное условие

1. Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
2. x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .

Наибольшее и наименьшее значение функции на промежутке

Шаги вычислений:

1. Ищется производная f»(x) ;
2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .

пример функции, которая обратно самой себе, но не обладает свойствами четности/нечетности

Графики функций/ Исследовать

Учитель очень удивится увидев твоё верное решение😉

Введите график функции

Исследуем график функции y=f(x), для этого задайте функцию f(x).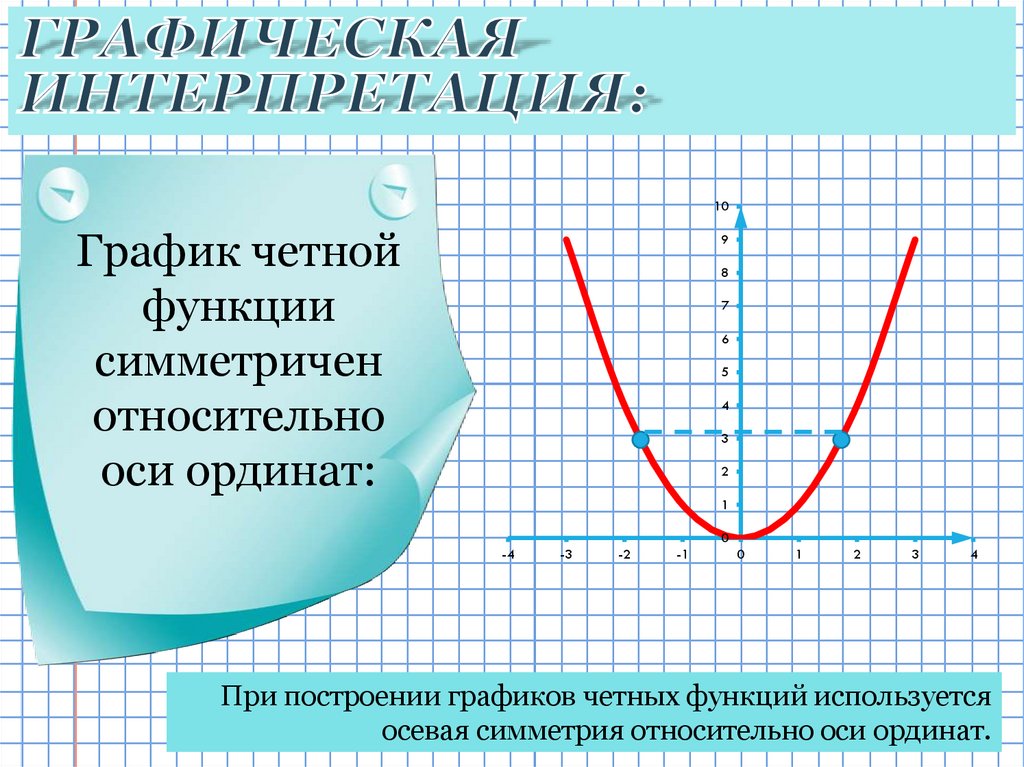 2*arctgh(x)*arcctgh(x)

Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

• Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
• Умеет определять точки пересечения графика функции с осями координат: Да
• Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
• Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости):
  Да
• Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
• Горизонтальные асимптоты графика функции: Да
• Наклонные асимптоты графика функции: Да
• Четность и нечетность функции: Да
• Минимум и максимум функции: Да

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от

x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

×

Где учитесь?

Для правильного составления решения, укажите:

(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое

Определить, является ли функция четной или нечетной функцией

Четная или нечетная функция, онлайн-исчисление

Сводка:

Калькулятор для определения, является ли функция четной и нечетной функцией.

is_odd_or_even_function онлайн

---

Описание:

Калькулятор может определить, является ли функция четной или нечетной . Напомним, что функция f четна, если f (-x) = f (x), функция нечетна, если f (-x) = -f (x). Когда функция не является ни нечетной, ни нечетной, калькулятор указывает шаги расчета, которые приводят к результату. Когда функция четная, компьютер возвращает 0, когда нечетная, компьютер возвращает значение 1, Когда функция не является ни нечетной, ни нечетной, она возвращает значение -1.

Синтаксис:

• is_odd_or_even_function(функция)

---

Примеры:

• is_odd_or_even_function(`exp(x)+exp(-x)`) , возвращает 0, поскольку функция является четной.
• is_odd_or_even_function(`exp(x)-exp(-x)`) возвращает 1, поскольку функция нечетная.

Расчет онлайн с помощью is_odd_or_even_function (калькулятор четных или нечетных функций)

См. также

Список связанных калькуляторов:

• Калькулятор четных или нечетных функций: is_odd_or_even_function. Калькулятор для определения, является ли функция четной функцией и нечетной функцией.
• Калькулятор разложения на частичные дроби: partial_fraction_decomposition. Калькулятор позволяет разбить рациональную дробь на простые элементы.
• Калькулятор производных: производная. Калькулятор производной позволяет пошагово вычислить производную функции по переменной.
• Калькулятор расширения Тейлора: taylor_series_expansion. Калькулятор ряда Тейлора позволяет вычислить разложение Тейлора функции.
• Интегральный калькулятор: интегральный. Калькулятор интегралов вычисляет онлайн интеграл функции между двумя значениями, результат выдается в точном или приближенном виде.
• Калькулятор неопределенного интеграла: первообразная. Калькулятор первообразной позволяет рассчитать первообразную онлайн с подробностями и шагами расчета.
• Калькулятор лимита: лимит. Калькулятор лимита позволяет рассчитать лимит функции с подробным описанием и шагами расчета.

---

Список связанных упражнений:

• Четные и нечетные функции : Цель этого исправленного упражнения — определить четность функции (указать, является ли функция четной или нечетной).
• Определить четность функции по ее графическому представлению : Цель этого исправленного упражнения — графически определить четность функции (указать, является ли функция четной или нечетной).

---

Напоминания о курсах, калькуляторы, упражнения и игры: Реальные функции

 

Калькулятор четных или нечетных функций

Чтобы использовать калькулятор четных или нечетных функций, введите функцию и нажмите «Рассчитать».

РЕКЛАМА

Функция

РЕКЛАМА

РЕКЛАМА

Содержание:

• Калькулятор четных и нечетных функций
• Что такое четные и нечетные функции?
• Как определить четные и нечетные функции?

Дайте нам отзыв

✎

✉

РЕКЛАМА

Калькулятор четной или нечетной функции 

Калькулятор четной или нечетной функции классифицирует входную функцию как четную, нечетную или никакую.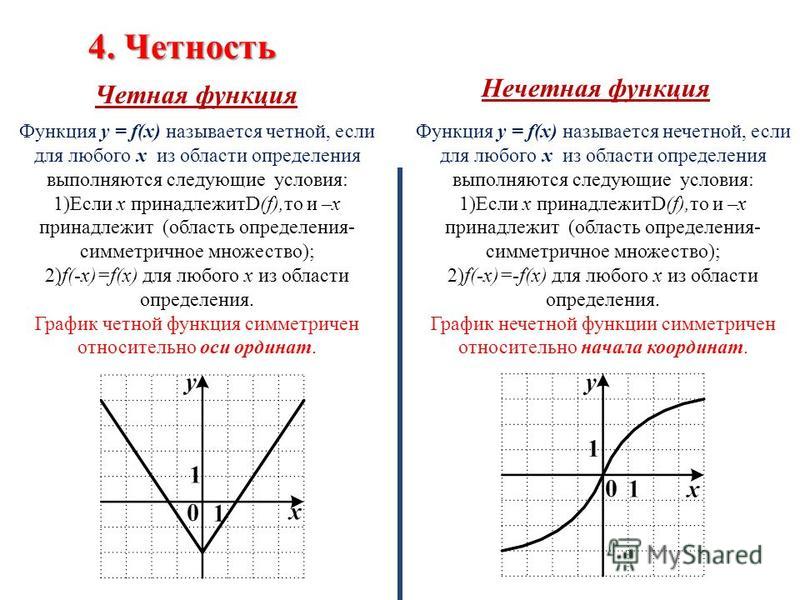 Этот инструмент особенно полезен для сложных функций, включающих тригонометрию, логарифмирование и т. д.

Что такое четные и нечетные функции?

Четные функции — это те, которые удовлетворяют следующему уравнению: как исходное значение. Например, когда f(x ² ) и x = -1, ответ равен 1.

Графики таких функций симметричны, как функции параболы и cosx.

                                            Функция косинуса 
        
Нечетные функции противоположны четным. Уравнение, которому удовлетворяет нечетная функция:

                                          F (x) = — F(x)

Таким образом, такие функции дают противоположное значение исходной функции. Такие экспоненты, как x, x ³ , x ⁵ и т. д., составляют нечетную функцию. Но следует отметить, что не каждый четный показатель является четной функцией, и не каждый нечетный показатель является нечетной функцией, такой как (x + 1) ⁴ и (х — 1) ³ .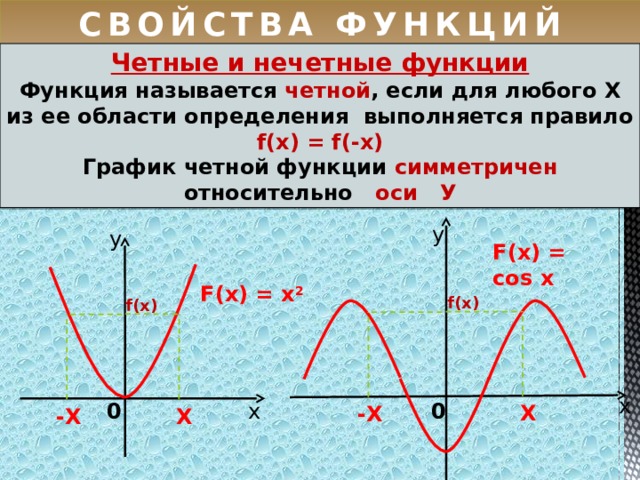

Некоторые функции ни четные, ни нечетные . Это функции, которые оказываются где-то между одинаковыми и прямо противоположными значениями.

Как определить четные и нечетные функции?

Используйте для этой цели калькулятор нечетных или четных функций. Для идентификации без использования калькулятора поставьте в функции -x.

Примеры:

1. Возьмем функцию -5x
   4 — 7. Как она выглядит? четным или нечетным? Всегда лучше решать. Подставьте -x в функцию.

= -5x ⁴ — 7x ² 
= -5(-x) ⁴ -7(-x) ²
= -5(x) ^{4 — 1(x)}

)

Мы получили значение, с которого начали. Это означает, что указанная выше функция четная.

2. Следующая функция 6x + 4x ³ . Это даже? Вы никогда не должны говорить, прежде чем решить это должным образом.

Поместите -x вместо x.

= 6х + 4х ³
= 6(-х) + 4(-х) ³
= -6x -4x ³

Как видите, это будет нанесено на противоположную сторону графика.