Видео с вопросами: Решение абсолютных неравенств с одной переменной
Стенограмма видео
Решите, что абсолютное значение 𝑥 минус шесть меньше или равно пяти.
Итак, первое, что вы заметите в этом вопросе, это вертикальные линии. И эти вертикальные линии означают абсолютное значение или модуль 𝑥 минус шесть. Итак, если мы подумаем об этом как об абсолютном значении 𝑎 или модуле 𝑎. Что это на самом деле означает? Но это означает расстояние между 𝑎 и нулем. Таким образом, не имеет значения, положительное оно или отрицательное, потому что оно все равно будет на одном и том же расстоянии от нуля.
Таким образом, если у нас на самом деле есть что-то вроде модуля 𝑥 или абсолютное значение 𝑥 равно 𝑎 как уравнение, то оно на самом деле будет иметь два решения: 𝑥 равно 𝑎 или 𝑥 равно отрицательному 𝑎 потому что они оба на расстоянии 𝑎 от нуля. Итак, теперь у нас есть понимание того, что такое абсолютное значение или модуль. Как мы можем использовать его для решения нашего неравенства? Задолго до того, как мы сможем решить вопрос, связанный с неравенством, мы должны посмотреть, как неравенство будет работать со знаком модуля.
Итак, давайте рассмотрим модуль или абсолютное значение 𝑥 меньше трех. Но это означает, что все точки отстоят от нуля менее чем на три единицы. Итак, давайте посмотрим, как это будет выглядеть на нашей числовой прямой. Ну, во-первых, вы можете видеть, что у нас есть открытые круги. И это потому, что меньше. Не меньше или равно. Если он меньше или равен или больше или равен, они будут окрашены. Но это показывает, что все значения, которые находятся менее чем в трех единицах от 𝑥, изменяются от отрицательных трех до трех, вызывая любое значение в пределах этого меньше трех единиц от нуля.
Таким образом, это можно записать как 𝑥 больше отрицательной тройки или меньше трех. Таким образом, мы говорим, что модуль или абсолютное значение 𝑥 меньше трех можно записать таким образом в виде составного неравенства. Хорошо, отлично! Так что это дает нам кое-что для работы, и мы попытаемся решить. Модуль или абсолютное значение 𝑥 минус шесть меньше или равно пяти, потому что мы можем переписать наш модуль или абсолютное значение в неравенстве как 𝑥 минус шесть больше или равно минус пять, но меньше или равно пяти.
И мы можем это сделать, потому что это меньшее неравенство, чем в нашем примере.
Это работает немного по-другому, если это больше, чем неравенство. Теперь, чтобы решить это неравенство, мы добавим шесть к каждому разделу. Итак, мы собираемся прибавить шесть к минус пяти, шесть к 𝑥 минус шесть и шесть к пяти. Итак, когда мы это сделаем, нашим первым значением будет единица, потому что минус пять добавить шесть равно единице, затем наши следующие значения будут 𝑥, потому что 𝑥 минус шесть добавить шесть будет просто 𝑥, и, наконец, у нас будет 11, потому что пять добавить шесть будет одиннадцать. Следовательно, мы можем сказать, что решение модуля 𝑥 минус шесть меньше или равно пяти, если 𝑥 больше или равно единице, но меньше или равно 11.
Неравенства с модулями (Часть 1)
Здравствуйте. Теперь, когда мы обсудили уравнения, включающие модуль, мы расширим эти знания для решения неравенств аналогичной формы (т. е. линейных неравенств).
Пример 1 Решите уравнение |x| > 3.
Решение Я проиллюстрирую два разных метода, оба из которых вытекают из определений, которые мы обсуждали ранее.
Метод 1
Определение модуля говорит мне, что
\( |x| = \begin{cases}
x& \text{ if } x\ge 0 \\
-x& \text{ if } x < 0
\end{cases} \)
Итак, когда х ≥ 0, |х| можно заменить на x, поэтому нужно решить неравенство x > 3.
А при x < 0 |x| равно –x, и на этот раз мы должны решить –x > 3.
Ну, решать особо нечего: первый случай дает x > 3 , а второй дает x < –3 .
Другими словами, неравенство |x| >
В интервальной записи решение можно представить как
x ϵ (–∞, –3) U (3, ∞)
Давайте попробуем подставить некоторые из этих значений в исходное неравенство, просто для уверенности.
Возьмем x = 5. Тогда |x| = |5| = 5 > 3, значит, x = 5 удовлетворяет неравенству.
Если взять x = –6, то |x| = |–6| = 6 > 3, что снова означает, что -6 является допустимым решением.
Попробуйте еще несколько значений самостоятельно, как внутри, так и вне набора решений, для проверки.
Метод 2
Теперь мы будем использовать второе определение. Напомним, что |х| представляет собой расстояние x от 0 на числовой прямой.
Таким образом, мы можем перефразировать это как «Найти число, расстояние до которого от начала координат больше 3».
Сначала найдем числа, расстояние которых от начала координат равно 3. Таких чисел, как мы видели ранее, два, 3 и –3.
Теперь нам нужны числа, расстояние которых от 0 до больше 3. Вы можете это понять?
Если x = 3, то расстояние x от 0 равно точно 3. Если мы хотим, чтобы это расстояние увеличилось (т. е. стало больше 3), то мы должны двигаться к правому из 3. То есть , в области, где x > 3.
Аналогично, когда x = –3, то он находится на расстоянии 3 от 0.
И, если мы хотим, чтобы это расстояние стало больше 3, то мы должны перейти к оставил из -3. То есть мы должны оставаться в области, где x < –3.
Перетащите точку, обозначенную x в апплете ниже, чтобы понять, что я имею в виду.
Объединив эти два случая, мы получим решение в виде
x < –3 или x > 3
Попробуем еще.
Пример 2 Найдите значения y, для которых |y| < 5,
Решение Геометрически этот вопрос спрашивает: «Найдите все числа на числовой прямой, расстояние от которых до начала координат меньше 5».
Сначала найдем числа, расстояние которых от начала координат равно 5. Эти числа, как мы уже знаем, равны 5 и -5.
Теперь мы хотим найти те числа, расстояние которых от начала координат меньше , чем 5.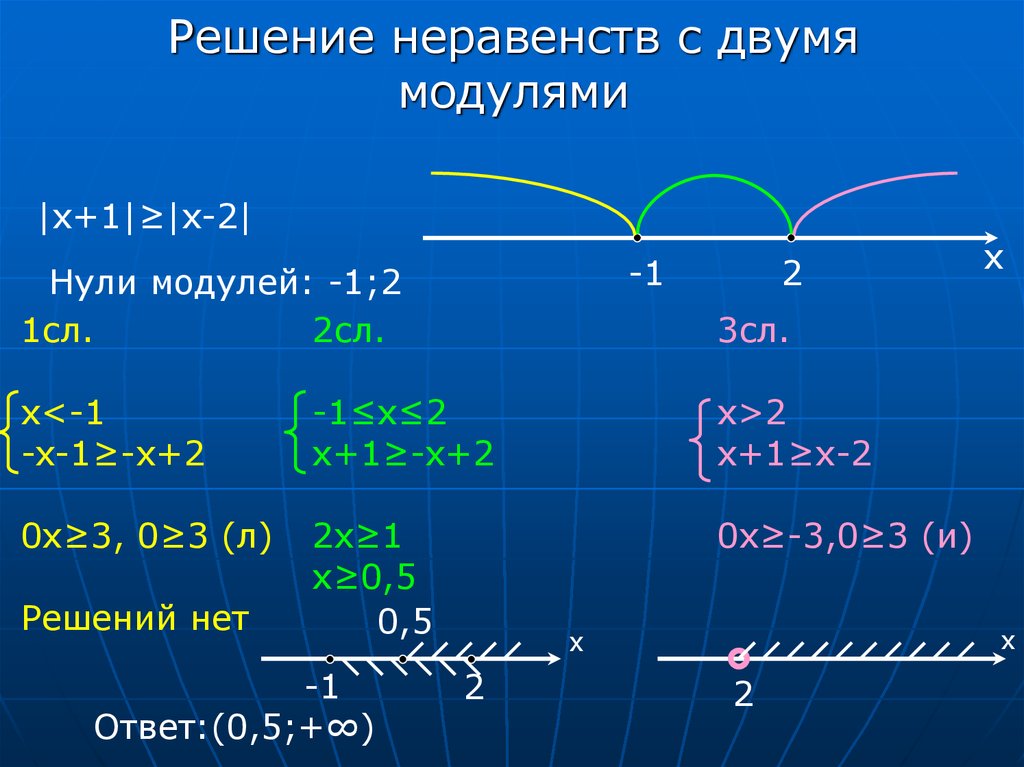
Как вы думаете, где находятся все эти числа?
Поэкспериментируйте с точкой, представляющей y для исследования.
Как вы могли видеть, искомые числа — это те, которые лежат в пределах области, ограниченной –5 и 5. То есть все значения y такие, что –5 < y < 5.
Ну вот и все . Решение неравенства |y| < 5 равно
–5 < y < 5
В интервальной записи решение можно представить как
y ϵ (–5, 5)
Давайте также рассмотрим аналитический метод.
Решить |y| < 5, мы рассмотрим два случая, основываясь на определении |y|.
Случай 1 : y ≥ 0
Здесь |y| = y и, следовательно, исходное неравенство становится y < 5, что представляет само решение.
Так же, как и в случае уравнений, решение y < 5 справедливо только в случае, когда y ≥ 0.
Чтобы убедиться в этом, подставим y = – 7 в исходное уравнение, где y < 5, но y ≱ 0. Мы получим LHS как |–7|, что равно 7 и 7 ≮ 5 (т. е. не удовлетворяет неравенству).
Следовательно, для этого случая нам нужно объединяет
0 ≤ y < 5
Теперь рассмотрим другой случай.
Случай 2 : y < 0
Здесь |y| = – у. Исходное неравенство принимает вид – y < 5, что дает y > – 5.
Объединив решение с условием случая, мы получим
–5 < y < 0
Со всеми случаями покончено. Итак, окончательное решение:
–5 < y < 0 ИЛИ 0 ≤ y < 5
, которые можно объединить и выразить как
–5 < y < 5
Мы получаем то же решение, что и при визуальном методе. Еще раз попытайтесь понять, как создавать эти «кейсы» и комбинировать их с решениями, которые вы получаете.
Мы предпочитаем работать с числовым методом, когда это возможно. Но во многих задачах вам может понадобиться аналитический метод.
Подведем итоги того, что мы уже сделали
|x| > 3 => х < –3 или х > 3
|г| < 5 => –5 < y < 5
Мы можем расширить это знание, чтобы решать такие уравнения, как |w| ≤ 6 и |z| ≥ 4 тоже.
|ш| ≤ 6 => –6 ≤ w ≤ 6
|z| ≥ 4 => z ≤ –4 или z ≥ 4
Внимательно изучите образец. По мере того, как вы будете больше практиковаться, вы сможете начать писать решения для таких простых уравнений напрямую, без использования числовой прямой или создания случаев.
Давайте рассмотрим несколько крайних случаев этих неравенств.
Пример 3 Найдите x: |x| ≥ 0
Решение Глядя на предыдущие шаблоны, мы могли бы написать что-то вроде
x ≤ 0 или x ≥ 0
Это означает, что x может быть практически любым действительным числом. Другими словами, x ϵ R.
Но давайте еще раз посмотрим на это неравенство с точки зрения геометрии.
Неравенство |x| ≥ 0 просит нас найти все числа, расстояние которых от начала координат больше или равно нулю (или неотрицательно).
Но это верно для любого числа , не так ли? Выберите любое число на числовой прямой — его расстояние от начала координат будет равно 9.
0070 всегда больше или равно нулю.
Смотрите сами.
Следовательно, решение неравенства таково: «x может быть любым действительным числом» или x ϵ R.
Можете ли вы решить неравенство |x| > 0 самостоятельно? (Может ли x быть любым действительным числом ?)
Пример 4 Решите неравенство |x| < 0.
Решение Это неравенство требует от нас найти число x такое, что его расстояние от начала координат меньше 0 (или отрицательно).
Возможно ли это? Могут ли расстояния быть отрицательными? Неа.
Опять же, смотрите сами.
Следовательно, неравенство не имеет решения. Или |х| < 0 =>
х ϵ ø.Сможете ли вы решить неравенство |x| ≤ 0 самостоятельно? (Это тоже не имеет решения?)
Еще пара примеров, и мы закончим.
Пример 5 Решите уравнение |y| ≥ –5.
Решение Прежде чем вы начнете писать что-то странное вроде
|y| ≥ –5 => y ≥ –5 или y ≤ –(–5),
давайте посмотрим на это неравенство геометрически.
Неравенство требует от нас найти все числа, расстояние от которых до начала координат больше или равно -5.
Расстояние никогда не может равняться , равному и -5. Но может ли оно быть больше –5? Да!
Расстояние |y| по определению всегда неотрицательно (т.е. |y| ≥ 0). Следовательно, всегда на больше –5 (или –23, –140 или любого отрицательного числа).
Следовательно, решение этого неравенства равно
y ϵ R
То есть y может быть любым вещественным числом. Попробуйте подставить некоторые значения y для проверки.
Пример 6 Решите уравнение |z| < –4.
Решение Опять же, не будем спешить писать что-то вроде
|z| < –4 => –(–4) < z < –4 😖
, как мы узнали из первых двух примеров.
По определению |z| ≥ 0. Это означает, что |z| никогда не может быть меньше -4. К сожалению, это неравенство не имеет решения.
Рассмотрим также аналитический метод. Возьмем два случая: z ≥ 0 и z < 0.
Случай 1 : z ≥ 0
Здесь неравенство принимает вид z < –4, что и является решением. Но мы отклоним это решение, так как оно нарушает условие случая 1. (Все равно попробуйте подставить любое значение z, меньшее –4, чтобы проверить).
Случай 2: z < 0
Здесь неравенство принимает вид –z < –4, что дает z > 4. Мы снова отклоним это решение, так как оно нарушает условие случая 2. (Вы можете снова подставьте любое значение z больше 4 для проверки.)
В обоих случаях мы отклонили решения. Следовательно, неравенство |z| < –4 не имеет решения.
На этом мы подошли к концу урока. Пожалуйста, просмотрите все примеры еще раз и убедитесь, что вы понимаете как методы, так и особенно крайние случаи.
Следующие таблицы обобщают то, что мы узнали на этом уроке.
1. а > 0
| Неравенство | Раствор |
| |х| > а | х < –а или х > а |
| |х| < а | –а < х < а |
| |х| ≥ | х ≤ –а или х ≥ а |
| |х| < а | –а ≤ х ≤ |
2.