Смежные и вертикальные углы — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Смежные и вертикальные углы
2. Повторение:
1. Что такое луч? Как он обозначается?2. Какая фигура называется углом?
3. Какой угол называется развёрнутым?
4. Какой угол называется острым?
Прямым? Тупым?
3. СМЕЖНЫЕ УГЛЫ
Практическое задание:1. Построить острый
угол АОВ;
2.
 Провести луч ОС,
Провести луч ОС,являющийся
продолжением луча ОА.
А
О
В
АОВ и
ВОС – смежные углы
С
4. Определение:
Два угла, у которых одна сторона общая и дведругие являются продолжением одна другой
называются смежными углами.
В
А
О
С
5. Свойство смежных углов
1. Какой угол АОС?2. Чему равна градусная
мера угла?
3. На какие углы делит
луч ОВ этот угол?
4. Чему равна сумма
В
этих углов?
А
О
• 1. АОС развёрнутый
• 2.180˚
• 3. АОВ и ВОС
• 4.180˚
С
6. ВЫВОД:
АОВ +ВОС =180˚
Сумма смежных углов равна 180˚
7. Упражнения для закрепления
1.Начертите три угла: острый, прямой, тупой.Для каждого из этих углов начертите
смежный угол.
Решение:
8. 2. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
9. 3. Верно ли утверждение: если смежные углы равны, то они прямые?
10. ВЕРТИКАЛЬНЫЕ УГЛЫ
Практическое задание:1.
 построим острый угол;
построим острый угол;2. выделим его дугой и
обозначим цифрой 1;
3. построим продолжение
сторон угла 1;
4. отметим дугой угол, стороны
которого являются
продолжением сторон угла 1 и
обозначим его цифрой 2
1
2
11. Определение
Два угла называются вертикальными, еслистороны одного угла являются продолжением
сторон другого.
3
1
2
4
1и
2 – вертикальные углы
12. Свойство вертикальных углов
Дано:1=35˚
3, 4
Найти:
Решение:
1, 3-смежные
3=180˚-35˚=145˚
1, 4-смежные
4=180˚-35˚=145˚
3= 4=145˚, но
3 и 4-вертикальные
3
2
1
4
Вывод:
Вертикальные углы
равны.
13. Упражнения для закрепления
1. При пересечении двухпрямых а и в сумма
каких-то углов равна 60˚.
Какие это углы?
Ответ: вертикальные
углы, т.к. сумма смежных
углов равна 180˚.
2. При пересечении двух
прямых а и в разность
каких-то углов равна 30˚.

Какие это углы?
Ответ: смежные, т.к.
разность вертикальных
углов равна 0˚
14. Итог урока:
• Определение смежных и вертикальных углов и ихсвойств:
1) Если углы смежные, то их сумма равна 180˚.
2) Если углы вертикальные, то они равны.
English Русский Правила
Смежные и вертикальные углы. Их свойства
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.

Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение.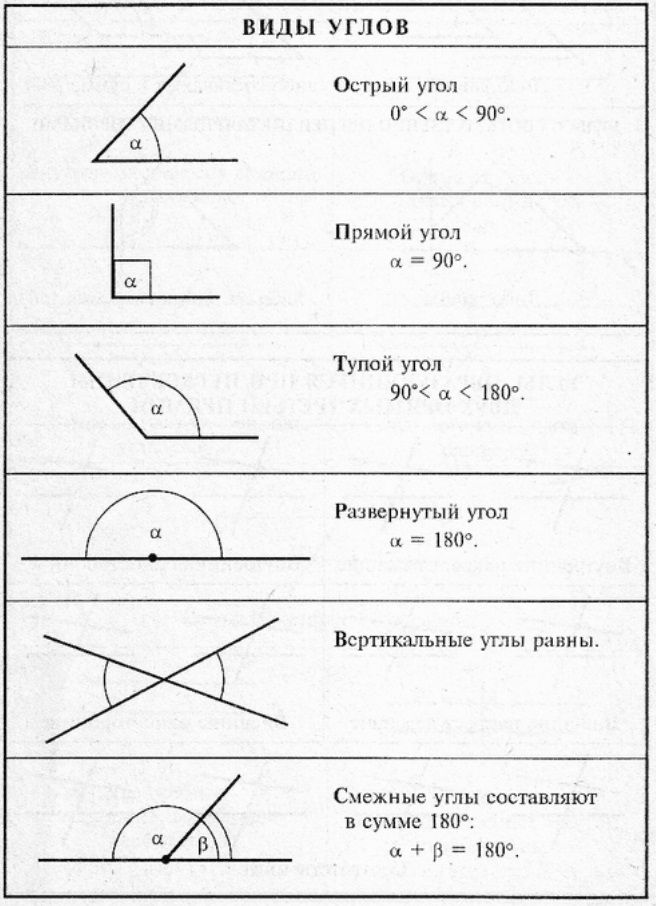 Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Другие материалы
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).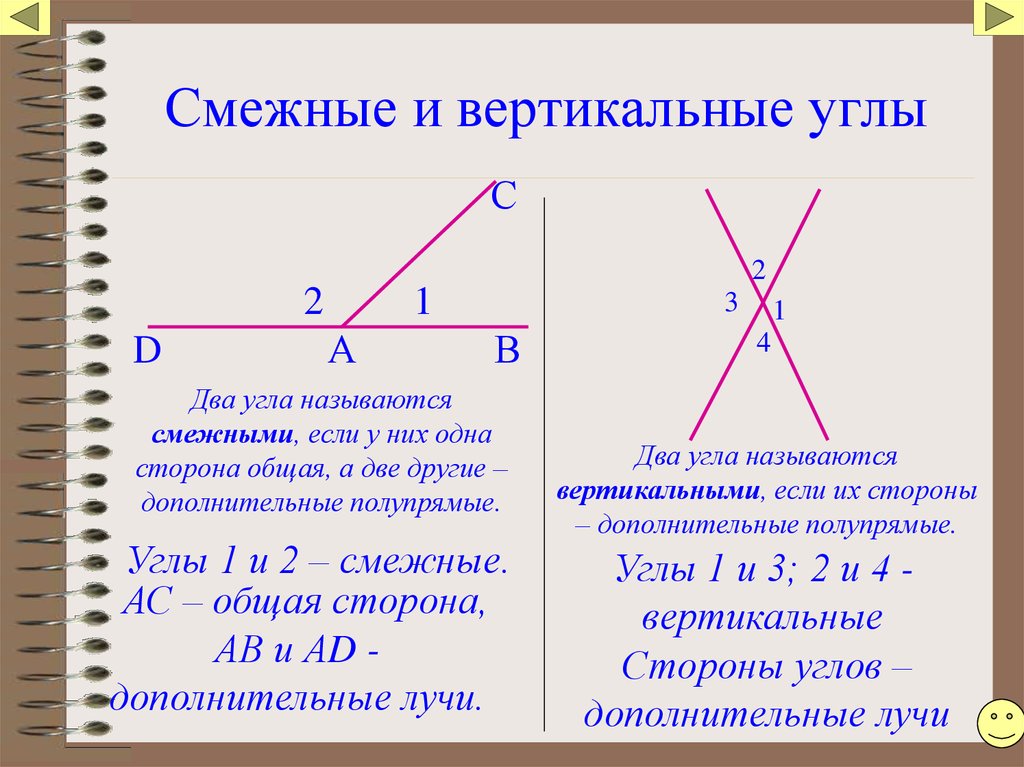
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
по теме: Смежные и вертикальные углы, их свойства.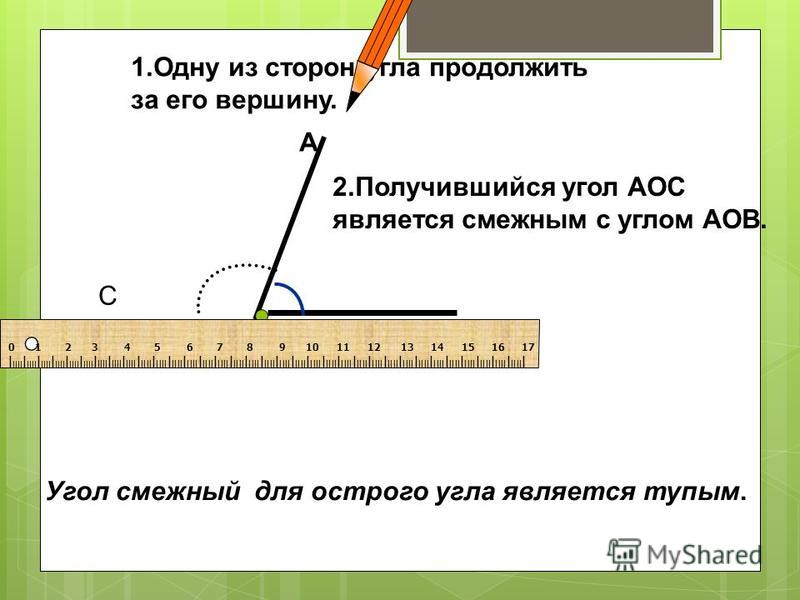
(3 занятия)
В результате изучения темы нужно:
УМЕТЬ:
Понятия: смежных и вертикальных углов, перпендикулярных прямых
Различать понятия смежные и вертикальные углы
Теоремы смежных и вертикальных углов
Решать задачи с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Строить смежные и вертикальные углы, перпендикулярные прямые
ЛИТЕРАТУРА:
1. Геометрия. 7 класс. Ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7 класс. К.О.Букубаева, А.Т. Миразова. Алматы « Атамұра ». 2012
3. Геометрия. 7 класс. Методическое руководство. К.О.Букубаева. Алматы « Атамұра ». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. Алматы « Атамұра ». 2012
5. Геометрия. 7 класс. Сборник задач и упражнений. К.О.Букубаева, А.Т.Миразова. Алматы « Атамұра ». 2012
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях,
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому,
кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
ЗАДАНИЕ №1.
Прочитай определение и выучи (2б):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучи и запиши в тетрадь теорему: (2б)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ ДОВ –данные смежные углы
ОД — общая сторона
Доказать:
∠ АОД + ∠ ДОВ = 180
Доказательство:
На основе аксиомы III 4:
∠ АОД + ∠ ДОВ = ∠ АОВ.
∠ АОВ — развернутый. Следовательно,
∠ АОД + ∠ ДОВ = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то смежные с ними углы равны;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Запомни!
Угол, равный 90°, называется прямым углом.
Угол, меньше 90°, называется острым углом.
Угол, больше 90° и меньше 180°, называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, смежный с прямым углом, прямой;
2) угол, смежный с острым углом, тупой;
3) угол, смежный с тупым углом, острый.
4) Рассмотри образец решения з адачи:
а) Дано: ∠ h k и ∠ kl — смежные; ∠ h k больше ∠ kl на 50° .
Найти: ∠ h k и ∠ kl .
Решение: Пусть ∠ kl = х, тогда ∠ h k = х + 50°. По свойству о сумме смежных углов ∠ kl + ∠ h k = 180°.
х + х + 50° = 180°;
2х = 180° — 50°;
2х = 130°;
х = 65°.
∠ kl = 65°; ∠ h k = 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть ∠ kl = х, тогда ∠ h k = 3х
х + 3х = 180°; 4х = 180°; х = 45°; ∠ kl = 45°; ∠ hk = 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найди ошибки в определениях: (2б)
Пройди проверку №1
Задание №2
1)Построй 2 смежных угла так, чтобы их общая сторона проходила через точку C и сторона одного из углов совпадала с лучом AB. (2б)
(2б)
2). Практическая работа на открытие свойства смежных углов: (5б)
Ход работы
1. Построй угол смежный углу а , если а : острый, прямой, тупой.
2. Измерь величины углов.
3.Данные измерений занеси в таблицу.
4. Найди соотношение между величинами углов а и .
5. Сделай вывод о свойстве смежных углов.
Пройди проверку №2
Задание №3
Начертите неразвернутый ∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Проведите луч О, являющийся продолжение луча ОА, и луч ОД, являющийся продолжение луча ОВ.
Запишите в тетради: углы ∠ АОВ и ∠ СОД называются вертикальными. (3б)
Выучи и запиши в тетрадь: (4б)
Определение: Углы, у которых стороны одного из них являются дополнительными лучами другого, называются вертикальными углами.
1 и
Лучи
OF
и
OA
,
OC
и
OE
являются попарно дополнительными лучами.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые а и b пересекаются в точке О. ∠ 1 и ∠ 2 –вертикальные углы.
∠ АОС-развернутый, значит ∠ АОС= 180°. Однако ∠ 1+ ∠ 2= ∠ АОС, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
Также имеем, что ∠ ДОВ= 180°, отсюда ∠ 2+ ∠ 3= 180°, или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то ∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов:(2б)
6) Найди ошибку в определении:(2б).
Пройди проверку №3
Задание №4
1)Практическая работа на открытие свойства вертикальных углов:(5б)
Ход работы:
1.Построй угол β вертикальный углу α , если α :
острый, прямой, тупой.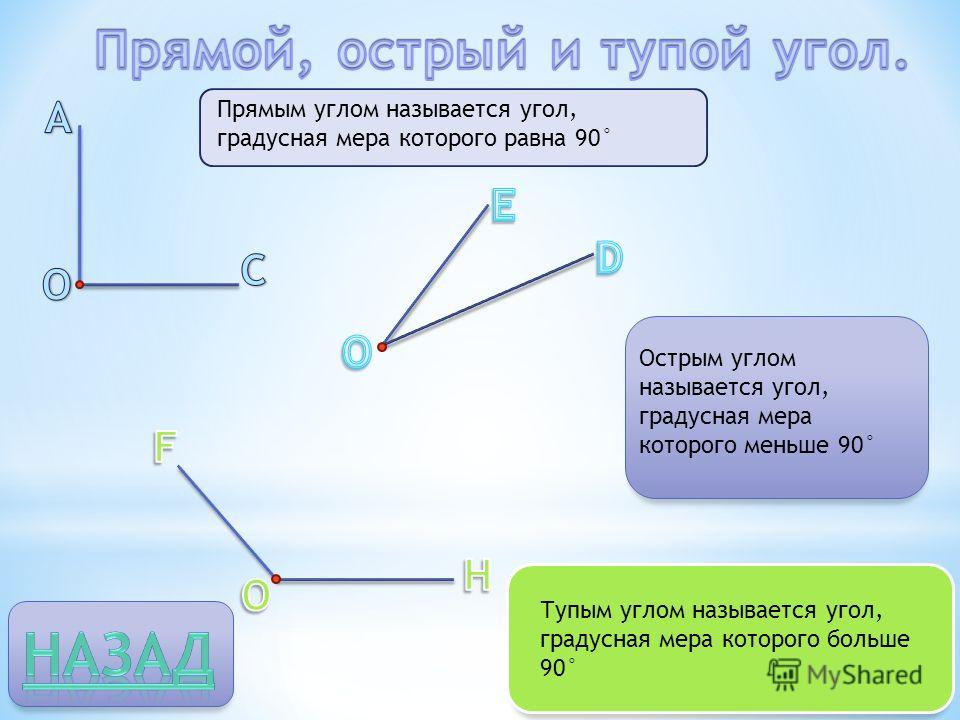
2.Измерь величины углов.
3.Данные измерений занеси в таблицу
4.Найди соотношение между величинами углов α и β.
5.Сделай вывод о свойстве вертикальных углов.
2)Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотри образец решения з адачи.
Задача. Прямые АВ и СД пересекаются в точке О так, что ∠ AOД = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы АОД и АОС смежные, поэтому ∠ BOC = 180° — 35° = 145°.
2) Углы АОС и ВОС также смежные, поэтому ∠ BOC = 180° — 145° = 35°.
Значит, ∠ BOC = ∠ АОД = 35°, причем эти углы являются вертикальными. Вопрос: верно ли утверждение, что любые вертикальные углы равны?
3) Решение задач на готовых чертежах: (3б)
1. Найти углы АОВ, АОD, COD.
3) Найти углы BOC, FOA.: (3б)
3. Найди на рисунке смежные и вертикальные углы. Пусть известны величины двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти величины остальных углов, не выполняя измерений (2б)
Пройди проверку №4
Задание №5
Проверь свои знания, выполнив проверочную работу №1
Задание №6
1) Самостоятельно докажи свойства вертикальных углов и запиши эти доказательства в тетрадь. (3б)
(3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то остальные углы также прямые.
2) Реши на выбор две задачи:
1.Градусные меры смежных углов относятся как 7:2. Найдите эти углы.(2б)
2.Один из углов, образовавшихся при пересечении двух прямых, в 11 раз меньше другого.Найдите каждый из углов.(3б)
3.Найдите смежные углы,если их разность и их сумма относятся как 2:9.(3б)
Задание №7
Молодец! Можешь приступать к проверочной работе №2.
Проверочная работа №1.
Реши на выбор любой из вариантов (10б)
Вариант 1
г)
Смежные
д) Начертите (на глаз) угол в 30° и
е) Какие углы называются вертикальными?
Два угла называются вертикальными, если орни равны.
ж) Из точки А провести две прямые, перпендикулярные прямой а
Можно провести только одну прямую.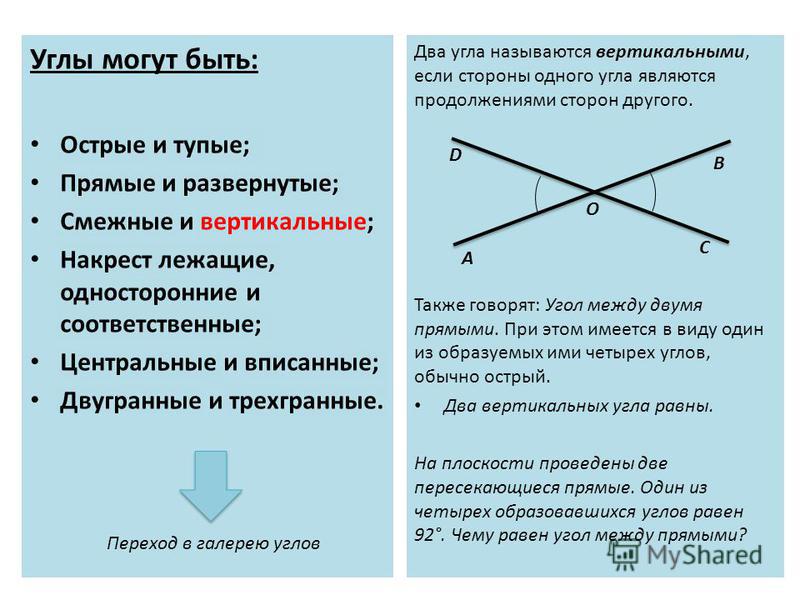
Вариант 2
1.Ученик, отвечая на вопросы учителя, дал соответствующие ответы. Проверьте, верны ли они, пометив в третьем столбике словом «ДА», «НЕТ», «НЕ ЗНАЮ». В случает «НЕТ» запишите там же верный ответ или добавьте недостающее.
Д)
Нет. Они вертикальные
Е) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными прямыми.
2. Назовите вертикальные углы на данном рисунке.
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Проверочная работа №2.
Реши на выбор любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4б)
Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 240°, меньше суммы двух других. (6б)
(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма относятся как 5:8(4б)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если один из них на 60°, больше суммы двух других.(6б)
Итого:10 баллов
«5»-10баллов;
«4»-8-9 баллов;
«3»-5-7 баллов.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис.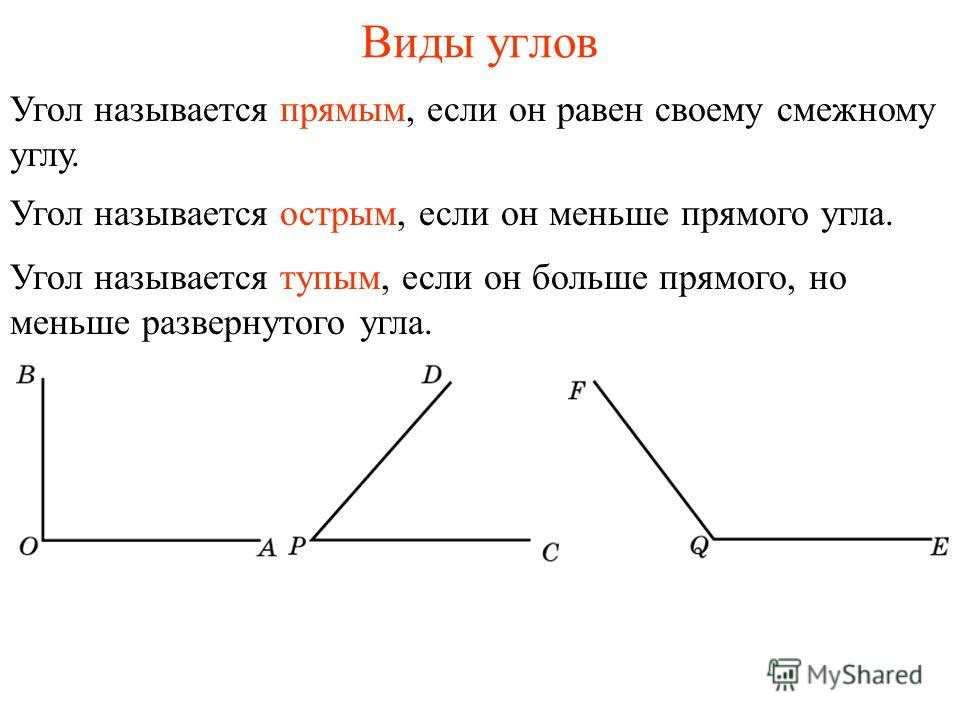 2).
2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4).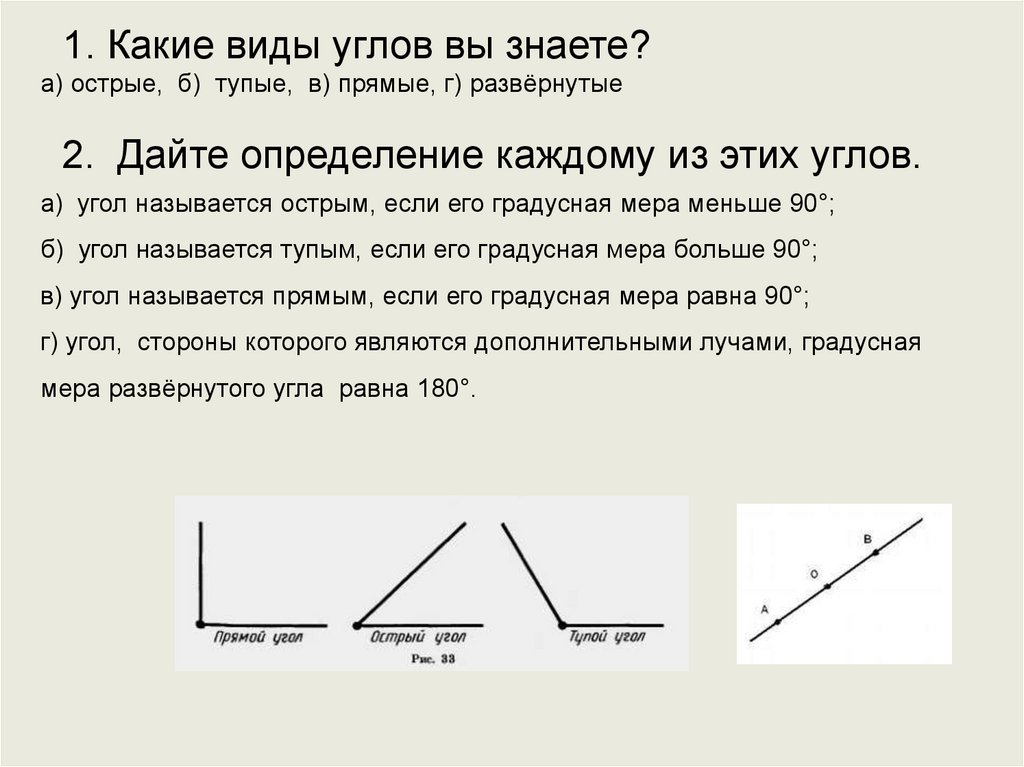 Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».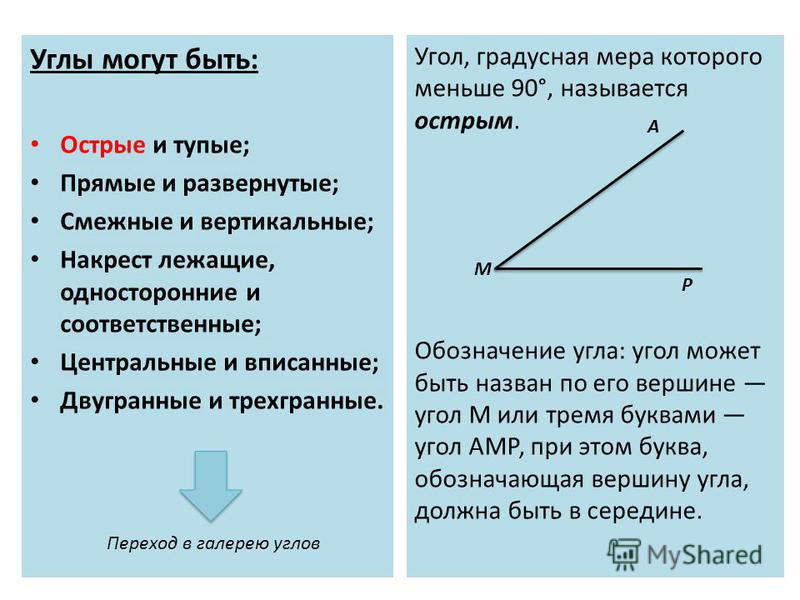
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°.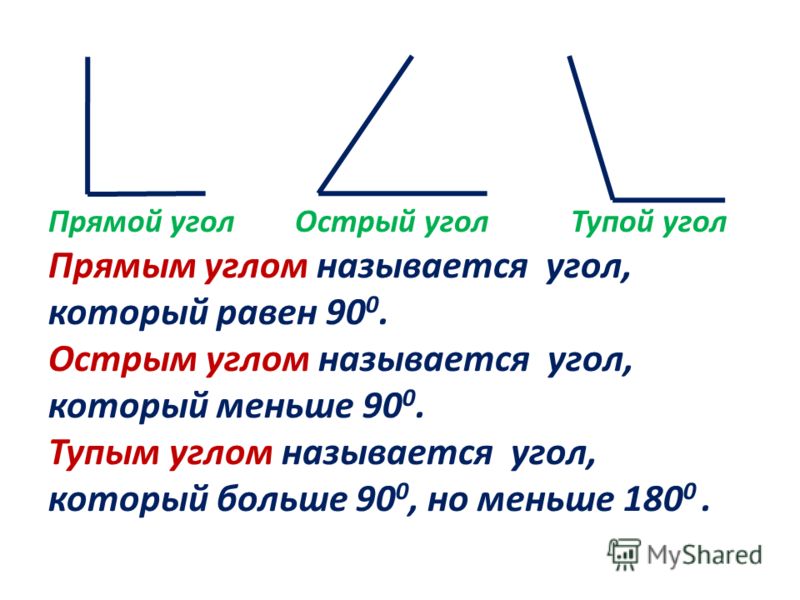 Найти величину каждого из четырех углов.
Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Типы углов
Существует множество различных типов углов, которые можно классифицировать на основе следующих характеристик.
- Magnithy из угла
- Вращение Угол
- А Пара Углов
- У углов , когда Transversal Создает две параллельные линии
. угол, а затем мы покажем все различные типы углов.
Что такое углы?
Обратите внимание, что угол образуется, когда два луча, также называемые плечами угла, встречаются в общей конечной точке, называемой вершиной угла.
На рисунке выше вершина показана красной точкой, а плечи показаны синим цветом.
Классификация углов по величине
Определим основные углы. Вот список из 7 типов углов в зависимости от величины угла.
- Острый угол
- Прямой угол
- Тупой угол
- Прямой угол
- Угол отражения
- Полный угол поворота
- Нулевой угол
Внимательно изучите изображения, чтобы понять их, а затем быстро распознать основные углы.
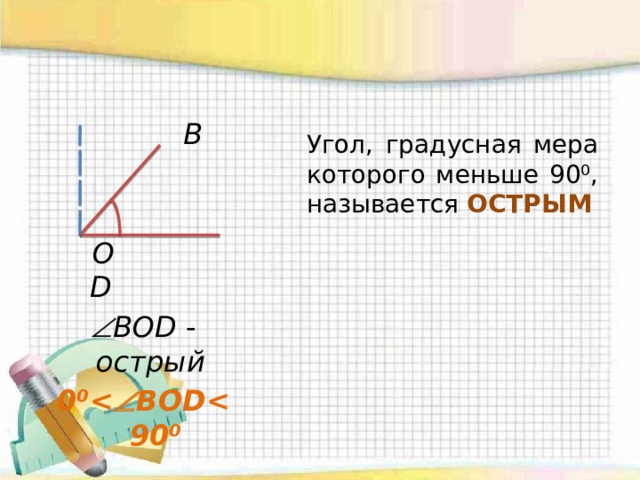
Острый угол:
Угол, градусная мера которого меньше 90 градусов, является острым углом. Например, если величина угла 89 градусов, то угол острый. Нижний угол — острый угол.
Прямой угол:
Угол, градусная мера которого ровно 90 градусов. Далее идет прямой угол.
Тупой угол:
Угол, градусная мера которого больше 90 градусов, но меньше 180 градусов, является тупым углом. Таким образом, он находится между 90 и 180 градусами. Например, если градусная мера угла равна 150 градусам, то угол тупой. Дальше идет тупой угол.
Дальше идет тупой угол.
Угол прямой:
Угол, мера которого ровно 180 градусов. Таким образом, прямой угол выглядит как прямая линия. Далее идет прямой угол.
Угол рефлекса:
Угол, величина которого больше 180 градусов, но меньше 360 градусов. Например, если мера угла составляет 235 градусов, угол является рефлекторным углом. Ниже приведен угол рефлекса.
Полный угол поворота:
Угол, градусная мера которого составляет ровно 360 градусов, является полным углом поворота. Полный угол поворота состоит из 4 прямых углов. Ниже приведен полный угол поворота.
Нулевой угол:
Угол, мера которого ровно 0 градусов, является нулевым углом. При нулевом угле оба плеча лежат на одной линии. Ниже приведен угол нулевой степени.
Классификация углов на основе поворота угла
Два типа углов образуются, когда угол измеряется либо против часовой стрелки, либо по часовой стрелке.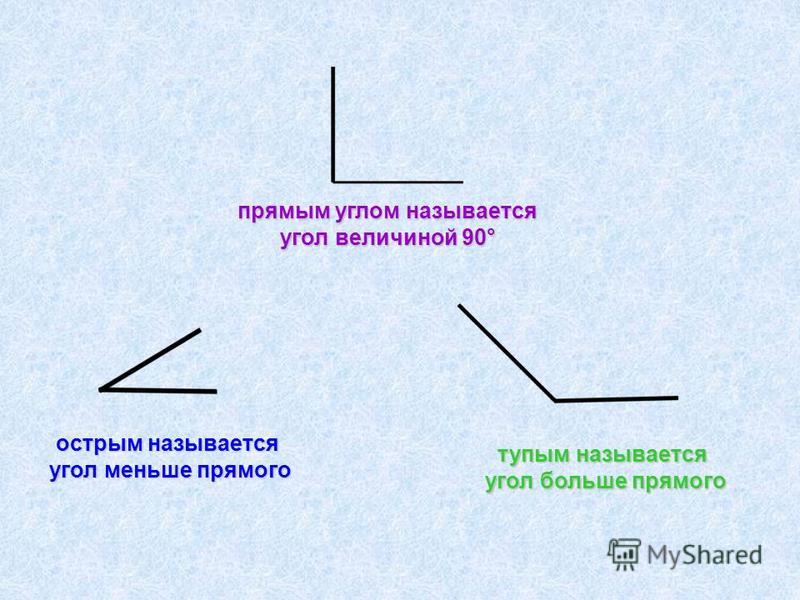
Если мы измеряем угол против часовой стрелки или в направлении, противоположном движению стрелок часов, угол является положительным углом. Угол ниже положительный угол.
Если мы измерим угол по часовой стрелке или в том же направлении, что и стрелки часов, угол будет отрицательным. Угол ниже — отрицательный угол.
Типы углов на основе пары углов
Вот список из 4 типов углов на основе пары углов.
- Смежные углы
- Дополнительные углы
- Дополнительные углы
- Вертикальные углы
Смежные углы:
Прием и регистрация
Приемная комиссия и регистратор могут помочь вам с различными вопросами, связанными с зачислением, такими как подача заявления, запрос выписки или регистрация на занятия .
Свяжитесь с приемной комиссией и регистратором
Узнайте больше об очистке от менингита
Запросите или отправьте стенограммы
Консультирование Наши консультанты и тренеры ACE It здесь, чтобы убедиться, что вы на правильном пути и выполнили все требования, чтобы вы были приняты, зачислены и на пути к успешному будущему.
Связь с консультированием и тестированием
Информация для студентов с двойным кредитом
Связаться с ACE It Coach
Оплата обучения в колледжеФинансовая помощь может помочь вам подать заявку на получение помощи, разобраться в типах помощи и получить предложенные средства. Вы можете совершать платежи и настраивать планы платежей в кассе.
Связь с отделом финансовой помощи
Связь с кассой (бизнес-офис)
Обязательное тестированиеВсе новые студенты, стремящиеся к получению степени, должны сдать экзамен Texas Success Initiative (TSI). Чтобы поддержать наших студентов в этот кризис, мы теперь предоставляем услуги тестирования как онлайн, так и на территории кампуса.
Узнайте больше и зарегистрируйтесь на экзамен TSI
Пройдите предварительную оценку TSI перед сдачей экзамена TSI
Начало занятий
Помощь с технологиями У нас есть точки доступа, руководства, точки доступа и руководства 900 помочь настроить электронную почту на телефоне.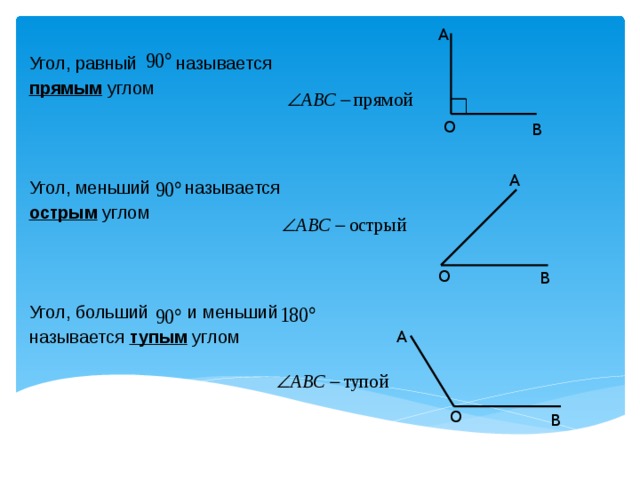 Отдел дистанционного обучения может помочь ответить на вопросы, касающиеся виртуального кампуса (D2L).
Отдел дистанционного обучения может помочь ответить на вопросы, касающиеся виртуального кампуса (D2L).Узнайте, как сбросить пароль
Подключение к виртуальному кампусу (D2L) Поддержка
Совершите экскурсию по виртуальному кампусу
Запросите личную точку доступа или ноутбук
Настройте электронную почту BC на своем iPhone или Android
Получение оценки
Возникли проблемы с академической поддержкойСвязь с центром письма
Связь с математическим центром
Свяжитесь с библиотекарем
Свяжитесь с руководителем SI, чтобы получить помощь в изучении курса естествознания
Посмотрите видео о Центре успеха студентов
Доступ к услугам на территории кампуса Необходимо составить тест или купить книгу ? Такие службы, как книжный магазин и службы обучения, по-прежнему открыты, чтобы помочь вам в течение семестра.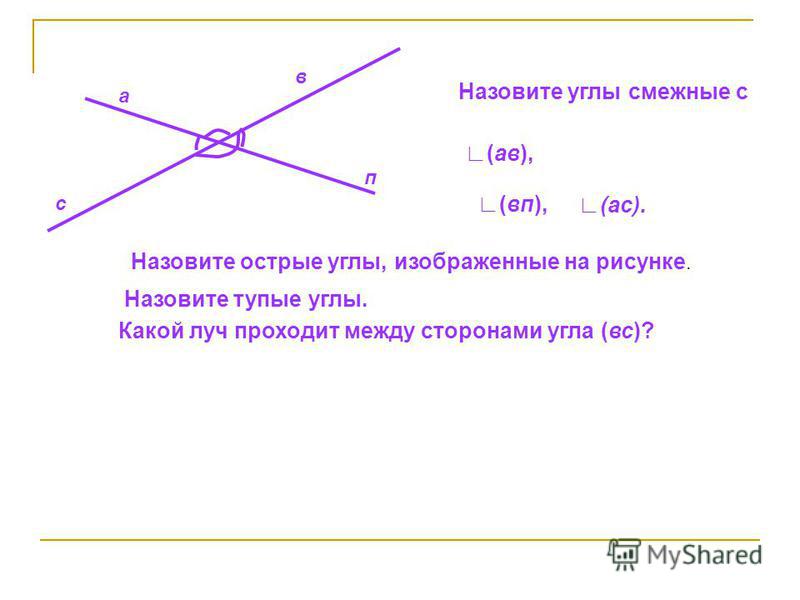 Обратитесь в службу ИТ-поддержки, чтобы получить помощь с учетной записью учащегося и потребностями, связанными с технологиями.
Обратитесь в службу ИТ-поддержки, чтобы получить помощь с учетной записью учащегося и потребностями, связанными с технологиями.
Связь со службой технической поддержки
Посетите веб-сайт книжного магазина Британской Колумбии
Составьте тест или обратитесь за помощью в Службу обучения
Рука помощи
Продовольственная и экстренная помощь
У нас есть экстренная помощь, чтобы помочь учащимся дело неопределенности и стресса.
Свяжитесь с отделом здоровья и основных потребностей
Запросите информацию о GatorMart (Foodbank Британской Колумбии)
Посмотрите видео о GatorMart (Foodbank Британской Колумбии)
Подать заявку на экстренную помощь
Планирование образования и карьеры
Наша приверженность успеху учащихся лежит в основе всего, что мы делаем. Какими бы ни были ваши карьерные цели, мы здесь, чтобы помочь вам их достичь.
Связаться с тренером ACEit
Запрос на беседу с консультантом
Проверить Центр карьеры
Посмотреть видео о Центре карьеры
Сделать перерыв в виртуальном мероприятии
30211
Мы здесь, чтобы продолжать помогать вам за пределами классной комнаты, обеспечивая качественное участие студентов и оздоровительные мероприятия, которые дополняют академические программы и улучшают образовательный опыт.

 Поскольку 30 градусов + 60 градусов = 90 градусов, угол x является дополнением угла y (другим способом сказать, что они дополняют друг друга).
Поскольку 30 градусов + 60 градусов = 90 градусов, угол x является дополнением угла y (другим способом сказать, что они дополняют друг друга).
