1.2.5. Независимые события
Рассмотрим определение независимости событий, которое отражает понятие реальной независимости несвязанных событий.
Определение. События называются Независимыми, Если появление одного из них не влияет на вероятность появления другого.
Пример 1.12. Предположим, что подбрасывают два игральных кубика независимо друг от друга. Пространство элементарных событий состоит из упорядоченных пар чисел (N = 36):
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
Рассмотрим два события.
Событие A = { число очков на первом кубике > 4 } состоит из всех пар пятой и шестой строк ( M = 12) и имеет вероятность P(A) = .
Событие B = { число очков на втором кубике < 4 } состоит из всех пар первых трех столбцов (
Очевидно, что эти события причинно не связаны друг с другом и Независимы в этом смысле.Найдем Вероятность произведениЯ этих событий.
Событие AB состоит из шести пар выпадающих цифр (M = 6 )
{ (5,1) (5,2) (5,3) (6,1) (6,2) (6,3) }
И имеет вероятность P (AB)= . Очевидно, что выполняется равенство P(AB) = P(A) P(B). Оно отражает независимость событий A и B.
Определение. События A и B называются Независимыми, если выполняется равенство P(AB) = P(A)
P(B) , (1.4)Т. е. Вероятность произведения двух Независимых Событий равна Произведению Вероятностей этих событий.
В противном случае события считают зависимыми.
Пример 1.13. (продолжение примера 1.12).
Рассмотрим событие C = {сумма очков равна 8}. Оно состоит из 5 пар
{(2,6) (3,5) (4,4) (5,3) (6,2)}
И имеет вероятность P(C)=.
Событие, которое получается как Произведение События A На событие C, состоит из пар {(5,3) (6,2)} и имеет вероятность
P(AC)=.
Так как P(AC) ¹ P(A) P(C) = = , то события A и C следует считать Зависимыми.
Свойство 6
P(A +В) = p(A) + Р(В) — P(A) p(В).
(***)
Примечания:
А) Формулы (*), (**), (***) позволяют вычислить вероятность суммы двух любых событий.
Б) Если требуется вычислить вероятность Суммы трех и более событий, то вычисление надо производить, введя замену переменных таким образом, чтобы поэтапно свести расчет к вычислению вероятности суммы двух событий.
Например, найти P(A +В +С + D ) = P ( R + K) =P(R )+ P(K ) – P(RK),
Где R=A +B, K = C + D. Тогда по формуле 1.3 находим
Р(R) =p( A +B ) = p(A) +P(B) – P(AB), P(K) = P(C + D) = P(C) + P(D) – P(CD), Значения которых надо подставить в исходную формулу.
| < Предыдущая | Следующая > |
|---|
14. Приведите примеры зависимых и независимых событий
Зависимые события — два события называются
Независимые события — два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет.
15. Что такое составное событие? Приведите примеры составных событий и их разложение на элементарные. (Сложение и умножение вероятностей)
Теоремы сложения и умножения вероятностей
Теорема. Вероятность появления одного их двух несовместных событий, неважно какого, равна сумме вероятностей этих событий, т.е.
.
Следствие. Сумма вероятностей
противоположных событий равна 1, т.
е
.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления, т.е.Пример1.
Если 25% покупателей предпочитают батончики «Биг-Байт», а 50% — «Труфл», тогда вероятность того, что покупатель предпочтет «Биг-Байт» или «Труфл», рассчитывается следующим образом.
Имеем: P («Биг-Байт») = 25% = 0.25.
Аналогично: P («Труфл») = 50% = 0.50.
Следовательно, так как эти события взаимно исключают друг друга, то: P («Биг-Байт» или «Труфл») — P («Биг-Байт») + P («Труфл») = 0.25 + 0.5 = 0.75 (или 75%).
Пример2.
При выборочной проверке качества 200 «домашних» кондитерских изделий компании «Даунбрукс» получены следующие результаты:
Качество: Высшее Приемлемое Брак
Количество изделий: 140 40 20
То
есть, согласно этой выборке: P
(Высшее) == 140/200 = 0.
Аналогично, Р (Приемлемое) = 40/200 = 0.2 и P (Брак) = 20/200 «=0.1.
Все три категории качества взаимно исключают друг друга. Таким образом, чтобы, например, рассчитать вероятность получения изделий высшего и приемлемого качества, необходимо:
P (Высшее или Приемлемое) = P (Высшее) + P (Приемлемое) = 0.7 + 0.2 = 0.9 (или 90%).
Пример3.
Предыдущий пример можно применить к иллюстрации дополняющих друг друга событий. Например, рассмотрим вероятность «получения брака» или «неполучения брака». Эти два события дополняют друг друга, так как одно или другое событие должно наступить. Кроме того, они взаимно исключают друг друга, так как не могут наступить одновременно: ведь невозможно одновременно получить изделие, которое и было бы бракованным и не было им! Таким образом, совокупная вероятность того, что получится брак и не получится брак, должна равняться 1 (100%). Это можно записать в следующем виде:
P
(Брак или Не брак) = P
(Брак) +P
(Не брак) =1.
Следовательно, путем трансформации получаем:
P (Не брак) = 1 — P (Брак).
Возьмем значения из предыдущего примера: Р (Брак) = 0.1. Следовательно, P (Не брак) = 1 — 0.1 = 0.9 (или 90%). Данный пример иллюстрирует другое правило, которое в общем виде можно записать следующим образом:
P (не X) = 1 — Р (X).
То есть, если, например, вероятность получения изделий высшего качества равна 0.7, тогда вероятность получения изделий не высшего качества равна 1 — 0.7 = 0.3 (или 30%).
Независимые мероприятия — GCSE по математике
Введение
Что такое независимые события?
Как рассчитать вероятность независимых событий
Рабочий лист независимого события
Распространенные заблуждения
Практика вопросов о независимых мероприятиях
Независимые мероприятия Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое независимые события?
Как рассчитать вероятность независимых событий
Рабочий лист независимого события
Распространенные заблуждения
Практикуйте независимые вопросы событий
Независимые мероприятия Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о независимых событиях, в том числе о том, что такое независимые события и как рассчитать вероятность возникновения независимых событий.
Существуют также листы расчета вероятности на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое независимые события?
Независимые события — это события, на которые не влияет возникновение других событий. Например, если мы бросаем кубик дважды, результаты первого и второго бросков не влияют друг на друга — они независимы.
Если два события независимы, то
\textbf{P(A} и \textbf{B) = P(A) × P(B)} .
Это называется правилом умножения.
Давайте рассмотрим пример.
Если мы бросаем кости дважды, мы можем найти вероятность того, что выпадут две шестерки.
Вероятность выпадения 6 равна \frac{1}{6} .
Таким образом, вероятность выпадения 6 и 6 равна
\frac{1}{6} \times\frac{1}{6} = \frac{1}{36}.
Пошаговое руководство: Вероятность объединенных событий
Что такое независимые события?
Как рассчитать вероятность независимых событий
Для расчета вероятности независимых событий:
- Подтвердить, что события независимы.
- Определите вероятности событий.
- Умножьте вероятности.
Объясните, как рассчитать вероятность независимых событий
Таблица вероятности (включает независимые события)
Получите бесплатную таблицу независимых событий, содержащую более 20 вопросов и ответов по вероятности. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксТаблица вероятности (включает независимые события)
Получите бесплатную таблицу независимых событий, содержащую более 20 вопросов и ответов по вероятности. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры независимых событий
Пример 1: определение независимых событий
Посмотрите на события ниже. Какая совокупность событий не является независимой?
- Бросив кубик, выпало 6, подбросили монету и выпал орёл.
- Подбрасывание двух монет и выпадение двух орлов.
- Выбор синего шара из мешка с синими и желтыми шарами, а затем выбор другого синего шара из того же мешка.
- Ученица 5 класса с каштановыми волосами и ростом 3 фута.
Независимость определяется тем, что события не влияют друг на друга.
Когда вы бросаете кубик и подбрасываете монету, результат одного не влияет на результат другого, поэтому события независимы .
Когда вы подбрасываете две монеты, результат одной не влияет на другую, поэтому события независимы .
Когда вы выбираете мяч из мешка, вы меняете количество мячей в мешке, поэтому результат выбора первого мяча повлияет на результат выбора второго мяча (например, если вы выберете синий шар в первый раз, вероятность выбора синего шара во второй раз уменьшится). Следовательно, это зависимых событий.
Цвет чьих-то волос не влияет на размер ноги, поэтому события независимы .
Пример 2: вероятность двух независимых событий
Вероятность того, что Том забудет свой физический набор, равна 0,3. Вероятность того, что Ной забудет свой физический набор, равна 0,1. События независимы.
Рассчитайте вероятность того, что и Том, и Ной забудут свои наборы физкультуры в один и тот же день.
Подтвердите, что события независимы.
В вопросе нам говорят, что события независимы.
Определите вероятности событий.
Первым событием является то, что Том забывает свой набор физкультуры. Вероятность того, что Том забудет свой физический набор, равна 0,3.
Во-вторых, Ной забывает свой физкультурный набор. Вероятность того, что Ной забудет свой физический набор, равна 0,1.
Умножьте вероятности.
Вероятность того, что Том и Ной забудут свои наборы физкультуры, равна 9.0003
0,3 х 0,1 = 0,03.
Пример 3: вероятность трех независимых событий
Рэйчел подбрасывает три одинаковые монеты.
Найдите вероятность того, что все три монеты выпадут решкой.
Подтвердите, что события независимы.
Результат каждой монеты не зависит от других монет, поэтому события независимы.
Определите вероятности событий.
Поскольку монеты честные, вероятность того, что у каждой монеты выпадет решка, равна \frac{1}{2}.
Умножьте вероятности.
Вероятность выпадения трех решек равна
\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8} .
Пример 4: использование древовидной диаграммы
Ниам играет в настольный теннис в субботу и в бадминтон в воскресенье. Различные результаты представлены на древовидной диаграмме ниже.
Вычислите вероятность того, что Ниам выиграет обе игры.
Подтвердите, что события независимы.
Исход одной игры не влияет на исход другой игры, поэтому события независимы.
Определите вероятности событий.
Вероятность того, что Ниам выиграет в настольный теннис, равна 0,4, а вероятность того, что Ниам выиграет в бадминтон, равна 0,7.
Умножьте вероятности.
Вероятность того, что Ниам выиграет в настольный теннис и бадминтон, равна
0,4 х 0,7=0,28.
Пример 5: определение вероятности отдельных событий
У Зайнаб есть две упаковки сладостей. Она выбирает по одной конфете из каждого мешка. Вероятность того, что Зайнаб выберет леденец из первого мешка, равна \frac{1}{6}, а вероятность того, что она выберет леденец из обоих мешков, равна \frac{1}{15} .
Какова вероятность того, что она выберет леденец из второго мешка?
Подтвердите, что события независимы.
Тип сладости, взятой из одного мешка, не влияет на сладость, взятую из другого мешка, поэтому события независимы.
Определите вероятности событий.
Вероятность того, что Зайнаб выберет леденец из первого мешка, равна \frac{1}{6}, а вероятность того, что она выберет леденец из обоих мешков, равна \frac{1}{15}.
Умножьте вероятности.
Если мы обозначим вероятность выбора леденца из второго мешка \text{P(L)}, то
\frac{1}{6} \times \text{P(L)}=\frac{ 1}{15}.
Решение этой
\begin{выровнено}
\text{P(L)}&=\frac{1}{15} \div\frac{1}{6}\\\\
&=\frac{1}{15} \times \frac{6}{1}\\\\
&=\frac{6}{15} \text{ или } \frac{2}{5}
\end{выровнено}
Пример 6: нахождение вероятности отдельных событий
Рози дважды подбрасывает монету с пристрастием. Вероятность того, что Рози выпадет два орла, равна 0,64.
Найдите вероятность того, что Рози выпадет орлом при одном подбрасывании монеты.
Подтвердите, что события независимы.
Результаты первого броска монеты не повлияют на второй бросок монеты, поэтому события независимы.
Определите вероятности событий.
Здесь мы знаем только, что вероятность того, что Рози выпадет две решки, равна 0,64.
Умножьте вероятности.
Если мы назовем вероятность того, что Рози выпадет решка \text{P(H)}, то
\text{P(H)} \times \text{P(H)} = 0,64.
Решение этой
Вероятность выпадения орла при одном подбрасывании монеты составляет 0,8.
Распространенные заблуждения
- Неправильное умножение или деление дробей
Чтобы умножить дробь, умножьте числители и умножьте знаменатели. Чтобы разделить дроби, переверните вторую и умножьте.
- Сложение вероятностей вместо их умножения
Для независимых событий P(A и B) = P(A) \×P(B).
Для взаимоисключающих событий P(A или B) = P(A) + P(B).
Практические вопросы по независимым событиям
Бросание двух костей и выпадение каждой из них на 6.
Дождь, идущий 20 декабря 2020 г. и 20 декабря 2021 г.
Подбрасывание монеты, выпадение решки и выбор короля из колоды карт.
Выбрать одну карту из колоды карт, а затем вторую карту и оба раза получить туз.
Если вы выберете одну карту из колоды карт, вы измените количество оставшихся карт и, следовательно, вероятность каждого результата для следующего розыгрыша.
Выбор одной карты, а затем второй карты из колоды карт не являются независимыми событиями.
\frac{3}{4}
\frac{1}{8}
\frac{1}{2}
\frac{1}{4}
четное число равно \frac{1}{2}.
Вероятность вытащить алмаз из колоды карт равна \frac{1}{4}.
Вероятность того, что события A и B произойдут одновременно, равна
\frac{1}{2} \times \frac{1}{4} = \frac{1}{8}.
Вероятность того, что поезд опоздает в любой из дней, равна 0,3.
Вероятность того, что поезд опоздает в 1-й, 2-й и 3-й день, равна
0,3 х 0,3 х 0,3 = 0,027.
Вероятность того, что Сэм выберет бутерброд с сыром, равна 0,7, а вероятность того, что Сэм выберет виноград, равна 0,8.
Вероятность того, что Сэм выберет бутерброд с сыром и виноград, равна
0,7 х 0,8=0,56.
Если мы назовем вероятность того, что Пит попадет в яблочко \text{P(P)}, то
\begin{выровнено} 0,1 \times \text{P(P)}&=0,02\\\\ \text{P(P)}&=0,02 \div 0,1\\\\ &=0,2 \end{выровнено}
\фрак{2}{25}
\фрак{2}{5} 9{2}&=\frac{4}{25}\\\\ \text{P(6)}&=\sqrt{\frac{4}{25}}\\\\ \text{P(6)}&=\frac{2}{5} \end{выровнено}
Независимые соревнования Вопросы GCSE
1. Элери бросает кубик и подбрасывает две монеты. Найдите вероятность того, что Элери выпадет 4 на кубике и решка выпадет на обеих монетах.
(2 балла)
Показать ответ
\frac{1}{6} \times \frac{1}{2} \times \frac{1}{2}
(1)
=\фракция{1}{24}
(1)
2. (a) Из мешка с красным и зеленым шариками достают шарик. Мрамор заменяют, а затем берут второй мрамор. На древовидной диаграмме ниже показаны возможные результаты.
Вставьте пропущенные числа на древовидной диаграмме.
(b) Найдите вероятность того, что будут подняты два зеленых шарика.
(3 балла)
Показать Ответ
(A)
RED 0,8 и зеленый 0,2
(1)
(B)
0,2 х 0,2
(1)
0,04
(1)
3.
Рози дважды бросает кубик со смещением. Вероятность того, что она выкинет четное число в обоих бросках, равна 0,16.
Найдите вероятность того, что она выкинет нечетное число на обоих бросках.
9{2}=0,36
(1)
Контрольный список обучения
Теперь вы научились:
- Идентифицировать независимые события
- Вычислять вероятность независимых событий 2 9005 Застрял?
- Вероятность
- Формула условной вероятности
- Экспериментальная вероятность
- Калькулятор вероятности события
- Вероятность того, что независимые события происходят последовательно, может быть найдена путем перемножения результатов.
- Если вероятность одного события не влияет на вероятность другого события, события независимы.
- Если вероятность одного события влияет на вероятность другого события, события являются зависимыми.
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Независимые события — определение, формула, решенные примеры, часто задаваемые вопросы
Эндрю внимательно наблюдает за жонглером в цирке. У него есть несколько цветных булав для жонглирования: 1 красная, 2 зеленые и остальные 3 синие.
Внезапно он совершает ошибку. Одна из булав для жонглирования падает и снова поднимается. Теперь из его руки выпадает и вторая дубинка для жонглирования. Какова вероятность того, что первая клюшка для жонглирования синяя, а вторая клюшка для жонглирования зеленая? Ответ может быть довольно запутанным. Клубы, которые может выбрать Эндрю, не зависят от каких-либо предыдущих инцидентов, и поэтому клубы могут быть любого цвета. Такие события называются независимыми событиями, и на них не влияют предыдущие события. Итак, давайте узнаем о таких событиях.
В этой статье мы узнаем о независимых событиях и о том, как найти вероятность как зависимых, так и независимых событий. Оба эти события являются частью вероятности и во многом связаны между собой. Мы также исследуем разницу между независимыми и зависимыми событиями и подход к ним. Вы можете ознакомиться с решенными примерами, чтобы узнать больше об уроке, и попробовать свои силы в решении нескольких интересных практических вопросов о независимых событиях в конце страницы.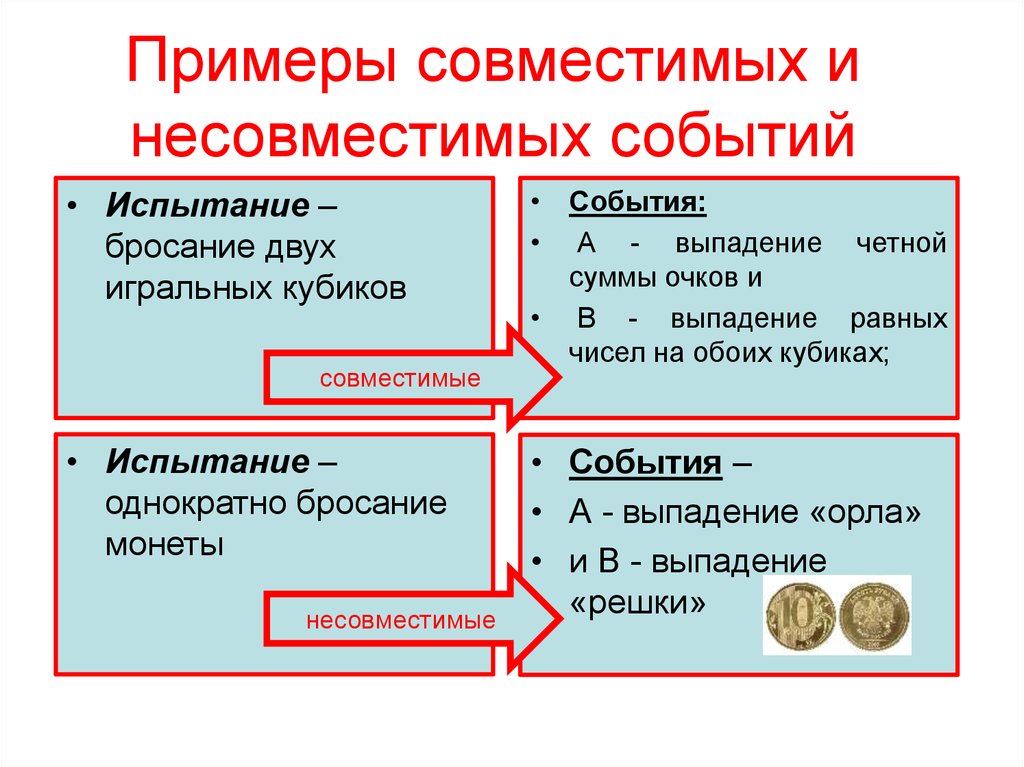
| 1. | Что такое независимые события? |
| 2. | Разница между независимыми событиями и зависимыми событиями |
| 3. | Определение вероятности независимых событий |
| 4. | Метод определения независимого события |
| 5. | Решенные примеры для независимых событий |
| 6. | Практические вопросы по независимым событиям |
| 7. | Часто задаваемые вопросы о независимых мероприятиях |
Что такое независимые события?
Два события называются независимыми, если исход одного события не влияет на исход другого. Или мы можем сказать, что если одно событие не влияет на вероятность другого события, оно называется независимым событием. Независимые события по вероятности отражают события реальной жизни.
Чтобы понять это, мы можем привести несколько примеров, например, хорошие оценки на экзамене не влияют на то, что делают соседи. Точно так же поездка на такси на рынок никак не повлияет на поиск любимого фильма на YouTube. Другими словами, независимое событие не зависит от того, произойдет ли другое событие раньше.
Какие существуют типы независимых событий? В вероятности есть два типа событий, которые часто классифицируются как зависимые события или независимые события. Изучим их отличие.
Разница между независимыми событиями и зависимыми событиями
Разница между независимыми и зависимыми событиями указана в таблице ниже.
| Независимые события | Зависимые события |
| 1. Относится к наступлению одного события, не влияющему на вероятность другого события. | 1. Относится к возникновению одного события, влияющего на вероятность другого события. |
2.Пример: а) Кататься на велосипеде и смотреть любимый фильм на ноутбуке. | 2.Пример: а) Несвоевременное пополнение счета за телефон и приостановка обслуживания звонков. б) Покупка нескольких лотерейных билетов и выигрыш в лотерею. Чем больше билетов мы купили, тем выше наши шансы на победу. c) Предположим, у вас есть коробка, содержащая 10 зеленых яблок и 5 красных яблок. Если мы возьмем красное яблоко и съедим его правильно, у нас будет условие, что мы не можем снова заменить его другими яблоками, которые находятся в коробке, поэтому, не заменяя его, вероятность получить другое красное яблоко во второй попытке сильно изменится, потому что ты достал красное яблоко в первый раз. |
3. Формулу можно записать так: P(A и B) = P(A)×P(B)P(A и B) = P(A)×P(B) | 3. Формулу можно записать так: P(B и A)=P(A)×P(B после A) |
Такие события называются зависимыми событиями.Определение вероятности независимых событий
Для нахождения вероятности независимых событий мы должны воспользоваться формулой условной вероятности, которая приведена ниже: Если вероятность событий А и В равна Р(А) и Р(В) соответственно, то условная вероятность события B такое, что событие A уже произошло, называется P(A/B). Формула условной вероятности представлена ниже.
\[ P\left( \dfrac AB \right)=\dfrac {P(A \cap B)}{P(B)} \text {или} \dfrac {P(B \cap A)}{ P(B)}\]
Дано, P(A) должно быть больше 0. P(A) меньше 0 означает, что событие A невозможно. В \(P(A \cap B)\) пересечение обозначает сложную вероятность события.
Давайте подробно найдем вероятность независимых событий на примере. Предположим, у нас есть коробка, в которой 10 игрушек, из которых 7 разноцветных и 3 синих. На основании этого мы знаем, что вероятность нарисовать одну разноцветную игрушку равна 7 к 10, или 0,7, а вероятность нарисовать синюю игрушку 3 к 10, или 0,3·9.0003
Метод идентификации независимых событий
Прежде чем применять формулы вероятности, необходимо определить независимое событие. Несколько шагов для проверки того, относится ли вероятность к зависимым или независимым событиям:
Шаг 1 : Проверьте, могут ли события происходить в любом порядке? Если да, перейдите к шагу 2 или перейдите к шагу 3. Если да, перейдите к шагу 4 или перейдите к шагу 3 9.0092 Шаг 3 : Событие независимое. Используйте формулу независимых событий и получите ответ.
Шаг 4: Событие является зависимым.
Воспользуйтесь формулой зависимого события и получите ответ.
Советы и рекомендации по независимым мероприятиям
Вы можете использовать приведенные ниже советы и рекомендации для решения проблем на независимых мероприятиях.
Часто задаваемые вопросы о независимых мероприятиях
Примеры независимых событий?
Независимые события — это события, возникновение которых не зависит ни от каких других событий.
Например, если мы подбрасываем монету в воздухе и получаем результат «Орел», то снова, если мы подбрасываем монету, но на этот раз мы получаем результат «Решка». В обоих случаях возникновение обоих событий не зависит друг от друга.
Как узнать, является ли событие независимым?
События A и B независимы, если верно равенство P(A ∩ B) = P(A) · P(B). Вы можете использовать это уравнение, чтобы проверить, являются ли события независимыми; умножьте вероятности двух событий вместе, чтобы увидеть, равны ли они вероятности того, что они оба произошли вместе.
Каково правило для независимых событий?
Если вероятность событий A и B равна P(A) и P(B) соответственно, то эти два события независимы, если выполняется любое из следующих условий: P(A|B)=P(A), P( B|A)=P(B) и P(A и B)=P(A)⋅P(B)
Как определить, является ли событие независимым или зависимым?
Два события A и B называются независимыми, если факт возникновения одного события не влияет на вероятность появления другого.
Также, если возникновение одного события влияет на вероятность возникновения другого события, два события называются зависимыми.
Может ли событие быть взаимоисключающим и независимым?
Взаимоисключающими в математике являются наборы событий, которые не могут произойти одновременно. Например: при подбрасывании монеты может выпасть либо орел, либо решка, но не то и другое одновременно. Это, конечно, означает, что взаимоисключающие события не являются независимыми, а независимые события не могут быть взаимоисключающими.
Являются ли независимые события непересекающимися?
Два непересекающихся события никогда не могут быть независимыми, за исключением случая, когда одно из событий равно нулю. События считаются непересекающимися, если они никогда не происходят одновременно. Например, быть первокурсником и быть второкурсником можно было бы считать непересекающимися событиями. Независимые события — это несвязанные события.