Нод 35 и 24: НОД и НОК для 24 и 35 (с решением)

alexxlab / / Разное

Наибольший общий делитель. Взаимно простые числа

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Наибольший общий делитель.
Взаимно простые числа
1
Решите уравнения, записывая только ответы.
3
д
84 : л = 14;
84 : т = 7;
84 : е = 21;
84 : л = 4;
84 : ь = 3;
84 : д = 28;
84 : е = 6;
84 : и = 12;
4
е
6
л
л=6
т = 12
е=4
л = 21
ь = 28
д=3
е = 14
и=7
7 12 14 21 28

и т е л ь
Расположите ответы в порядке возрастания.
Назовите, какое слово получилось. Дайте определение
делителя натурального числа.
2
3
875
175
35
7
1
5
5
5
7
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
4
2376
1188
594
297
99
33
11
1
2
2
2
2
3
3
11
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
5
5625
1875
625
125
25
5
1
3
3
5
5
5
5
Назовите наибольший делитель, отличный
от самого числа. Как его найти?
6
1. Разложите числа на простые множители.
2. Выпишите общие простые множители.
3. Найдите произведение полученных простых
множителей.
24 2
60 2
12 2
30 2
6 2
15 3
3 3
55
1
1
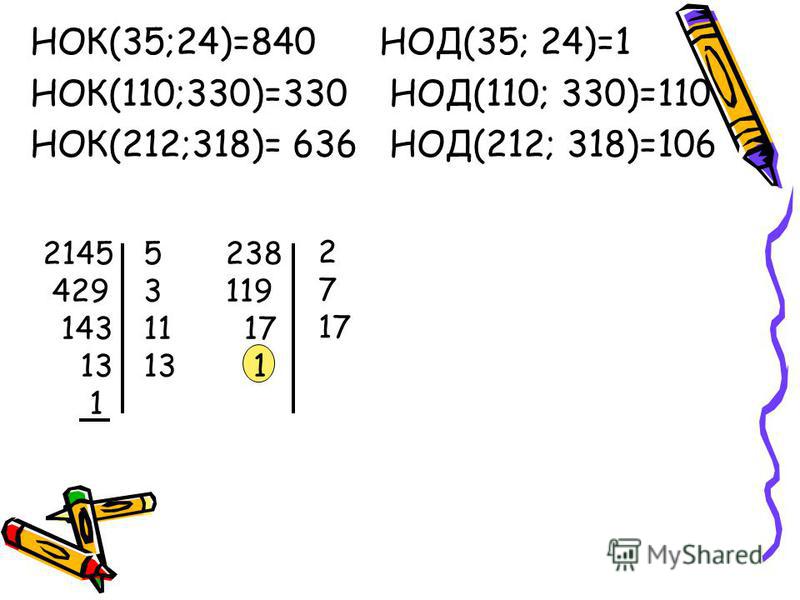
24 = 2 ∙ 2 ∙ 2 ∙ 3;
60 = 2 ∙ 2 ∙ 3 ∙ 5
НОД(24;60) = 2 ∙ 2 ∙ 3 = 12.
7
50 2
25 5
5 5
1
50 = 2 ∙ 5 ∙ 5;
175 5
35 5
77
1
175 = 5 ∙ 5 ∙ 7
НОД(50;175) = 5 ∙ 5= 25
8
675 3
225 3
75 3
25 5
5 5
1
675 = 3 ∙ 3 ∙ 3 ∙ 5 ∙ 5;
875 5
175 5
35 5
77
1
875 = 5 ∙ 5 ∙ 5 ∙ 7
НОД(675;875) = 5 ∙ 5= 25
9
7920 2
3960 2
1980 2
990 2
495 3
165 3
55 5
11 11
1
594 2
297 3
99 3
33 3
11 11
1
7920 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 11
594 = 2 ∙ 3 ∙ 3 ∙ 3 ∙ 11
НОД(7920;594) = 2 ∙ 3 ∙ 3 ∙ 11 = 198
10
Чтобы найти наибольший общий делитель
нескольких натуральных чисел, надо:
1) разложить их на простые множители;
2) из множителей, входящих в каждое разложение
подчеркнуть общие множители;
3) найти произведение подчеркнутых множителей.
Если все данные числа делятся на одно из них, то
это число и является наибольшим общим
делителем данных чисел.
11
В одной корзине 32 яблока, в другой корзине 40 груш. Какое наибольшее
количество одинаковых наборов можно составить, используя эти фрукты.
Найти
наибольшее
число,
на
Что нужно
сделать, чтобы
ответить
на вопрос
задачи?
которое делятся
числа
32 и 40, то
есть найти их наибольший общий
делитель.
40 груш
32 яблока
НОД (32; 40) = 8.
Ответ: 8 наборов.
12
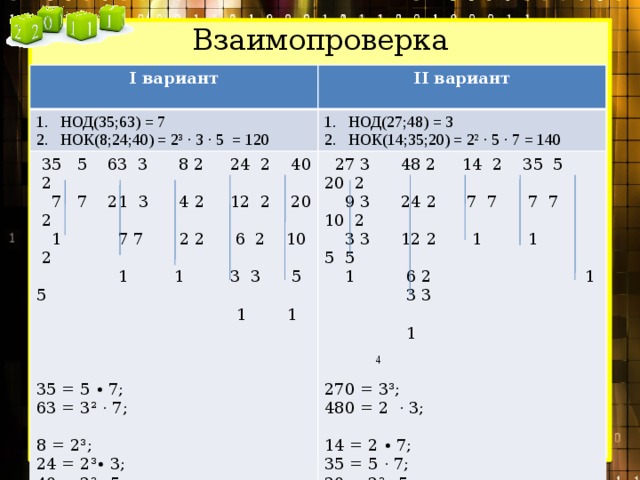
Для каждой пары чисел: 35 и 88; 25 и 9; 5 и 3; 7 и 8;
Найдите все делители каждого числа.
Подчеркните их общие делители.
Выделите их наибольший общий делитель.
35: 1, 5, 7, 35
88: 1, 2, 4, 8, 11, 22, 44, 88
НОД (35; 88) = 1.
25: 1, 5, 25
9: 1, 3, 9
НОД (25; 9) = 1;
5: 1, 5
3: 1, 3
НОД( 5; 3) = 1;
7: 1, 7
8: 1, 8
НОД (7; 8) = 1.
13
НОД (35; 88) = 1
НОД (25; 9) = 1
НОД( 5; 3) = 1
НОД (7; 8) = 1
14
Ребята получили на новогодней елке одинаковые подарки.
Во всех подарках вместе было 123 апельсина и 82 яблока.
Сколько ребят присутствовало на елке? Сколько апельсинов
и сколько яблок было в каждом подарке?
82 яблока
123 апельсина
Сколько ребят -?
Сколько яблок — ?
Сколько апельсинов -?
апельсинов
и яблок
Как Количество
узнать,НОД
сколько
ребят
Найти
чисел
123 было
и 82. на елке?
должно делиться на одно и то же
наибольшее число.
НОД (123; 82) = 41, значит, 41 человек.
123 : 41 = 3 (ап.)
82 : 41 = 2 (ябл.)
Ответ: ребят 41, апельсинов 3, яблок 2.
15
Для поездки за город работникам завода было выделено несколько автобусов, с
одинаковым числом мест в каждом автобусе. 424 человека поехали в лес, а 477
человек — на озеро. Все места в автобусах были заняты, и ни одного человека не
осталось без места. Сколько автобусов было выделено и сколько пассажиров было
в каждом автобусе?
Найти НОД чисел
424 и 477. 424 2
НОД (424; 477) = 53,
212 2
значит, 53 пассажира в
106 2
одном автобусе. 2

[Решено] Последовательность обхода в прямом порядке бинарного дерева поиска:

Последовательность обхода в прямом порядке:

25, 15, 10, 4, 12, 22, 18, 24, 50, 35, 31, 44, 70, 66, 90

Что из следующего является последовательностью обхода одного и того же дерева в обратном порядке?

  1. 4, 12, 10, 18, 24, 15, 22, 31, 44, 50, 66, 90, 70, 35, 25
  2. 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25
  3. 4, 10, 12, 15, 18, 22, 24, 25, 31, 35, 44, 50, 66, 70, 90
  4. 90, 70, 66, 50, 44, 35, 31, 25, 24, 22, 18, 15, 12, 10, 4

Вариант 2: 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25

Бесплатно

ST 1: Электрические цепи

3,2 тыс. пользователей

20 вопросов

20 баллов

20 минут

Правильный ответ: вариант 2.

Понятие :

Чтобы построить бинарное дерево из заданных последовательностей обхода, одна из последовательностей обхода должна быть неупорядоченной. Другая последовательность обхода может быть либо Preorder, либо Postorder. Мы знаем, что неупорядоченный обход бинарного дерева поиска всегда осуществляется в порядке возрастания.

Последовательность обхода бинарного дерева поиска в прямом порядке дерево поиска,

4, 10, 12, 15, 18, 22, 24, 25, 31, 35, 44, 50, 66, 70, 90

Обход в обратном порядке — это тип обхода, при котором мы сначала посещаем левое поддерево в обратном порядке, затем правое поддерево в обратном порядке, а затем посетите корневой узел.

Почтовый заказ= 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25

Следовательно, правильный ответ: 4, 12, 10, 18, 24, 22, 15, 31, 44, 35, 66, 90, 70, 50, 25.

Дополнительная информация

Обход дерева

 

Поток метода

 Заказ предзаказ почтовый заказ

Конверс Заказать

 Конверс Предзаказ Converse Постзаказ
  1. Слева
  2. Корень
  3. Право
  1. Корень
  2. Левый
  3. Право
  1. Слева
  2. Право
  3. Корень
  1. Справа
  2. Корень
  3. Левый
  1. Корень
  2. Право
  3. Левый
  1. Справа
  2. Левый
  3. Корень
Скачать решение PDF

Поделиться в WhatsApp

Последние обновления помощника инженера UPPCL

Последнее обновление: 8 февраля 2023 г.

Уведомление о присоединении к UPPCL AE опубликовано 8 февраля 2023 г. Ранее результат UPPCL AE для Civit был опубликован 17 декабря 2022 г.! Это со ссылкой на Advt. № 05/VSA/2022/AE/Civil. Результат был выпущен в виде файла PDF, и кандидаты могут проверить свои регистрационные номера в формате PDF, нажав Ctrl+F. Также обратите внимание, что набор также продолжается на 14 вакансий AE Civil (Объявление № 05/VSA/2022/AE/Civil). Процесс отбора для UPPCL AE включает CBT и личное собеседование. Заработная плата окончательно назначенных кандидатов будет соответствовать уровню 10 Матрицы оплаты труда.

[Решено] Последовательность обхода бинарного дерева поиска в прямом порядке: 35, 39, 30

  • 15, 20, 10, 23, 25, 42, 35, 39, 30
  • 15, 10, 23, 25, 20, 35, 42, 39, 30

    • : 5 Опция , 10, 23, 25, 20, 35, 42, 39, 30

    Бесплатно

    CT 1: соотношение и пропорция

    13,8 тыс. пользователей

    10 вопросов

    16 баллов

    30 минут

    Правильный ответ « вариант 4″.

    КОНЦЕПЦИЯ:

    Двоичное дерево поиска (BST) также известно как упорядоченное дерево или отсортированное двоичное дерево.

    Это бинарное дерево со следующими свойствами:

    1. левое поддерево узла содержит только узлы с ключом-значением меньше значения ключа узла.

    2.  правое поддерево узла содержит только узлы с ключом-значением больше , чем значение ключа узла.

    Существует три типа обхода:

    1. Обход по порядку: В этом обходе будет проходить первый левый узел, корневой узел, затем правый узел.

    2. Обход предварительного заказа : В этом обходе будет проходить первый корневой узел, левый узел, а затем правый узел.

    3. Обход в обратном порядке : В этом обходе будет проходить первый левый узел, затем будет проходить правый узел, затем корневой узел.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *